Further Examination of the Pulsed- and Steady-Pedestal Paradigms under Hypothetical Parvocellular- and Magnocellular-Biased Conditions
Abstract
1. Introduction
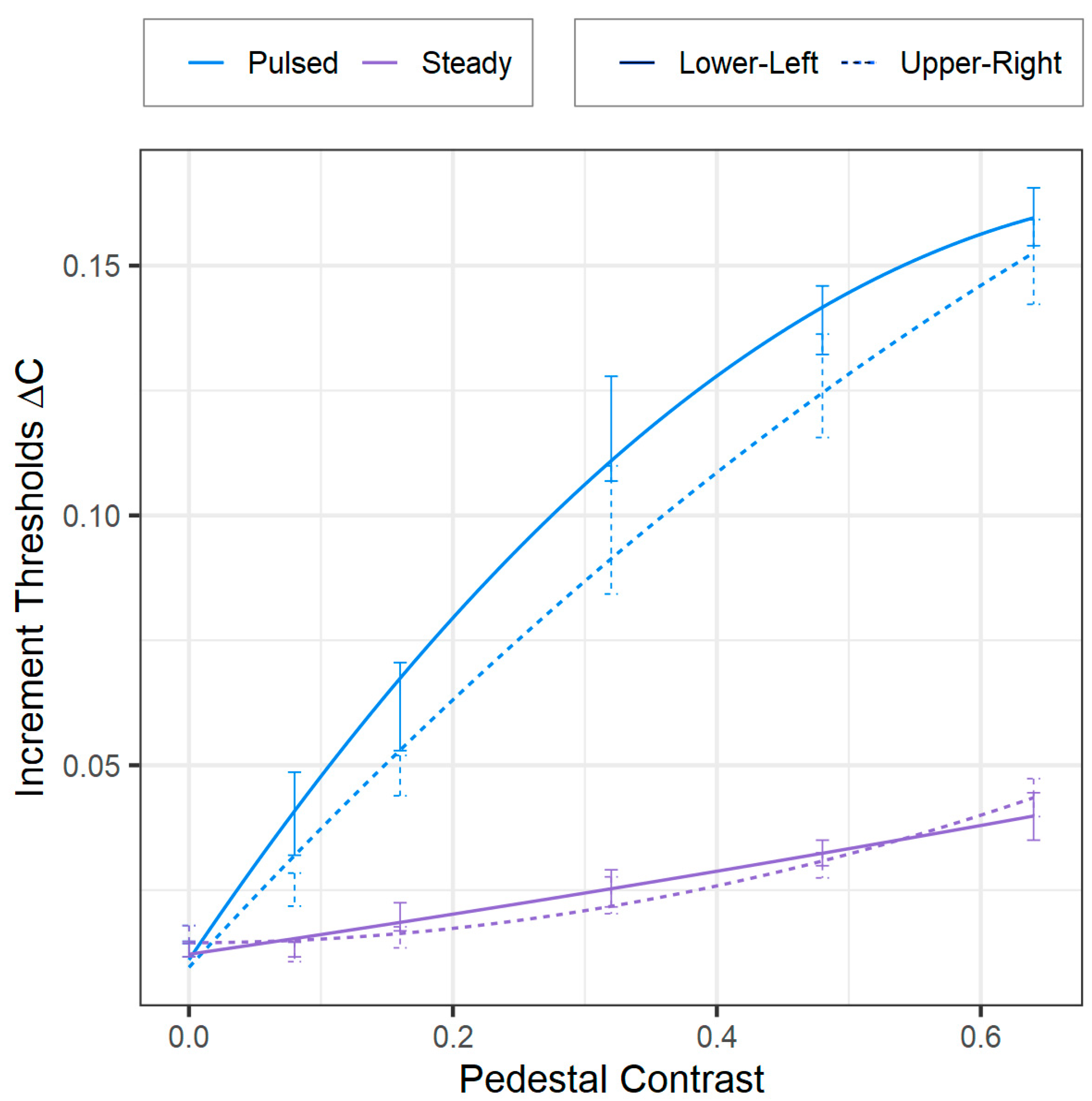
- The pulsed-pedestal paradigm would yield a steeper ΔC vs. C function in comparison to the steady-pedestal paradigm. This expectation arose from the premise that the pulsed-pedestal requires both detection and discrimination (i.e., a more difficult task), whereas the steady pedestal primarily focuses on discrimination (i.e., an easier task);
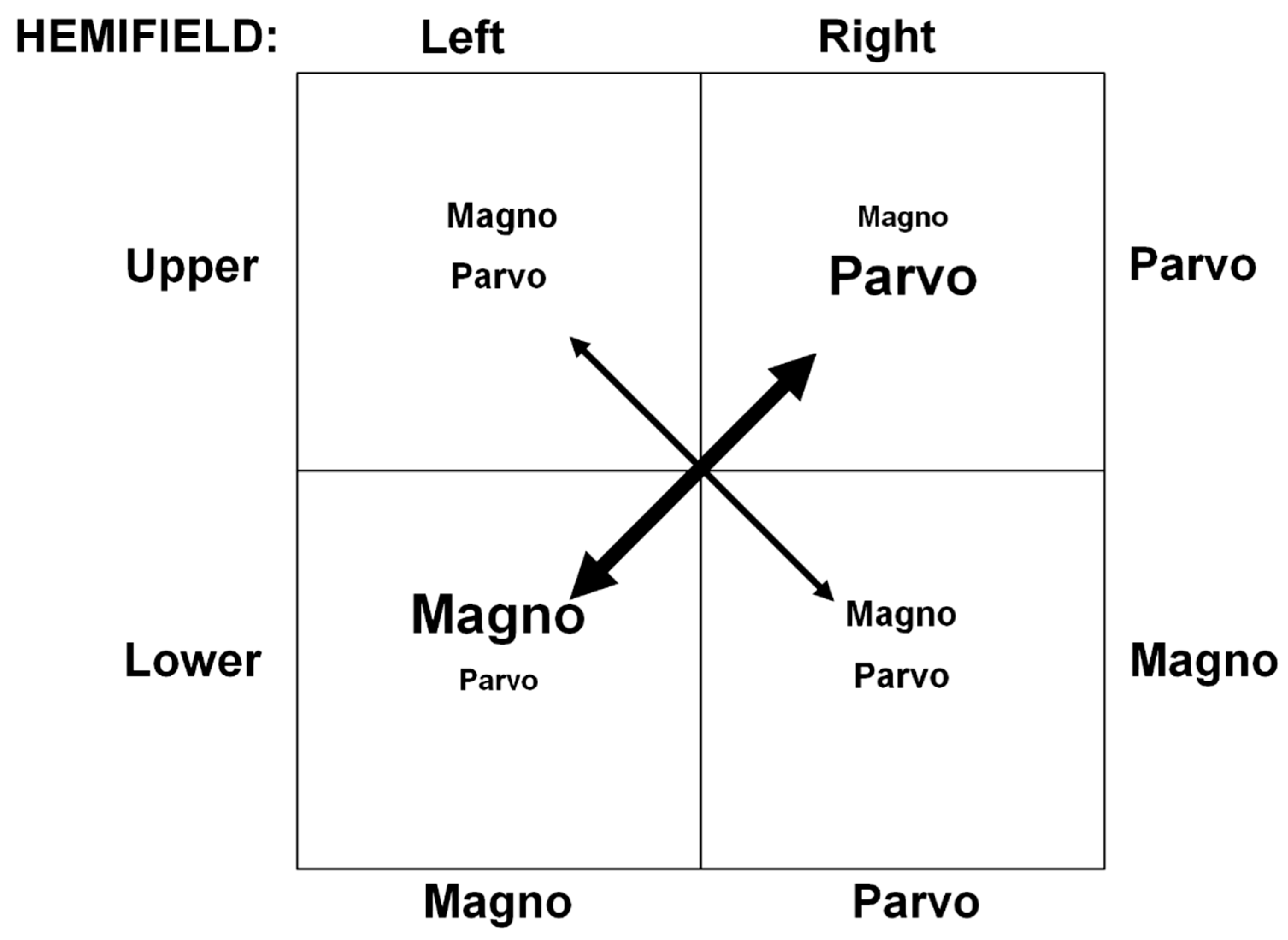
- Our expectations regarding visual-field influences on ΔCs varied for the pulsed-pedestal and steady-pedestal paradigms, in part due to these task-demand differences. Overall, ΔCs were expected to be lower in the upper-right vs. lower-left VF due to the bias for P-system processing in the upper-right VF. Our expectations were less clear about ΔCs in the lower-left VF due our position that both paradigms target the P-system and our uncertainty about how the bias towards M-system processing there would interact with the task demands of the two paradigms. For the pulsed-pedestal paradigm, ΔCs were expected to be lower in the upper-right VF compared to the lower-left. This hypothesis was in line with both our stance and Pokorny and Smith’s [10] because both the upper-right VF and the pulsed-pedestal paradigm would be predominantly influenced by P-system processing. Our expectations diverge from Pokorny and Smith’s because of our position that the steady-pedestal paradigm also targets the P-system. According to Pokorny and Smith’s research, ΔCs should be lower in the lower-left than in the upper-right VF (i.e., opposite of the pulsed pedestal) reflecting the combined influence of the steady-pedestal paradigm targeting the M-system and the stronger influence of M-system processing in the lower-left VF. By comparison, we anticipated a conflict in the bias towards the M and P systems in response to stimuli presented in the M-biased lower-left VF under the P-biased steady-pedestal paradigm. This conflict might negate the pattern predicted by Pokorny and Smith or possibly even reverse the pattern of results.
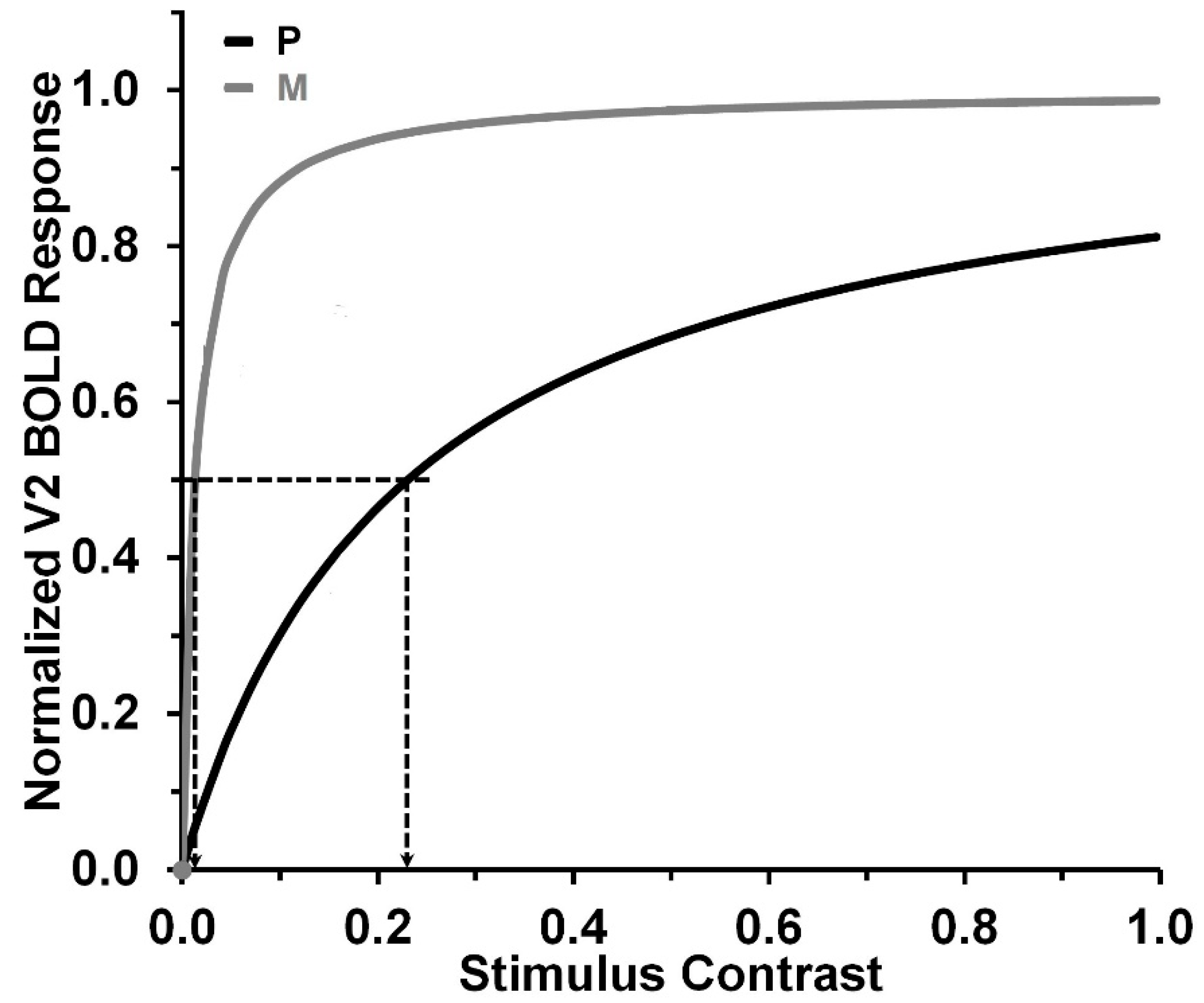
- The ΔCs under red and green light should be similar, as both paradigms predominantly engage the P-system. Therefore, any suppressive effect of red light on the M-system should not impact P-system mediated performance.
2. Materials and Methods
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leonova, A.; Pokorny, J.; Smith, V.C. Spatial frequency processing in inferred PC- and MC-pathways. Vis. Res. 2003, 43, 2133–2139. [Google Scholar] [CrossRef]
- McAnany, J.J.; Levine, M.W. Magnocellular and parvocellular visual pathway contributions to visual field anisotropies. Vis. Res. 2007, 47, 2327–2336. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zele, A.J.; Pokorny, J.; Lee, D.Y.; Ireland, D. Anisometropic amblyopia: Spatial contrast sensitivity deficits in inferred magnocellular and parvocellular vision. Investig. Ophthalmol. Vis. Sci. 2007, 48, 3622–3631. [Google Scholar] [CrossRef]
- Kulikowski, J.J.; Tolhurst, D.J. Psychophysical evidence for sustained and transient detectors in human vision. J. Physiol. 1973, 232, 149–162. [Google Scholar] [CrossRef]
- Legge, G.E. Sustained and transient mechanisms in human vision: Temporal and spatial properties. Vis. Res. 1978, 18, 69–81. [Google Scholar] [CrossRef] [PubMed]
- Wilson, H.R. Spatiotemporal characterization of a transient mechanism in the human visual system. Vis. Res. 1980, 20, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.C.; Breitmeyer, B.G.; Lovegrove, W.J.; Gutierrez, C. Metacontrast with masks varying in spatial frequency and wavelength. Vis. Res. 1991, 31, 2017–2023. [Google Scholar] [CrossRef]
- Breitmeyer, B.G.; Ganz, L. Temporal studies with flashed gratings: Inferences about human transient and sustained channels. Vis. Res. 1977, 17, 861–865. [Google Scholar] [CrossRef]
- Pokorny, J. Review: Steady and pulsed pedestals, the how and why of post-receptoral pathway separation. J. Vis. 2011, 11, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Pokorny, J.; Smith, V.C. Psychophysical signatures associated with magnocellular and parvocellular pathway contrast gain. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 1997, 14, 2477–2486. [Google Scholar] [CrossRef]
- Breitmeyer, B.G.; May, J.G.; Heller, S.S. Metacontrast reveals asymmetries at red–green isoluminance. J. Opt. Soc. Am. A 1991, 8, 1324–1329. [Google Scholar] [CrossRef]
- Brown, J.M.; Plummer, R. When figure–ground segregation fails: Exploring antagonistic interactions in figure–ground perception. Atten. Percept. Psychophys. 2020, 82, 3618–3635. [Google Scholar] [CrossRef] [PubMed]
- Breitmeyer, B.G.; Breier, J.I. Effects of background color on reaction time to stimuli varying in size and contrast: Inferences about human M channels. Vis. Res. 1994, 34, 1039–1045. [Google Scholar] [CrossRef] [PubMed]
- Bedwell, J.S.; Brown, J.M.; Orem, D.M. The effect of a red background on location backward masking by structure. Percept. Psychophys. 2008, 70, 503–507. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Awasthi, B.; Williams, M.A.; Friedman, J. Examining the role of red background in magnocellular contribution to face perception. PeerJ 2016, 4, e1617. [Google Scholar] [CrossRef] [PubMed]
- Merigan, W.H.; Maunsell, J.H. How parallel are the primate visual pathways? Annu. Rev. Neurosci. 1993, 16, 369–402. [Google Scholar] [CrossRef] [PubMed]
- Croner, L.J.; Kaplan, E. Receptive fields of P and M ganglion cells across the primate retina. Vis. Res. 1995, 35, 7–24. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, E.; Shapley, R.M. The primate retina contains two types of ganglion-cells, with high and low contrast sensitivity. Proc. Natl. Acad. Sci. USA 1986, 83, 2755–2757. [Google Scholar] [CrossRef] [PubMed]
- De Monasterio, F.M.; Schein, S.J. Protan-like spectral sensitivity of foveal Y ganglion cells of the retina of macaque monkeys. J. Physiol. 1980, 299, 385–396. [Google Scholar] [CrossRef]
- Livingstone, M.S.; Hubel, D.H. Anatomy and physiology of a color system in the primate visual-cortex. J. Neurosci. 1984, 4, 309–356. [Google Scholar] [CrossRef]
- Wiesel, T.N.; Hubel, D.H. Spatial and chromatic interactions in the lateral geniculate body of the rhesus monkey. J. Neurophysiol. 1966, 29, 1115–1156. [Google Scholar] [CrossRef] [PubMed]
- Kosslyn, S.M. Seeing and imagining in the cerebral hemispheres: A computational approach. Psychol. Rev. 1987, 94, 148–175. [Google Scholar] [CrossRef] [PubMed]
- Kosslyn, S.M.; Chabris, C.F.; Marsolek, C.J.; Koenig, O. Categorical versus coordinate spatial relations: Computational analyses and computer simulations. J. Exp. Psychol. Hum. Percept. Perform. 1992, 18, 562–577. [Google Scholar] [CrossRef] [PubMed]
- Previc, F.H. Functional specialization in the lower and upper visual fields in humans: Its ecological origins and neurophysiological implications. Behav. Brain Sci. 1990, 13, 519–542. [Google Scholar] [CrossRef]
- Previc, F.H. The neuropsychology of 3-D space. Psychol. Bull. 1998, 124, 123–164. [Google Scholar] [CrossRef] [PubMed]
- Peyrin, C.; Baciu, M.; Segebarth, C.; Marendaz, C. Cerebral regions and hemispheric specialization for processing spatial frequencies during natural scene recognition. An event-related fMRI study. NeuroImage 2004, 23, 698–707. [Google Scholar] [PubMed]
- Peyrin, C.; Mermillod, M.; Chokron, S.; Marendaz, C. Effect of temporal constraints on hemispheric asymmetries during spatial frequency processing. Brain Cogn. 2006, 62, 214–220. [Google Scholar] [CrossRef] [PubMed]
- Peyrin, C.; Schwartz, S.; Seghier, M.; Michel, C.; Landis, T.; Vuilleumier, P. Hemispheric specialization of human inferior temporal cortex during coarse-to-fine and fine-to-coarse analysis of natural visual scenes. NeuroImage 2005, 28, 464–473. [Google Scholar] [CrossRef] [PubMed]
- Niebauer, C.L.; Christman, S.D. Upper and lower visual field differences in categorical and coordinate judgments. Psychon. Bull. Rev. 1998, 5, 147–151. [Google Scholar] [CrossRef]
- Hugrass, L.; Verhellen, T.; Morrall-Earney, E.; Mallon, C.; Crewther, D.P. The effects of red surrounds on visual magnocellular and parvocellular cortical processing and perception. J. Vis. 2018, 18, 1–13. [Google Scholar] [CrossRef]
- McAnany, J.J.; Alexander, K.R. Contrast sensitivity for letter optotypes vs. gratings under conditions biased toward parvocellular and magnocellular pathways. Vis. Res. 2006, 46, 1574–1584. [Google Scholar] [CrossRef]
- Sun, H.; Swanson, W.H.; Arvidson, B.; Dul, M.W. Assessment of contrast gain signature in inferred magnocellular and parvocellular pathways in patients with glaucoma. Vis. Res. 2008, 48, 2633–2641. [Google Scholar] [CrossRef]
- Alexander, K.R.; Barnes, C.S.; Fishman, G.A.; Pokorny, J.; Smith, V.C. Contrast sensitivity deficits in inferred magnocellular and parvocellular pathways in retinitis pigmentosa. Investig. Ophthalmol. Vis. Sci. 2004, 45, 4510–4519. [Google Scholar] [CrossRef][Green Version]
- McKendrick, A.M.; Badcock, D.R.; Morgan, W.H. Psychophysical measurement of neural adaptation abnormalities in magnocellular and parvocellular pathways in glaucoma. Investig. Ophthalmol. Vis. Sci. 2004, 45, 1846–1853. [Google Scholar] [CrossRef] [PubMed]
- McKendrick, A.M.; Sampson, G.P.; Walland, M.J.; Badcock, D.R. Contrast sensitivity changes due to glaucoma and normal aging: Low-spatial-frequency losses in both magnocellular and parvocellular pathways. Investig. Ophthalmol. Vis. Sci. 2007, 48, 2115–2122. [Google Scholar] [CrossRef]
- Brooks, C.J.; Chan, Y.M.; Fielding, J.; White, O.B.; Badcock, D.R.; McKendrick, A.M. Visual contrast perception in visual snow syndrome reveals abnormal neural gain but not neural noise. Brain 2022, 145, 1486–1498. [Google Scholar] [CrossRef]
- Kelemen, O.; Kiss, I.; Benedek, G.; Kéri, S. Perceptual and cognitive effects of antipsychotics in first-episode schizophrenia: The potential impact of GABA concentration in the visual cortex. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2013, 47, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Qian, Y.; Bi, H.-Y.; Coltheart, M. The visual magnocellular-dorsal dysfunction in Chinese children with developmental dyslexia impedes Chinese character recognition. Sci. Rep. 2014, 4, 7068. [Google Scholar] [CrossRef] [PubMed]
- Greenaway, R.; Davis, G.; Plaisted-Grant, K. Marked selective impairment in autism on an index of magnocellular function. Neuropsychologia 2013, 51, 592–600. [Google Scholar] [CrossRef]
- Song, J.; Breitmeyer, B.G.; Brown, J.M. Examining Increment thresholds as a function of pedestal contrast under hypothetical parvo- and magnocellular-biased conditions. Atten. Percept. Psychophys. 2024, 86, 213–220. [Google Scholar] [CrossRef]
- Sclar, G.; Maunsell, J.H.R.; Lennie, P. Coding of image-contrast in central visual pathways of the macaque monkey. Vis. Res. 1990, 30, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, E.; Purpura, K.; Shapley, R.M. Contrast affects the transmission of visual information through the mammalian lateral geniculate nucleus. J. Physiol. 1987, 391, 267–288. [Google Scholar] [CrossRef]
- Rathbun, D.L.; Alitto, H.J.; Warland, D.K.; Usrey, W.M. Stimulus Contrast and Retinogeniculate Signal Processing. Front. Neural Circuits 2016, 10, 175669. [Google Scholar] [CrossRef]
- Sclar, G. Expression of “retinal” contrast gain control by neurons of the cat’s lateral geniculate nucleus. Exp. Brain Res. 1987, 66, 589–596. [Google Scholar] [CrossRef]
- Scholl, B.; Latimer, K.W.; Priebe, N.J. A retinal source of spatial contrast gain control. J. Neurosci. 2012, 32, 9824–9830. [Google Scholar] [CrossRef] [PubMed]
- Archer, D.R.; Alitto, H.J.; Usrey, W.M. Stimulus contrast affects spatial integration in the lateral geniculate nucleus of macaque monkeys. J. Neurosci. 2021, 41, 6246–6256. [Google Scholar] [CrossRef]
- Carandini, M.; Heeger, D.J. Summation and division by neurons in primate visual cortex. Science 1994, 264, 1333–1336. [Google Scholar] [CrossRef] [PubMed]
- Ohzawa, I.; Sclar, G.; Freeman, R. Contrast gain control in the cat visual cortex. Nature 1982, 298, 266–268. [Google Scholar] [CrossRef] [PubMed]
- Ohzawa, I.; Sclar, G.; Freeman, R.D. Contrast gain control in the cat’s visual system. J. Neurophysiol. 1985, 54, 651–667. [Google Scholar] [CrossRef]
- Tootell, R.B.; Nasr, S. Columnar segregation of magnocellular and parvocellular streams in human extrastriate cortex. J. Neurosci. 2017, 37, 8014–8032. [Google Scholar] [CrossRef]
- Anderson, S.F.; Kelley, K.; Maxwell, S.E. Sample-size planning for more accurate statistical power: A method adjusting sample effect sizes for publication bias and uncertainty. Psychol. Sci. 2017, 28, 1547–1562. [Google Scholar] [CrossRef] [PubMed]
- Peirce, J.W. Generating stimuli for neuroscience using PsychoPy. Front. Neuroinform. 2009, 2, 343. [Google Scholar] [CrossRef] [PubMed]
- Watson, A.B.; Pelli, D.G. Quest—A bayesian adaptive psychometric method. Percept. Psychophys. 1983, 33, 113–120. [Google Scholar] [CrossRef]
- Smith, V.C.; Sun, V.C.; Pokorny, J. Pulse and steady-pedestal contrast discrimination: Effect of spatial parameters. Vis. Res. 2001, 41, 2079–2088. [Google Scholar] [CrossRef] [PubMed]

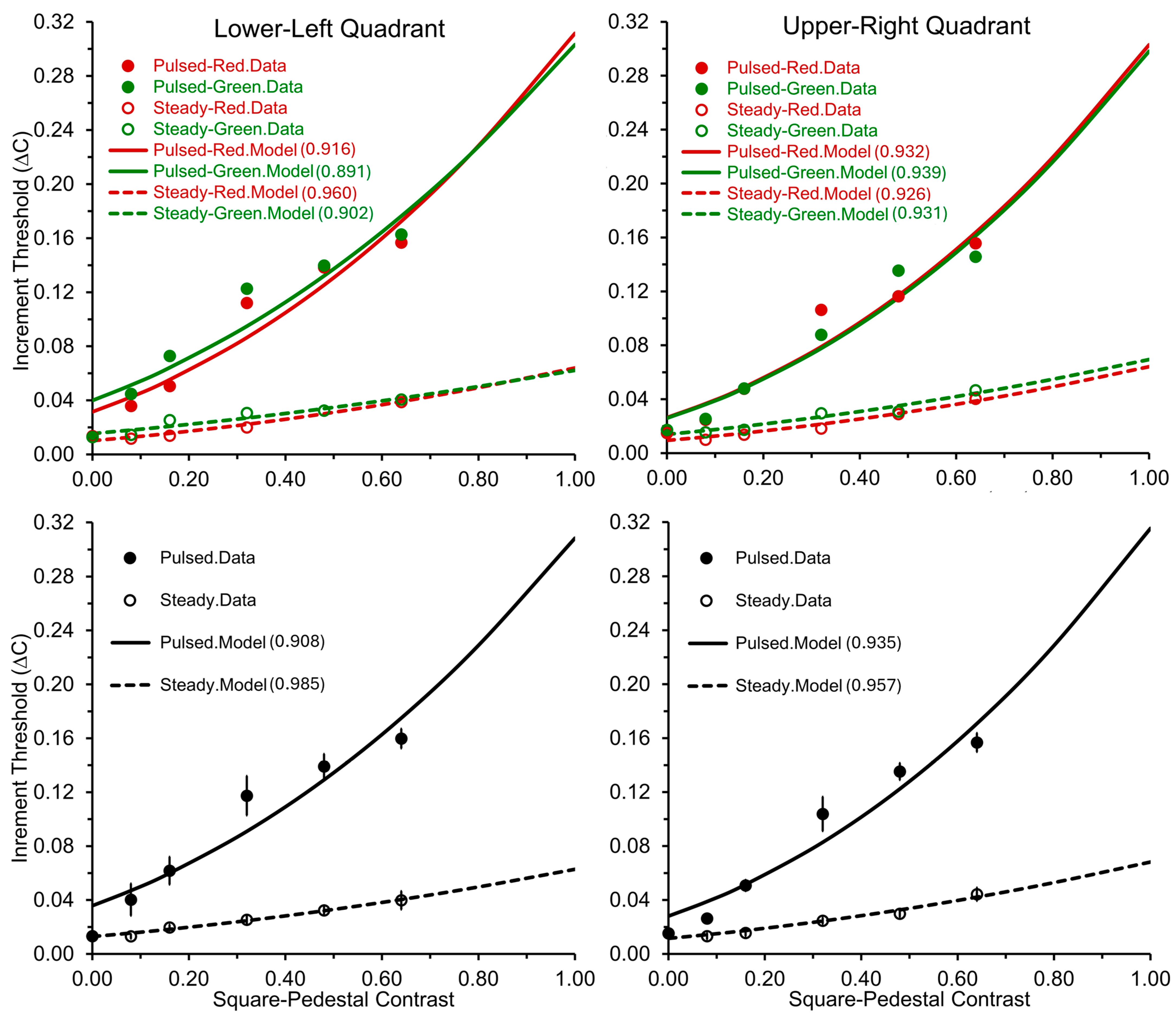
| Paradigm | VF Quadrant | Gain |
|---|---|---|
| Pulsed | Lower-left | 1.297 |
| Upper-right | 1.069 | |
| 1.183 | ||
| Steady | Lower-left | 0.838 |
| Upper-right | 0.740 | |
| 0.789 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Breitmeyer, B.G.; Brown, J.M. Further Examination of the Pulsed- and Steady-Pedestal Paradigms under Hypothetical Parvocellular- and Magnocellular-Biased Conditions. Vision 2024, 8, 28. https://doi.org/10.3390/vision8020028
Song J, Breitmeyer BG, Brown JM. Further Examination of the Pulsed- and Steady-Pedestal Paradigms under Hypothetical Parvocellular- and Magnocellular-Biased Conditions. Vision. 2024; 8(2):28. https://doi.org/10.3390/vision8020028
Chicago/Turabian StyleSong, Jaeseon, Bruno G. Breitmeyer, and James M. Brown. 2024. "Further Examination of the Pulsed- and Steady-Pedestal Paradigms under Hypothetical Parvocellular- and Magnocellular-Biased Conditions" Vision 8, no. 2: 28. https://doi.org/10.3390/vision8020028
APA StyleSong, J., Breitmeyer, B. G., & Brown, J. M. (2024). Further Examination of the Pulsed- and Steady-Pedestal Paradigms under Hypothetical Parvocellular- and Magnocellular-Biased Conditions. Vision, 8(2), 28. https://doi.org/10.3390/vision8020028





