The Use of Visualizations to Improve Bayesian Reasoning: A Literature Review
Abstract
1. Introduction
2. Methods
3. Visualizations That Have Been Effective
4. Classroom Teaching of Visualizations to Improve Bayesian Reasoning
5. The Creation of New Visualizations
6. Adding Interactivity to Visualizations May Be Helpful
7. Some Mixed Results
8. Consideration of Other Factors When Studying Visualizations
8.1. Natural Frequencies Versus Probabilities
8.2. Problem Format
8.3. Individual Differences
9. Future Directions
- Exploring the interaction between certain visualizations and natural frequencies vs. probabilities. There seems to be a potential for an interesting interaction between the use of (certain) visualizations and the use of natural frequencies vs. probabilities in the problem prompt. Some of the reviewed literature started investigating this possibility, but more studies that use either different visualizations or a wider range of visualizations are needed;
- Narrowing down visualizations. As exemplified in Figure 1/Table 1, there are a lot of visualizations that are used in this research area, with some more popular than others. We recommend narrowing down the types of visualizations that are studied so that we can have more knowledge on a smaller set instead of less knowledge over a larger set, and even the standardization of the names of the visualizations (currently there are multiple names to refer to the same thing) to reduce confusion.
- 3.
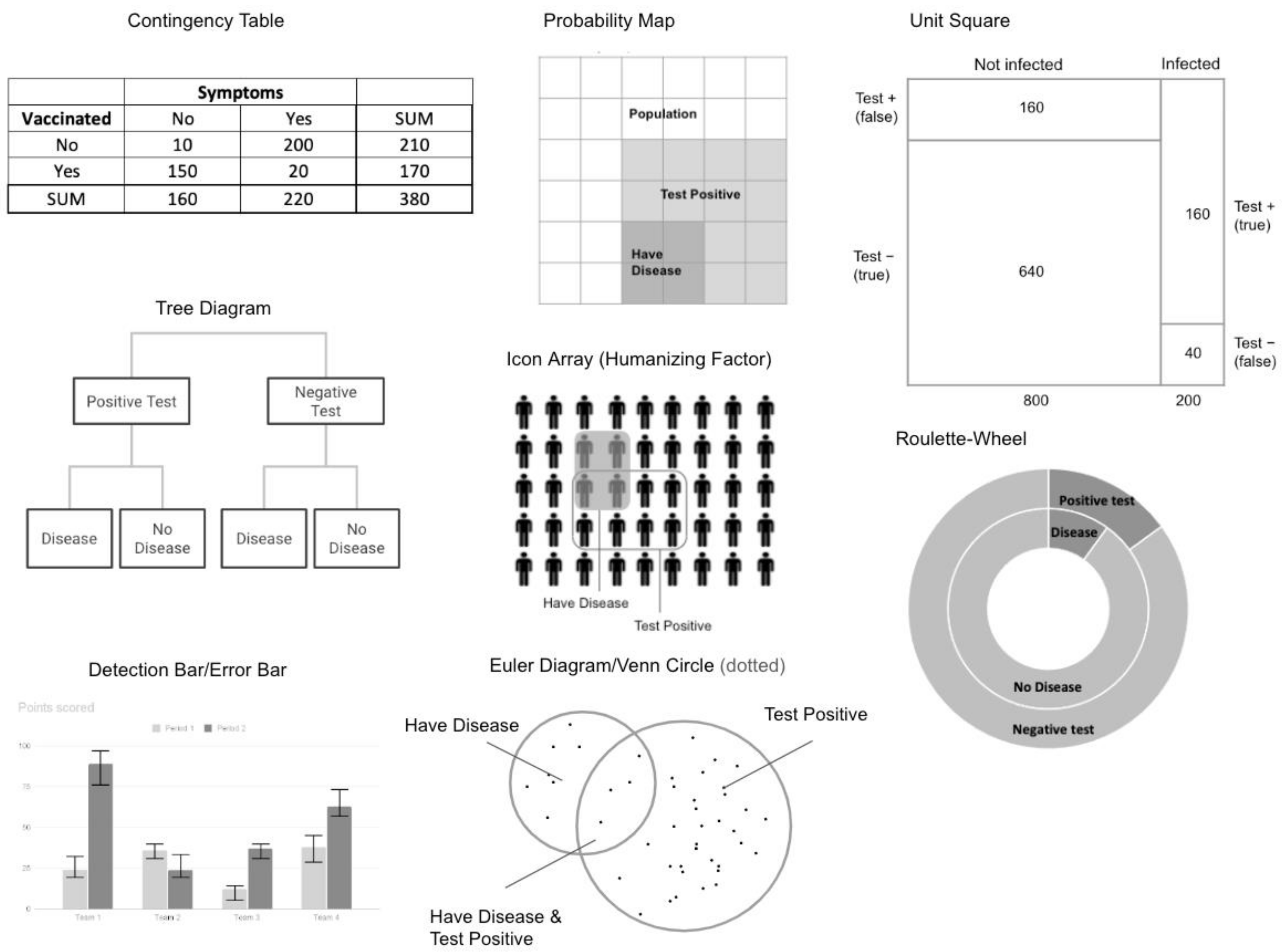
- Understanding the importance of key features of certain visualizations. We should be more deliberate in our comparison between different visualizations and choose visualizations (to include in studies) according to either testing competing hypotheses or identifying which features in those visualizations are helpful to students. For example, visualizations can be grouped based on whether quantitative information is presented in a discrete or continuous fashion or based on whether the quantitative information presented is a number, countable item, or area. These features can be used as an independent variable (e.g., area), and the visualizations (e.g., roulette wheel, unit square, probability map) can be chosen to match.
- 4.
- Consideration of other problem formats. Problem format is not commonly studied or manipulated alongside visualizations but should be considered. Whether problems are framed to be condition-focused (typical format, i.e., the base rate of having a condition/disease is the main focus) or test-focused (i.e., the base rate of a positive/negative test result is the main focus) seems to affect the solution rates across participants [49]. Some considerations are obvious, like making sure that the type of quantitative information (natural frequency vs. probability) matches the problem and the visualization. Bayesian reasoning is typically used in risk assessment and judgment, and with that, problems typically have a negative framing or very serious (health) outcomes. It would be interesting to see studies that manipulate positive vs. negative framing (e.g., test positive/negative vs. is healthy/ill) and see whether this influences over or underestimation. Cover studies of other more relatable contexts, such as social rejection/inclusion, could also be explored.
- 5.
- Greater consideration of individual differences. This literature review identified individual differences as a potential limiting factor for the effectiveness of visualizations. Future studies should investigate which simplifications and modifications (of visualizations and problem prompts) would be helpful to those with low numeracy skills. Additionally, other individual differences that could influence the effectiveness of visualizations or Bayesian reasoning, in general, should be explored. For example, things like risk aversion could bias probability estimates to be over or under the actual probability.
- 6.
- Varying level interactivity and use with certain visualizations. This seems to be the most lacking area of research. We can see this area of research going in two directions: (1) assessing a wide range of interactivity levels or comparing digital to physical manipulations and (2) including interactivity with each of the commonly studied visualizations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gerd, G.; Hoffrage, U. How to Improve Bayesian Reasoning Without Instruction: Frequency Formats. Psychol. Rev. 1995, 102, 684–704. [Google Scholar]
- Khan, A.; Breslav, S.; Glueck, M.; Hornbæk, K. Benefits of visualization in the Mammography Problem. Int. J. Hum.-Comput. Stud. 2015, 83, 94–113. [Google Scholar] [CrossRef]
- McDowell, M.; Jacobs, P. Meta-analysis of the effect of natural frequencies on Bayesian reasoning. Psychol. Bull. 2017, 143, 1273–1312. [Google Scholar] [CrossRef] [PubMed]
- Kahneman, D.; Tversky, A. On the psychology of prediction. Psychol. Rev. 1973, 80, 237–251. [Google Scholar] [CrossRef]
- Bayes, T. An Essay Toward Solving a Problem in the Doctrine of Chances. Philos. Trans. R. Soc. Lond. 1764, 53, 370–418. [Google Scholar] [CrossRef]
- Albert, J. Teaching Inference about Proportions Using Bayes and Discrete Models. J. Stat. Educ. 1995, 3, 1–16. [Google Scholar] [CrossRef]
- Johnson, E.D.; Tubau, E. Words, numbers, & numeracy: Diminishing individual differences in Bayesian reasoning. Learn. Individ. Differ. 2013, 28, 34–40. [Google Scholar] [CrossRef]
- Benoy, F.; Rodgers, P. Evaluating the Comprehension of Euler Diagrams. In Proceedings of the 2007 11th International Conference Information Visualization (IV’07), Zurich, Switzerland, 4–6 July 2007; pp. 771–780. [Google Scholar] [CrossRef]
- Binder, K.; Krauss, S.; Wiesner, P. A New Visualization for Probabilistic Situations Containing Two Binary Events: The Frequency Net. Front. Psychol. 2020, 11, 750. [Google Scholar] [CrossRef]
- Binder, K.; Krauss, S.; Schmidmaier, R.; Braun, L.T. Natural frequency trees improve diagnostic efficiency in Bayesian reasoning. Adv. Health Sci. Educ. 2021, 26, 847–863. [Google Scholar] [CrossRef]
- Ebinder, K.; Krauss, S.; Ebruckmaier, G. Effects of visualizing statistical information—An empirical study on tree diagrams and 2 × 2 tables. Front. Psychol. 2015, 6, 1186. [Google Scholar] [CrossRef]
- Böcherer-Linder, K.; Eichler, A. The Impact of Visualizing Nested Sets. An Empirical Study on Tree Diagrams and Unit Squares. Front. Psychol. 2017, 7, 2026. [Google Scholar] [CrossRef] [PubMed]
- Böcherer-Linder, K.; Eichler, A. How to Improve Performance in Bayesian Inference Tasks: A Comparison of Five Visualizations. Front. Psychol. 2019, 10, 267. [Google Scholar] [CrossRef] [PubMed]
- Brase, G.L. Pictorial representations in statistical reasoning. Appl. Cogn. Psychol. 2008, 23, 369–381. [Google Scholar] [CrossRef]
- Brase, G.L. The power of representation and interpretation: Doubling statistical reasoning performance with icons and frequentist interpretations of ambiguous numbers. J. Cogn. Psychol. 2013, 26, 81–97. [Google Scholar] [CrossRef]
- Bruckmaier, G.; Binder, K.; Krauss, S.; Kufner, H.-M. An Eye-Tracking Study of Statistical Reasoning With Tree Diagrams and 2 × 2 Tables. Front. Psychol. 2019, 10, 632. [Google Scholar] [CrossRef]
- Büchter, T.; Eichler, A.; Steib, N.; Binder, K.; Böcherer-Linder, K.; Krauss, S.; Vogel, M. How to Train Novices in Bayesian Reasoning. Mathematics 2022, 10, 1558. [Google Scholar] [CrossRef]
- Cole, W.G. Understanding Bayesian reasoning via graphical displays. ACM SIGCHI Bull. 1989, 20, 381–386. [Google Scholar] [CrossRef]
- Cole, W.G.; Davidson, J.E. Graphic Representation Can Lead To Fast and Accurate Bayesian Reasoning. Proc. Symp. Comput. Appl. Med. Care 1989, 5, 227–231. [Google Scholar]
- Eichler, A.; Böcherer-Linder, K.; Vogel, M. Different Visualizations Cause Different Strategies When Dealing With Bayesian Situations. Front. Psychol. 2020, 11, 1897. [Google Scholar] [CrossRef]
- Gaissmaier, W.; Wegwarth, O.; Skopec, D.; Müller, A.-S.; Broschinski, S.; Politi, M.C. Numbers can be worth a thousand pictures: Individual differences in understanding graphical and numerical representations of health-related information. Health Psychol. 2012, 31, 286–296. [Google Scholar] [CrossRef]
- Garcia-Retamero, R.; Hoffrage, U. Visual representation of statistical information improves diagnostic inferences in doctors and their patients. Soc. Sci. Med. 2013, 83, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Gigerenzer, G.; Multmeier, J.; Föhring, A.; Wegwarth, O. Do children have Bayesian intuitions? J. Exp. Psychol. Gen. 2021, 150, 1041–1070. [Google Scholar] [CrossRef] [PubMed]
- Kurzenhäuser, S.; Hoffrage, U. Teaching Bayesian reasoning: An evaluation of a classroom tutorial for medical students. Med. Teach. 2002, 24, 516–521. [Google Scholar] [CrossRef] [PubMed]
- Kunzelmann, A.K.; Binder, K.; Fischer, M.R.; Reincke, M.; Braun, L.T.; Schmidmaier, R. Improving Diagnostic Efficiency with Frequency Double-Trees and Frequency Nets in Bayesian Reasoning. MDM Policy Pract. 2022, 7, 23814683221086623. [Google Scholar] [CrossRef]
- Micallef, L.; Dragicevic, P.; Fekete, J.-D. Assessing the Effect of Visualizations on Bayesian Reasoning through Crowdsourcing. IEEE Trans. Vis. Comput. Graph. 2012, 18, 2536–2545. [Google Scholar] [CrossRef]
- Ottley, A.; Peck, E.M.; Harrison, L.T.; Afergan, D.; Ziemkiewicz, C.; Taylor, H.A.; Han, P.K.J.; Chang, R. Improving Bayesian Reasoning: The Effects of Phrasing, Visualization, and Spatial Ability. IEEE Trans. Vis. Comput. Graph. 2015, 22, 529–538. [Google Scholar] [CrossRef]
- Alvitta, O.; Aleksandra, K.; Johnson, C.R.; Evan, M.P. The Curious Case of Combining Text and Visualization. In Proceedings of the EUROVIS 2019, Porto, Portugal, 3–7 June 2019. [Google Scholar]
- Reani, M.; Peek, N.; Jay, C. How different visualizations affect human reasoning about uncertainty: An analysis of visual behaviour. Comput. Hum. Behav. 2018, 92, 55–64. [Google Scholar] [CrossRef]
- Sirota, M.; Kostovičová, L.; Juanchich, M. The effect of iconicity of visual displays on statistical reasoning: Evidence in favor of the null hypothesis. Psychon. Bull. Rev. 2014, 21, 961–968. [Google Scholar] [CrossRef]
- Starns, J.J.; Cohen, A.L.; Bosco, C.; Hirst, J. A visualization technique for Bayesian reasoning. Appl. Cogn. Psychol. 2019, 33, 234–251. [Google Scholar] [CrossRef]
- Markus, V.; Katharina, B.L. The effect of visualizing statistical information in Bayesian reasoning problems. In Proceedings of the ICOTS10 (2018), Invited Paper. Kyoto, Japan, 8–13 July 2018. [Google Scholar]
- Witt, J.K.; Dhami, M.K. Visual organization of icon arrays affects bayesian reasoning and risk judgments. J. Appl. Res. Mem. Cogn. 2022, in press. [Google Scholar] [CrossRef]
- Wu, C.M.; Meder, B.; Filimon, F.; Nelson, J.D. Asking better questions: How presentation formats influence information search. J. Exp. Psychol. Learn. Mem. Cogn. 2017, 43, 1274–1297. [Google Scholar] [CrossRef] [PubMed]
- Yamagishi, K. Facilitating Normative Judgments of Conditional Probability: Frequency or Nested Sets? Exp. Psychol. 2003, 50, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Zikmund-Fisher, B.J.; Witteman, H.O.; Dickson, M.; Fuhrel-Forbis, A.; Kahn, V.C.; Exe, N.L.; Valerio, M.; Holtzman, L.G.; Scherer, L.D.; Fagerlin, A. Blocks, Ovals, or People? Icon Type Affects Risk Perceptions and Recall of Pictographs. Med. Decis. Mak. 2014, 34, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Maggio, L.A.; Cate, O.T.; Irby, D.M.; O’Brien, B.C. Designing evidence-based medicine training to optimize the transfer of skills from the classroom to clinical practice: Applying the four component instructional design model. Acad. Med. J. Assoc. Am. Med. Coll. 2015, 90, 1457–1461. [Google Scholar] [CrossRef] [PubMed]
- Wopereis, I.; Frerejean, J.; Brand-Gruwel, S. Information Problem Solving Instruction in Higher Education: A Case Study on Instructional Design. In Information Literacy: Moving Toward Sustainability, Proceedings of the Third European Conference, ECIL 2015, Tallinn, Estonia, 19–22 October 2015; Revised Selected, Papers; Kurbanoğlu, S., Boustany, J., Špiranec, S., Grassian, E., Mizrachi, D., Roy, L., Eds.; Springer: Cham, Switzerland, 2015; pp. 293–302. ISBN 978-331-928-197-1. [Google Scholar]
- Sarfo, F.K.; Elen, J. Developing technical expertise in secondary technical schools: The effect of 4C/ID learning environments. Learn. Environ. Res. 2007, 10, 207–221. [Google Scholar] [CrossRef]
- Tsai, J.; Miller, S.; Kirlik, A. Interactive Visualizations to Improve Bayesian Reasoning. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2011, 55, 385–389. [Google Scholar] [CrossRef]
- Vallée-Tourangeau, G.; Abadie, M.; Vallée-Tourangeau, F. Interactivity fosters Bayesian reasoning without instruction. J. Exp. Psychol. Gen. 2015, 144, 581–603. [Google Scholar] [CrossRef]
- Mosca, A.; Alvitta, O.; Remco, C. Does Interaction Improve Bayesian Reasoning With Visualization? In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 8–13 May 2021; Association for Computing Machinery: New York, NY, USA; Volume 609, pp. 1–14. [Google Scholar] [CrossRef]
- Zhu, L.; Gigerenzer, G. Children can solve Bayesian problems: The role of representation in mental computation. Cognition 2006, 98, 287–308. [Google Scholar] [CrossRef]
- Hoffrage, U.; Gigerenzer, G. Using natural frequencies to improve diagnostic inferences. Acad. Med. 1998, 73, 538–540. [Google Scholar] [CrossRef]
- Mellers, B.; McGraw, A.P. How to Improve Bayesian Reasoning: Comment on Gigerenzer and Hoffrage. Psychol. Rev. 1995, 106, 417–424. [Google Scholar] [CrossRef]
- Sirota, M.; Kostovičová, L.; Vallée-Tourangeau, F. Now you Bayes, now you don’t: Effects of set-problem and frequency-format mental representations on statistical reasoning. Psychon. Bull. Rev. 2015, 22, 1465–1473. [Google Scholar] [CrossRef] [PubMed]
- Brase, G. What facilitates Bayesian reasoning? A crucial test of ecological rationality versus nested sets hypotheses. Psychon. Bull. Rev. 2021, 28, 703–709. [Google Scholar] [CrossRef] [PubMed]
- Brase, G.L.; Hill, W.T. Adding up to good Bayesian reasoning: Problem format manipulations and individual skill differences. J. Exp. Psychol. Gen. 2017, 146, 577–591. [Google Scholar] [CrossRef]
- Talboy, A.N.; Schneider, S.L. Focusing on what matters: Restructuring the presentation of Bayesian reasoning problems. J. Exp. Psychol. Appl. 2018, 24, 440–458. [Google Scholar] [CrossRef] [PubMed]
- Vince, K.; Chan, S.; Fang, X. Improving User Performance in Conditional Probability Problems with Computer-Generated Diagrams. In Human-Computer Interaction. Users and Contexts of Use; Lecture Notes in Computer Science; Kurosu, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Cohen, A.L.; Staub, A. Within-subject consistency and between-subject variability in Bayesian reasoning strategies. Cogn. Psychol. 2015, 81, 26–47. [Google Scholar] [CrossRef]
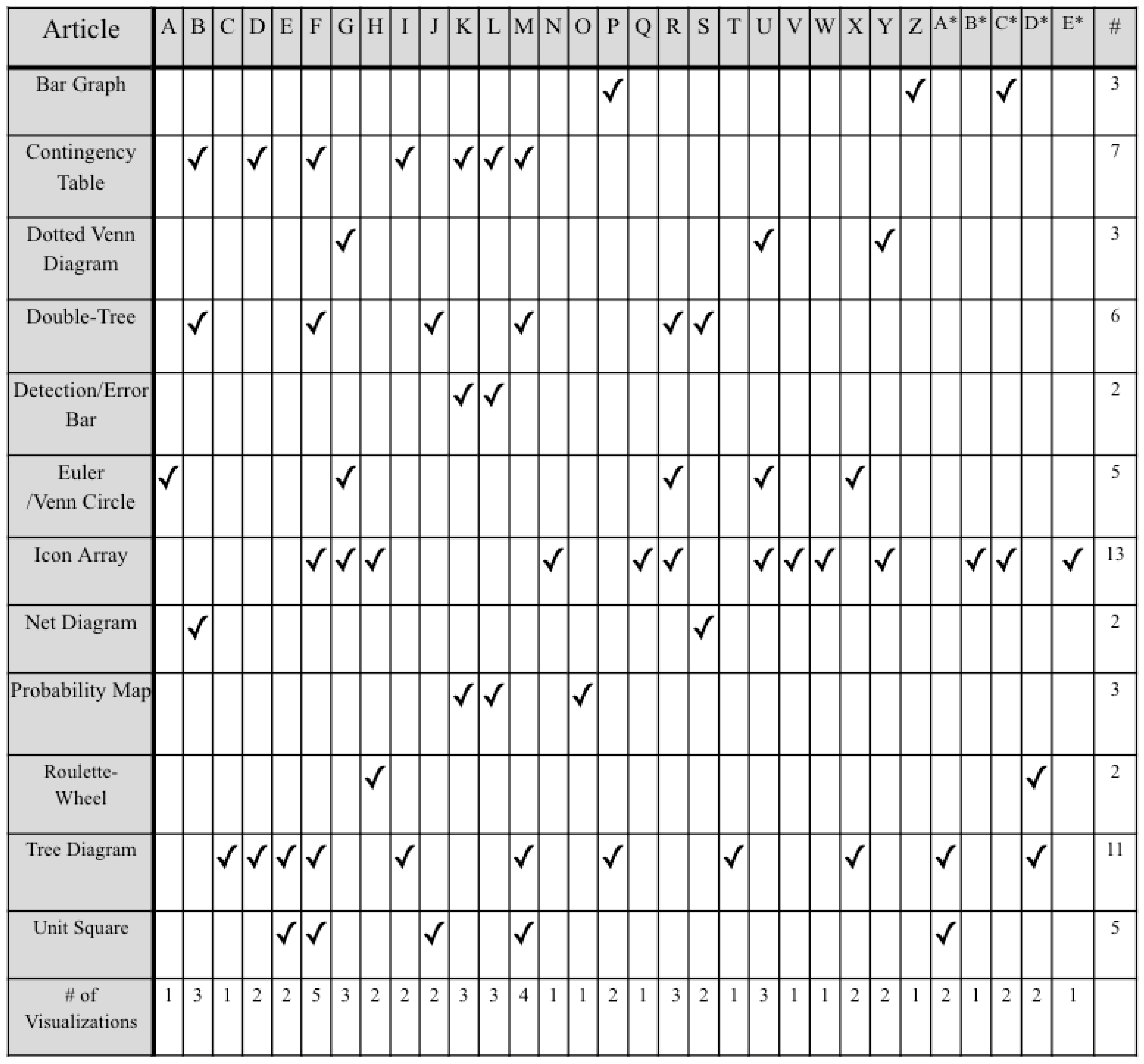
| Reference ID | Reference |
|---|---|
| A | Benoy and Rodgers (2007) [8] |
| B | Binder et al. (2020) [9] |
| C | Binder et al. (2021) [10] |
| D | Binder et al. (2015) [11] |
| E | Böcherer-Linder & Eichler (2017) [12] |
| F | Böcherer-Linder & Eichler (2019) [13] |
| G | Brase (2009) [14] |
| H | Brase (2014) [15] |
| I | Bruckmaier et al. (2019) [16] |
| J | Büchter et al. (2022) [17] |
| K | Cole (1989) [18] |
| L | Cole & Davidson (1989) [19] |
| M | Eichler et al. (2020) [20] |
| N | Gaissmaier et al. (2012) [21] |
| O | Garcia-Retamero et al. (2013) [22] |
| P | Gigerenzer and Hoffrage (1995) [1] |
| Q | Gigerenzer et al. (2021) [23] |
| R | Khan et al. (2015) [2] |
| S | Kunzelmann et al. (2022) [24] |
| T | Kurzenhäuser and Hoffrage (2002) [25] |
| U | Micallef et al. (2012) [26] |
| V | Ottley et al. (2016) [27] |
| W | Ottley et al. (2019) [28] |
| X | Reani et al. (2019) [29] |
| Y | Sirota et al. (2014) [30] |
| Z | Starns et al. (2019) [31] |
| A * | Vogel & Böcherer-Linder (2018) [32] |
| B * | Witt & Dhami (2022) [33] |
| C * | Wu et al. (2017) [34] |
| D * | Yamagishi (2003) [35] |
| E * | Zikmund-Fisher et al. (2014) [36] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, L.; Lo, S.; Liu, Z. The Use of Visualizations to Improve Bayesian Reasoning: A Literature Review. Vision 2023, 7, 17. https://doi.org/10.3390/vision7010017
Cui L, Lo S, Liu Z. The Use of Visualizations to Improve Bayesian Reasoning: A Literature Review. Vision. 2023; 7(1):17. https://doi.org/10.3390/vision7010017
Chicago/Turabian StyleCui, Lucy, Stephanie Lo, and Zili Liu. 2023. "The Use of Visualizations to Improve Bayesian Reasoning: A Literature Review" Vision 7, no. 1: 17. https://doi.org/10.3390/vision7010017
APA StyleCui, L., Lo, S., & Liu, Z. (2023). The Use of Visualizations to Improve Bayesian Reasoning: A Literature Review. Vision, 7(1), 17. https://doi.org/10.3390/vision7010017




