Reliable, Fast and Stable Contrast Response Function Estimation
Abstract
1. Introduction
2. Material and Methods
2.1. Curve Fitting
2.2. Computational Model
2.3. Optimization Criteria
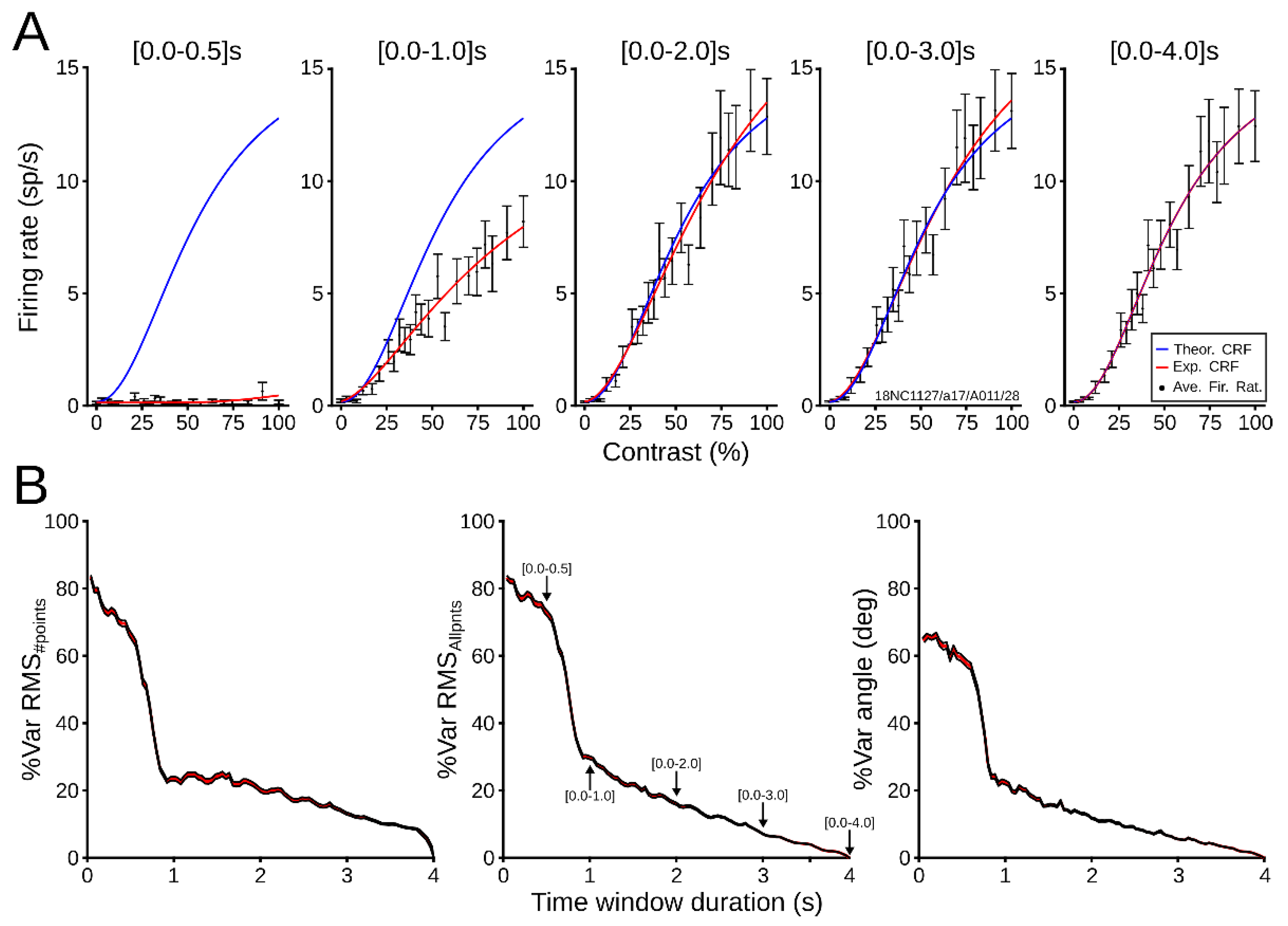
2.3.1. Error Estimation of CRF
2.3.2. Temporal Error Estimation
2.3.3. Monte Carlo Method
2.4. Metric Spacing or Scales
2.5. Experimental Conditions
2.5.1. Animal Preparation
2.5.2. Visual Stimuli
2.5.3. Electrophysiological Recordings and Data Acquisition
2.5.4. Experiment Termination
2.6. Statistical Analysis and Data Analysis
3. Results
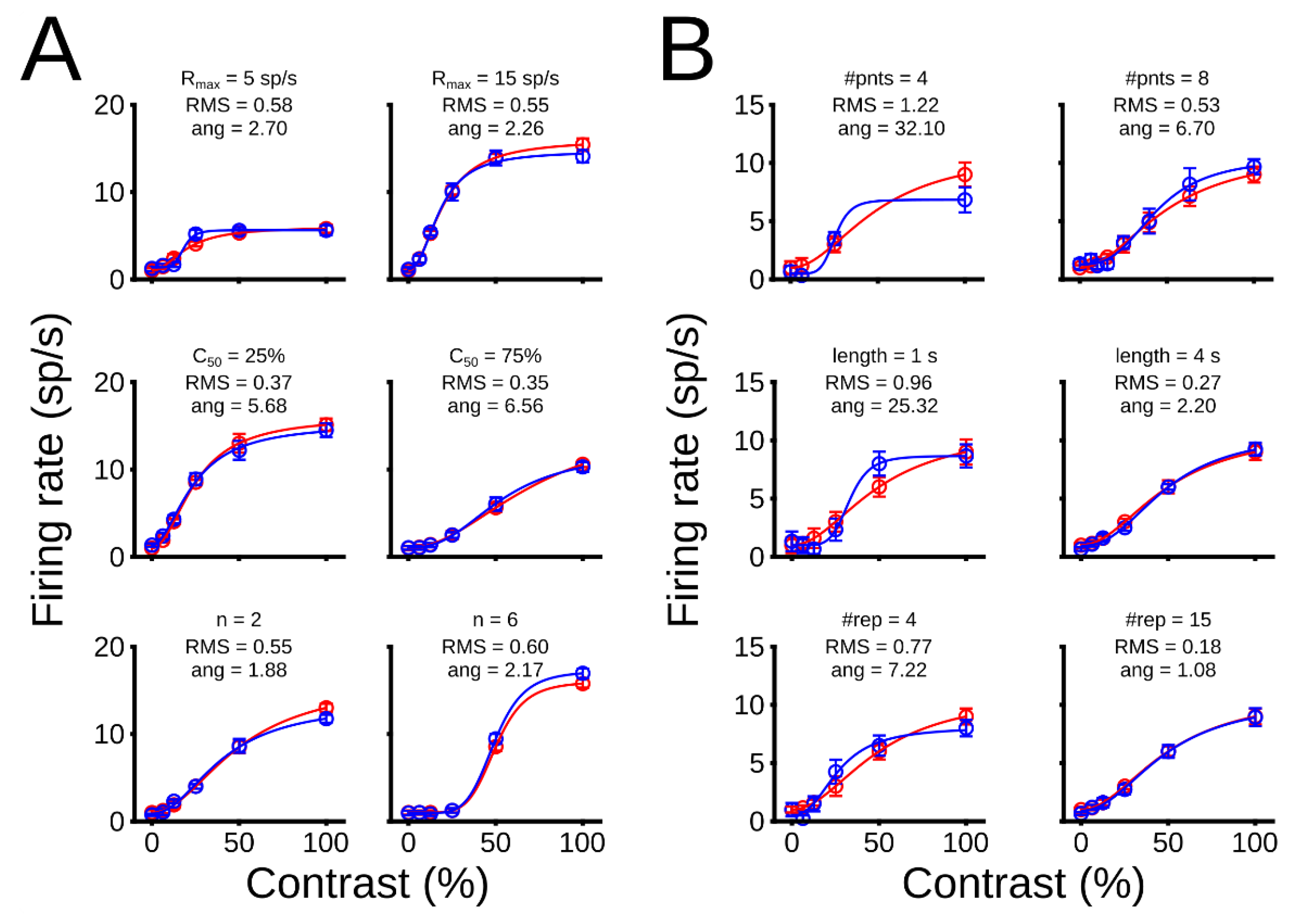
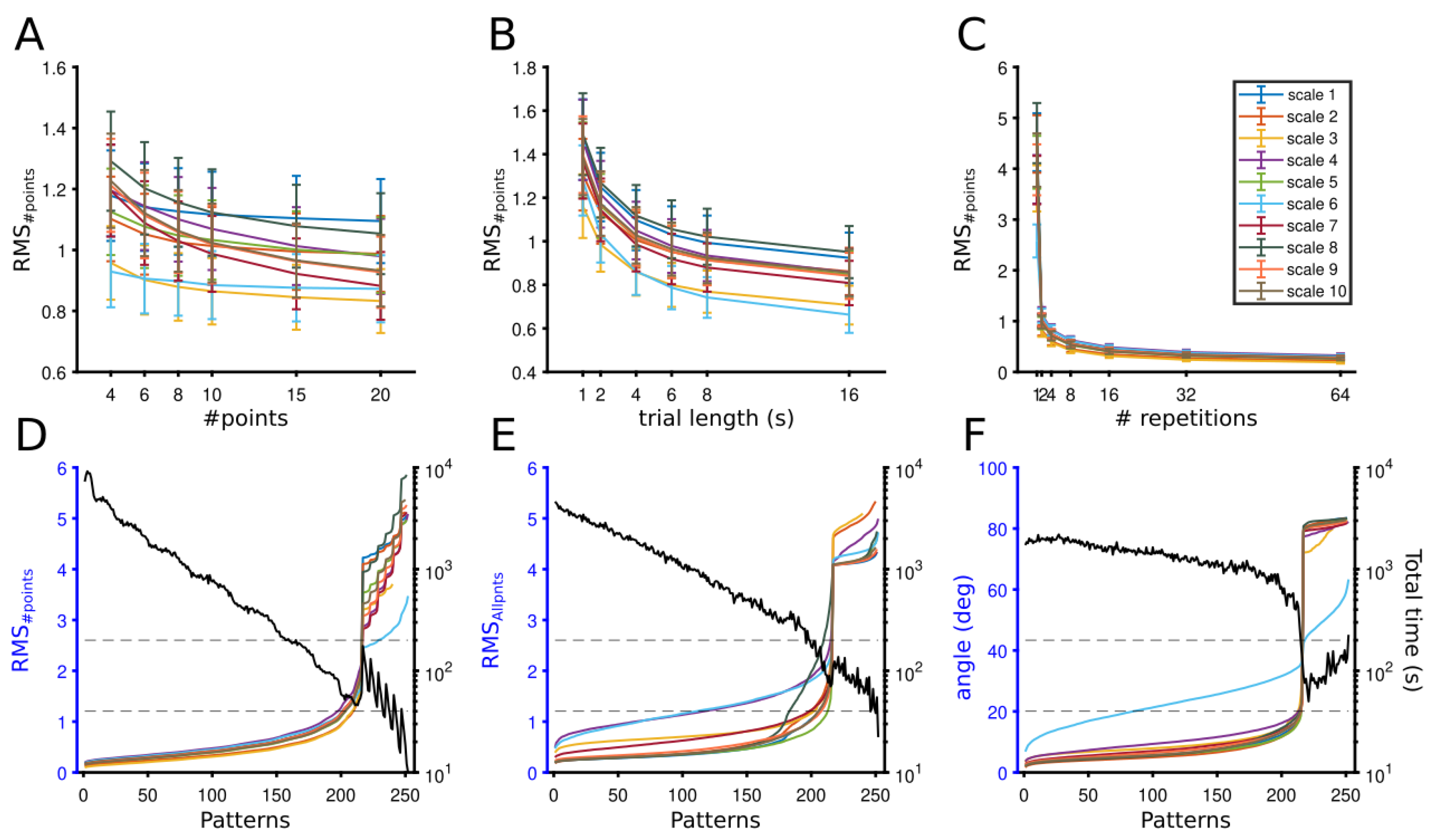
3.1. Theoretical Results
3.1.1. Theoretical Optimization of Experimental Conditions
3.1.2. Optimization Point
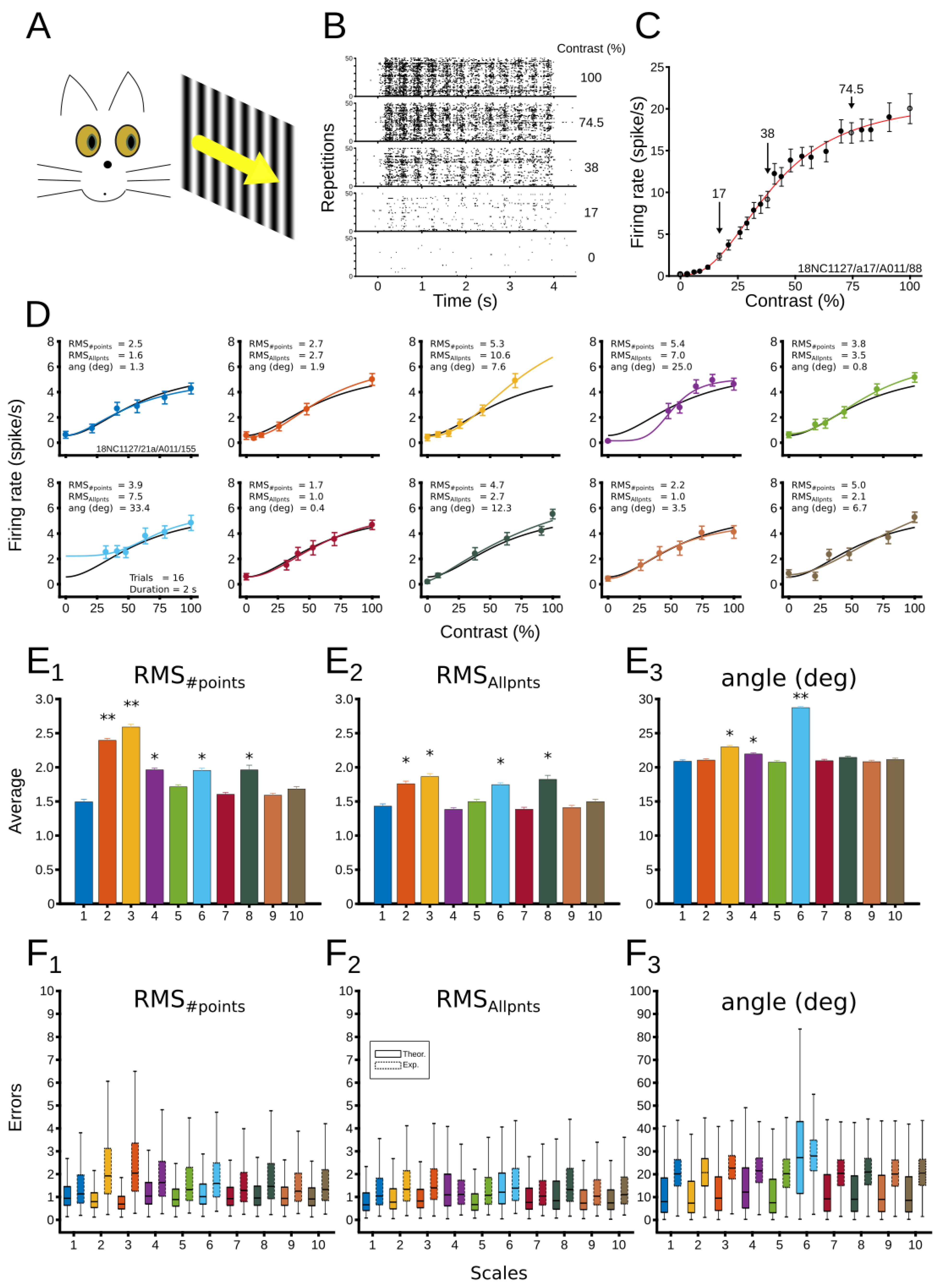
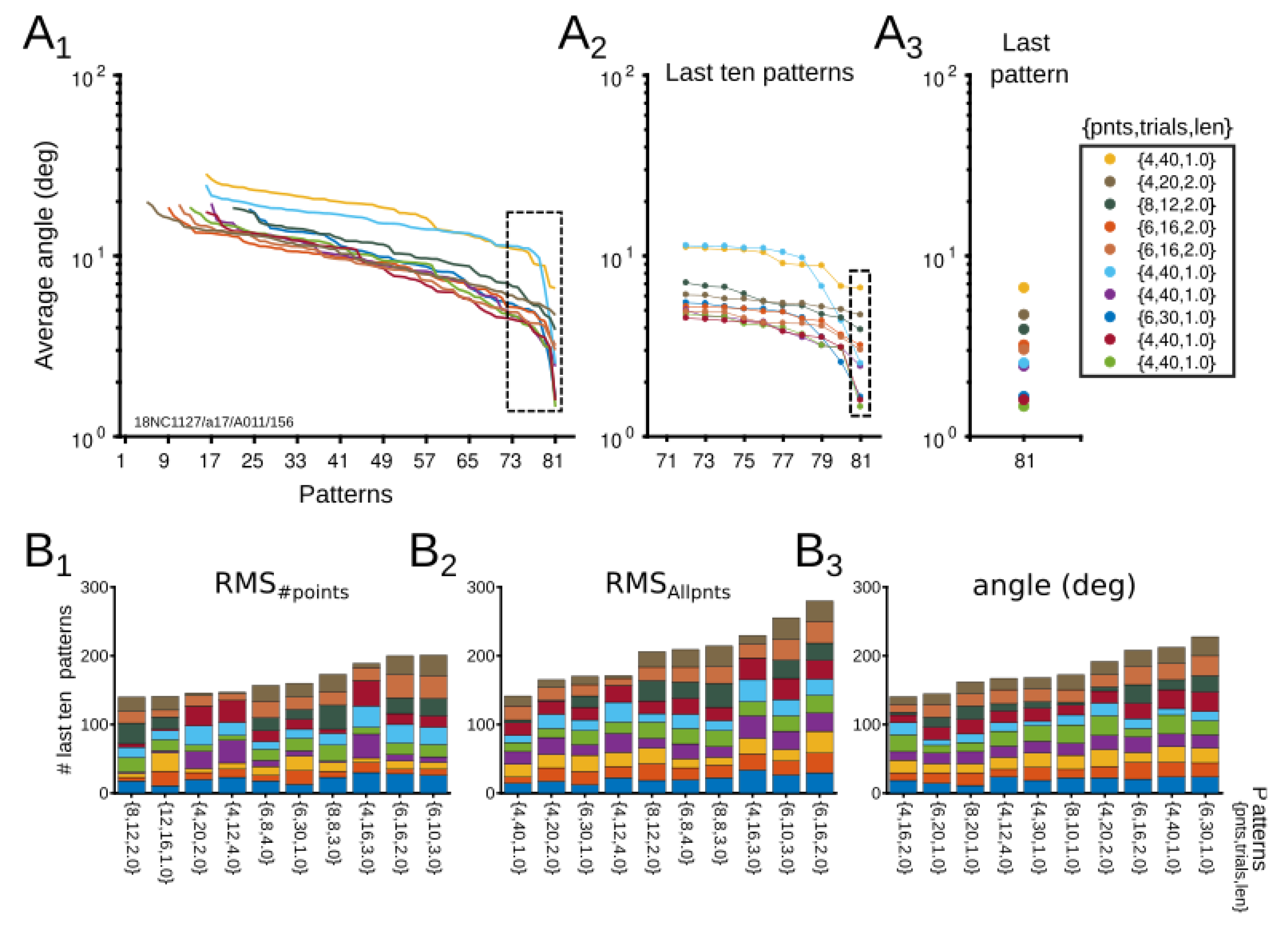
3.2. Experimental Results
3.2.1. Evaluation of Patterns’ Performance
3.2.2. Dynamical CRF Characterization
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, A.; Charles, A.S.; Koay, S.A.; Gauthier, J.L.; Thiberge, S.Y.; Pillow, J.W.; Tank, D.W. Volumetric two-photon imaging of neurons using stereoscopy (vTwINS). Nat. Methods 2017, 14, 420–426. [Google Scholar] [CrossRef] [PubMed]
- Bleia, D.; Smythd, P. Science and data science. Proc. Natl. Acad. Sci. USA 2017, 114, 8689–8692. [Google Scholar] [CrossRef] [PubMed]
- Zhong-Lin, L.; Dosher, B. Adaptive Psychophysical Procedures. In Visual Psychophysics from Laboratory to Theory; The MIT Press: Cambridge, MA, USA, 2013; pp. 351–384. [Google Scholar]
- Jun, J.J.; Steinmetz, N.A.; Siegle, J.H.; Denman, D.J.; Bauza, M.; Barbarits, B.; Lee, A.K.; Anastassiou, C.A.; Andrei, A.; Aydin, C.; et al. Fully integrated silicon probes for high-density recording of neural activity. Nature 2017, 551, 232–236. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, D.G.; Hamilton, D.B. Striate cortex of monkey and cat: Contrast response function. J. Neurophysiol. 1982, 48, 217–237. [Google Scholar] [CrossRef]
- Albrecht, D.; Wilson, S.; Crane, A. Nonlinear properties of visual cortex neurons: Temporal dynamics, stimulus selectivity, neural performance. In The Visual Neurosciences; Chalupa, L., Werner, J., Eds.; The MIT Press: Cambridge, MA, USA, 2003; pp. 747–764. [Google Scholar]
- Naka, K.I.; Rushton, W.A.H. S-potentials from luminosity units in the retina of fish (Cyprinidae). J. Physiol. 1966, 185, 587–599. [Google Scholar] [CrossRef]
- Moré, J.J.; Sorensen, D.C. Computing a Trust Region Step. SIAM J. Sci. Stat. Comput. 1983, 4, 553–572. [Google Scholar] [CrossRef]
- DeGroot, M.; Schervish, M. The Bootstrap. Probability and Statistics; Addison—Wesley: Boston, MA, USA, 2002; pp. 753–763. [Google Scholar]
- Bergh, G.V.D.; Zhang, B.; Arckens, L.; Chino, Y.M. Receptive-field properties of V1 and V2 neurons in mice and macaque monkeys. J. Comp. Neurol. 2010, 518, 2051–2070. [Google Scholar] [CrossRef]
- Contreras, D.; Palmer, L. Response to Contrast of Electrophysiologically Defined Cell Classes in Primary Visual Cortex. J. Neurosci. 2003, 23, 6936–6945. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.; Naud, R.; Paninski, L. Adaptation and firing patterns. In Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: New York, NY, USA, 2014; pp. 136–167. [Google Scholar]
- Angelucci, A.; Shushruth, S. Beyond the classical receptive field: Surround modulation in primary visual cortex. In The New Visual Neurosciences; Chalupa, L., Werner, J., Eds.; The MIT Press: Cambridge, MA, USA, 2013; pp. 425–444. [Google Scholar]
- Movshon, J.A.; Thompson, I.D.; Tolhurst, D.J. Spatial and temporal contrast sensitivity of neurones in areas 17 and 18 of the cat’s visual cortex. J. Physiol. 1978, 283, 101–120. [Google Scholar] [CrossRef]
- Villeneuve, M.; Vanni, M.; Casanova, C. Modular organization in area 21a of the cat revealed by optical imaging: Comparison with the primary visual cortex. Neuroscience 2009, 164, 1320–1333. [Google Scholar] [CrossRef]
- Zumbroich, T.J.; Blakemore, C. Spatial and temporal selectivity in the suprasylvian visual cortex of the cat. J. Neurosci. 1987, 7, 482–500. [Google Scholar] [CrossRef] [PubMed]
- Friend, S.M.; Baker, C.L. Spatio-temporal frequency separability in area 18 neurons of the cat. Vis. Res. 1993, 33, 1765–1771. [Google Scholar] [CrossRef]
- Bonds, A. Temporal dynamics of contrast gain in single cells of the cat striate cortex. Vis. Neurosci. 1991, 6, 239–255. [Google Scholar] [CrossRef] [PubMed]
- Siegle, J.H.; Lopez, A.C.; Patel, Y.A.; Abramov, K.; Ohayon, S.; Voigts, J. Open Ephys: An open-source, plugin-based platform for multichannel electrophysiology. J. Neural Eng. 2017, 14, 045003. [Google Scholar] [CrossRef]
- Rossant, C.; Kadir, S.N.; Goodman, D.F.M.; Schulman, J.; Hunter, M.L.D.; Saleem, A.B.; Grosmark, A.; Belluscio, M.; Denfield, G.H.; Ecker, A.S.; et al. Spike sorting for large, dense electrode arrays. Nat. Neurosci. 2016, 19, 634–641. [Google Scholar] [CrossRef]
- Murgas, K.A.; Wilson, A.M.; Michael, V.; Glickfeld, L.L. Unique Spatial Integration in Mouse Primary Visual Cortex and Higher Visual Areas. J. Neurosci. 2020, 40, 1862–1873. [Google Scholar] [CrossRef]
- Goodyear, B.G.; Menon, R.S. Effect of luminance contrast on BOLD fMRI response in human primary visual areas. J. Neurophysiol. 1998, 79, 2204–2207. [Google Scholar] [CrossRef]
- Pestilli, F.; Carrasco, M.; Heeger, D.J.; Gardner, J.L. Attentional Enhancement via Selection and Pooling of Early Sensory Responses in Human Visual Cortex. Neuron 2011, 72, 832–846. [Google Scholar] [CrossRef]
- Morrone, M.C.; Burr, D.C. Evidence for the existence and development of visual inhibition in humans. Nature 1986, 321, 235–237. [Google Scholar] [CrossRef]
- Tsai, J.J.; Wade, A.R.; Norcia, A.M. Dynamics of Normalization Underlying Masking in Human Visual Cortex. J. Neurosci. 2012, 32, 2783–2789. [Google Scholar] [CrossRef]
- Candy, T.R.; Skoczenski, A.M.; Norcia, A.M. Normalization Models Applied to Orientation Masking in the Human Infant. J. Neurosci. 2001, 21, 4530–4541. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, D.G.; Farrar, S.B.; Hamilton, D.B. Spatial contrast adaptation characteristics of neurones recorded in the cat’s visual cortex. J. Physiol. 1984, 347, 713–739. [Google Scholar] [CrossRef] [PubMed]
- Katzner, S.; Busse, L.; Carandini, M. GABAA Inhibition Controls Response Gain in Visual Cortex. J. Neurosci. 2011, 31, 5931–5941. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Williford, T.; Maunsell, J.H.R. Spatial Attention and the Latency of Neuronal Responses in Macaque Area V4. J. Neurosci. 2007, 27, 9632–9637. [Google Scholar] [CrossRef] [PubMed]
- Lima, B.; Cardoso, M.M.B.; Sirotin, Y.B.; Das, A. Stimulus-related neu roimaging in task-engaged subjects is best predicted by concurrent spiking. J. Neurosci. 2014, 42, 13878–13891. [Google Scholar] [CrossRef]
- Sharpee, T.O.; Victor, J.D. Contextual modulation of V1 receptive fields depends on their spatial symmetry. J. Comput. Neurosci. 2008, 26, 203–218. [Google Scholar] [CrossRef]
- Tailby, C.; Solomon, S.; Dhruv, N.; Majaj, N.J.; Sokol, S.H.; Lennie, P. A New Code for Contrast in the Primate Visual Pathway. J. Neurosci. 2007, 27, 3904–3909. [Google Scholar] [CrossRef]
- Cavanaugh, J.R.; Bair, W.; Movshon, J.A. Nature and Interaction of Signals From the Receptive Field Center and Surround in Macaque V1 Neurons. J. Neurophysiol. 2002, 88, 2530–2546. [Google Scholar] [CrossRef]
- Camillo, D.; Ahmadlou, M.; Saiepour, M.H.; Yasaminshirazi, M.; Levelt, C.N.; Heimel, J.A. Visual Processing by Calretinin Expressing Inhibitory Neurons in Mouse Primary Visual Cortex. Sci. Rep. 2018, 8, 12355. [Google Scholar] [CrossRef]
- Hudson, A.E.; Schiff, N.D.; Victor, J.D.; Purpura, K.P. Attentional modulation of adaptation in V4. Eur. J. Neurosci. 2009, 30, 151–171. [Google Scholar] [CrossRef]
- Long, M.; Jiang, W.; Liu, D.; Yao, H. Contrast-dependent orientation discrimination in the mouse. Sci. Rep. 2015, 5, 15830. [Google Scholar] [CrossRef] [PubMed]
- Olsen, S.; Bortone, D.S.; Adesnik, H.; Scanziani, M. Gain control by layer six in cortical circuits of vision. Nature 2012, 483, 47–52. [Google Scholar] [CrossRef] [PubMed]




| CRF Parameter | Values for Simulations | Units | |
|---|---|---|---|
| Functional | Rmax | 5, 7, 10, 16, 32 | spk/s |
| C50 | 20, 40, 50, 60, 80 | % | |
| B | 1, 2, 4 | spk/s | |
| n | 1, 2, 3, 6 | - | |
| Experimental | Trial Length | 1, 2, 4, 6, 8, 16 | s |
| # contrast points | 4, 6, 8, 10, 15, 20 | - | |
| # repetitions | 1, 2, 4, 8, 16, 32, 64 | - |
| Implementation | ||||
|---|---|---|---|---|
| Scale | Lower Bound | Upper Bound | Description | |
| 1 | Linear | 0.0 | 1.0 | Linearly spaced |
| 2 | Logarithmic | −1.2 | 0.0 | Concentrated around 0 |
| 3 | Logarithmic | −1.0 | −0.15 | Concentrated around 0.25 |
| 4 | Logarithmic | −0.3 | 0.0 | Concentrated around 1 |
| 5 | Logarithmic | −0.7 | 0.0 | Concentrated around 0.75 |
| * 6 | Logarithmic | −0.5 | 0.0 | Same as 5 without 0 |
| 7 | Logarithmic | −0.5 | −0.15 | Concentrated around 0.5 |
| 8 | Linear | 0.1 | 0.9 | Same as 7 but linearly spaced |
| 9 | Linear | 0.25 | 0.75 | Same as 8 but less spread out |
| 10 | Logarithmic | −0.7 | −0.1 | Log-concentrated around 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortes, N.; Demers, M.; Ady, V.; Ikan, L.; Casanova, C. Reliable, Fast and Stable Contrast Response Function Estimation. Vision 2022, 6, 62. https://doi.org/10.3390/vision6040062
Cortes N, Demers M, Ady V, Ikan L, Casanova C. Reliable, Fast and Stable Contrast Response Function Estimation. Vision. 2022; 6(4):62. https://doi.org/10.3390/vision6040062
Chicago/Turabian StyleCortes, Nelson, Marc Demers, Visou Ady, Lamyae Ikan, and Christian Casanova. 2022. "Reliable, Fast and Stable Contrast Response Function Estimation" Vision 6, no. 4: 62. https://doi.org/10.3390/vision6040062
APA StyleCortes, N., Demers, M., Ady, V., Ikan, L., & Casanova, C. (2022). Reliable, Fast and Stable Contrast Response Function Estimation. Vision, 6(4), 62. https://doi.org/10.3390/vision6040062





