The Sternberg Paradigm: Correcting Encoding Latencies in Visual and Auditory Test Designs
Abstract
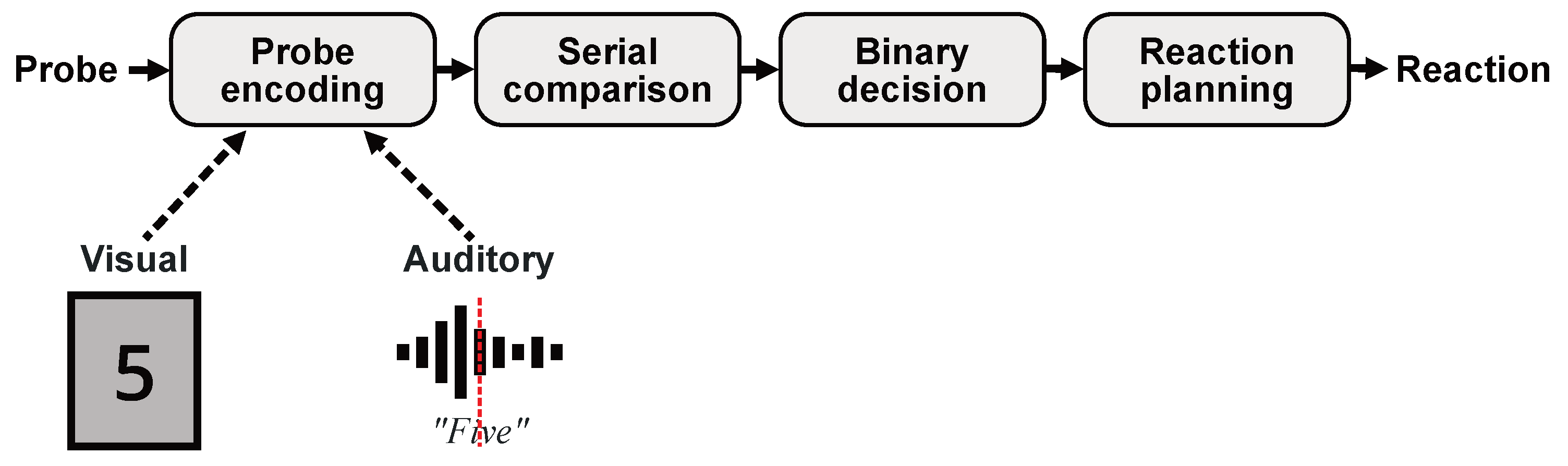
1. Introduction
2. Materials and Methods
2.1. Participants
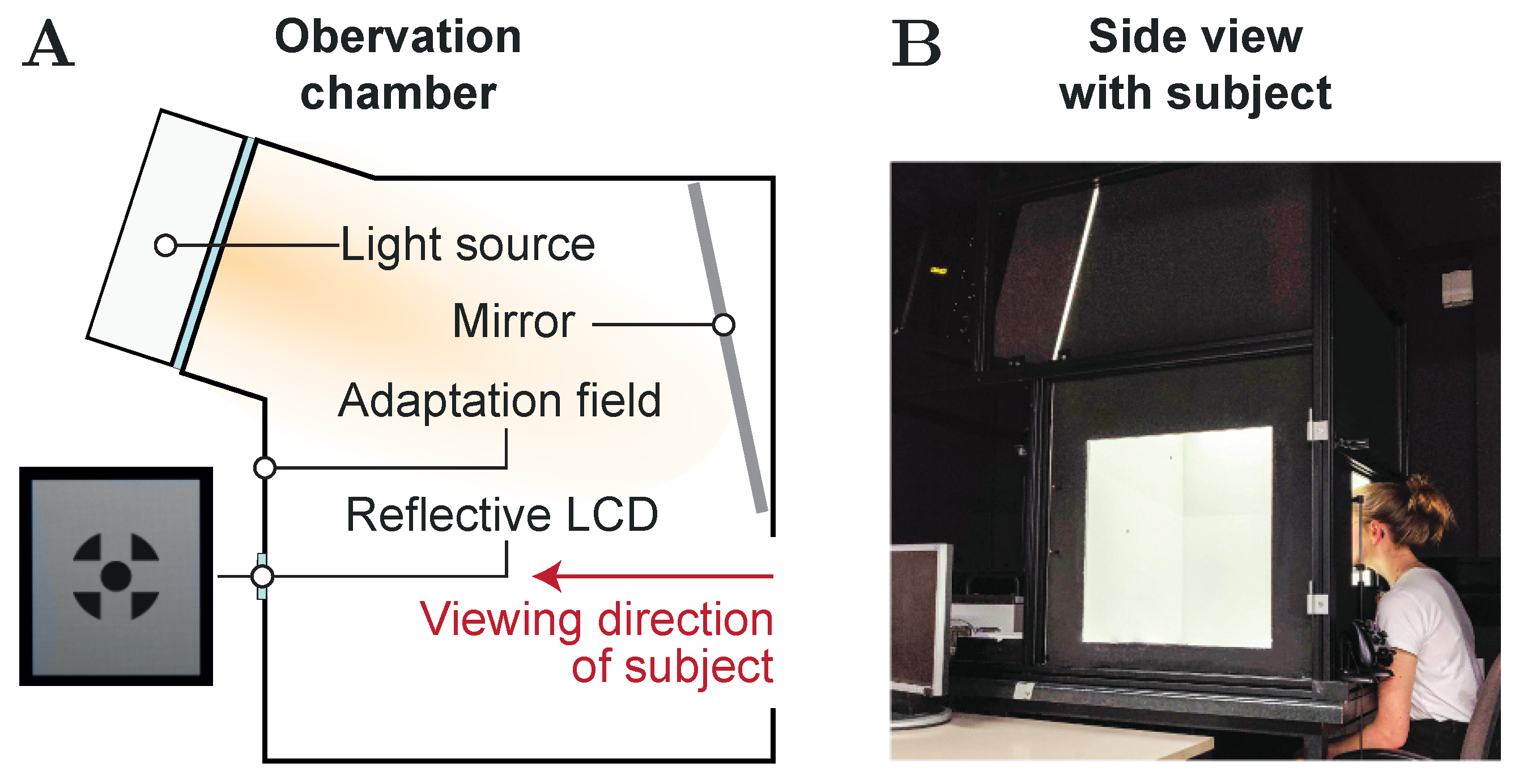
2.2. Experimental Setup
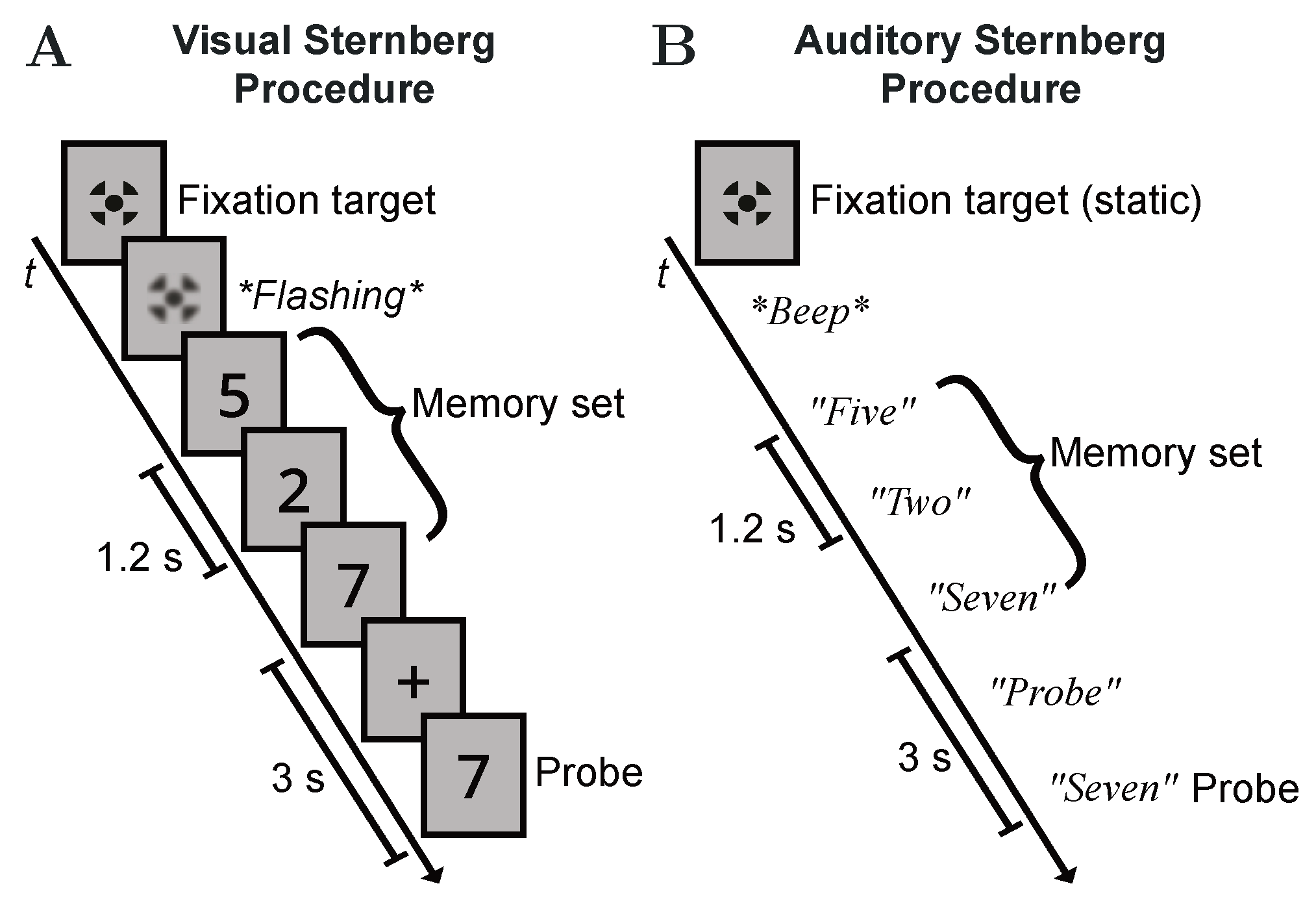
2.3. Test Procedure
2.4. Statistical Analysis
3. Results
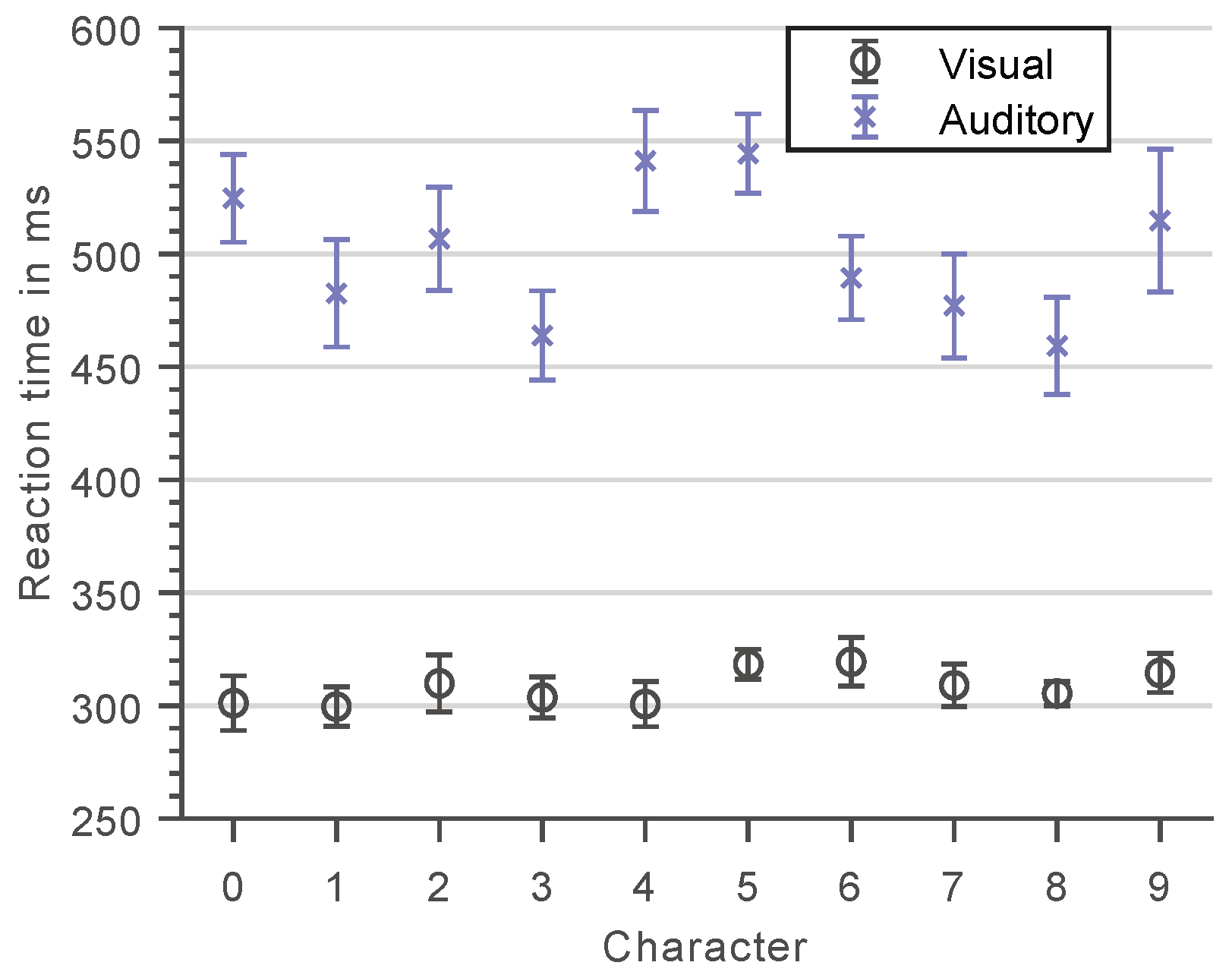
3.1. Character-Specific Encoding Times
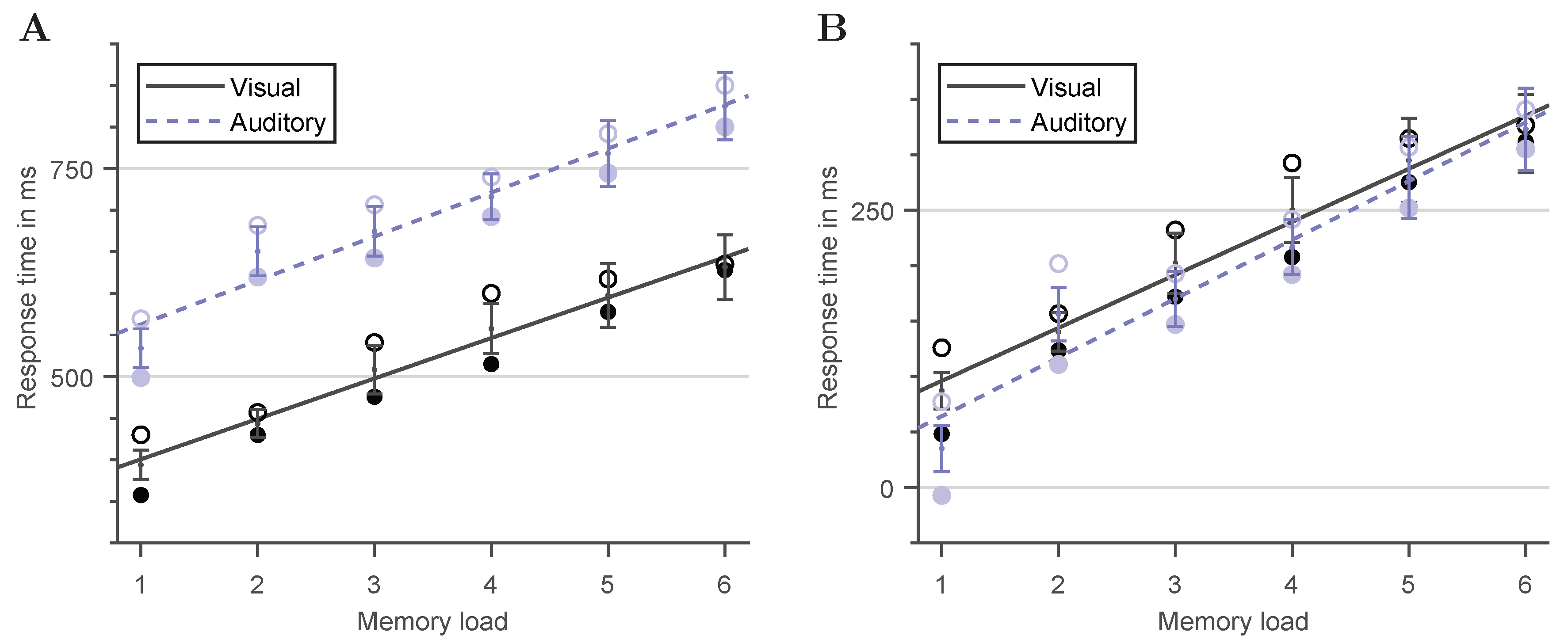
3.2. Visual versus Auditory Sternberg Task Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hayhoe, M.M.; Bensinger, D.G.; Ballard, D.H. Task constraints in visual working memory. Vis. Res. 1998, 38, 125–137. [Google Scholar] [CrossRef]
- Engle, R.W. Role of working-memory capacity in cognitive control. Curr. Anthropol. 2010, 51, S17–S26. [Google Scholar] [CrossRef]
- Luck, S.J.; Zhang, W. Continuous versus discrete models of visual working memory capacity. J. Vis. 2013, 13, 1364. [Google Scholar] [CrossRef]
- Pollard, M.A.; Courage, M.L. Working memory capacity predicts effective multitasking. Comput. Hum. Behav. 2017, 76, 450–462. [Google Scholar] [CrossRef]
- Baddeley, A. Working memory. Curr. Biol. 2010, 20, R136–R140. [Google Scholar] [CrossRef] [PubMed]
- Luck, S.J.; Vogel, E.K. The capacity of visual working memory for features and conjunctions. Nature 1997, 390, 279–281. [Google Scholar] [CrossRef] [PubMed]
- Ho, H.Z.; Baker, L.A.; Decker, S.N. Covariation between intelligence and speed of cognitive processing: Genetic and environmental influences. Behav. Genet. 1988, 18, 247–261. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, A.C.; Spinath, F.M.; Riemann, R.; Borkenau, P.; Angleitner, A. Genetic and environmental influences on two measures of speed of information processing and their relation to psychometric intelligence: Evidence from the German observational study of adult twins. Intelligence 2000, 28, 267–289. [Google Scholar] [CrossRef]
- Luciano, M.; Wright, M.; Smith, G.A.; Geffen, G.M.; Geffen, L.B.; Martin, N.G. Genetic covariance among measures of information processing speed, working memory, and IQ. Behav. Genet. 2001, 31, 581–592. [Google Scholar] [CrossRef] [PubMed]
- Polderman, T.J.C.; Stins, J.F.; Posthuma, D.; Gosso, M.F.; Verhulst, F.C.; Boomsma, D.I. The phenotypic and genotypic relation between working memory speed and capacity. Intelligence 2006, 34, 549–560. [Google Scholar] [CrossRef][Green Version]
- Vinkhuyzen, A.A.E.; van der Sluis, S.; Boomsma, D.I.; de Geus, E.J.C.; Posthuma, D. Individual differences in processing speed and working memory speed as assessed with the Sternberg memory scanning task. Behav. Genet. 2010, 40, 315–326. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sternberg, S. High-Speed Scanning in Human Memory. Science 1966, 153, 652–654. [Google Scholar] [CrossRef]
- Whitney, P.; Hinson, J.M. Measurement of cognition in studies of sleep deprivation. Prog. Brain Res. 2010, 185, 37–48. [Google Scholar] [CrossRef]
- Burle, B.; Bonnet, M. High-speed memory scanning: A behavioral argument for a serial oscillatory model. Cogn. Brain Res. 2000, 9, 327–337. [Google Scholar] [CrossRef]
- Sternberg, S. In defence of high-speed memory scanning. Q. J. Exp. Psychol. 2016, 69, 2020–2075. [Google Scholar] [CrossRef] [PubMed]
- Sternberg, S. Memory-scanning: Mental processes revealed by reaction-time experiments. Am. Sci. 1969, 57, 421–457. Available online: https://www.jstor.org/stable/27828738 (accessed on 25 March 2021). [PubMed]
- D’Esposito, M.; Postle, B.R.; Rypma, B. Prefrontal cortical contributions to working memory: Evidence from event-related fMRI studies. In Executive Control and the Frontal Lobe: Current Issues; Schneider, W.X., Owen, A.M., Duncan, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 3–11. [Google Scholar] [CrossRef]
- Rojas, D.C.; Teale, P.; Sheeder, J.L.; Reite, M.L. Neuromagnetic alpha suppression during an auditory Sternberg task: Evidence for a serial, self-terminating search of short-term memory. Cogn. Brain Res. 2000, 10, 85–89. [Google Scholar] [CrossRef]
- Wolach, I.; Pratt, H. The mode of short-term memory encoding as indicated by event-related potentials in a memory scanning task with distractions. Clin. Neurophysiol. 2001, 112, 186–197. [Google Scholar] [CrossRef]
- Jensen, O.; Gelfand, J.; Kounios, J.; Lisman, J.E. Oscillations in the alpha band (9–12 Hz) increase with memory load during retention in a short-term memory task. Cereb. Cortex 2002, 12, 877–882. [Google Scholar] [CrossRef] [PubMed]
- Jensen, O.; Tesche, C.D. Frontal theta activity in humans increases with memory load in a working memory task. Eur. J. Neurosci. 2002, 15, 1395–1399. [Google Scholar] [CrossRef] [PubMed]
- Schack, B.; Klimesch, W. Frequency characteristics of evoked and oscillatory electroencephalic activity in a human memory scanning task. Neurosci. Lett. 2002, 331, 107–110. [Google Scholar] [CrossRef]
- Singhal, A.; Fowler, B. The effects of memory scanning on the late Nd and P300: An interference study. Psychophysiology 2005, 42, 142–150. [Google Scholar] [CrossRef] [PubMed]
- Leiberg, S.; Lutzenberger, W.; Kaiser, J. Effects of memory load on cortical oscillatory activity during auditory pattern working memory. Brain Res. 2006, 1120, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Pesonen, M.; Björnberg, C.H.; Hämäläinen, H.; Krause, C.M. Brain oscillatory 1–30 Hz EEG ERD/ERS responses during the different stages of an auditory memory search task. Neurosci. Lett. 2006, 399, 45–50. [Google Scholar] [CrossRef]
- Altamura, M.; Elvevåg, B.; Blasi, G.; Bertolino, A.; Callicott, J.H.; Weinberger, D.R.; Mattay, V.S.; Goldberg, T.E. Dissociating the effects of Sternberg working memory demands in prefrontal cortex. Psychiatry Res. Neuroimaging 2007, 154, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Pelosi, L.; Slade, T.; Blumhardt, L.D.; Sharma, V.K. Working memory dysfunction in major depression: An event-related potential study. Clin. Neurophysiol. 2000, 111, 1531–1543. [Google Scholar] [CrossRef]
- Ahn, K.H.; Youn, T.; Cho, S.S.; Ha, T.H.; Ha, K.S.; Kim, M.S.; Kwon, J.S. N-methyl-D-aspartate receptor in working memory impairments in schizophrenia: Event-related potential study of late stage of working memory process. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2003, 27, 993–999. [Google Scholar] [CrossRef]
- Archibald, C.J.; Wei, X.; Scott, J.N.; Wallace, C.J.; Zhang, Y.; Metz, L.M.; Mitchell, J.R. Posterior fossa lesion volume and slowed information processing in multiple sclerosis. Brain 2004, 127, 1526–1534. [Google Scholar] [CrossRef][Green Version]
- Johnson, M.R.; Morris, N.A.; Astur, R.S.; Calhoun, V.D.; Mathalon, D.H.; Kiehl, K.A.; Pearlson, G.D. A functional magnetic resonance imaging study of working memory abnormalities in schizophrenia. Biol. Psychiatry 2006, 60, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Karrasch, M.; Laine, M.; Rinne, J.O.; Rapinoja, P.; Sinervä, E.; Krause, C.M. Brain oscillatory responses to an auditory-verbal working memory task in mild cognitive impairment and Alzheimer’s disease. Int. J. Psychophysiol. 2006, 59, 168–178. [Google Scholar] [CrossRef]
- Schlösser, R.G.M.; Koch, K.; Wagner, G.; Nenadic, I.; Roebel, M.; Schachtzabel, C.; Axer, M.; Schultz, C.; Reichenbach, J.R.; Sauer, H. Inefficient executive cognitive control in schizophrenia is preceded by altered functional activation during information encoding: An fMRI study. Neuropsychologia 2008, 46, 336–347. [Google Scholar] [CrossRef]
- Rypma, B.; Berger, J.S.; Genova, H.M.; Rebbechi, D.; D’Esposito, M. Dissociating age-related changes in cognitive strategy and neural efficiency using event-related fMRI. Cortex 2005, 41, 582–594. [Google Scholar] [CrossRef]
- Tait, R.; Martin-Iverson, M.; Michie, P.T.; Dusci, L. The effects of cigarette consumption on the Sternberg visual memory search paradigm. Addiction 2000, 95, 437–446. [Google Scholar] [CrossRef]
- Moulton, P.L.; Boyko, L.N.; Fitzpatrick, J.L.; Petros, T.V. The effect of Ginkgo biloba on memory in healthy male volunteers. Physiol. Behav. 2001, 73, 659–665. [Google Scholar] [CrossRef]
- Verster, J.C.; Volkerts, E.R.; Verbaten, M.N. Effects of alprazolam on driving ability, memory functioning and psychomotor performance: A randomized, placebo-controlled study. Neuropsychopharmacology 2002, 27, 260–269. [Google Scholar] [CrossRef]
- Allain, H.; Bentue-Ferrer, D.; Tarral, A.; Gandon, J.M. Effects on postural oscillation and memory functions of a single dose of zolpidem 5 mg, zopiclone 3.75 mg and lormetazepam 1 mg in elderly healthy subjects. A randomized, cross-over, double-blind study versus placebo. Eur. J. Clin. Pharmacol. 2003, 59, 179–188. [Google Scholar] [CrossRef] [PubMed]
- Wickens, C.D.; Hyman, F.; Dellinger, J.; Taylor, H.; Meador, M. The Sternberg memory search task as an index of pilot workload. Ergonomics 1986, 29, 1371–1383. [Google Scholar] [CrossRef]
- Okamoto, Y.; Nakagawa, S. Effects of light wavelength on MEG ERD/ERS during a working memory task. Int. J. Psychophysiol. 2016, 104, 10–16. [Google Scholar] [CrossRef]
- Tan, C.H.; Low, K.A.; Schneider-Garces, N.; Zimmerman, B.; Fletcher, M.A.; Maclin, E.L.; Chiarelli, A.M.; Gratton, G.; Fabiani, M. Optical measures of changes in cerebral vascular tone during voluntary breath holding and a Sternberg memory task. Biol. Psychol. 2016, 118, 184–194. [Google Scholar] [CrossRef] [PubMed]
- van der Wel, P.; van Steenbergen, H. Pupil dilation as an index of effort in cognitive control tasks: A review. Psychon. Bull. Rev. 2018, 25, 2005–2015. [Google Scholar] [CrossRef] [PubMed]
- Van Gerven, P.W.M.; Paas, F.; Van Merriënboer, J.J.G.; Schmidt, H.G. Memory load and the cognitive pupillary response in aging. Psychophysiology 2004, 41, 167–174. [Google Scholar] [CrossRef]
- Porter, G.; Troscianko, T.; Gilchrist, I.D. Effort during visual search and counting: Insights from pupillometry. Q. J. Exp. Psychol. 2007, 60, 211–229. [Google Scholar] [CrossRef] [PubMed]
- Kursawe, M.A.; Zimmer, H.D. Costs of storing colour and complex shape in visual working memory: Insights from pupil size and slow waves. Acta Psychol. 2015, 158, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Unsworth, N.; Robison, M.K. Individual differences in the allocation of attention to items in working memory: Evidence from pupillometry. Psychon. Bull. Rev. 2015, 22, 757–765. [Google Scholar] [CrossRef]
- Unsworth, N.; Robison, M.K. Tracking working memory maintenance with pupillometry. Atten. Percept. Psychophys. 2018, 80, 461–484. [Google Scholar] [CrossRef] [PubMed]
- Hess, E.H.; Polt, J.M. Pupil size in relation to mental activity during simple problem-solving. Science 1964, 143, 1190–1192. [Google Scholar] [CrossRef] [PubMed]
- Kahneman, D. Attention and Effort; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Beatty, J. Task-evoked pupillary responses, processing load, and the structure of processing resources. Psychol. Bull. 1982, 91, 276–292. [Google Scholar] [CrossRef]
- Rondeel, E.; Van Steenbergen, H.; Holland, R.; van Knippenberg, A. A closer look at cognitive control: Differences in resource allocation during updating, inhibition and switching as revealed by pupillometry. Front. Hum. Neurosci. 2015, 9, 494. [Google Scholar] [CrossRef]
- Van Der Meer, E.; Beyer, R.; Horn, J.; Foth, M.; Bornemann, B.; Ries, J.; Kramer, J.; Warmuth, E.; Heekeren, H.R.; Wartenburger, I. Resource allocation and fluid intelligence: Insights from pupillometry. Psychophysiology 2010, 47, 158–169. [Google Scholar] [CrossRef]
- Bijleveld, E.; Custers, R.; Aarts, H. The unconscious eye opener: Pupil dilation reveals strategic recruitment of resources upon presentation of subliminal reward cues. Psychol. Sci. 2009, 20, 1313–1315. [Google Scholar] [CrossRef]
- Chase, W.G.; Calfee, R.C. Modality and similarity effects in short-term recognition memory. J. Exp. Psychol. 1969, 81, 510–514. [Google Scholar] [CrossRef]
- Wingfield, A. Effects of serial position and set size in auditory recognition memory. Mem. Cogn. 1973, 1, 53–55. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wingfield, A.; Branca, A.A. Strategy in high-speed memory search. J. Exp. Psychol. 1970, 83, 63–67. [Google Scholar] [CrossRef]
- Wingfield, A.; Bolt, R.A. Memory search for multiple targets. J. Exp. Psychol. 1970, 85, 45–50. [Google Scholar] [CrossRef]
- Zandi, B.; Klabes, J.; Khanh, T.Q. Prediction accuracy of L- and M-cone based human pupil light models. Sci. Rep. 2020, 10, 10988. [Google Scholar] [CrossRef]
- Zandi, B.; Khanh, T.Q. Deep learning-based pupil model predicts time and spectral dependent light responses. Sci. Rep. 2021, 11, 841. [Google Scholar] [CrossRef]
- Thaler, L.; Schütz, A.C.; Goodale, M.A.; Gegenfurtner, K.R. What is the best fixation target? The effect of target shape on stability of fixational eye movements. Vis. Res. 2013, 76, 31–42. [Google Scholar] [CrossRef]
- Rea, M.S. Toward a model of visual performance: Foundations and data. J. Illum. Eng. Soc. 1986, 15, 41–57. [Google Scholar] [CrossRef]
- Brainard, D.H. The psychophysics toolbox. Spat. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef] [PubMed]
- Kleiner, M.; Brainard, D.; Pelli, D. What’s new in psychtoolbox-3. Perception 2007, 36, 14. [Google Scholar] [CrossRef]
- Laird, N.M.; Ware, J.H. Random-Effects Models for Longitudinal Data. Biometrics 1982, 38, 963–974. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R. A theory of memory retrieval. Psychol. Rev. 1978, 85, 59–108. [Google Scholar] [CrossRef]
- Ratcliff, R.; Rouder, J.N. Modeling response times for two-choice decisions. Psychol. Sci. 1998, 9, 347–356. [Google Scholar] [CrossRef]
- Schubert, A.L.; Frischkorn, G.T.; Hagemann, D.; Voss, A. Trait characteristics of diffusion model parameters. J. Intell. 2016, 4, 7. [Google Scholar] [CrossRef]
- Voss, A.; Voss, J. Fast-dm: A free program for efficient diffusion model analysis. Behav. Res. Methods 2007, 39, 767–775. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Voss, J. Diffusion Model Analysis with Fast-dm-30. Available online: https://www.psychologie.uni-heidelberg.de/ae/meth/fast-dm/ (accessed on 25 April 2021).
| Memory Load | Visual | Auditory |
|---|---|---|
| M1 | 0.975 (0 .038) | 0.995 (0.020) |
| M2 | 0.975 (0.048) | 0.995 (0.020) |
| M3 | 0.975 (0.055) | 0.985 (0.043) |
| M4 | 0.971 (0.064) | 0.990 (0.027) |
| M5 | 0.966 (0.050) | 0.975 (0.048) |
| M6 | 0.912 (0.101) | 0.971 (0.040) |
| Visual | Auditory | |||||||
|---|---|---|---|---|---|---|---|---|
| Memory Load | a | a | ||||||
| M1 | 0.14 (0.48) | 0.70 (0.46) | 0.29 (0.07) | 0.11 (0.07) | 0.02 (0.26) | 0.67 (0.27) | 0.42 (0.08) | 0.13 (0.11) |
| M2 | 0.33 (0.93) | 0.57 (0.32) | 0.36 (0.04) | 0.16 (0.09) | 0.21 (0.67) | 0.84 (0.30) | 0.47 (0.07) | 0.16 (0.11) |
| M3 | 0.11 (0.37) | 0.67 (0.24) | 0.39 (0.07) | 0.17 (0.11) | −0.06 (0.26) | 0.79 (0.29) | 0.52 (0.08) | 0.16 (0.14) |
| M4 | 0.09 (0.33) | 0.74 (0.22) | 0.43 (0.09) | 0.21 (0.17) | −0.05 (0.17) | 0.84 (0.22) | 0.55 (0.08) | 0.18 (0.12) |
| M5 | 0.00 (0.20) | 0.73 (0.30) | 0.44 (0.08) | 0.18 (0.12) | −0.05 (0.11) | 0.92 (0.34) | 0.56 (0.10) | 0.25 (0.09) |
| M6 | −0.03 (0.86) | 0.75 (0.42) | 0.48 (0.09) | 0.17 (0.13) | −0.11 (0.20) | 0.97 (0.29) | 0.61 (0.11) | 0.18 (0.13) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klabes, J.; Babilon, S.; Zandi, B.; Khanh, T.Q. The Sternberg Paradigm: Correcting Encoding Latencies in Visual and Auditory Test Designs. Vision 2021, 5, 21. https://doi.org/10.3390/vision5020021
Klabes J, Babilon S, Zandi B, Khanh TQ. The Sternberg Paradigm: Correcting Encoding Latencies in Visual and Auditory Test Designs. Vision. 2021; 5(2):21. https://doi.org/10.3390/vision5020021
Chicago/Turabian StyleKlabes, Julian, Sebastian Babilon, Babak Zandi, and Tran Quoc Khanh. 2021. "The Sternberg Paradigm: Correcting Encoding Latencies in Visual and Auditory Test Designs" Vision 5, no. 2: 21. https://doi.org/10.3390/vision5020021
APA StyleKlabes, J., Babilon, S., Zandi, B., & Khanh, T. Q. (2021). The Sternberg Paradigm: Correcting Encoding Latencies in Visual and Auditory Test Designs. Vision, 5(2), 21. https://doi.org/10.3390/vision5020021






