Spatial Frequency Tuning and Transfer of Perceptual Learning for Motion Coherence Reflects the Tuning Properties of Global Motion Processing
Abstract
:1. Introduction
1.1. Specificity
1.2. Perceptual Learning and the Visual Hierarchy
1.3. Low- and High-Level Perception of Motion
1.4. Studying Motion Perception
1.5. Feedback in Perceptual Learning
2. Our Study
2.1. Experiment 1
2.2. Experiment 2: Main Study
3. Methods and Materials
3.1. Participants
3.2. Experiment 1
3.3. Experiment 2
3.3.1. Training Stimuli
3.3.2. Testing Stimuli (Pre and Post)
- Global motion: Stimuli were identical to those described in the training session, with the following exceptions. In order to standardise the stimuli across the viewing conditions of the two monitors, the standard deviations of the testing elements were 6.4 arc minutes (broadband), 28.4 arc minutes (low-frequency) and 7.0 arc minutes (high-frequency). Stimuli were presented within a mid-grey rectangle measuring 15.9° × 15.9°, and each element moved a fixed distance of 8 arc minutes.
- Contrast sensitivity: Stimuli were static oriented Gabor patches (see Figure 4), with a spatial frequency of 1 cycle per degree (/°) or 4 cycles/°, presented in the centre of the screen on a mid-grey background, tilted either ±20° away from vertical. The Gaussian envelope of the Gabor stimulus had a standard deviation of 1.1°. Seven levels of contrast (0.05, 0.1, 0.15, 0.175, 0.2, 0.3, 0.4% Michelson Contrast) were presented.
3.4. Procedure
3.5. Statistical Methodology
Interpreting the Changes to the Psychometric Function
4. Results
4.1. Statistical Methods
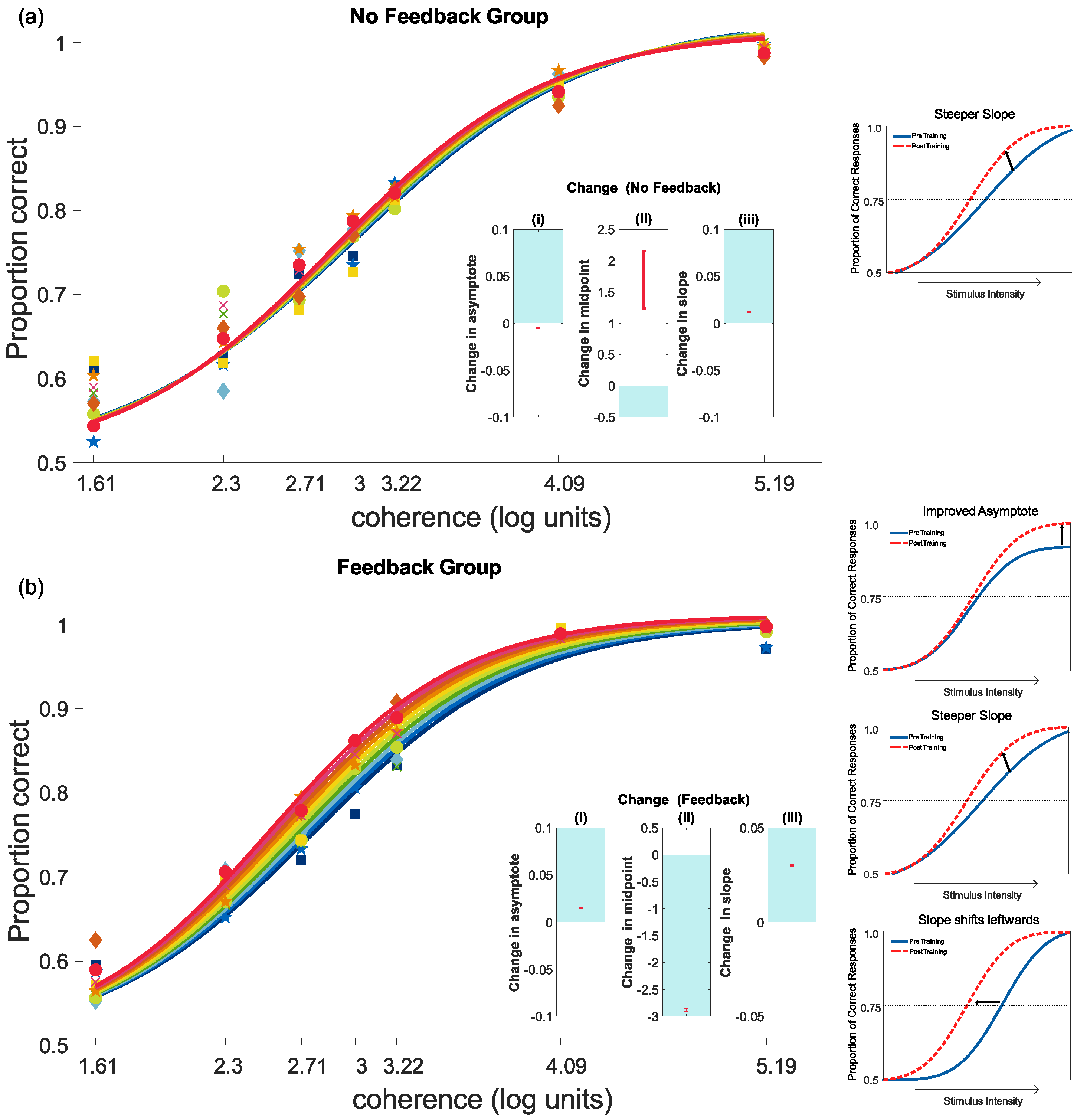
4.2. Feedback and Perceptual Learning: Experiment 1
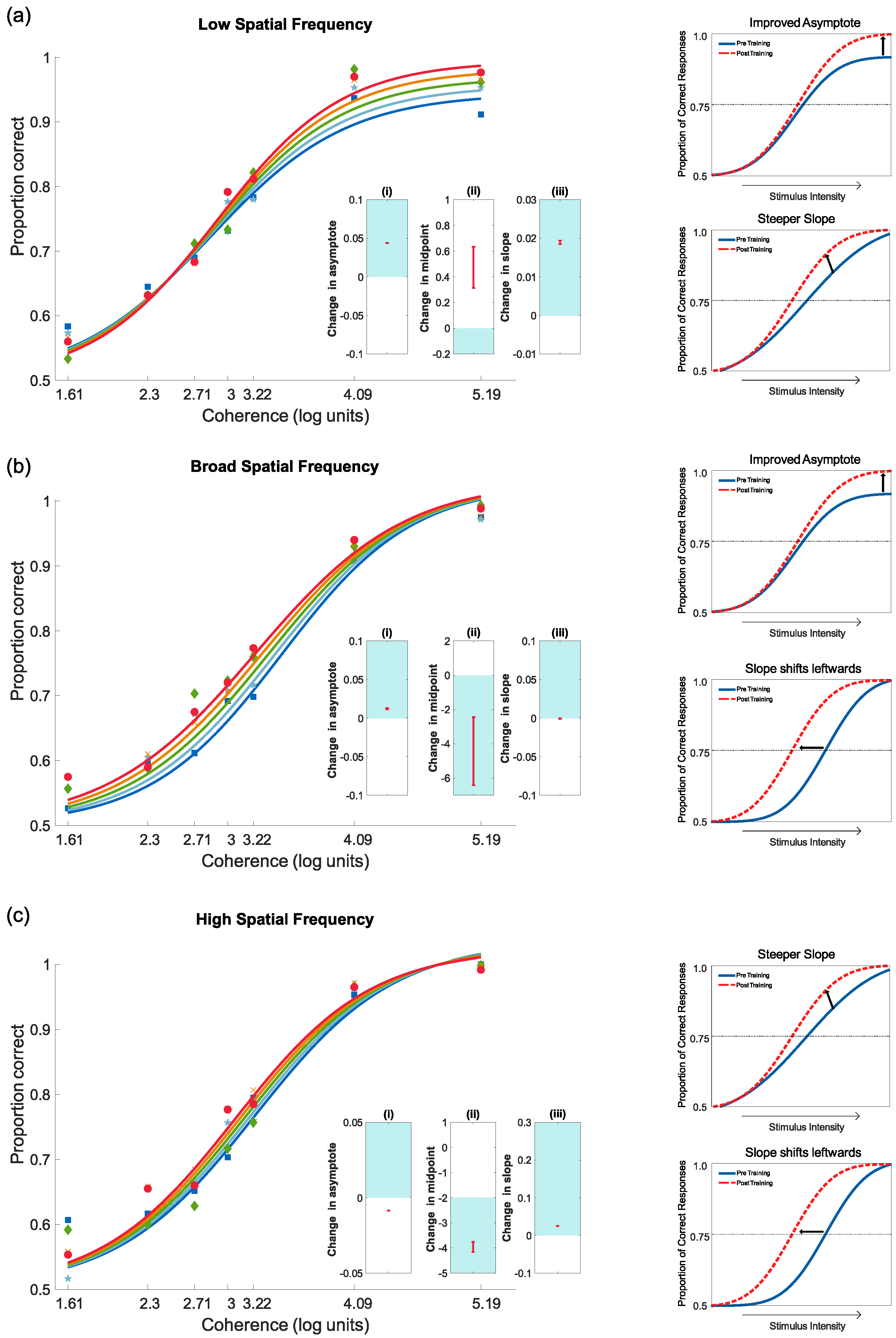
4.3. Feedback and Perceptual Learning: Experiment 2
4.3.1. Training Results
4.3.2. Pre- and Post-Test Results for Motion Coherence
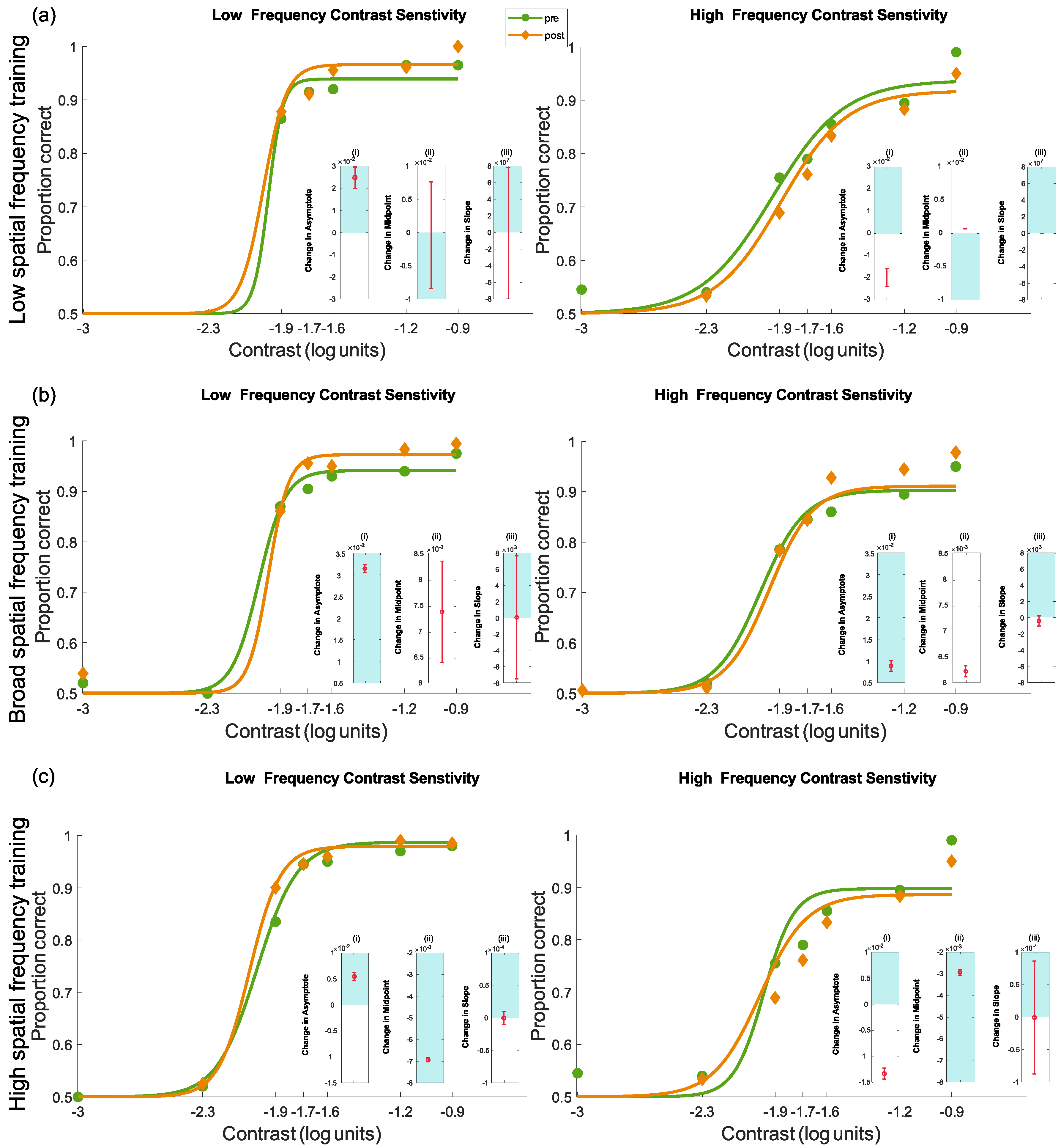
4.3.3. Pre- and Post-Test Results for Contrast Sensitivity
5. Discussion
Main Findings
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Campana, G.; Maniglia, M. Editorial: Improving visual deficits with perceptual learning. Front. Psychol. 2015, 6, 491. [Google Scholar] [CrossRef] [PubMed]
- Tan, D.T.; Fong, A. Efficacy of neural vision therapy to enhance contrast sensitivity function and visual acuity in low myopia. J. Cataract Refract. Surg. 2008, 34, 570–577. [Google Scholar] [CrossRef]
- Camilleri, R.; Pavan, A.; Ghin, F.; Battaglini, L.; Campana, G. Improvement of uncorrected visual acuity (UCVA) and contrast sensitivity (UCCS) with perceptual learning and transcranial random noise stimulation (tRNS) in individuals with mild myopia. Front. Psychol. 2014, 5, 1234. [Google Scholar] [CrossRef] [PubMed]
- Camilleri, R.; Pavan, A.; Ghin, F.; Campana, G. Improving myopia via perceptual learning: Is training with lateral masking the only (or the most) efficacious technique? Atten. Percept. Psychophys. 2014, 76, 2485–2494. [Google Scholar] [CrossRef] [PubMed]
- Camilleri, R.; Pavan, A.; Campana, G. The application of online transcranial random noise stimulation and perceptual learning in the improvement of visual functions in mild myopia. Neuropsychologia 2016, 89, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Hess, R.F.; Hayes, A.; Field, D.J. Contour integration and cortical processing. J. Physiol. Paris 2003, 97, 105–119. [Google Scholar] [CrossRef] [PubMed]
- Levi, D.M.; Li, R.W. Perceptual learning as a potential treatment for amblyopia: A mini-review. Vis. Res. 2009, 49, 2535–2549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polat, U. Making perceptual learning practical to improve visual functions. Vis. Res. 2009, 49, 2566–2573. [Google Scholar] [CrossRef] [Green Version]
- Huxlin, K.R.; Martin, T.; Kelly, K.; Riley, M.; Friedman, D.I.; Burgin, W.S.; Hayhoe, M. Perceptual relearning of complex visual motion after V1 damage in humans. J. Neurosci. 2009, 29, 3981–3991. [Google Scholar] [CrossRef] [PubMed]
- Sahraie, A.; Trevethan, C.T.; MacLeod, M.J.; Murray, A.D.; Olson, J.A.; Weiskrantz, L. Increased sensitivity after repeated stimulation of residual spatial channels in blindsight. Proc. Natl. Acad. Sci. USA 2006, 103, 14971–14976. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trevethan, C.T.; Urquhart, J.; Ward, R.; Gentleman, D.; Sahraie, A. Evidence for perceptual learning with repeated stimulation after partial and total cortical blindness. Adv. Cogn. Psychol. 2012, 8, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Sagi, D. Perceptual learning in Vision Research. Vis. Res. 2011, 51, 1552–1566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seitz, A.R.; Watanabe, T. A unified model for perceptual learning. Trends Cogn. Sci. 2005, 9, 329–334. [Google Scholar] [CrossRef] [PubMed]
- Fahle, M. Perceptual learning: Specificity versus generalization. Curr. Opin. Neurobiol. 2005, 15, 154–160. [Google Scholar] [CrossRef] [PubMed]
- Ahissar, M.; Hochstein, S. Task difficulty and the specificity of perceptual learning. Lett. Nat. 1997, 387, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Fiorentini, A.; Berardi, N. Perceptual learning specific for orientation and spatial frequency. Nature 1980, 287, 43–44. [Google Scholar] [CrossRef] [PubMed]
- Karni, A.; Sagi, D. Where practice makes perfect in texture discrimination: Evidence for primary visual cortex plasticity. Proc. Natl. Acad. Sci. USA 1991, 88, 4966–4970. [Google Scholar] [CrossRef]
- Ball, K.; Sekuler, R. A specific and enduring improvement in visual motion discrimination. Science 1982, 218, 697–698. [Google Scholar] [CrossRef]
- Lu, Z.L.; Hua, T.; Huang, C.B.; Zhou, Y.; Dosher, B.A. Visual perceptual learning. Neurobiol. Learn. Mem. 2011, 95, 145–151. [Google Scholar] [CrossRef]
- Fahle, M. Specificity of learning curvature, orientation, and vernier discriminations. Vis. Res. 1997, 37, 1885–1895. [Google Scholar] [CrossRef] [Green Version]
- Schoups, A.A.; Vogels, R.; Orban, G.A. Human perceptual learning in identifying the oblique orientation: Retinotopy, orientation specificity and monocularity. J. Physiol. 1995, 483, 797–810. [Google Scholar] [CrossRef] [PubMed]
- Campana, G.; Casco, C. Learning in combined-feature search: Specificity to orientation. Percept. Psychophys. 2003, 65, 1197–1207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sowden, P.T.; Rose, D.; Davies, I.R.L. Perceptual learning of luminance contrast detection: Specific for spatial frequency and retinal location but not orientation. Vis. Res. 2002, 42, 1249–1258. [Google Scholar] [CrossRef]
- Fahle, M.; Edelman, S. Long-term learning in vernier acuity: Effects of stimulus orientation, range and of feedback. Vis. Res. 1993, 33, 397–412. [Google Scholar] [CrossRef]
- Fahle, M.; Edelman, S.; Poggio, T. Fast perceptual learning in hyperacuity. Vis. Res. 1995, 35, 3003–3013. [Google Scholar] [CrossRef] [Green Version]
- Poggio, T.; Fahle, M.; Edelman, S. Fast perceptual learning in visual hyperacuity. Science 1992, 256, 1018–1021. [Google Scholar] [CrossRef] [Green Version]
- Shiu, L.P.; Pashler, H. Improvement in line orientation discrimination is retinally local but dependent on cognitive set. Percept. Psychophys. 1992, 52, 582–588. [Google Scholar] [CrossRef]
- DeValois, R.L.; Albrecht, D.G.; Thonrell, L.G. Spatial Frequency Selectivity of Cells in Macaque Visual Cortex. Vis. Res. 1982, 22, 545–559. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106–154. [Google Scholar] [CrossRef]
- Movshon, J.A.; Thompson, I.D.; Tolhurst, D.J. Spatial and temporal contrast sensitivity of neurones in areas 17 and 18 of the cat visual cortex. J. Physiol. 1978, 283, 101–120. [Google Scholar] [CrossRef]
- Livingstone, M.; Hubel, D.H. Segregation of Form, Color, Movement, and Depth: Anatomy, Physiology, and Perception. Science 1988, 240, 740–749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Movshon, J.A.; Newsome, W.T. Visual response properties of striate cortical neurons projecting to area MT in macaque monkeys. J. Neurosci. 1996, 16, 7733–7741. [Google Scholar] [CrossRef] [PubMed]
- Furlan, M.; Smith, A.T. Global Motion Processing in Human Visual Cortical Areas V2 and V3. J. Neurosci. 2016, 36, 7314–7324. [Google Scholar] [CrossRef] [PubMed]
- Lamme, V.A.F. Recurrent corticocortical interactions in neural disease. Arch. Neurol. 2003, 60, 178–184. [Google Scholar] [CrossRef] [PubMed]
- Simoncelli, E.P.; Heeger, D.J. A Model of Neuronal Responses in Visual Area MT. Vis. Res. 1998, 38, 743–761. [Google Scholar] [CrossRef]
- Levi, A.; Shaked, D.; Tadin, D.; Huxlin, K.R. Is improved contrast sensitivity a natural consequence of visual training? J. Vis. 2015, 14, 1158. [Google Scholar] [CrossRef]
- Ball, K.; Sekuler, R. Direction-specific improvement in motion discrimination. Vis. Res. 1987, 27, 953–965. [Google Scholar] [CrossRef]
- McGovern, D.P.; Webb, B.S.; Peirce, J.W. Transfer of perceptual learning between different visual tasks. J. Vis. 2012, 12, 4. [Google Scholar] [CrossRef]
- Garcia, A.; Kuai, S.G.; Kourtzi, Z. Differences in the time course of learning for hard compared to easy training. Front. Psychol. 2013, 4, 110. [Google Scholar] [CrossRef]
- Felleman, D.J.; Van Essen, D.C. Receptive field properties of neurons in area V3 of macaque monkey extrastriate cortex. J. Neurophysiol. 1987, 57, 889–920. [Google Scholar] [CrossRef] [Green Version]
- Hubel, D.H.; Wiesel, T.N. Receptive fields and functional acrhitecture in two nonstriate visual areas (18 and 19) of the cat. J. Neurophysiol. 1965, 28, 229–289. [Google Scholar] [CrossRef] [PubMed]
- Mikami, A.; Newsome, W.T.; Wurtz, R.H. Motion selectivity in macaque visual cortex. II. Spatiotemporal range of directional interactions in MT and V1. J. Neurophysiol. 1986, 55, 1328–1339. [Google Scholar] [CrossRef] [PubMed]
- Sillito, A.M.; Cudeiro, J.; Jones, H.E. Always returning: Feedback and sensory processing in visual cortex and thalamus. Trends Neurosci. 2006, 29, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Zeki, S. Functional organization of a visual area in the posterior bank of the superior temporal sulcus of the rhesus monkey. J. Physiol. 1974, 236, 549–573. [Google Scholar] [CrossRef] [PubMed]
- Amano, K.; Edwards, M.; Badcock, D.R.; Nishida, S. Spatial-frequency tuning in the pooling of one- and two-dimensional motion signals. Vis. Res. 2009, 49, 2862–2869. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bex, P.J.; Dakin, S.C. Comparison of the spatial-frequency selectivity of local and global motion detectors. J. Opt. Soc. Am. 2002, 19, 670–677. [Google Scholar] [CrossRef] [PubMed]
- Burr, D.; Thompson, P. Motion psychophysics: 1985–2010. Vis. Res. 2011, 51, 1431–1456. [Google Scholar] [CrossRef]
- Gilbert, C.D.; Sigman, M.; Crist, R.E. The Neural Basis of Perceptual Learning Review. Neuron 2001, 31, 681–697. [Google Scholar] [CrossRef]
- Nishida, S. Advancement of motion psychophysics: Review 2001–2010. J. Vis. 2011, 11, 11. [Google Scholar] [CrossRef]
- Sincich, L.C.; Horton, J.C. The Circutrly of V1 and V2: Integration of Color, Form, and Motion. Annu. Rev. Neurosci. 2005, 28, 303–326. [Google Scholar] [CrossRef]
- Rockland, K.S.; Knutson, T. Feedback Connections From Area Mt Of The Squirrel-Monkey To Areas V1 And V2. J. Comp. Neurol. 2000, 425, 345–368. [Google Scholar] [CrossRef]
- Pascual-Leone, A.; Walsh, V. Fast Backprojections from the Motion to the Primary Visual Area Necessary for Visual Awareness. Science 2001, 292, 510–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silvanto, J.; Cowey, A.; Lavie, N.; Walsh, V. Striate cortex (V1) activity gates awareness of motion. Nat. Neurosci. 2005, 8, 143–144. [Google Scholar] [CrossRef] [PubMed]
- Romei, V.; Chiappini, E.; Hibbard, P.B.; Avenanti, A. Empowering Reentrant Projections from V5 to V1 Boosts Sensitivity to Motion. Curr. Biol. 2016, 26, 2155–2160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hochstein, S.; Ahissar, M. Hierarchies and reverse hierarchies in the Visual System. Neuron 2002, 36, 791–804. [Google Scholar] [CrossRef]
- Ahissar, M.; Hochstein, S. The reverse hierarchy theory of visual perceptual learning. Trends Cogn. Sci. 2004, 8, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Adelson, E.H.; Movshon, J.A. Phenomenal coherence of moving visual patterns. Nature 1982, 300, 523–525. [Google Scholar] [CrossRef]
- Wilson, H.R.; Ferrera, V.P.; Yo, C. A Psychophysically Motivated Model for 2-Dimensional Motion Perception. Vis. Neurosci. 1992, 9, 79–97. [Google Scholar] [CrossRef] [PubMed]
- An, X.; Gong, H.; Qian, L.; Wang, X.; Pan, Y.; Zhang, X.; Yang, Y.; Wang, W. Distinct Functional Organizations for Processing Different Motion Signals in V1, V2, and V4 of Macaque. J. Neurosci. 2012, 32, 13363–13379. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Zhu, S.; Chen, M.; Han, C.; Xu, H.; Hu, J.; Fang, Y.; Lu, H.D. A Motion direction preference map in monkey V4. Neuron 2013, 78, 376–388. [Google Scholar] [CrossRef]
- Newsome, W.T.; Britten, K.H.; Movshon, J.A. Neuronal correlates of a perceptual decision. Nature 1989, 341, 52–54. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, K.; Pasternak, T. Transient and permanent deficits in motion perception after lesions of cortical areas MT and MST in the macaque monkey. Cereb. Cortex 1999, 9, 90–100. [Google Scholar] [CrossRef] [PubMed]
- Britten, K.H.; Shadlen, M.N.; Newsome, W.T.; Movshon, J.A. The analysis of visual motion: A comparison of neuronal and psychophysical performance. J. Neurosci. 1992, 12, 4745–4765. [Google Scholar] [CrossRef] [PubMed]
- Newsome, W.T.; Park, B.; York, N.; Brook, S. A Selective Impairment of Motion Perception Following Lesions of the Middle Temporal Visual Area (MT). J. Neurosci. 1988, 8, 2201–2211. [Google Scholar] [CrossRef] [PubMed]
- Rees, G.; Friston, K.; Koch, C. A direct quantitative relationship between the functional properties of human and macaque V5. Nat. Neurosci. 2000, 3, 716–723. [Google Scholar] [CrossRef] [PubMed]
- Braddick, O.J. Segmentation versus integration in visual motion processing. Trends Neurosci. 1993, 16, 263–268. [Google Scholar] [CrossRef]
- Cowey, A.; Campana, G.; Walsh, V.; Vaina, L.M. The role of human extra-striate visual areas V5/MT and V2/V3 in the perception of the direction of global motion: A transcranial magnetic stimulation study. Exp. Brain Res. 2006, 171, 558–562. [Google Scholar] [CrossRef]
- Hedges, J.H.; Gartshteyn, Y.; Kohn, A.; Rust, N.C.; Shadlen, M.N.; Newsome, W.T.; Movshon, J.A. Dissociation of neuronal and psychophysical responses to local and global motion. Curr. Biol. 2011, 21, 2023–2028. [Google Scholar] [CrossRef]
- Lui, L.L.; Bourne, J.A.; Rosa, M.G.P. Spatial and temporal frequency selectivity of neurons in the middle temporal visual area of new world monkeys (Callithrix jacchus). Eur. J. Neurosci. 2007, 25, 1780–1792. [Google Scholar] [CrossRef]
- Pasternak, T.; Merigan, W.H. Motion Perception following Lesions of the Superior Temporal Sulcus in the Monkey. Cereb. Cortex 1994, 4, 247–259. [Google Scholar] [CrossRef]
- Vaina, L.M.; Sundareswaran, V.; Harris, J.G. Learning to ignore: Psychophysics and computational modeling of fast learning of direction in noisy motion stimuli. Cogn. Brain Res. 1995, 2, 155–163. [Google Scholar] [CrossRef]
- Dakin, S.C.; Mareschal, I.; Bex, P.J. Local and global limitations on direction integration assessed using equivalent noise analysis. Vis. Res. 2005, 45, 3027–3049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tibber, M.S.; Kelly, M.G.; Jansari, A.; Dakin, S.C.; Shepherd, A.J. An inability to exclude visual noise in migraine. Investig. Ophthalmol. Vis. Sci. 2014, 55, 2539–2546. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.W.; Sekuler, R. Coherent global motion percepts from stochastic local motions. Vis. Res. 1984, 24, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Scarfe, P.; Glennerster, A. Humans Use Predictive Kinematic Models to Calibrate Visual Cues to Three-Dimensional Surface Slant. J. Neurosci. 2014, 34, 10394–10401. [Google Scholar] [CrossRef] [PubMed]
- Shibata, K.; Yamagishi, N.; Ishii, S.; Kawato, M. Boosting perceptual learning by fake feedback. Vis. Res. 2009, 49, 2574–2585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herzog, M.H.; Aberg, K.C.; Frémaux, N.; Gerstner, W.; Sprekeler, H. Perceptual learning, roving and the unsupervised bias. Vis. Res. 2012, 61, 95–99. [Google Scholar] [CrossRef]
- Herzog, M.H.; Fahle, M. A recurrent model for perceptual learning. J. Opt. Technol. 1999, 66, 836. [Google Scholar] [CrossRef]
- Herzog, M.H.; Fahle, M. The Role of Feedback in Learning a Vernier Discrimination Task. Vis. Res. 1997, 37, 2133–2141. [Google Scholar] [CrossRef]
- Maniglia, M.; Pavan, A.; Sato, G.; Contemori, G.; Montemurro, S.; Battaglini, L.; Casco, C. Perceptual learning leads to long lasting visual improvement in patients with central vision loss. Restor. Neurol. Neurosci. 2016, 34, 697–720. [Google Scholar] [CrossRef] [Green Version]
- Dobres, J.; Watanabe, T. Response feedback triggers long-term consolidation of perceptual learning independently of performance gains. J. Vis. 2012, 12, 9. [Google Scholar] [CrossRef] [PubMed]
- Seitz, A.R.; Nanez, J.E.; Holloway, S.; Tsushima, Y.; Watanabe, T. Two cases requiring external reinforcement in perceptual learning. J. Vis. 2006, 6, 9. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lu, Z.L.; Dosher, B.A. Mixed training at high and low accuracy levels leads to perceptual learning without feedback. Vis. Res. 2012, 61, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Petrov, A.A.; Dosher, B.A.; Lu, Z.L. The dynamics of perceptual learning: An incremental reweighting model. Psychol. Rev. 2005, 112, 715–743. [Google Scholar] [CrossRef] [PubMed]
- Vaina, L.M.; Belliveau, J.W.; des Roziers, E.B.; Zeffiro, T.A. Neural systems underlying learning and representation of global motion. Proc. Natl. Acad. Sci. USA 1998, 95, 12657–12662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petrov, A.A.; Dosher, B.A.; Lu, Z.L. Perceptual learning without feedback in non-stationary contexts: Data and model. Vis. Res. 2006, 46, 3177–3197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brainard, D.H. The psychophysics toolbox. Spat. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef] [PubMed]
- Kleiner, M.; Brainard, D.; Pelli, D.; Ingling, A.; Murray, R.; Broussard, C. What’s new in Psychtoolbox-3. Perception 2007, 36, 1–16. [Google Scholar] [CrossRef]
- Pelli, D.G. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spat. Vis. 1997, 10, 437–442. [Google Scholar] [CrossRef]
- Moscatelli, A.; Mezzetti, M.; Lacquaniti, F. Modeling psychophysical data at the population-level: The generalized linear mixed model. J. Vis. 2012, 12, 26. [Google Scholar] [CrossRef]
- Agresti, A. Categorical Data Analysis, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Gold, J.I.; Law, C.T.; Connolly, P.; Bennur, S. Relationships Between the Threshold and Slope of Psychometric and Neurometric Functions During Perceptual Learning: Implications for Neuronal Pooling. J. Neurophysiol. 2010, 103, 140–154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swanson, W.H.; Birch, E.E. Extracting thresholds from noisy psychophysical data. Percept. Psychophys. 1992, 51, 409–422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ling, S.; Carrasco, M. Sustained and transient covert attention enhance the signal via different contrast response functions. Vis. Res. 2006, 46, 1210–1220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herrmann, K.; Montaser-Kouhsari, L.; Carrasco, M.; Heeger, D.J. When size matters: Attention affects performance by contrast or response gain. Nat. Neurosci. 2010, 13, 1554–1561. [Google Scholar] [CrossRef] [PubMed]
- Donovan, I.; Carrasco, M. Exogenous attention facilitates location transfer of perceptual learning. J. Vis. 2015, 15, 1–16. [Google Scholar] [CrossRef]
- Reynolds, J.H.; Heeger, D.J. The Normalization Model of Attention. Neuron 2009, 61, 168–185. [Google Scholar] [CrossRef] [Green Version]
- Zylberberg, A.; Roelfsema, P.R.; Sigman, M. Variance misperception explains illusions of confidence in simple perceptual decisions. Conscious. Cogn. 2014, 27, 246–253. [Google Scholar] [CrossRef]
- Talluri, B.C.; Hung, S.C.; Seitz, A.R.; Seriès, P. Confidence-based integrated reweighting model of task-difficulty explains location-based specificity in perceptual learning. J. Vis. 2015, 15, 17. [Google Scholar] [CrossRef]
- Chiappini, E.; Silvanto, J.; Hibbard, P.B.; Avenanti, A.; Romei, V. Strengthening functionally specific neural pathways with transcranial brain stimulation. Curr. Biol. 2018, 28, R735–R736. [Google Scholar] [CrossRef] [Green Version]
- Fertonani, A.; Pirulli, C.; Miniussi, C. Random Noise Stimulation Improves Neuroplasticity in Perceptual Learning. J. Neurosci. 2011, 31, 15416–15423. [Google Scholar] [CrossRef] [Green Version]
- Campana, G.; Camilleri, R.; Pavan, A.; Veronese, A.; Giudice, G.L. Improving visual functions in adult amblyopia with combined perceptual training and transcranial random noise stimulation (tRNS): A pilot study. Front. Psychol. 2014, 5, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Moret, B.; Camilleri, R.; Pavan, A.; Lo Giudice, G.; Veronese, A.; Rizzo, R.; Campana, G. Differential effects of high-frequency transcranial random noise stimulation (hf-tRNS) on contrast sensitivity and visual acuity when combined with a short perceptual training in adults with amblyopia. Neuropsychologia 2018, 114, 125–133. [Google Scholar] [CrossRef] [PubMed]
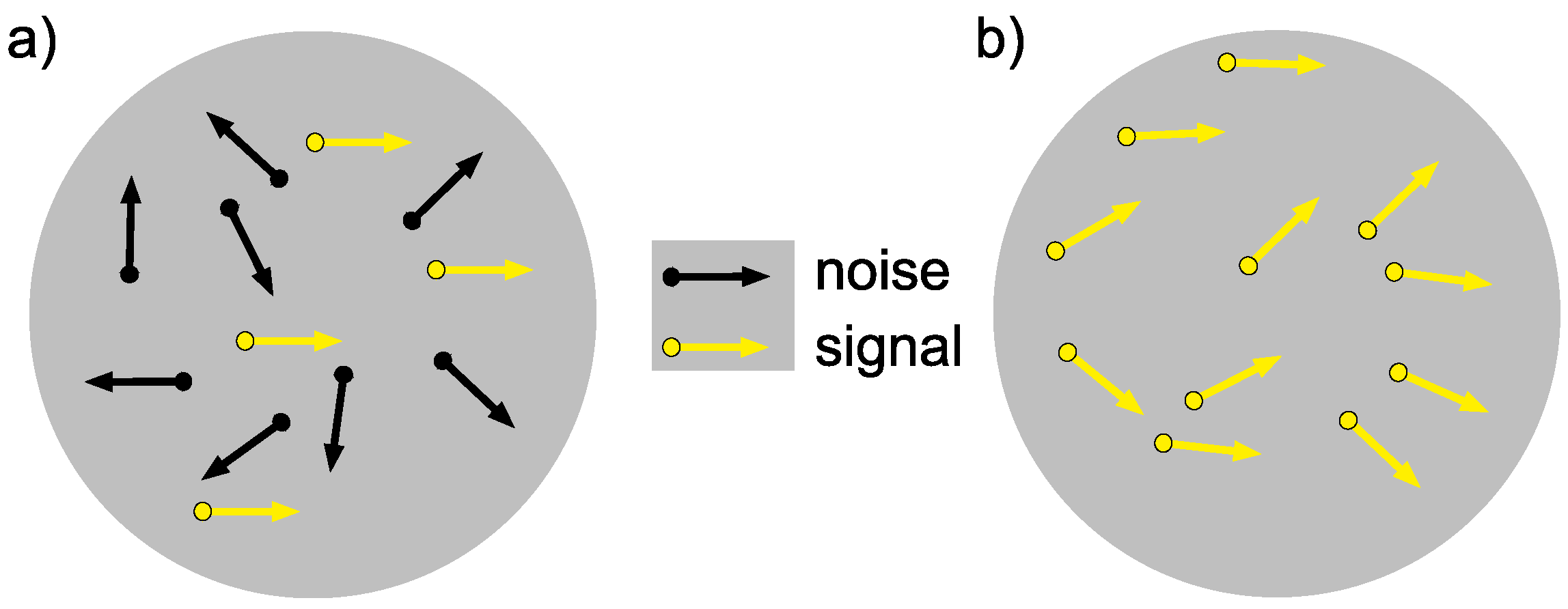
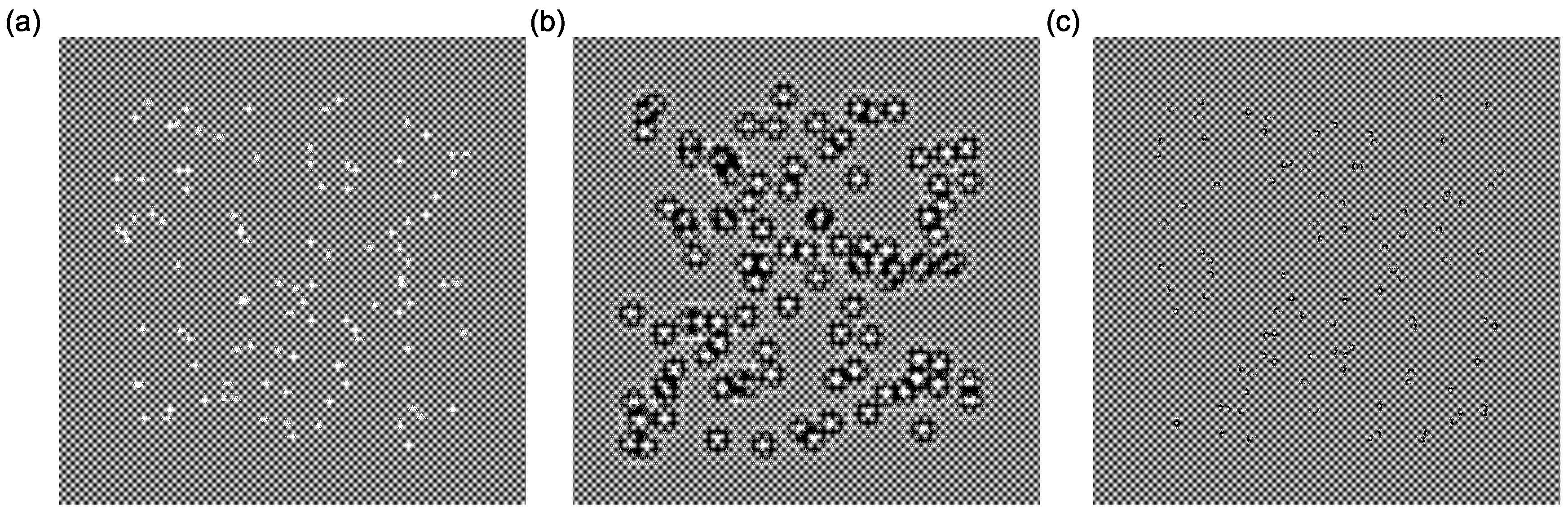
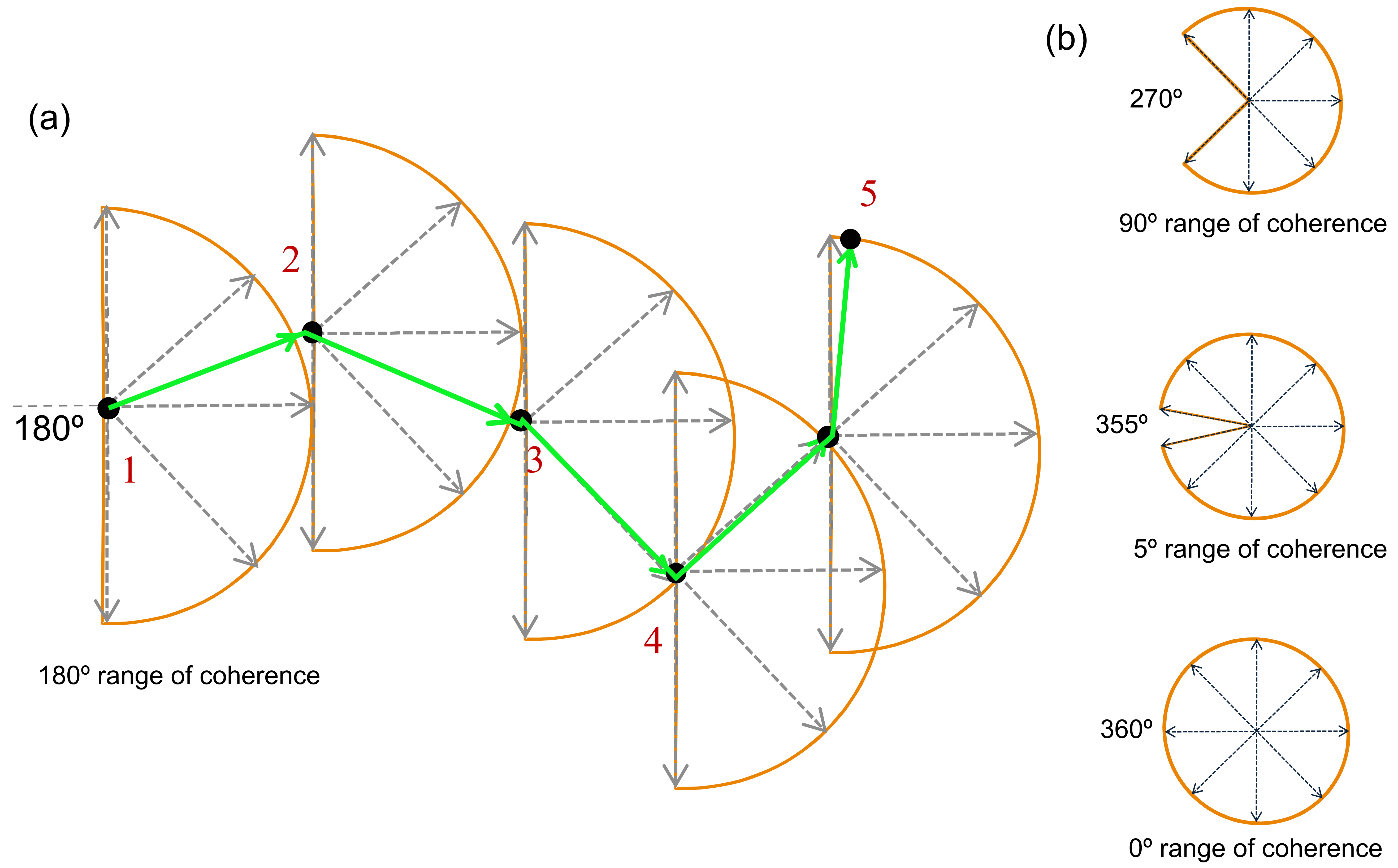

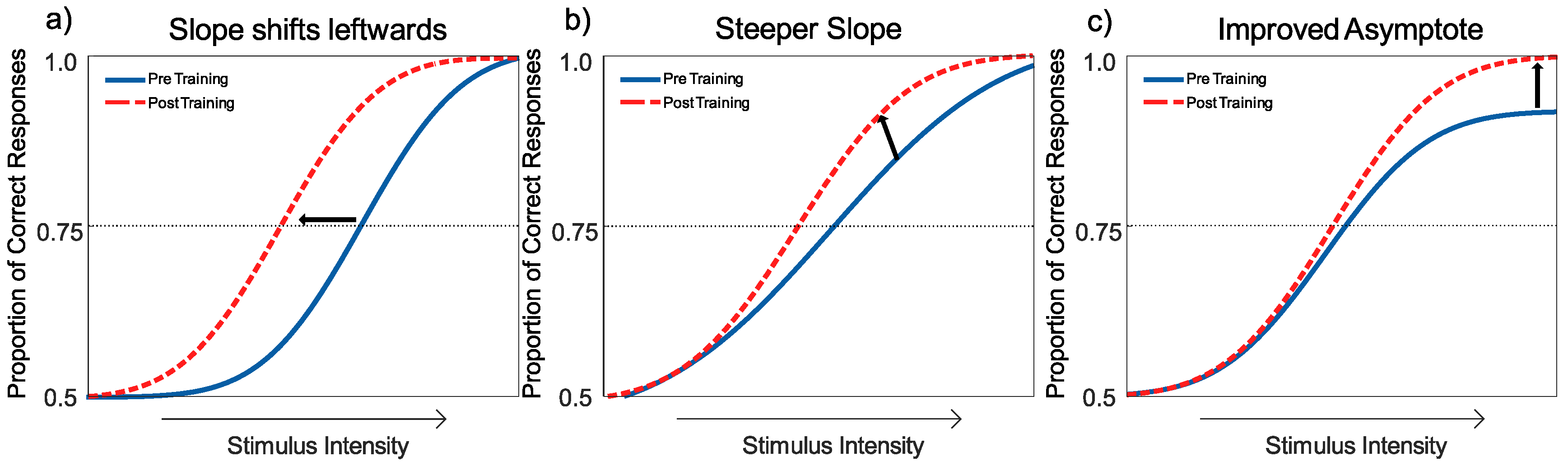
| Coherence ° | Accuracy (%) |
|---|---|
| 180 | 98.1 |
| 60 | 96.0 |
| 25 | 80.4 |
| 20 | 77.7 |
| 15 | 73.5 |
| 10 | 64.1 |
| 5 | 61.5 |
| Feedback Condition | −2LL | ΔDOF | p |
|---|---|---|---|
| Feedback | 1528.96 | 10 | <0.0001 |
| No Feedback | 1428.24 | 10 | <0.0001 |
| Training Frequency | −2LL | ΔDOF | p |
|---|---|---|---|
| Low | 641.53 | 10 | <0.0001 |
| Broad | 618.32 | 10 | <0.0001 |
| High | 765.47 | 10 | <0.0001 |
| Training Frequency | Tested Frequency | −2LL | ΔDOF | p |
|---|---|---|---|---|
| Low | Low | 123.29 | 10 | <0.0001 |
| Low | Broad | 146.17 | 10 | <0.0001 |
| Low | High | 176.96 | 10 | <0.0001 |
| Broad | Low | 161.96 | 10 | <0.0001 |
| Broad | Broad | 158.93 | 10 | <0.0001 |
| Broad | High | 168.91 | 10 | <0.0001 |
| High | Low | 98.04 | 10 | <0.0001 |
| High | Broad | 207.56 | 10 | <0.0001 |
| High | High | 197.53 | 10 | <0.0001 |
| Training Frequency | Tested Frequency | −2LL | ΔDOF | p |
|---|---|---|---|---|
| Low | Low | 234.87 | 8 | <0.0001 |
| Low | High | 161.14 | 8 | <0.0001 |
| Broad | Low | 268.60 | 8 | <0.0001 |
| Broad | High | 206.31 | 8 | <0.0001 |
| High | Low | 276.63 | 8 | <0.0001 |
| High | High | 209.01 | 8 | <0.0001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asher, J.M.; Romei, V.; Hibbard, P.B. Spatial Frequency Tuning and Transfer of Perceptual Learning for Motion Coherence Reflects the Tuning Properties of Global Motion Processing. Vision 2019, 3, 44. https://doi.org/10.3390/vision3030044
Asher JM, Romei V, Hibbard PB. Spatial Frequency Tuning and Transfer of Perceptual Learning for Motion Coherence Reflects the Tuning Properties of Global Motion Processing. Vision. 2019; 3(3):44. https://doi.org/10.3390/vision3030044
Chicago/Turabian StyleAsher, Jordi M., Vincenzo Romei, and Paul B. Hibbard. 2019. "Spatial Frequency Tuning and Transfer of Perceptual Learning for Motion Coherence Reflects the Tuning Properties of Global Motion Processing" Vision 3, no. 3: 44. https://doi.org/10.3390/vision3030044
APA StyleAsher, J. M., Romei, V., & Hibbard, P. B. (2019). Spatial Frequency Tuning and Transfer of Perceptual Learning for Motion Coherence Reflects the Tuning Properties of Global Motion Processing. Vision, 3(3), 44. https://doi.org/10.3390/vision3030044







