Distinguishing Hemodynamics from Function in the Human LGN Using a Temporal Response Model
Abstract
1. Introduction
2. Experimental Procedures
2.1. Subjects
2.2. Display Hardware
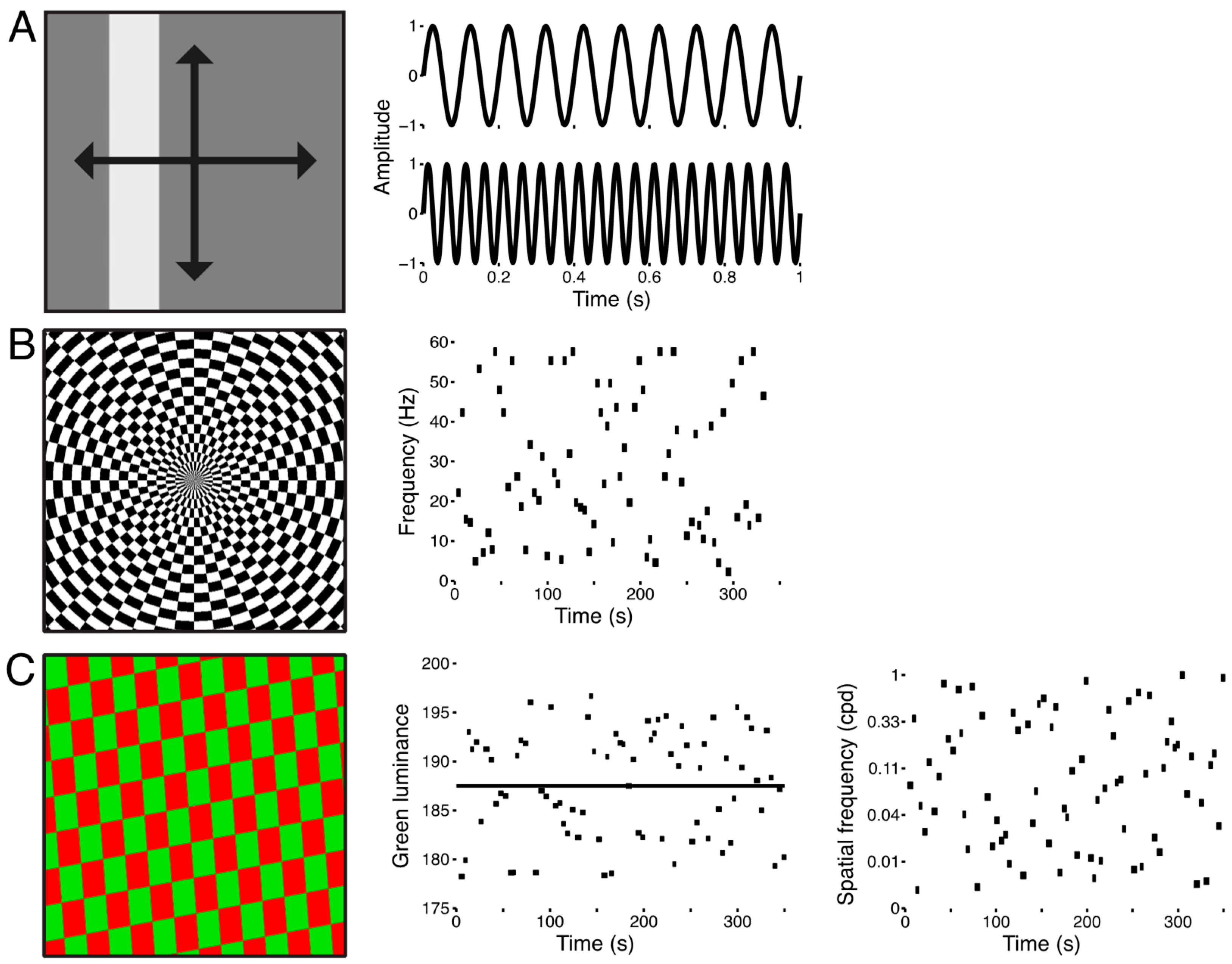
2.3. Visual Stimuli and Procedure
2.4. Data Acquisition
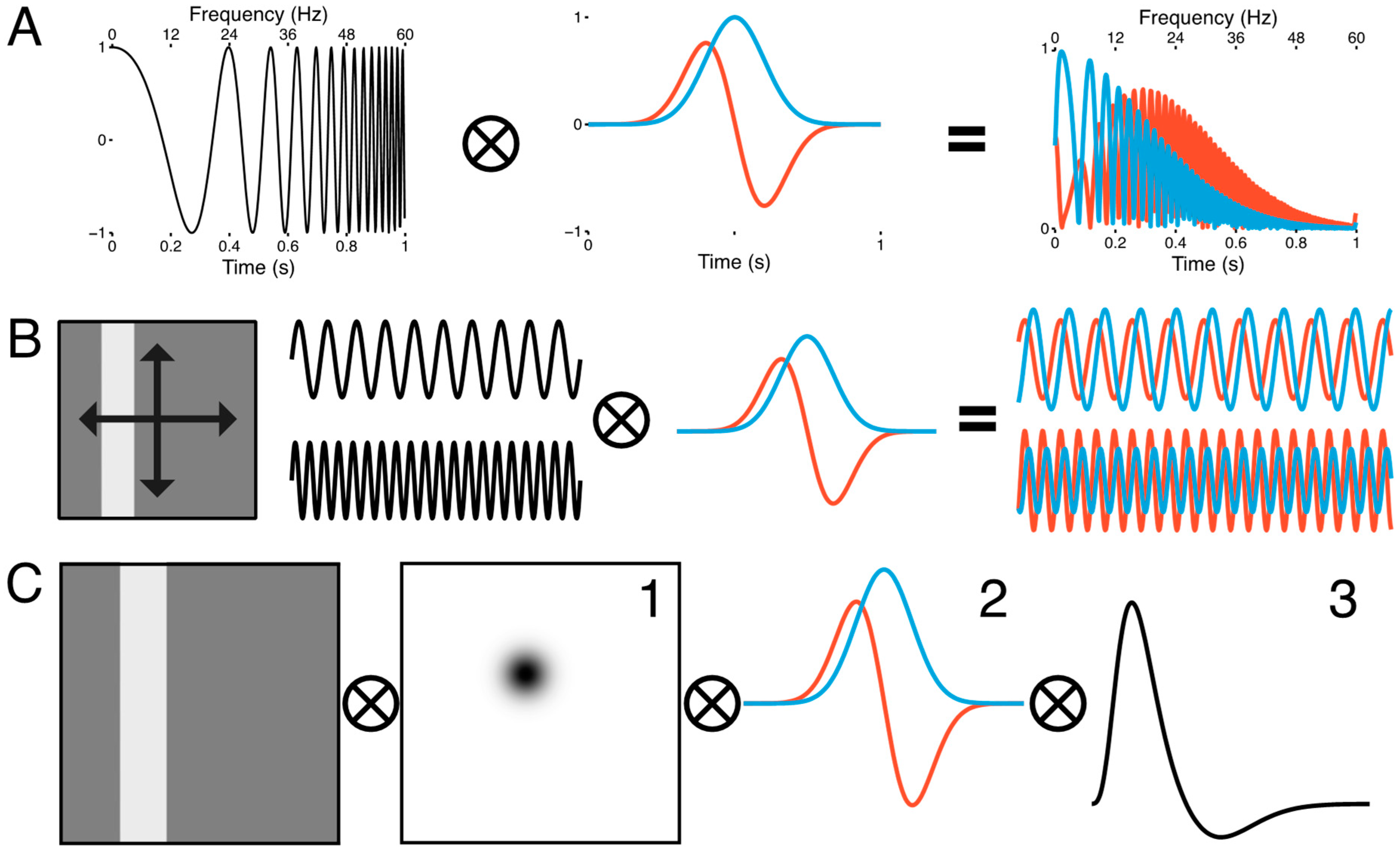
2.5. Population Receptive Field Estimation
2.6. Model-Free Functional Segmentation of the LGN
3. Results
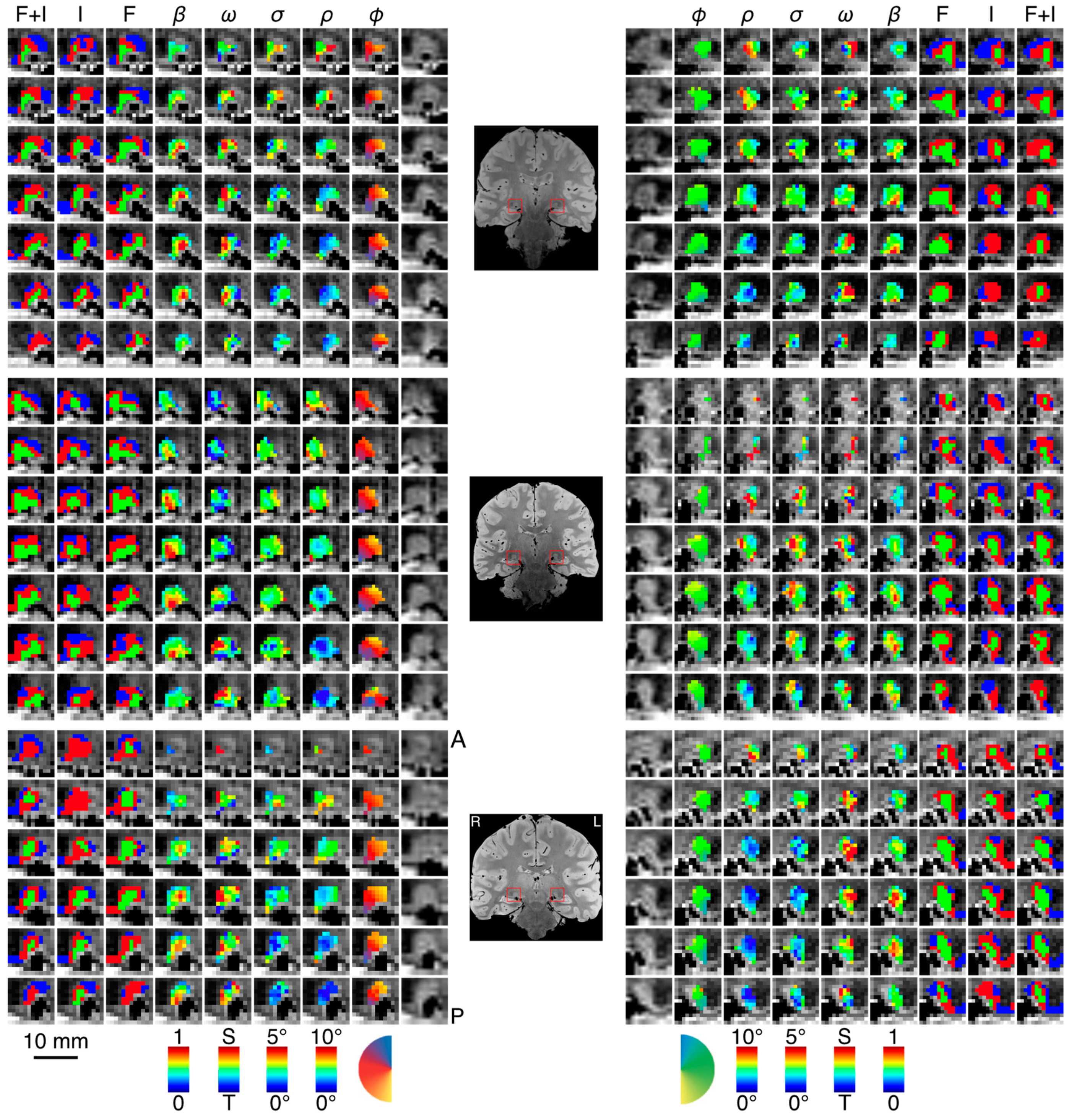
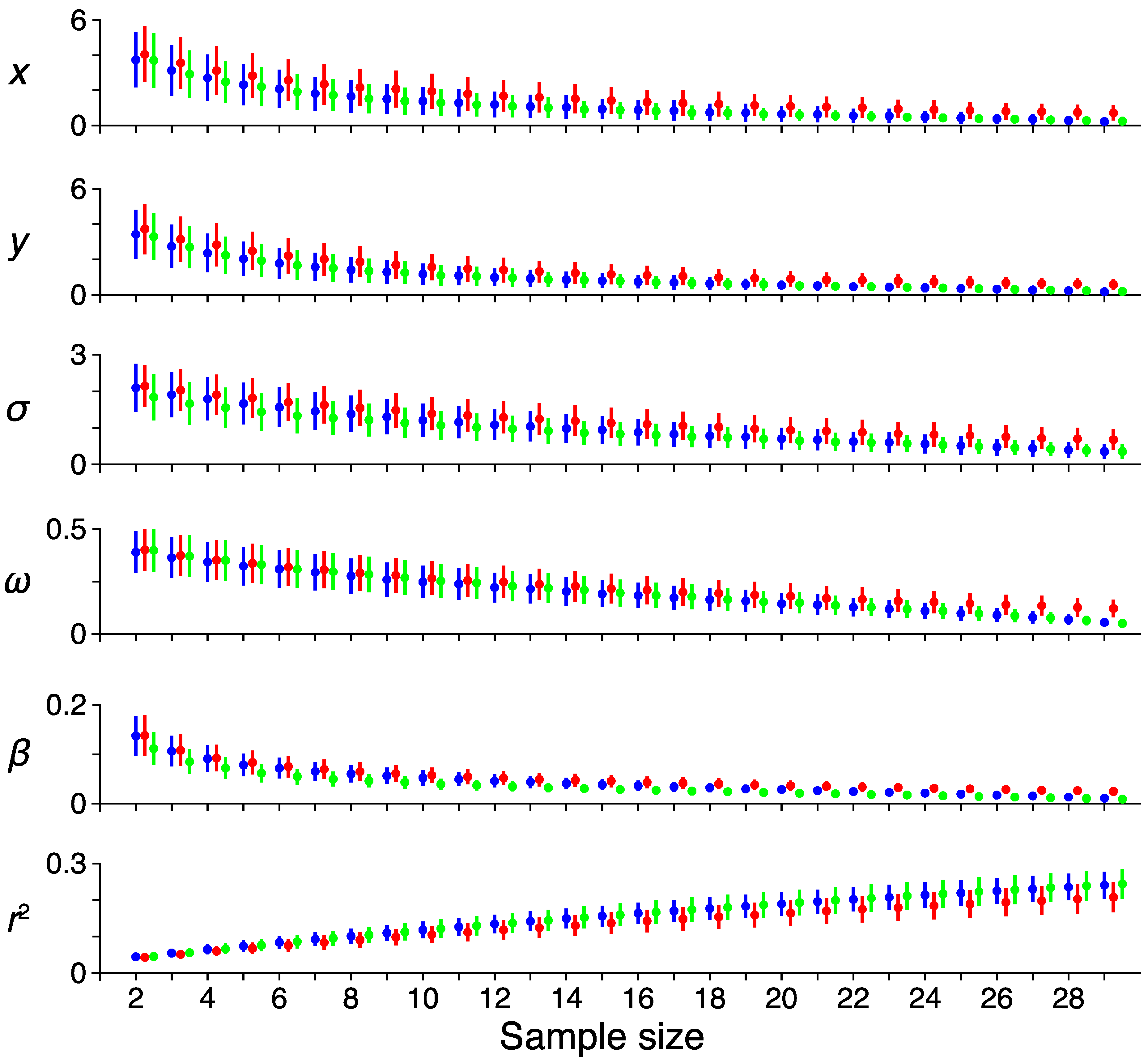
3.1. Spatiotemporal pRF Model Estimates
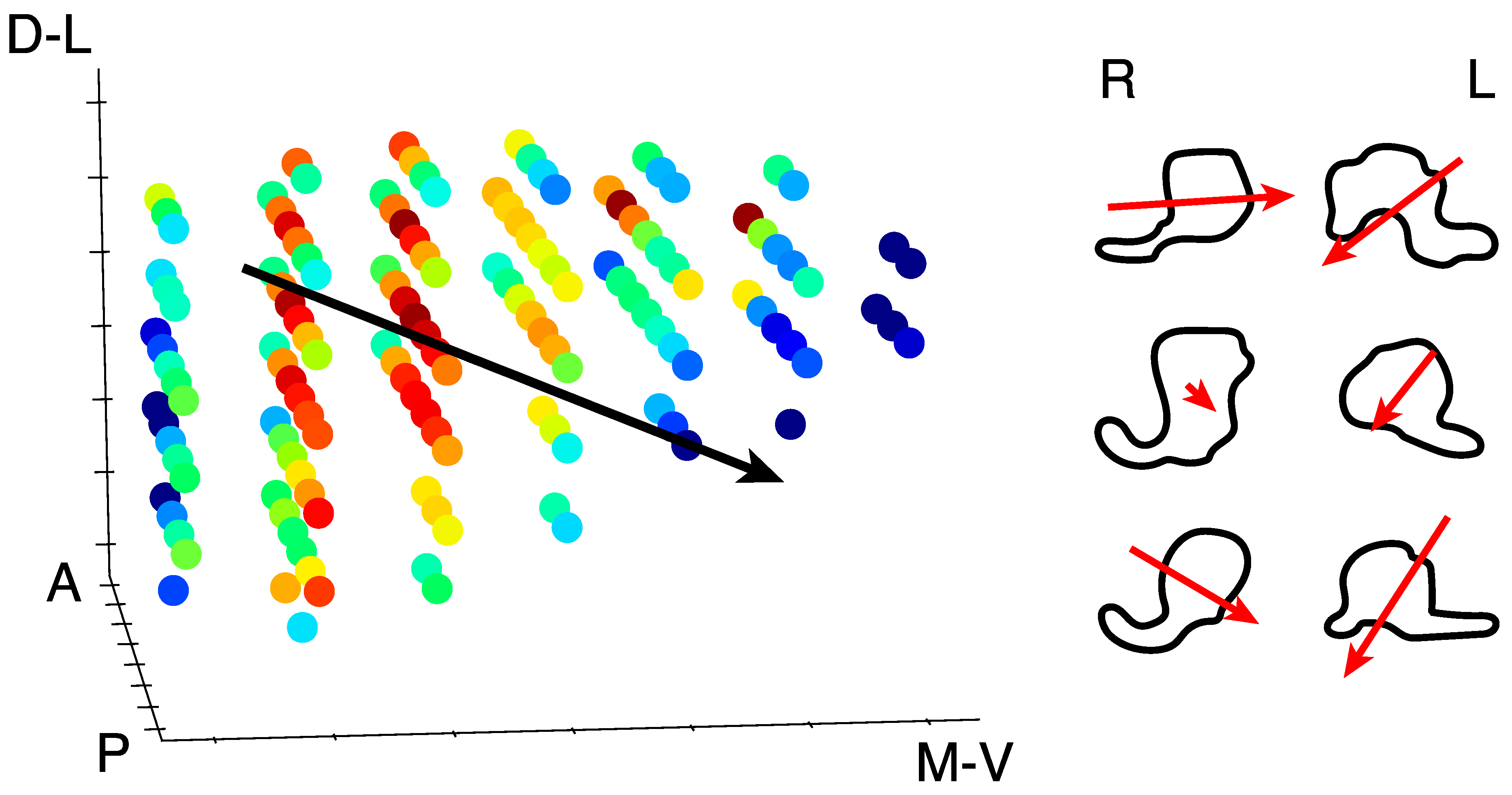
3.2. Model-Free Data-Driven Segmentation of the LGN
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- DeSimone, K.; Viviano, J.D.; Schneider, K.A. Population receptive field estimation reveals new retinotopic maps in human subcortex. J. Neurosci. 2015, 35, 9836–9847. [Google Scholar] [CrossRef] [PubMed]
- Schneider, K.A. Subcortical mechanisms of feature-based attention. J. Neurosci. 2011, 31, 8643–8653. [Google Scholar] [CrossRef] [PubMed]
- Schneider, K.A.; Kastner, S. Effects of sustained spatial attention in the human lateral geniculate nucleus and superior colliculus. J. Neurosci. 2009, 29, 1784–1795. [Google Scholar] [CrossRef] [PubMed]
- Schneider, K.A.; Richter, M.C.; Kastner, S. Retinotopic organization and functional subdivisions of the human lateral geniculate nucleus: A high-resolution functional magnetic resonance imaging study. J. Neurosci. 2004, 24, 8975–8985. [Google Scholar] [CrossRef] [PubMed]
- Viviano, J.D.; Schneider, K.A. Interhemispheric interactions of the human thalamic reticular nucleus. J. Neurosci. 2015, 35, 2026–2032. [Google Scholar] [CrossRef] [PubMed]
- Stein, J. The magnocellular theory of developmental dyslexia. Dyslexia 2001, 7, 12–36. [Google Scholar] [CrossRef] [PubMed]
- Stein, J.; Walsh, V. To see but not to read; the magnocellular theory of dyslexia. Trends Neurosci. 1997, 20, 147–152. [Google Scholar] [CrossRef]
- Denison, R.N.; Vu, A.T.; Yacoub, E.; Feinberg, D.A.; Silver, M.A. Functional mapping of the magnocellular and parvocellular subdivisions of human LGN. NeuroImage 2014, 102, 358–369. [Google Scholar] [CrossRef]
- Zhang, P.; Wen, W.; Sun, X.; He, S. Selective reduction of fMRI responses to transient achromatic stimuli in the magnocellular layers of the LGN and the superficial layer of the SC of early glaucoma patients. Hum. Brain Mapp. 2016, 37, 558–569. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, H.; Wen, W.; He, S. Layer-specific response properties of the human lateral geniculate nucleus and superior colliculus. NeuroImage 2015, 111, 159–166. [Google Scholar] [CrossRef]
- Abbie, A.A. The blood supply of the lateral geniculate body, with a note on the morphology of the choroidal arteries. J. Anat. 1933, 67, 491–521. [Google Scholar] [PubMed]
- Brainard, D.H. The Psychophysics Toolbox. Spat. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef] [PubMed]
- Pelli, D.G. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spat. Vis. 1997, 10, 437–442. [Google Scholar] [CrossRef] [PubMed]
- Tansley, B.W.; Boynton, R.M. Chromatic border perception: The role of red- and green-sensitive cones. Vis. Res. 1978, 18, 683–697. [Google Scholar] [CrossRef]
- Power, J.D.; Barnes, K.A.; Snyder, A.Z.; Schlaggar, B.L.; Petersen, S.E. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage 2012, 59, 2142–2154. [Google Scholar] [CrossRef] [PubMed]
- Dumoulin, S.O.; Wandell, B.A. Population receptive field estimates in human visual cortex. NeuroImage 2008, 39, 647–660. [Google Scholar] [CrossRef] [PubMed]
- Thirion, B.; Duchesnay, E.; Hubbard, E.; Dubois, J.; Poline, J.-B.; Lebihan, D.; Dehaene, S. Inverse retinotopy: Inferring the visual content of images from brain activation patterns. NeuroImage 2006, 33, 1104–1116. [Google Scholar] [CrossRef] [PubMed]
- Maunsell, J.H.R.; Ghose, G.M.; Assad, J.A.; McAdams, C.J.; Boudreau, C.E.; Noerager, B.D. Visual response latencies of magnocellular and parvocellular LGN neurons in macaque monkeys. Vis. Neurosci. 1999, 16, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Schiller, P.H.; Malpeli, J.G. Functional specificity of lateral geniculate nucleus laminae of the rhesus monkey. J. Neurophysiol. 1978, 41, 788–797. [Google Scholar] [CrossRef]
- Solomon, S.G.; Peirce, J.W.; Dhruv, N.T.; Lennie, P. Profound contrast adaptation early in the visual pathway. Neuron 2004, 42, 155–162. [Google Scholar] [CrossRef]
- De Valois, R.L.; Cottaris, N.P. Inputs to directionally selective simple cells in macaque striate cortex. Proc. Natl. Acad. Sci. USA 1998, 95, 14488–14493. [Google Scholar] [CrossRef] [PubMed]
- Stigliani, A.; Jeska, B.; Grill-Spector, K. Encoding model of temporal processing in human visual cortex. Proc. Natl. Acad. Sci. USA 2017, 114, E11047–E11056. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Benson, N.C.; Kay, K.N.; Winawer, J. Compressive temporal summation in human visual cortex. J. Neurosci. 2018, 38, 691–709. [Google Scholar] [CrossRef] [PubMed]
- Glover, G.H. Deconvolution of impulse response in event-related BOLD fMRI. NeuroImage 1999, 9, 416–429. [Google Scholar] [CrossRef]
- Fletcher, R.; Powell, M.J.D. A rapidly convergent descent method for minimization. Comput. J. 1963, 6, 163–168. [Google Scholar] [CrossRef]
- DeSimone, K.; Rokem, A.; Schneider, K. Popeye: A population receptive field estimation tool. J. Open Source Softw. 2016, 1, 103. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Thompson, J.K.; Peterson, M.R.; Freeman, R.D. High resolution neuro-metabolic coupling in the lateral geniculate nucleus. In Proceedings of the Society for Neuroscience Annual Meeting 2003, New Orleans, LA, USA, 4–9 November 2003. Program number 68.9. [Google Scholar]
- Das, A.; Gilbert, C.D. Long-range horizontal connections and their role in cortical reorganization revealed by optical recording of cat primary visual cortex. Nature 1995, 375, 780–784. [Google Scholar] [CrossRef]
- Menon, R.S.; Goodyear, B.G. Submillimeter functional localization in human striate cortex using BOLD contrast at 4 Tesla: Implications for the vascular point-spread function. Magn. Reson. Med. 1999, 41, 230–235. [Google Scholar] [CrossRef]
- Giraldo-Chica, M.; Hegarty, J.P.; Schneider, K.A. Morphological differences in the lateral geniculate nucleus associated with dyslexia. NeuroImage Clin. 2015, 7, 830–836. [Google Scholar] [CrossRef]
- Schneider, K.A.; Kastner, S. Visual responses of the human superior colliculus: A high-resolution functional magnetic resonance imaging study. J. Neurophysiol. 2005, 94, 2491–2503. [Google Scholar] [CrossRef]
- Berens, P. CircStat: A MATLAB toolbox for circular statistics. J. Stat. Softw. 2009, 31, 1–21. [Google Scholar] [CrossRef]
- Amano, K.; Wandell, B.A.; Dumoulin, S.O. Visual field maps, population receptive field sizes, and visual field coverage in the human MT+ complex. J. Neurophysiol. 2009, 102, 2704–2718. [Google Scholar] [CrossRef]
- Harvey, B.M.; Dumoulin, S.O. The relationship between cortical magnification factor and population receptive field size in human visual cortex: Constancies in cortical architecture. J. Neurosci. 2011, 31, 13604–13612. [Google Scholar] [CrossRef]
- Kay, K.N.; Winawer, J.; Mezer, A.; Wandell, B.A. Compressive spatial summation in human visual cortex. J. Neurophysiol. 2013, 110, 481–494. [Google Scholar] [CrossRef]
- Engel, S.A. The development and use of phase-encoded functional MRI designs. NeuroImage 2012, 62, 1195–1200. [Google Scholar] [CrossRef]
- Engel, S.A.; Rumelhart, D.E.; Wandell, B.A.; Lee, A.T.; Glover, G.H.; Chichilnisky, E.-J.; Shadlen, M.N. fMRI of human visual cortex. Nature 1994, 369, 525. [Google Scholar] [CrossRef]
- Sereno, M.I.; Dale, A.M.; Reppas, J.B.; Kwong, K.K.; Belliveau, J.W.; Brady, T.J.; Rosen, B.R.; Tootell, R.B. Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science 1995, 268, 889–893. [Google Scholar] [CrossRef]
- Ma, Y.; Ward, B.D.; Ropella, K.M.; DeYoe, E.A. Comparison of randomized multifocal mapping and temporal phase mapping of visual cortex for clinical use. NeuroImage Clin. 2013, 3, 143–154. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, P.; Qiu, J.; Fang, F. Perceptual learning of contrast detection in the human lateral geniculate nucleus. Curr. Biol. 2016, 26, 3176–3182. [Google Scholar] [CrossRef]
- Bayram, A.; Karahan, E.; Bilgiç, B.; Ademoglu, A.; Demiralp, T. Achromatic temporal-frequency responses of human lateral geniculate nucleus and primary visual cortex. Vis. Res. 2016, 127, 177–185. [Google Scholar] [CrossRef]

| Left Hemisphere | Right Hemisphere | |
|---|---|---|
| LGN | 255 ± 14 | 251 ± 22 |
| LGN, r2 > 0.10 | 69 ± 2 | 65 ± 6 |
| Flicker | Isoluminance | Flicker + Isoluminance | |||||||
|---|---|---|---|---|---|---|---|---|---|
| pRF Parameter | β | SE | p-Value | β | SE | p-Value | β | SE | p-Value |
| φ polar angle | 0.02 | 0.012 | 0.086 | 0.02 | 0.02 | 0.44 | 0.04 | 0.01 | 0.016 |
| ρ eccentricity | −0.04 | 0.013 | <0.01 | −0.09 | 0.02 | <0.01 | −0.03 | 0.02 | 0.079 |
| σ receptive field size | −0.03 | 0.017 | 0.035 | 0.12 | 0.03 | <0.01 | −0.05 | 0.02 | 0.012 |
| ω weight | −0.004 | 0.013 | 0.78 | −0.10 | 0.03 | <0.01 | −0.03 | 0.02 | 0.061 |
| β amplitude | −0.07 | 0.014 | <0.0001 | −0.31 | 0.02 | <0.0001 | −0.17 | 0.01 | <0.0001 |
| μ baseline | 0.03 | 0.012 | 0.015 | 0.05 | 0.02 | 0.019 | 0.05 | 0.01 | <0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
DeSimone, K.; Schneider, K.A. Distinguishing Hemodynamics from Function in the Human LGN Using a Temporal Response Model. Vision 2019, 3, 27. https://doi.org/10.3390/vision3020027
DeSimone K, Schneider KA. Distinguishing Hemodynamics from Function in the Human LGN Using a Temporal Response Model. Vision. 2019; 3(2):27. https://doi.org/10.3390/vision3020027
Chicago/Turabian StyleDeSimone, Kevin, and Keith A. Schneider. 2019. "Distinguishing Hemodynamics from Function in the Human LGN Using a Temporal Response Model" Vision 3, no. 2: 27. https://doi.org/10.3390/vision3020027
APA StyleDeSimone, K., & Schneider, K. A. (2019). Distinguishing Hemodynamics from Function in the Human LGN Using a Temporal Response Model. Vision, 3(2), 27. https://doi.org/10.3390/vision3020027





