The Effect of Stimulus Area on Global Motion Thresholds in Children and Adults
Abstract
1. Introduction
2. Materials and Methods
2.1. Power Analyses
2.2. Participants
2.3. Apparatus
2.4. Stimuli and Experimental Conditions
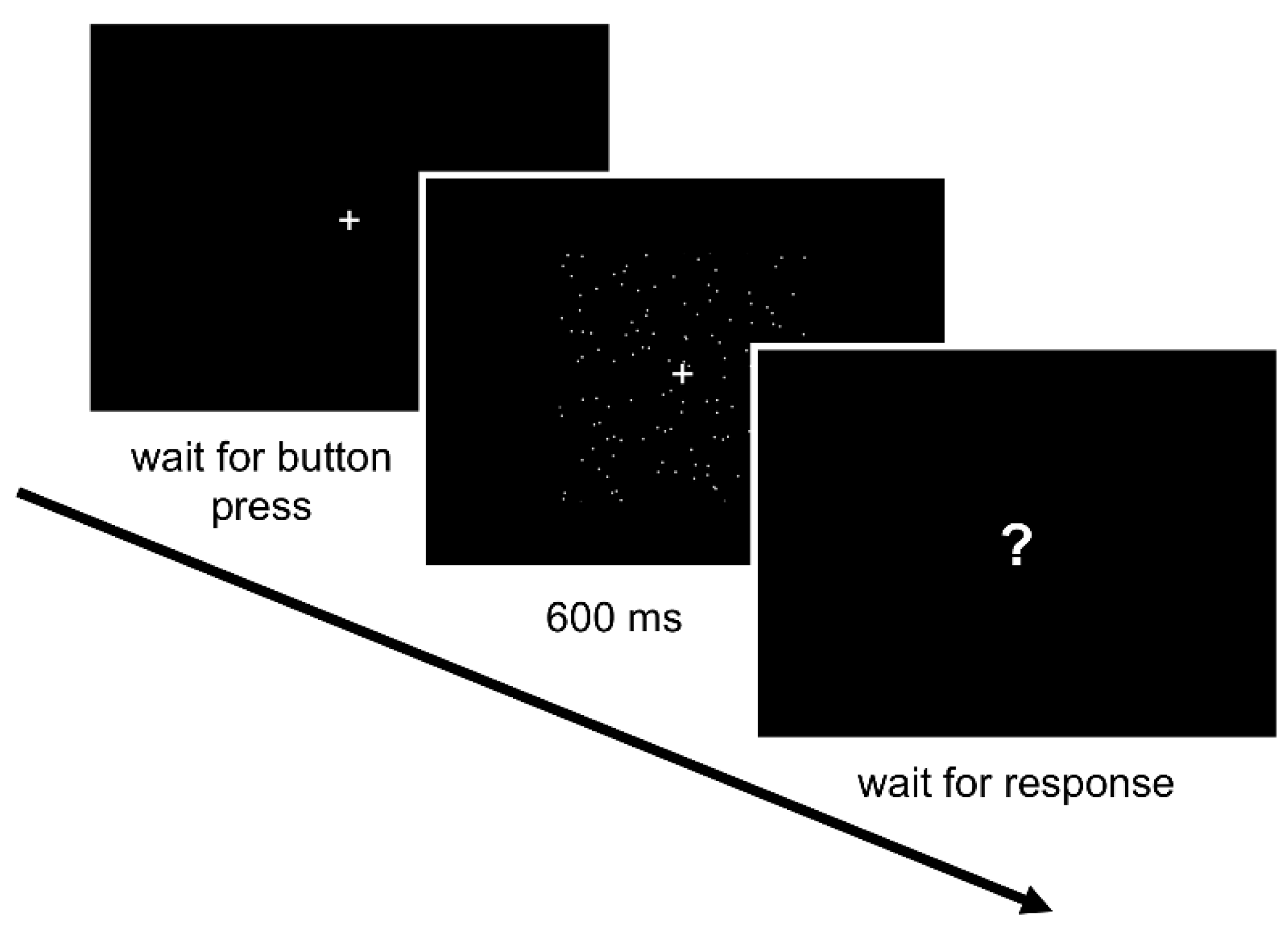
2.5. Procedure
2.6. Data Analysis
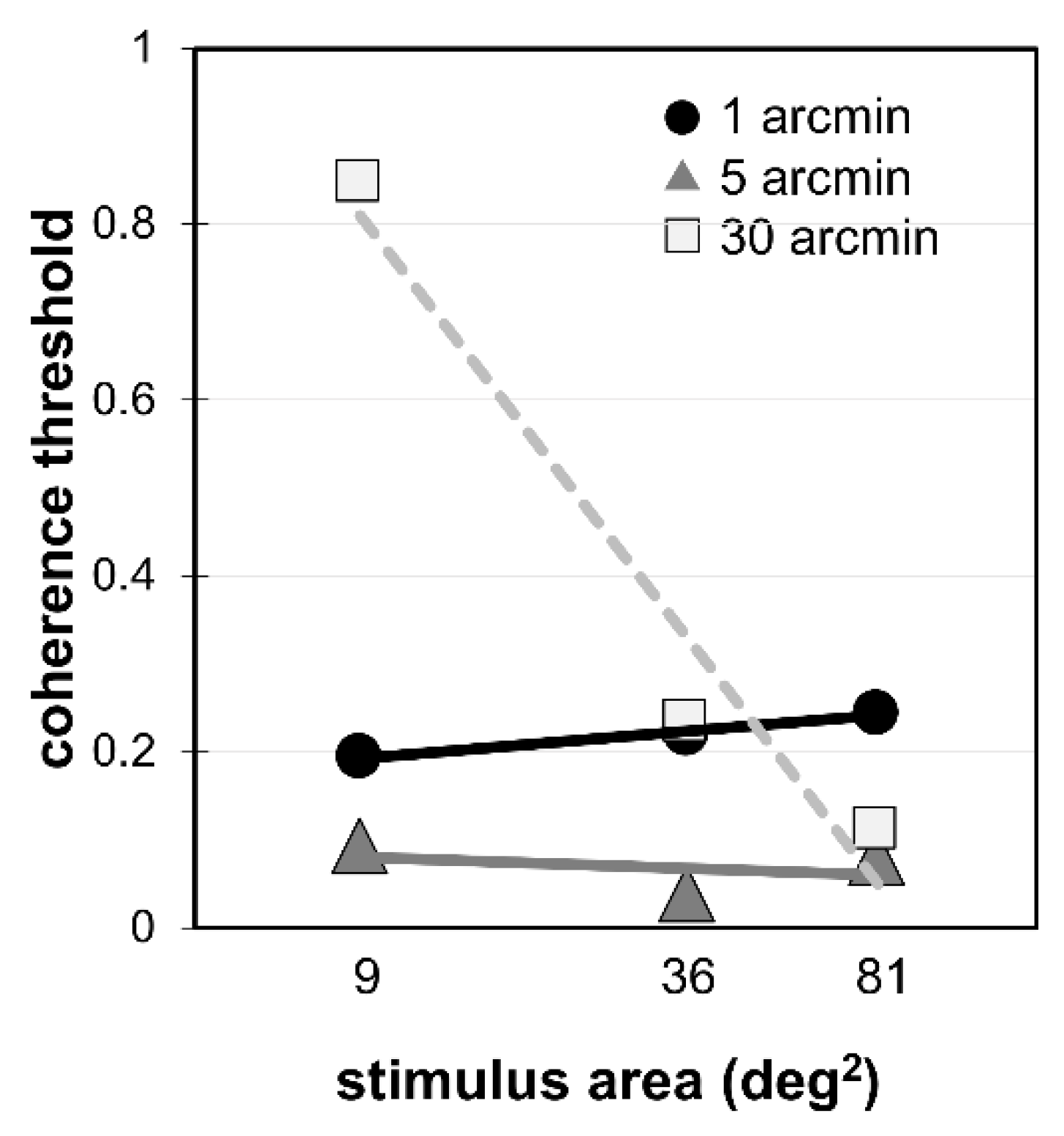
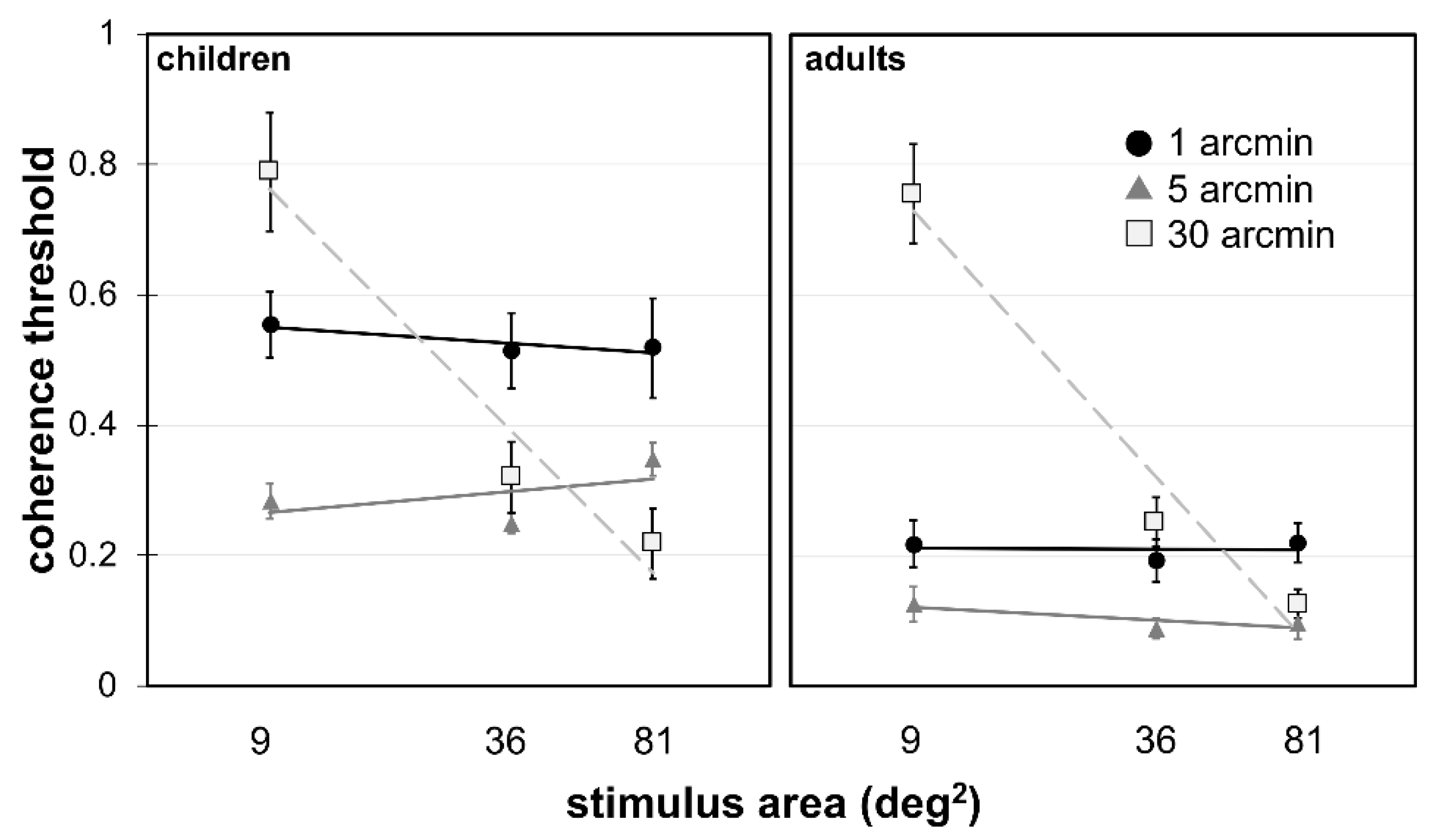
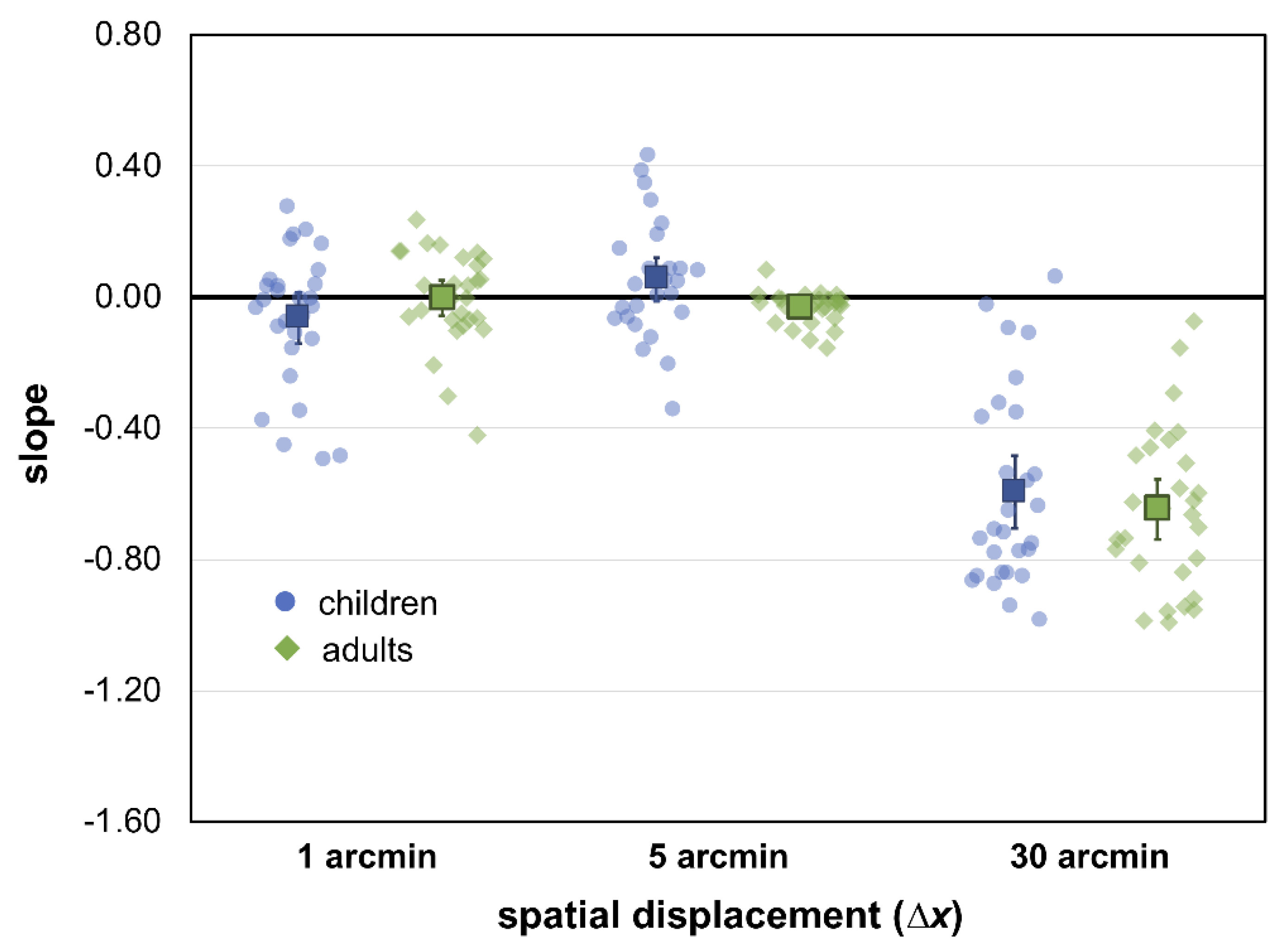
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bogfjellmo, L.G.; Bex, P.J.; Falkenberg, H.K. The development of global motion discrimination in school aged children. J. Vis. 2014, 14, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Narasimhan, S.; Giaschi, D. The effect of dot speed and density on the development of global motion perception. Vis. Res. 2012, 62, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Ellemberg, D.; Lewis, T.L.; Dirks, M.; Maurer, D.; Ledgeway, T.; Guillemot, J.-P.; Lepore, F. Putting order into the development of sensitivity to global motion. Vis. Res. 2004, 44, 2403–2411. [Google Scholar] [CrossRef]
- Ellemberg, D.; Lewis, T.L.; Maurer, D.; Lee, B.; Ledgeway, T.; Guilemot, J.P.; Lepore, F. The effect of displacement on sensitivity to first- and second-order global motion in 5-year-olds and adults. See. Perceiv. 2010, 23, 517–532. [Google Scholar] [PubMed]
- Kiorpes, L.; Price, T.; Hall-Haro, C.; Movshon, J.A. Development of sensitivity to global form and motion in macaque monkeys (macaca nemestrina). Vis. Res. 2012, 63, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Kiorpes, L.; Movshon, J.A. Development of sensitivity to visual motion in macaque monkeys. Vis. Neurosci. 2004, 21, 851–859. [Google Scholar] [CrossRef] [PubMed]
- Meier, K.; Giaschi, D. The maturation of global motion perception depends on the spatial and temporal offsets of the stimulus. Vis. Res. 2014, 95, 61–67. [Google Scholar] [CrossRef]
- Meier, K.; Giaschi, D. Effect of spatial and temporal stimulus parameters on the maturation of global motion perception. Vis. Res. 2017, 135, 1–9. [Google Scholar] [CrossRef]
- Meier, K.; Sum, B.; Giaschi, D. Global motion perception in children with amblyopia as a function of spatial and temporal stimulus parameters. Vis. Res. 2016, 127, 18–27. [Google Scholar] [CrossRef]
- Lewis, T.L.; Ellemberg, D.; Maurer, D.; Dirks, M.; Wilkinson, F.; Wilson, H.R. A window on the normal development of sensitivity to global form in glass patterns. Perception 2004, 33, 409–418. [Google Scholar] [CrossRef]
- Hadad, B.; Maurer, D.; Lewis, T.L. The effects of spatial proximity and collinearity on contour integration in adults and children. Vis. Res. 2010, 50, 772–778. [Google Scholar] [CrossRef]
- Kovács, I.; Kozma, P.; Feher, A.; Benedek, G. Late maturation of visual spatial integration in humans. PNAS 1999, 96, 12204–12209. [Google Scholar] [CrossRef] [PubMed]
- Kiorpes, L.; Bassin, S.A. Development of contour integration in macaque monkeys. Vis. Neurosci. 2003, 20, 567–575. [Google Scholar] [CrossRef]
- Barlow, H.; Tripathy, S.P. Correspondence noise and signal pooling in the detection of coherent visual motion. J. Neurosci. 1997, 17, 7954–7966. [Google Scholar] [CrossRef]
- Talcott, J.B.; Hansen, P.C.; Assoku, E.L.; Stein, J.F. Visual motion sensitivity in dyslexia: Evidence for temporal and energy integration deficits. Neuropsychologia 2000, 38, 935–943. [Google Scholar] [CrossRef]
- Parrish, E.E.; Giaschi, D.E.; Boden, C.; Dougherty, R. The maturation of form and motion perception in school age children. Vis. Res. 2005, 45, 827–837. [Google Scholar] [CrossRef]
- Hutchinson, C.V.; Ledgeway, T. Spatial summation of first-order and second-order motion in human vision. Vis. Res. 2010, 50, 1766–1774. [Google Scholar] [CrossRef] [PubMed]
- Downing, C.J.; Movshon, J.A. Spatial and temporal summation in the detection of motion in stochastic random dot displays. Invest. Ophthalmol. Vis. Sci. 1989, 30. [Google Scholar]
- Boulton, J.C. Two mechanisms for the detection of slow motion. J. Opt. Soc. Am. A 1987, 4, 1634–1642. [Google Scholar] [CrossRef] [PubMed]
- Baker, C.L.; Braddick, O.J. The basis of area and dot number effects in random dot motion perception. Vis. Res. 1982, 22, 1253–1259. [Google Scholar] [CrossRef]
- Chang, J.J.; Julesz, B. Displacement limits for spatial frequency filtered random-dot cinematograms in apparent motion. Vis. Res. 1983, 23, 1379–1385. [Google Scholar] [CrossRef]
- Eagle, R.A.; Rogers, B.J. Effects of dot density, patch size and contrast on the upper spatial limit for direction discrimination in random-dot kinematograms. Vis. Res. 1997, 37, 2091–2102. [Google Scholar] [CrossRef]
- Baker, C.L.J.; Braddick, O.J. Eccentricity-dependent scaling of the limits for short-range apparent motion perception. Vis. Res. 1985, 25, 803–812. [Google Scholar] [CrossRef]
- Anderson, S.J.; Burr, D.C. Receptive field size of human motion detection units. Vis. Res. 1987, 27, 621–635. [Google Scholar] [CrossRef]
- Anderson, S.J.; Burr, D.C. Spatial summation properties of directionally selective mechanisms in human vision. J. Opt. Soc. Am. A 1991, 8, 1330–1339. [Google Scholar] [CrossRef] [PubMed]
- Newsome, W.T.; Mikami, A.; Wurtz, R.H. Motion selectivity in macaque visual cortex. Iii. Psychophysics and physiology of apparent motion. J. Neurophysiol. 1986, 55, 1340–1351. [Google Scholar] [CrossRef] [PubMed]
- Faul, F.; Erdfelder, E.; Lang, A.-G.; Buchner, A. G* power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 2007, 39, 175–191. [Google Scholar] [CrossRef]
- Born, R.T.; Bradley, D.C. Structure and function of visual area MT. Ann. Rev. Neurosci. 2005, 28, 157–189. [Google Scholar] [CrossRef]
- Birch, E.; Williams, C.; Drover, J.; Fu, V.; Cheng, C.; Northstone, K.; Courage, M.; Adams, R. Randot preschool stereoacuity test: Normative data and validity. J. Am. Assoc. Pediatr. Ophthalmol. Strabismus 2008, 12, 23–26. [Google Scholar] [CrossRef]
- Brainard, D.H. The psychophysics toolbox. Spatial. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef]
- Kleiner, M.; Brainard, D.; Pelli, D. What’s new in psychtoolbox-3? Perception 2007, 36. ECVP Abstract Supplement. [Google Scholar] [CrossRef]
- Pelli, D.G. The videotoolbox software for visual psychophysics: Transforming numbers into movies. Spatial. Vis. 1997, 10, 437–442. [Google Scholar] [CrossRef]
- Regan, D. Low contrast letter charts and sinewave grating tests in ophthalmological and neurological disorders. Clin. Vis. Sci. 1988, 2, 235–250. [Google Scholar]
- Hyvärinen, L.; Näsänen, R.; Laurinen, P. New visual acuity test for pre-school children. Acta Ophthalmol. 1980, 58, 507–511. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.L. Hybrid adaptive procedure for estimation of psychometric functions. J. Acoust. Soc. Am. 1981, 69, 1763–1769. [Google Scholar] [CrossRef] [PubMed]
- Leek, M.R.; Hanna, T.E.; Marshall, L. Estimation of psychometric functions from adaptive tracking procedures. Percept. Psychophys. 1992, 51, 247–256. [Google Scholar] [CrossRef]
- Watson, A.B.; Pelli, D.G. Quest: A Bayesian adaptive psychometric method. Percept. Psychophys. 1983, 33, 113–120. [Google Scholar] [CrossRef]
- Prins, N.; Kingdom, F.A.A. Applying the model-comparison approach to test specific research hypotheses in psychophysical research using the Palamedes toolbox. Front. Psychol. 2018, 9, 1250. [Google Scholar] [CrossRef]
- Wichmann, F.A.; Hill, N.J. The psychometric function: I. Fitting, sampling, and goodness of fit. Percept. Psychophys. 2001, 63, 1293–1313. [Google Scholar] [CrossRef]
- Pilly, P.K.; Seitz, A.R. What a difference a parameter makes: A psychophysical comparison of random dot motion algorithms. Vis. Res. 2009, 49, 1599–1612. [Google Scholar] [CrossRef]
- McKee, S.P.; Welch, L. Sequential recruitment in the discrimination of velocity. J. Opt. Soc. Am. A 1985, 2, 243–251. [Google Scholar] [CrossRef] [PubMed]
- Nakayama, K.; Silverman, G.H. Temporal and spatial characteristics of the upper displacement limit for motion in random dots. Vis. Res. 1984, 24, 293–299. [Google Scholar] [CrossRef]
- Hess, R.F.; Mansouri, B.; Dakin, S.C.; Allen, H.A. Integration of local motion is normal in amblyopia. J. Opt. Soc. Am. A 2006, 23, 986–992. [Google Scholar] [CrossRef]
- Falkenberg, H.K.; Simpson, W.A.; Dutton, G.N. Development of sampling efficiency and internal noise in motion detection and discrimination in school-aged children. Vis. Res. 2014, 100, 8–17. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meier, K.; Giaschi, D. The Effect of Stimulus Area on Global Motion Thresholds in Children and Adults. Vision 2019, 3, 10. https://doi.org/10.3390/vision3010010
Meier K, Giaschi D. The Effect of Stimulus Area on Global Motion Thresholds in Children and Adults. Vision. 2019; 3(1):10. https://doi.org/10.3390/vision3010010
Chicago/Turabian StyleMeier, Kimberly, and Deborah Giaschi. 2019. "The Effect of Stimulus Area on Global Motion Thresholds in Children and Adults" Vision 3, no. 1: 10. https://doi.org/10.3390/vision3010010
APA StyleMeier, K., & Giaschi, D. (2019). The Effect of Stimulus Area on Global Motion Thresholds in Children and Adults. Vision, 3(1), 10. https://doi.org/10.3390/vision3010010




