Accurate Model-Based Point of Gaze Estimation on Mobile Devices
Abstract
1. Introduction
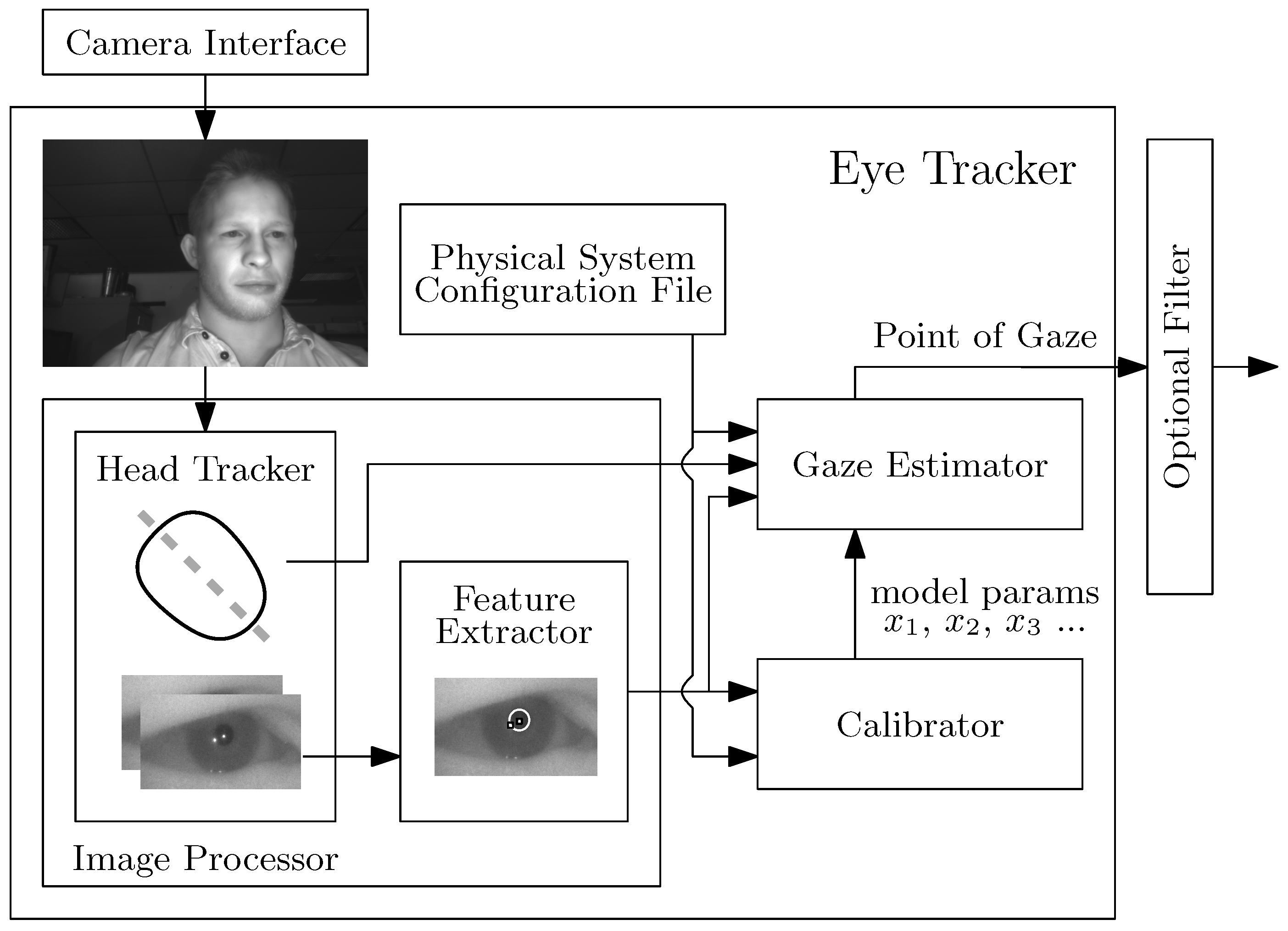
2. Materials and Methods
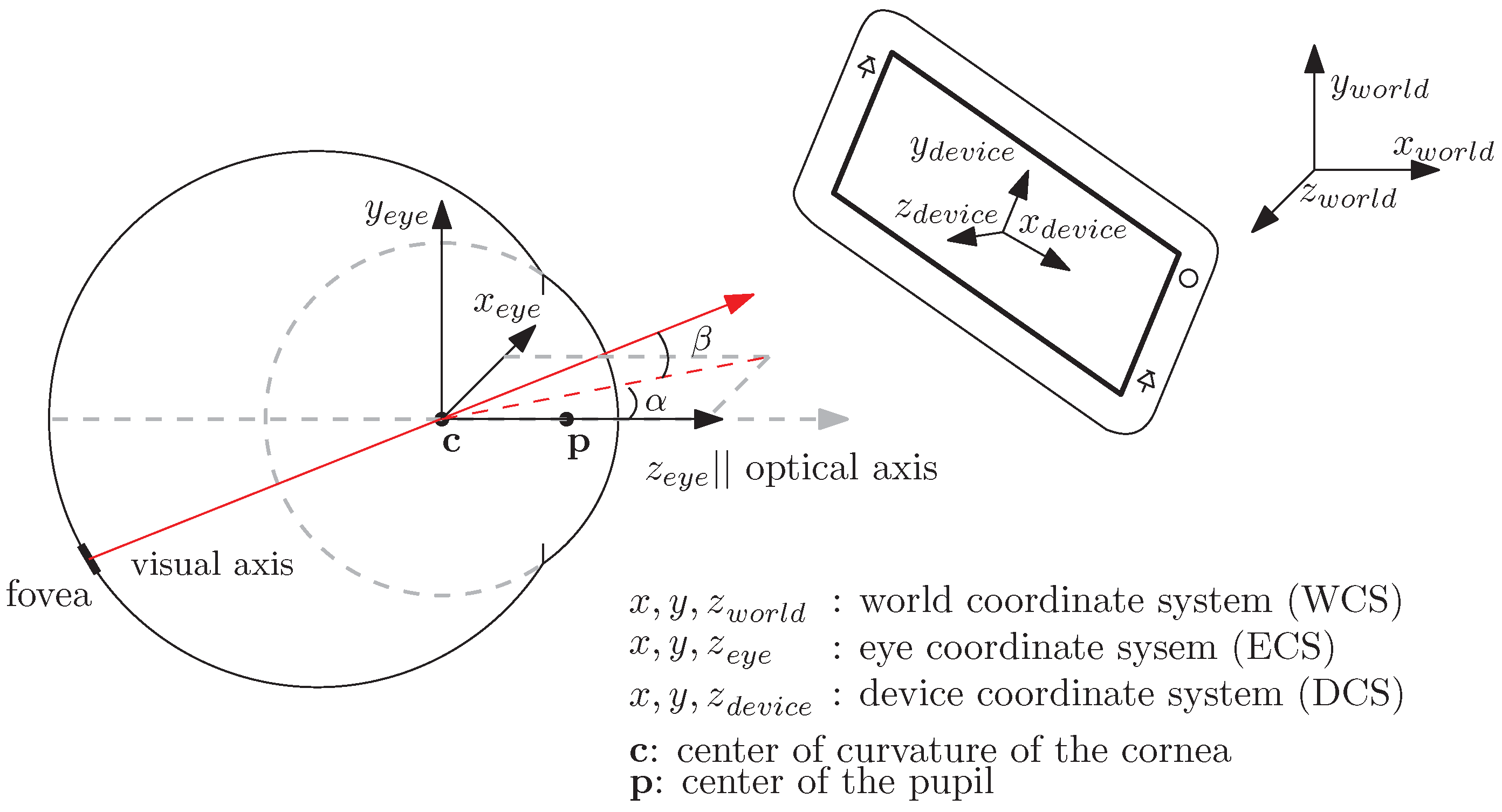
2.1. Mathematical Model
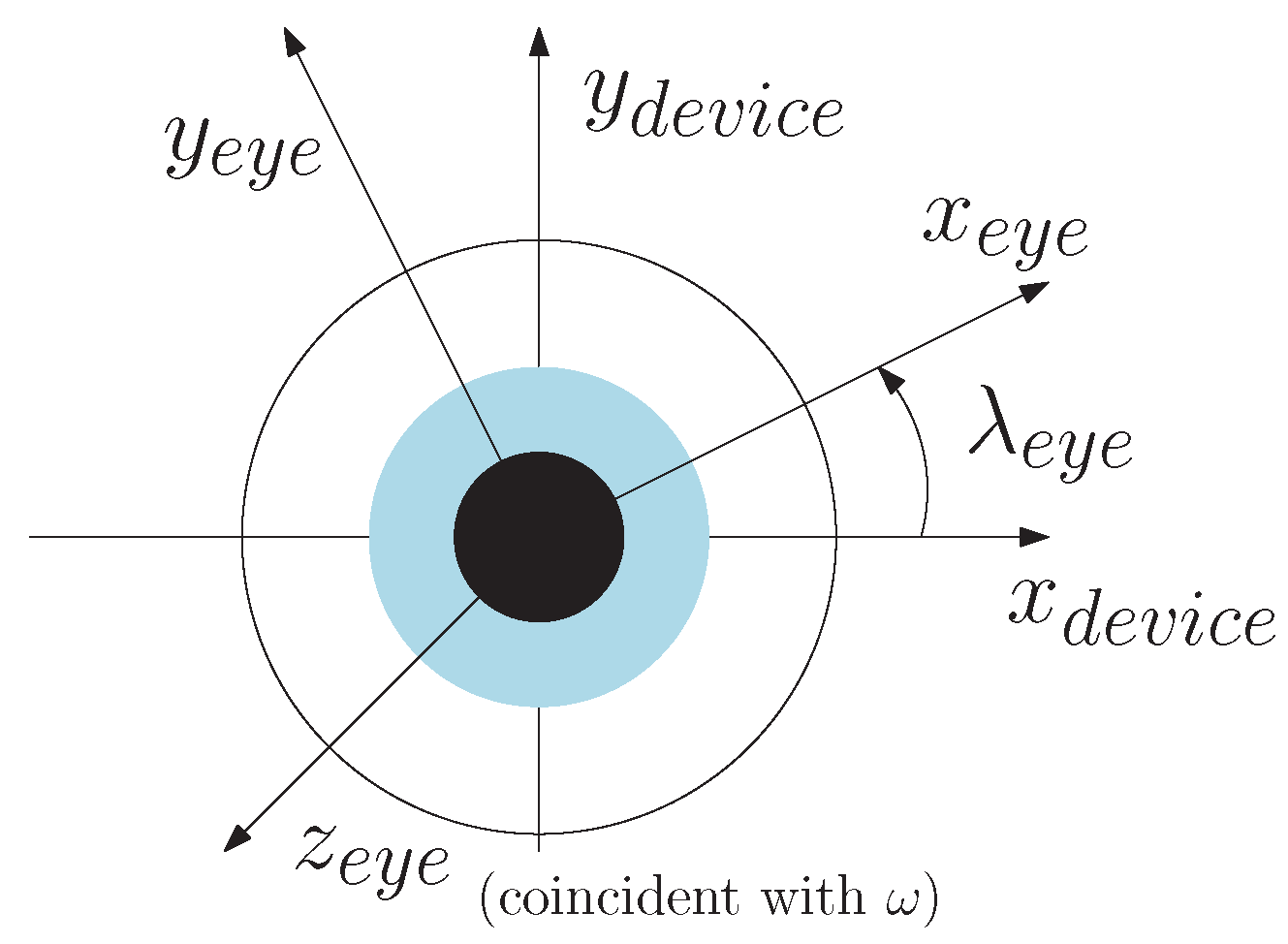
2.2. Quantifying the Effects of Relative Roll on POG Estimation
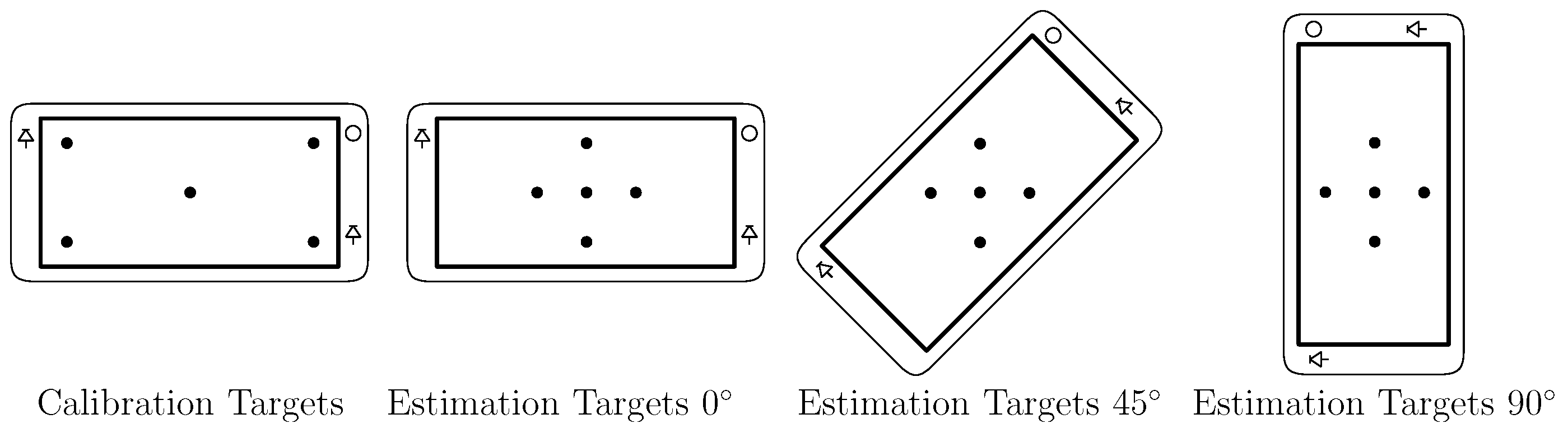
2.3. Experimental Procedure
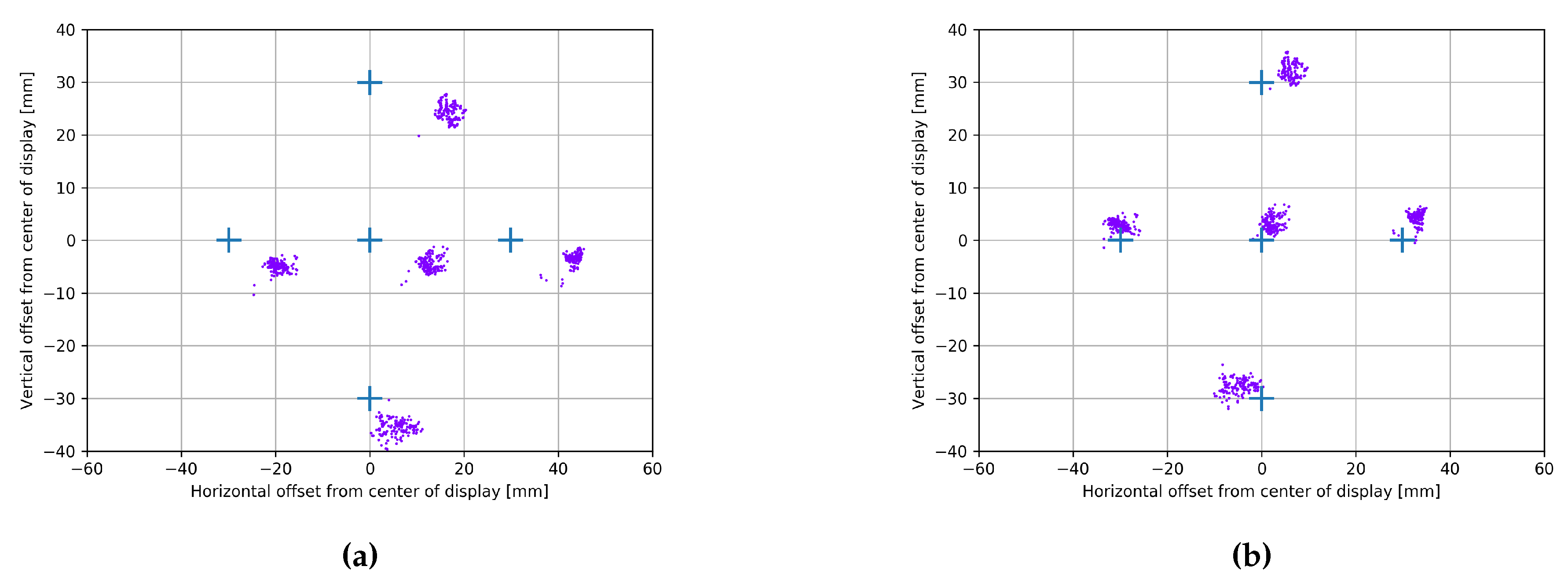
3. Experiment Results
4. Discussion and Conclusions
4.1. Limitations
4.2. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hervet, G.; Guérard, K.; Tremblay, S.; Chtourou, M.S. Is banner blindness genuine? Eye tracking internet text advertising. Appl. Cognit. Psychol. 2011, 25, 708–716. [Google Scholar] [CrossRef]
- Resnick, M.; Albert, W. The Impact of Advertising Location and User Task on the Emergence of Banner Ad Blindness: An Eye-Tracking Study. Int. J. Hum. Comput. Interact. 2014, 30, 206–219. [Google Scholar] [CrossRef]
- Rayner, K. Eye movements in reading and information processing: 20 years of research. Psychol. Bull. 1998, 124, 372–422. [Google Scholar] [CrossRef] [PubMed]
- Duggan, G.B.; Payne, S.J. Skim Reading by Satisficing: Evidence from Eye Tracking. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Vancouver, BC, Canada, 7–12 May 2011; pp. 1141–1150. [Google Scholar] [CrossRef]
- Mazzei, A.; Eivazi, S.; Marko, Y.; Kaplan, F.; Dillenbourg, P. 3D Model-based Gaze Estimation in Natural Reading: A Systematic Error Correction Procedure Based on Annotated Texts. In Proceedings of the Symposium on Eye Tracking Research and Applications, Safety Harbor, FL, USA, 26–28 March 2014; pp. 87–90. [Google Scholar] [CrossRef]
- Wang, J.G.; Sung, E.; Venkateswarlu, R. Estimating the eye gaze from one eye. Comput. Vis. Image Underst. 2005, 98, 83–103. [Google Scholar] [CrossRef]
- Vertegaal, R.; Dickie, C.; Sohn, C.; Flickner, M. Designing attentive cell phone using wearable eyecontact sensors. In Proceedings of the CHI’02 ACM Extended Abstracts on Human Factors in Computing Systems, Minneapolis, MN, USA, 20–25 April 2002; pp. 646–647. [Google Scholar] [CrossRef]
- Nagamatsu, T.; Yamamoto, M.; Sato, H. MobiGaze: Development of a gaze interface for handheld mobile devices. In Proceedings of the CHI’10 ACM Extended Abstracts on Human Factors in Computing Systems, Atlanta, GA, USA, 10–15 April 2010; pp. 3349–3354. [Google Scholar] [CrossRef]
- Liu, D.; Dong, B.; Gao, X.; Wang, H. Exploiting eye tracking for smartphone authentication. In International Conference on Applied Cryptography and Network Security; Springer: New York, NY, USA, 2015; pp. 457–477. [Google Scholar] [CrossRef]
- Khamis, M.; Hasholzner, R.; Bulling, A.; Alt, F. GTmoPass: Two-factor authentication on public displays using gaze-touch passwords and personal mobile devices. In Proceedings of the 6th ACM International Symposium on Pervasive Displays, Lugano, Switzerland, 7–9 June 2017; p. 8. [Google Scholar] [CrossRef]
- Wood, E.; Bulling, A. EyeTab: Model-based Gaze Estimation on Unmodified Tablet Computers. In Proceedings of the ETRA ’14 Symposium on Eye Tracking Research and Applications, Safety Harbor, FL, USA, 26–28 March 2014; pp. 207–210. [Google Scholar] [CrossRef]
- Krafka, K.; Khosla, A.; Kellnhofer, P.; Kannan, H.; Bhandarkar, S.; Matusik, W.; Torralba, A. Eye Tracking for Everyone. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2176–2184. [Google Scholar] [CrossRef]
- Huang, M.X.; Li, J.; Ngai, G.; Leong, H.V. Screenglint: Practical, in-situ gaze estimation on smartphones. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 2546–2557. [Google Scholar] [CrossRef]
- Huang, Q.; Veeraraghavan, A.; Sabharwal, A. TabletGaze: Dataset and analysis for unconstrained appearance-based gaze estimation in mobile tablets. Mach. Vis. Appl. 2017, 28, 445–461. [Google Scholar] [CrossRef]
- Kao, C.W.; Yang, C.W.; Fan, K.C.; Hwang, B.J.; Huang, C.P. An adaptive eye gaze tracker system in the integrated cloud computing and mobile device. In Proceedings of the 2011 IEEE International Conference on the Machine Learning and Cybernetics (Icmlc), Guilin, China, 10–13 July 2011; Volume 1, pp. 367–371. [Google Scholar]
- Holland, C.; Garza, A.; Kurtova, E.; Cruz, J.; Komogortsev, O. Usability evaluation of eye tracking on an unmodified common tablet. In Proceedings of the CHI’13 Extended Abstracts on Human Factors in Computing Systems, Paris, France, 27 April–2 May 2013; pp. 295–300. [Google Scholar]
- Holland, C.; Komogortsev, O. Eye tracking on unmodified common tablets: Challenges and solutions. In Proceedings of the Symposium on Eye Tracking Research and Applications, Santa Barbara, CA, USA, 28–30 March 2012; pp. 277–280. [Google Scholar]
- Ishimaru, S.; Kunze, K.; Utsumi, Y.; Iwamura, M.; Kise, K. Where are you looking at?-feature-based eye tracking on unmodified tablets. In Proceedings of the 2013 IEEE 2nd IAPR Asian Conference on Pattern Recognition (ACPR), Naha, Japan, 5–8 November 2013; pp. 738–739. [Google Scholar]
- Wang, J.G.; Sung, E. Gaze determination via images of irises. Image Vis. Comput. 2001, 19, 891–911. [Google Scholar] [CrossRef]
- Hansen, D.W.; Pece, A.E. Eye tracking in the wild. Comput. Vis. Image Underst. 2005, 98, 155–181. [Google Scholar] [CrossRef]
- Hohlfeld, O.; Pomp, A.; Link, J.Á.B.; Guse, D. On the applicability of computer vision based gaze tracking in mobile scenarios. In Proceedings of the 17th International Conference on Human-Computer Interaction with Mobile Devices and Services, Copenhagen, Denmark, 24–27 August 2015; pp. 427–434. [Google Scholar]
- Guestrin, E.; Eizenman, M. General theory of remote gaze estimation using the pupil center and corneal reflections. IEEE Trans. Biomed. Eng. 2006, 53, 1124–1133. [Google Scholar] [CrossRef] [PubMed]
- Guestrin, E.D.; Eizenman, M. Remote Point-of-gaze Estimation Requiring a Single-point Calibration for Applications with Infants. In Proceedings of the 2008 Symposium on Eye Tracking Research, Savannah, GA, USA, 26–28 March 2008; pp. 267–274. [Google Scholar]
- Model, D.; Eizenman, M. An Automatic Personal Calibration Procedure for Advanced Gaze Estimation Systems. IEEE Trans. Biomed. Eng. 2010, 57, 1031–1039. [Google Scholar] [CrossRef] [PubMed]
- Keralia, D.; Vyas, K.; Deulkar, K. Google project tango, a convenient 3D modeling device. Int. J. Curr. Eng. Technol. 2014, 4, 3139–3142. [Google Scholar]
- Miller, E.F. Counterrolling of the human eyes produced by head tilt with respect to gravity. Acta Oto-Laryngol. 1962, 54, 479–501. [Google Scholar] [CrossRef]
- Maxwell, J.S.; Schor, C.M. Adaptation of torsional eye alignment in relation to head roll. Vis. Res. 1999, 39, 4192–4199. [Google Scholar] [CrossRef]
- Boles, W.; Boashash, B. A human identification technique using images of the iris and wavelet transform. IEEE Trans. Signal Process. 1998, 46, 1185–1188. [Google Scholar] [CrossRef]
- Hepp, K. On Listing’s law. Commun. Math. Phys. 1990, 132, 285–292. [Google Scholar] [CrossRef]
- Khamis, M.; Baier, A.; Henze, N.; Alt, F.; Bulling, A. Understanding Face and Eye Visibility in Front-Facing Cameras of Smartphones used in the Wild. In Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, Montreal, QC, Canada, 21–26 April 2018; p. 280. [Google Scholar]
- Wang, K.; Ji, Q. Hybrid Model and Appearance Based Eye Tracking with Kinect. In Proceedings of the Ninth Biennial ACM Symposium on Eye Tracking Research & Applications, Charleston, South Carolina, 14–17 March 2016; pp. 331–332. [Google Scholar]


| Average Gaze Error (mm) | Average Gaze Error (Degrees) | ||||||
|---|---|---|---|---|---|---|---|
| Subject | Method | R-Roll | R-Roll | R-Roll | R-Roll | R-Roll | R-Roll |
| 01 | 2 | 5.07 | 4.7 | 5.05 | 0.96 | 0.89 | 0.96 |
| 1 | 4.91 | 11.11 | 15.96 | 0.93 | 2.12 | 2.75 | |
| 02 | 2 | 3.73 | 4.55 | 5.18 | 0.71 | 0.86 | 0.98 |
| 1 | 3.52 | 9.08 | 14.39 | 0.67 | 1.73 | 2.74 | |
| 03 | 2 | 3.15 | 4.77 | 4.12 | 0.60 | 0.91 | 0.78 |
| 1 | 3.14 | 11.91 | 18.42 | 0.59 | 2.27 | 3.51 | |
| 04 | 2 | 7.23 | 5.94 | 10.05 | 1.38 | 1.13 | 1.91 |
| 1 | 7.31 | 15.44 | 24.66 | 1.39 | 2.94 | 4.69 | |
| Average | 2 | 4.80 | 4.99 | 6.10 | 0.92 | 0.95 | 1.16 |
| 1 | 4.72 | 11.88 | 18.36 | 0.90 | 2.26 | 3.50 | |
| Subject | 01 | 02 | 03 | 04 | ||||
|---|---|---|---|---|---|---|---|---|
| 1.73 | 1.21 | 1.78 | 2.67 | |||||
| 0.5 | 0.28 | 0.92 | 0.25 | |||||
| 1.37 | 2.54 | 0.94 | 1.75 | 1.53 | 2.83 | 2.06 | 3.81 | |
| 1.22 | 2.08 | 0.86 | 1.76 | 1.36 | 2.72 | 1.81 | 2.78 | |
| 0.15 | 0.46 | 0.08 | 0.01 | 0.17 | 0.11 | 0.25 | 1.03 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brousseau, B.; Rose, J.; Eizenman, M. Accurate Model-Based Point of Gaze Estimation on Mobile Devices. Vision 2018, 2, 35. https://doi.org/10.3390/vision2030035
Brousseau B, Rose J, Eizenman M. Accurate Model-Based Point of Gaze Estimation on Mobile Devices. Vision. 2018; 2(3):35. https://doi.org/10.3390/vision2030035
Chicago/Turabian StyleBrousseau, Braiden, Jonathan Rose, and Moshe Eizenman. 2018. "Accurate Model-Based Point of Gaze Estimation on Mobile Devices" Vision 2, no. 3: 35. https://doi.org/10.3390/vision2030035
APA StyleBrousseau, B., Rose, J., & Eizenman, M. (2018). Accurate Model-Based Point of Gaze Estimation on Mobile Devices. Vision, 2(3), 35. https://doi.org/10.3390/vision2030035





