Apparent Motion Perception in the Praying Mantis: Psychophysics and Modelling
Simple Summary
Abstract
1. Introduction
2. Results
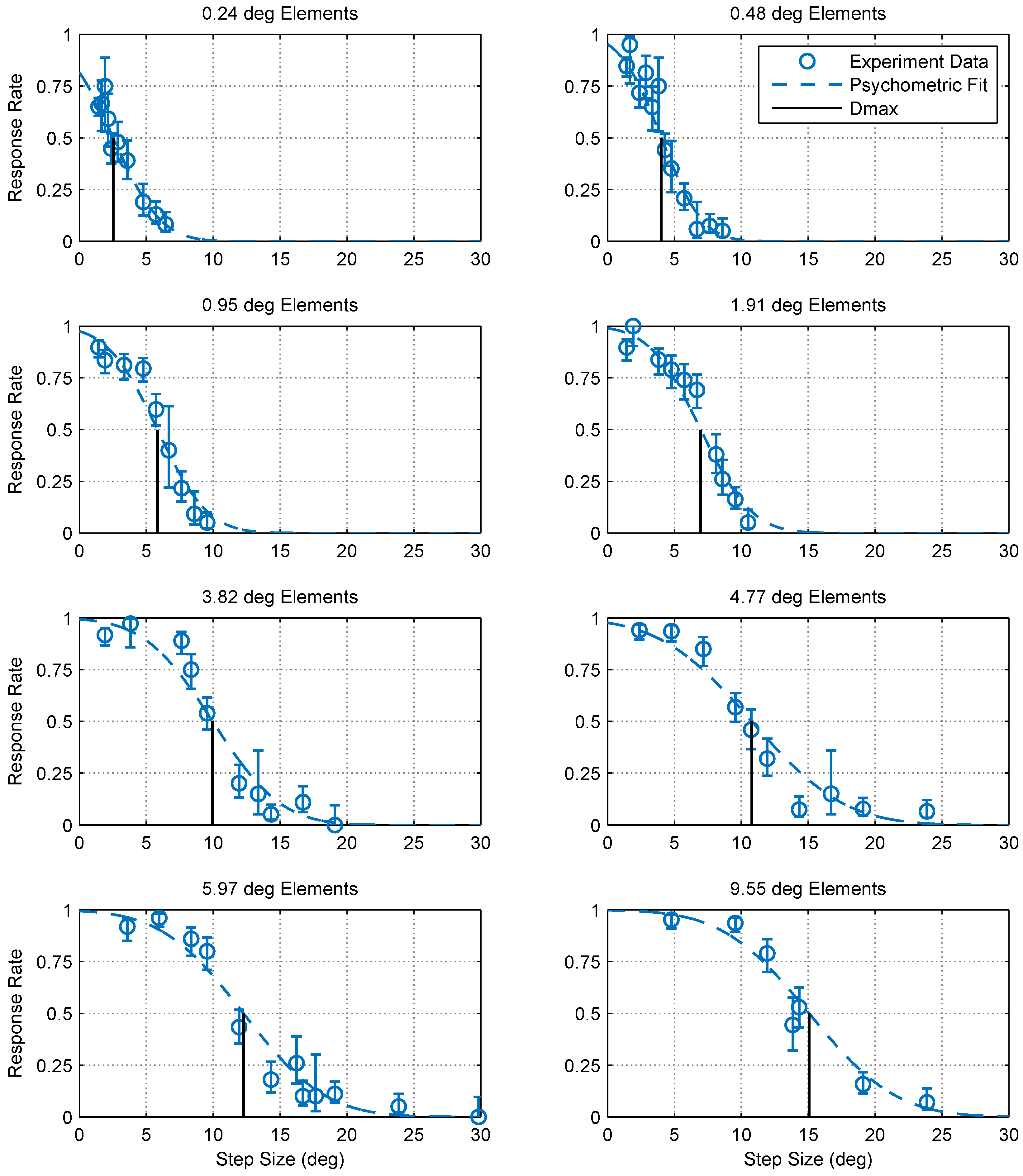
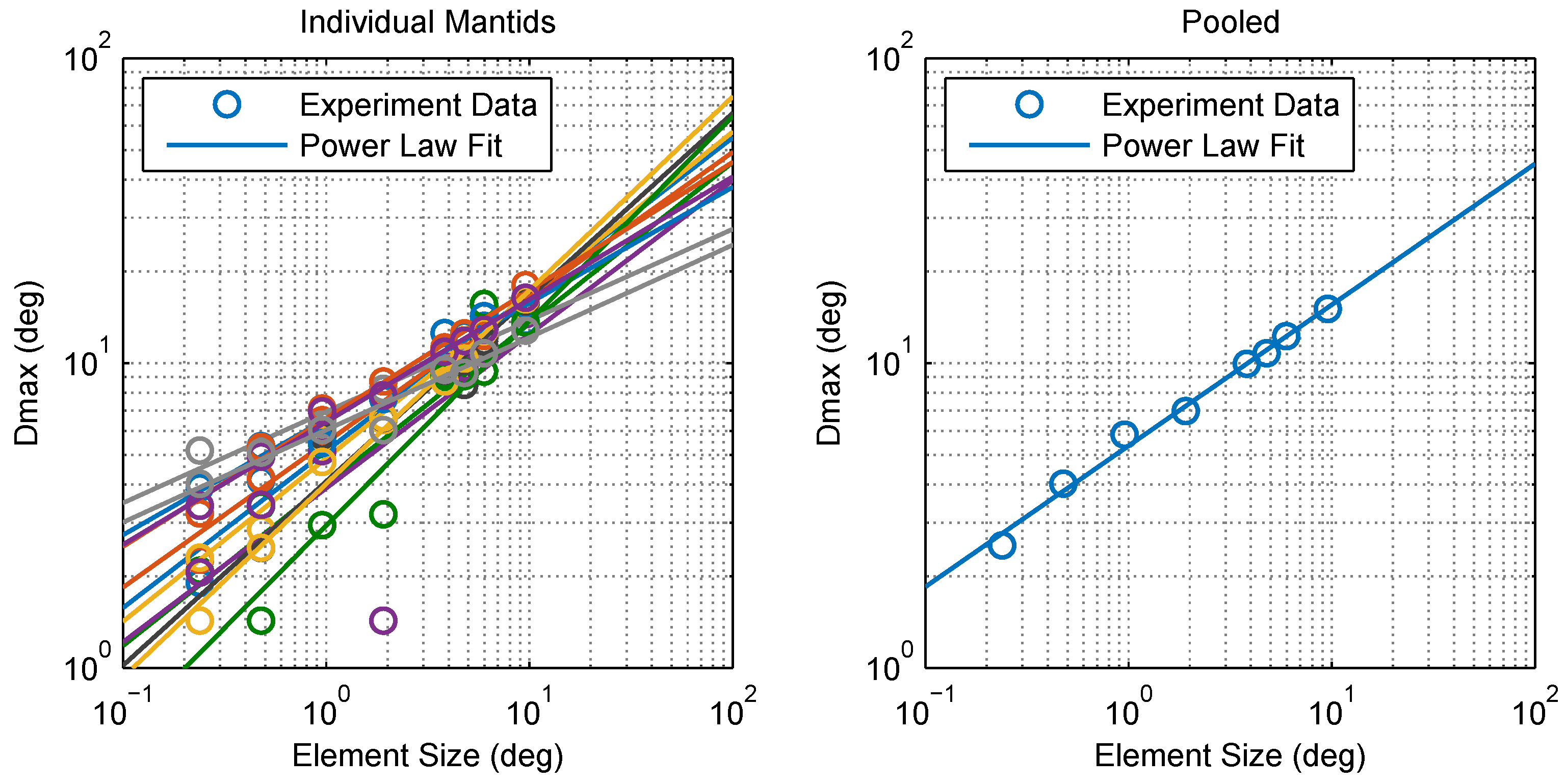
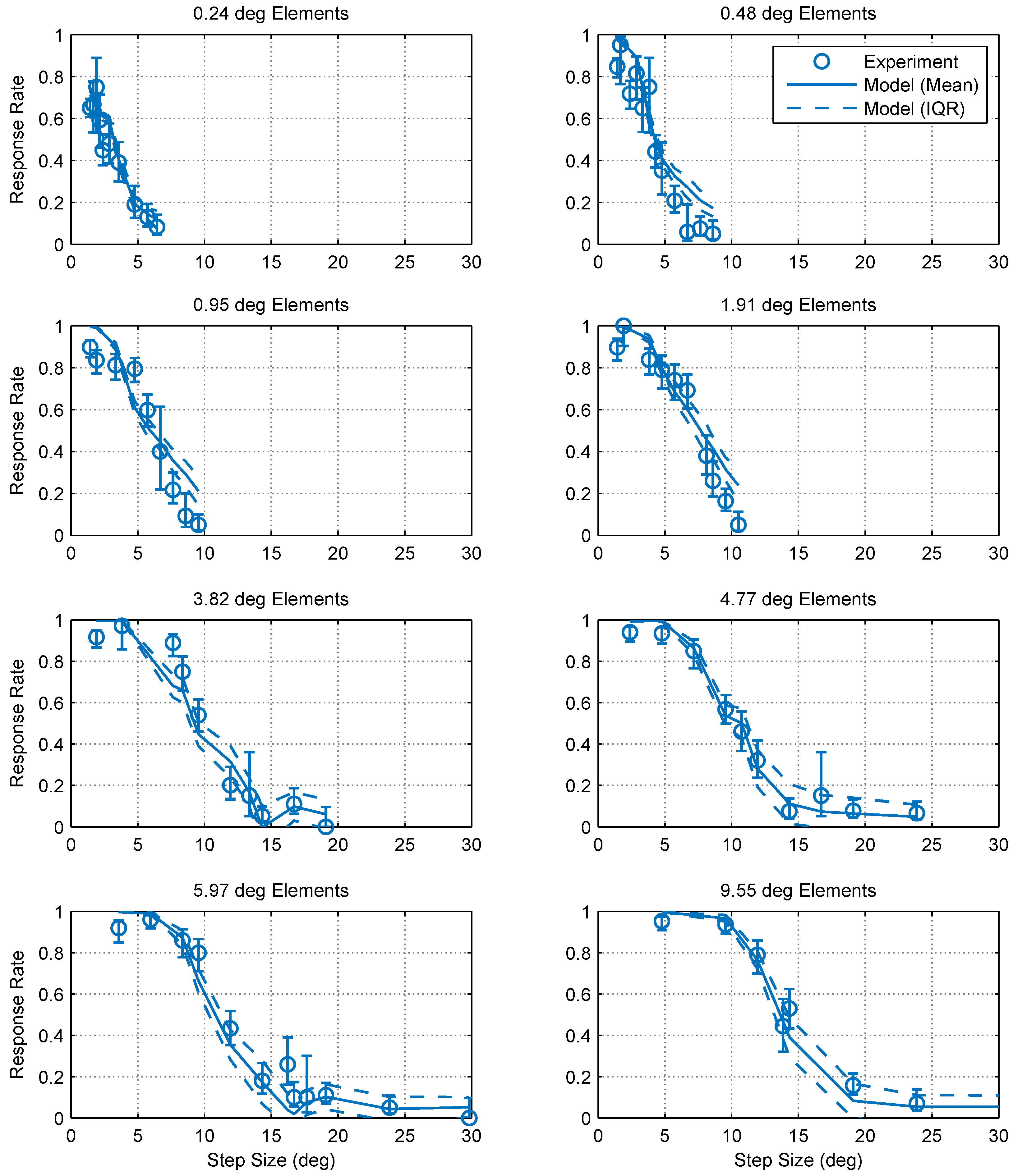
2.1. Experimental Findings
2.2. Modeling and Simulation
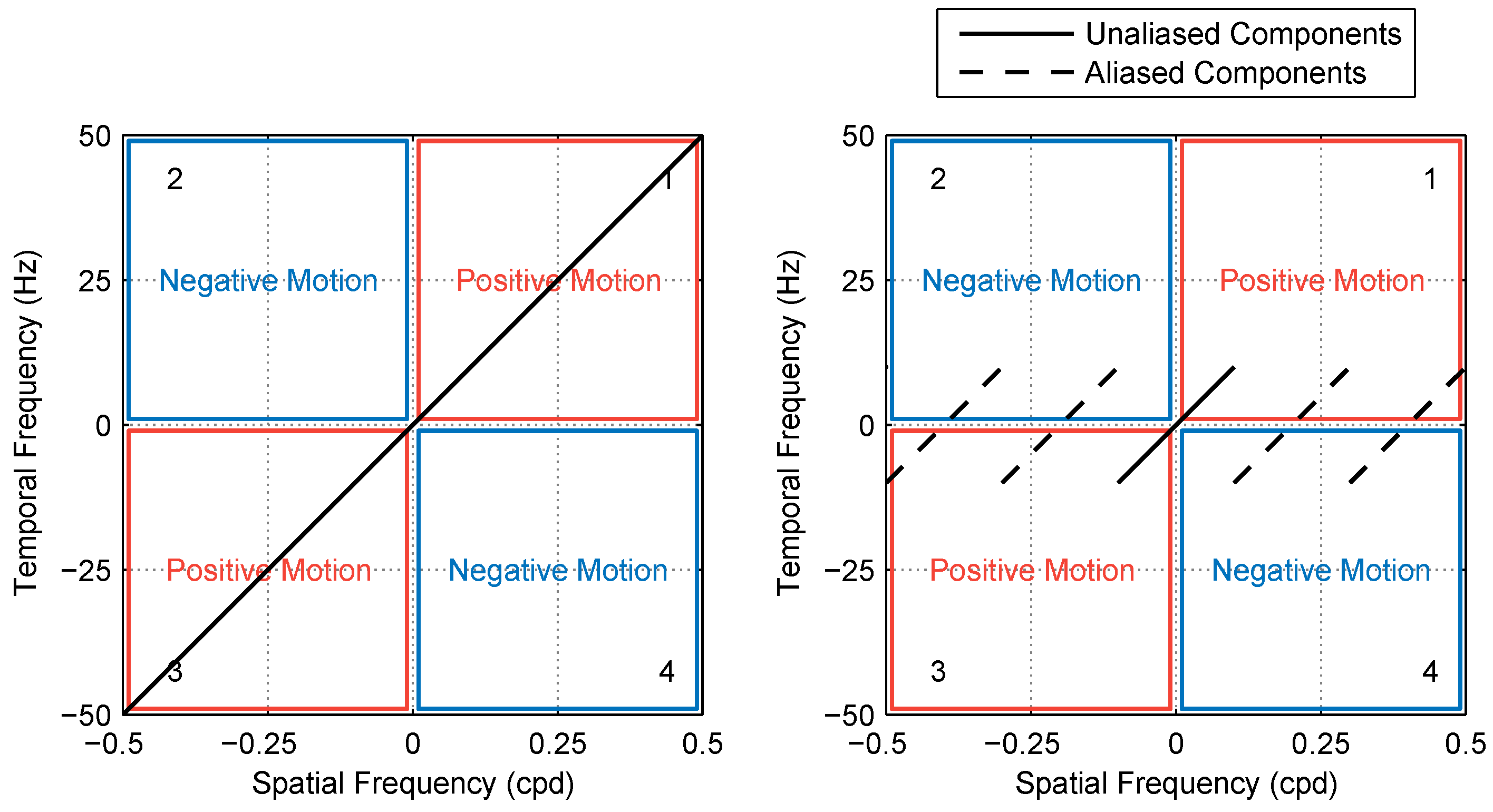
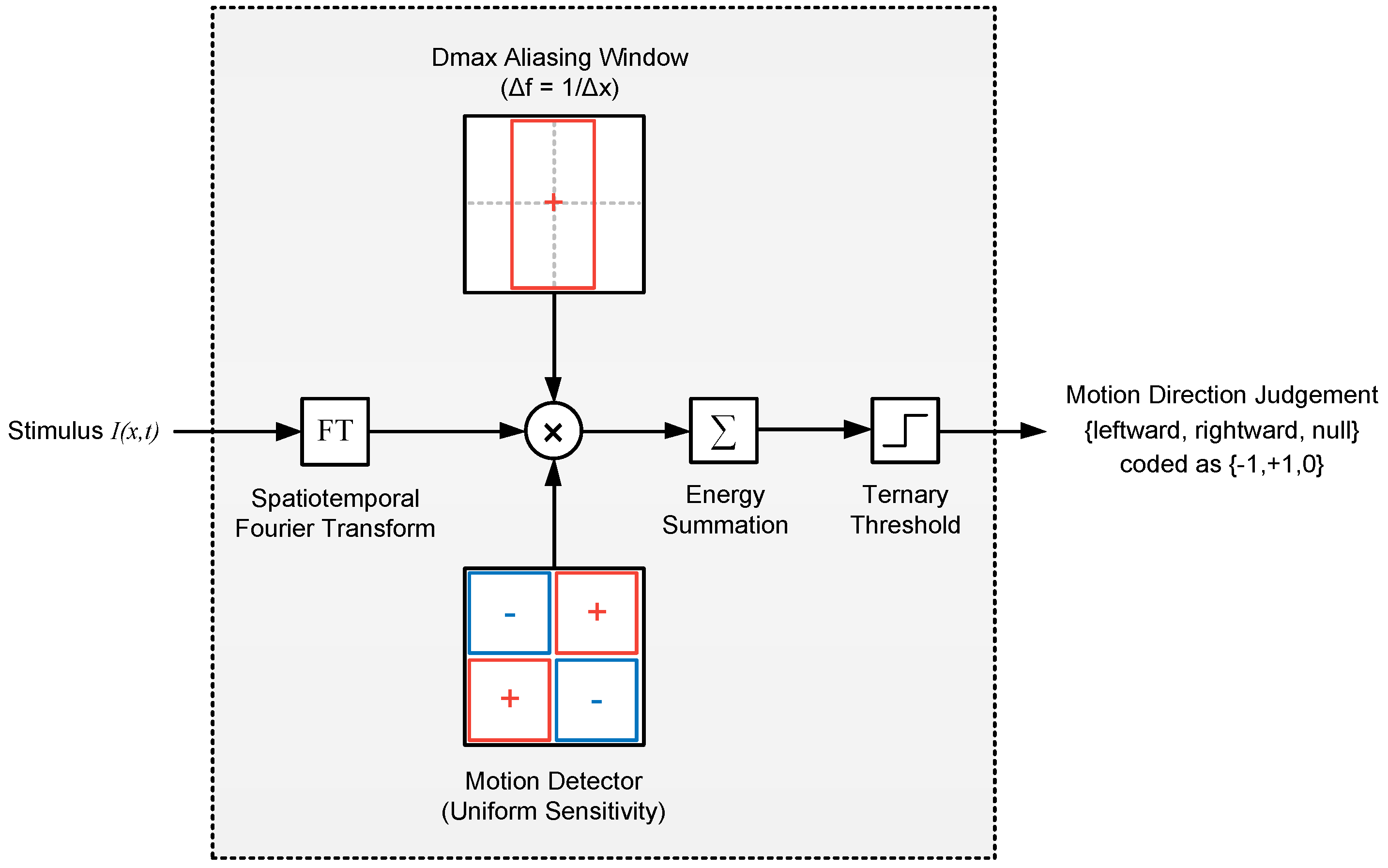
2.2.1. Model 1: Fourier Energy
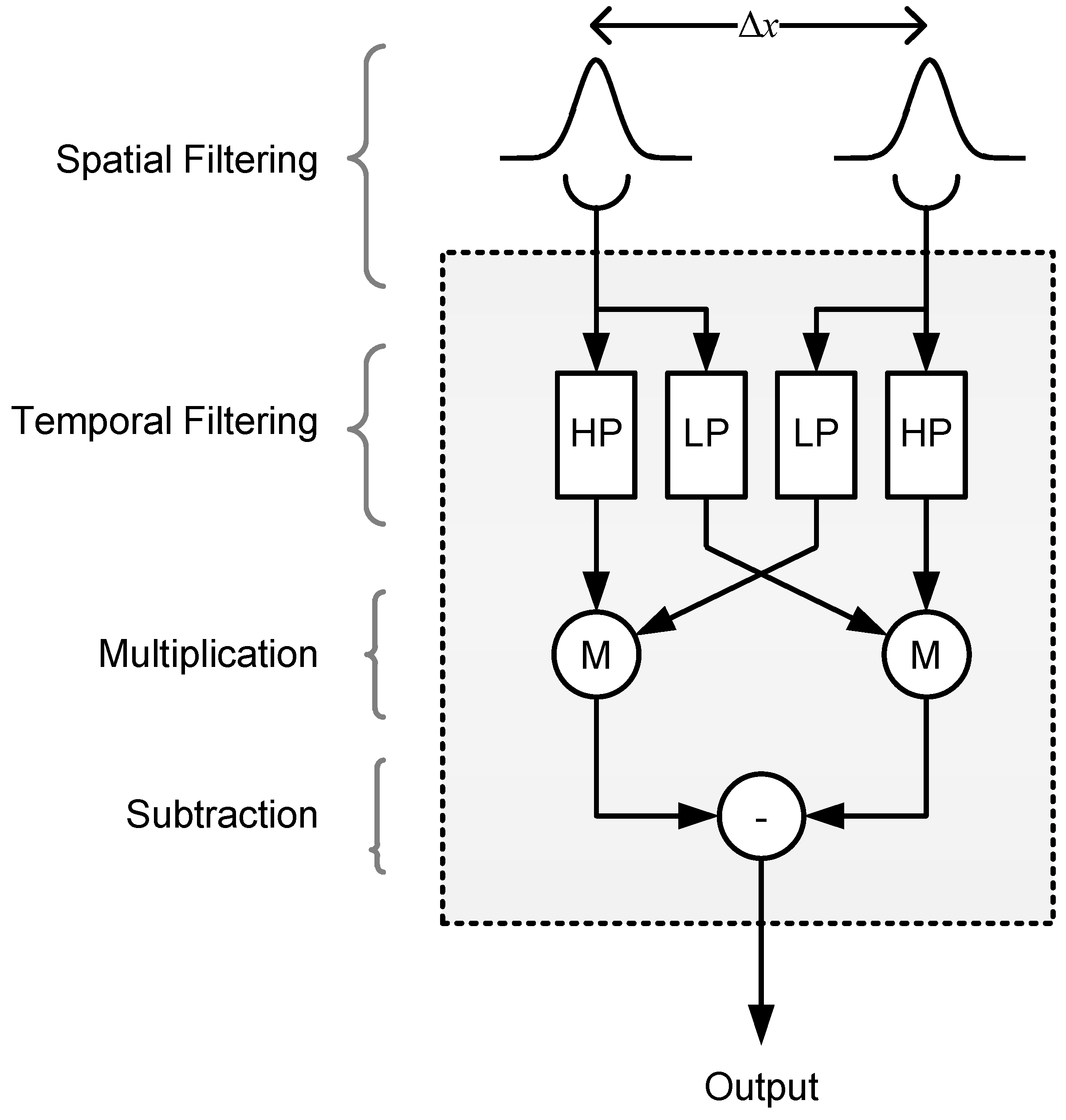
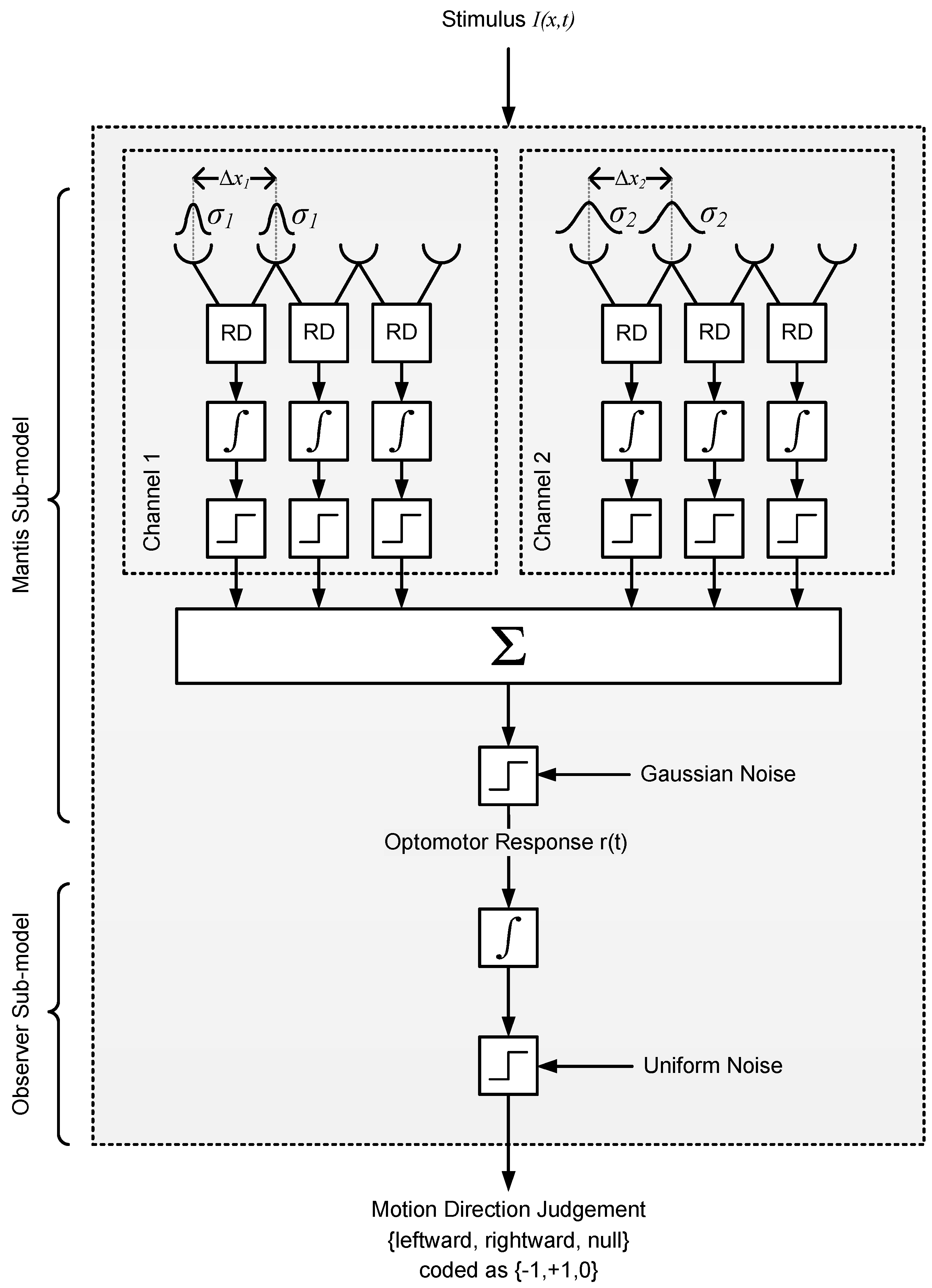
2.2.2. Model 2: Reichardt Detector
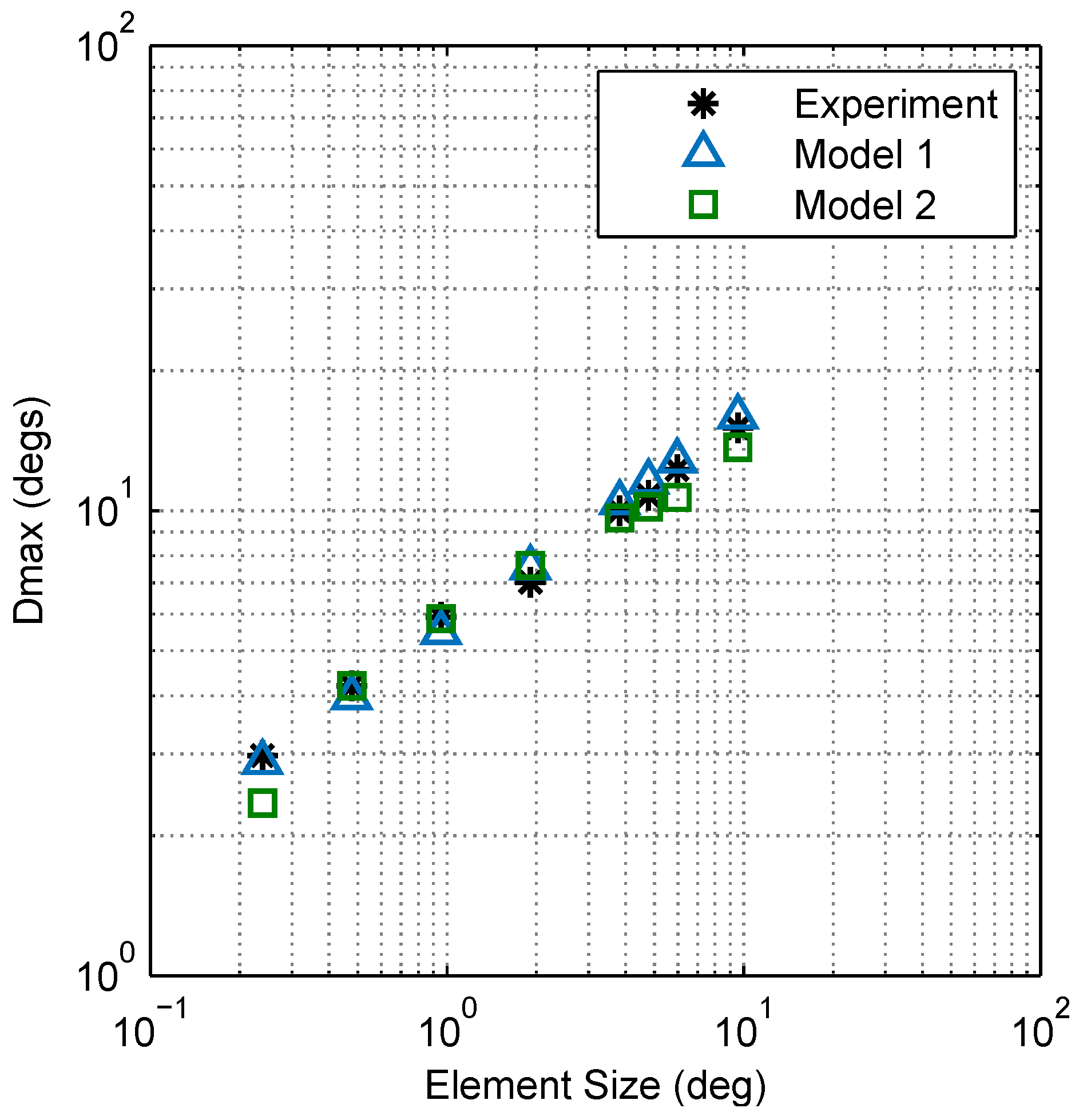
2.2.3. Model Comparison
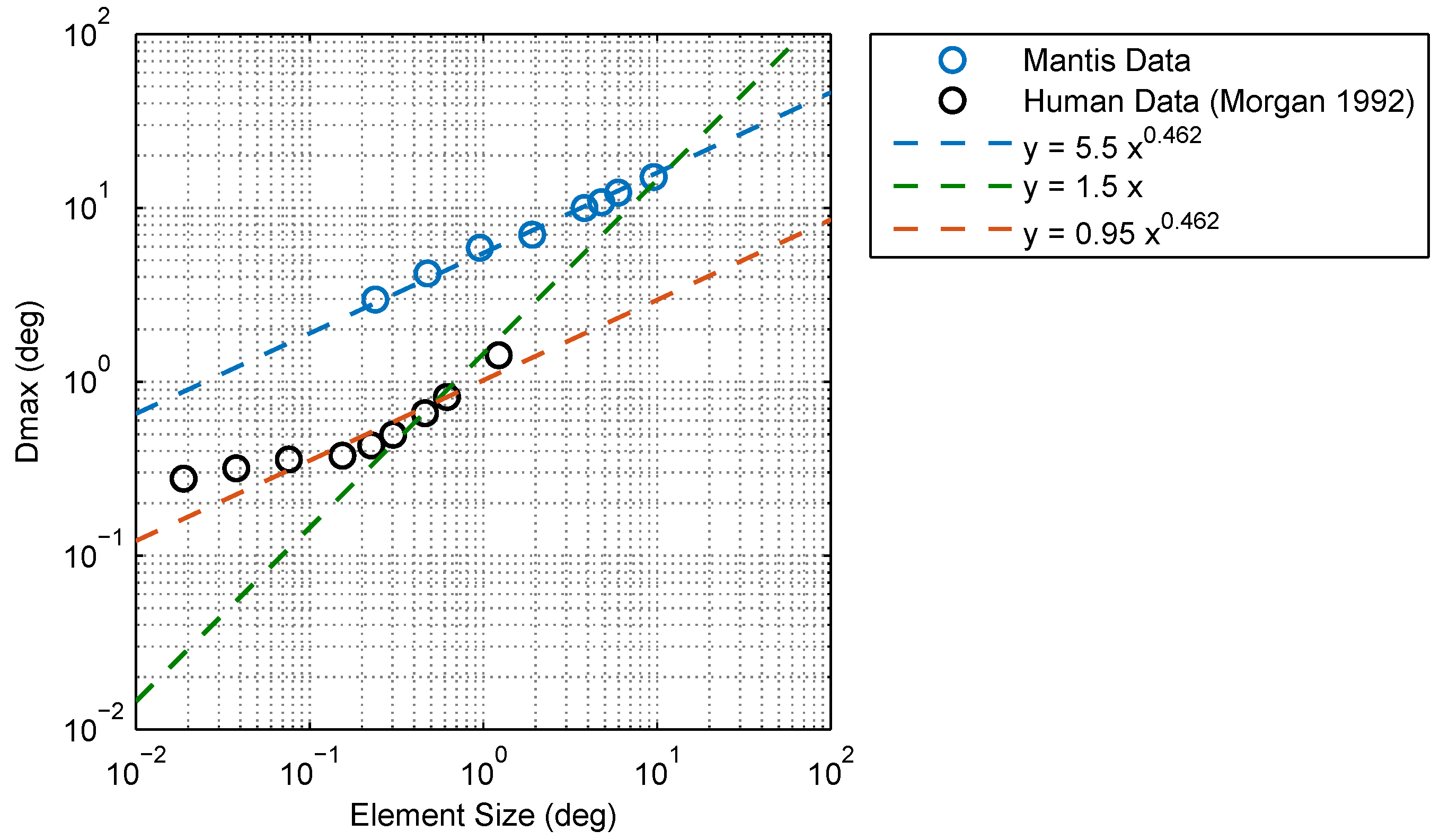
3. Discussion
4. Methods
4.1. Insects
4.2. Experimental Setup
4.3. Experimental Procedure
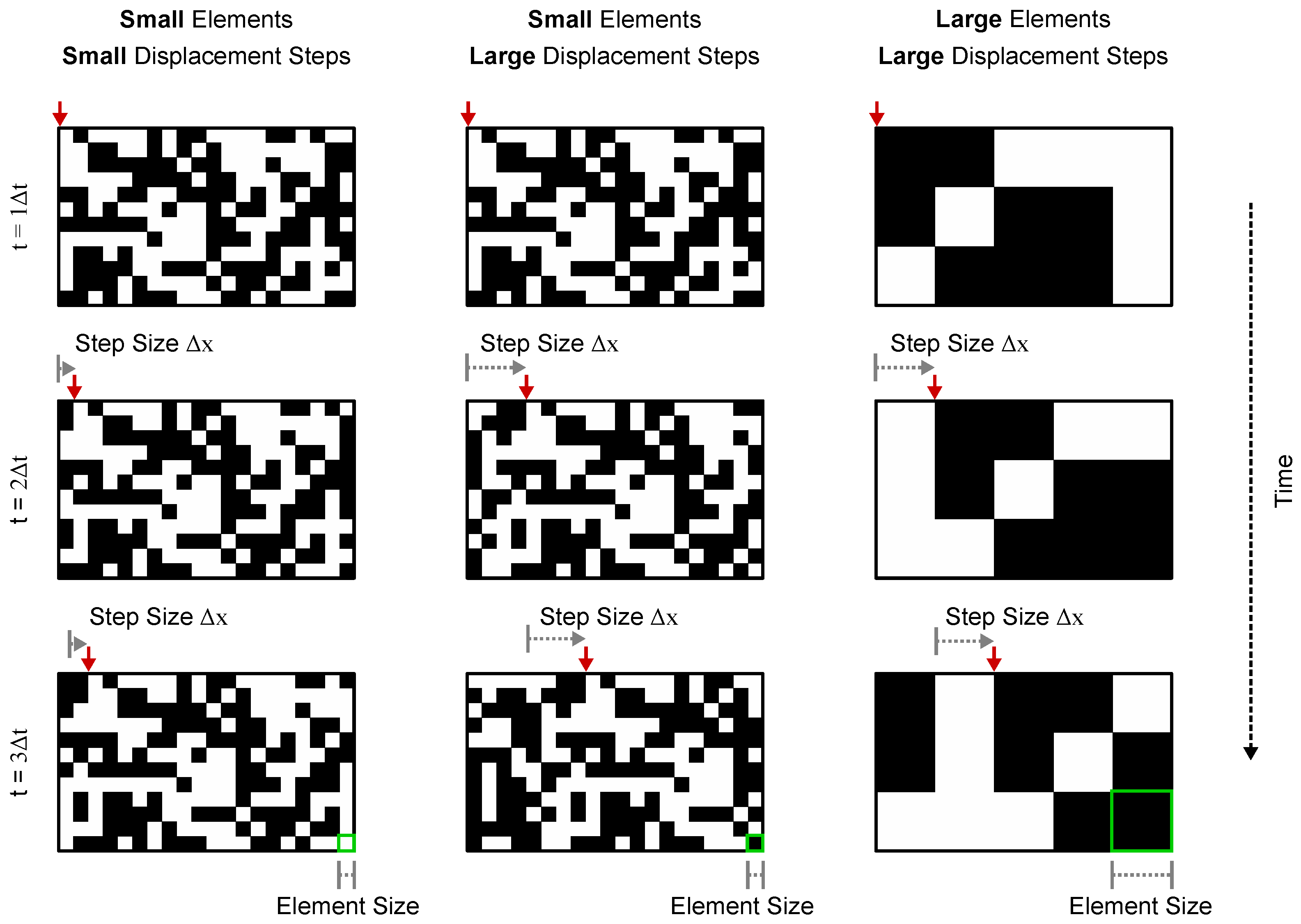
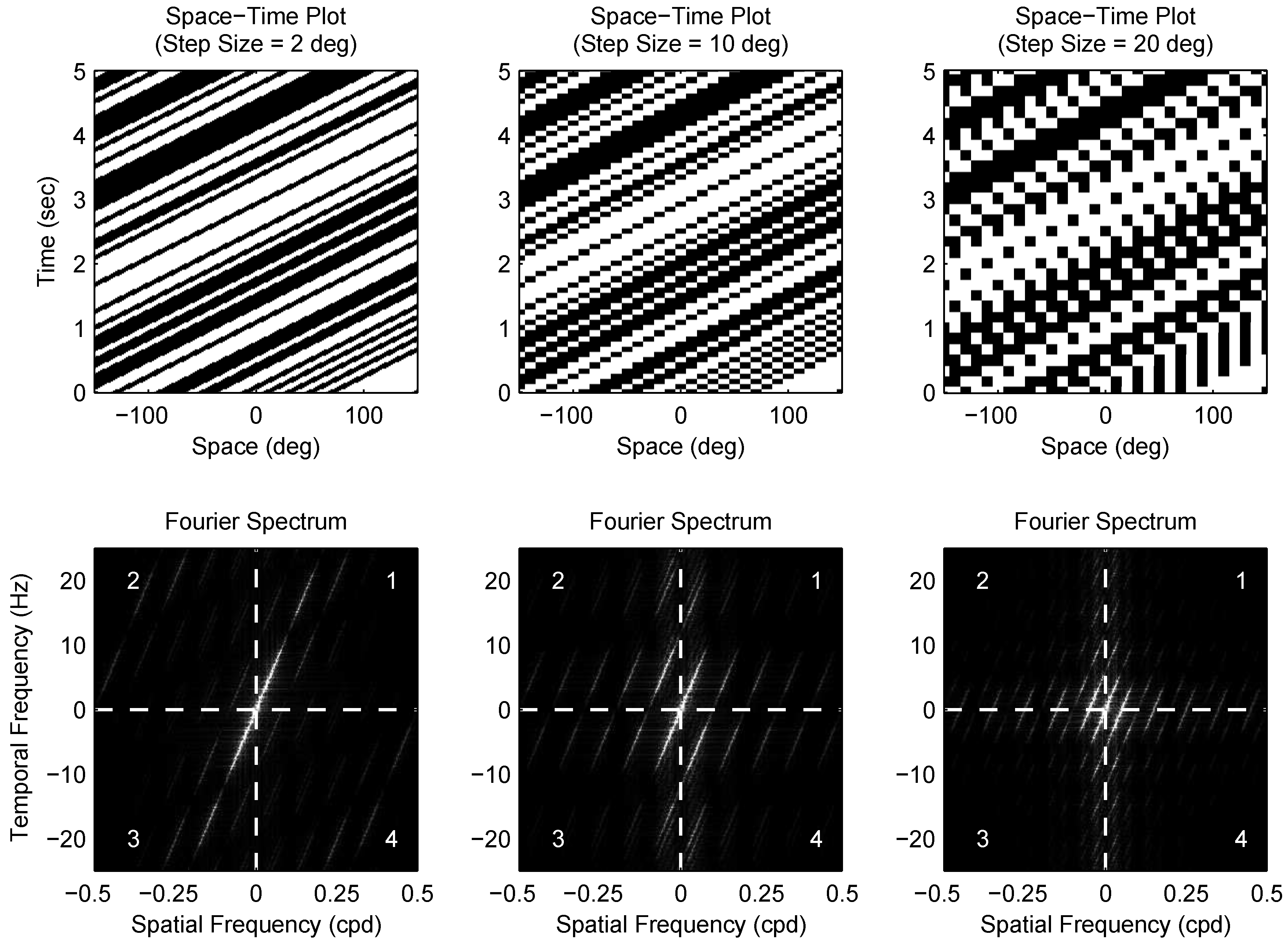
4.4. Visual Stimulus
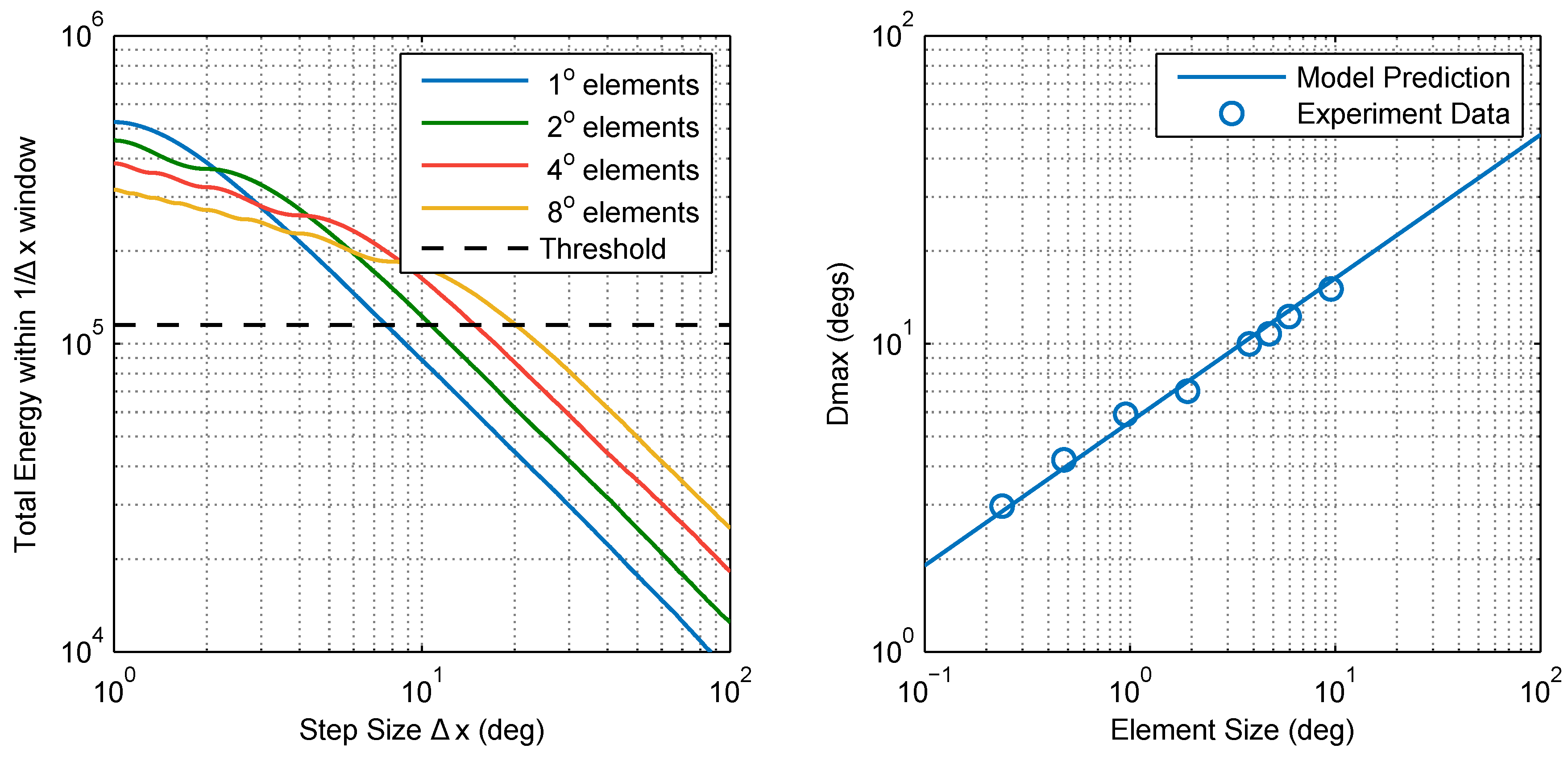
4.5. Calculating Dmax
4.6. Simulation and Model Fitting
4.6.1. Model 1
4.6.2. Model 2
5. Data Availability
Author Contributions
Funding
Conflicts of Interest
References
- Braddick, O. A short-range process in apparent motion. Vis. Res. 1974, 14, 519–527. [Google Scholar] [CrossRef]
- Cavanagh, P.; Boeglin, J.; Favreau, O.E. Perception of motion in equiluminous kinematograms. Perception 1985, 14, 151–162. [Google Scholar] [CrossRef] [PubMed]
- Morgan, M. Spatial filtering precedes motion detection. Nature 1992, 355, 344–346. [Google Scholar] [CrossRef] [PubMed]
- Sato, T. Reversed apparent motion with random dot patterns. Vis. Res. 1989, 29, 1749–1758. [Google Scholar] [CrossRef]
- Chang, J.J.; Julesz, B. Displacement limits for spatial frequency filtered random-dot cinematograms in apparent motion. Vis. Res. 1983, 23, 1379–1385. [Google Scholar] [CrossRef]
- Tripathy, S.P.; Shafiullah, S.N.; Cox, M.J. Influence of correspondence noise and spatial scaling on the upper limit for spatial displacement in fully-coherent random-dot kinematogram stimuli. PLoS ONE 2012, 7, e42995. [Google Scholar] [CrossRef] [PubMed]
- Adelson, E.H.; Bergen, J.R. Spatiotemporal energy models for the perception of motion. JOSA A 1985, 2, 284–299. [Google Scholar] [CrossRef]
- Hassenstein, B.; Reichardt, W. Systemtheoretische analyse der zeit-, reihenfolgen-und vorzeichenauswertung bei der bewegungsperzeption des rüsselkäfers chlorophanus. Z. Naturforsch. B 1956, 11, 513–524. [Google Scholar] [CrossRef]
- Borst, A. Fly visual course control: Behaviour, algorithms and circuits. Nat. Rev. Neurosci. 2014, 15, 590–599. [Google Scholar] [CrossRef] [PubMed]
- Nityananda, V.; Tarawneh, G.; Jones, L.; Busby, N.; Herbert, W.; Davies, R.; Read, J.C. The contrast sensitivity function of the praying mantis Sphodromantis lineola. J. Comp. Physiol. A 2015, 201, 741–750. [Google Scholar] [CrossRef] [PubMed]
- Tarawneh, G.; Nityananda, V.; Rosner, R.; Errington, S.; Herbert, W.; Cumming, B.G.; Read, J.C.; Serrano-Pedraza, I. Invisible noise obscures visible signal in insect motion detection. Sci. Rep. 2017, 7, 3496. [Google Scholar] [CrossRef] [PubMed]
- Tarawneh, G.; Nityananda, V.; Rosner, R.; Errington, S.; Herbert, W.; Arranz-Paraíso, S.; Busby, N.; Tampin, J.; Read, J.; Serrano-Pedraza, I. Contrast thresholds reveal different visual masking functions in humans and praying mantises. Biol. Open 2018, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wichmann, F.A.; Hill, N.J. The psychometric function: I. Fitting, sampling, and goodness of fit. Percept. Psychophys. 2001, 63, 1293–1313. [Google Scholar] [CrossRef] [PubMed]
- Nityananda, V.; Tarawneh, G.; Errington, S.; Serrano-Pedraza, I.; Read, J. The optomotor response of the praying mantis is driven predominantly by the central visual field. J. Comp. Physiol. A 2017, 203, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Bahl, A.; Ammer, G.; Schilling, T.; Borst, A. Object tracking in motion-blind flies. Nat. Neurosci. 2013, 16, 730–738. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, M.; Lehrer, M.; Kirchner, W.; Zhang, S. Range perception through apparent image speed in freely flying honeybees. Vis. Neurosci. 1991, 6, 519–535. [Google Scholar] [CrossRef] [PubMed]
- Borst, A.; Bahde, S. Visual information processing in the fly’s landing system. J. Comp. Physiol. A 1988, 163, 167–173. [Google Scholar] [CrossRef]
- Borst, A.; Haag, J.; Reiff, D.F. Fly motion vision. Ann. Rev. Neurosci. 2010, 33, 49–70. [Google Scholar] [CrossRef] [PubMed]
- Rossel, S. Regional differences in photoreceptor performance in the eye of the praying mantis. J. Comp. Physiol. 1979, 131, 95–112. [Google Scholar] [CrossRef]
- Borst, A. Neural circuits for elementary motion detection. J. Neurogenet. 2014, 28, 361–373. [Google Scholar] [CrossRef] [PubMed]
- Emerson, R.C.; Bergen, J.R.; Adelson, E.H. Directionally selective complex cells and the computation of motion energy in cat visual cortex. Vis. Res. 1992, 32, 203–218. [Google Scholar] [CrossRef]
- Movshon, J.A.; Thompson, I.D.; Tolhurst, D.J. Spatial summation in the receptive fields of simple cells in the cat’s striate cortex. J. Physiol. 1978, 283, 53–77. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T. High-Level Motion Processing: Computational, Neurobiological, and Psychophysical Perspectives; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Smith, A.; Ledgeway, T. Motion detection in human vision: a unifying approach based on energy and features. R. Soc. Lond. B Biolog. Sci. 2001, 268, 1889–1899. [Google Scholar] [CrossRef] [PubMed]
- Baker, C.L.; Braddick, O.J. The basis of area and dot number effects in random dot motion perception. Vis. Res. 1982, 22, 1253–1259. [Google Scholar] [CrossRef]
- Nakayama, K.; Silverman, G.H. Temporal and spatial characteristics of the upper displacement limit for motion in random dots. Vis. Res. 1984, 24, 293–299. [Google Scholar] [CrossRef]
- Todd, J.T.; Norman, J.F. The effects of spatiotemporal integration on maximum displacement thresholds for the detection of coherent motion. Vis. Res. 1995, 35, 2287–2302. [Google Scholar] [CrossRef]
- Nishida, S.; Sato, T. Positive motion after-effect induced by bandpass-filtered random-dot kinematograms. Vis. Res. 1992, 32, 1635–1646. [Google Scholar] [CrossRef]
- Snowden, R.; Braddick, O. The combination of motion signals over time. Vis. Res. 1989, 29, 1621–1630. [Google Scholar] [CrossRef]
- Snowden, R.; Braddick, O. Extension of displacement limits in multiple-exposure sequences of apparent motion. Vis. Res. 1989, 29, 1777–1787. [Google Scholar] [CrossRef]
- Von Fermi, G.; Richardt, W. Optomotorische reaktionen der fliege Musca domestica. Kybernetik 1963, 2, 15–28. [Google Scholar] [CrossRef]
- Eckert, H. Optomotorische Untersuchungen am visuellen System der Stubenfliege Musca domestica L. Kybernetik 1973, 14, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Joesch, M.; Plett, J.; Borst, A.; Reiff, D.F. Response properties of motion-sensitive visual interneurons in the lobula plate of Drosophila melanogaster. Curr. Biol. 2008, 18, 368–374. [Google Scholar] [CrossRef] [PubMed]
- Schnell, B.; Joesch, M.; Forstner, F.; Raghu, S.V.; Otsuna, H.; Ito, K.; Borst, A.; Reiff, D.F. Processing of horizontal optic flow in three visual interneurons of the Drosophila brain. J. Neurophysiol. 2010, 103, 1646–1657. [Google Scholar] [CrossRef] [PubMed]
- Rister, J.; Pauls, D.; Schnell, B.; Ting, C.Y.; Lee, C.H.; Sinakevitch, I.; Morante, J.; Strausfeld, N.J.; Ito, K.; Heisenberg, M. Dissection of the peripheral motion channel in the visual system of Drosophila melanogaster. Neuron 2007, 56, 155–170. [Google Scholar] [CrossRef] [PubMed]
- Joesch, M.; Schnell, B.; Raghu, S.V.; Reiff, D.F.; Borst, A. ON and OFF pathways in Drosophila motion vision. Nature 2010, 468, 300–304. [Google Scholar] [CrossRef] [PubMed]
- Brainard, D.H.; Vision, S. The psychophysics toolbox. Spat. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef] [PubMed]
- Pelli, D.G. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spat. Vis. 1997, 10, 437–442. [Google Scholar] [CrossRef] [PubMed]
- Kleiner, M.; Brainard, D.; Pelli, D. What’s new in Psychophysics Toolbox-3? [ECVP Abstract Supplement]. Perception 2007, 36, 1–16. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarawneh, G.; Jones, L.; Nityananda, V.; Rosner, R.; Rind, C.; Read, J.C.A. Apparent Motion Perception in the Praying Mantis: Psychophysics and Modelling. Vision 2018, 2, 32. https://doi.org/10.3390/vision2030032
Tarawneh G, Jones L, Nityananda V, Rosner R, Rind C, Read JCA. Apparent Motion Perception in the Praying Mantis: Psychophysics and Modelling. Vision. 2018; 2(3):32. https://doi.org/10.3390/vision2030032
Chicago/Turabian StyleTarawneh, Ghaith, Lisa Jones, Vivek Nityananda, Ronny Rosner, Claire Rind, and Jenny C. A. Read. 2018. "Apparent Motion Perception in the Praying Mantis: Psychophysics and Modelling" Vision 2, no. 3: 32. https://doi.org/10.3390/vision2030032
APA StyleTarawneh, G., Jones, L., Nityananda, V., Rosner, R., Rind, C., & Read, J. C. A. (2018). Apparent Motion Perception in the Praying Mantis: Psychophysics and Modelling. Vision, 2(3), 32. https://doi.org/10.3390/vision2030032





