Annual Performance Progression in Swimming Across Competition Levels and Race Distances
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Data Collection and Analysis
2.3. Statistical Analysis
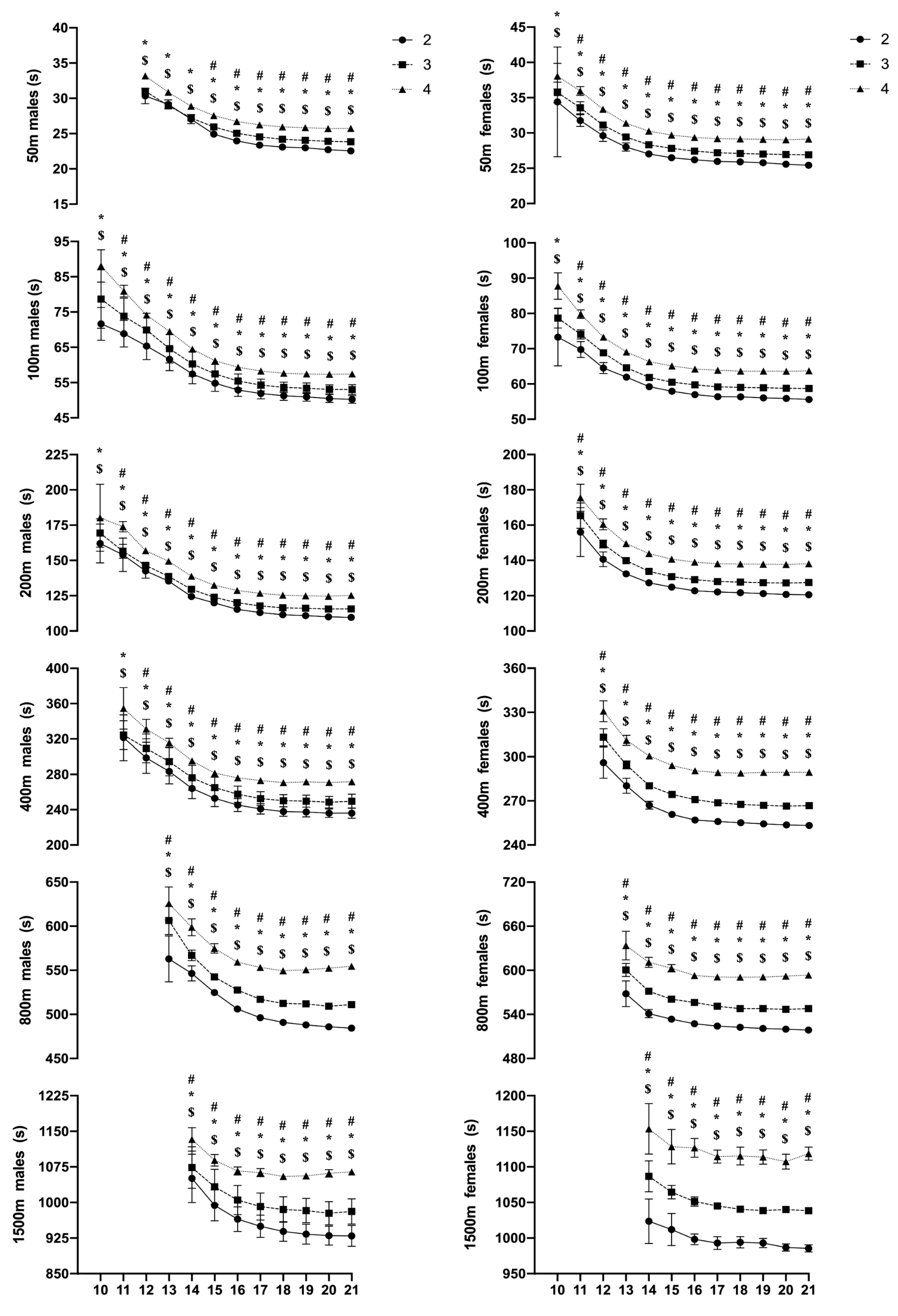
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LMM | Linear mixed model |
| REML | Restricted maximum likelihood |
| ICC | Intra-class correlation coefficient |
| M | Males |
| F | Females |
References
- Dweck, C.S. Self-Theories: Their Role in Motivation, Personality, and Development; Psychology Press: Philadelphia, PA, USA, 2000. [Google Scholar]
- Gollwitzer, P.M.; Sheeran, P. Implementation Intentions and Goal Achievement: A Meta-Analysis of Effects and Processes. Adv. Exp. Soc. Psychol. 2006, 38, 69–119. [Google Scholar] [CrossRef]
- Brustio, P.; Cardinale, M.; Lupo, C.; De Pasquale, P.; Boccia, G. Being a Top Swimmer During the Early Career Is Not a Prerequisite for Success: A Study on Sprinter Strokes. J. Sci. Med. Sport 2021, 24, 1272–1277. [Google Scholar] [CrossRef] [PubMed]
- Brustio, P.R.; Cardinale, M.; Lupo, C.; Boccia, G. Don’t Throw the Baby Out with the Bathwater: Talent in Swimming Sprinting Events Might Be Hidden at Early Age. Int. J. Sports Physiol. Perform. 2022, 17, 1550–1557. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.J.; Marinho, D.A.; Bragada, J.A.; Silva, A.J.; Barbosa, T.M. Stability of Elite Freestyle Performance from Childhood to Adulthood. J. Sports Sci. 2011, 29, 1183–1189. [Google Scholar] [CrossRef] [PubMed]
- Dormehl, S.J.; Robertson, S.J.; Williams, C.A. Modelling the Progression of Male Swimmers’ Performances through Adolescence. Sports 2016, 4, 2. [Google Scholar] [CrossRef]
- Costa, M.J.; Marinho, D.A.; Reis, V.M.; Silva, A.J.; Marques, M.C.; Bragada, J.A.; Barbosa, T.M. Tracking the Performance of World-Ranked Swimmers. J. Sports Sci. Med. 2010, 9, 411–417. [Google Scholar]
- Post, A.K.; Koning, R.H.; Visscher, C.; Elferink-Gemser, M.T. Multigenerational Performance Development of Male and Female Top-Elite Swimmers–A Global Study of the 100 m Freestyle Event. Scand. J. Med. Sci. Sports 2020, 30, 564–571. [Google Scholar] [CrossRef]
- Allen, S.V.; Vandenbogaerde, T.J.; Hopkins, W.G. Career Performance Trajectories of Olympic Swimmers: Benchmarks for Talent Development. Eur. J. Sport Sci. 2014, 14, 643–651. [Google Scholar] [CrossRef]
- Born, D.P.; Stöggl, T.; Lorentzen, J.; Romann, M.; Björklund, G. Predicting Future Stars: Probability and Performance Corridors for Elite Swimmers. J. Sci. Med. Sport 2024, 27, 113–118. [Google Scholar] [CrossRef]
- IOC Olympics. Available online: https://olympics.com/en/ (accessed on 25 July 2025).
- Canada, S. Natation. In Long Term Athlete Development Strategy; Swimming Canada: Ottawa, ON, Canada, 2008; ISBN 978-0-9809299-0-4. [Google Scholar]
- Gastin, P.B. Energy System Interaction and Relative Contribution during Maximal Exercise. Sports Med. 2001, 31, 725–741. [Google Scholar] [CrossRef]
- Peyrebrune, M.C.; Toubekis, A.G.; Lakomy, H.K.A.; Nevill, M.E. Estimating the Energy Contribution during Single and Repeated Sprint Swimming. Scand. J. Med. Sci. Sports 2014, 24, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Alshdokhi, K.; Petersen, C.; Clarke, J. Improvement and Variability of Adolescent Backstroke Swimming Performance by Age. Front. Sports Act. Living 2020, 2, 46. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Navarro, J.J.; López-Belmonte, Ó.; Gay, A.; Cuenca-Fernández, F.; Arellano, R. A New Model of Performance Classification to Standardize the Research Results in Swimming. Eur. J. Sport Sci. 2023, 23, 478–488. [Google Scholar] [CrossRef] [PubMed]
- Allen, S.V.; Hopkins, W.G. Age of Peak Competitive Performance of Elite Athletes: A Systematic Review. Sports Med. 2015, 45, 1431–1441. [Google Scholar] [CrossRef]
- Aquatics, W. Swimming Rules and Swimming Points. Available online: https://www.worldaquatics.com/rules/competition-regulations (accessed on 10 September 2024).
- Shapiro, J.R.; Klein, S.L.; Morgan, R. Stop Controlling for Sex and Gender in Global Health Research. BMJ Glob. Health 2021, 6, 6–8. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using SPSS; SAGE: New York, NY, USA, 2009; ISBN 9781847879066. [Google Scholar]
- Crowley, E.; Harrison, A.J.; Lyons, M. The Impact of Resistance Training on Swimming Performance: A Systematic Review. Sports Med. 2017, 47, 2285–2307. [Google Scholar] [CrossRef]
- Chatard, J.; Stewart, A.M. Training Load and Performance in Swimming. In World Book of Swimming: From Science to Performance; Seifert, L., Chollet, D., Mujika, I., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2011; pp. 359–373. ISBN 9781616682026. [Google Scholar]
- Mechsner, F.; Kerzel, D.; Knoblich, G.; Prinz, W. Perceptual Basis of Bimanual Coordination. Nature 2001, 414, 69–73. [Google Scholar] [CrossRef]
- Hirtz, P.; Starosta, W. Sensitive and Critical Periods of Motor Co-Ordination Development and Its Relation to Motor Learning. J. Hum. Kinet. 2002, 7, 19–28. [Google Scholar]
- Malina, R.M.; Rogol, A.D.; Cumming, S.P.; E Silva, M.J.C.; Figueiredo, A.J. Biological Maturation of Youth Athletes: Assessment and Implications. Br. J. Sports Med. 2015, 49, 852–859. [Google Scholar] [CrossRef]
- Silva, A.F.; Figueiredo, P.; Vilas-Boas, J.P.; Fernandes, R.J.; Seifert, L. The Effect of a Coordinative Training in Young Swimmers’ Performance. Int. J. Environ. Res. Public Health 2022, 19, 7020. [Google Scholar] [CrossRef]
- Nugent, F.J.; Comyns, T.M.; Warrington, G.D. Quality Versus Quantity Debate in Swimming: Perceptions and Training Practices of Expert Swimming Coaches. J. Hum. Kinet. 2017, 57, 147–158. [Google Scholar] [CrossRef][Green Version]
- Silva, A.F.; Ribeiro, J.; Vilas-Boas, J.P.; Figueiredo, P.; Alves, F.; Seifert, L.; Fernandes, R.J. Integrated Analysis of Young Swimmers’ Sprint Performance. Mot. Control 2019, 23, 354–364. [Google Scholar] [CrossRef]
- Ganzevles, S.P.M.; Beek, P.J.; Daanen, H.A.M.; Coolen, B.M.A.; Truijens, M.J. Differences in Swimming Smoothness between Elite and Non-Elite Swimmers. Sports Biomech. 2023, 22, 675–688. [Google Scholar] [CrossRef] [PubMed]
- Morais, J.E.; Barbosa, T.M.; Neiva, H.P.; Marques, M.C.; Marinho, D.A. Young Swimmers’ Classification Based on Performance and Biomechanical Determinants: Determining Similarities Through Cluster Analysis. Mot. Control 2022, 26, 396–411. [Google Scholar] [CrossRef] [PubMed]
- Born, D.P.; Stäcker, I.; Romann, M.; Stöggl, T. Competition Age: Does It Matter for Swimmers? BMC Res. Notes 2022, 15, 82. [Google Scholar] [CrossRef] [PubMed]
- Myer, G.D.; Jayanthi, N.; Difiori, J.P.; Faigenbaum, A.D.; Kiefer, A.W.; Logerstedt, D.; Micheli, L.J. Sport Specialization, Part I: Does Early Sports Specialization Increase Negative Outcomes and Reduce the Opportunity for Success in Young Athletes? Sports Health 2015, 7, 437–442. [Google Scholar] [CrossRef]
- Raedeke, T.D. Is Athlete Burnout More than Just Stress? A Sport Commitment Perspective. J. Sport Exerc. Psychol. 1997, 19, 396–417. [Google Scholar] [CrossRef]
| Performance Level | Level 4 | Level 3 | Level 2 | |||
|---|---|---|---|---|---|---|
| Distance | M | F | M | F | M | F |
| 50 m | 5849 | 3196 | 2645 | 1707 | 264 | 214 |
| 100 m | 4452 | 2661 | 3925 | 2151 | 824 | 363 |
| 200 m | 2601 | 1457 | 2889 | 1773 | 515 | 395 |
| 400 m | 1108 | 920 | 1759 | 1211 | 760 | 255 |
| 800 m | 498 | 384 | 862 | 687 | 318 | 194 |
| 1500 m | 303 | 150 | 691 | 287 | 356 | 86 |
| Performance Level | Age Categories [Years] | Linear Mixed Model Analysis | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9–10 | 10–11 | 11–12 | 12–13 | 13–14 | 14–15 | 15–16 | 16–17 | 17–18 | 18–19 | 19–20 | 20–21 | |||||
| 50 m n = 8751 | 2 | - | - | −7.6 ± 2.96 [−10.71, −4.5] | −5.14 ± 4.08 [−7.5, −2.78] | −5.68 ± 2.35 [−6.63, −4.73] | −5.83 ± 3.34 [−6.74, −4.91] | −3.70 ± 2.17 # [−4.16, −3.24] | −2.93 ± 2.08 [−3.31, −2.55] | −1.94 ± 2.28 [−2.33, −1.54] | −0.73 ± 1.81 # [−1.02, −0.43] | −1.28 ± 1.88 [−1.57, −1] | −0.92 ± 1.66 [−1.16, −0.69] | R2c= 0.36 ICC = 1.08−15 | (a) F[9|28282] = 342.4 | p < 0.001 |
| 3 | - | - | −7.34 ± 7.13 [−8.74, −5.94] | −7.02 ± 4.65 [−7.7, −6.35] | −6.42 ± 3.6 [−6.82, −6.03] | −4.72 ± 2.79 # [−4.94, −4.49] | −3.46 ± 2.39 # [−3.62, −3.3] | −2.20 ± 2.29 # [−2.33, −2.07] | −1.66 ± 2.16 # [−1.77, −1.55] | −0.78 ± 2.08 # [−0.89, −0.67] | −0.72 ± 2.06 [−0.82, −0.61] | −0.26 ± 2.03 # [−0.35, −0.16] | (b) F[2|28282] = 0.5 | p = 0.600 | ||
| 4 | - | - | −8.20 ± 5.11 [−8.82, −7.58] | −7.19 ± 4.24 # [−7.57, −6.81] | −6.41 ± 3.68 # [−6.65, −6.16] | −4.61 ± 3.02 # [−4.76, −4.45] | −3.29 ± 2.76 # [−3.41, −3.17] | −2.11 ± 2.39 # [−2.2, −2.02] | −1.34 ± 2.33 # [−1.43, −1.25] | −0.63 ± 2.28 # [−0.72, −0.53] | −0.51 ± 2.28 [−0.6, −0.42] | −0.05 ± 2.55 # * [−0.14, 0.04] | (c) F[18|28282] = 2.9 | p < 0.001 | ||
| 100 m n = 9201 | 2 | −12.01 ± 2.11 [−13.96, −10.1] | −7.42 ± 5.25 # [−10.21, −4.62] | −7.54 ± 4.38 [−8.85, −6.22] | −7.02 ± 3.25 [−7.77, −6.28] | −6.57 ± 3.35 [−7.2, −5.95] | −4.86 ± 2.48 # [−5.2, −4.52] | −3.50 ± 2.25 # [−3.75, −3.24] | −2.24 ± 1.97 # [−2.43, −2.05] | −1.85 ± 2.13 [−2.04, −1.66] | −0.86 ± 1.82 # [−1.02, −0.7] | −0.9 ± 1.74 [−1.05, −0.75] | −0.60 ± 1.73 [−0.74, −0.46] | R2c= 0.43 ICC = 1.64−14 | (a) F[11|32349] = 1153 | p < 0.001 |
| 3 | −12.99 ± 5.93 [−15.62, −10.4] | −9.54 ± 5.65 [−10.77, −8.31] | −8.8 ± 5.35 [−9.57, −8.03] | −7.49 ± 4.25 # [−7.93, −7.06] | −6.74 ± 3.47 # [−7.01, −6.47] | −4.80 ± 2.90 # [−4.97, −4.62] | −3.50 ± 2.48 # [−3.63, −3.38] | −2.10 ± 2.11 # [−2.2, −2.01] | −1.54 ± 2.11 # [−1.63, −1.45] | −0.62 ± 2.21 # [−0.72, −0.53] | −0.69 ± 2.07 [−0.78, −0.6] | −0.08 ± 2.08 * [−0.16, 0] | (b) F[2|32349] = 7.93 | p < 0.001 | ||
| 4 | −12.00 ± 5.00 [−14.34, −9.66] | −10.28 ± 5.12 * [−11.36, −9.2] | −8.61 ± 5.88 # [−9.39, −7.83] | −8.00 ± 4.48 [−8.4, −7.6] | −7.10 ± 3.96 # [−7.37, −6.83] | −5.15 ± 3.32 # [−5.33, −4.97] | −3.59 ± 3.13 # [−3.74, −3.45] | −2.18 ± 2.65 # [−2.29, −2.06] | −1.38 ± 2.54 # [−1.49, −1.27] | −0.60 ± 2.34 # [−0.71, −0.49] | −0.44 ± 2.46 [−0.56, −0.32] | 0.02 ± 2.61 * [−0.09, 0.13] | (c) F[22|32349] = 5.37 | p < 0.001 | ||
| 200 m n = 6005 | 2 | −6.25 ± 3.90 [−12.45, −0.04] | −9.15 ± 5.73 [−13.93, −4.36] | −6.48 ± 4.13 [−8.54, −4.43] | −6.21 ± 3.38 [−7.34, −5.08] | −6.89 ± 3.37 [−7.71, −6.06] | −4.59 ± 2.50 # [−5.01, −4.17] | −3.52 ± 2.59 [−3.86, −3.17] | −2.26 ± 2.13 # [−2.51, −2.02] | −1.52 ± 2.24 [−1.76, −1.27] | −0.81 ± 2.10 [−1.03, −0.58] | −0.72 ± 2.25 [−0.95, −0.48] | −0.39 ± 2.05 [−0.6, −0.18] | R2c= 0.37 ICC = 9.37−15 | (a) F[11|20519] = 623.68 | p < 0.001 |
| 3 | −10.24 ± 7.21 [−16.26, −4.21] | −8.44 ± 6.39 [−10.91, −5.96] | −8.83 ± 5.50 * [−10.07, −7.59] | −7.28 ± 4.23 [−7.91, −6.65] | −6.63 ± 3.31 [−6.97, −6.28] | −4.77 ± 2.86 # [−4.98, −4.57] | −3.35 ± 2.68 # [−3.51, −3.2] | −1.99 ± 2.14 # [−2.1, −1.88] | −1.34 ± 2.05 # [−1.44, −1.24] | −0.44 ± 2.22 # [−0.55, −0.33] | −0.47 ± 2.11 [−0.57, −0.37] | 0.12 ± 2.55 # [0.01, 0.24] | (b) F[2|20519] = 6.5 | p = 0.002 | ||
| 4 | −11.27 ± 5.31 [−19.72, −2.81] | −8.25 ± 3.98 [−9.82, −6.67] | −8.87 ± 3.78 [−9.79, −7.96] | −7.13 ± 4.32 # [−7.8, −6.45] | −7.29 ± 3.87 [−7.68, −6.9] | −4.95 ± 3.56 # [−5.22, −4.69] | −3.38 ± 3.04 # [−3.58, −3.19] | −1.99 ± 2.89 # [−2.16, −1.82] | −1.21 ± 2.91 # [−1.38, −1.04] | −0.35 ± 2.86 # [−0.53, −0.17] | −0.44 ± 2.73 [−0.61, −0.26] | 0.19 ± 3.36 # [0, 0.37] | (c) F[22|20519] = 3.4 | p < 0.001 | ||
| 400 m n = 3627 | 2 | - | −8.37 ± 2.46 [−10.43, −6.32] | −6.01 ± 3.39 [−7.51, −4.5] | −6.48 ± 3.65 [−7.48, −5.47] | −5.88 ± 3.06 [−6.43, −5.33] | −4.48 ± 2.51 # [−4.82, −4.14] | −3.23 ± 2.21 # [−3.48, −2.99] | −1.97 ± 1.96 # [−2.15, −1.78] | −1.44 ± 1.75 [−1.6, −1.28] | −0.41 ± 1.92 # [−0.58, −0.24] | −0.62 ± 2.05 [−0.8, −0.44] | −0.11 ± 2.3 [−0.3, 0.08] | R2c= 0.33 ICC = 2.64−15 | (a) F[8|12638] = 235.6 | p < 0.001 |
| 3 | - | −9.43 ± 5.00 [−12.78, −6.07] | −9.05 ± 3.41 * [−10.28, −7.82] | −6.94 ± 3.65 # [−7.59, −6.29] | −6.45 ± 3.44 [−6.86, −6.03] | −4.55 ± 3.01 # [−4.81, −4.28] | −3.07 ± 2.68 # [−3.27, −2.87] | −1.94 ± 2.46 # [−2.1, −1.78] | −1.12 ± 2.25 # [−1.26, −0.97] | −0.37 ± 2.36 # [−0.52, −0.21] | −0.28 ± 2.41 [−0.44, −0.12] | 0.33 ± 2.74 # * [0.17, 0.49] | (b) F[2|12638] = 3.2 | p = 0.968 | ||
| 4 | - | −6.53 ± 4.60 [−11.36, −1.69] | −8.94 ± 4.19 * [−10.6, −7.29] | −7.17 ± 4.22 [−8.09, −6.25] | −6.40 ± 3.76 [−6.97, −5.84] | −4.47 ± 3.45 # [−4.88, −4.07] | −2.72 ± 3.82 # [−3.1, −2.34] | −1.80 ± 3.83 # [−2.15, −1.46] | −1.20 ± 2.86 [−1.46, −0.94] | −0.07 ± 2.90 # [−0.36, 0.23] | −0.23 ± 3.12 [−0.55, 0.1] | 0.17 ± 3.51 # * [−0.13, 0.46] | (c) F[16|12638] = 1.8 | p = 0.034 | ||
| 800 m n = 1678 | 2 | - | - | - | −8.31 ± 4.72 [−14.17, −2.44] | −4.73 ± 2.42 [−5.68, −3.77] | −4.31 ± 2.52 [−4.89, −3.73] | −3.44 ± 2.15 [−3.83, −3.05] | −2.41 ± 2.01 [−2.72, −2.11] | −1.3 ± 2.15 [−1.61, −0.99] | −0.7 ± 2.08 [−1.0, −0.4] | −0.63 ± 2.01 [−0.91, −0.35] | −0.41 ± 2.12 [−0.68, −0.13] | R2c= 0.30 ICC = 0.01 | (a) F[9|5426] = 201.3 | p < 0.001 |
| 3 | - | - | - | −4.62 ± 3.47 [−6.29, −2.95] | −6.79 ± 3.16 [−7.6, −5.98] | −4.49 ± 2.96 [−4.93, −4.05] | −3.03 ± 2.8 # [−3.35, −2.71] | −2.12 ± 2.42 [−2.36, −1.89] | −1.06 ± 2.18 [−1.26, −0.86] | −0.29 ± 2.31 [−0.5, −0.07] | −0.36 ± 2.26 [−0.57, −0.15] | 0.21 ± 2.35 [0.02, 0.41] | (b) F[2|3673] = 0.02 | p = 0.982 | ||
| 4 | - | - | - | −6.4 ± 3.18 [−8.16, −4.64] | −6.67 ± 3.37 [−7.67, −5.67] | −4.35 ± 2.59 [−4.82, −3.87] | −2.95 ± 2.95 # [−3.42, −2.47] | −1.86 ± 3.0 [−2.27, −1.44] | −1.04 ± 2.44 [−1.36, −0.72] | −0.28 ± 2.61 [−0.65, 0.09] | −0.11 ± 3.3 [−0.62, 0.4] | 0.40 ± 3.57 [−0.03, 0.84] | (c) F[18|5311] = 2.13 | p = 0.003 | ||
| 1500 m n = 1350 | 2 | - | - | - | - | −4.78 ± 2.68 [−5.97, −3.59] | −4.45 ± 2.62 [−5.02, −3.87] | −3.07 ± 1.92 # [−3.4, −2.74] | −1.95 ± 1.8 # [−2.21, −1.69] | −1.27 ± 1.89 [−1.53, −1.01] | −0.74 ± 1.83 [−0.99, −0.49] | −0.47 ± 1.7 [−0.68, −0.25] | −0.09 ± 1.87 [−0.31, 0.14] | R2c= 0.30 ICC = 0.02 | (a) F[7|4197] = 204.7 | p < 0.001 |
| 3 | - | - | - | - | −6.04 ± 2.75 [−6.85, −5.23] | −4.23 ± 2.73 # [−4.69, −3.76] | −2.83 ± 2.67 # [−3.17, −2.5] | −1.61 ± 2.3 # [−1.86, −1.36] | −0.99 ± 2.19 [−1.21, −0.76] | −0.3 ± 2.08 # [−0.52, −0.08] | −0.45 ± 2.04 [−0.66, −0.23] | 0.15 ± 2.02 [−0.04, 0.34] | (b) F[2|1569] = 1.1 | p = 0.339 | ||
| 4 | - | - | - | - | −7.1 ± 4.13 * [−9.08, −5.11] | −4.48 ± 3.52 # [−5.4, −3.57] | −2.61 ± 2.76 # [−3.19, −2.02] | −1.49 ± 3.24 [−2.1, −0.89] | −0.77 ± 2.52 [−1.22, −0.33] | −0.54 ± 2.34 [−0.97, −0.1] | −0.15 ± 2.72 [−0.7, 0.39] | 0.17 ± 2.69 [−0.26, 0.6] | (c) F[14|4305] = 1.9 | p = 0.021 | ||
| Performance Level | Age Categories [Years] | Linear Mixed Model Analysis | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9–10 | 10–11 | 11–12 | 12–13 | 13–14 | 14–15 | 15–16 | 16–17 | 17–18 | 18–19 | 19–20 | 20–21 | |||||
| 50 m n = 5117 | 2 | −15.02 ± 5.17 [−27.87, −2.17] | −8.53 ± 4.45 # [−11.72, −5.34] | −6.69 ± 3.84 [−8.82, −4.57] | −6.10 ± 2.54 [−7.36, −4.83] | −3.37 ± 2.60 # [−4.21, −2.53] | −2.37 ± 2.16 [−2.9, −1.83] | −1.76 ± 2.07 [−2.17, −1.35] | −1.30 ± 1.96 [−1.64, −0.95] | −0.65 ± 1.82 [−0.98, −0.33] | −0.70 ± 2.01 [−1.06, −0.34] | −0.86 ± 1.68 [−1.13, −0.58] | −0.65 ± 1.61 [−0.9, −0.41] | R2c= 0.34 ICC = 1.44−14 | (a) F[11|18231] = 312.2 | p < 0.001 |
| 3 | −12.19 ± 5.08 [−15.27, −9.12] | −8.51 ± 4.95 # [−9.98, −7.04] | −7.24 ± 3.77 [−8.1, −6.37] | −5.77 ± 4.19 # [−6.37, −5.17] | −3.68 ± 2.63 # [−3.95, −3.41] | −2.33 ± 2.26 # [−2.52, −2.15] | −1.41 ± 1.95 # [−1.55, −1.27] | −0.91 ± 2.08 [−1.05, −0.78] | −0.49 ± 1.99 [−0.62, −0.36] | −0.31 ± 2.10 [−0.46, −0.17] | −0.31 ± 2.00 [−0.44, −0.17] | −0.21 ± 2.04 [−0.33, −0.09] | (b) F[2|18231] = 3.3 | p = 0.037 | ||
| 4 | −12.12 ± 6.08 [−15.14, −9.1] | −9.03 ± 4.14 # * [−9.91, −8.16] | −7.26 ± 3.98 # [−7.9, −6.63] | −5.86 ± 3.35 # [−6.2, −5.51] | −3.74 ± 2.99 # [−3.96, −3.51] | −2.33 ± 2.75 # [−2.5, −2.17] | −1.24 ± 2.37 # [−1.37, −1.12] | −0.69 ± 2.40 # [−0.81, −0.57] | −0.25 ± 2.30 # [−0.37, −0.14] | −0.09 ± 2.28 [−0.22, 0.04] | −0.12 ± 2.30 [−0.25, 0.02] | 0.21 ± 2.45 [0.09, 0.33] | (c) F[22|18231] = 1.3 | p = 0.136 | ||
| 100 m n = 5175 | 2 | −20.81 ± 16.55 [−169.5, 127.92] | −8.34 ± 4.11 # [−10.39, −6.3] | −7.53 ± 3.33 [−8.88, −6.19] | −5.95 ± 3.68 [−6.99, −4.92] | −3.90 ± 2.76 # [−4.47, −3.34] | −2.50 ± 1.85 # [−2.81, −2.19] | −1.79 ± 1.86 [−2.06, −1.51] | −1.15 ± 1.84 [−1.4, −0.9] | −0.46 ± 1.77 [−0.7, −0.23] | −0.74 ± 2.03 [−1.01, −0.47] | −0.43 ± 1.78 [−0.66, −0.2] | −0.44 ± 1.95 [−0.67, −0.2] | R2c= 0.41 ICC = 3.33−15 | (a) F[11|19776] = 593.9 | p < 0.001 |
| 3 | −14.35 ± 6.94 * [−17.8, −10.9] | −9.81 ± 4.93 # [−10.91, −8.72] | −8.74 ± 4.56 [−9.48, −8] | −6.13 ± 3.70 # [−6.55, −5.71] | −4.44 ± 3.08 # [−4.71, −4.17] | −2.42 ± 2.46 # [−2.6, −2.25] | −1.57 ± 2.00 # [−1.7, −1.45] | −1.08 ± 2.08 [−1.2, −0.96] | −0.44 ± 1.94 # [−0.55, −0.33] | −0.06 ± 2.29 [−0.2, 0.07] | −0.23 ± 2.01 [−0.35, −0.11] | −0.06 ± 2.33 [−0.18, 0.06] | (b) F[2|19776] = 22.6 | p < 0.001 | ||
| 4 | −13.29 ± 6.22 * [−16.05, −10.53] | −10.46 ± 5.24 # [−11.53, −9.4] | −8.95 ± 4.94 # [−9.66, −8.25] | −6.40 ± 3.95 # [−6.78, −6.03] | −4.33 ± 3.39 # [−4.59, −4.08] | −2.48 ± 2.97 # [−2.66, −2.29] | −1.46 ± 2.69 # [−1.61, −1.31] | −0.76 ± 2.68 # [−0.9, −0.62] | −0.32 ± 2.70 [−0.47, −0.17] | 0.10 ± 2.64 [−0.07, 0.27] | −0.16 ± 2.69 [−0.33, 0.02] | 0.20 ± 2.78 [0.05, 0.35] | (c) F[22|19776] = 6.9 | p < 0.001 | ||
| 200 m n = 3625 | 2 | - | −8.86 ± 4.31 [−12.85, −4.87] | −7.01 ± 3.80 [−8.97, −5.06] | −5.58 ± 2.79 [−6.49, −4.66] | −4.16 ± 2.91 [−4.81, −3.5] | −2.37 ± 2.03 # [−2.71, −2.03] | −1.84 ± 1.93 [−2.12, −1.56] | −0.88 ± 1.76 [−1.11, −0.65] | −0.59 ± 1.81 [−0.82, −0.36] | −0.42 ± 1.97 [−0.67, −0.16] | −0.44 ± 1.71 [−0.65, −0.22] | −0.14 ± 1.87 [−0.36, 0.07] | R2c= 0.33 ICC = 0.00 | (a) F[10|13352] = 425.99 | p < 0.001 |
| 3 | - | −11.56 ± 5.61 [−13.83, −9.3] | −8.14 ± 3.59 # [−8.96, −7.32] | −6.52 ± 3.72 # [−7.04, −5.99] | −4.32 ± 3.11 # [−4.64, −4.01] | −2.51 ± 2.35 # [−2.7, −2.32] | −1.53 ± 1.96 # [−1.67, −1.39] | −0.90 ± 2.00 # [−1.02, −0.77] | −0.36 ± 1.97 # [−0.48, −0.24] | −0.17 ± 2.21 [−0.31, −0.02] | −0.05 ± 2.27 [−0.2, 0.09] | 0.10 ± 2.32 [−0.04, 0.23] | (b) F[2|13352] = 12.35 | p < 0.001 | ||
| 4 | - | −8.48 ± 7.64 [−11.71, −5.25] | −7.89 ± 4.60 [−9.09, −6.68] | −6.57 ± 3.62 # [−7.14, −6] | −4.15 ± 3.46 # [−4.52, −3.78] | −2.43 ± 2.78 # [−2.67, −2.19] | −1.57 ± 2.65 # [−1.78, −1.36] | −0.91 ± 2.64 # [−1.11, −0.72] | −0.31 ± 2.75 # [−0.52, −0.1] | −0.08 ± 2.97 [−0.33, 0.18] | −0.08 ± 2.59 [−0.31, 0.15] | 0.38 ± 2.82 [0.17, 0.59] | (c) F[22|13354] = 2.9 | p < 0.001 | ||
| 400 m n = 2386 | 2 | - | - | −6.93 ± 1.93 [−8.54, −5.32] | −5.26 ± 3.13 [−6.49, −4.02] | −3.89 ± 2.24 [−4.5, −3.29] | −2.63 ± 2.19 [−3.1, −2.15] | −1.82 ± 1.75 [−2.14, −1.49] | −0.89 ± 1.73 [−1.18, −0.6] | −0.48 ± 1.52 [−0.71, −0.24] | −0.38 ± 1.69 [−0.65, −0.12] | −0.21 ± 1.72 [−0.48, 0.05] | −0.07 ± 2.00 [−0.36, 0.22] | R2c= 0.29 ICC = 0.00 | (a) F[10|8712] = 229.2 | p < 0.001 |
| 3 | - | - | −6.93 ± 4.01 [−8.1, −5.75] | −6.00 ± 3.66 [−6.61, −5.39] | −3.99 ± 2.97 # [−4.36, −3.63] | −2.40 ± 2.62 # [−2.66, −2.13] | −1.43 ± 1.98 # [−1.6, −1.25] | −0.83 ± 2.33 [−1.02, −0.65] | −0.42 ± 2.20 [−0.6, −0.25] | −0.21 ± 2.31 [−0.39, −0.02] | −0.14 ± 2.22 [−0.32, 0.04] | 0.09 ± 2.25 [−0.06, 0.24] | (b) F[2|8712] = 5.2 | p = 0.006 | ||
| 4 | - | - | −8.72 ± 5.14 [−10.34, −7.1] | −6.31 ± 3.99 # [−7.07, −5.55] | −4.07 ± 3.54 # [−4.52, −3.63] | −2.42 ± 3.12 # [−2.75, −2.09] | −1.20 ± 2.83 # [−1.47, −0.92] | −0.84 ± 2.78 [−1.11, −0.58] | −0.34 ± 2.88 [−0.62, −0.05] | −0.23 ± 2.74 [−0.53, 0.06] | 0.18 ± 2.85 [−0.14, 0.49] | 0.25 ± 3.06 [−0.04, 0.53] | (c) F[20|8712] = 1.9 | p = 0.012 | ||
| 800 m n = 1265 | 2 | - | - | - | −3.94 ± 3.06 [−6.13, −1.75] | −3.93 ± 2.01 [−4.6, −3.26] | −1.99 ± 1.76 # [−2.44, −1.54] | −1.53 ± 1.86 [−1.95, −1.11] | −0.96 ± 1.73 [−1.3, −0.62] | −0.51 ± 1.45 [−0.78, −0.24] | −0.33 ± 1.45 [−0.61, −0.06] | −0.36 ± 1.56 [−0.65, −0.08] | −0.23 ± 1.75 [−0.52, 0.06] | R2c= 0.22 ICC = 0.00 | (a) F[9|4284] = 108.9 | p < 0.001 |
| 3 | - | - | - | −6.06 ± 3.15 | −3.91 ± 2.74 # | −2.44 ± 2.47 # | −1.21 ± 2.04 # | −0.83 ± 1.87 | −0.52 ± 1.99 | −0.18 ± 1.96 | −0.18 ± 1.95 | 0.04 ± 2.31 | (b) F[2|4284] = 0.105 | p = 0.902 | ||
| [−7.13, −4.99] | [−4.43, −3.39] | [−2.78, −2.09] | [−1.45, −0.97] | [−1.03, −0.63] | [−0.73, −0.31] | [−0.39, 0.03] | [−0.39, 0.03] | [−0.17, 0.26] | ||||||||
| 4 | - | - | - | −5.44 ± 2.97 [−7.02, −3.86] | −3.59 ± 3.17 [−4.41, −2.77] | −2.39 ± 3.09 [−2.99, −1.8] | −1.31 ± 2.56 # [−1.73, −0.89] | −0.63 ± 2.59 [−1.04, −0.23] | −0.64 ± 2.32 [−1.01, −0.27] | −0.60 ± 2.42 [−1.01, −0.18] | 0.22 ± 2.42 [−0.19, 0.63] | 0.29 ± 2.67 [−0.08, 0.66] | (c) F[18|4284] = 1.6 | p = 0.055 | ||
| 1500 m n =523 | 2 | - | - | - | - | −3.46 ± 2.67 [−6.26, −0.65] | −1.63 ± 1.27 [−2.4, −0.86] | −1.27 ± 2.07 [−2.09, −0.45] | −0.67 ± 1.38 [−1.16, −0.18] | −0.58 ± 1.86 [−1.19, 0.02] | −0.75 ± 1.81 [−1.34, −0.16] | −0.69 ± 1.29 [−1.12, −0.27] | 0.01 ± 2.02 [−0.53, 0.55] | R2c= 0.13 ICC = 0.00 | (a) F[7|1361] = 20.9 | p < 0.001 |
| 3 | - | - | - | - | −3.12 ± 2.17 [−4.93, −1.31] | −2.53 ± 2.57 [−3.28, −1.77] | −1.63 ± 2.17 [−2.1, −1.16] | −0.76 ± 2.01 [−1.13, −0.39] | −0.79 ± 1.67 [−1.11, −0.48] | −0.32 ± 1.45 [−0.6, −0.03] | −0.13 ± 1.78 [−0.44, 0.17] | −0.11 ± 1.88 [−0.38, 0.16] | (b) F[2|1361] = 0.5 | p = 0.584 | ||
| 4 | - | - | - | - | −3.79 ± 2.72 [−5.74, −1.85] | −3.82 ± 2.85 [−5.73, −1.9] | −1.26 ± 2.71 # [−2.11, −0.41] | −0.89 ± 2.80 [−1.67, −0.11] | 0.04 ± 2.12 [−0.6, 0.68] | −0.03 ± 2.30 [−0.71, 0.65] | −0.40 ± 2.22 [−1.07, 0.26] | −0.07 ± 2.26 [−0.55, 0.41] | (c) F[14|1361] = 1.5 | p = 0.115 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Navarro, J.J.; Born, D.-P. Annual Performance Progression in Swimming Across Competition Levels and Race Distances. J. Funct. Morphol. Kinesiol. 2025, 10, 297. https://doi.org/10.3390/jfmk10030297
Ruiz-Navarro JJ, Born D-P. Annual Performance Progression in Swimming Across Competition Levels and Race Distances. Journal of Functional Morphology and Kinesiology. 2025; 10(3):297. https://doi.org/10.3390/jfmk10030297
Chicago/Turabian StyleRuiz-Navarro, Jesús J., and Dennis-Peter Born. 2025. "Annual Performance Progression in Swimming Across Competition Levels and Race Distances" Journal of Functional Morphology and Kinesiology 10, no. 3: 297. https://doi.org/10.3390/jfmk10030297
APA StyleRuiz-Navarro, J. J., & Born, D.-P. (2025). Annual Performance Progression in Swimming Across Competition Levels and Race Distances. Journal of Functional Morphology and Kinesiology, 10(3), 297. https://doi.org/10.3390/jfmk10030297








