Design of a Fiber Temperature and Strain Sensor Model Using a Fiber Bragg Grating to Monitor Road Surface Conditions
Abstract
1. Introduction
- Thermocouples: Thermocouples are sensors that utilize the potential difference that occurs at the junction of two different metals when the temperature changes. Thermocouples can measure temperature extremes of 2000 °C or higher. However, their accuracy and sensitivity are much lower than FBG-based fiber sensors. Thermocouples are also susceptible to electrical interference and require frequent calibration.
- Resistive thermometers (RTDs): RTDs, or resistive thermometers, measure temperature based on the change in resistance of the metal as the temperature changes. They provide a high accuracy over a range of −200 °C to +850 °C, but their sensitivity and stability can decrease over time. RTDs also require electrical connections, which can limit their use in extreme environments.
- Infrared sensors: Infrared sensors measure temperature by the radiant heat energy of an object. They are suitable for non-contact monitoring and can operate over a wide temperature range, but their accuracy depends on the emissivity of the surface, and they may be ineffective in the presence of dust, smoke, or other interference.
- Temperature-compensated electrical strain gauges: Strain gauges measure mechanical strain, but their accuracy can be compromised by changes in temperature. Complex circuitry and calibration are required to compensate for temperature effects, but even with temperature compensation, these sensors can be less accurate than FBG-based fiber sensors.
2. Materials and Methods

- Gauss function ;
- Raised sine function (Raised sine) ;
- Sine function (Sinc) ;
- Tangent function (Tanh) ;
- Blackman function ;
- Hamming function ;
- Cosine function (Cosine) ;
- Cauchy function (Cauchy) .
- The sensors should be as small as possible to minimize interference with the pavement layers.
- For strain measurement, the stiffness of the sensors should match the stiffness of the pavement mix to properly evaluate the mechanical properties of the pavement.
- The sensors should be able to withstand the maximum loads experienced during pavement construction, such as temperature and compression.
- For long-term pavement monitoring, the sensors should be resistant to corrosion and thermo-mechanical conditions.
3. Results
3.1. Characteristics of the Bragg Grid with Respect to Temperature Fluctuations and Strain
3.2. Model of Fiber Temperature Sensor Based on in MATLAB R2022b Environment
- Length of the grating;
- Refractive index neff;
- Number of grid periods;
- Bragg wavelength;
- Apodization profile;
- Average value of the refractive index modulation;
- Amplitude of the refractive index modulation;
- Grid period;
- Refractive index of the core in a fiber without a grating.
- Light source;
- Test probe;
- Placed in a measuring probe;
- Spectrum analyzer;
- Measuring element used to measure temperature.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alavi, A.H.; Hasni, H.; Lajnef, N.; Chatti, K. Continuous health monitoring of pavement systems using smart sensing technology. Constr. Build. Mater. 2016, 114, 719–736. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, H.; Ma, S.; Xu, H. Quality control of asphalt pavement compaction using fibre Bragg grating sensing technology. Constr. Build. Mater. 2013, 54, 53–59. [Google Scholar]
- Timm, D.H.; Priest, A.L.; McEwen, T.V. Design and Instrumentation of the Structural Pavement Experiment at the NCAT Test Track; National Center for Asphalt Technology, Auburn University: Auburn, AL, USA, 2004. [Google Scholar]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, W.; Huang, Y.; Wang, H.; Jianping, H.; Huang, M.; Jinping, O. Optical fiber Bragg grating sensor assembly for 3D strain monitoring and its case study in highway pavement. Mech. Syst. Signal Process. 2012, 28, 36–49. [Google Scholar] [CrossRef]
- Song, I.; Little, D.N.; Masad, E.A.; Lytton, R. Comprehensive evaluation of damage in asphalt mastics using X-ray CT; continuum mechanics and micromechanics. J. Assoc. Asph. Paving Technol. 2005, 74, 885–920. [Google Scholar]
- Liu, H.Y.; Liang, D.K.; Zeng, J. Long period fiber grating transverse load effect-based sensor for asphalt pavement pressure field measurements. Sens. Actuators A Phys. 2016, 168, 262–266. [Google Scholar] [CrossRef]
- Kashaganova, G.; Orazaliyeva, S.; Balbayev, G.; Alimseitova, Z.; Carbone, G. Application of Apodized s in Information Security Systems Mechanisms and Machine Science. In Proceedings of the I4SDG Workshop 2021: IFToMM for Sustainable Development Goals 1, Online, 25–26 November 2021; Springer International Publishing: Cham, Switzerland, 2022; Volume 108, pp. 451–460. [Google Scholar]
- Jian-Neng, W.; Jaw-Luen, T. Using Sensors to Monitor Pavement Structures. J. Transp. Res. Board 2005, 1913, 165–176. [Google Scholar]
- Kashaganova, G.; Kozbakova, A.; Kartbayev, T.; Balbayev, G.; Togzhanova, K.; Alimseitova, Z.; Orazaliyeva, S. Research of a Fiber Sensor Based on for Road Surface Monitoring. J. Electron. 2023, 12, 2491. [Google Scholar] [CrossRef]
- Kisala, P. Optoelectronic sensor for simultaneous and independent temperature and elongation measurement using Bragg gratings. Prz. Elektrotech. 2012, 11, 343–346. [Google Scholar]
- Wen, X.; Zhang, D.; Qian, Y.; Li, J.; Fei, N. Improving the peak wavelength detection accuracy of Sn–doped, H2–loaded FBG high temperature sensors by wavelet filter and Gaussian curve fitting. Sens. Actuators A Phys. 2012, 174, 91–95. [Google Scholar] [CrossRef]
- Peng, H.; Su, Y.; Ye, Z.; Zhou, B. A novel fiber Bragg grating sensor for weak pressure measurement based on the Stokes parameter. Opt. Fiber Technol. 2012, 18, 485–489. [Google Scholar] [CrossRef]
- An, J.; Liu, T.; Jin, Y. Fiber optic vibration sensor based on the tilted fiber Bragg grating. Adv. Mater. Sci. Eng. 2013, 2013, 545013. [Google Scholar] [CrossRef]
- Makovec, A.; Berruti, G.; Consales, M.; Giordano, M.; Petagna, P.; Buontempo, S.; Breglio, G.; Szillasi, Z.; Beni, N.; Cusano, A. Radiation hard polyimide–coated FBG optical sensors for relative humidity monitoring in the CMS experiment at CERN. J. Instrum. 2014, 9, C03040. [Google Scholar] [CrossRef]
- Song, L.; Fang, F.; Zhao, J. Study on viscosity measurement using fiber Bragg grating micro–vibration. Meas. Sci. Technol. 2013, 24, 015301. [Google Scholar] [CrossRef]
- Kisala, P. Detection of material defects with indirect method by determining the linear expansion with FBG sensor. Prz. Elektrotech. 2013, 89, 29–33. [Google Scholar]
- Kahandawa, G.C.; Epaarachchi, J.; Wang, H.; Lau, K.T. Use of FBG sensors for SHM in aerospace structures. Photonic Sens. 2012, 2, 203–214. [Google Scholar] [CrossRef]
- Luo, B.; Zhao, M.; Zhou, X.; Shi, S.; Han, X.; Wang, Y. Etched fiber Bragg grating for refractive index distribution measurement. Opt. Int. J. Light Electron Opt. 2013, 124, 2777–2780. [Google Scholar] [CrossRef]
- Garcia, I.; Zubia, J.; Durana, G.; Aldabaldetreku, G.; Illarramendi, M.A.; Villatoro, J. Optical fiber sensors for aircraft structural health monitoring. Sensors 2015, 15, 15494–15519. [Google Scholar] [CrossRef]
- Lee, B.H.; Kim, Y.H.; Park, K.S.; Eom, J.B.; Kim, M.J.; Rho, B.S.; Choi, H.Y. Interferometric fiber optic sensors. Sensors 2012, 12, 2467–2486. [Google Scholar] [CrossRef]
- Gao, P.; Chen, X.; Feng, W. Simultaneous measurement of external refractive index and temperature based on long–period–grating–inscribed Sagnac interferometer and fiber Bragg grating. Rev. Sci. Instrum. 2012, 83, 105001. [Google Scholar] [CrossRef]
- Hernández-Acosta, M.A.; Martines-Arano, H.; Soto-Ruvalcaba, L.; Martínez-González, C.L.; Martínez-Gutiérrez, H.; Torres-Torres, C. Fractional thermal transport and twisted light induced by an optical two-wave mixing in single-wall carbon nanotubes. Int. J. Therm. Sci. 2020, 147, 106136. [Google Scholar] [CrossRef]
- Pan, J.; Hou, W.; Wang, L.; Zou, Z.; Xiao, F. Design and experimental study of a fiber Bragg grating strain sensor with enhanced sensitivity. Appl. Opt. 2022, 61, 8172–8179. [Google Scholar] [CrossRef] [PubMed]
- Bilodeau, F.; Johnson, D.C.; Theriault, S.; Malo, B.; Albert, J.; Hill, K.O. An all-fiber dense-wavelength multiplexer/demultiplexer using photoimprinted Bragg gratings. IEEE Photonics Technol. Lett. 1995, 7, 388–390. [Google Scholar] [CrossRef]
- Dianov, E.M.; Grekov, M.V.; Bufetov, L.A.; Vasiliev, S.A.; Medvedkov, O.I.; Plotnichenko, V.G.; Koltashev, V.V.; Belov, A.V.; Bubnov, M.M.; Semjonov, S.L.; et al. CW high power 1.24 nm and 1.48 μm Raman lasers based on low loss phosphosilicate fibre. Electron. Lett. 1997, 33, 1542–1544. [Google Scholar] [CrossRef]
- Archambbault, J.L.; Grubb, S.G. Fiber Gratings in lasers and amplifiers. J. Light. Technol 1997, 15, 1378–1390. [Google Scholar] [CrossRef]
- Bird, D.M.; Armitage, J.R.; Kashyap, R.; Fatah, R.M.A.; Cameron, K.H. Narrow line semiconductor laser using fiber grating. Electron. Lett. 1991, 27, 1115–1116. [Google Scholar] [CrossRef]
- Vengsarkar, A.M.; Pedrazzani, J.R.; Judkins, J.B.; Lemaire, P.J.; Bergano, N.S.; Davidson, C.R. Long-period fiber-grating-based gain equalizers. Opt. Lett. 1996, 21, 336–338. [Google Scholar] [CrossRef] [PubMed]
- Protopopov, V.N.; Karpov, V.I.; Medvedkov, O.I.; Vasiliev, S.A.; Grekov, M.V.; Dianov, E.M.; Palto, S.P. Temperature sensor based on fiber Bragg grating. In Proceedings of the SPIE 4083, Advances in Fiber Optics, Moscow, Russia, 1 March 2000; pp. 224–228. [Google Scholar]
- Dianov, E.M.; Kurkov, A.S.; Medvedkov, O.I.; Vasiliev, S.A. Application of photo induced long-period fiber gratings in optical sensors. In Proceedings of the European Conference on Lasers and Electro-Optics 1996, CLEO/Europe’96, Hamburg, Germany, 8–13 September 1996. [Google Scholar]
- Dianov, E.M.; Kurkov, A.S.; Medvedkov, O.I.; Vasiliev, S.A. Photo induced long-period fiber grating as a promising sensor element. In Proceedings of the Eurosensors X The 10th European Conference on Solid-State Transducers, Leuven, Belgium, 8–11 September 1996; Volume 5, pp. 1–128. [Google Scholar]
- Gu, X.J. Wavelength-division multiplexing isolation fiber filter and light source using cascaded long-period fiber gratings. Opt. Lett. 1998, 23, 509–510. [Google Scholar] [CrossRef]
- Starodubov, D.S.; Grubsky, V.; Feinberg, J. All-fiber band pass filter with adjustable transmission. In Proceedings of the Optical Fiber Communication Conference 1999, OFC’P9, San Diego, CA, USA, 21–26 February 1999; pp. 138–140. [Google Scholar]
- Starodubov, D.S.; Grubsky, V.; Skorucak, A.; Feinberg, J.; Cai, J.X.; Feng, K.M.; Willner, A.E. Novel fiber amplitude modulators for dynamic channel power equalization in WDM systems. In Proceedings of the Optical Fiber Communication Conference 1998, OFC’98, San Jose, CA, USA, 16–22 February 1997. [Google Scholar]
- Kashaganova, G.B. Research and Optimization of Spectral Characteristics of Fiber Optic Bragg Gratings. Doctoral Dissertation, Almaty, Kazakhstan, 2017; p. 120. [Google Scholar]
- Kashaganova, G.B. Study of the main parameters of fiber sensors based on inclined fiber Bragg grids and the influence of external factors on them. Bull. KazATC 2022, 4, 537–545. [Google Scholar]
- Dong, Y.; Bao, X.; Chen, L. Distributed temperature sensing based on birefringence effect on transient Brillouin grating in a polarization-maintaining photonic crystal fiber. Opt. Lett. 2009, 34, 2590–2592. [Google Scholar] [CrossRef]
- Kalimoldayev, M.; Kalizhanova, A.; Wójcik, W.; Kashaganova, G.; Amirgaliyeva, S.; Dasibekov, A.; Kozbakova, A.; Aitkulov, Z. Research of the Spectral Characteristics of Apodized fiber bragg gratings. In ITM Web of Conferences; EDP Sciences: Paris, France, 2018; ISSN 2271-2097. [Google Scholar] [CrossRef]
- Wagener, J.L.; Strasser, T.A.; Pedrazzani, J.R.; DeMarco, J.; DiGiovanni, D. Fiber Grating Optical Spectrum Analyzer Tap. In Proceedings of the 11th International Conference on Integrated Optics and Optical Fibre Communications; 23rd European Conference on Optical Communications IOOC-ECOC97, Edinburgh, UK, 22–25 September 1997; IET: London, UK, 1997; pp. 65–68. [Google Scholar] [CrossRef]
- Faiyaz, N.M.; Omi, A.I.; Faisal, M. Optimization of Apodization Profile of Chirped fiber Bragg grating for Chromatic Dispersion Compensation Using Chirped Apodized FBG. In Proceedings of the International Conference on Electrical Engineering and Information & Communication Technology (ICEEICT), Dhaka, Bangladesh, 10–12 April 2014; pp. 1–5. [Google Scholar]
- Khan, S.S.A.; Islam, M.S. Chromatic Dispersion Compensation Using Linearly Chirped Apodized fiber Bragg grating. In Proceedings of the International Conference on Electrical & Computer Engineering (ICECE 2010), Dhaka, Bangladesh, 18–20 December 2010; pp. 9–12. [Google Scholar]
- Bandyopadhyay, S.; Biswas, P.; Pal, A.; Bhadra, S.K.; Dasgupta, K. Empirical Relations for Design of Linear Edge Filters Using Apodized Linearly Chirped. J. Light. Technol. 2008, 26, 3853–3859. [Google Scholar] [CrossRef]
- Farahi, F.; Webb, D.J.; Jones, J.D.C.; Jackson, D.A. Simultaneous measurement of temperature and strain: Cross-sensitivity considerations. J. Light. Technol. 1990, 8, 138–142. [Google Scholar] [CrossRef]
- Jin, W.; Michie, W.C.; Thursby, G.; Konstantaki, M.; Culshaw, B. Simultaneous measurement of strain and temperature: Error analysis. Opt. Eng. 1997, 36, 598–609. [Google Scholar] [CrossRef]
- Xu, M.G.; Archambault, J.L.; Reekie, L.; Dakin, J.P. Simultaneous measurement of strain and temperature using fibre grating sensors. Proc. SPIE 1994, 2360, 191–194. [Google Scholar]
- Xu, M.G.; Archambault, J.L.; Reekie, L.; Dakin, J.P. Discrimination between strain and temperature effects using dual-wavelength fibre grating sensors. Electron. Lett. 1994, 30, 1085–1087. [Google Scholar] [CrossRef]
- Chehura, E.; James, S.W.; Tatam, R.P. Temperature and strain discrimination using a single tilted fibre Bragg grating. Opt. Commun. 2007, 275, 344–347. [Google Scholar] [CrossRef]
- James, S.W.; Dockney, M.L.; Tatam, R.P. Simultaneous independent temperature and strain measurement using in-fibre Bragg grating sensors. Electron. Lett. 1996, 32, 1133–1134. [Google Scholar] [CrossRef]
- Cavaleiro, P.M.; Aráujo, F.M.; Ferreira, L.A.; Santos, J.L.; Farahi, F. Simultaneous measurement of strain and temperature using Bragg gratings written in germanosilicate and boron-codoped germanosilicate fibers. IEEE Photonics Technol. Lett. 1999, 11, 1635–1637. [Google Scholar] [CrossRef]
- Guan, B.O.; Tam, H.Y.; Chan, H.L.W.; Choy, C.L.; Demokan, M.S. Discrimination between strain and temperature with a single. Microw. Opt. Technol. Lett. 2002, 33, 200–202. [Google Scholar] [CrossRef]
- Frazão, O.; Santos, J.L. Simultaneous measurement of strain and temperature using a Bragg grating structure written in germanosilicate fibres. J. Opt. A Pure Appl. Opt. 2004, 6, 553–556. [Google Scholar] [CrossRef]
- Patrick, H.J.; Williams, G.M.; Kersey, A.D.; Pedrazzani, J.R.; Vengsarkar, A.M. Hybrid long period fiber grating sensor for strain temperature discrimination. IEEE Photonics Technol. Lett. 1996, 8, 1223–1225. [Google Scholar] [CrossRef]
- Guan, B.O.; Tam, H.Y.; Tao, X.M.; Dong, X.Y. Simultaneous strain and temperature measurement using a superstructure. IEEE Photonics Technol. Lett. 2000, 12, 675–677. [Google Scholar] [CrossRef]
- Frazao, O.; Romero, R.; Rego, G.; Marques, P.V.S.; Salgado, H.M.; Santos, J.L. Sampled fibre Bragg grating sensors for simultaneous strain and temperature measurement. Electron. Lett. 2002, 38, 693–695. [Google Scholar] [CrossRef]
- Frazao, O.; Marques, L.M.; Baptista, J.M. Fibre Bragg grating interrogation based on high-birefringence fiber loop mirror for strain-temperature discrimination. Microw. Opt. Technol. Lett. 2006, 48, 2326–2328. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Light. Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Tosi, D. Review and Analysis of peak tracking techniques for sensors. Sensors 2017, 17, 2368. [Google Scholar] [CrossRef]


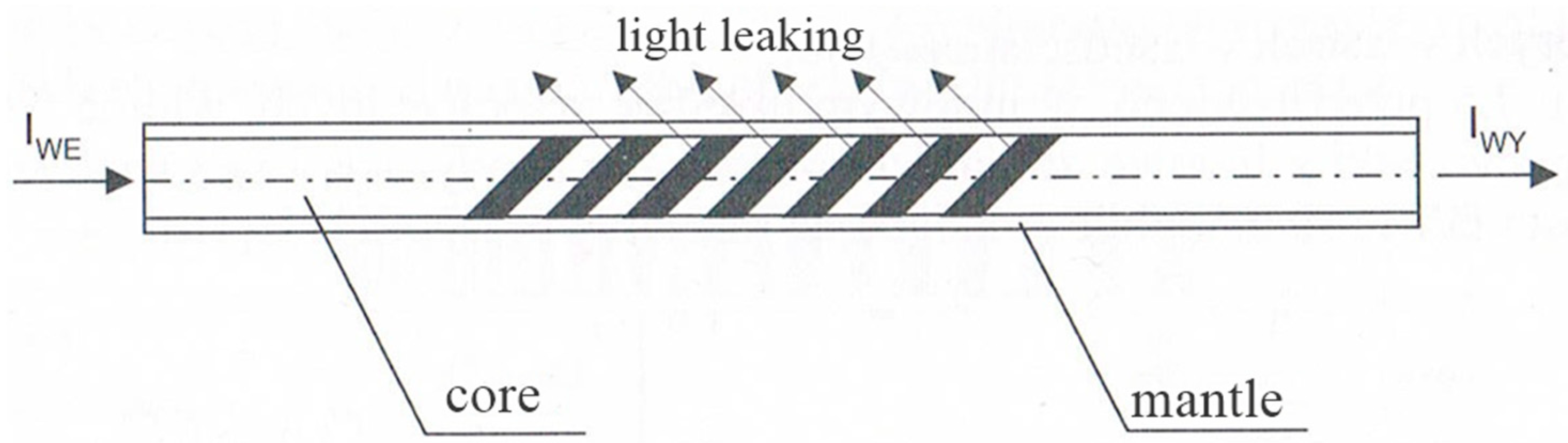
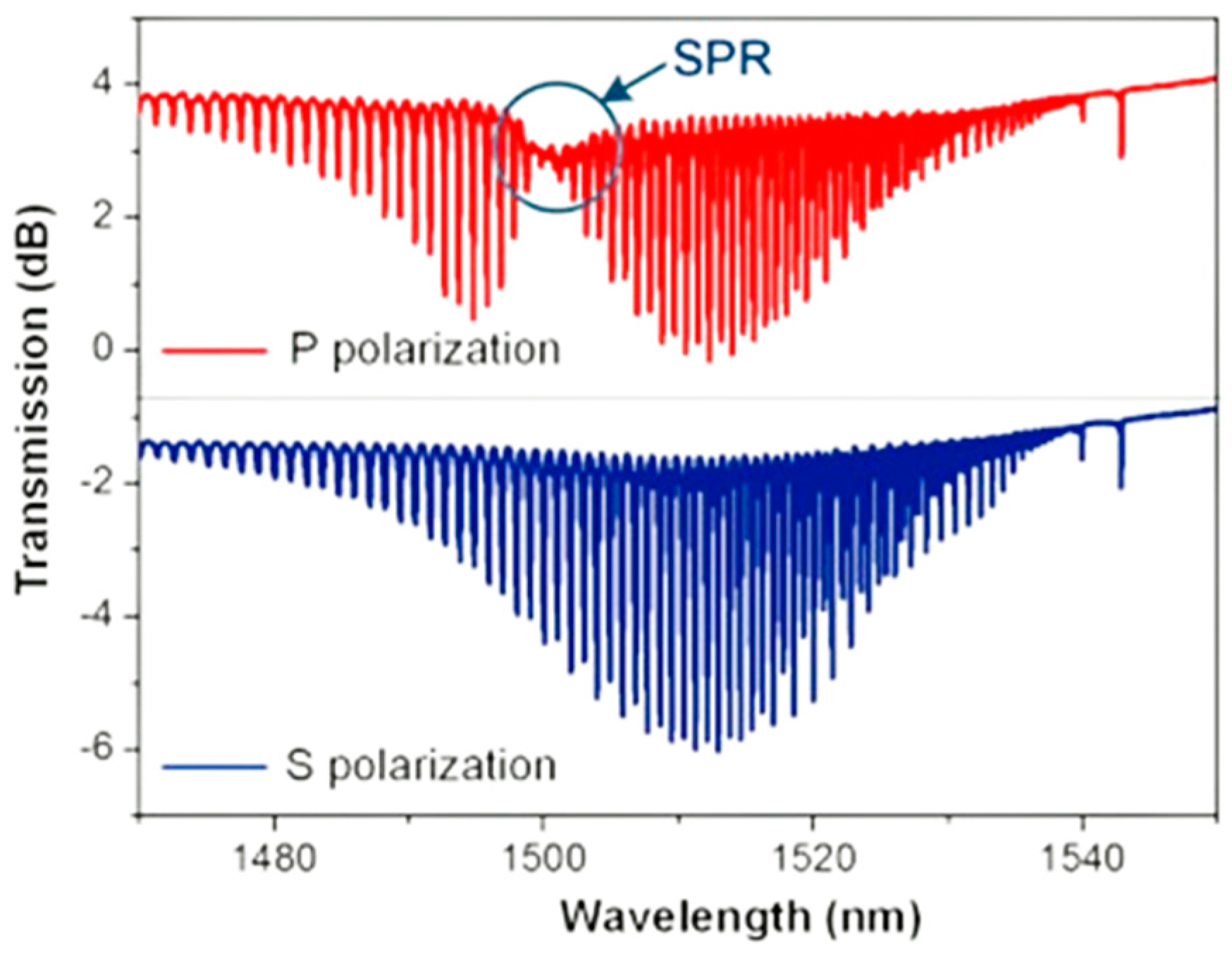


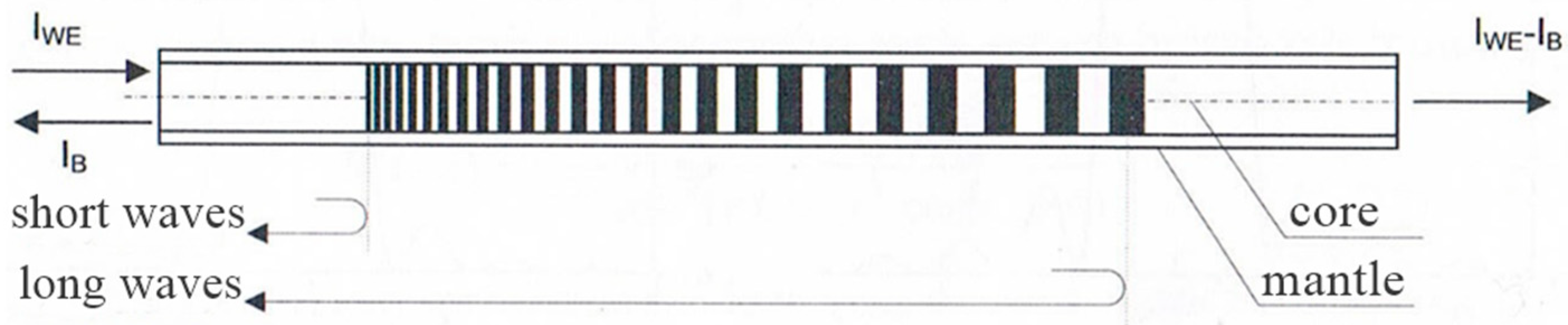
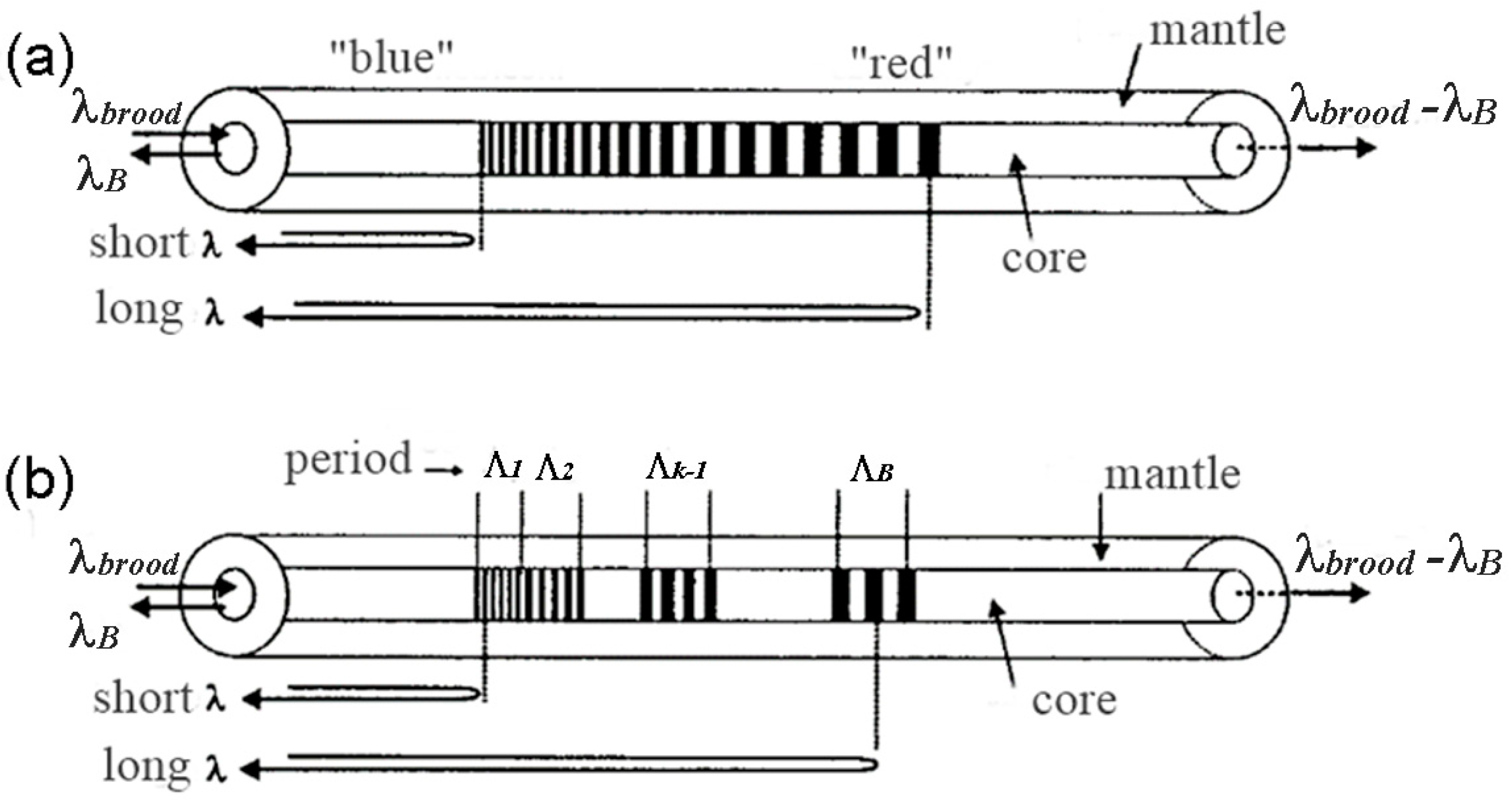



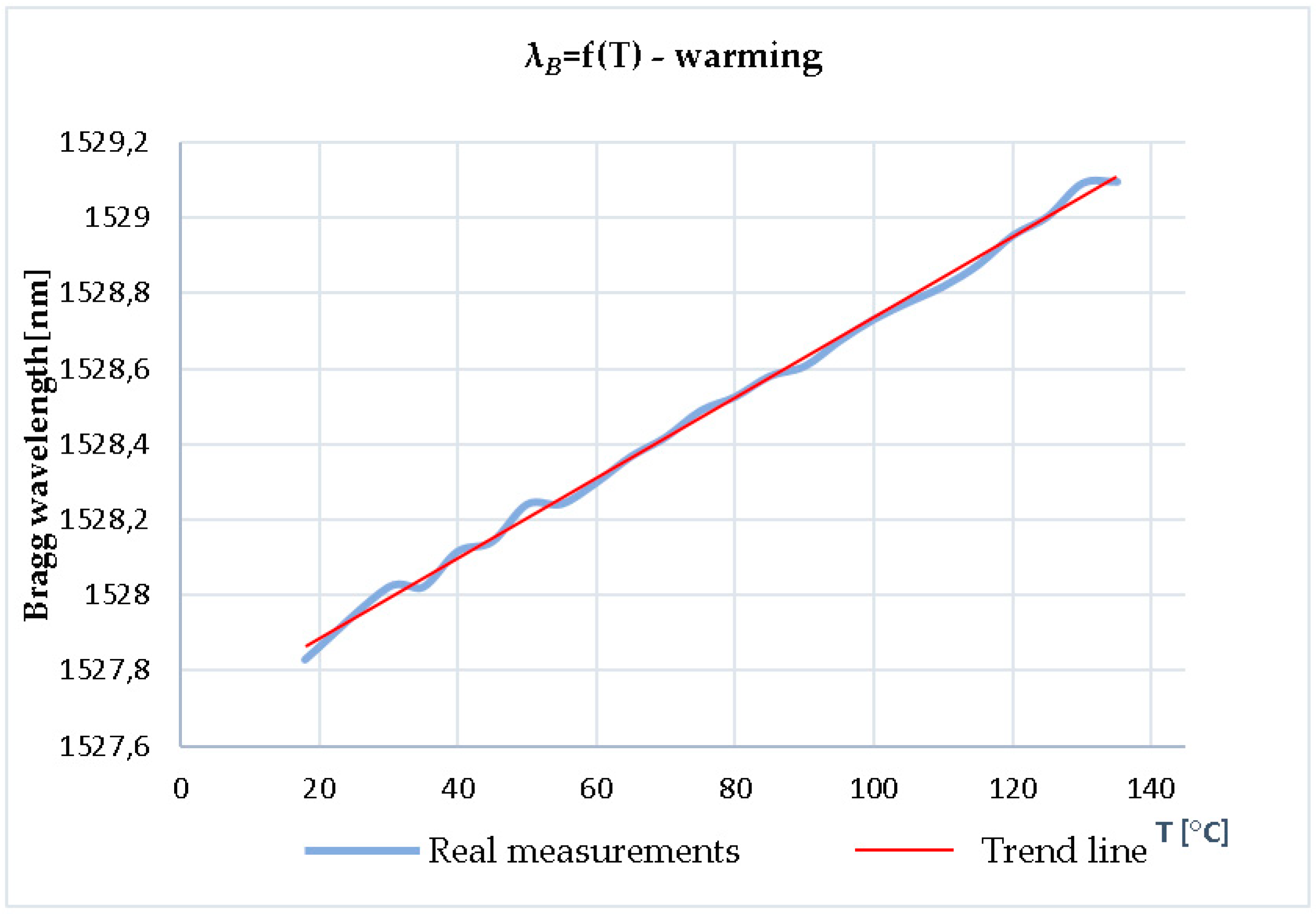
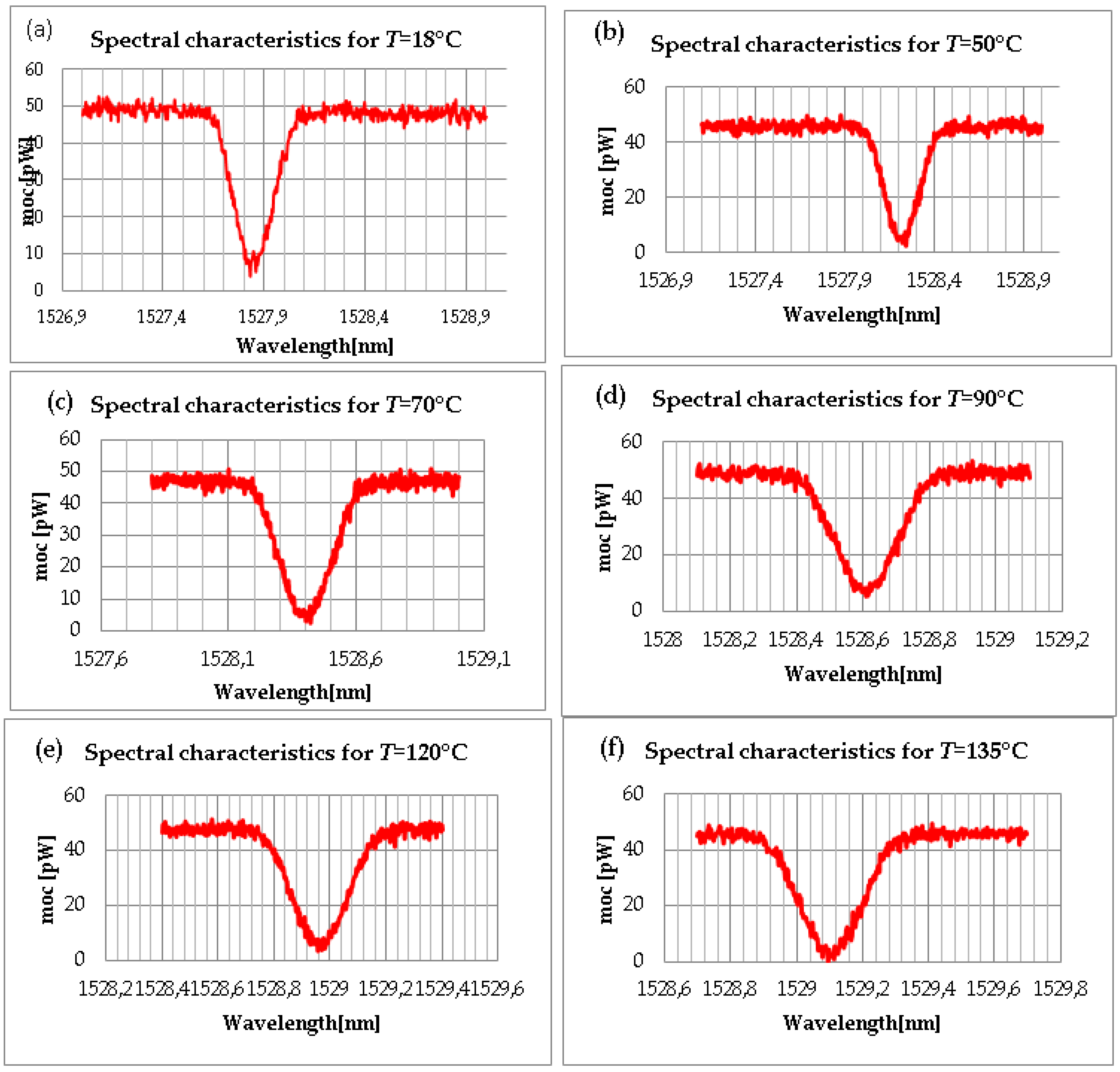
| ΛB [nm] | T [°C] |
|---|---|
| 1527.83 | 18 |
| 1528.022 | 30 |
| 1528.022 | 35 |
| 1528.117 | 40 |
| 1528.143 | 45 |
| 1528.242 | 50 |
| 1528.243 | 55 |
| 1528.3 | 60 |
| 1528.369 | 65 |
| 1528.42 | 70 |
| 1528.49 | 75 |
| 1528.527 | 80 |
| 1528.582 | 85 |
| 1528.608 | 90 |
| 1528.675 | 95 |
| 1528.733 | 100 |
| 1528.778 | 105 |
| 1528.82 | 110 |
| 1528.877 | 115 |
| 1528.955 | 120 |
| 1529.005 | 125 |
| 1529.093 | 130 |
| 1529.097 | 135 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashaganova, G.; Kozbakova, A.; Kartbayev, T.; Togzhanova, K.; Alimseitova, Z.; Sergazin, G. Design of a Fiber Temperature and Strain Sensor Model Using a Fiber Bragg Grating to Monitor Road Surface Conditions. Inventions 2024, 9, 100. https://doi.org/10.3390/inventions9050100
Kashaganova G, Kozbakova A, Kartbayev T, Togzhanova K, Alimseitova Z, Sergazin G. Design of a Fiber Temperature and Strain Sensor Model Using a Fiber Bragg Grating to Monitor Road Surface Conditions. Inventions. 2024; 9(5):100. https://doi.org/10.3390/inventions9050100
Chicago/Turabian StyleKashaganova, Gulzhan, Ainur Kozbakova, Timur Kartbayev, Kulzhan Togzhanova, Zhuldyz Alimseitova, and Gani Sergazin. 2024. "Design of a Fiber Temperature and Strain Sensor Model Using a Fiber Bragg Grating to Monitor Road Surface Conditions" Inventions 9, no. 5: 100. https://doi.org/10.3390/inventions9050100
APA StyleKashaganova, G., Kozbakova, A., Kartbayev, T., Togzhanova, K., Alimseitova, Z., & Sergazin, G. (2024). Design of a Fiber Temperature and Strain Sensor Model Using a Fiber Bragg Grating to Monitor Road Surface Conditions. Inventions, 9(5), 100. https://doi.org/10.3390/inventions9050100








