Control on Flow Separation over a Cylinder by a Ferrofluid Film Adsorbed by a Magnet
Abstract
1. Introduction
2. Materials and Methods
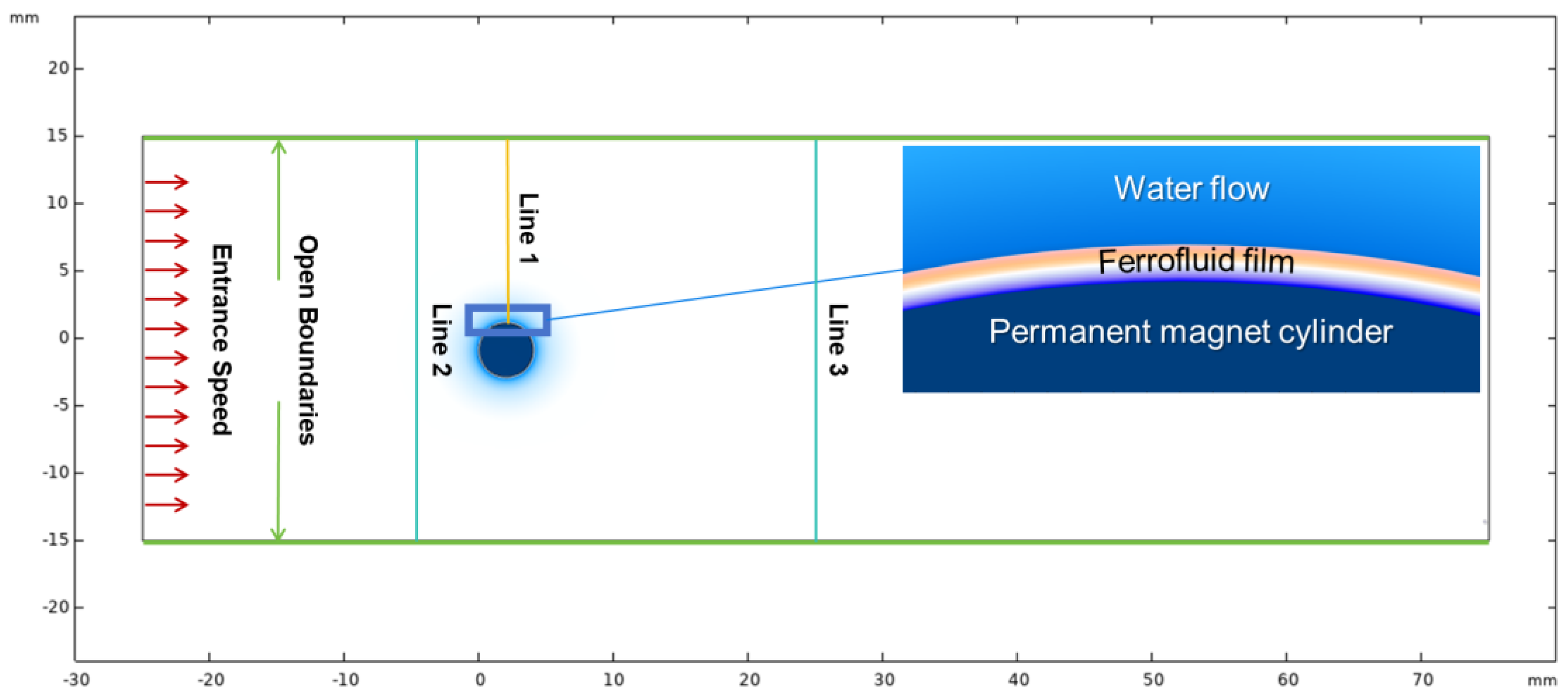
2.1. Flow Configuration
2.2. Numerical Method
2.3. Numerical Procedures
3. Result and Analysis
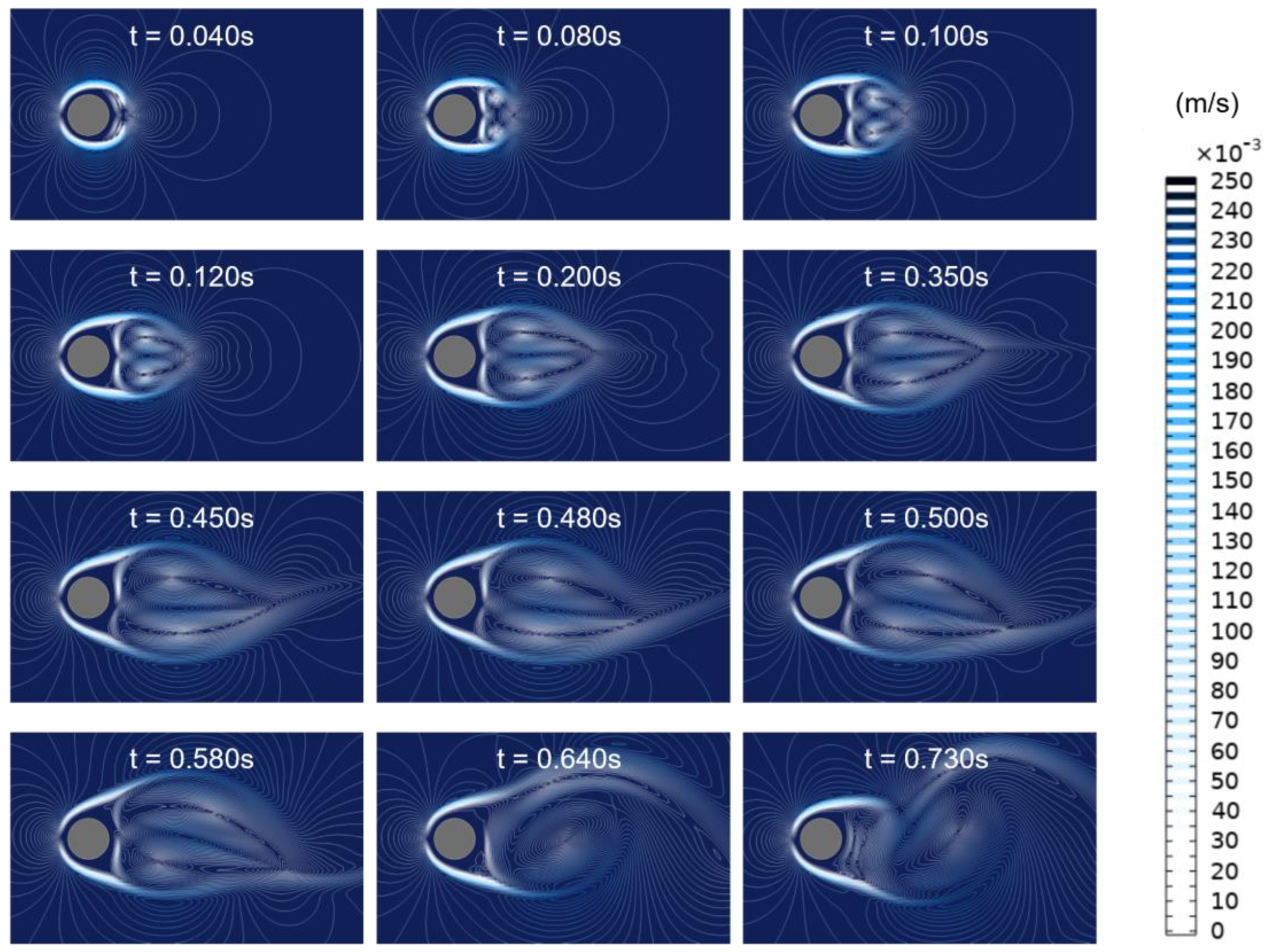
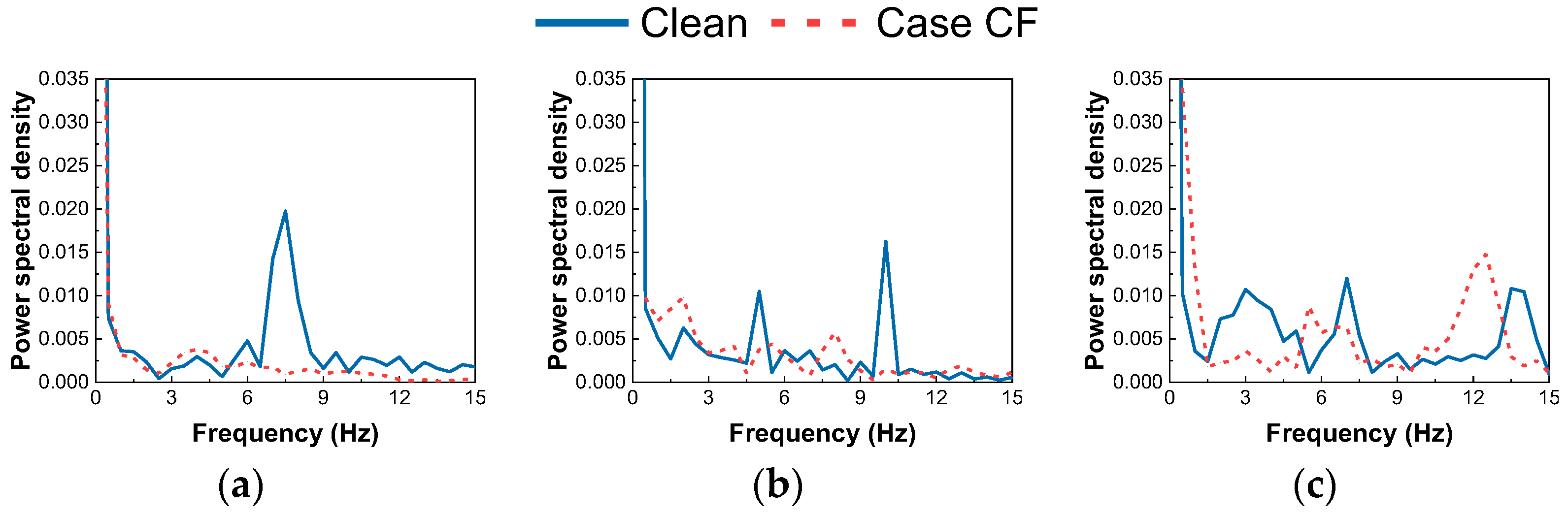
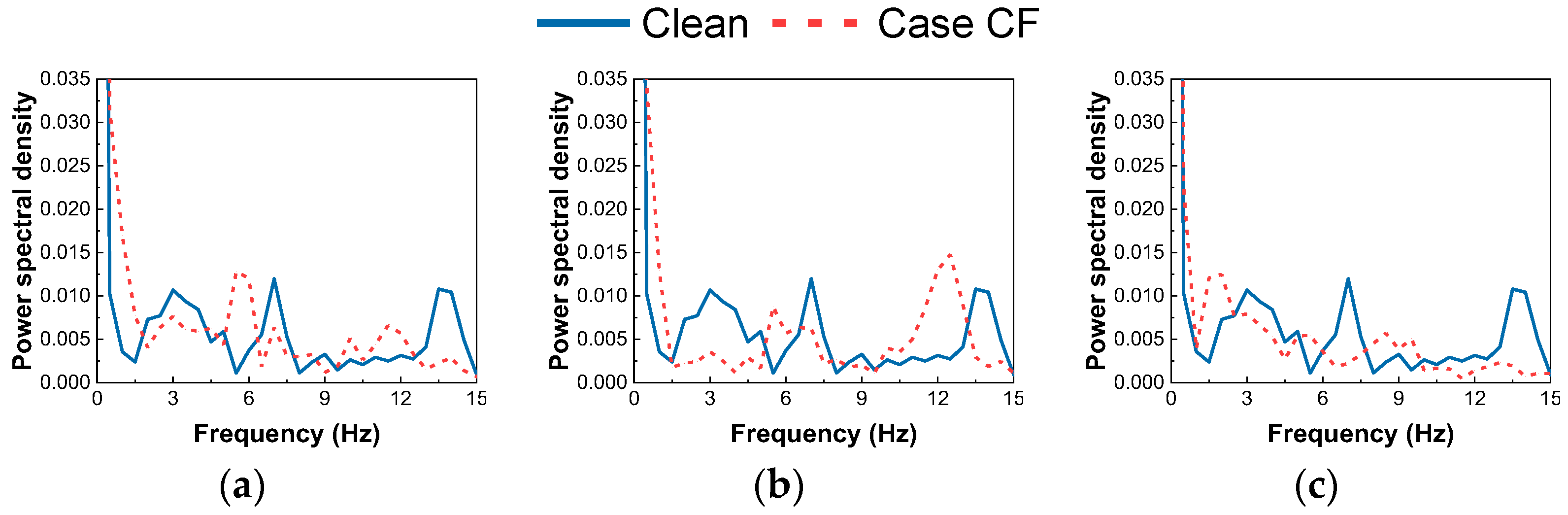
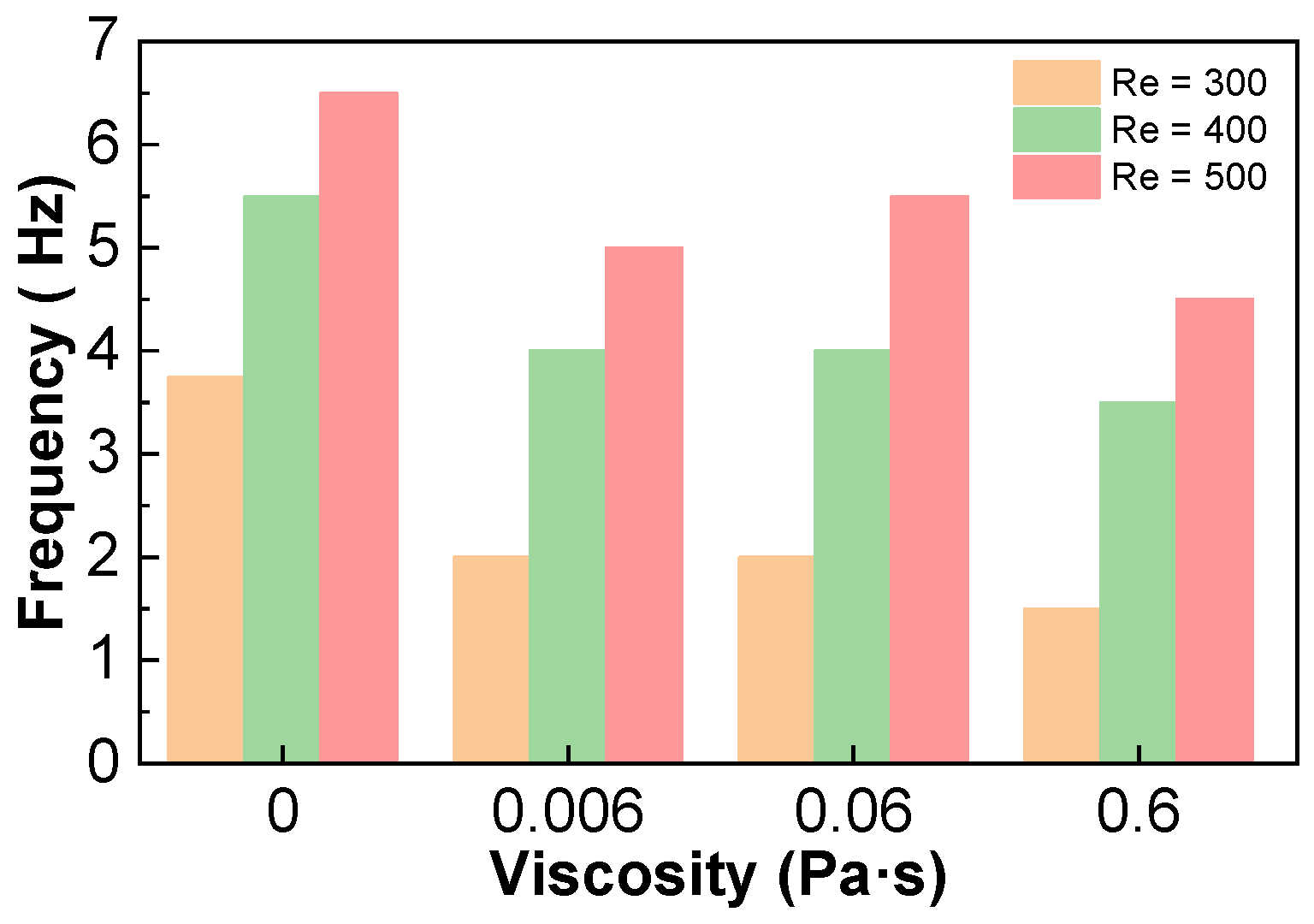
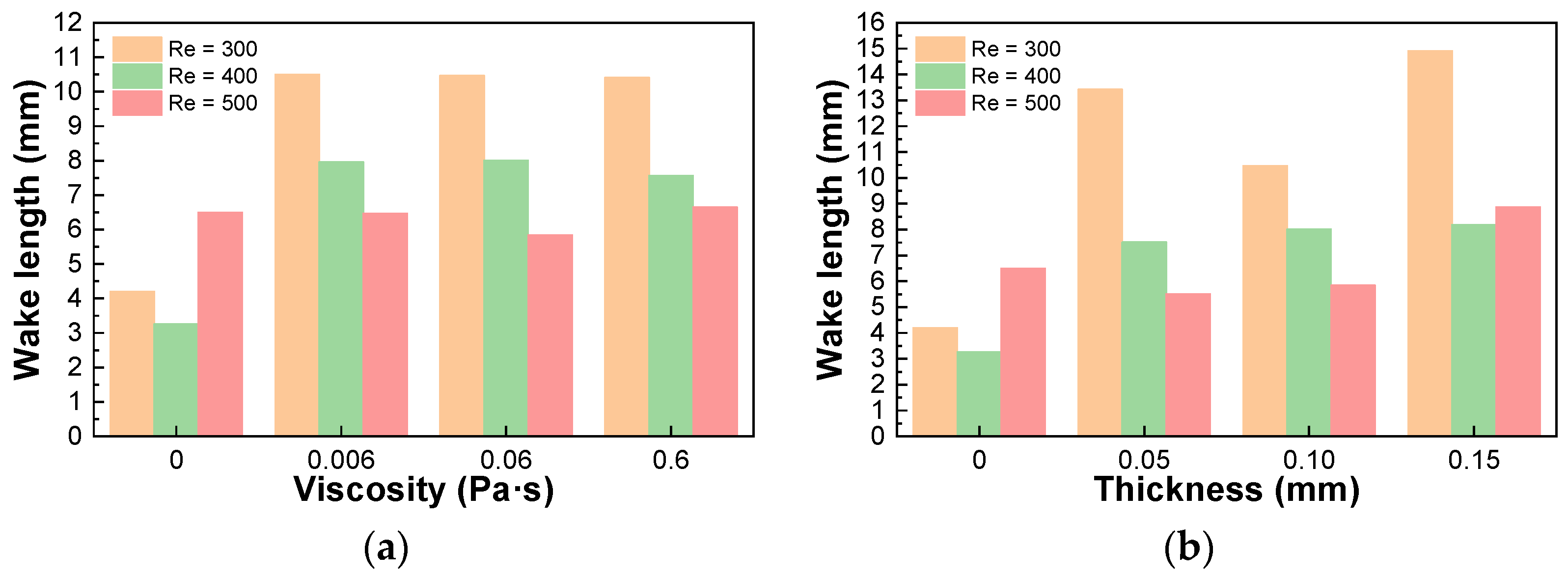
3.1. Vortex Shedding Process
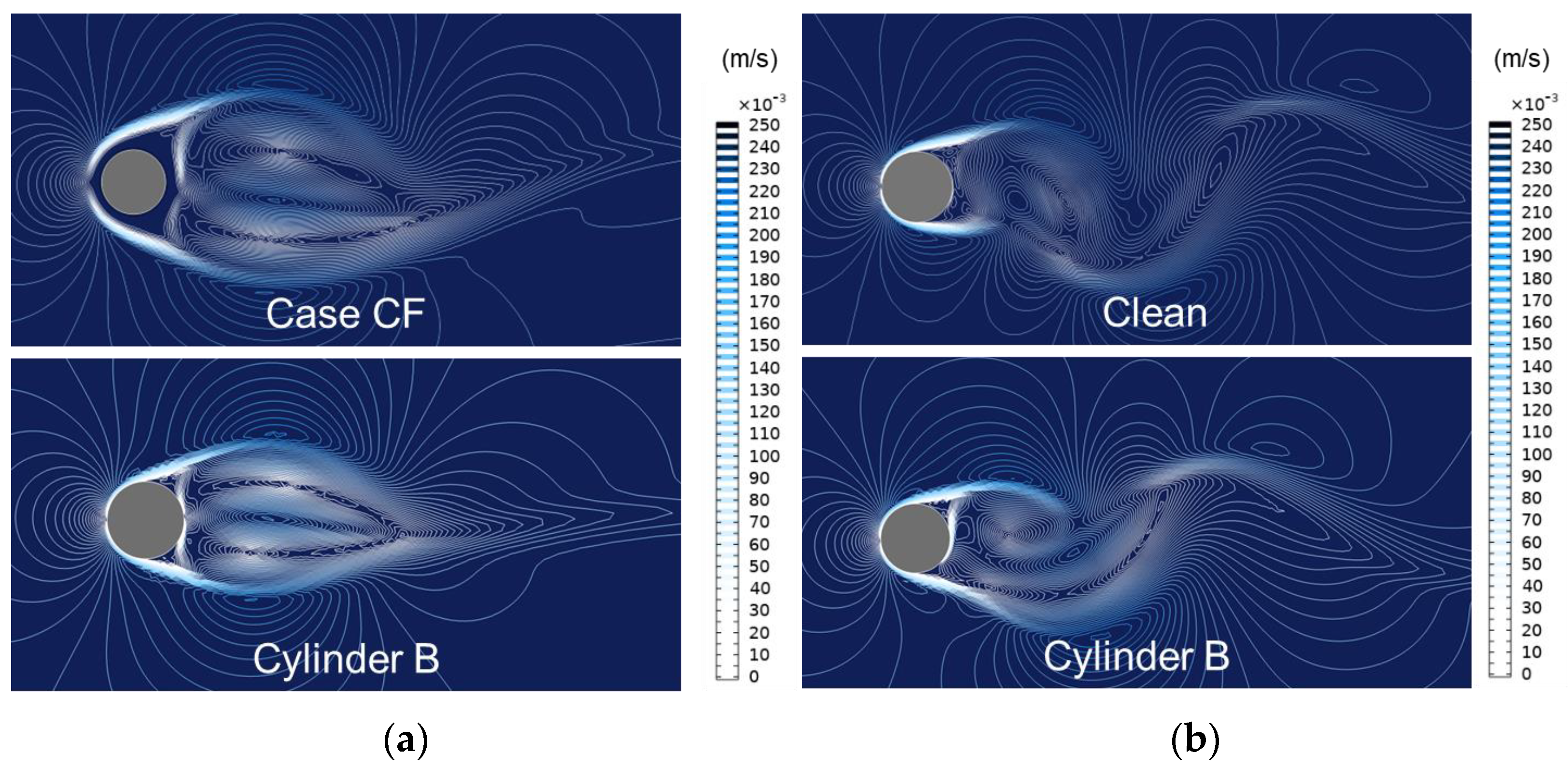
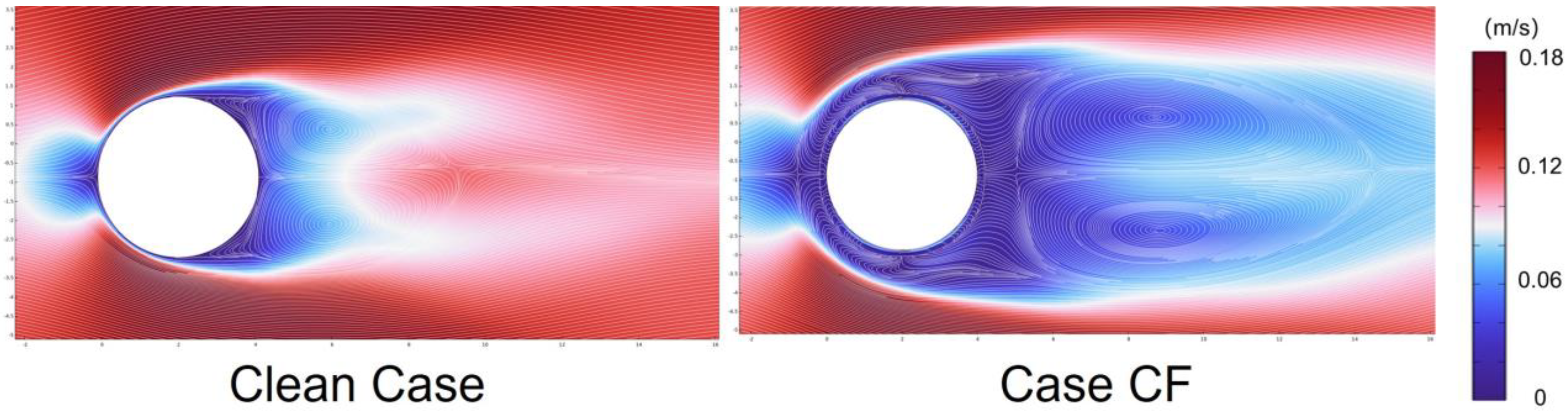
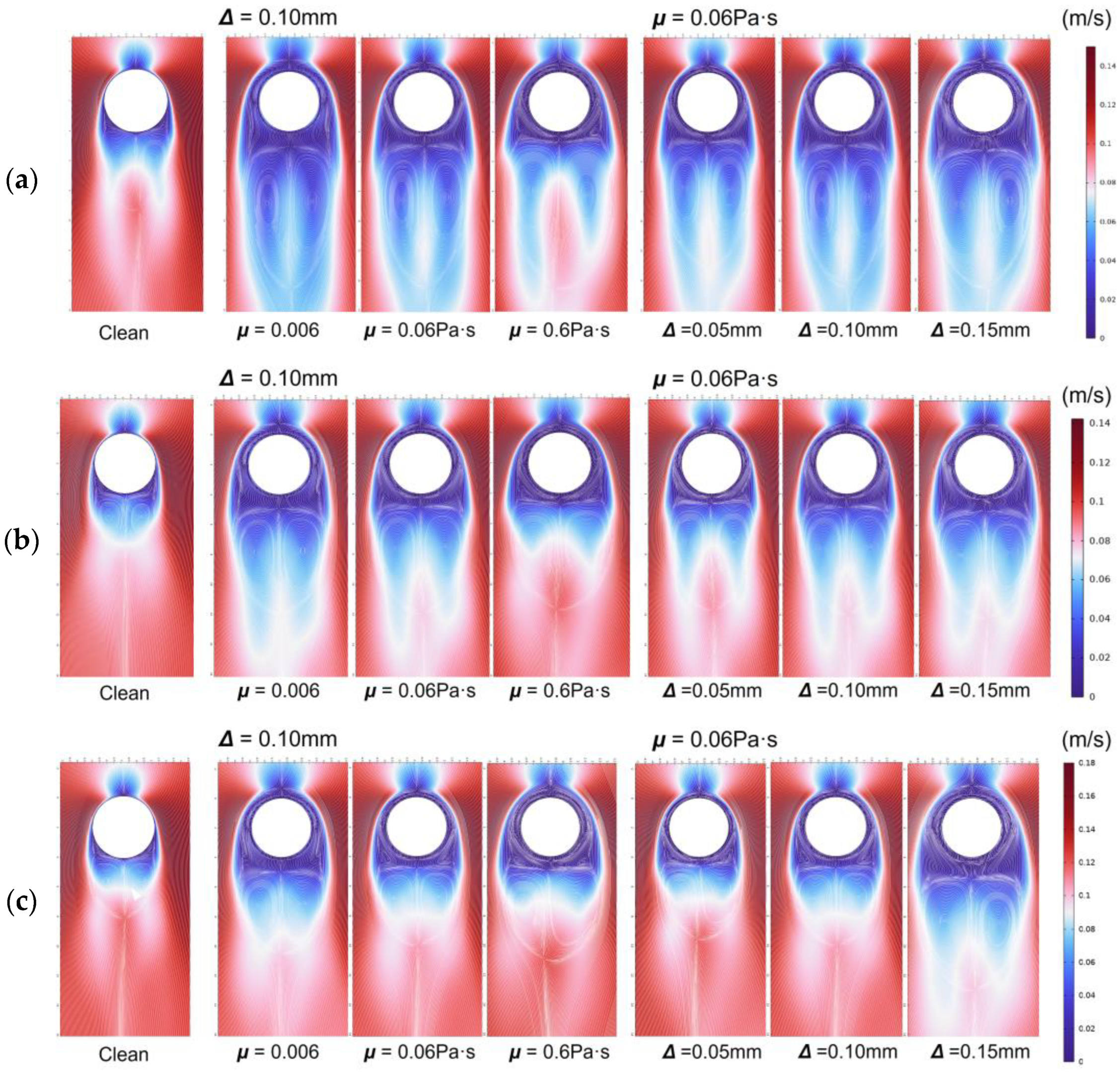
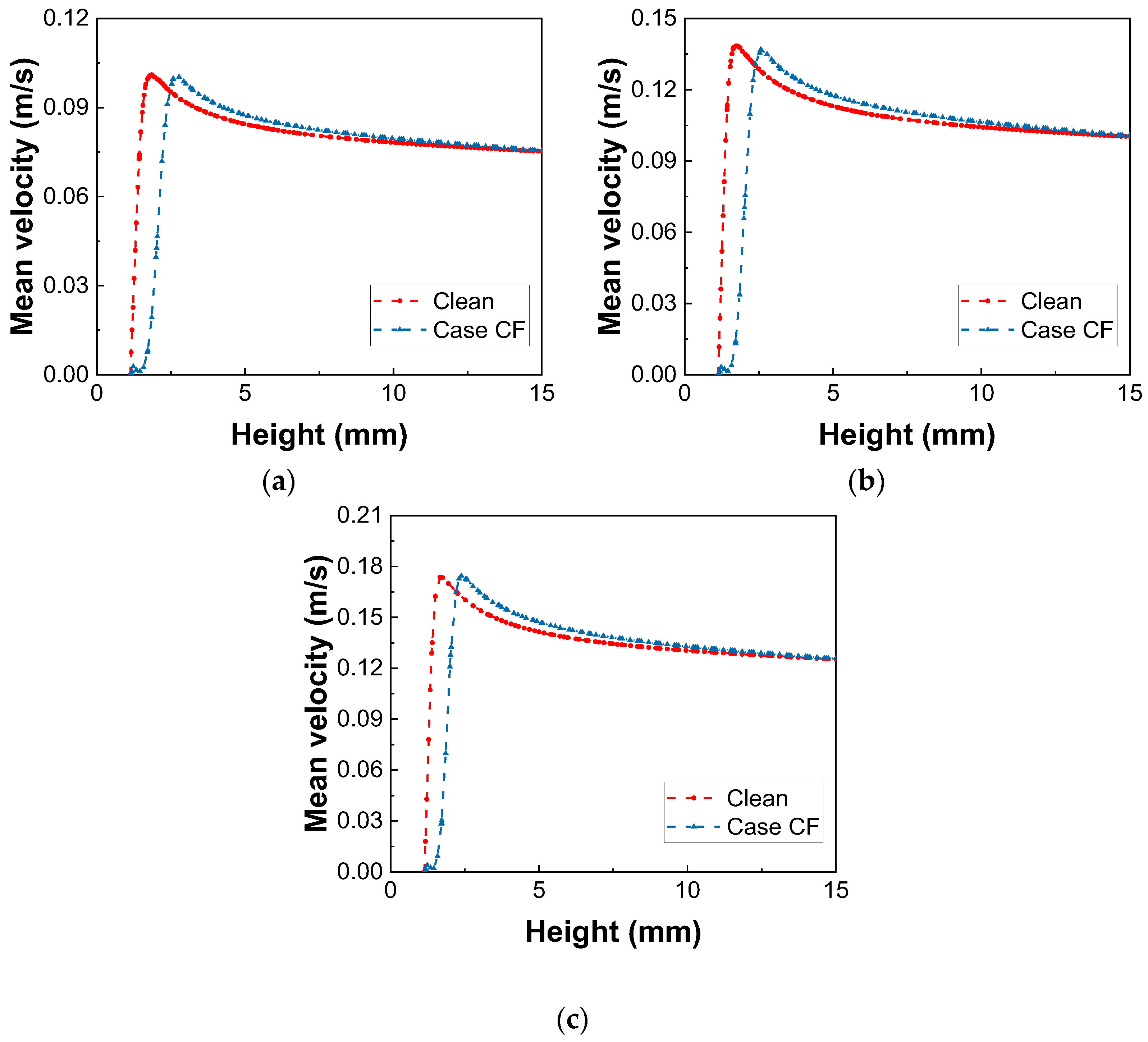
3.2. Velocity Distribution
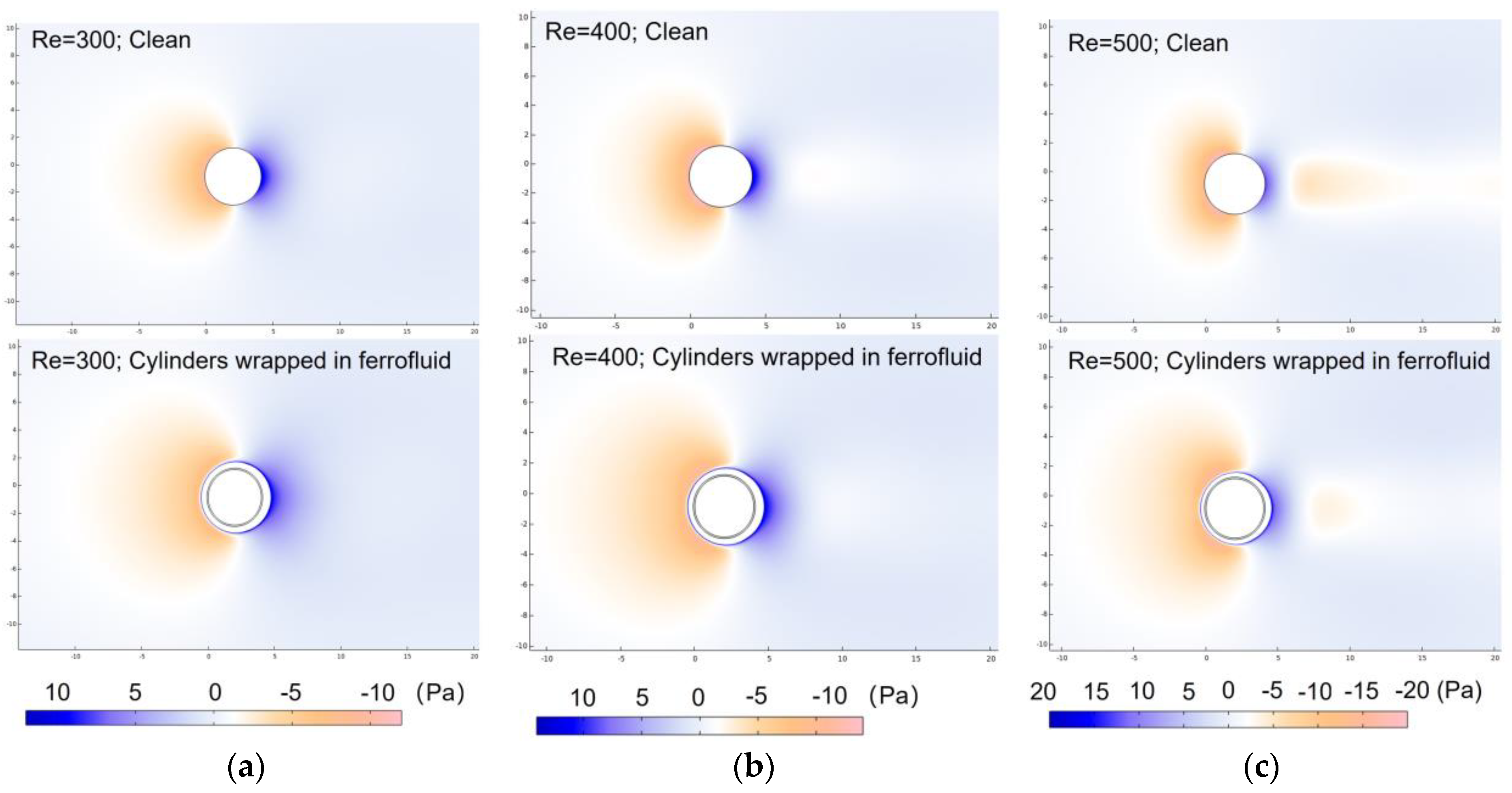
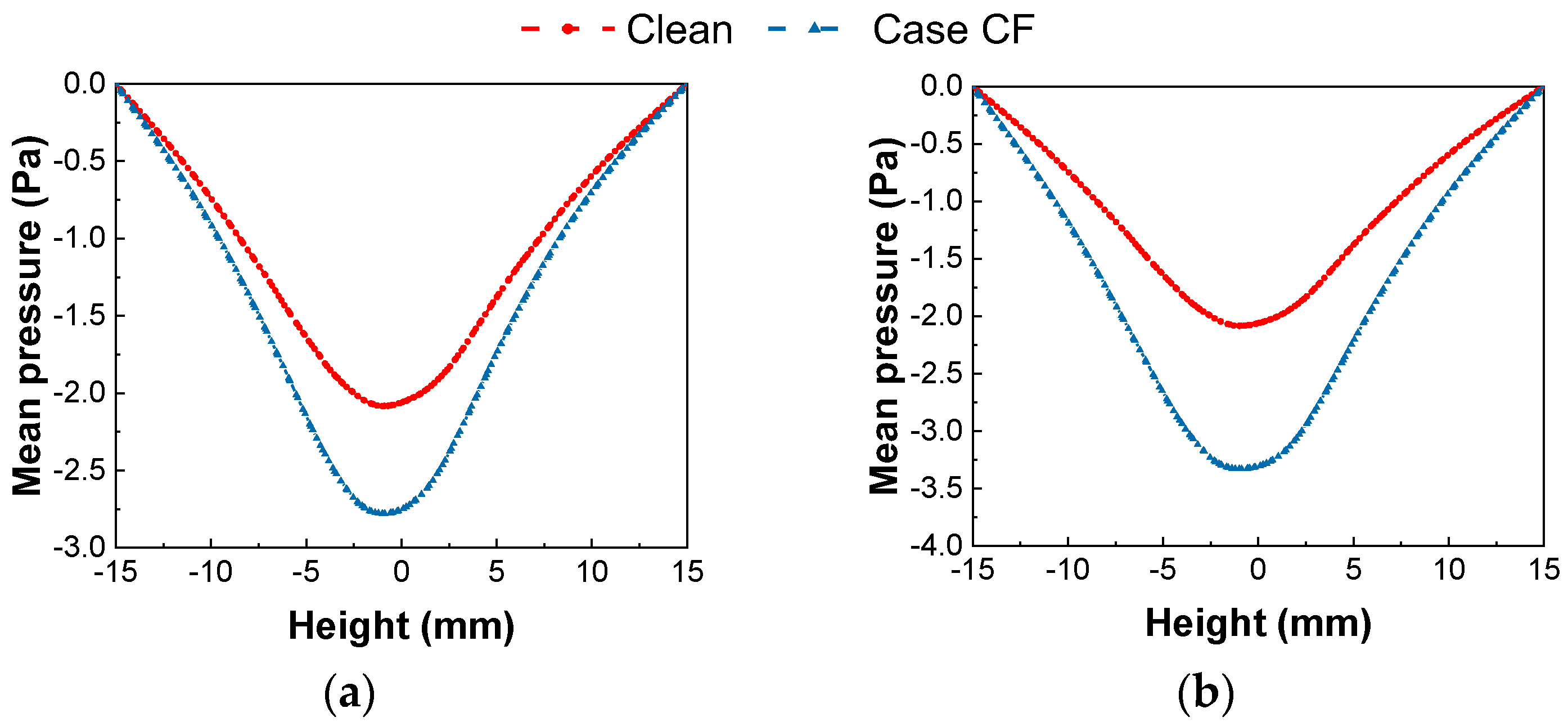
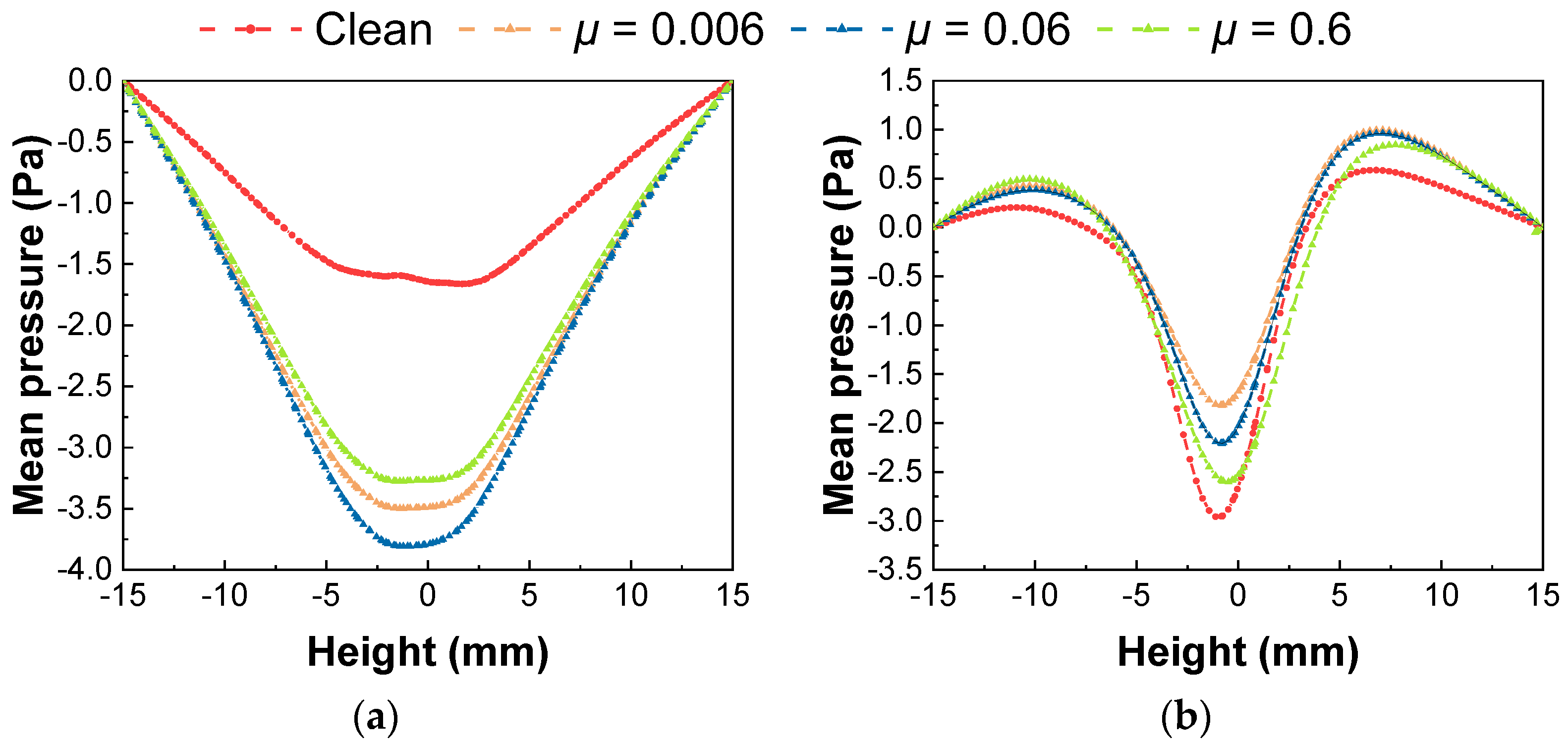
3.3. Pressure Distribution
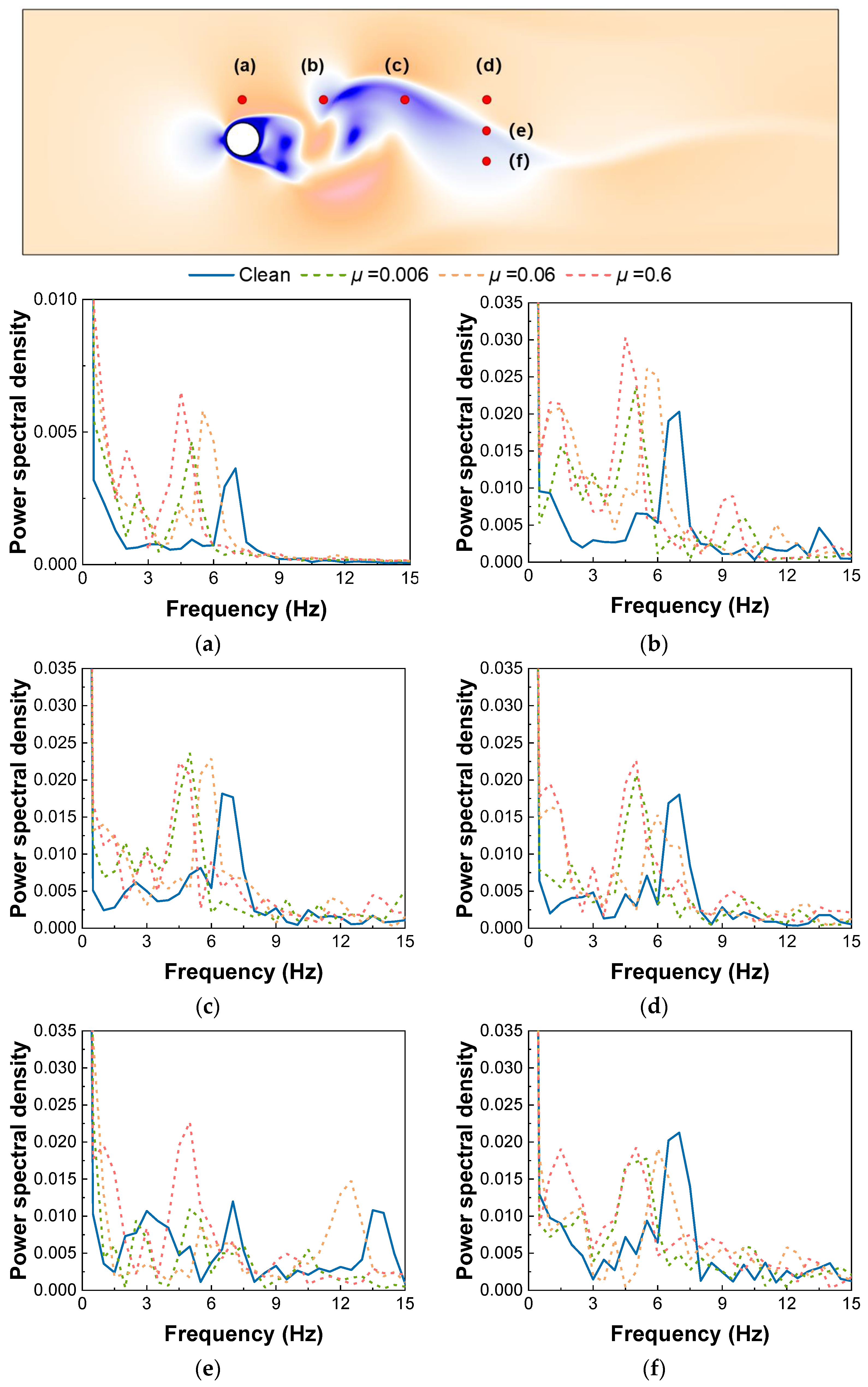
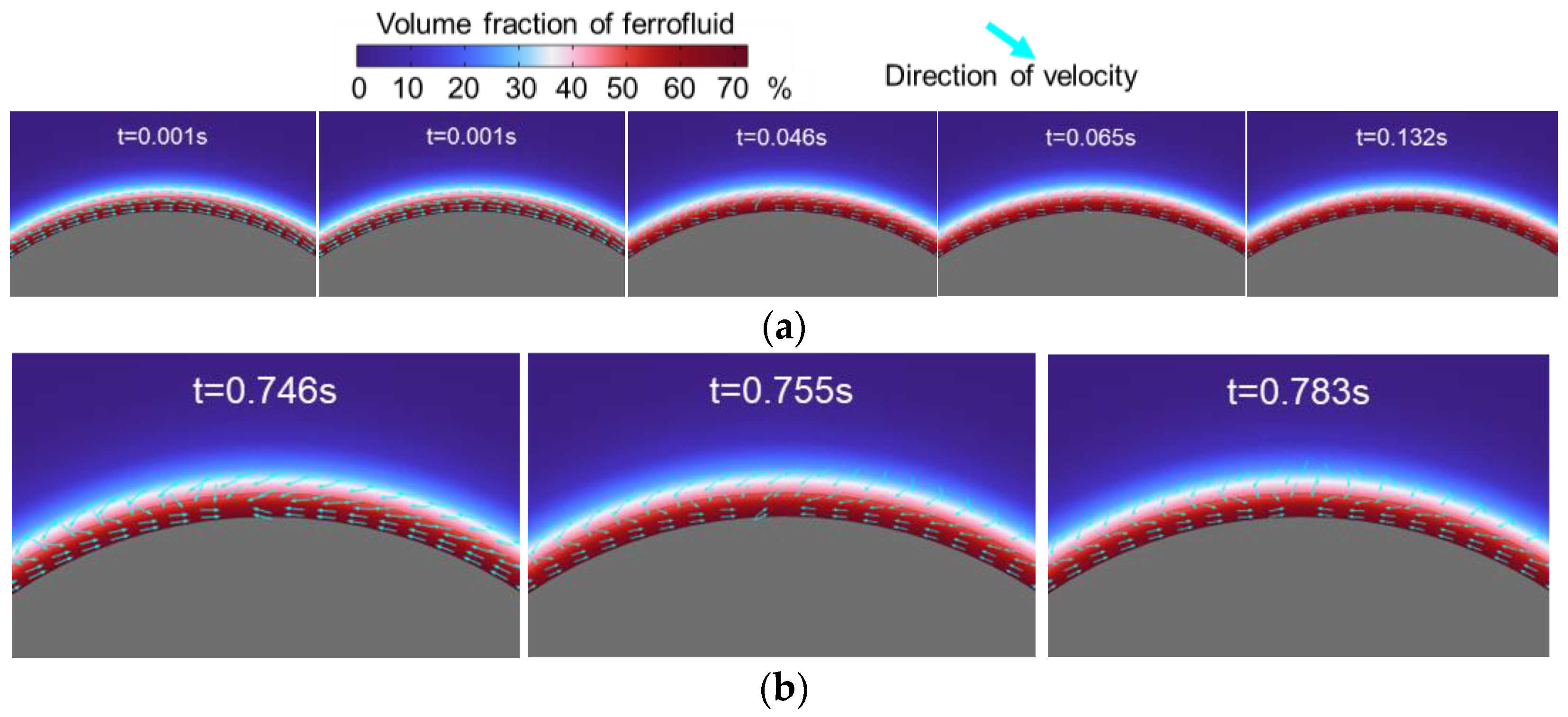
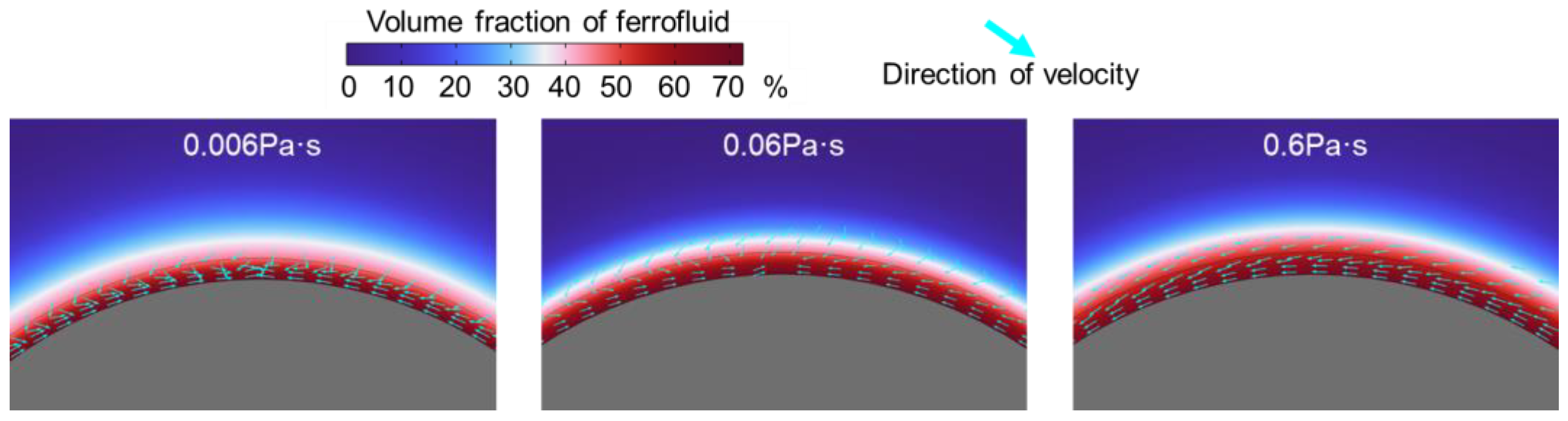
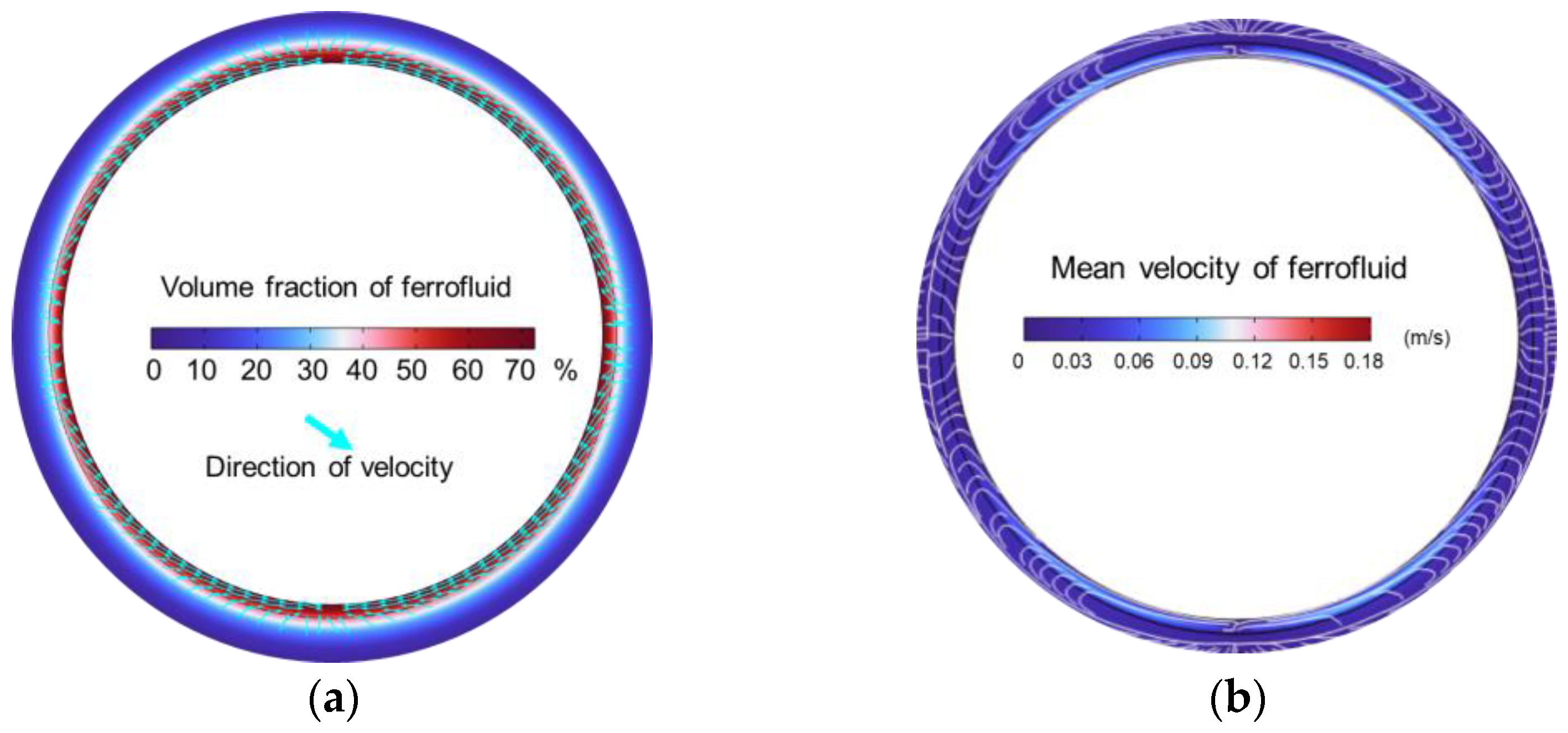
3.4. Flow Motion inside the Ferrofluid
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, W.-L.; Huang, Y.; Chen, C.; Yu, H.; Gao, D. Review of active control of circular cylinder flow. Ocean Eng. 2022, 258, 111840. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, L. Flow separation around a square cylinder at low to moderate Reynolds numbers. Phys. Fluids 2020, 32, 044103. [Google Scholar] [CrossRef]
- Heil, M.; Rosso, J.; Hazel, A.L.; Brøns, M. Topological fluid mechanics of the formation of the Kármán-vortex street. J. Fluid Mech. 2017, 812, 199–221. [Google Scholar] [CrossRef]
- Sohankar, A.; Norberg, C.; Davidson, L. Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 1999, 11, 288–360. [Google Scholar] [CrossRef]
- Choi, H. Control of flow over a bluff body. In Fifth International Symposium on Turbulence and Shear Flow Phenomena; Begel House Inc.: Danbury, CT, USA, 2007. [Google Scholar] [CrossRef]
- Lee, S.J.; Lim, H.C.; Han, M.; Lee, S.S. Flow control of circular cylinder with a V-grooved micro-riblet film. Fluid Dyn. Res. 2005, 37, 246. [Google Scholar] [CrossRef]
- Lim, H.C.; Lee, S.J. Flow control of circular cylinders with longitudinal grooved surfaces. AIAA J. 2002, 40, 2027–2036. [Google Scholar] [CrossRef]
- Huang, S. VIV suppression of a two-degree-of-freedom circular cylinder and drag reduction of a fixed circular cylinder by the use of helical grooves. J. Fluids Struct. 2011, 27, 1124–1133. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X. Aeroacoustic investigation of asymmetric oblique trailing-edge serrations enlighted by owl wings. Phys. Fluids 2022, 34, 015113. [Google Scholar] [CrossRef]
- Gao, D.; Huang, Y.; Chen, W.L.; Chen, G.; Li, H. Control of circular cylinder flow via bilateral splitter plates. Phys. Fluids 2019, 31, 057105. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, W.L.; Yang, Z.F. The control mechanism of the soft trailing fringe on the flow characteristics over an airfoil. Phys. Fluids 2022, 34, 95112. [Google Scholar] [CrossRef]
- Brücker, C. Interaction of flexible surface hairs with near-wall turbulence. J. Phys. Condens. Matter 2011, 23, 184120. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, M.; Sakaue, H. Microfibers coating for drag reduction by flocking technology. Coatings 2018, 8, 464. [Google Scholar] [CrossRef]
- Lin, L.; Deng, Z.; Chen, W.; Li, H.; Gao, D. Flow control of a circular cylinder by self-adaptive furry microfibers. Phys. Fluids 2022, 34, 105128. [Google Scholar] [CrossRef]
- Bashtovoi, V.G.; Krakov, M.S.; Taits, E.M. Intensification of heat transfer and reduction of the resistance under conditions of flow in channels with a magnetic-fluid coating. 1. Planar coating. J. Eng. Phys. 1990, 58, 435–439. [Google Scholar] [CrossRef]
- Krakov, M.S. Experiments involving a cylindrical magnet coated with a magnetic fluid in a transverse flow. Magnetohydrodynamics 1989, 1, 61–64. [Google Scholar]
- Jin, X.; Dai, M.; Zou, X.; Laima, S. Suppression of flow separation around a finite wall-mounted square cylinder by suction at the side leading edge. Phys. Fluids 2024, 36, 017120. [Google Scholar] [CrossRef]
- Lam, K.M. Vortex shedding flow behind a slowly rotating circular cylinder. J. Fluids Struct. 2009, 25, 245–262. [Google Scholar] [CrossRef]
- Toms, B.A. Observation on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proc. Int. Rheol. Congr. 1948, 2, 131–141. [Google Scholar]
- Li, F.; Bo, Y.; Wei, J.; Kawaguchi, Y. Surfactant Turbulence Reduction; Higher Education Publishing House: Beijing, China, 2012; p. 220. ISBN 9787040343151. [Google Scholar]
- Solomon, B.R.; Khalil, K.S.; Varanasi, K.K. Correction to Drag Reduction using Lubricant-Impregnated Surfaces in Viscous Laminar Flow. Langmuir 2016, 32, 8287. [Google Scholar] [CrossRef][Green Version]
- Deutsch, S.; Castano, J. Microbubble skin friction reduction on an axisymmetric body. Phys. Fluids 1986, 29, 3590–3596. [Google Scholar] [CrossRef]
- Madavan, N.K.; Detusch, S.; Merkle, C.L. Measurements of local skin friction in a microbubble–modified turbulent boundary layer. Fluid. Mech. 1985, 156, 37–256. [Google Scholar] [CrossRef]
- Krakov, M.S. Flow separation control by means of magnetic fluid. Izv. Akad. Nauk. SSSR Mekh. Zhidk. Gaza 1984, 39, 119–122. [Google Scholar] [CrossRef]
- Krakov, M.S.; Kamiyama, S. Steady flow past a circular cylinder coated with magnetic fluid: Flow structure, drag reduction and coating deformation. J. Fluid Mech. 1995, 295, 1–22. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Secchi, E.; Holzner, M. Magnetic fluid film enables almost complete drag reduction across laminar and turbulent flow regimes. Commun. Phys. 2024, 7, 30. [Google Scholar] [CrossRef]
- Krakov, M.S.; Maskalik, E.S.; Medvedev, V.F. Hydrodynamic resistance of pipelines with a magnetic fluid coating. Fluid Dynam. 1989, 24, 715–720. [Google Scholar] [CrossRef]
- Outokesh, M.; Amiri, H.A.; Miansari, M. Numerical insights into magnetic particle enrichment and separation in an integrated droplet microfluidic system. Chem. Eng. Process.-Process Intensif. 2022, 170, 108696. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G. A conservative level set method for two phase flow. J. Comput. Phys. 2005, 210, 225–246. [Google Scholar] [CrossRef]
- Kholardi, M.D.; Farhadi, M. Understanding droplet formation in T-shaped channels with magnetic field influence: A computational investigation. Phys. Fluids 2024, 36, 053302. [Google Scholar] [CrossRef]
- Ganguly, R.; Sen, S.; Puri, I.K. Thermomagnetic convection in a square enclosure using a line dipole. Phys. Fluids 2004, 16, 2228–2236. [Google Scholar] [CrossRef]
- Norberg, C. Fluctuating lift on a circular cylinder: Review and new measurements. J. Fluids Struct. 2003, 17, 57–96. [Google Scholar] [CrossRef]
- Dunne, P.; Adachi, T.; Dev, A.A.; Sorrenti, A.; Giacchetti, L.; Bonnin, A.; Bourdon, C.; Mangin, P.H.; Coey, J.M.D.; Doudin, B.; et al. Liquid flow and control without solid walls. Nature 2020, 581, 58–62. [Google Scholar] [CrossRef]




| Material | ρ (kg/m3) | μ (Pa·s) | Δ (mm) |
|---|---|---|---|
| Water | 1000 | 0.001 | / |
| Ferrofluid | 1200 | 0.006, 0.06, 0.6 | 0.05, 0.1, 0.15 |
| u (m/s) | Re |
|---|---|
| 0.075 | 300 |
| 0.1 | 400 |
| 0.125 | 500 |
| Re = 300 | St | Error |
|---|---|---|
| Numerical simulation | 0.2000 | 0.79% |
| Empirical function | 0.2016 [32] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.; Xie, H.; Liu, Z.; Zhai, X.; Zhang, H.; Li, X. Control on Flow Separation over a Cylinder by a Ferrofluid Film Adsorbed by a Magnet. Inventions 2024, 9, 65. https://doi.org/10.3390/inventions9030065
Wei C, Xie H, Liu Z, Zhai X, Zhang H, Li X. Control on Flow Separation over a Cylinder by a Ferrofluid Film Adsorbed by a Magnet. Inventions. 2024; 9(3):65. https://doi.org/10.3390/inventions9030065
Chicago/Turabian StyleWei, Chunyun, Hongjia Xie, Zixuan Liu, Xinfeng Zhai, Hongna Zhang, and Xiaobin Li. 2024. "Control on Flow Separation over a Cylinder by a Ferrofluid Film Adsorbed by a Magnet" Inventions 9, no. 3: 65. https://doi.org/10.3390/inventions9030065
APA StyleWei, C., Xie, H., Liu, Z., Zhai, X., Zhang, H., & Li, X. (2024). Control on Flow Separation over a Cylinder by a Ferrofluid Film Adsorbed by a Magnet. Inventions, 9(3), 65. https://doi.org/10.3390/inventions9030065









