Abstract
The purpose of this study is to employ and improve evolutionary algorithms, namely the genetic algorithm (GA) and the differential evolution algorithm (DE), to extract the parameters of the equivalent circuit model (ECM) of a bifacial photovoltaic module using the representative model of a diode with five parameters (1D5P). The objective is to simulate the characteristics of the I–V curves for various irradiation and temperature scenarios. A distinctive feature of this study is the exclusive use of the information in the technical sheet of the bifacial module to conduct the entire extraction and simulation process, eliminating the need to resort to external sources of data or experimental data. To validate the methods, a comparison was made between the simulation results and the data provided by the bifacial module manufacturer, contemplating different scenarios of irradiation and temperature. The DE was the most accurate algorithm for the 1D5P model, which presented a maximum average error of 1.57%. In comparison, the GA presented a maximum average error of 1.98% in the most distant scenario of STC conditions. Despite the errors inherent to the simulations, none of the algorithms presented relative errors greater than 8%, which represents a satisfactory modeling for the different operational conditions of the bifacial photovoltaic modules.
1. Introduction
With the pursuit of economic growth and industrial development, the world’s dependence on electricity is becoming ever more significant. Even though investments in the energy sector will fall by 20% from their 2020 levels [1], significant effort has been invested in expanding energy generation capacity, increasing the efficiency of conventional energy sources, and developing new energy sources.
The global energy matrix is based mainly on non-renewable sources, such as coal, oil, and derivatives [2]. However, the increase in technological development also contributes to the development of new sources of energy generation, i.e., renewable sources, which, in addition to enabling improved reliability in the electrical system, allow for a variation in the world’s energy matrix, thus reducing the environmental impacts caused by fossil fuels. In addition to this scenario, the decrease in fossil fuel reserves and the environmental impacts associated with non-renewable energies have considerably increased the interest in sustainable, renewable, and ecologically sound energy sources [3,4], such as those derived from bioethanol [5], wind energy [6], biomass [7], and photovoltaic Energy [8].
Within this scenario, solar energy stands out as one of the leading renewable energy sources that is being captured and transformed through photovoltaic panels. The growing number of installed photovoltaic systems has been remarkable, as evidenced by [3], which showed that, by the end of 2018, more than 500 GW of power had been generated through photovoltaic panels worldwide.
Furthermore, as indicated by [9] in 2021, photovoltaics reached a level of 1 TWh generated for the first time, while other renewable sources, such as wind, reached an export of 2 TWh. In its projections report, the International Energy Agency (IEA) estimates that, by 2050, photovoltaic energy production could represent approximately 11% of the total world electricity production [10].
It is undeniable that photovoltaic energy is becoming one of the best choices in the power generation sector. This is mainly because the energy generated through photovoltaic modules is a renewable and inexhaustible source of energy, as highlighted by [11].
Despite the reductions in fees and taxes granted by the government in recent years, as well as investments in technological advancements and improvements in energy efficiency and production capacity that have led to a significant decrease in system costs, the acquisition of photovoltaic equipment still requires a substantial investment [12]. In addition, installation and engineering costs are considerable, as pointed out by the International Energy Agency [1], especially when it comes to large installations, such as power plants.
In this context, conducting studies and simulations that analyze the relationship between the photovoltaic generation system and deployment area, combined with the detection of possible failures in energy generation or the tracking system, has the potential to increase accuracy in the dimensioning process, thus avoiding financial losses [13,14].
Within the literature, several methods aim to represent a photovoltaic cell; the most accepted is the representation of the solar cell through an electrical circuit composed of a current source, a passive element, and resistances that configure its operation, in which the values of the represented elements are determined through algorithms and evolutionary computation due to their high degree of complexity. However, there are also models with greater complexity that are composed of a current source in parallel with two passive elements. These algorithms, despite being validated, tend to consume greater processing power and, in certain operating conditions, present greater errors [15]. Thus, the representation of energy generation from a photovoltaic module is carried out through simulations of photovoltaic electrical properties that are modeled by an electrical equivalence circuit [16]. Several types of ECM have been suggested over time, among which the single diode model stands out [14,16].
To extract the parameters of the PV model, mathematical or computational methods are used to solve nonlinear equations [17]. There are a wide variety of optimization techniques used in parameter extraction, including the use of evolutionary algorithms, such as the genetic algorithm (GA), differential evolution algorithm (DE), and others [18]. In addition to evolutionary algorithms, several computational techniques using bio-inspired algorithms are applied, such as the particle swarm algorithm [16].
However, in the literature, there are no standardized methods to characterize bifacial photovoltaic modules as observed in conventional ones since bifacial characteristics are not a linear combination of monofacial characteristics [19]. Therefore, the objective of this study is to conduct simulations and performance evaluations of bifacial photovoltaic modules under different irradiation and temperature conditions using the one diode and five configurations (1D5P) model. This analysis will be performed using algorithms inspired by nature, specifically the genetic algorithm (GA) and the differential evolution algorithm (DE). The objective is to extract the parameters of the ECM equations using only the data present in the specifications provided by the Canadian manufacturer [20].
The manuscript is organized as follows: Section 2 presents the materials and methods. It begins with Section 2.1, which presents how irradiation and temperature impact the I–V curve of a photovoltaic module. Section 2.2 presents the equivalent circuit of a photovoltaic module, followed by Section 2.2.1 and Section 2.2.2, which present the ideal ECM of a photovoltaic cell, followed by the representation of a photovoltaic cell using the one diode and five parameter method (1D5P). Section 2.3 presents the concepts used to extract the parameters necessary to represent the photovoltaic modules and the fitness function. The next section presents the concepts of evolutionary algorithms, as well as the steps of their implementation, and then, Section 3 first presents the parameters found through the algorithms used, followed by the simulations and I–V curves of each implementation at different temperatures and irradiation scenarios. Finally, Section 4 presents the conclusions obtained through the methods developed and implemented.
2. Materials and Methods
2.1. Influence of Temperature and Irradiation on the I–V Curve of a Photovoltaic Cell
Since many power conversion drives are sized by the maximum DC power installed in them, one of the most significant characteristics of photovoltaic modules is the power they generate at their maximum power point (Pmp). To do this, it is necessary to analyze the module’s I–V curve to find the point of highest generation, where the maximum power (Pm) will be the intersection of the maximum power current (Imp) and the maximum power voltage (Vmp). In this context, the importance of analyzing the I–V curve of photovoltaic modules is highlighted, in addition to such curves representing the relationship between the two parameters, it is also used to identify PV failures [21].
Although the power (Wp) is the characteristic by which a module is identified, its effectiveness and energy production are intrinsically linked to external elements. These factors include the operating temperature of the cells, the presence of dirt on the surface of the modules, the amount of solar radiation received, and exposure to wind action [22].
In the context of identifying the extent of the impacts of temperature and irradiation on the efficiency of energy generation, several studies were carried out to better understand these consequences.
Due to the electrical nature of an electron, this particle is directly influenced by solar radiation. This occurs due to the excitation of electrons caused by the incidence of solar photons. In this way, the current generated by sunlight maintains a proportional relationship with the intensity of the radiation that reaches the semiconductor material.
On the other hand, temperature has a negative effect on the cell. This effect results from the thermal agitation of the materials, which intensifies with increasing temperature. This process speeds up the recombination of electron pairs, resulting in a decrease in the number of free electrons. Consequently, the P-N junction experiences an increase in voltage that results in a decrease in voltage at the cell’s output terminals [23].
It is important to note that an increase in solar radiation translates into a simultaneous increase in the current generated by sunlight. Figure 1 [16] below illustrates the I–V graph of a photovoltaic module when subject to variations in temperature and irradiation.
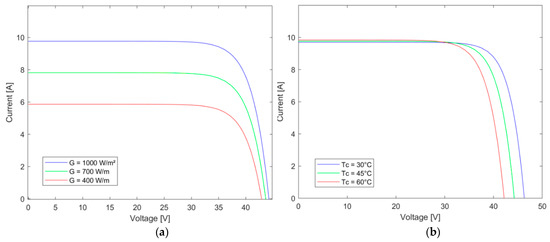
Figure 1.
(a) Influence of irradiation on the I–V curve of a photovoltaic cell. (b) Influence of temperature on the I–V curve of a photovoltaic cell.
2.2. Equivalent Circuit Modeling of a Bifacial Photovoltaic Module
A set of photovoltaic cells connected in series is called a photovoltaic module [11], and the cells most used in the construction of commercial photovoltaic modules are those with monocrystalline silicon and polycrystalline silicon [24,25].
Within the categories of photovoltaic modules, two main groups stand out: monofacial and bifacial. As the name suggests, bifacial modules are equipped with cells on both sides of the module, allowing solar radiation to be captured on both sides of the panel [26].
Bifacial modules were developed from conventional ones and have, as their main characteristic, the ability to capture photons and generate energy on both sides, the front and the back. The front face receives direct solar irradiation, and the rear receives both diffuse solar irradiation and irradiation reflected by the ground, called albedo [27].
The extra power obtained at the rear of the module allows a gain from 5 to 30% when compared to a conventional equivalent module, depending on how and where the module is installed, the gain varies depending on the surface where the modules were installed [28].
This phenomenon, called the photoelectric effect, is especially noticeable in silicon due to its peculiar atomic structure, which consists of four electrons forming bonds with their neighbors and configuring as a crystalline lattice [25]. However, for the phenomenon to occur, the two layers that make up the silicon must be charged with inverse polarities, one positively and the other negatively, so the silicon must be doped with impurities. In order to perform the modeling of a bifacial photovoltaic panel, it is essential to identify the parameters that reflect the physical phenomena observed in the equipment. For this, developing an electrical model that resembles the real system is necessary. This procedure is of crucial importance as it enables an accurate estimate of the energy generated by the module and the electrical parameters under any circumstances [16].
As mentioned in [29], a photovoltaic cell can be described in an analogous way by means of an equivalent electrical circuit, in which an electric current source operates in parallel with a diode. The current source generates direct electrical current, while the diode represents the P-N semiconductor found in photovoltaic cells. In this scenario, the diode ideality factor assumes fundamental importance in characterizing the behavior of the P-N junction, serving as an indication of how close or far the junction is from ideal conditions. This parameter is intrinsically related to the manufacturing characteristics of the diode, including the type of material used and the doping level. Its value is confined to a range that varies between 1 and 2, where values close to 1 signal a diode performance that is more in line with the ideal, as discussed in [30].
However, an equivalent scheme containing only these two elements is not adequately comprehensive to trace the I–V curve of an actual photovoltaic panel [31] since the ohmic losses of the material and the internal dissipation in the cell are not taken into account. Consequently, the most prevalent models in the literature, which aim to represent a commercial photovoltaic cell, are based on a current source connected to a diode and resistors that capture ohmic losses and dissipation.
2.2.1. Modelling of a Photovoltaic Cell
The way a photovoltaic cell can be presented through an electrical circuit includes the combination of an electric current source and a diode [29], as illustrated in the single-line circuit shown in Figure 2 below.
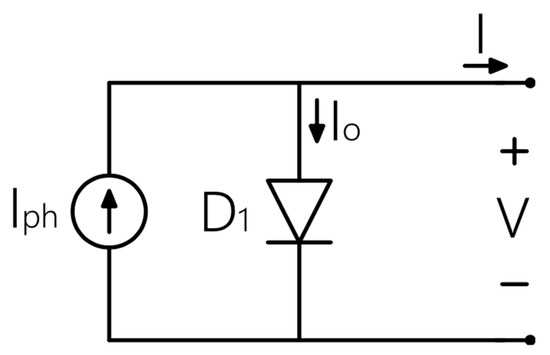
Figure 2.
ECM of a photovoltaic cell.
Equation (1) below describes the ECM of Figure 2:
where the current flowing through a diode ( is given by:
where I is the output current of the cell (A); is the inverse saturation current of the diode (A); is the elementary charge of the electron (1.602 × 10−19 coulombs); is the Boltzmann constant (1.31 × 10−23) J/K); is the cell temperature (K); is the ideality factor of the diode; and V is the cell output voltage (V).
However, the circuit shown in Figure 2 represents an idealized scenario in which the losses inherent to photovoltaic cells are not considered. These losses will be addressed in the one diode and five parameters (1D5P) model, which will be discussed in the next topic.
2.2.2. One Diode Five Parameter Model (1D5P)
The one diode five parameter model (1D5P) or single diode model (SDM), as commonly found in the literature, are the most widely used equivalent electrical circuit models in the literature used to represent a photovoltaic cell [32,33]. According to [30], a photovoltaic cell is composed of a photo-generated current (Iph) that is produced by the flow of light that generates a continuous electric current and by its resistances.
In the scope of modeling an equivalent circuit to obtain the best representation of a photovoltaic cell, a model with one diode and five parameters approaches the real configuration due to the inclusion of two resistances in the equivalent circuit, and (). The series resistance () encompasses two intrinsic resistances to the photovoltaic cell: the resistance of the semiconductor material in its P-N junction and the resistance between the material and the metallic terminals that capture the photogenerated current [25], while (), which is connected in parallel to the current source, represents the impurities and defects in the structure, mainly close to the edges, creating an internal path for the leakage current and reducing the current effectively generated by the device [25]. According to [34,35] the equivalent electrical circuit of the 1D5P model can be represented as shown in Figure 3.
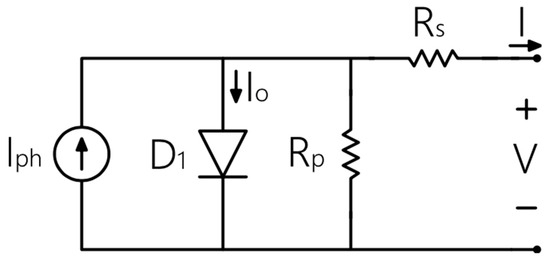
Figure 3.
Circuit equivalent 1D5P.
Thus, when analyzing the electrical circuit, the result is five unknown parameters that need to be extracted in this model: the inverse saturation current of the diode ), the ideality factor of the diode (), the photogenerated current , the series resistance () and the parallel resistance (). The five parameters to be obtained are present in the characteristic equation of the model with one diode and five parameters, obtained from Kirchhoff’s law, and express the electric current as follows.
However, because a bifacial photovoltaic module is composed of several cells connected in series, the term () is added to Equation (3). Thus, the equation is now represented by:
2.3. Concepts for Parameter Extraction
Regardless of the evolutionary algorithm used, there are shared concepts between the methods. The term “individual” refers to the proposed solution to the problem, in this case, the parameters that need to be obtained. This collection of individuals is known as the “population”.
The initial step in extracting parameters through evolutionary algorithms involves creating an initial population composed of randomly generated Np individuals. However, certain limitations are applied, mainly to define the ranges in which the parameter values are feasible from a physical point of view. These ranges can be further adjusted to more likely values if enough information is available. Table 1 displays the ranges of values for each parameter in both models [16].

Table 1.
Parameter ranges for creating the initial population in a SDM model, Genetic Algorithm and Differential Evolution.
In this study, we will use the standard test conditions (STC) as a reference point, since it is possible to find all the values of the main points of the I–V curve for this condition in the datasheet of a bifacial photovoltaic module. Terms followed by “ref” are taken from data provided by the manufacturer under standard conditions.
Another important operation common to all algorithms in this study is the criterion for evaluating individuals. This criterion, known as the fitness function, aims to verify whether the parameters fit the model. This function is derived from the ECM equation. In the case addressed in this work, in the model with one diode and five parameters, Equation (4) is used. To determine the fitness, it is necessary to set the model equation equal to zero and apply it to each of the points found in the data sheet of the module under the reference conditions, that is, the open circuit voltage (, 0), maximum power point (, ), and short circuit current (0, ). Substituting the obtained data and the physical constants, the system will present three equations where the unknowns will be the parameters that the algorithm needs to extract. To ensure that the values remain positive, the Root Mean Squared Error (RMSE) criterion is used. The equation is presented in Equation (5) below.
where N represents the number of experimental points used. The fitness of the 1D5P model is represented by:
where for the 1D5P model, representing the parameters to be extracted by the algorithm.
2.4. Evolutionary Algorithms
2.4.1. Genetic Algorithm (GA)S
The genetic algorithm (GA) was developed by [36] and was considered an evolutionary algorithm paradigm [37]. Holland employed Charles Darwin’s evolutionary theory as an analogy for natural selection and reproduction processes, adapting these ideas to the computational environment. In this scenario, the element tasked with solving problems is called a chromosome or individual. Each chromosome contains M information, which represents the parameters to be later extracted by the algorithm. The initial step for applying the algorithm involves the generation of the initial population, executed in a pseudo-random way, adopting Np = 50 and limits specified in Table 1. Next, each individual generated is evaluated according to its aptitude (fitness), and the algorithm progresses according to the flowchart are outlined in Figure 4. In this path, the following operators are employed: GA Selection, GA Crossing and GA Mutation, as described in Section 2.4.1.2, Section 2.4.1.3 and Section 2.4.1.4, respectively. This recursive process lasts until Ng reaches a value of 3000. The choices of Np and Ng are supported by the parameter refinement process explained in Section 3.1.
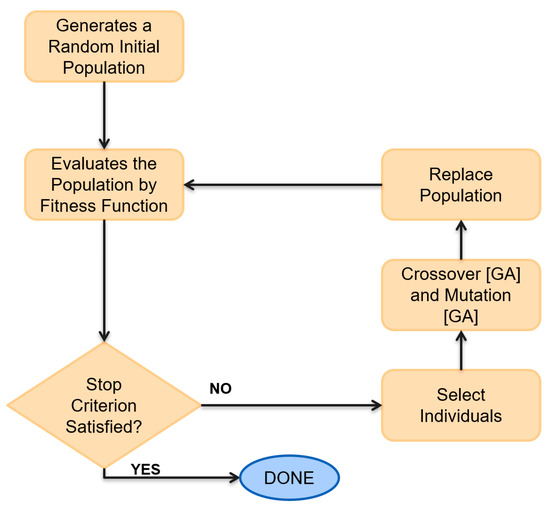
Figure 4.
Genetic algorithm flowchart.
2.4.1.1. Genetic Algorithm Coding
The basis for applying genetic algorithms to any problem, be it search or optimization, starts with properly representing the problem. This representation is crucial to allow genetic algorithms to act efficiently on it [38].
Genetic algorithms operate by manipulating populations of individuals or chromosomes. A chromosome is an array of data expressed as vectors or sequences of binary, real, or a combination of both. It encapsulates a potential solution to the problem being optimized, in the case of this study, the representative parameters of a photovoltaic cell.
Three different approaches can represent chromosomes: binary, integer, or real. This representation is referred to as the genetic algorithm alphabet. The choice between these three types depends on the nature of the class of problems to be solved [39]. The fitness function evaluates each individual of the population, the result of the fitness function applied to each individual of the population is defined by fPop.
The complete set of all possible configurations a chromosome can adopt constitutes its search space, as [38] mentioned.
2.4.1.2. Selection for GA
According to [40,41] the tournament method is one of the main methods used for the selection operator. In summary, this operator is implemented as follows: Nt individuals are extracted from the temporary population, forming the set Pt, which will be the individuals that will compete in the tournament. The tournament winner will be the individual from the Pt set with the lowest fitness value. Thus, this individual is inserted into the population for the next iteration. This procedure is repeated Np times to complete the population.
2.4.1.3. Crossover for GA
The crossover step is the genetic operator with the greatest impact in genetic algorithms (GA). Inspired by the process of sexual reproduction in living beings, as [42] pointed out, this phase aims to create offspring by mixing the genetic characteristics of the previously selected parents.
We define the crossover probability parameter as , which defines the probability of an individual being selected for this purpose. This parameter is unique; therefore, all individuals present in the population have the same chance of reproducing regardless of the evaluation of the fitness function. According to [16], the higher this rate, the faster the new structures will be introduced into the population. But if this rate is too high, structures with good aptitudes can be removed faster than the ability of selection can create better structures.
In this operator, all individuals randomly receive an index between 0 and 1 that will define whether they will be selected for the crossover or not in the case where = 0.3, All individuals that have indices lower than 0.3 are selected for genetic recombination, in which they are subjected to the exchange of information with each other and are added to the initial population, causing an increase in the number of individuals in the same population.
2.4.1.4. Mutation for GA
The purpose of this genetic operator is to introduce genetic traits in the members of the population, which may or may not be relevant for each individual. This adjustment in genetic characteristics happens in a specific way within each individual. The mutation process is controlled by a fixed parameter , mutation probability, which is generally recommended as 1% [43]. However, this parameter can be changed to increase the algorithm’s search area, knowing that a very high rate makes the algorithm essentially random.
According to [44], a very common way to perform this operator is as follows: given a real vector , a very common way to generate a descendant by mutation is:
where j denotes the jth component of r that was selected for mutation and is a random variable. The use of a normal (Gaussian) distribution, with zero mean and variance , has been one of the main ways to introduce mutation in real coding individuals.
After mutation, the population is reevaluated, but only the mutated individuals and those generated in the crossover need to be effectively evaluated.
2.4.2. Differential Evolution Algorithm (DE)
Similar to the genetic algorithm, the differential evolution algorithm (DE) employs Charles Darwin’s evolutionary theory to execute this method in the computational context. For this reason, DE is also classified as a bio-inspired algorithm [45].
The differential evolution method was proposed by [46] with the goal of creating a population meta-heuristic dedicated to the optimization of functions in continuous spaces, that is, for parameters with values belonging to the group of real numbers [46,47]. The steps of this algorithm are similar to those of the genetic algorithm; however, the distinctive element of this approach resides in the exploitation of information intrinsic to the population to incorporate disturbances in individuals. This process differs from associating disturbances to predefined probabilities [44].
In this algorithm, each individual is called a target vector and contains D information, representing the parameters to be extracted. Like other algorithms, the initial procedure consists of generating the initial population, which is created pseudo-randomly, adopting Np = 50 and intervals as specified in Table 1. Subsequently, each particle is submitted to evaluation through the fitness function, and the algorithm proceeds as outlined in the flowchart of Figure 5, using the operators: ED Mutation, ED Crossover and ED Selection, which are detailed in Section 2.4.2.1, Section 2.4.2.2, and Section 2.4.2.3, respectively. This recursive process is performed until Ng = 300 is reached. The values chosen for Np and Ng are based on the fine-tuning of parameters highlighted in Section 3.1.

Figure 5.
Differential evolution algorithm flowchart.
2.4.2.1. Mutation to DE
For each member of the population , with , a new vector is produced using Equation (8).
where are distinct values chosen from {1, 2, …, }, which are mutually distinct and different items of index i.
After completing the mutation process, the matrix of mutated individuals is obtained, in which each individual is denoted by
2.4.2.2. Crossover to DE
In order to obtain diversity in the mutated parameters, the Differential Evolution Crossover Operator is implemented. Let be the target vector under analysis and be the respective mutated vector, obtained by Equation (8). The vector , called a trial vector, is obtained as follows:
where , CR ∈ [0, 1] is a constant that defines the crossover rate, and Ii is a randomly chosen index ∈{1,…,M}, which guarantees that receives at least one component of .
2.4.2.3. Selection for DE
After the mutation and crossover steps, in which all Np vectors served as target vectors, the selection of vectors that will be preserved for the next generation is completed using a greedy criterion, which means always choosing the best alternative that seems most promising at that time.
With as the target vector under analysis and as its respective trial vector, the differential evolution selection operator is completed as follows:
If has a fitness value greater than the fitness value of , then ;
Otherwise,
At the end of the selection process, we have the new population formed by the target vectors , with .
Finally, by combining the selection, crossover, and mutation operators as shown in the flowchart in Figure 5, we obtain the standard version of the differential evolution algorithm (or details on other variants, see, for example [48,49]).
2.5. Plot I–V Curve
After extracting the parameters performed by the algorithms mentioned in the previous topics, it is possible to carry out simulations for any irradiation and temperature indices. This is possible through Equations (9) and (10) below, which allow the updating of and to different operating conditions [50].
where and is the irradiation in W/m2.
where represents the diffusion factor of the diode (V) and denotes the temperature coefficient of the short-circuit current.
The value of the parameter changes proportionally to the irradiance value, as indicated by Equation (11) below [51]. On the other hand, in this method, the values of m and remain unchanged.
In this way, acquiring the I–V curve of a bifacial module using the 1D5P model is feasible when applying Equation (3). This allows the determination of the bifacial photovoltaic module’s currents, voltages, and output powers according to the desired conditions.
The implementation of the algorithms for calculating the parameters and generating the graphics was carried out using the MATLAB™ software (Version R2023b 23.2) [52], where all lines of code were developed without applying a toolbox.
3. Results and Discussions
As Section 2 of this study shows, evolutionary algorithms extract essential parameters from models under reference conditions. Thus, Table 2 presents the parameter values found using the genetic algorithm and the differential evolution algorithm for the 1D5P model of the bifacial solar module CANADIAN CS3W-410PB-AG.

Table 2.
Parameters extracted by GA and DE from the CANADIAN CS3W-410PB-AG bifacial photovoltaic module.
With the extracted parameters, it becomes possible to adjust them for different values of temperature and irradiation by using the auxiliary equations presented in Section 2.5 of this study. This makes it possible to simulate I–V curves for specific scenarios.
To evaluate the effectiveness of the algorithms, simulations were carried out in four different scenarios. The first occurs under STC conditions with G = 1000 W/m2 and cell temperature T = 25 °C, the second with an irradiation of G = 600 W/m2 and cell temperature T = 20 °C, the third with G = 1100 W/m2 and T = 60 °C, and finally, the nominal operating temperature (NOCT) with G = 800 W/m2 and T ≅ 44 °C. As observed in the selected irradiation and temperature values, such data address several scenarios of operational conditions in which the simulations encompass both optimistic scenarios, such as the third case, and pessimistic scenarios of low irradiation and low temperature, represented by the second case. The first case was simulated according to the standard test conditions informed in the datasheet by the manufacturer of the bifacial module; the second case was simulated according to [53], where it is indicated that European irradiation and temperature are milder than the temperatures found in places of high irradiation, such as in Brazil, which approaches the third condition simulated in this work [54]. Finally, the last case concerns the NOCT conditions, which are more frequent [55] and serve to validate the effectiveness of the schemes employed in typical situations.
Figure 6 shows the superimposition of the curves generated by the GA and DE evolutionary algorithms using the 1D5P model under reference conditions (STC). Both curves are compared with data provided by [20]. Table 3 indicates the points of (, 0), (, ), (0, ) and the average relative error (e%) of the data obtained through the parameters in relation to the manufacturer’s values. The relative percentage error (e%) is calculated according to Equation (12), where valuedata represents the value presented by the manufacturer and the valuesimulated is the value found through the simulation, and the maximum power point is found by the product of the current by the voltage .
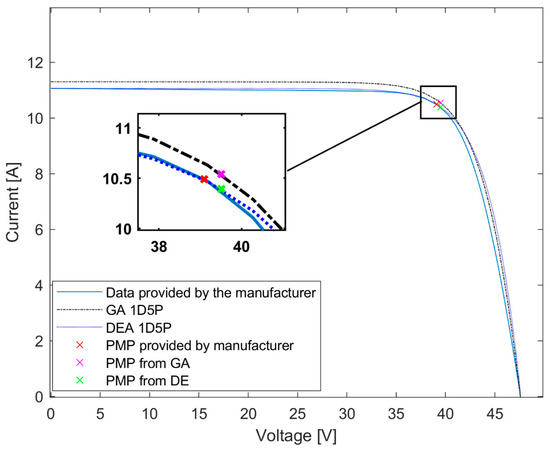
Figure 6.
Superposition of the I–V curves generated by GA and DE in the 1D5P model under operating conditions G = 1000 W/m2 and T = 25 °C.

Table 3.
Points of interest of the different methods on STC conditions with G = 1000 W/m2 and T = 25 °C.
Through Table 3, it is possible to verify that the simulations using the 1D5P model obtained slightly better results when combined with the differential evolution algorithm than with the genetic algorithm. The average error found through the GA was 1.04%, while for the DE it was 0.45%. Thus, it is evident that, for the STC conditions, the differential evolution algorithm tends to represent in a more efficient way the bifacial module.
In general, the results were positive for the STC conditions since the worst case occurred in the short-circuit current where the relative error was 2.08% presented by the GA.
Similar to the previous case, Figure 7, Figure 8 and Figure 9 show the superimposition of the curves generated by the evolutionary algorithms and the data provided by CANADIAN SOLAR [20] under the conditions specified at the beginning of this topic.
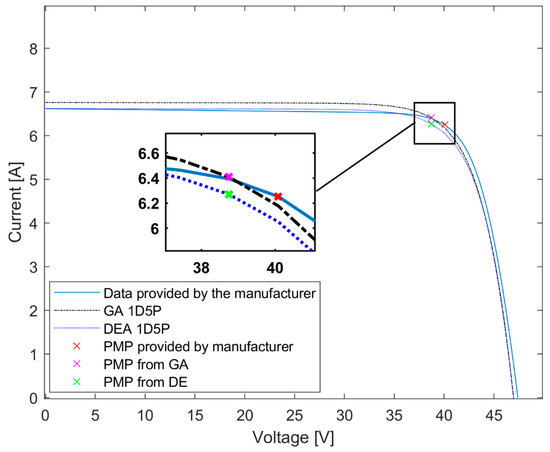
Figure 7.
Superposition of the I–V curves generated by GA and DE in the 1D5P model under operating conditions G = 600 W/m2 and T = 20 °C.
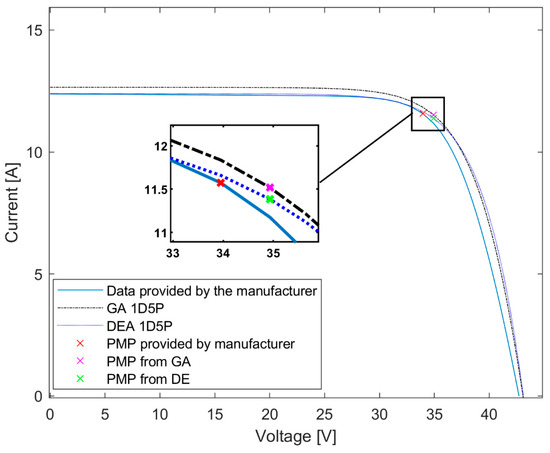
Figure 8.
Superposition of the I–V curves generated by GA and DE in the 1D5P model under operating conditions G = 1100 W/m2 and T = 60 °C.
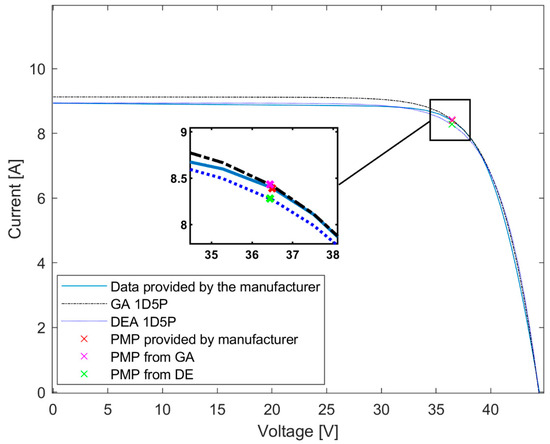
Figure 9.
Superposition of the I–V curves generated by GA and DE in the 1D5P model under operating conditions G = 800 W/m2 and T ≅ 44 °C.
Table 4, Table 5 and Table 6 show the points of interest (, 0), (, ), (0, ) and the respective relative errors of each method. It is important to emphasize that the data provided by CANADIAN SOLAR, except for the standard test conditions and nominal operating temperature, are generated from simulations made in the PVSYST software (Version 2020) [56].

Table 4.
Points of interest of the different methods under the conditions G = 600 W/m2 and T = 20 °C.

Table 5.
Points of interest of the different methods under the conditions G = 1100 W/m2 and T = 60 °C.

Table 6.
Points of interest of the different methods under the conditions G = 800 W/m2 and T ≅ 44 °C.
Analyzing Figure 7, Figure 8 and Figure 9, as well as their respective tables, it is observed that the 1D5P method combined with GA and DE had good results in the simulated scenarios, with the best result being the DE, where the average error in the simulation of low irradiation and temperature with G = 600 W/m2 and T = 20 °C was 1.57%, the average error for the third case with G = 1100 W/m2 and T = 60 °C was 1.37%, and finally, a 0.81% error for the NOCT case. However, despite the GA presenting a larger error than the DE, the algorithm still had good results, with an average error of 1.98% in the most complex simulated condition, in which G = 600 W/m2 and T = 20 °C.
A crucial observation is that, as conditions move away from STC conditions, the error increases. This phenomenon arises from the fact that the reference parameters are obtained from the technical sheet under STC conditions. The same characteristics can be observed in [15] where, according to the I–V curves were simulated in conditions far from the STC conditions, the accentuated error is visible by yourself. However, even choosing a more complex condition with G = 600 W/m2 and Tc = 20 °C, the algorithms presented errors of less than 8%. In studies such as the one conducted by [57], in which several approaches to modeling and obtaining parameters of photovoltaic modules were evaluated with the purpose of examining the effectiveness and accuracy of each method, the finding from Chenni’s method [50] stood out as the most accurate. This indicates that this error range is acceptable for simulating photovoltaic modules.
3.1. Definition of Np and Ng Parameters
As detailed in item 2, as the value of the fitness function approaches zero, the parameters adjust more and more to the model. Therefore, the criteria to determine the values of Np (number of individuals in the population) and Ng (number of iterations) were established, with the priority that the calculated value of the fitness function (fitness) was the closest to zero and was limited to a maximum of . However, if aptitude convergence did not occur within a period of up to 2 s, the selected parameters would be those that originated from the minimum aptitude value in up to 2 s. Table 7 presents the fitness values for different combinations of Np and Ng, summarizing the search for more appropriate values for each simulation scheme conducted in the research (fine-tuning of parameters). It is important to note that the time in Table 7 only serves as a reference point to compare the computational cost of the three methods employed superficially. It should be noted that the simulations were performed on a machine with a GTX 1650 4 GB, an I5-10300H processor, and 12GB of RAM.

Table 7.
Refined settings of the Np and Ng parameters.
Analyzing Table 7, it is observed that the number of iterations and the number of individuals in the initial population directly impact the value of the fitness function, thus, with the relative increase of Ng and Np, the value of the fitness function tends to approach zero despite having a higher operational cost due to processing the Np individuals to be analyzed individually with their M characteristics.
4. Conclusions
This study used evolutionary optimization algorithms, such as the genetic algorithm (GA) and the differential evolution algorithm (DE) to obtain the parameters of the ECM of a photovoltaic module in the 1D5P model. The objective was to simulate the I–V characteristic curves for various irradiation and temperature conditions, using the information available in the module’s technical sheet. Additionally, a comparative analysis was carried out between the results obtained by each method and the data provided by the Canadian module manufacturer, considering different irradiation and temperature scenarios.
In general, the DE was the evolutionary algorithm that stood out with the best performance. It registered maximum relative errors of 1.02% in the standard test conditions (STC) and 3.34% in the scenario furthest from the reference conditions. On the other hand, the GA presented more significant errors, reaching a maximum relative error of 2.08% in the STC conditions and 3.34% in a simulation that deviated from the reference conditions. With regard to the simulations of scenarios three and four, both algorithms exhibited solid performance, registering maximum relative errors of 2.88% for both of them.
One of the most significant contributions of this study is the conclusion that using the 1D5P model results in a good representation of bifacial photovoltaic modules. This conclusion is evidenced by the low errors found by the evolutionary algorithms in the different simulations carried out in this study, both close to the reference conditions and in more extreme operational conditions.
Author Contributions
Conceptualization, G.H.G., R.K. and C.M.G.A.; methodology, G.H.G., L.L.P. and R.K.; software, G.H.G., L.L.P. and R.K.; validation, G.H.G.; formal analysis, G.H.G. and C.M.G.A.; investigation, G.H.G., L.L.P., G.P.d.A. and O.C.d.M.L.; resources, G.P.d.A., O.C.d.M.L. and R.K.; data curation, G.H.G. and L.L.P.; writing—original draft preparation, G.H.G., L.L.P. and C.M.G.A.; writing—review and editing, G.P.d.A., O.C.d.M.L. and R.K.; visualization, G.H.G.; supervision, C.M.G.A. and G.P.d.A.; project administration, G.H.G., G.P.d.A. and C.M.G.A.; funding acquisition, C.M.G.A. All authors have read and agreed to the published version of the manuscript.
Funding
Coordination for the Improvement of Higher Education Personnel—Brazil (CAPES) and the National Council for Scientific and Technological Development (CNPq).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors wish to thank the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.
Conflicts of Interest
The authors declare no conflict of interest.
References
- International Energy Agency. Renewables 2021—Analysis and Forecast to 2026. 2021. Available online: https://iea.blob.core.windows.net/assets/5ae32253-7409-4f9a-a91d-1493ffb9777a/Renewables2021-Analysisandforecastto2026.pdf (accessed on 1 August 2023).
- International Energy Agency. World Energy Outlook 2021. 2021. Available online: https://www.iea.org/reports/world-energy-outlook-2021 (accessed on 1 August 2023).
- Haegel, N.M.; Atwater, H.; Barnes, T.; Breyer, C.; Burrell, A.; Chiang, Y.-M.; De Wolf, S.; Dimmler, B.; Feldman, D.; Glunz, S.; et al. Terawatt-Scale Photovoltaics: Transforming Global Energy. Science 2019, 364, 836–838. [Google Scholar] [CrossRef]
- Kurbatova, T.; Perederii, T. Global Trends in Renewable Energy Development. In Proceedings of the 2020 IEEE KhPI Week of Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 5–10 October 2020; pp. 260–263. [Google Scholar] [CrossRef]
- Freitas, H.; Olivo, J.; Andrade, C. Optimization of Bioethanol In Silico Production Process in a Fed-Batch Bioreactor Using Non-Linear Model Predictive Control and Evolutionary Computation Techniques. Energies 2017, 10, 1763. [Google Scholar] [CrossRef]
- Nwaigwe, K.N. Assessment of wind energy technology adoption, application and utilization: A critical review. Int. J. Environ. Sci. Technol. 2022, 19, 4525–4536. [Google Scholar] [CrossRef]
- Almeida, E.L.; Andrade, C.M.G.; Andreo Dos Santos, O. Production of Biodiesel via Catalytic Processes: A Brief Review. Int. J. Chem. React. Eng. 2018, 16, 20170130. [Google Scholar] [CrossRef]
- Alhmoud, L. Why Does the PV Photovoltaic Solar Power Plant Operate Ineffectively? Energies 2023, 16, 4074. [Google Scholar] [CrossRef]
- Maia, S.; Demôro, L. Power Transition Trends. 2022. Available online: https://assets.bbhub.io/professional/sites/24/BNEF-Power-Transition-Trends-2022_FINAL.pdf (accessed on 6 June 2023).
- International Energy Agency Technology Roadmap Solar Photovoltaic Energy. 2014. Available online: http://mdvseia.org/wp-content/uploads/2015/05/Technology-Roadmap-Solar-PV-2014-version.pdf (accessed on 6 July 2023).
- Lopes Filho, G.; Franco Pereira, R.A.; Vieira Teles, F.H. Estimação De Parâmetros De Painéis Fotovoltaicos Utilizando O Algoritmo Fireflycom Atualização Em Função Da Irradiância E Temperatura. VII Congresso Brasileiro de Energia Solar 2018. Gramado. Available online: https://anaiscbens.emnuvens.com.br/cbens/article/view/365/365 (accessed on 3 April 2023).
- IPEA—Instituto De Pesquisa Econômica Aplicada. Viabilidade Econômica de Sistemas Fotovoltaicos No Brasil e Possíveis Efeitos No Setor Elétrico. 2018; Governo Federal. Available online: https://portalantigo.ipea.gov.br/agencia/images/stories/PDFs/TDs/td_2388.pdf (accessed on 7 October 2023).
- Da Rocha Queiroz, J.; Da Silva Souza, A.; Gussoli, M.K.; De Oliveira, J.C.D.; Andrade, C.M.G. Construction and Automation of a Microcontrolled Solar Tracker. Processes 2020, 8, 1309. [Google Scholar] [CrossRef]
- Tifidat, K.; Maouhoub, N.; Askar, S.S.; Abouhawwash, M. Numerical Procedure for Accurate Simulation of Photovoltaic Module Performance Based on Single-Diode Model Parameters. Energy Rep. 2023, 9, 5532–5544. [Google Scholar] [CrossRef]
- Provensi, L.L.; Souza, R.M.; Grala, G.H.; Bargamasco, R.; Krummenauer, R.; Andrade, C.M.G. Modeling and Simulation os Photovoltaic Modules Using Bio-Inspired Algorithms. Inventions 2023, 8, 107. [Google Scholar] [CrossRef]
- Provensi, L.L.; Grala, G.H.; Zukeram Junior, E.S.; Alcantara, G.P.; Krummenauer, R.; Andrade, C.M.G. Modeling of the operating characteristics of photovoltaic modules based on particle swarm optimization. Environ. Prog. Sustain. Energy 2022, 41, e13831. [Google Scholar] [CrossRef]
- Koohi-Kamali, S.; Rahim, N.A.; Mokhlis, H.; Tyagi, V.V. Photovoltaic electricity generator dynamic modeling methods for smart grid applications: A review. Renew. Sustain. Energy Rev. 2016, 57, 131–172. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.J.; Duck, B.C. A hybrid wind driven-based fruit fly optimization algorithm for identifying the parameters of a double-diode photovoltaic cell model considering degradation effects. Sustain. Energy Technol. Assess. 2022, 50, 101685. [Google Scholar] [CrossRef]
- Guerrero-Lemus, R.; Vega, R.; Kim, T.; Kimm, A.; Shephard, L. Bifacial solar photovoltaics—A technology review. Renew. Sustain. Energy Rev. 2016, 60, 1533–1549. [Google Scholar] [CrossRef]
- Canadian Solar. Datasheet of Canadian Solar BiHiKu CS3W-410PB-AG Module; 2019. 2020. Available online: https://www.canadiansolar.com/wp-content/uploads/2019/12/Canadian_Solar-Datasheet-BiHiKu_CS3W-PB-AG_EN.pdf (accessed on 28 May 2023).
- Kongphet, V.; Migan-Dubois, A.; Delpha, C.; Lechenadec, J.-Y.; Diallo, D. Low-Cost I–V Tracer for PV Fault Diagnosis Using Single-Diode Model Parameters and I–V Curve Characteristics. Energies 2022, 15, 5350. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. Operating temperature of photovoltaic modules: A survey of pertinent correlations. Renew. Energy 2008, 34, 23–29. [Google Scholar] [CrossRef]
- Rodrigues, P. Extraction of Parameters of Photovoltaic Modules from the Solution of Nonlinear Equation Systems Using Thrust Region Techniques. Master’s Thesis, Universidade Federal de Uberlândia, Uberlândia, Brazil, 2012. [Google Scholar] [CrossRef]
- Kwak, J.I.; Nam, S.-H.; Kim, L.; An, Y.-J. Potential Environmental Risk of Solar Cells: Current Knowledge and Future Challenges. J. Hazard. Mater. 2020, 392, 122297. [Google Scholar] [CrossRef]
- Pinho, J.T.; Galdino, M.A. Manual de Engenharia para Sistemas Fotovoltaicos; CEPEL—CRESESB: Rio de Janeiro, Brazil, 2014. [Google Scholar]
- Sahu, P.K.; Roy, J.N.; Chakraborty, C.; Sundaram, S. A New Model for Estimating the Energy Extraction from Bifacial Photovoltaic Modules. Energies 2021, 14, 5089. [Google Scholar] [CrossRef]
- Benda, V. Crystalline Silicon Solar Cell and Module Technology. In A Comprehensive Guide to Solar Energy Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 181–213. [Google Scholar]
- Mesquita, D.B.; Silva, J.L.; Moreira, H.S.; Kitayama, M.; Villalva, M.G. A review and analysis of technologies applied in PV modules. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gholami, A.; Ameri, M.; Zandi, M.; Gavagsaz Ghoachani, R. A single-diode model for photovoltaic panels in variable environmental conditions: Investigating dust impacts with experimental evaluation. Sustain. Energy Technol. Assess. 2021, 47, 101392. [Google Scholar] [CrossRef]
- Reis, L.R.d.D. Determination of Photovoltaic Module Parameters Using the Newton-Raphson Method and Genetic Algorithms. Ph.D. Dissertation, Universidade Federal de Uberlândia, Uberlândia, Brazil, 2018. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell Modeling and Model Parameter Estimation Techniques for Photovoltaic Simulator Applications: A Review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter Extraction of Solar Cells Using Particle Swarm Optimization. J. Appl. Phys. 2009, 105, 094502. [Google Scholar] [CrossRef]
- Mittal, M.; Bora, B.; Sexena, S.; Gaur, A.M. Performance prediction of PV module using electrical equivalent model and artificial neural network. Sol. Energy 2018, 176, 104–117. [Google Scholar] [CrossRef]
- Lidaighbi, S.; Elyaqouti, M.; Ben Hmamou, D.; Saadaoui, D.; Assalaou, K.; Arjdal, E. A new hybrid method to estimate the single-diode model parameters of solar photovoltaic panel. Energy Convers. Manag. X 2022, 15, 100234. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Massago, S. Introdução ao Algoritmo Genético. 2013. Available online: https://www.dm.ufscar.br/profs/sadao/download/?file=article/algoritmosgeneticos.pdf (accessed on 28 March 2023).
- Silva, A.J.M. Implementação de um Algoritmo Genético Utilizando o Modelo de Ilhas. Master’s Thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil, 2005. Available online: https://www.livrosgratis.com.br/ler-livro-online-38007/implementacao-de-um-algoritmo-genetico-utilizando-o-modelo-de-ilhas (accessed on 6 April 2023).
- Miranda, M.N. Algoritmos Genéticos: Fundamentos e Aplicações; Universidade Federal do Rio de Janeiro: Rio de Janeiro, Brazil, 2017; Available online: http://www.nce.ufrj.br/GINAPE/VIDA/alggenet.htm (accessed on 3 April 2023).
- Back, T. Selective Pressure in Evolutionary Algorithms: A Characterization of Selection Mechanisms. In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; IEEE: Piscataway, NJ, USA, 1994; pp. 57–62. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Deb, K. A Comparison of Selection Schemes Used in Genetic Algorithms. In Foundations of Genetic Algorithms; Rawlins, G.J.E., Ed.; Morgan Kaufmann: Burlington, MA, USA, 1991; pp. 69–93. [Google Scholar]
- Cunha, V.H.; Campos, E.S.; Guimaraes, L.C.; Dantas, M.J.P. Algoritmo Genético de Codificação Real Aplicado a Otimização de Funções de Benchmark. XLVIII Simpósio Brasileiro de Pesquisas Operacionais. 2016. Available online: http://www.din.uem.br/sbpo/sbpo2016/pdf/155947.pdf (accessed on 2 June 2023).
- Fogarty, T.C. Varying the Mutation Probability in Genetic Algorithms. In Proceedings of the 3rd International Conference on Genetic Algorithms, San Francisco, CA, USA, 1 June 1989; pp. 104–109. [Google Scholar]
- Boccato, L.; Krummenauer, R.; Attux, R.; Lopes, A. Application of natural computing algorithms to maximum likelihood estimation of direction of arrival. Signal Process. 2012, 92, 1338–1352. [Google Scholar] [CrossRef]
- Qin, A.K.; Suganthan, P.N. Self-adaptive Differential Evolution Algorithm for Numerical Optimization. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation Anais, Edinburgh, UK, 2–5 September 2005; IEEE: Piscataway, NJ, USA, 2005. Available online: http://ieeexplore.ieee.org/document/1554904/ (accessed on 3 April 2023).
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces. J. Glob. Optim. 1995, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K.; Rainer, M.; Storn, R.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Computat. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Chenni, R.; Makhlouf, M.; Kerbache, T.; Bouzid, A. A Detailed Modeling Method for Photovoltaic Cells. Energy 2007, 32, 1724–1730. [Google Scholar] [CrossRef]
- Pinto, C.S.B.S. Experimental Validation of the Five-Parameter and One-Diode Model for Photovoltaic Panels. Master’s Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2016. [Google Scholar]
- Mathworks. Matlab Software. Available online: https://www.mathworks.com/products/matlab.html (accessed on 1 May 2023).
- Bocca, A.; Bergamasco, L.; Fasano, M.; Bottaccioli, L.; Chiavazzo, E.; Macii, A.; Asinari, P. Multiple-Regression Method for Fast Estimation of Solar Irradiation and Photovoltaic Energy Potentials over Europe and Africa. Energies 2018, 11, 3477. [Google Scholar] [CrossRef]
- Ministério Da Agricultura E Pecuária. Instituto Nacional de Meteorologia. 2023. Available online: https://portal.inmet.gov.br/normais (accessed on 2 May 2023).
- Sun, V.; Asanakham, A.; Deethayat, T.; Kiatsiriroat, T. Evaluation of nominal operating cell temperature (NOCT) of glazed photovoltaic thermal module. Case Stud. Therm. Eng. 2021, 28, 101361. [Google Scholar] [CrossRef]
- PVSYST. PVSYST Photovoltaic Software. 2023. Available online: https://www.pvsyst.com/ (accessed on 2 May 2023).
- Aoun, N.; Bailek, N. Evaluation of mathematical methods to characterize the electrical parameters of photovoltaic modules. Energy Convers. Manag. 2019, 193, 25–38. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).