Abstract
The ejector drives unreacted hydrogen from the anode to improve fuel utilization ratio and discharges redundant water to prevent flooding and shutdown in the proton exchange membrane fuel cell (PEMFC). However, the traditional fixed structure ejector cannot meet the recycling requirements in the whole dynamic working condition of the fuel cell. In this article, a part nested four-nozzle (PNFN) ejector is proposed to enhance the hydrogen recycling efficiency under variable working conditions of the PEMFC by restricting the nozzle flow as 10%, 20%, 20%, and 50% of the fuel cell-rated power, respectively. Systematical analyses are performed on the experimentally verified 3D model to study inner flow characteristics and performance under different nozzle running modes. The results indicate that the PNFN ejector satisfies the recirculation ratio requirements in the power range of 34–220 kW within the 7–9 bar suitable supply pressure. By comparing with traditional ejectors, the PNFN ejector has a wider working range and especially outputs better performance in the low power range.
1. Introduction
Large fossil energy consumption brings a series of environmental issues, such as energy crisis, greenhouse effect, and so on [1,2,3,4]. A green and effective energy conversion technology is the proton exchange membrane fuel cell (PEMFC), which converts chemical energy directly into electric energy without burning and without being affected by heat engine efficiency [5,6,7,8].
The hydrogen recycle subsystem provides fuel for continuous electrochemical reactions and electric power generation of fuel cells. The advantages of the ejector for hydrogen recirculation systems include its small volume, lack of noise, inexpensive cost, straightforward construction, and no power consumption [9,10,11].
In recent years, research results show that the ejector driven PEMFC hydrogen recycle system can significantly increase fuel utilization efficiency [12,13]. Kim et al. [14] invented an ejector for the PEMFC of the submarine and experimental verification indicated that the ejector can meet the PEMFC anode hydrogen requirements. Dadvar et al. [15] proposed a design approach for the ejector based on the relationship between the ejector and the stack parameters (cell number, battery active area, etc.). Yin et al. [16] put forward a sequential procedure for optimizing the ejector geometry based on the ejector numerical model in three dimensions for PEMFC anode recycling. Maghsoodi et al. [17] investigated the impact of four crucial geometries (nozzle exit position (NXP), mixing chamber length, diffusion chamber length, and diffusion angle of diffusion chamber) on the ejector performance. Apart from the four geometries, Yang et al. [18] also investigated two other parameters (nozzle outlet diameter and mixing chamber diameter) that affect the performance of the ejector. Pei et al. [19] investigated how the area ratio (the ratio of the mixing chamber diameter to the nozzle diameter) and NXP affect ejector performance. The results show that the ejector’s ejection capability declines rapidly when the area ratio and NXP are too large or too small. Wang et al. [20] found that nozzle length and nozzle angle have an impact on the ejector performance. Amin et al. [21] designed a new type of ejector nozzle and studied the gas-liquid two-phase flow inside the ejector by computational fluid dynamics (CFD) technology. The results show that the two fluids mix more uniformly and the ejector has better ejection performance. The aforementioned studies are primarily concerned with ejector structural optimization and its effects on ejection performance in the PEMFC anode recycle system.
Some scholars have also conducted investigation on ejectors operation in variable working conditions. Brunner et al. [22] proposed a variable structure ejector, whose nozzle structure may be altered to enable the ejector to operate at a wide range with regard to a low-power PEMFC. The outcomes showed that the ejector performs well during cycles where the output power is between 7 and 17 kW. Jenssen et al. [23] created a model of the variable structure ejector for the cascade PEMFC system. One could draw the conclusion that the ejector in the PEMFC with low output power has a high recirculation ratio. He et al. [24] combined ejector and blower to increase the operating range of the PEMFC system. Nikiforow [25] built a control strategy for the three-way solenoid valve to change the ejector primary flow in the variable working condition of PEMFC. Hwang [9] installed the solenoid valve and proportional valve on the fuel delivery line of the ejector. This method can achieve stable hydrogen delivery for the PEMFC system and expand the ejector working range to a certain extent.
The above-mentioned research results mainly focus on the small power PEMFC under rated power of 80 kW, but the results cannot be directly generalized to high-power PEMFC applications for the nonlinear properties of fluids and electrochemistry. With the current rapid development towards high-power PEMFC, it is important to design an ejector that can meet the recycling requirements in the dynamic condition of the high-power PEMFC system. Therefore, this study proposes a part nested four-nozzle (PNFN) ejector for the high rated power fuel cell of 170 kW. The four nozzles are designed with 10%, 20%, 20%, and 50% of the fuel cell rated power. By altering the operation model of the nozzles, the four-nozzle ejector can enhance the hydrogen recirculation performance to satisfy the high-power fuel cell’s recycling requirements under varying working conditions.
2. PNFN Ejector Design Method
2.1. Ejector in the PEMFC Operating Theory
The anode hydrogen recirculation system with a single nozzle ejector is depicted in Figure 1 Diagram of an anode hydrogen recirculation system with a single nozzle ejector. The ejector is made up of a nozzle, a suction chamber, a mixing chamber with constant pressure, constant area, and a diffusion chamber. The pressure-reducing valve lowers the high-pressure hydrogen coming from the hydrogen tank. Next, low-pressure hydrogen (primary flow (PF)) expands via the nozzle, transforming the hydrogen’s pressure potential energy into kinetic energy. The secondary flow (unreacted hydrogen (SF)) from the PEMFC stack anode is sucked into the ejector’s suction chamber. After that, the SF and the PF are then combined in the mixing chamber. The combined gas then enters the fuel cell anode after passing through the diffusion chamber.
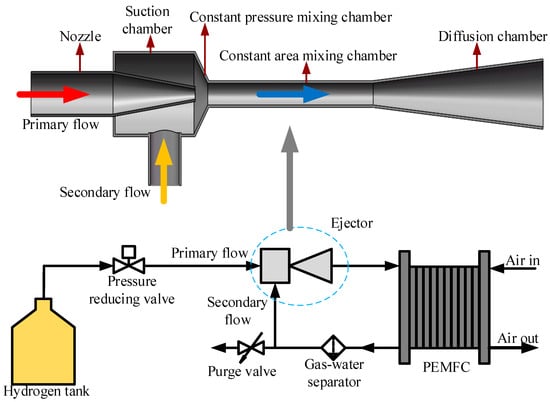
Figure 1.
Diagram of an anode hydrogen recirculation system with a single nozzle ejector.
In the recycling process, the ejector can increase fuel usage rate while also releasing fuel cell anode water. In the fuel cell system, the relationship between the different hydrogen mass flows about the ejector is expressed as follows:
where is the mass of hydrogen entering the fuel cell, and are the hydrogen mass of the recirculated (unreacted) and consumed in the fuel cell, respectively.
The hydrogen mass entering the fuel cell in the fuel cell system is greater than the hydrogen mass that should have theoretically responded. The following equation can be used to express the hydrogen excess coefficient , which represents the actual mass of hydrogen entering the fuel cell:
2.2. Structural Design of the PNFN Ejector
It is important that PEMFC rated power, mass flow rate, cell voltage, and other geometric parameters for the ejector design.
According to fuel cell parameters, the hydrogen PF mass flow is calculated as follows:
where is the fuel cell’s rated power of the, is the hydrogen molar mass, and are the single cell voltage and Faraday constant, respectively.
Designing the nozzle structure is the key step for the ejector. The following formulas are used to compute the nozzle throat area :
where is the critical velocity, is the ratio of the specific heat of gas, is the relative pressure, is the PF pressure, is the gaseous critical pressure, is the gas constant, and is the gaseous critical temperature.
Aiming at a 170 kW (Pe) high-power fuel cell, this study proposes a new type of four-nozzle ejector. The conventional single-nozzle ejector is designed under certain operating points of the fuel cell. When the fuel cell power changes in a large scale, the performance of the conventional single-nozzle ejector will sharply decrease and therefore, it cannot meet the flow requirements. So, we design the multi-nozzle ejector to improve the performance of the ejector under full operating range. We select four nozzles (10%, 20%, 20%, and 50% of the fuel cell rated power) because this type can meet the whole power requirements by combining nozzles with different working modes. If the number of nozzles is lower than four, the ejector cannot work at the whole power range of the fuel cell, and when the number of nozzles is greater than four, the ejector’s structure will be too complicated.
The nozzle that meets 10% of rated power is called the first nozzle (N1). The second nozzle (N2) and the third nozzle (N3) are identical nozzle applied to 20% of rated power. The nozzle of 50% rated power is called the fourth nozzle (N4). Combined with the different power nozzles, the PNFN ejector can operate throughout the fuel cell’s whole power range. The operation modes of ejector in different powers based on the number of nozzles working are shown in Table 1.

Table 1.
The ejector operation mode.
In the four-nozzle ejector, the hydrogen supply flow of each nozzle is equal to the percentage of the hydrogen supply flow of the fuel cell at its rated operating condition, and the throat area of each nozzle is equal to the percentage of the total throat area. Combined with the above formula, the throat area of each nozzle is calculated as follows:
where is the nozzle (x) diameter, x = 1, 2, 3, 4.
The ejector design process is illustrated in Figure 2.
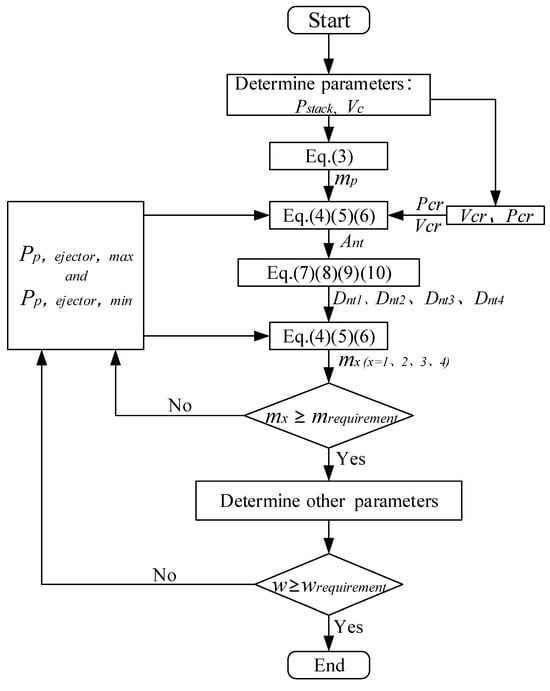
Figure 2.
Design process of the PNFN ejector.
Table 2 shows the diameter of the four nozzles carried out with the above iterative calculation process.

Table 2.
The diameter of the four nozzles.
The PEMFC system uses the recirculation ratio () to assess the performance of the ejector, which is defined as:
here is the PF mass flow rate, is the SF mass flow rate.
The recirculation ratio () for the PNFN ejector can be calculated using the formula below:
where, , , and are the mass flow rate of the N1, N2, N3 and N4, respectively.
In addition to the ejector nozzle, the performance and mass flow rate of the ejector are significantly influenced by other structural factors, such as NXP, mixing chamber diameter, diffusion chamber length, and others. These values are determined by multiple simulations. When the minimum recirculation ratio exceeds 0.50, the ejector design process is over, or else, redesign the ejector structure. Table 3 displays the values of the PNFN ejector’s other geometric parameters.

Table 3.
The PNFN ejector geometric parameters value.
The PNFN ejector structure diagram and 3D model diagram are shown in Figure 3a and Figure 3b, respectively.
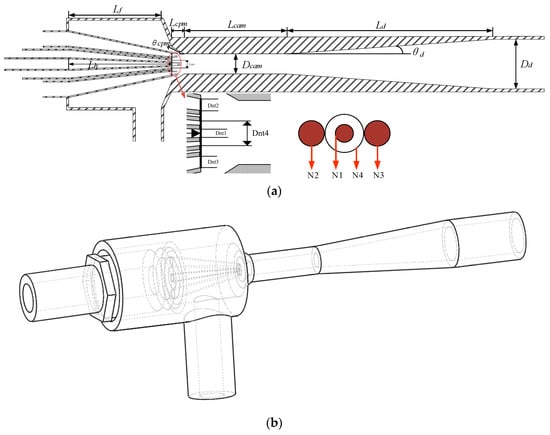
Figure 3.
(a)The PNFN ejector structure diagram; (b) 3D model diagram.
3. Numerical Model and Simulation
3.1. Governing Equation
To analyze performance and optimize the geometric structure of the ejector by using computational fluid dynamics (CFD) under various operating conditions. For the numerical simulation of the ejector, the following assumptions are made:
- (1)
- The walls are considered adiabatic.
- (2)
- The internal gas is considered an ideal gas.
- (3)
- The inner fluid of the ejector is fully mixed.
- (4)
- The inner fluid is regarded as compressible fluid.
The conservation equations governing the ejector can be stated as follows using the aforementioned presumptions:
Continuity equation:
Momentum equation:
Energy equation:
Species transport equation and the ideal gas relationship:
The inner fluid of the ejector occurs in various flow phenomena including mixing, turbulence, backflow, etc. In this paper, the RNG turbulence model is adopted, which can simulate jet impingement, SF, and whirlwind complex flow phenomena. Because previous studies [26,27] have accomplished many experiments to compare the SST turbulence model with the RNG turbulence model for the PEMFC ejector. The results show that the RNG turbulence model is appropriate for the full working condition PEMFC ejector model, it is represented as follows:
where, , , represents the turbulent kinetic energy generated, represents the turbulent kinetic energy generated, represents the fluctuating expansion to total dissipation ratio in compressible turbulent, and are the reciprocal of an effective Prandtl number.
3.2. Grid Generation
Grid generation is one of the important components of CFD and the stability and precision of the numerical calculation are determined by the grid’s quality. Ansys software serves as grid generator and solver for governing equations. The grid numbers will affect simulation result. For the region with intensive gradient change, the grid density needs to be encrypted. In order to improve the accuracy of fluid flow simulation, the nozzle outlet grid needs a fine refinement treatment. Figure 4 shows the final grid results.
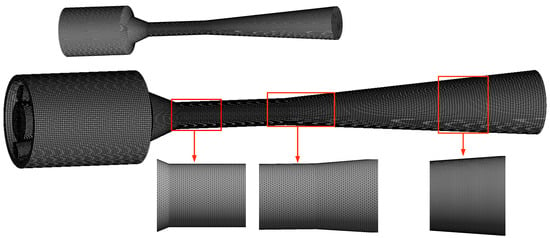
Figure 4.
The grids of the PNFN ejector model.
3.3. Boundary Conditions
The simulated boundary conditions in this study are set in accordance with the PEMFC’s real operational settings (Table 4).

Table 4.
The actual operating conditions of the PEMFC.
The PF inlet and the SF inlet are set to the pressure inlet and the outlet is set to the outlet pressure. In addition, the PF temperature is 293 K same as the environmental temperature, the SF temperature and the outlet temperature are both 338 K same as the fuel cell stack temperature. The fluid that flows near the wall takes the standard wall function method.
3.4. Grid Independence Verification
The grid independence verification of the models guarantees the accuracy and reliability of the results. Three grid models are studied including sparse grid with 785,242 elements, medium grid with 1,245,316 elements, and encrypted grid with 1,613,454 elements. The simulated working gas is dry hydrogen, and the results are compared with each other under the same conditions (the PF pressure, the SF pressure and the outlet pressure are 7.0 bar, 1.9 bar and 2.1 bar, respectively). Figure 5a shows the static pressure on the internal axis of the ejector under the three different grid numbers. With varying numbers of grids, the static pressure trend is the same, and the values for medium and encrypted grids are quite close. Figure 5b shows the connection between the recirculation ratio and model gird number at different operation modes of the ejector. The results show that the simulation data are also quite close to each other.
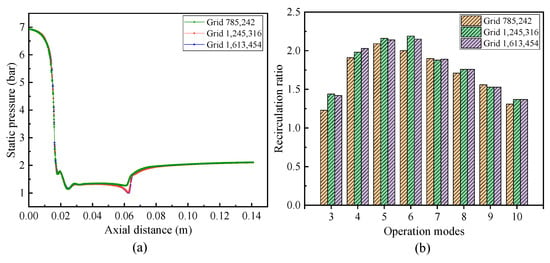
Figure 5.
Grid independent validation. (a)The static pressure distribution on the axis under different grids (Mode 10). (b) The comparison of the recirculation ratio at different operation modes.
Two groups of ejector operation mode are selected to verify the deviation from PF, SF, and recirculation ratio as shown in Table 5 and Table 6. The deviation can be expressed by the following equation:
where is the nth calculated value.

Table 5.
Grid independence validation results (Mode 4).

Table 6.
Grid independence validation results (Mode 6).
From the tables, the deviation becomes smaller when the grid number increases in the two modes. The deviations of the three factors of the mode 6 between medium and fine grid are decreased to 0.35%, 1.95%, and 1.61%, respectively. The deviations between the medium and fine grids are far less than that between the coarse and medium grids.
In CFD numerical simulation, the level of grid quality is related to calculation accuracy and calculation time. Although the higher of the model grid quality and more accurate results are, the calculation time is longer. Considering the calculation accuracy and the calculation time, the medium grid model is selected to accomplish the following numerical simulation.
4. Experimental Facility and Model Verification
4.1. Experimental Facility
Figure 6a,b are the diagrammatic sketch and system schematic of the experimental facility. The experimental setup consists of an ejector, a buffer tank, pressure sensors, mass flow meters, a pressure-reducing valve, a needle valve, an evacuation valve, and a computer. A 3D printing technology is used to manufacture the ejector and nozzles. The nozzles need to be switched on in turn to evaluate the performance of each mode. Considering the safety of the experiment, nitrogen is substituted for hydrogen as the supply gas. In order to meet the experimental requirements, the gas pressure from the cylinder needs to be reduced by the pressure-reducing valve. The mass flow meter is used for measuring the PF mass flow rate and SF mass flow rate, and the pressure sensor is used for checking the pressure of the ejector inlet and outlet. To achieve simulation of the pressure drop in the fuel cell stack, evacuation valve, buffer tank, and needle valve are employed. In addition, the experimental temperature is 293 K, and the flow data and pressure data are collected and stored in the computer.
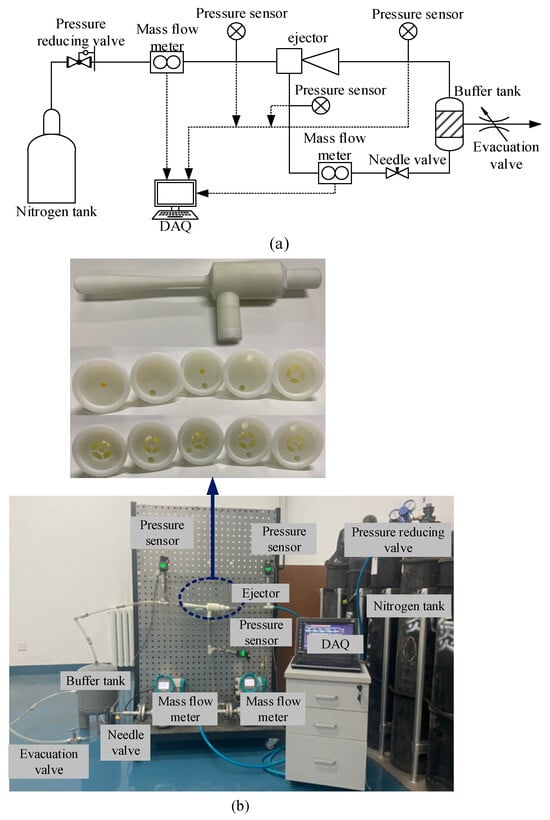
Figure 6.
(a) Diagrammatic sketch of the experimental facility. (b) System schematic of the experimental facility.
4.2. Model Verification
Experimental data is used to validate the CFD model. In the experimental process, the PF pressure is set at 6.0 bar and 7.0 bar by changing the opening of the pressure-reducing valve. The SF pressure and outlet pressure are set at 1.9 bar and 2.1 bar by adjusting the opening of the needle valve and evacuation valve. The experimental conditions are the same as the simulation conditions. As given in Figure 7, the experimental data agree with the simulation data and relative errors are within 7%. The deviation perhaps results from the experimental instrumentation measurement errors and the machining errors of the ejector prototype. Hence, the simulation model can predict the performance of ejector accurately.
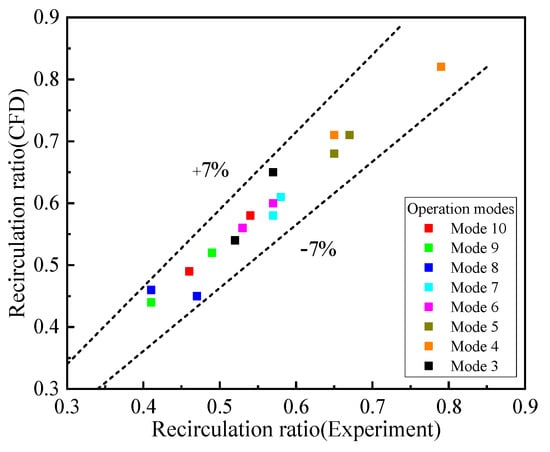
Figure 7.
Comparison of experiment and simulation data.
5. Results and Analysis
This part investigates the interior flow field and ejector performance using 3D numerical simulation. The recirculation ratio of ejector is systematically studied under different power and PF pressure conditions.
5.1. Characteristics of the PNFN Ejector’s Flow
Figure 8 shows two-dimensional velocity image and velocity streamlined diagram of the PNFN ejector under the different operation modes. The operating conditions are as follows: the dry hydrogen serves as the working fluid, the PF pressure is 7.0 bar, the SF pressure is 1.9 bar, the outlet pressure is 2.1 bar. The operation modes are shown on the left side of Figure 8a.
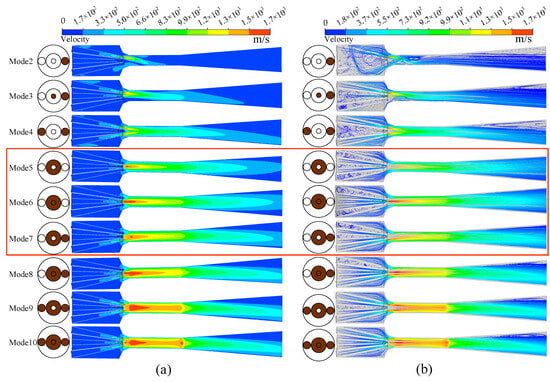
Figure 8.
Velocity flow field diagram of the PNFN ejector. (a) Velocity image. (b) Velocity streamline.
In the red frame of the two pictures, we can see that inner fluid of the ejector flow along the central axis and the ejector inner flow mechanism is more stable under three modes. From the perspective of flow mechanism, the ejector performance is best under these three modes. The ejector performance is best when the toroidal fourth nozzle and the circular first nozzle work at the same time in mode 6. The superposition of two flows stream in the same direction generates higher velocity, consequently, produces lower pressure which makes the SF be easily sucked. In operation mode 7, the fourth nozzle and the second nozzle work together. In this case, the vortex and backflow phenomena are not found in the ejector inner fluid although there is a certain angle between the fourth nozzle and the second nozzle that may cause partial energy loss. Therefore, the ejector performance is relatively good in this mode. When the fuel cell power changes, the ejector can work at these three modes to meet the recycling requirements by changing the PF pressure. In other modes, either fluid impacts the constant-area mixing chamber wall causing energy losses, or several streams of fluid crashes causing lots of energy lost, or constant-area mixing chamber entrance appears choking phenomenon, resulting in ejector inner appears serious vortex and backflow phenomenon.
5.2. Performance of the PNFN Ejector
Except structural parameters of the ejector, the PF pressure and outlet pressure significantly affects how well the ejector performs. Figure 9 demonstrates the effects of the PF pressure and the outlet pressure on the recirculation ratio and mass flow of the SF under the fixed SF pressure of 1.9 bar.
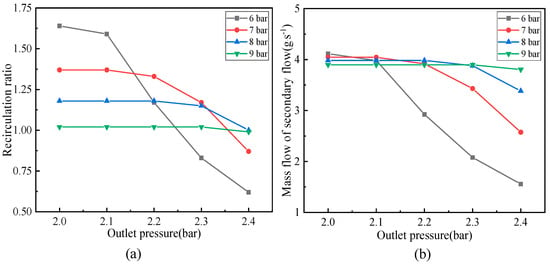
Figure 9.
(a) PF pressure and outlet pressure’s impact on recirculation ratio. (b) The impact of the PF pressure and outlet pressure on the mass flow of SF.
As can be seen from the pictures, when the PF pressure is lower than 9 bar, the recirculation ratio and mass flow of SF are easy to be influenced by the outlet pressure. When the PF pressure is fixed, the lower the outlet pressure is, the larger recirculation ratio is. When the outlet pressure is 2.0 bar, each recirculation ratio reaches its maximum value, in which the lower the PF pressure is, the larger the recirculation ratio can be.
The performance of the ejector is significantly impacted by PF pressure and output pressure. When the PF pressure is fixed, the ejector performance decreases with the outlet pressure increasing. The ejector performance is best when the PF pressure is 6.0 bar and outlet pressure is 2.0 bar.
5.3. Performance of the PEMFC System’s PNFN Ejector in Terms of Recirculation
Figure 10 and Figure 11 illustrate performances of the PNFN ejector under different operation modes.
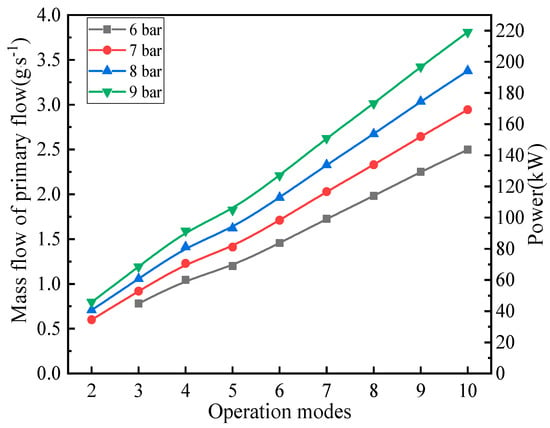
Figure 10.
The mass flow of PF and power change at different operation modes.
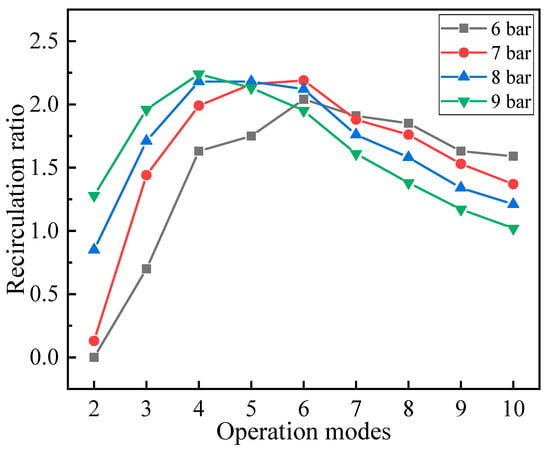
Figure 11.
The PNFN ejector’s recirculation performance.
The mass flow of PF and the power range of the PNFN ejector relate to the operation modes of the ejector. The working range of the ejector is determined by the mass flow of PF for meeting the power requirement of the PEMFC system. When all the nozzles are working, the ejector can only work at the power of 150 kW when the PF pressure is 6.0 bar and beyond the rated power 170 kW of the fuel cell with the PF pressure increases 7.0 bar. It can be seen in Figure 10 that higher PF pressure makes the rated power can be fulfilled more easily.
Figure 11 shows the change of recirculation ratio with the ejector operation modes at different PF pressures. The maximum recirculation ratio is 1.28 when the pressure is 9 bar and the ejector operates at mode 2. All recirculation ratios reach the maximum value of 2.24 under different PF pressures when the ejector operates in modes 4–6.
The ejector can operate in the 34–220 kW power range by switching operation mode when the PF pressure is in the range of 7.0 bar to 9.0 bar. In the lower power range, increasing the PF pressure can increase the ejector’s performance. The PNFN ejector not only expands the PEMFC’s operating range, but also adjusts the PF pressure to keep the recirculation ratio above 1.0 which meets the recycling requirement of the PEMFC.
5.4. Performance Comparison of the PNFN and Traditional Ejectors
The traditional ejector is usually designed at a certain operating point of the PEMFC. The performance of the traditional ejector sharply declines and therefore it is difficult meet the power requirements when the PEMFC deviates from the rated power. However, the PNFN ejector can solve the problem and work at a wide power range.
The PNFN ejector at each mode corresponds to a throat diameter of the traditional ejector that Equation (4) can be used to determine the throat diameter of the traditional ejector. Table 7 demonstrates the throat diameter of the traditional ejector while other structures keep fixed.

Table 7.
Throat diameter of traditional ejector corresponds to PNFN ejector mode.
The PNFN ejector and traditional ejector’s recirculation ratios are displayed in Figure 12. The two types of ejectors are compared under the same conditions of the PF pressure of 7.0 bar, the SF pressure of 1.9 bar, and the outlet pressure is 2.1 bar.
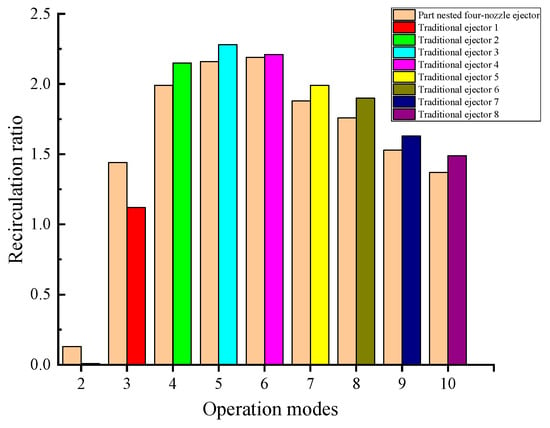
Figure 12.
Comparison between two type of ejectors.
The recirculation ratio of the PNFN ejector and the traditional ejector exhibit the similar trend, as can be shown in Figure 12. The recirculation ratio of the PNFN ejector is almost equal to that of the corresponding traditional ejector. When the PEMFC’s output power is low, the PNFN ejector has a better recirculation ratio that is hard for the traditional ejector to achieve. The performance of the PNFN ejector is good more than the traditional single nozzle ejector. The PNFN ejector can contain working ranges of the many traditional ejectors and overcome the problem that the failure of traditional ejector in variable working conditions.
5.5. Performance Comparison of Different Configuration Four-Nozzle Ejector
The four nozzles have multiple layout styles with the equal mass flow rate. The ejector performance is largely affected by the ejector nozzle position. The typical nozzle combination types are compared.
Plan 1, the N4 comprises the N1 with the same central axis. The N2 and the N3 have axial symmetry that are distributed on both sides of the N4 at angle of 180°, as shown in Figure 13a.
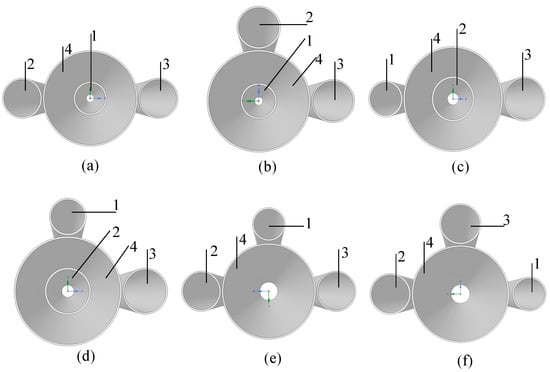
Figure 13.
(a–f) Diagram of plans 1 to 6.
Plan 2, the N4 comprises the N1 with the same central axis. The N2 and the N3 are distributed on adjacent sides of the N4 at angle of 90°, as shown in Figure 13b.
Plan 3, the N4 comprises the N2 (or the N3) with the same central axis. The N3 (or the N2) and the N1 are distributed on opposite sides of the N4 at angle of 180°, as shown in Figure 13c.
Plan 4, the N4 comprises the N2 (or the N3) with the same central axis. The N3 (or the N2) and the N1 are distributed on adjacent sides of the N4 at angle of 180°, as shown in Figure 13d.
Plan 5, the N4 is on the central axis while the N2 and the N3 have axial symmetry distributed on both sides of the N4 at angle of 180°. The N1 locates at another orientation with the N2 and N3 at angle of 90°, as shown in Figure 13e.
Plan 6, the N4 is on the central axis. The N2 and the N3 are distributed on adjacent sides of the N4 at angle of 90°. The N1 is distributed on the other side of the N4 at angle of 90° with the N2 (or the N3), as shown in Figure 13f.
Plan 7, the N4 comprises the N1, the N2 and the N3. The N4 is divided into three regions with each region angle of 120°. The nozzle is drawn on the central plane of each region. The angle of the central axis of the adjacent two nozzles is 120°. The diameter of the N4 is enlarged accordingly in this plan to ensure the fluid flow mass same as in other plans, as shown in Figure 14.
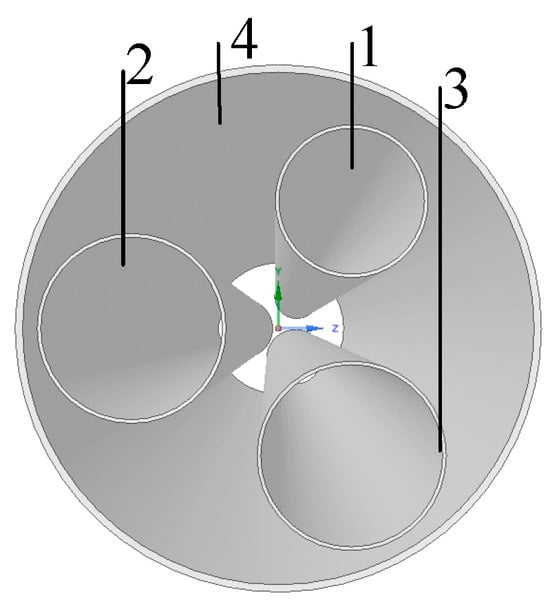
Figure 14.
Diagram of Plan 7.
In Figure 13 and Figure 14, the number 1, 2, 3, and 4 represents the N1, N2, N3, and N4, respectively, Blue and green arrows represent the x and y axis of the three-dimensional coordinate axis.
The ejector plans are compared under the same conditions. The dry hydrogen is selected as the working gas under the PF pressure of 7.0 bar, the SF pressure of 1.9 bar, and the outlet pressure of 2.1 bar. The recirculation ratio is used to assess the ejector’s performance. Table 8 shows the recirculation ratio value of seven types of ejectors at different operation modes. Figure 15 is ejector curve of the recirculation ratio with different plans.

Table 8.
The values of the recirculation ratio of different plans.
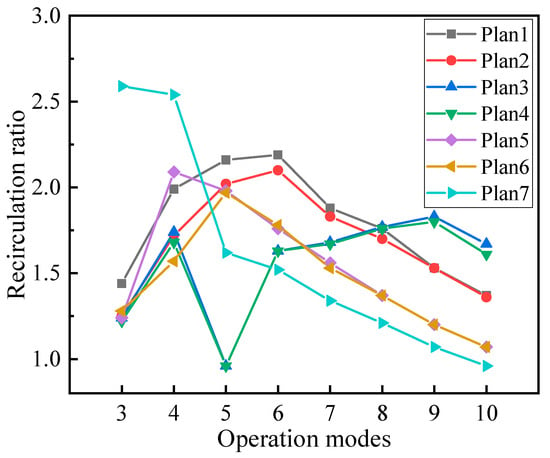
Figure 15.
Recirculation ratio curve of the ejector.
It can be seen from the Figure 15 that the performance of Plan 1 is better than that of Plan 2, Plan 5, and Plan 6 in general. As for Plan 3 and Plan 4, their performance curves are very close. Their recirculation ratio values are equal to Plan 1 in operation mode 8. In operation mode 8, the recirculation ratio of Plan 3 and Plan 4 has the minimum value of 0.96. The performance of Plan 7 is better than Plan 1 in mode 3 and mode 4. The performance of Plan 1 is far higher than Plan 7 when the operation modes are 5–10. The performance curve of Plan 7 is descending with the minimum value of 0.96 in mode 10.
By comparing seven types of ejectors, the performance of Plan 3, Plan 4, and Plan 7 are better than that of Plan 1 in individual modes, but performance of Plan 1 is better than that of the other plans at most modes. In general, Plan 1 as previously mentioned has the best overall performance.
6. Conclusions
In this study, a new type of part nested four-nozzle (PNFN) ejector is proposed in order to substitute for the traditional ejector to meet the hydrogen recycle requirement in the high-power PEMFC system within the full power range. The four nozzles are designed at 10%, 20%, 20%, and 50% of the PEMFC rated power. The internal flow properties and recirculation performance of the PNFN ejector are studied using a 3D numerical model of the device. The PNFN ejector can meet the flow requirements in the high-power fuel cell full power range by switching the nozzle’s working conditions. The main conclusions are as follows:
- The ejector inner flow field is at the most stable state and ejector performance reach the best value point when the first nozzle and the fourth nozzle (mode 6) work together. By observing the velocity field image and velocity streamline map, the ejector inner flow mechanism becomes more complex with the increase of working nozzles.
- The PNFN ejector with different operation modes can operate in the 34–220 kW power range with the recirculation ratio above 1.0 when the PF pressure range is between 7–9 bar.
- The PNFN ejector performs better than the traditional single nozzle ejector in the whole power range. It’s worth noting that the PNFN ejector has better performance compared to traditional ejectors in the low power zone.
- The performance of the PNFN ejector (Plan 1) is better than other combined plans by comparing the typical combined plans of the four nozzles.
Author Contributions
Conceptualization, C.W., L.W. and X.W.; methodology, C.W., L.W. and X.W.; Investigation, A.Y.; Soft, A.Y.; Writing—original draft, A.Y.; Writing—review & editing, C.W., L.W. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
The work was funded by the National Key Research and Development Program of China (Grant No. 2019YFB1504700), the National Natural Science Foundation of China (Grant No. 52306256) and China Postdoctoral Science Foundation (Grant No. 2023M732048).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | area (m2) | λ | stoichiometric ratio/thermal conductivity (W m−1 K−1) |
| D | diameter (m) | μ | dynamic viscosity (N s m−2) |
| Dq,m | mass diffusion coefficient (m2 s−1) | ρ | density (kg m−3) |
| DT,q | Thermal diffusion coefficient (m2 s−1) | ω | recirculation ratio |
| E | total energy (J kg−1) | μ | dynamic viscosity (N s m−2) |
| F | Faraday’s constant (C mol−1) | ρ | density (kg m−3) |
| gravitational acceleration (m s−2) | Subscript | ||
| GbGk | turbulence kinetic energy generation (J m−3 s−1) | r | recirculated hydrogen |
| h | enthalpy (J kg−1) | c | hydrogen consumption |
| I | unit tensor diffusion flux (kg m−2 s−1) | cam | constant-area mixing chamber |
| k | turbulent kinetic energy (m2 s−2) | cpm | constant-pressure mixing chamber |
| L | length (m) | d | diffusion |
| m | mass flow rate (kg s−1) | H2 | hydrogen |
| M | molar weight (kg mol−1) | i, j | direction |
| P | pressure (Pa) | nt | nozzle throat |
| Pstack | power (W) | N1 | first nozzle |
| R | gas constant (J mol−1 K−1) | N2 | second nozzle |
| Sct | Schmidt number | N3 | |
| T | temperature (K) | N4 | fourth nozzle |
| vcr | critical velocity (m s−1) | Abbreviations | |
| velocity vector (m s−1) | CFD | computational fluid dynamics | |
| Vc | single cell voltage (V) | NXP | nozzle exit position |
| Y | mass fraction | PEMFC | polymer electrolyte membrane fuel cell |
| YM | the fluctuating expansion to total dissipation ratio in compressible turbulent | PNFN | part nested four-nozzle |
| Greek letters | PF | primary flow | |
| ε | turbulence kinetic energy dissipation rate (m2 s−3) | SF | secondary flow |
| θ | angle (°) | ||
| inverse effective Prandtl numbers | |||
| κ | specific heat ratio | ||
References
- Liu, Z.; Chen, J.; Liu, H.; Yan, C.; Hou, Y.; He, Q.; Zhang, J.; Hissel, D. Anode purge management for hydrogen utilization and stack durability improvement of PEM fuel cell systems. Appl. Energy 2020, 275, 115110. [Google Scholar] [CrossRef]
- Rodosik, S.; Poirot-Crouvezier, J.-P.; Bultel, Y. Simplified anode architecture for PEMFC systems based on alternative fuel feeding: Experimental characterization and optimization for automotive applications. Int. J. Hydrogen Energy 2020, 45, 19720–19732. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, W.; Xiao, B.; Liu, Q.; Yang, L.; Covaci, A.; Zhu, L. Bioavailability and biomagnification of organophosphate esters in the food web of Taihu Lake, China: Impacts of chemical properties and metabolism. Environ. Int. 2019, 125, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Yousefi, N. Optimal parameter identification of PEMFC stacks using Adaptive Sparrow Search Algorithm. Int. J. Hydrogen Energy 2021, 46, 9541–9552. [Google Scholar] [CrossRef]
- Chen, H.; Song, Z.; Zhao, X.; Zhang, T.; Pei, P.; Liang, C. A review of durability test protocols of the proton exchange membrane fuel cells for vehicle. Appl. Energy 2018, 224, 289–299. [Google Scholar] [CrossRef]
- Kazim, A. Introduction of PEM fuel-cell vehicles in the transportation sector of the United Arab Emirates. Appl. Energy 2003, 74, 125–133. [Google Scholar] [CrossRef]
- Pei, P.; Chen, H. Main factors affecting the lifetime of Proton Exchange Membrane fuel cells in vehicle applications: A review. Appl. Energy 2014, 125, 60–75. [Google Scholar] [CrossRef]
- Li, W.; Wang, X.; Wang, L.; Jia, L.; Song, R.; Fu, Z.; Xu, W. An LSTM and ANN Fusion Dynamic Model of a Proton Exchange Membrane Fuel Cell. IEEE Trans. Ind. Inform. 2023, 19, 5743–5751. [Google Scholar] [CrossRef]
- Hwang, J.-J. Passive hydrogen recovery schemes using a vacuum ejector in a proton exchange membrane fuel cell system. J. Power Sources 2014, 247, 256–263. [Google Scholar] [CrossRef]
- Li, F.; Du, J.; Zhang, L.; Li, J.; Li, G.; Zhu, G.; Ouyang, M.; Chai, J.; Li, H. Experimental determination of the water vapor effect on subsonic ejector for proton exchange membrane fuel cell (PEMFC). Int. J. Hydrogen Energy 2017, 42, 29966–29970. [Google Scholar] [CrossRef]
- Toghyani, S.; Afshari, E.; Baniasadi, E. A parametric comparison of three fuel recirculation system in the closed loop fuel supply system of PEM fuel cell. Int. J. Hydrogen Energy 2019, 44, 7518–7530. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, X.; Tu, Z.; Chan, S.H. Droplet Dynamics in a Proton Exchange Membrane Fuel Cell with Ejector-Based Recirculation. Energy Fuels 2021, 35, 11533–11544. [Google Scholar] [CrossRef]
- Liu, Y.; Tu, Z.; Chan, S.H. Applications of ejectors in proton exchange membrane fuel cells: A review. Fuel Process. Technol. 2021, 214, 106683. [Google Scholar] [CrossRef]
- Kim, M.; Sohn, Y.-J.; Cho, C.-W.; Lee, W.-Y.; Kim, C.-S. Customized design for the ejector to recirculate a humidified hydrogen fuel in a submarine PEMFC. J. Power Sources 2008, 176, 529–533. [Google Scholar] [CrossRef]
- Dadvar, M.; Afshari, E. Analysis of design parameters in anodic recirculation system based on ejector technology for PEM fuel cells: A new approach in designing. Int. J. Hydrogen Energy 2014, 39, 12061–12073. [Google Scholar] [CrossRef]
- Yin, Y.; Fan, M.; Jiao, K.; Du, Q.; Qin, Y. Numerical investigation of an ejector for anode recirculation in proton exchange membrane fuel cell system. Energy Convers. Manag. 2016, 126, 1106–1117. [Google Scholar] [CrossRef]
- Maghsoodi, A.; Afshari, E.; Ahmadikia, H. Optimization of geometric parameters for design a high-performance ejector in the proton exchange membrane fuel cell system using artificial neural network and genetic algorithm. Appl. Therm. Eng. 2014, 71, 410–418. [Google Scholar] [CrossRef]
- Yang, Y.; Du, W.; Ma, T.; Lin, W.; Cong, M.; Yang, H.; Yu, Z. Numerical studies on ejector structure optimization and performance prediction based on a novel pressure drop model for proton exchange membrane fuel cell anode. Int. J. Hydrogen Energy 2020, 45, 23343–23352. [Google Scholar] [CrossRef]
- Pei, P.; Ren, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S.; Jia, X. Numerical studies on wide-operating-range ejector based on anodic pressure drop characteristics in proton exchange membrane fuel cell system. Appl. Energy 2019, 235, 729–738. [Google Scholar] [CrossRef]
- Wang, L.; Yan, J.; Wang, C.; Li, X. Numerical study on optimization of ejector primary nozzle geometries. Int. J. Refrig. 2017, 76, 219–229. [Google Scholar] [CrossRef]
- Amin, B.; Tavousi, E.; Noghrehabadi, A.; Behbahani-Nejad, M. Study of a novel inlet geometry for ejectors. Int. J. Refrig. 2022, 139, 113–127. [Google Scholar] [CrossRef]
- Brunner, D.A.; Marcks, S.; Bajpai, M.; Prasad, A.K.; Advani, S.G. Design and characterization of an electronically controlled variable flow rate ejector for fuel cell applications. Int. J. Hydrogen Energy 2012, 37, 4457–4466. [Google Scholar] [CrossRef]
- Jenssen, D.; Berger, O.; Krewer, U. Improved PEM fuel cell system operation with cascaded stack and ejector-based recirculation. Appl. Energy 2017, 195, 324–333. [Google Scholar] [CrossRef]
- He, J.; Choe, S.-Y.; Hong, C.-O. Analysis and control of a hybrid fuel delivery system for a polymer electrolyte membrane fuel cell. J. Power Sources 2008, 185, 973–984. [Google Scholar] [CrossRef]
- Nikiforow, K.; Koski, P.; Ihonen, J. Discrete ejector control solution design, characterization, and verification in a 5 kW PEMFC system. Int. J. Hydrogen Energy 2017, 42, 16760–16772. [Google Scholar] [CrossRef]
- Xue, H.; Wang, L.; Zhang, H.; Jia, L.; Ren, J. Design and investigation of multi-nozzle ejector for PEMFC hydrogen recirculation. Int. J. Hydrogen Energy 2020, 45, 14500–14516. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S.; Xing, C. Numerical and experimental investigation on an ejector designed for an 80 kW polymer electrolyte membrane fuel cell stack. J. Power Sources 2019, 415, 25–32. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).