Fault Location Method for Overhead Power Line Based on a Multi-Hypothetical Sequential Analysis Using the Armitage Algorithm
Abstract
:1. Introduction
- Relative and angular errors of measuring current and voltage transformers;
- Harmonic components in currents and voltages recorded in an emergency mode [33];
- Current waveform distortions associated with saturation of electromagnetic measuring current transformers;
- The presence of transient resistance at the site of fault on OHPLs;
- Uneven distribution of resistivity along the OHPL [36];
- Not taking into account the capacitive component of the OHPL relative to the ground in the FL algorithm;
- Neglect of mutual induction in the corridors of joint passage of OHPLs [39];
- Errors in the initial data on the resistivity of sections of OHPLs;
- Not taking into account the resistance of bypass connections, etc.
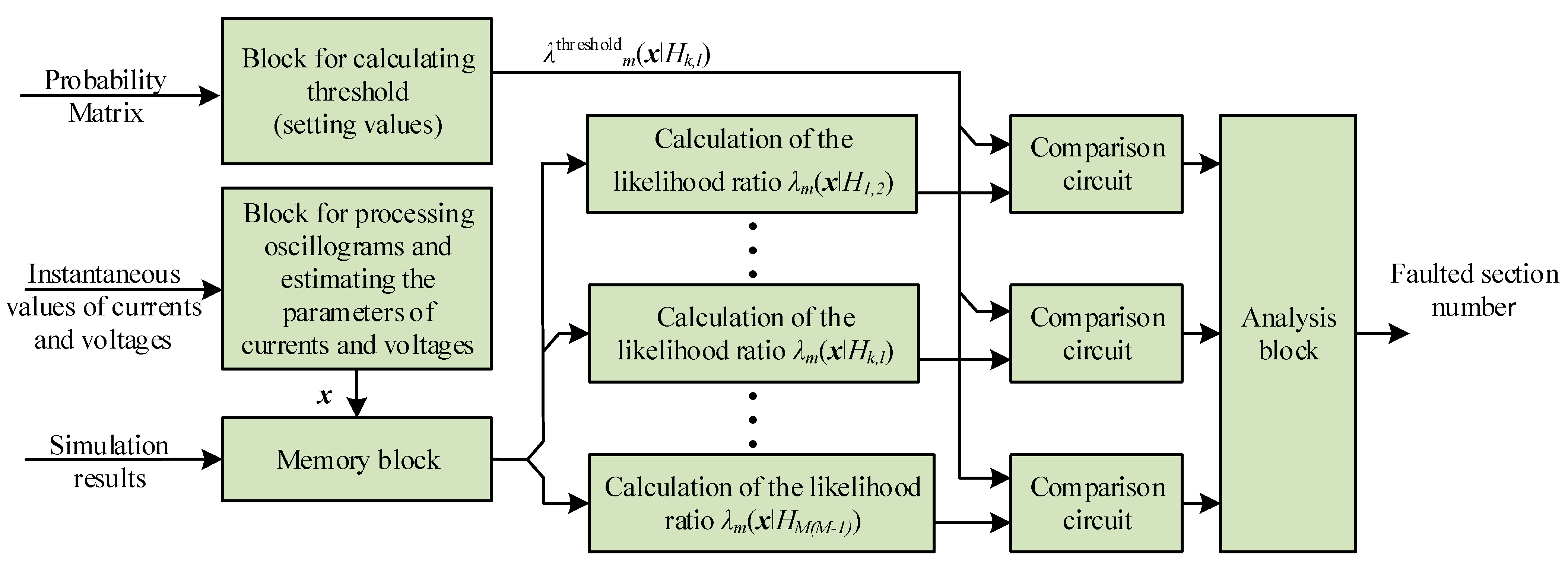
2. Materials and Methods
- Complete the experiment by accepting the hypothesis H1 (fault in section No. 1).
- Complete the experiment by accepting the H2 hypothesis (fault in section No. 2).
- ………
- Complete the experiment by accepting the HM hypothesis (fault in section No. M).
- Continue the experiment by making additional observations.
3. Results and Discussion
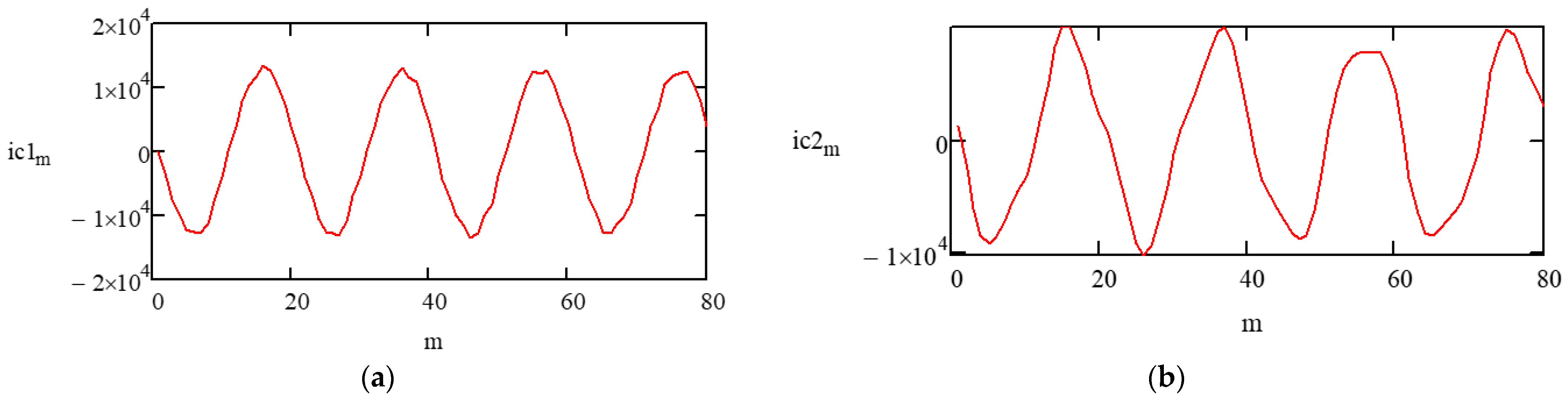
+ L·(I′(m)/dtm + I″(m)/dtm)].
+ 0.15I″[R·sin(2πfi(td + m·ts))+ L·cos(2πfi(td + m·ts))]}/
{(I′(1 − k·rnd(m)) + I″)·[R·sin(2πf(td + m·ts)) + L·cos(2πf(td + m·ts))]
+ 0.15I″[R·sin(2πfi(td + m·ts)) + L·cos(2πfi(td + m·ts))]};
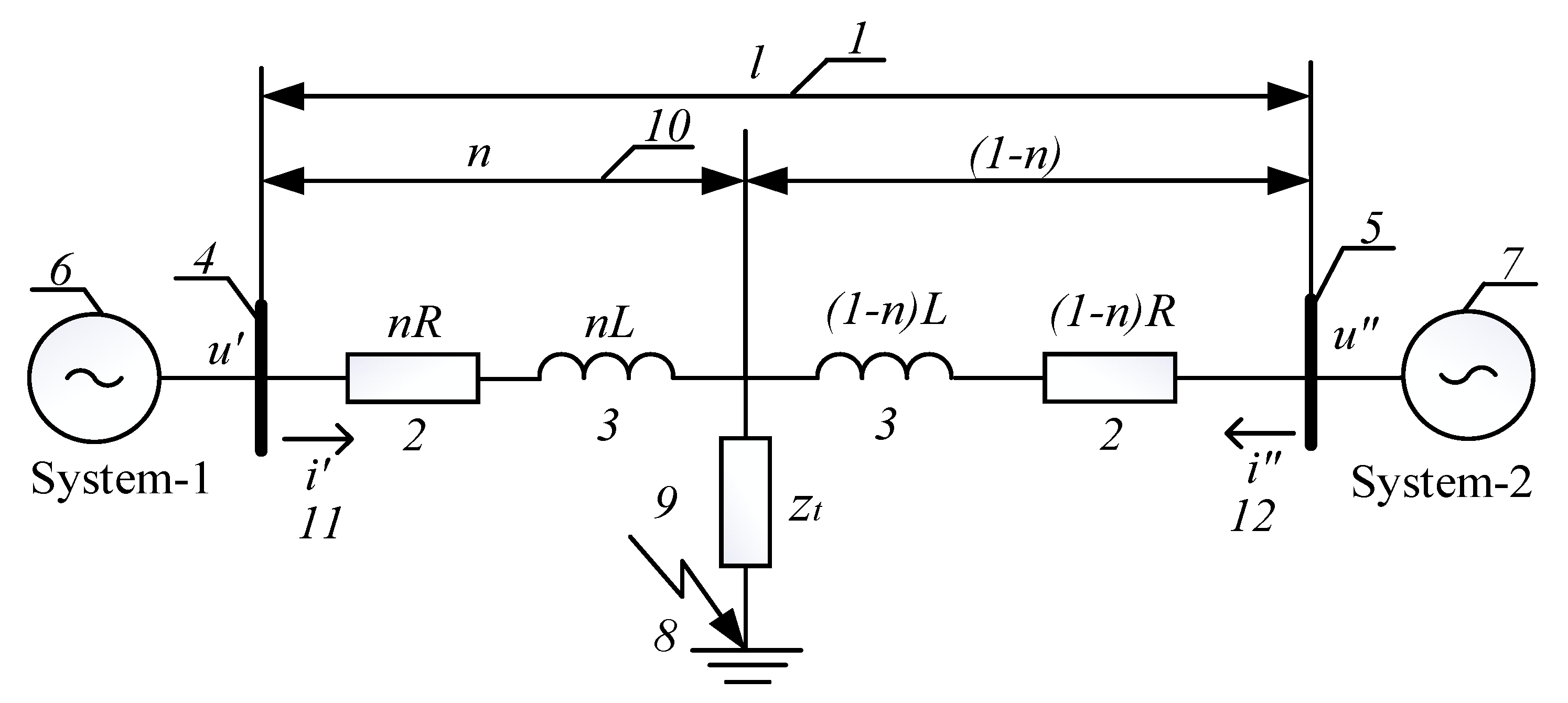
u′(m) = U + I′·(1 − k·rnd(m))·[nR·sin(2πf(td + m·ts)) + nL·cos(2πf(td + m·ts))],
ui″(m) = U + (1 − n)·R[I″·sin(2πf(td + m·ts)) + 0.15I″·sin(2πfi(td + m·ts))]
+ (1 − n)L·[I″·sin(2πf(td + m·ts)) + 0.15I″·sin(2πfi(td + m·ts))],
- At m = 20; ni and (20) = 0.486; ∆x = l·(n − ni) = 50 × (0.5 − 0.486) = 0.7 (km);
- At m = 60; ni and (60) = 0.526; ∆x = l·(n − ni) = 50 × (0.5 − 0.526) = −1.30 (km).
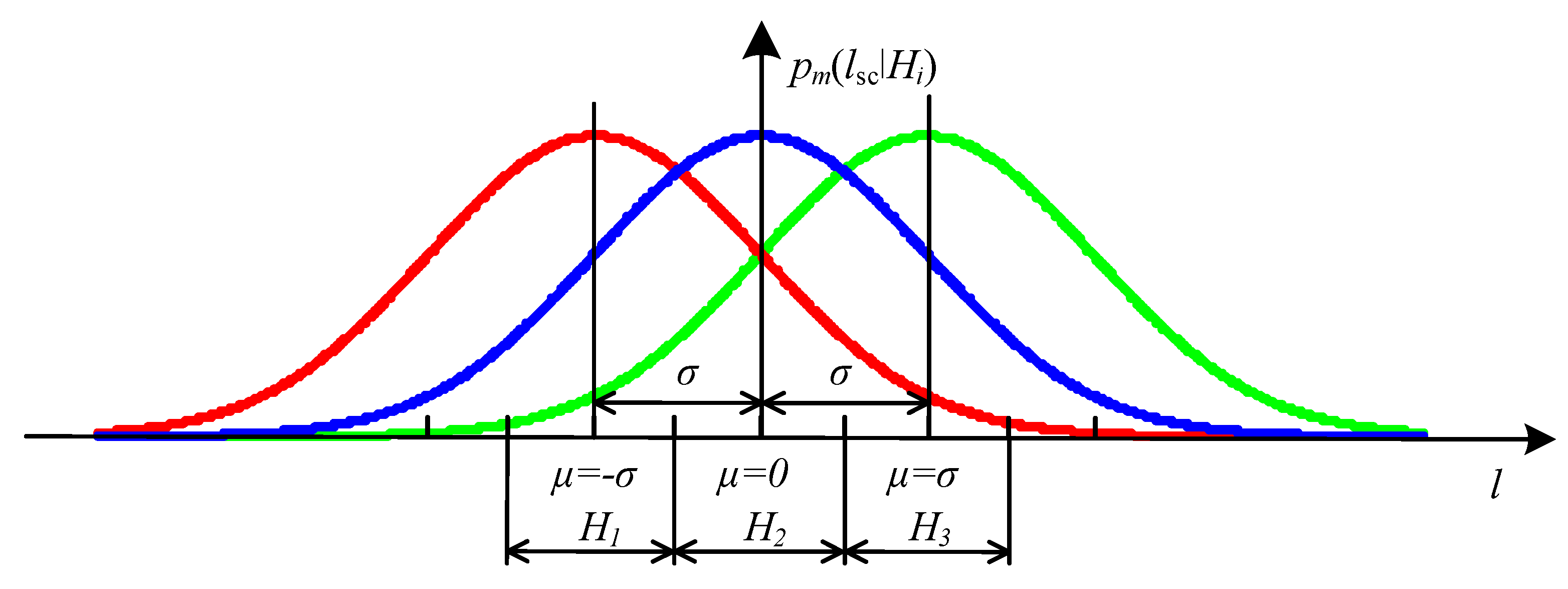
- Multi-criteria sequential analysis using the Armitage algorithm as applied to FL for OHPLs by EMP leads to the selection of a faulted section in the interval M[lsc] ± σ/2 = 25.185 ± 0.835 (km);
- The sequential analysis procedure does not require significant time costs, allowing us to make a decision about the faulted section in two steps, practically without affecting the speed of the OHPL fault algorithm;
- There is no need to use special computational methods to increase the speed of FL for OHPLs;
- The speed of making a decision on the fault location on OHPLs when implementing sequential analysis depends on the degree of distortion of currents and voltages in emergency mode oscillograms, including deviations of power quality parameters from standard values [85].
- Overlaps as a result of thunderstorms;
- Falling of trees onto wires without breaking the wire or overlapping onto tree branches;
- Overlap with the destruction of insulators, for example, due to unauthorized persons shooting at the garland from a hunting rifle;
- Overlap from the wire to the support body as a result of strong winds, ice, and frost deposits;
- Blocking the wire from passing large-sized machinery and agricultural machinery;
- Breakage of lightning protection cables followed by an SC of the phase wire(s) to the ground;
- A break with a wire falling to the ground;
- Uncoupling of the insulator string;
- Throwing metal objects onto overhead line wires by unauthorized persons;
- Other reasons.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| FL | fault location |
| OHPL | overhead power line |
| EMP | emergency mode parameters |
| RP | relay protection |
| SC | short circuit |
| PMU | phasor measurement unit |
References
- Voropai, N. Electric Power System Transformations: A Review of Main Prospects and Challenges. Energies 2020, 13, 5639. [Google Scholar] [CrossRef]
- Suliman, A.S.; Ahmed, B.M.; Elareefi, M.B.; Elrahman, E.A.E.A.; Arbab, E.A.; Abdulwahab, M.M. Monitoring System for Overhead Power Transmission Lines in Smart Grid System Using Internet of Things. Univ. Khartoum Eng. J. 2022, 12, 1. [Google Scholar] [CrossRef]
- Savina, N.V.; Varygina, A.O. Selection of an optimal cable brand for high-voltage overhead power lines based on criterion analysis. Ipolytech J. 2023, 27, 339–353. [Google Scholar] [CrossRef]
- Korotkevich, M.A.; Podgaisky, S.I. On the Expediency of Laying Cable Power Lines with a Voltage of 6–35 kV Outside Settlements Instead of Overhead Power Lines. ENERGETIKA Proc. CIS High. Educ. Inst. Power Eng. Assoc. 2022, 65, 463–476. [Google Scholar] [CrossRef]
- Nazemi M Dehghanian, P.; Darestani, Y.M.; Jinshun, S.J. Parameterized Wildfire Fragility Functions for Overhead Power Line Conductors. Power Syst. IEEE Trans. Power Syst. 2023, 99, 1–11. [Google Scholar] [CrossRef]
- Gonçalves, A.C.R.; Marques, M.C.; Loureiro, S.; Nieto, R.; Liberato, M.L.R. Disruption risk analysis of the overhead power lines in Portugal. Energy 2022, 263, 125583. [Google Scholar] [CrossRef]
- Li, P.; Qiu, R.; Wang, M.; Wang, X.; Jaffry, S.; Xu, M.; Huang, K.; Huang, Y. Online Monitoring of Overhead Power Lines Against Tree Intrusion via a Low-cost Camera and Mobile Edge Computing Approach. J. Phys. Conf. Ser. 2023, 2422, 012018. [Google Scholar] [CrossRef]
- Farkhadzeh, E.M.; Muradaliev, A.Z.; Abdullaeva, S.A.; Nazarov, A.A. Quantitative Assessment of the Operational Reliability of Overhead Power Transmission Lines. Power Technol. Eng. 2022, 55, 790–796. [Google Scholar] [CrossRef]
- Listyukhin, V.A.; Pecherskaya, E.A.; Artamonov, D.; Zinchenko, T.O.; Anisimova, A.A. Improving the reliability of overhead power transmission lines through the introduction of information and measurement systems for monitoring their parameters. Meas. Monit. Manag. Control 2022, 3, 62–68. (In Russian) [Google Scholar] [CrossRef]
- Ilyushin, P.; Volnyi, V.; Suslov, K.; Filippov, S. Review of Methods for Addressing Challenging Issues in the Operation of Protection Devices in Microgrids with Voltages of up to 1 kV that Integrates Distributed Energy Resources. Energies 2022, 15, 9186. [Google Scholar] [CrossRef]
- Listyukhin, V.; Pecherskaya, E.; Gurin, S.; Anisimova, A.; Shepeleva, A. Analysis and classification of cause and effect factors affecting the operating modes of overhead power lines. AIP Conf. Proc. 2022, 2767, 020019. [Google Scholar] [CrossRef]
- Ilyushin, P.; Filippov, S.; Kulikov, A.; Suslov, K.; Karamov, D. Specific Features of Operation of Distributed Generation Facilities Based on Gas Reciprocating Units in Internal Power Systems of Industrial Entities. Machines 2022, 10, 693. [Google Scholar] [CrossRef]
- Gurevich, Y.E.; Kabikov, K.V. Peculiarities of Power Supply, Aimed at Failure-Free Operation of Industrial Consumers; ELEKS-KM: Moscow, Russia, 2005. (In Russian) [Google Scholar]
- Ilyushin, P.V. Emergency and post-emergency control in the formation of micro-grids. E3S Web Conf. 2017, 25, 02002. [Google Scholar] [CrossRef]
- Maly, A.S.; Shalyt, G.M.; Eisenfeld, A.I. Determination of the Places of Damage to Power Transmission Lines According to the Parameters of the Emergency Mode; Energiya: Moscow, Russia, 1972; 215p. (In Russian) [Google Scholar]
- Kezunovic, M.; Knezev, M. Selection of optimal fault location algorithm. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar] [CrossRef]
- Panahi, H.; Zamani, R.; Sanaye-Pasand, M.; Mehrjerdi, H. Advances in Transmission Network Fault Location in Modern Power Systems: Review, Outlook and Future Works. IEEE Access 2021, 9, 158599–158615. [Google Scholar] [CrossRef]
- Schwan, M.; Ettinger, A.; Gunaltay, S. Probabilistic reliability assessment in distribution network master plan development and in distribution automation implementation. In Proceedings of the CIGRE, 2012 Session, Paris, France, 26–30 August 2012. Rep. C4-203. [Google Scholar]
- Shor, Y.B. Statistical Methods of Analysis and Quality Control and Reliability; Soviet Radio: Moscow, Russia, 1962. (In Russian) [Google Scholar]
- Bollen, M.H.J.; Dirix, P.M.E. Simple model for post-fault motor behaviours for reliability/power quality assessment of industrial power systems. IEE Proc.—Gener. Transm. Distrib. 1996, 143, 56–60. [Google Scholar] [CrossRef]
- Powanga, L.; Kwakwa, P.A. Determinants of Electricity Transmission and Distribution Losses in South Africa. J. Renew. Energy 2023, 2023, 2376449. [Google Scholar] [CrossRef]
- Thomas, D.; Fung, J. Measuring downstream supply chain losses due to power disturbances. Energy Econ. 2022, 114, 106314. [Google Scholar] [CrossRef]
- Koks, E.E.; Pant, R.; Thacker, S.; Hall, J. Understanding Business Disruption and Economic Losses Due to Electricity Failures and Flooding. Int. J. Disaster Risk Sci. 2019, 10, 421–438. [Google Scholar] [CrossRef]
- Lacommare, K.; Eto, J. Cost of power interruptions to electricity consumers in the United States (US). Energy 2006, 31, 1845–1855. [Google Scholar] [CrossRef]
- Edomah, N. Effects of voltage sags, swell and other disturbances on electrical equipment and their economic implications. In Proceedings of the CIRED 2009—20th International Conference and Exhibition on Electricity Distribution—Part 1, Prague, Czech Republic, 8–11 June 2009; pp. 1–4. [Google Scholar]
- Shalyt, G.M. Determination of the Place of Damage in Electrical Networks; Energoatomizdat: Moscow, Russia, 1982; 312p. (In Russian) [Google Scholar]
- Krzysztof, G.; Kowalik, R.; Rasolomampionona, D.D.; Anwar, S. Traveling wave fault location in power transmission systems: An overview. J. Electr. Syst. 2011, 7, 287–296. [Google Scholar]
- Lachugin, V.F. Wave methods for determining the location of damage on overhead power lines. Relay Prot. Autom. 2023, 1, 58–61. (In Russian) [Google Scholar]
- Obalin, M.D.; Kulikov, A.L. Application of adaptive procedures in algorithms for determining the location of damage to power lines. Ind. Power Eng. 2013, 12, 35–39. (In Russian) [Google Scholar]
- Abbasi, F.; Abdoos, A.; Hosseini, S.M.; Sanaye-Pasand, M. New ground fault location approach for partially coupled transmission lines. Electr. Power Syst. Res. 2023, 216, 109054. [Google Scholar] [CrossRef]
- Sampaio, F.; Tofoli, F.L.; Melo, L.S.; Barroso, G.C.; Sampaio, R.F.; Leao, R. Adaptive fuzzy directional bat algorithm for the optimal coordination of protection systems based on directional overcurrent relays. Electr. Power Syst. Res. 2022, 211, 108619. [Google Scholar] [CrossRef]
- Aziz, T.; Lin, Z.; Waseem, M.; Liu, S. Review on optimization methodologies in transmission network reconfiguration of power systems for grid resilience. Int. Trans. Electr. Energy Syst. 2021, 31, e12704. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Pazderin, A.V. Approaches to organization of emergency control at isolated operation of energy areas with distributed generation. In Proceedings of the International Ural Conference on Green Energy (URALCON), Chelyabinsk, Russia, 4–6 October 2018. [Google Scholar] [CrossRef]
- Gurevich, Y.E.; Libova, L.E. Application of Mathematical Models of Electrical Load in Calculation of the Power Systems Stability and Reliability of Power Supply to Industrial Enterprises; ELEKS-KM: Moscow, Russia, 2008. (In Russian) [Google Scholar]
- Ilyushin, P.V.; Filippov, S.P. Under-frequency load shedding strategies for power districts with distributed generation. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25–29 March 2019. [Google Scholar] [CrossRef]
- Voitovich, P.A.; Lavrov, Y.A.; Petrova, N.F. Innovative technical solutions for the construction of ultra-compact high-voltage overhead power transmission lines. New Russ. Electr. Power Ind. 2018, 8, 44–57. (In Russian) [Google Scholar]
- Kosyakov, A.A.; Kuleshov, P.V.; Pogudin, A.L. The influence of the grounding device structure of a substation on the voltage of conducted interference of lightning currents. Russ. Electr. Eng. 2019, 90, 752–755. [Google Scholar] [CrossRef]
- Sharipov, U.B.; Égamnazarov, G.A. Calculating currents in lightning protection cables and in optical cables built into them during asymmetric short circuits in overhead transmission lines. Power Technol. Eng. 2017, 50, 673–678. [Google Scholar] [CrossRef]
- Shevchenko, N.Y.; Ugarov, G.G.; Kirillova, S.N.; Lebedeva, Y.V. Review and analysis of the design features of overhead power line wires with increased resistance to icy-wind loads. Quest. Electr. Technol. 2018, 4, 53–63. (In Russian) [Google Scholar]
- Kulikov, A.; Ilyushin, P.; Loskutov, A.; Suslov, K.; Filippov, S. WSPRT Methods for Improving Power System Automation Devices in the Conditions of Distributed Generation Sources Operation. Energies 2022, 15, 8448. [Google Scholar] [CrossRef]
- Saha, M.M.; Izykowski, J.; Rosolowski, E. Fault Location on Power Networks; Springer: London, UK, 2010; 437p. [Google Scholar]
- Visyashchev, A.N. Devices and Methods for Determining the Location of Damage on Power Transmission Lines: A textbook. At 2 h. h. 1; Publishing House of IrSTU: Irkutsk, Russia, 2001; 188p. (In Russian) [Google Scholar]
- Lebedev, V.; Filatova, G.; Timofeev, A. Increase of accuracy of the fault location methods for overhead electrical power lines. Adv. Mater. Sci. Eng. 2018, 2018, 3098107. [Google Scholar] [CrossRef]
- Arzhannikov, E.A.; Lukoyanov, V.Y.; Misrikhanov, M.S. Determining the Location of a Short Circuit on High−Voltage Power Transmission Lines; Shuin, V.A., Ed.; Energoatomizdat: Moscow, Russia, 2003; 272p. (In Russian) [Google Scholar]
- Ilyushin, P.V.; Shepovalova, O.V.; Filippov, S.P.; Nekrasov, A.A. The effect of complex load on the reliable operation of solar photovoltaic and wind power stations integrated into energy systems and into off-grid energy areas. Energy Rep. 2022, 8, 1515–1529. [Google Scholar] [CrossRef]
- Kulikov, A.L. Remote Determination of Power Line Damage Sites by Active Sensing Methods; Energoatomizdat: Moscow, Russia, 2006; 148p. (In Russian) [Google Scholar]
- Minullin, R.G. Detecting the faults of overhead electric-power lines by the location-probing method. Russ. Electr. Eng. 2017, 88, 61–70. [Google Scholar] [CrossRef]
- Kulikov, A.L.; Lukicheva, I.A. Determination of the place of damage to the power transmission line by the instantaneous values of the oscillograms of emergency events. Bull. Ivanovo State Power Eng. Univ. 2016, 5, 16–21. (In Russian) [Google Scholar]
- Ustinov, A.A.; Visyashchev, A.N. Iterative methods for determining the location of damage by the parameters of the emergency mode during one-way measurements on overhead power lines. Bull. IrSTU 2010, 5, 260–266. (In Russian) [Google Scholar]
- Kulikov, A.; Ilyushin, P.; Suslov, K.; Filippov, S. Estimating the Error of Fault Location on Overhead Power Lines by Emergency State Parameters Using an Analytical Technique. Energies 2023, 16, 1552. [Google Scholar] [CrossRef]
- Aboshady, F.M.; Thomas, D.W.P. A Wideband Single End Fault Location Scheme for Active Untransposed Distribution Systems. IEEE Trans. Smart Grid 2020, 11, 2115–2124. [Google Scholar] [CrossRef]
- Takagi, T.; Yamakoshi, Y.; Yamaura, Y.; Kondow, R.; Matsushima, T. Development of a new type fault locator using the one-terminal voltage and current data. IEEE Trans. Power Appl. Syst. 1982, PAS-101, 2892–2898. [Google Scholar] [CrossRef]
- Simeon, O.; Faithpraise, F.O.; Ibanga, J. Iterative Newton-Raphson-Based Impedance Method for Fault Distance Detection on Transmission Line. Int. Multiling. J. Sci. Technol. 2020, 5, 2805–2810. [Google Scholar] [CrossRef]
- Nagendra Reddy, P.L.V.; Mukunda, V.K.S.; Sushyanth, C.; Vanitha, V. Implementation of Novosel Simple Impedance Algorithm for fault location. IJCTA 2016, 9, 7589–7596. [Google Scholar]
- Schweitzer, E.O. A review of impedance-based fault locating experience. In Proceedings of the 14th Annual Iowa–Nebraska System Protection Seminar, Omaha, NE, USA, 12 October 1990; pp. 1–31. [Google Scholar]
- Suslov, K.V.; Solonina, N.N.; Solonina, Z.V.; Akhmetshin, A. Operational determination of the point of a short circuit in power lines. Power Eng. Res. Equip. Technol. 2023, 25, 71–83. [Google Scholar] [CrossRef]
- Bahmanyar, A.; Jamali, S.; Estebsari, A.; Bompard, E. A comparison framework for distribution system outage and fault location methods. Electr. Power Syst. Res. 2017, 145, 19–34. [Google Scholar] [CrossRef]
- Liao, Y. Transmission Line Fault Location Algorithms Without Requiring Line Parameters. Electr. Power Compon. Syst. 2008, 36, 1218–1225. [Google Scholar] [CrossRef]
- Stringfield, T.W.; Marihart, D.J.; Stevens, R.F. Fault location methods for overhead lines. IEEE Trans. Power Appar. Syst. 1957, 76, 518–530. [Google Scholar] [CrossRef]
- Born, E.; Jaeger, J. Device locates point of fault on transmission lines. Electr. World 1967, 168, 133–134. [Google Scholar]
- Senderovich, G.A.; Gryb, O.G.; Karpaliuk, I.T.; Shvets, S.V.; Zaporozhets, A.O.; Samoilenko, I.A. Automation of determining the location of damage of overhead power lines. Stud. Syst. Decis. Control 2021, 359, 35–53. [Google Scholar]
- Senderovich, G.A.; Gryb, O.G.; Karpaliuk, I.T.; Shvets, S.V.; Zaporozhets, A.O.; Samoilenko, I.A. Experimental studies of the method for determining location of damage of overhead power lines in the operation mode. Stud. Syst. Decis. Control 2021, 359, 55–77. [Google Scholar]
- Lyamets, Y.Y.; Antonov, V.I.; Efremov, V.A. Diagnostics of Power Transmission Lines. Electrotechnical Microprocessor Devices and Systems: Interuniversity Collection of Scientific Papers; Publishing House of the Chuvash State University: Cheboksary, Russia, 1992. (In Russian) [Google Scholar]
- Yu, C.S.; Liu, C.W.; Jiang, J.A. A new fault location algorithm for series compensated lines using synchronized phasor measurements. In Proceedings of the 2000 Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000. [Google Scholar] [CrossRef]
- Kezunovic, M.; Meliopoulos, S.; Venkatasubramanian, V.; Vittal, V. Application of Time-Synchronized Measurements in Power System Transmission Networks; Springer: New York, NY, USA, 2014. [Google Scholar]
- STO 56947007–29.240.55.159–2013; Standard Instructions for the Organization of Work to Determine the Places of Damage to Overhead Power Lines with a Voltage of 110 kV and above. Standard of the Organization of PJSC FGC UES: Moscow, Russia, 2013.
- Martynov, M.V. Method of interval determination of the place of damage to the power transmission line. Patent of the Russian Federation No. 2720949, 15 May 2020. (In Russian). [Google Scholar]
- Bykadorov, A.L.; Zarutskaya, T.A.; Muratova-Milekhina, A.S. Application of pattern recognition theory in determining the location of a short circuit in AC traction networks. Bull. RSUPS 2021, 2, 119–128. [Google Scholar] [CrossRef]
- Kulikov, A.L.; Shepovalova, O.V.; Ilyushin, P.V.; Filippov, S.P.; Chirkov, S.V. Control of electric power quality indicators in distribution networks comprising a high share of solar photovoltaic and wind power stations. Energy Rep. 2022, 8, 1501–1514. [Google Scholar] [CrossRef]
- Won, D.J.; Chung, I.Y.; Kim, J.M.; Moon, S.I.; Seo, J.C.; Choe, J.W. A new algorithm to locate power-quality event source with improved realization of distributed monitoring scheme. IEEE Trans. Power Deliv. 2006, 21, 1641–1647. [Google Scholar] [CrossRef]
- Shirman, Y.D. Radio-Electronic Systems: Fundamentals of Construction and Theory, 2nd ed.; Radio Engineering: Moscow, Russia, 2007; 510p. (In Russian) [Google Scholar]
- Armitage, P. Sequential analysis with more than two alternative hypotheses, and its relation to discriminant function analysis. J. R. Stat. Soc. 1950, 12, 137–144. Available online: https://api.semanticscholar.org/CorpusID:126310625 (accessed on 1 September 2023). [CrossRef]
- Ghosh, B.K.; Sen, P.K. Handbook of Sequential Analysis (Statistics: A Series of Textbooks and Monographs), 1st ed.; CRC Press: Boca Raton, FL, USA, 1991; 664p. [Google Scholar]
- Wald, A. Sequential Analysis; John Wiley and Sons: New York, NY, USA, 1947; 232p. [Google Scholar]
- Jouny, I.; Garber, F.D. Mary sequential hypothesis tests for automatic target recognition. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 473–483. [Google Scholar] [CrossRef]
- Kulikov, A.L.; Ilyushin, P.V.; Suslov, K.V.; Karamov, D.N. Coherence of digital processing of current and voltage signals at decimation for power systems with a large share of renewable power stations. Energy Rep. 2022, 8, 1464–1478. [Google Scholar] [CrossRef]
- Visyashchev, A.N.; Plenkov, E.R.; Tiguntsev, S.G. A method for Determining the Location of a Short Circuit on an Overhead Power Transmission Line with Unsynchronized Measurements from Its Two Ends. Patent of the Russian Federation No. 2508556, 27 February 2014. (In Russian). [Google Scholar]
- Varma, R.K.; Rahman, S.A.; Vanderheide, T.; Dang, M.D.N. Harmonic impact of a 20-MW PV solar farm on a utility distribution network. IEEE Power Energy Technol. Syst. J. 2016, 3, 89–98. [Google Scholar] [CrossRef]
- Torquato, R.; Freitas, W.; Hax, G.R.T.; Donadon, A.R.; Moya, R. High frequency harmonic distortions measured in a Brazilian solar farm. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 623–627. [Google Scholar]
- IEEE STD 519-2014; Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems/Transmission and Distribution Committee of the IEEE Power and Energy Society. The Institute of Electrical and Electronics Engineers: New York, NY, USA, 2014.
- Adineh, B.; Keypour, R.; Sahoo, S.; Davari, P.; Blaabjerg, F. Robust optimization based harmonic mitigation method in islanded microgrids. Int. J. Electr. Power Energy Syst. 2022, 137, 107631. [Google Scholar] [CrossRef]
- Saha, S.; Saleem, M.I.; Roy, T.K. Impact of high penetration of renewable energy sources on grid frequency behavior. Int. J. Electr. Power Energy Syst. 2022, 145, 108701. [Google Scholar] [CrossRef]
- Ribeiro, P.F.; Duque, C.A.; Silveira, P.M.; Cerqueira, A.S. Power Systems Signal Processing for Smart Grids; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Wentzel, E.S. Probability Theory: Textbook for University Students, 10th ed.; Academia: Moscow, Russia, 2005; 571p. (In Russian) [Google Scholar]
- Kulikov, A.; Ilyushin, P.; Suslov, K.; Filippov, S. Organization of Control of the Generalized Power Quality Parameter Using Wald’s Sequential Analysis Procedure. Inventions 2023, 8, 17. [Google Scholar] [CrossRef]
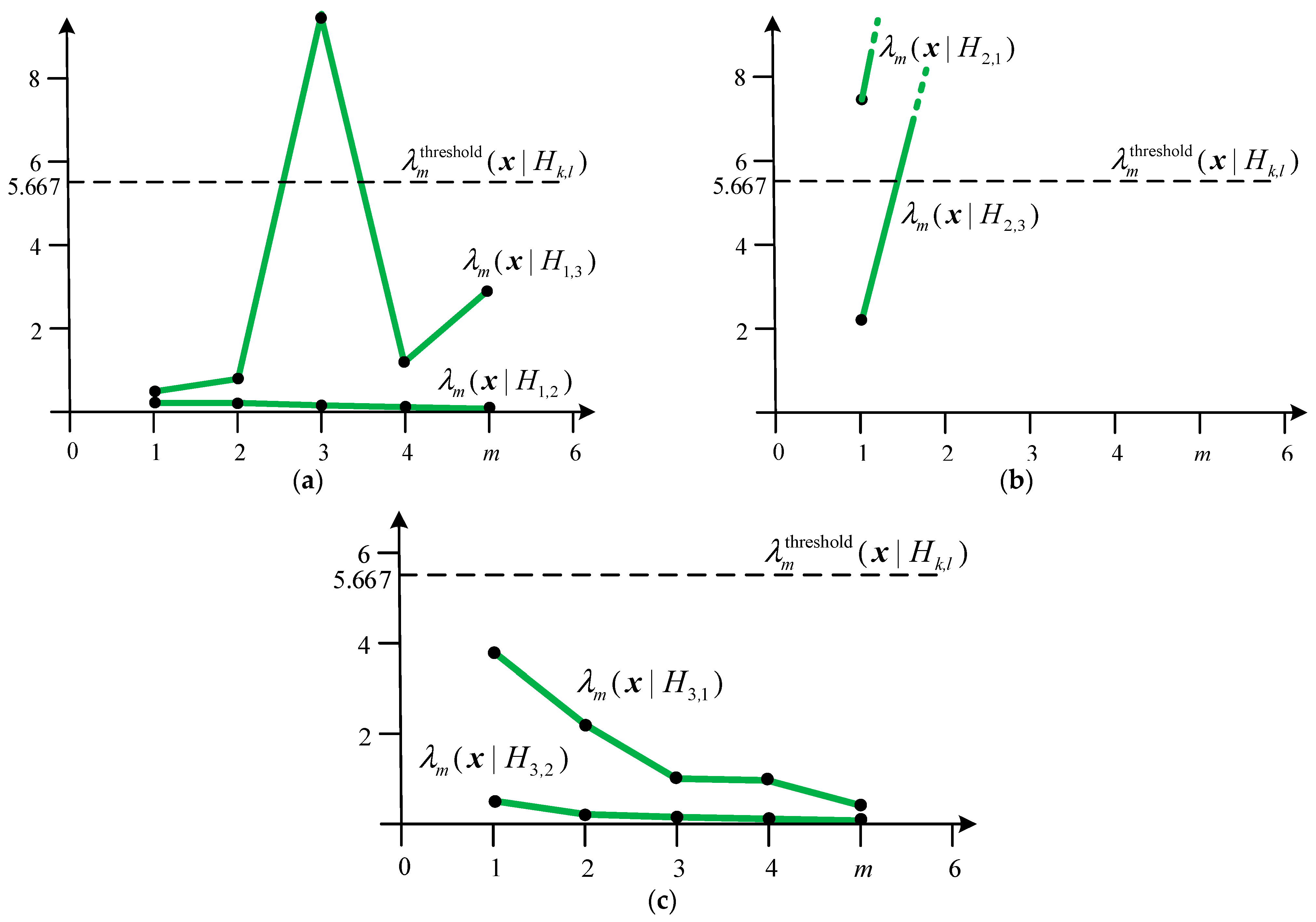
| Parameter | I′ (A) | I″ (A) | f (Hz) | ts (s) | L (H) | R (Ohm) | fi (Hz) | U (V) | n | k | td (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Meaning | 13,908.15 | 9030.13 | 50 | 0.0025 | 0.0643 | 12.5 | 135 | 29,323.83 | 0.5 | 0.15 | 0.003 |
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| lsc (km) | 25.85 | 24.9 | 23.7 | 26.35 | 24.6 | 25.6 | 25.7 | 27.36 | 23.75 | 25.05 |
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| λm(x|H1,2) | 0.131 | 0.043 | 0.047 | 0.004 | 0.002 | – | – | – | – | – |
| λm(x|H1,3) | 0.269 | 0.475 | 9.362 | 0.917 | 2.953 | – | – | – | – | – |
| λm(x|H2,1) | 7.608 | 23.098 | 23.236 | 298.12 | 669.88 | – | – | – | – | – |
| λm(x|H2,3) | 2.05 | 10.98 | 196.25 | 247.66 | 1790 | – | – | – | – | – |
| λm(x|H3,1) | 3.711 | 2.10 | 1.05 | 1.07 | 0.332 | – | – | – | – | – |
| λm(x|H3,2) | 0.488 | 0.091 | 0.005 | 0.004 | 0.0006 | – | – | – | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulikov, A.; Ilyushin, P.; Loskutov, A.; Filippov, S. Fault Location Method for Overhead Power Line Based on a Multi-Hypothetical Sequential Analysis Using the Armitage Algorithm. Inventions 2023, 8, 123. https://doi.org/10.3390/inventions8050123
Kulikov A, Ilyushin P, Loskutov A, Filippov S. Fault Location Method for Overhead Power Line Based on a Multi-Hypothetical Sequential Analysis Using the Armitage Algorithm. Inventions. 2023; 8(5):123. https://doi.org/10.3390/inventions8050123
Chicago/Turabian StyleKulikov, Aleksandr, Pavel Ilyushin, Anton Loskutov, and Sergey Filippov. 2023. "Fault Location Method for Overhead Power Line Based on a Multi-Hypothetical Sequential Analysis Using the Armitage Algorithm" Inventions 8, no. 5: 123. https://doi.org/10.3390/inventions8050123
APA StyleKulikov, A., Ilyushin, P., Loskutov, A., & Filippov, S. (2023). Fault Location Method for Overhead Power Line Based on a Multi-Hypothetical Sequential Analysis Using the Armitage Algorithm. Inventions, 8(5), 123. https://doi.org/10.3390/inventions8050123







