Obtaining Vortex Formation in Blood Flow by Particle Tracking: Echo-PV Methods and Computer Simulation
Abstract
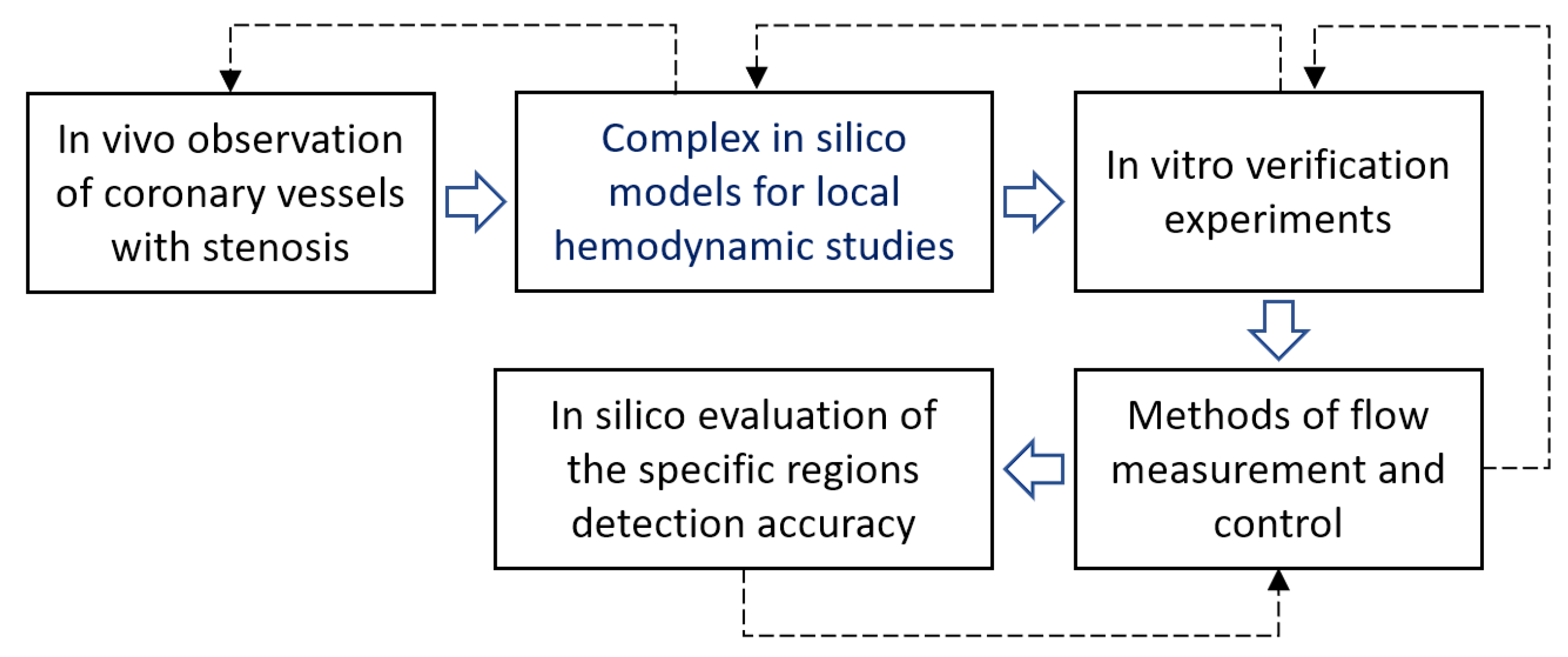
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup for Particle Echogenicity Testing in a Fluid Flow
2.2. Liquid–Particle Model: Equations Describing the Processes in the Dispersed and Liquid Phases
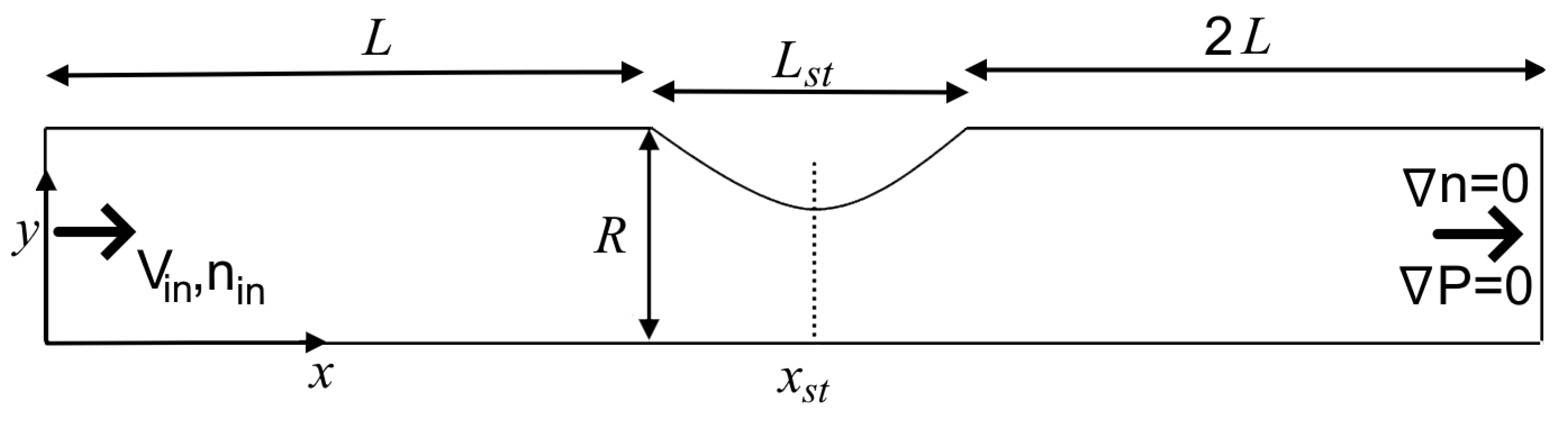
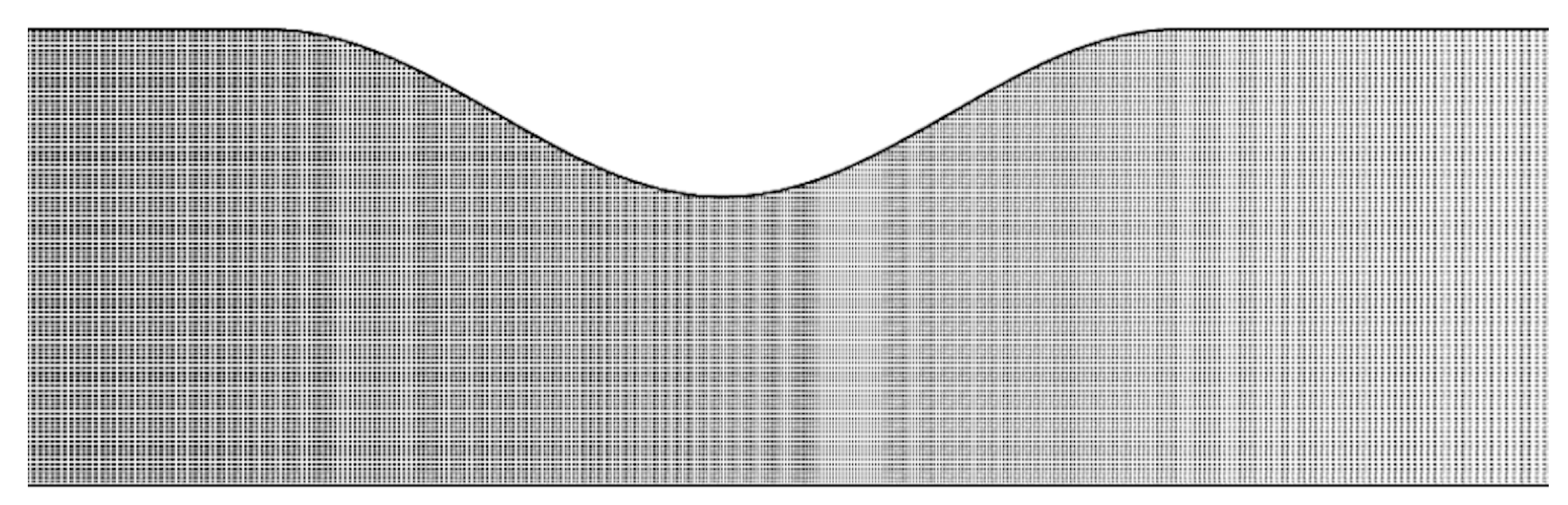
2.3. Design and Procedure of Simulations
3. Results and Discussion
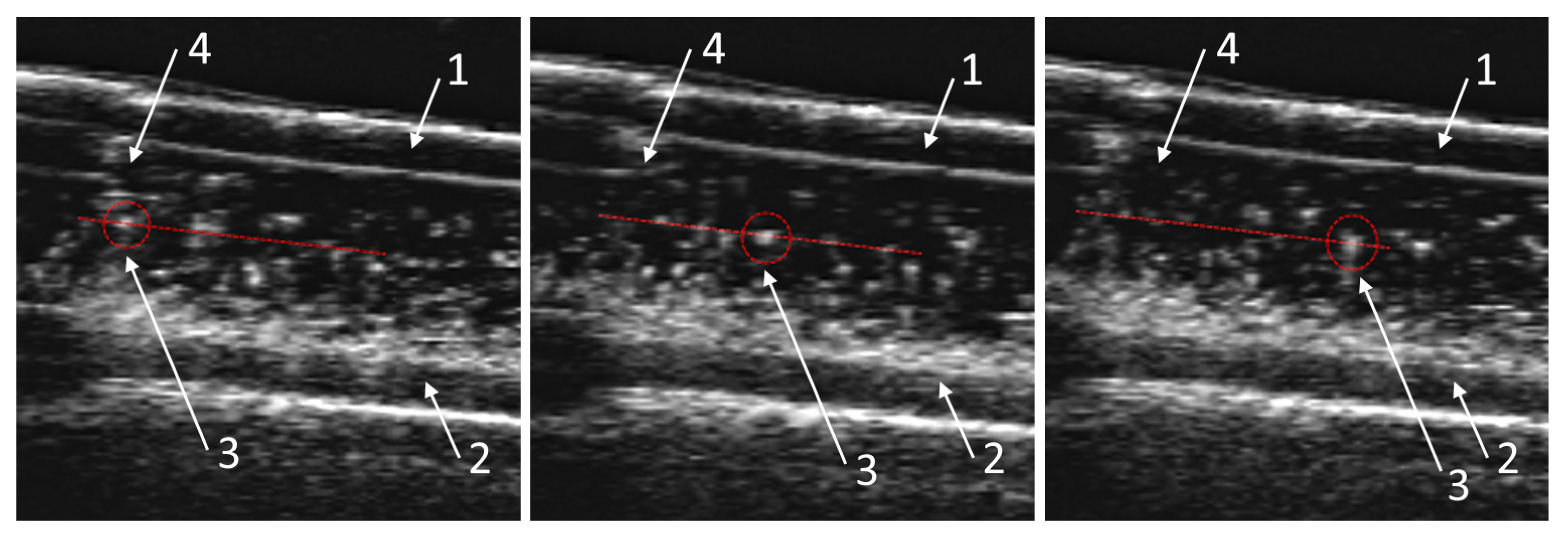
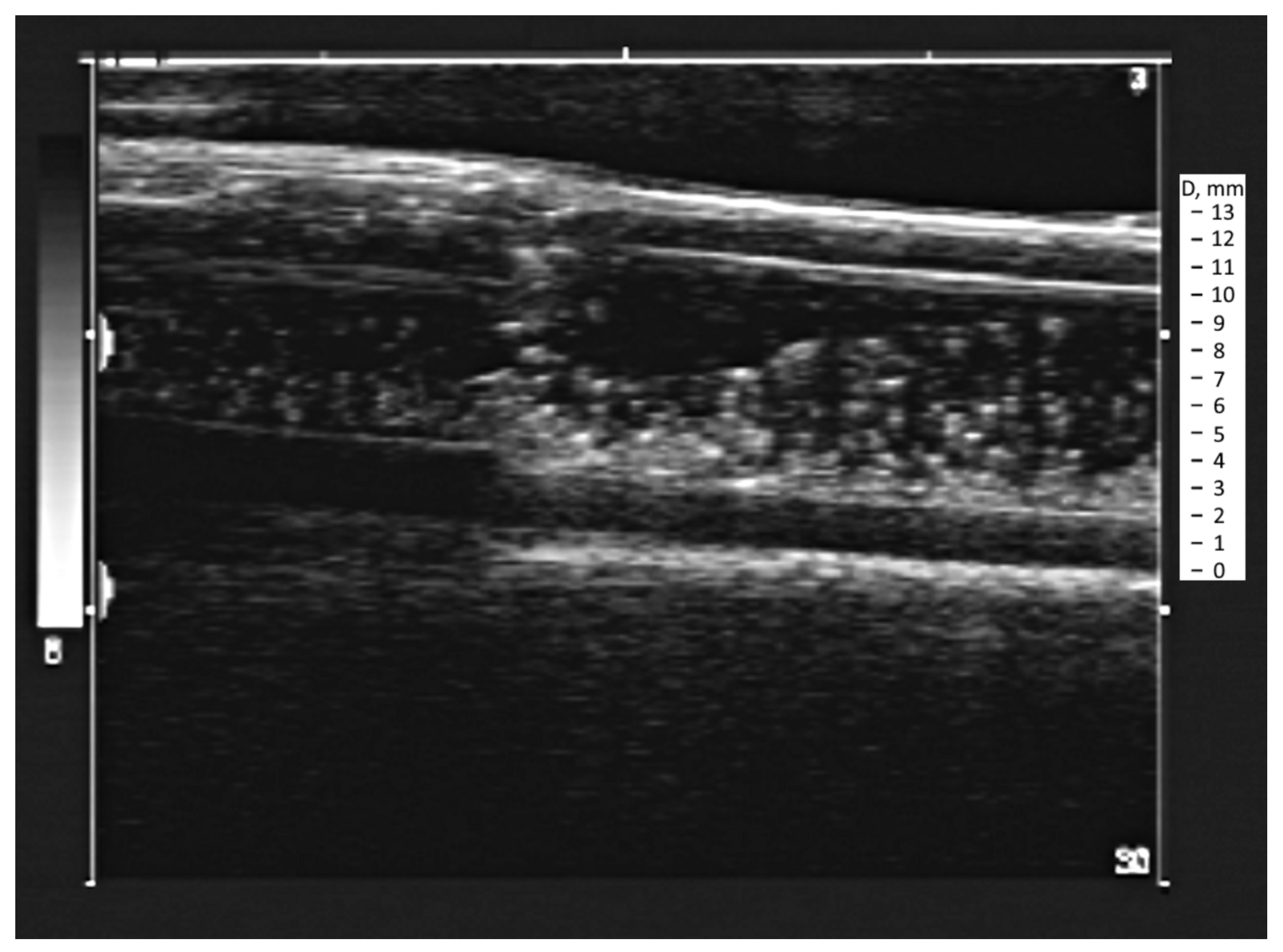
3.1. Obtaining the Vortex Zone by Echo-PV Tracking of Calcite Particles
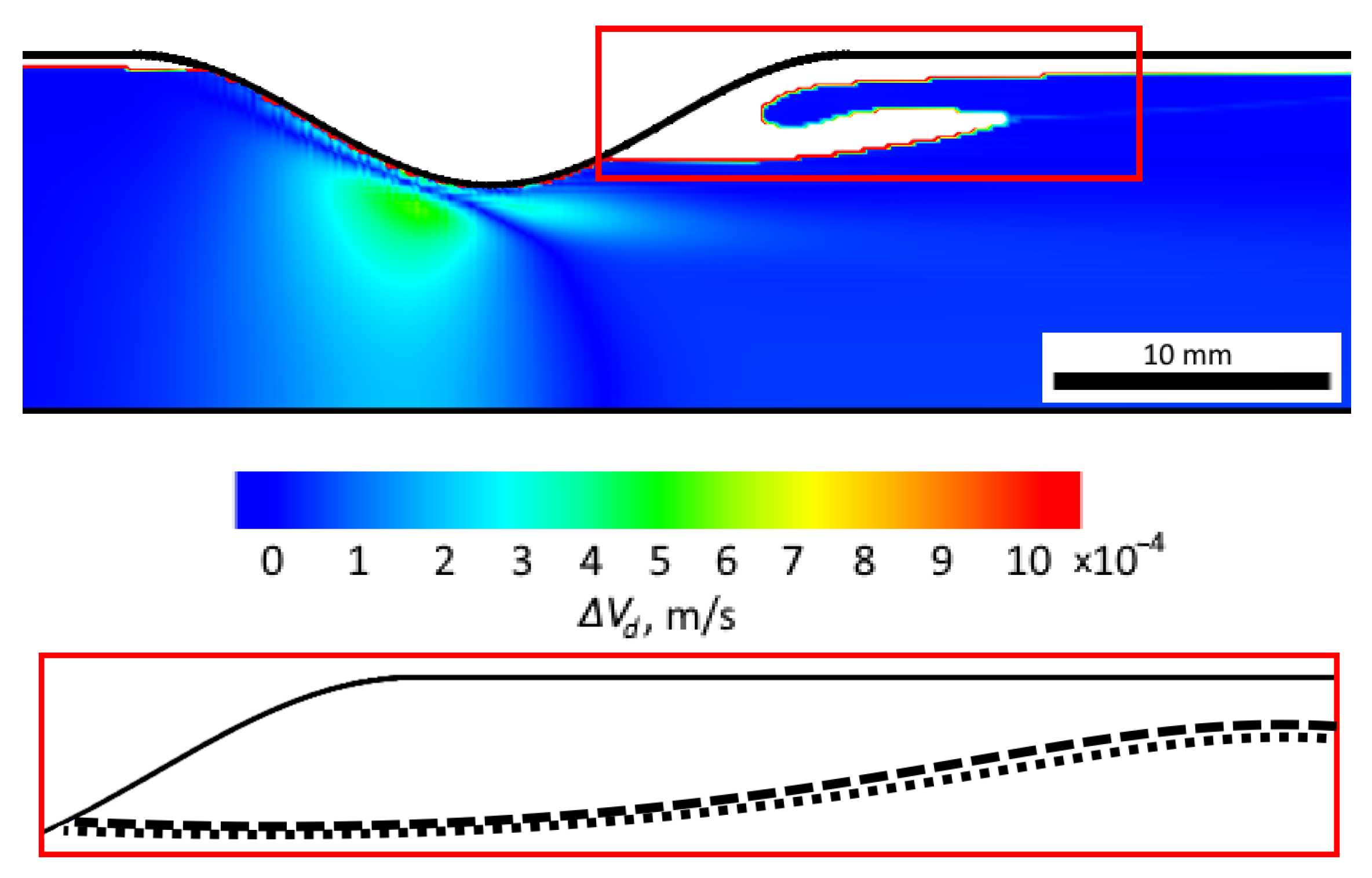
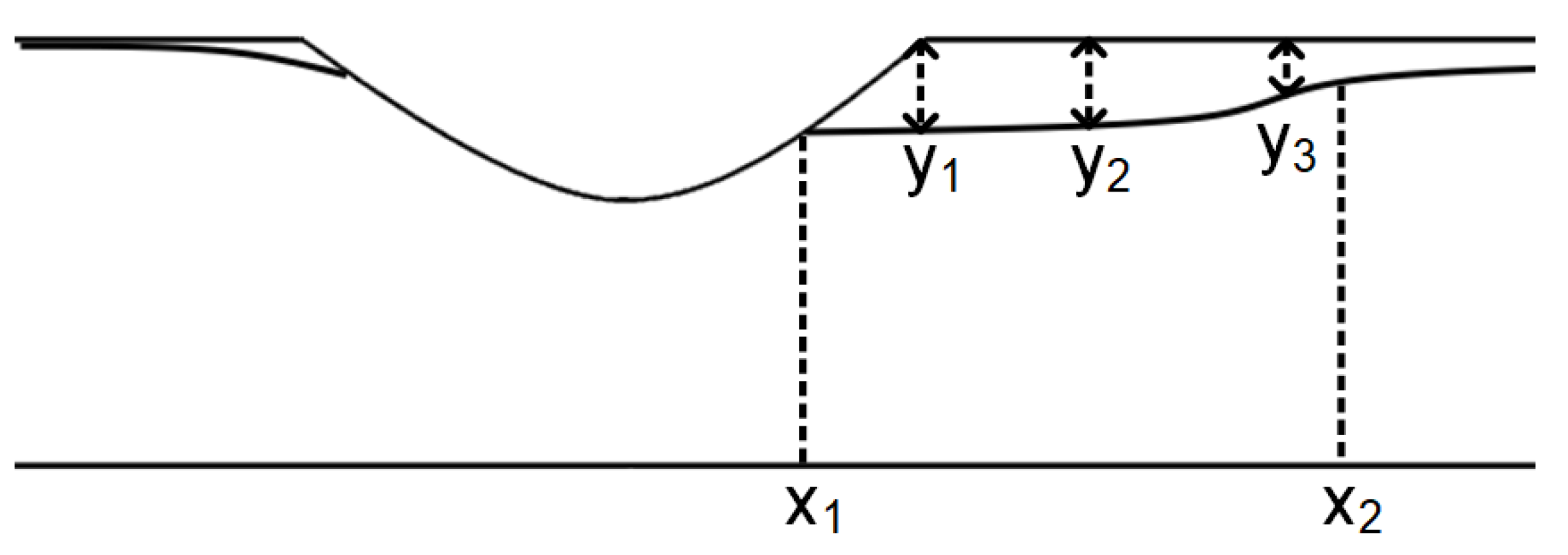
3.2. Computer Simulations and Accuracy Investigation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Azuma, T.; Fukushima, T. Flow patterns in stenotic blood vessel models. Biorheology 1976, 13, 337–355. [Google Scholar] [CrossRef]
- Kwak, B.R.; Bäck, M.; Bochaton-Piallat, M.L.; Caligiuri, G.; Daemen, M.J.; Davies, P.F.; Hoefer, I.E.; Holvoet, P.; Jo, H.; Krams, R.; et al. Biomechanical factors in atherosclerosis: Mechanisms and clinical implications. Eur. Heart J. 2014, 35, 3013–3020. [Google Scholar] [CrossRef]
- Chatzizisis, Y.S.; Coskun, A.U.; Jonas, M.; Edelman, E.R.; Feldman, C.L.; Stone, P.H. Role of endothelial shear stress in the natural history of coronary atherosclerosis and vascular remodeling: Molecular, cellular, and vascular behavior. J. Am. Coll. Cardiol. 2007, 49, 2379–2393. [Google Scholar] [CrossRef]
- Morbiducci, U.; Kok, A.M.; Kwak, B.R.; Stone, P.H.; Steinman, D.A.; Wentzel, J.J. Atherosclerosis at arterial bifurcations: Evidence for the role of haemodynamics and geometry. Thromb. Haemost. 2016, 115, 484–492. [Google Scholar] [CrossRef]
- Gimbrone, M.A., Jr.; Topper, J.N.; Nagel, T.; Anderson, K.R.; Garcia-Cardeña, G. Endothelial dysfunction, hemodynamic forces, and atherogenesis a. Ann. N. Y. Acad. Sci. 2000, 902, 230–240. [Google Scholar] [CrossRef]
- Chahed, N.; Peronneau, P.; Delouche, A.; Diebold, B. Velocity profiles and streamlines of a revolution post-stenotic flow. Biorheology 1991, 28, 383–400. [Google Scholar] [CrossRef]
- Buchanan, J., Jr.; Kleinstreuer, C.; Comer, J. Rheological effects on pulsatile hemodynamics in a stenosed tube. Comput. Fluids 2000, 29, 695–724. [Google Scholar] [CrossRef]
- Mallinger, F.; Drikakis, D. Instability in three-dimensional, unsteady, stenotic flows. Int. J. Heat Fluid Flow 2002, 23, 657–663. [Google Scholar] [CrossRef]
- Neofytou, P.; Drikakis, D. Effects of blood models on flows through a stenosis. Int. J. Numer. Methods Fluids 2003, 43, 597–635. [Google Scholar] [CrossRef]
- Cheng, L.; Robertson, J.; Clark, M. Numerical calculations of plane oscillatory non-uniform flow—II. Parametric study of pressure gradient and frequency with square wall obstacles. J. Biomech. 1973, 6, 521–538. [Google Scholar] [CrossRef]
- Daly, B.J. A numerical study of pulsatile flow through stenosed canine femoral arteries. J. Biomech. 1976, 9, 465–475. [Google Scholar] [CrossRef] [PubMed]
- Mandal, D.; Manna, N.; Chakrabarti, S. Influence of different bell-shaped stenoses on the progression of the disease, atherosclerosis. J. Mech. Sci. Technol. 2011, 25, 1933–1947. [Google Scholar] [CrossRef]
- Paul, M.C.; Molla, M.M.; Roditi, G. Large–Eddy simulation of pulsatile blood flow. Med. Eng. Phys. 2009, 31, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.; Liao, W.; Low, H. Numerical simulation of turbulent flow through series stenoses. Int. J. Numer. Methods Fluids 2003, 42, 717–740. [Google Scholar] [CrossRef]
- Starodumov, I.O.; Blyakhman, F.A.; Sokolov, S.Y.; Bessonov, I.S.; Zubarev, A.Y.; Alexandrov, D.V. In-silico study of hemodynamic effects in a coronary artery with stenosis. Eur. Phys. J. Spec. Top. 2020, 229, 3009–3020. [Google Scholar] [CrossRef]
- Starodumov, I.O.; Sokolov, S.Y.; Alexandrov, D.V.; Zubarev, A.Y.; Bessonov, I.S.; Chestukhin, V.V.; Blyakhman, F.A. Modelling of hemodynamics in bifurcation lesions of coronary arteries before and after myocardial revascularization. Phil. Trans. R. Soc. A 2022, 380, 20200303. [Google Scholar] [CrossRef]
- Starodumov, I.; Alexandrov, D.; Zubarev, A.; Toropova, L.; Sokolov, S.; Blyakhman, F. Influence of near-wall layer hemodynamics on blood flow in a vessel with stenosis. AIP Conf. Proc. 2023, 2803, 040002. [Google Scholar]
- Starodumov, I.O.; Sokolov, S.Y.; Blyakhman, F.A.; Zubarev, A.Y.; Fedotov, S.P.; Alexandrov, D.V. In silico study of magnetic nanoparticles transport in channels of various diameters in the presence of a constant magnetic field. Eur. Phys. J. Spec. Top. 2023, 232, 1207–1217. [Google Scholar] [CrossRef]
- Starodumov, I.; Makhaeva, K.; Zubarev, A.; Bessonov, I.; Sokolov, S.; Mikushin, P.; Alexandrov, D.; Chestukhin, V.; Blyakhman, F. Modeling of Local Hematocrit for Blood Flow in Stenotic Coronary Vessels. Fluids 2023, 8, 230. [Google Scholar] [CrossRef]
- Dirix, P.; Buoso, S.; Peper, E.; Kozerke, S. Synthesis of patient-specific multipoint 4D flow MRI data of turbulent aortic flow downstream of stenotic valves. Sci. Rep. 2022, 12, 16004. [Google Scholar] [CrossRef]
- Jhun, C.S.; Newswanger, R.; Cysyk, J.; Ponnaluri, S.; Good, B.; Manning, K.; Rosenberg, G. Dynamics of Blood Flows in Aortic Stenosis: Mild, Moderate, and Severe. ASAIO J. (Am. Soc. Artif. Intern. Organs 1992) 2021, 67, 666–674. [Google Scholar] [CrossRef] [PubMed]
- Gracka, M.; Lima, R.; Miranda, J.M.; Student, S.; Melka, B.; Ostrowski, Z. Red blood cells tracking and cell-free layer formation in a microchannel with hyperbolic contraction: A CFD model validation. Comput. Methods Programs Biomed. 2022, 226, 107117. [Google Scholar] [CrossRef]
- Abbasian, M.; Shams, M.; Valizadeh, Z.; Moshfegh, A.; Javadzadegan, A.; Cheng, S. Effects of different non-Newtonian models on unsteady blood flow hemodynamics in patient-specific arterial models with in-vivo validation. Comput. Methods Programs Biomed. 2020, 186, 105185. [Google Scholar] [CrossRef] [PubMed]
- Guerciotti, B.; Vergara, C. Computational comparison between Newtonian and non-Newtonian blood rheologies in stenotic vessels. In Biomedical Technology: Modeling, Experiments and Simulation; Springer: Berlin/Heidelberg, Germany, 2018; pp. 169–183. [Google Scholar]
- Liu, B.; Tang, D. Influence of non-Newtonian properties of blood on the wall shear stress in human atherosclerotic right coronary arteries. Mol. Cell. Biomech. MCB 2011, 8, 73. [Google Scholar]
- Hund, S.J.; Kameneva, M.V.; Antaki, J.F. A Quasi-Mechanistic Mathematical Representation for Blood Viscosity. Fluids 2017, 2, 10. [Google Scholar] [CrossRef]
- Wajihah, S.A.; Sankar, D. A review on non-Newtonian fluid models for multi-layered blood rheology in constricted arteries. Arch. Appl. Mech. 2023, 93, 1771–1796. [Google Scholar] [CrossRef]
- Ponalagusamy, R.; Manchi, R. A study on two-layered (K.L-Newtonian) model of blood flow in an artery with six types of mild stenoses. Appl. Math. Comput. 2020, 367, 124767. [Google Scholar] [CrossRef]
- Beris, A.N.; Horner, J.S.; Jariwala, S.; Armstrong, M.J.; Wagner, N.J. Recent advances in blood rheology: A review. Soft Matter 2021, 17, 10591–10613. [Google Scholar] [CrossRef]
- Rabby, M.G.; Shupti, S.P.; Molla, M.M. Pulsatile non-newtonian laminar blood flows through arterial double stenoses. J. Fluids 2014, 2014, 757902. [Google Scholar] [CrossRef]
- Rosenfeld, M. Validation of numerical simulation of incompressible pulsatile flow in a constricted channel. Comput. Fluids 1993, 22, 139–156. [Google Scholar] [CrossRef]
- Rosenfeld, M. A numerical study of pulsating flow behind a constriction. J. Fluid Mech. 1995, 301, 203–223. [Google Scholar] [CrossRef]
- Tutty, O. Pulsatile Flow in a Constricted Channel. J. Biomech. Eng. 1992, 114, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Mucci, R. Compact, Low Cost Particle Image Velocimetry System for the In Vitro Analysis of Cardiovascular Flows. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2021. [Google Scholar]
- Katritsis, D.; Theodorakakos, A.; Pantos, I.; Andriotis, A.; Efstathopoulos, E.; Siontis, G.; Karcanias, N.; Redwood, S.; Gavaises, M. Vortex formation and recirculation zones in left anterior descending artery stenoses: Computational fluid dynamics analysis. Phys. Med. Biol. 2010, 55, 1395. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Ong, P.K.; Yalcin, O.; Intaglietta, M.; Johnson, P.C. The cell-free layer in microvascular blood flow. Biorheology 2009, 46, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Shakeri, M.; Khodarahmi, I.; Sharp, M.K.; Amini, A.A. Optical imaging of steady flow in a phantom model of iliac artery stenosis: Comparison of CFD simulations with PIV measurements. SPIE Med. Imaging 2010, 7626, 187–194. [Google Scholar]
- Gülan, U.; Lüthi, B.; Holzner, M.; Liberzon, A.; Tsinober, A.; Kinzelbach, W. Experimental study of aortic flow in the ascending aorta via particle tracking velocimetry. Exp. Fluids 2012, 53, 1469–1485. [Google Scholar] [CrossRef]
- Roloff, C.; Stucht, D.; Beuing, O.; Berg, P. Comparison of intracranial aneurysm flow quantification techniques: Standard PIV vs stereoscopic PIV vs tomographic PIV vs phase-contrast MRI vs CFD. J. Neurointerv. Surg. 2019, 11, 275–282. [Google Scholar] [CrossRef]
- Buchmann, N.; Atkinson, C.; Jeremy, M.; Soria, J. Tomographic particle image velocimetry investigation of the flow in a modeled human carotid artery bifurcation. Exp. Fluids 2011, 50, 1131–1151. [Google Scholar] [CrossRef]
- Wu, X.; Gürzing, S.; Schinkel, C.; Toussaint, M.; Perinajová, R.; van Ooij, P.; Kenjereš, S. Hemodynamic Study of a Patient-Specific Intracranial Aneurysm: Comparative Assessment of Tomographic PIV, Stereoscopic PIV, In Vivo MRI and Computational Fluid Dynamics. In Cardiovascular Engineering and Technology; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–15. [Google Scholar]
- Fouras, A.; Kitchen, M.J.; Dubsky, S.; Lewis, R.; Hooper, S.B.; Hourigan, K. The past, present, and future of x-ray technology for in vivo imaging of function and form. J. Appl. Phys. 2009, 105, 102009. [Google Scholar] [CrossRef]
- Brum, J.; Bernal, M.; Barrere, N.; Negreira, C.; Cabeza, C. Vortex dynamics and transport phenomena in stenotic aortic models using echo-PIV. Phys. Med. Biol. 2021, 66, 055026. [Google Scholar] [CrossRef]
- Walker, A.M.; Scott, J.; Rival, D.E.; Johnston, C.R. In vitro post-stenotic flow quantification and validation using echo particle image velocimetry (Echo PIV). Exp. Fluids 2014, 55, 1–16. [Google Scholar] [CrossRef]
- DeMarchi, N.; White, C. Echo particle image velocimetry. JoVE J. Vis. Exp. 2012, 70, 4265. [Google Scholar]
- Blyakhman, F.; Safronov, A.; Starodumov, I.; Kuznetsova, D.; Kurlyandskaya, G. Remote Positioning of Spherical Alginate Ferrogels in a Fluid Flow by a Magnetic Field: Experimental and Computer Simulation. Gels 2023, 9, 711. [Google Scholar] [CrossRef] [PubMed]
- Blyakhman, F.A.; Sokolov, S.Y.; Safronov, A.P.; Dinislamova, O.A.; Shklyar, T.F.; Zubarev, A.Y.; Kurlyandskaya, G.V. Ferrogels ultrasonography for biomedical applications. Sensors 2019, 19, 3959. [Google Scholar] [CrossRef]
- Rayleigh, L. VIII. On the question of the stability of the flow of fluids. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1892, 34, 59–70. [Google Scholar] [CrossRef]
- Boothroyd, R.G. Flowing Gas-Solids Suspensions. J. Fluid Mech. 1971, 53, 591–592. [Google Scholar]
- Klyachko, L. Equations of motion of dust particles in dust collectors. Otop. Vent. 1934, 4, 27–29. [Google Scholar]
- James, P.; Hewitt, G.; Whalley, P. Droplet Motion in Two-Phase Flow; Technical Report; Nuclear Regulatory Commission: Washington, DC, USA, 1980; pp. 1484–1503. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Aksenov, A.A. Flowvision: Industrial computational fluid dynamics. Comput. Res. Model. 2017, 9, 5–20. [Google Scholar] [CrossRef]
- Couture, O.; Hingot, V.; Heiles, B.; Muleki-Seya, P.; Tanter, M. Ultrasound localization microscopy and super-resolution: A state of the art. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1304–1320. [Google Scholar] [CrossRef]
- Demeulenaere, O.; Mateo, P.; Ferrera, R.; Chiaroni, P.M.; Bizé, A.; Dai, J.; Sambin, L.; Gallet, R.; Tanter, M.; Papadacci, C.; et al. Assessment of coronary microcirculation alterations in a porcine model of no-reflow using ultrasound localization microscopy: A proof of concept study. EBioMedicine 2023, 94, 104727. [Google Scholar] [CrossRef]
- Demeulenaere, O.; Sandoval, Z.; Mateo, P.; Dizeux, A.; Villemain, O.; Gallet, R.; Ghaleh, B.; Deffieux, T.; Deméné, C.; Tanter, M.; et al. Coronary flow assessment using 3-dimensional ultrafast ultrasound localization microscopy. Cardiovasc. Imaging 2022, 15, 1193–1208. [Google Scholar] [CrossRef] [PubMed]
- Renaudin, N.; Demené, C.; Dizeux, A.; Ialy-Radio, N.; Pezet, S.; Tanter, M. Functional ultrasound localization microscopy reveals brain-wide neurovascular activity on a microscopic scale. Nat. Methods 2022, 19, 1004–1012. [Google Scholar] [CrossRef] [PubMed]
- Chong, W.K.; Papadopoulou, V.; Dayton, P.A. Imaging with ultrasound contrast agents: Current status and future. Abdom. Radiol. 2018, 43, 762–772. [Google Scholar] [CrossRef] [PubMed]
- Frinking, P.; Segers, T.; Luan, Y.; Tranquart, F. Three decades of ultrasound contrast agents: A review of the past, present and future improvements. Ultrasound Med. Biol. 2020, 46, 892–908. [Google Scholar] [CrossRef]


| Term | Method |
|---|---|
| Wall type boundary condition | No-slip condition |
| Symmetry type boundary condition | Impermeability condition |
| Inlet type boundary condition | Condition with a defined velocity field at the boundary |
| Free outlet type boundary condition | Condition with a zero static pressure gradient |
| Parameter | Value | Unit |
|---|---|---|
| 1055 | kg/m | |
| 0.004 | Pa s | |
| d (Aluminum particles) | 20 | µm |
| d (Calcite particles) | 200 | µm |
| (Aluminum particles) | 2700 | kg/m |
| (Calcite particles) | 2710 | kg/m |
| (Aluminum particles) | 11.3 × 10 | kg |
| (Calcite particles) | 9.7 × 10 | kg |
| Mesh Size (k) | Mean Velocity Particles (m/s) | Vortex Area (m) |
|---|---|---|
| 117 | 0.00523 | 0.00016728 |
| 320 | 0.00542 | 0.0001616 |
| 414 | 0.00557 | 0.000162 |
| 850 | 0.00598 | 0.000162 |
| Parameter (m) | Aluminum Particles | Calcite Particles | Difference (%) |
|---|---|---|---|
| 0.0673 | 0.0679 | 0.88 | |
| 0.094 | 0.096 | 2.08 | |
| Length | 0.0267 | 0.0281 | 4.98 |
| 0.0038 | 0.00379 | 0.26 | |
| 0.00395 | 0.00389 | 1.51 | |
| 0.0020 | 0.0019 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starodumov, I.; Sokolov, S.; Makhaeva, K.; Mikushin, P.; Dinislamova, O.; Blyakhman, F. Obtaining Vortex Formation in Blood Flow by Particle Tracking: Echo-PV Methods and Computer Simulation. Inventions 2023, 8, 124. https://doi.org/10.3390/inventions8050124
Starodumov I, Sokolov S, Makhaeva K, Mikushin P, Dinislamova O, Blyakhman F. Obtaining Vortex Formation in Blood Flow by Particle Tracking: Echo-PV Methods and Computer Simulation. Inventions. 2023; 8(5):124. https://doi.org/10.3390/inventions8050124
Chicago/Turabian StyleStarodumov, Ilya, Sergey Sokolov, Ksenia Makhaeva, Pavel Mikushin, Olga Dinislamova, and Felix Blyakhman. 2023. "Obtaining Vortex Formation in Blood Flow by Particle Tracking: Echo-PV Methods and Computer Simulation" Inventions 8, no. 5: 124. https://doi.org/10.3390/inventions8050124
APA StyleStarodumov, I., Sokolov, S., Makhaeva, K., Mikushin, P., Dinislamova, O., & Blyakhman, F. (2023). Obtaining Vortex Formation in Blood Flow by Particle Tracking: Echo-PV Methods and Computer Simulation. Inventions, 8(5), 124. https://doi.org/10.3390/inventions8050124








