Improved General Correlation for Condensation in Channels
Abstract
:1. Introduction
2. Shah Correlation
3. Present Research
3.1. Superheated Vapor Condensation Heat Transfer Models
3.2. Development of Improved Shah Correlation
3.3. The Modified/Improved Shah Correlation
3.3.1. Determining Regimes
Vertical Downflow
Horizontal Channels
3.3.2. Choice of Equivalent Diameter for Non-Circular Channels
4. Data Analysis
| Source | Geometry (Aspect Ratio) # | Dhyd (DHP) * mm | Fluid (Glide, K) ** | pr | G kg·m−2s−1 | x | ReLT | WeGT | FrLT | N | Deviation, % Mean Absolute Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shah [1] | Present | |||||||||||
| Al-Zaidi et al. [27] | Multi, rect. (0.4) | 5.7 (6.66) | HFE 7100 | 0.0455 | 86 | 0.990 | 164 | 32 | 0.702 | 1 | 92.7 92.7 | 2.1 −2.1 |
| Agarwal and Hrnjak [17] | Round | 6.1 | R-134a | 0.1889 0.3243 | 100 300 | 1.0 | 3325 12882 | 221 1692 | 0.118 1.24 | 2 | 138.0 138.0 | 1.1 1.1 |
| R-32 | 0.3321 0.5414 | 100 | 1.0 | 5679 7315 | 186 201 | 0.189 0.237 | 3 | 192.7 192.7 | 33.9 −33.9 | |||
| R-1234ze | 0.1584 0.2733 | 100 200 | 0.994 1.0 | 3239 8227 | 199 794 | 0.127 0.579 | 5 | 125.8 125.8 | 15.3 −7.3 | |||
| Kondu and Hrnjak [13] | Round | 6.1 | CO2 | 0.8109 0.9460 | 100 | 1.0 | 9692 12500 | 300 1101 | 0.295 0.406 | 2 | 152.5 152.5 | 39.5 −39.5 |
| R-410A | 0.5489 0.9438 | 100 200 | 0.99 1.0 | 7890 13592 | 235 1269 | 0.215 0.745 | 6 | 78.0 66.4 | 19.8 −18.5 | |||
| Azzolin et al. [28] | Multi, rect. | 3.38 | HFE-7000 | 0.0593 | 70 | 0.99 | 642 | 130 | 0.081 | 1 | 63.2 –63.2 | 63.2 −63.2 |
| Baird et al. [29] | Round, single | 1.95 | R-123 | 0.0789 | 550 | 0.99 | 1789 | 1232 | 17.9 | 1 | 59.0 59.0 | 59.0 59.0 |
| Zhuang et al. [30] | Round, single | 4.0 | Methane | 0.6489 | 254 | 0.99 | 30720 | 3241 | 199.0 | 1 | 9.6 9.6 | 9.6 9.6 |
| Matkovic et al. [31] | Round, single | 0.96 | R-32 | 0.4271 | 600 | 0.99 | 6052 | 1050 | 479 | 1 | 7.5 −7.5 | 7.5 −7.5 |
| Koyama et al. [32] | Multi, rect. | 0.807 | R-134a | 0.4177 | 273 652 | 0.99 | 1791 4278 | 184 1052 | 8.5 48.6 | 2 | 13.6 13.6 | 13.6 13.6 |
| Azer et al. [33] | Round, single | 12.7 | R-12 | 0.2498 | 210 | 0.99 | 213578 | 1495 | 0.23 | 1 | 26.9 −26.9 | 26.9 −26.9 |
| Jung et al. [34] | Round, single | 8.82 | R-410A (0.05 to 0.430 | 0.4917 | 200 | 0.99 | 18304 | 1057 | 0.48 | 1 | 23.7 −23.7 | 23.7 −23/7 |
| All sources | 0.807 12.7 | 0.0455 0.9460 | 70 652 | 0.99 1.0 | 164 213578 | 32 1692 | 0.081 479 | 27 | 95.0 83.5 | 22.1 −13.1 | ||
5. Discussion
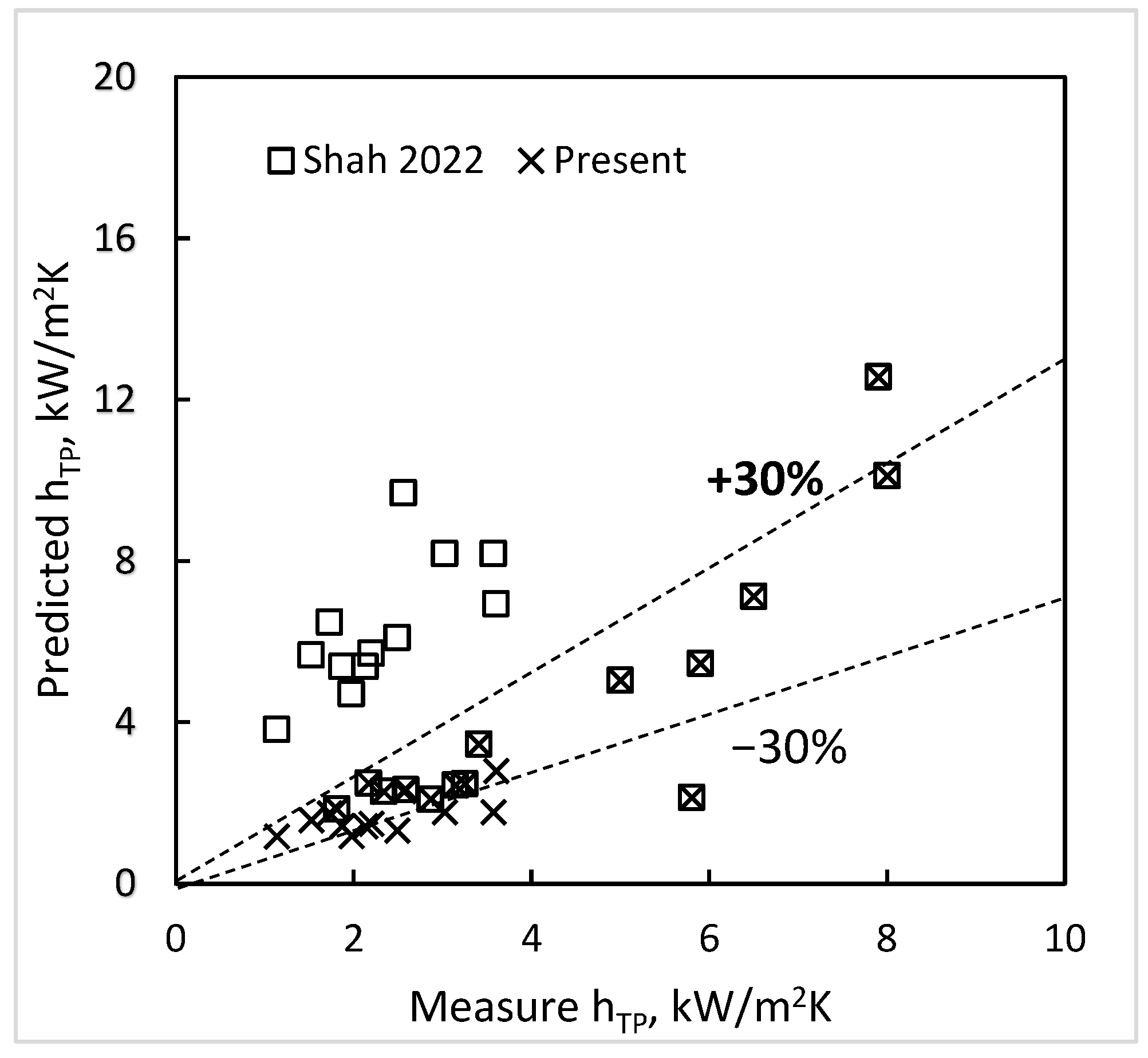
5.1. Data Showing Large Deviations
5.2. Effect of Weber Number
5.3. Data for All Qualities
5.4. Results for the Entire Database
6. Conclusions
- This improved accuracy is very important for the calculation of heat transfer during condensation of superheated vapors as widely used models for it require the heat transfer coefficient at x = 1.
- The present correlation has a MAD of 17.7% for the 8492 data points from 132 sources for horizontal and vertical channels. These include 51 fluids (water, refrigerants, chemicals, cryogens), diameters 0.08 to 49.0 mm, reduced pressures 0.0006 to 0.949, mass flux from 1.1 to 1400 kg·m−2s−1, various shapes (round, rectangular, triangular, etc.), single and multi-channels, and annuli.
- The MAD of other correlations was considerably higher. Their agreement was very poor for horizontal channels with WeGT < 100 (mini channel range) and for vertical channels.
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AD | Average deviation, (-) |
| CPG | Specific heat of vapor at constant pressure, J kg−1K−1 |
| D | inside diameter of tube, m |
| DHP | equivalent diameter based on perimeter with heat transfer, defined by Equation (21), m |
| DHYD | hydraulic equivalent diameter defined by Equation (22), m |
| FrLT | , (-) |
| G | total mass flux (liquid + vapor), kg m−2s−1 |
| g | acceleration due to gravity, m s−2 |
| h | heat transfer coefficient, W m−2 K−1 |
| hFC | forced convection singl-phase heat transfer coefficient of vapor, W m−2 K−1 |
| hI | heat transfer coefficient given by Equation (2), W m−2 K−1 |
| hGS | heat transfer coefficient assuming vapor phase flowing alone in the tube, W m−2 K−1 |
| hLS | heat transfer coefficient assuming liquid phase flowing alone in the tube, W m−2 K−1 |
| hLT | heat transfer coefficient with total mass flowing as liquid, W m−2 K−1 |
| hmix | heat transfer coefficient of mixture during condensation, W m−2 K−1 |
| hNu | heat transfer coefficient given by Eq.(3), the Nusselt equation, W m−2 K−1 |
| hSAT | Heat transfer coefficient of saturated vapor at x = 1, W m−2 K−1 |
| hTP | two-phase heat transfer coefficient, W m−2 K−1 |
| Jg | dimensionless vapor velocity defined by Equation (14) |
| k | thermal conductivity, W m−1 K−1 |
| MAD | Mean absolute deviation, (-) |
| N | number of data points, (-) |
| pr | reduced pressure, (-) |
| Pr | Prandtl number, (-) |
| q | Heat flux, Wm−2 |
| qlat | Heat flux due to phase change only, Wm−2 |
| ReGT | Reynolds number for all mass flowing as vapor = GDμG−1, (-) |
| ReLS | Reynolds number assuming liquid phase flowing alone, = G (1 − x)DμL−1, (-) |
| ReLT | Reynolds number for all mass flowing as liquid = GDμL−1, (-) |
| T | Temperature, K |
| TBP | Bubble point of mixture, K |
| TDP | Dew point of temperature, K |
| Tglide | (TDP − TBP), K |
| TSAT | saturation temperature, °C |
| Tw | wall temperature, °C |
| ΔT | = (TSAT − Tw), K |
| WeGT | Weber number for all mass flowing as vapor, defined by Equation (4), (-) |
| x | vapor quality, (-) |
| Z | Shah’s correlating parameter, =(1/x − 1)0.8 pr0.4, (-) |
| Greek | |
| μ | dynamic viscosity, Pa. s |
| ρ | density, kg m−3 |
| ∑ | Mathematical symbol for summation |
| σ | Surface tension, Nm−1 |
| Subscripts | |
| G | vapor |
| L | liquid |
References
- Shah, M.M. Improved correlation for heat transfer during condensation in mini and macrochannels. Int. J. Heat Mass Transf. 2022, 194, 123069. [Google Scholar] [CrossRef]
- Shah, M.M. A general correlation for heat transfer during film condensation inside pipes. Int. J. Heat Mass Transf. 1979, 22, 547–556. [Google Scholar] [CrossRef]
- Shah, M.M. An improved and extended general correlation for heat transfer during condensation in plain tubes. HVAC&R Res. 2009, 15, 889–913. [Google Scholar]
- Shah, M.M. General correlation for heat transfer during condensation in plain tubes: Further development and verification. ASHRAE Trans. 2013, 119, 3–11. [Google Scholar]
- McAdams, W.H. Heat Transmission, 3rd ed.; McGraw Hill: New York, NY, USA, 1954. [Google Scholar]
- Shah, M.M. A new flow pattern based general correlation for heat transfer during condensation in horizontal tubes. In Proceedings of the 15th International Heat Transfer Conference (IHTC-15), Kyoto, Japan, 10–15 August 2014. [Google Scholar]
- El Hajal, J.; Thome, J.R.; Cavallini, A. Condensation in horizontal tubes, part I: Two-phase flow pattern map. Int. J. Heat Mass Trans. 2003, 46, 3349–3363. [Google Scholar] [CrossRef]
- Shah, M.M. A new correlation for heat transfer during condensation in horizontal mini/micro channels. Int. J. Refrig. 2016, 64, 187–202. [Google Scholar] [CrossRef]
- Shah, M.M. Comprehensive correlations for heat transfer during condensation in conventional and mini/micro channels in all orientations. Int. J. Refrig. 2016, 67, 22–41. [Google Scholar] [CrossRef]
- Shah, M.M. Improved correlation for heat transfer during condensation in conventional and mini/micro channels. Int. J. Refrig. 2019, 98, 222–237. [Google Scholar] [CrossRef]
- Lee, C.C.; Teng, Y.J.; Lu, D.C. Investigation of condensation heat transfer of superheated R-22 vapor in a horizontal tube. In Experimental Heat Transfer, Fluid Mechanics, and Thermodynamics, Proceedings of the Second World Conference on Experimental Heat Transfer, Fluid Mechanics, and Thermodynamics, Dubrovnik, Yugoslavia, 23–28 June 1991; Keffer, J.F., Shah, R.K., Ganic, E.N., Eds.; Elsevier: New York, NY, USA, 1991; pp. 1051–1057. [Google Scholar]
- Gnielinski, V. New equation of heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 1976, 16, 359–367. [Google Scholar]
- Kondou, C.; Hrnjak, P.S. Condensation from superheated vapor flow of R744 and R410A at subcritical pressures in a horizontal smooth tube. Int. J. Heat Mass Transf. 2012, 55, 2779–2791. [Google Scholar] [CrossRef]
- Cavallini, A.; Del Col, D.; Doretti, L.; Matkovic, M.; Rossetto, L.; Zilio, C. Condensation in horizontal smooth tubes: A new heat transfer model for heat exchanger design. Heat Transf. Eng. 2006, 27, 31–38. [Google Scholar] [CrossRef]
- Petukhov, B.S. Heat transfer and friction in turbulent pipe flow with variable physical properties. Adv. Heat Transf. 1970, 6, 503–564. [Google Scholar]
- Agarwal, R.; Hrnjak, P.S. Effect of sensible heat, condensation in superheated and subcooled region incorporated in unified model for heat rejection in condensers in horizontal round smooth tubes. Appl. Therm. Eng. 2014, 71, 378–388. [Google Scholar] [CrossRef]
- Agarwal, R.; Hrnjak, P.S. Condensation in two phase and desuperheating zone for R1234ze(E), R134a and R32 in horizontal smooth tubes. Int. J. Refrig. 2015, 50, 172–183. [Google Scholar] [CrossRef]
- Webb, R.L. Convective condensation of superheated vapor. ASME J. Heat Transf. 1998, 120, 418–421. [Google Scholar] [CrossRef]
- Longo, G.A.; Righetti, G.; Claudio Zilio, C. A new computational procedure for refrigerant condensation inside herringbone-type Brazed Plate Heat Exchangers. Int. J. Heat Mass Transf. 2015, 82, 530–536. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, L.; McLinden, M.O. NIST Reference Fluid Thermodynamic and Transport Properties; REFPROP Version 9.1; NIST: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Bell, K.; Ghaly, M. An approximate generalized design method for multicomponent/partial condenser. Am. Inst. Chem. Eng. Symp. Ser. 1973, 69, 72–79. [Google Scholar]
- Kim, S.; Mudawar, I. Universal approach to predicting heat transfer coefficient for condensing mini/micro-channel flow. Int. J. Heat Mass Transf. 2013, 56, 238–250. [Google Scholar] [CrossRef]
- Dorao, C.A.; Fernandino, M. Simple and general correlation for heat trans- fer during flow condensation inside plain pipes. Int. J. Heat Mass Transf. 2018, 122, 290–305. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Moradkhani, M.A.; Valizadeh, M.; Zendehboudi, A.; Olazar, M. A general heat transfer correlation for flow condensation in single port mini and macro channels using genetic programming. Int. J. Refrig. 2020, 119, 376–389. [Google Scholar] [CrossRef]
- Moradkhani, M.A.; Hosseini, S.H.; Song, M. Robust and general predictive models for condensation heat transfer inside conventional and mini/micro channel heat exchangers. Appl. Therm. Eng. 2022, 201, 117737. [Google Scholar] [CrossRef]
- Ananiev, E.P.; Boyko, I.D.; Kruzhilin, G.N. Heat transfer in the presence of steam condensation in horizontal tubes. Int. Dev. Heat Transf. 1961, 2, 290–295. [Google Scholar]
- Al-Zaidi, A.H.; Mahmoud, M.M.; Karayiannis, T.G. Condensation flow patterns and heat transfer in horizontal microchannels. Exp. Therm. Fluid Sci. 2018, 90, 153–173. [Google Scholar] [CrossRef]
- Azzolin, M.; Bortolina, S.; Nguyen, L.P.L.; Lavieilleb, P.; Glushchuk, A.; Queeckers, P.; Miscevic, M.; Iorioc, C.S.; Del Col, D. Experimental investigation of in-tube condensation in microgravity. Int. Commun. Heat Mass Transf. 2018, 96, 69–79. [Google Scholar] [CrossRef]
- Baird, J.R.; Fletcher, D.F.; Haynes, B.S. Local condensation heat transfer rates in fine passages. Int. J. Heat Mass Transf. 2003, 46, 4453–4466. [Google Scholar] [CrossRef]
- Zhuang, X.R.; Chen, G.F.; Zou, X.; Song, Q.L.; Gong, M.Q. Experimental investigation on flow condensation of methane in a horizontal smooth tube. Int. J. Refrig. 2017, 78, 193–214. [Google Scholar] [CrossRef]
- Matkovic, M.; Cavallini, A.; Bortolin, S.; Del Col, D.; Rossetto, L. Heat transfer coefficient during condensation of a high pressure refrigerant inside a circular minichannel. In Proceedings of the 5th European Thermal-Sciences Conference, Eindhoven, The Netherland, 18–22 May 2008. [Google Scholar]
- Koyama, S.; Kuwahara, K.; Nakashita, K. Condensation of refrigerant in a multi-port channel. In Proceedings of the ASME 2003 1st International Conference on Microchannels and Minichannels, Rochester, NY, USA, 24–25 April 2003; pp. 193–205. [Google Scholar]
- Azer, N.Z.; Abis, L.V.; Soliman, H.M. Local heat transfer coefficients during annular flow con densation. ASHRAE Trans. 1972, 78, 135–143. [Google Scholar]
- Jung, D.; Cho, Y.; Park, K. Flow condensation heat transfer coefficients of R22, R134a, R407C, and R410A inside plain and microfin tubes. Int. J. Refrig. 2004, 27, 25–32. [Google Scholar] [CrossRef]
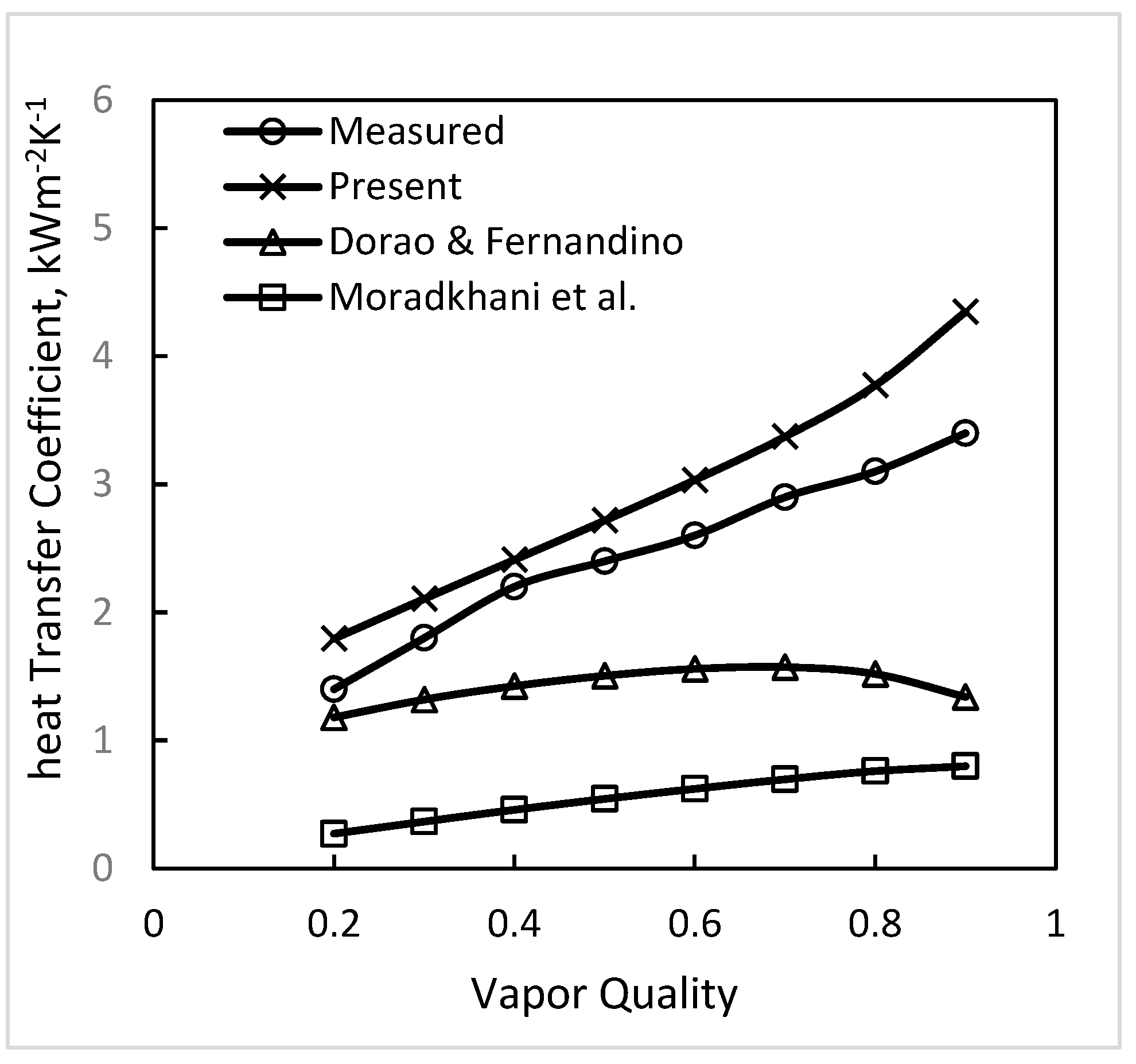
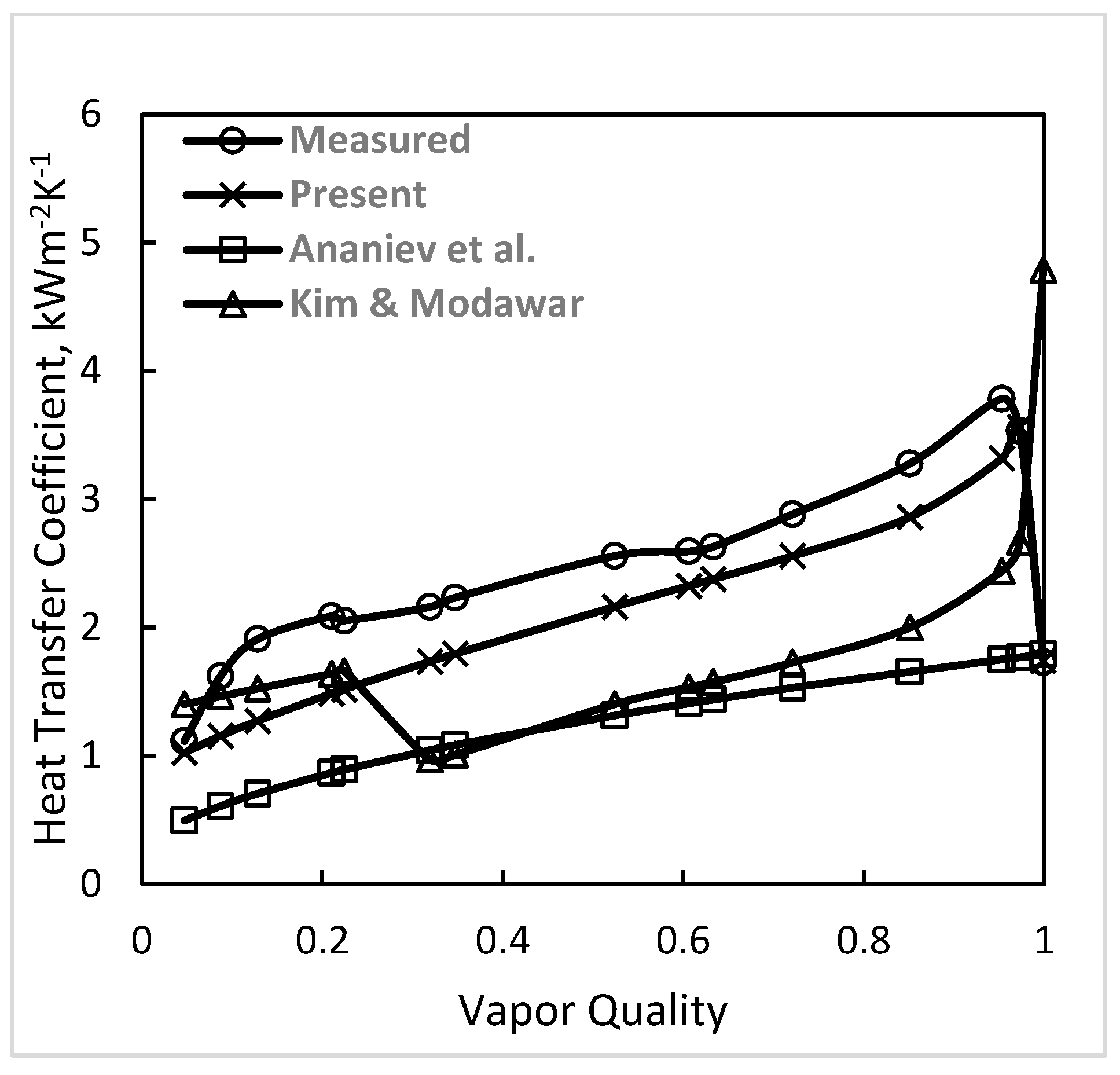
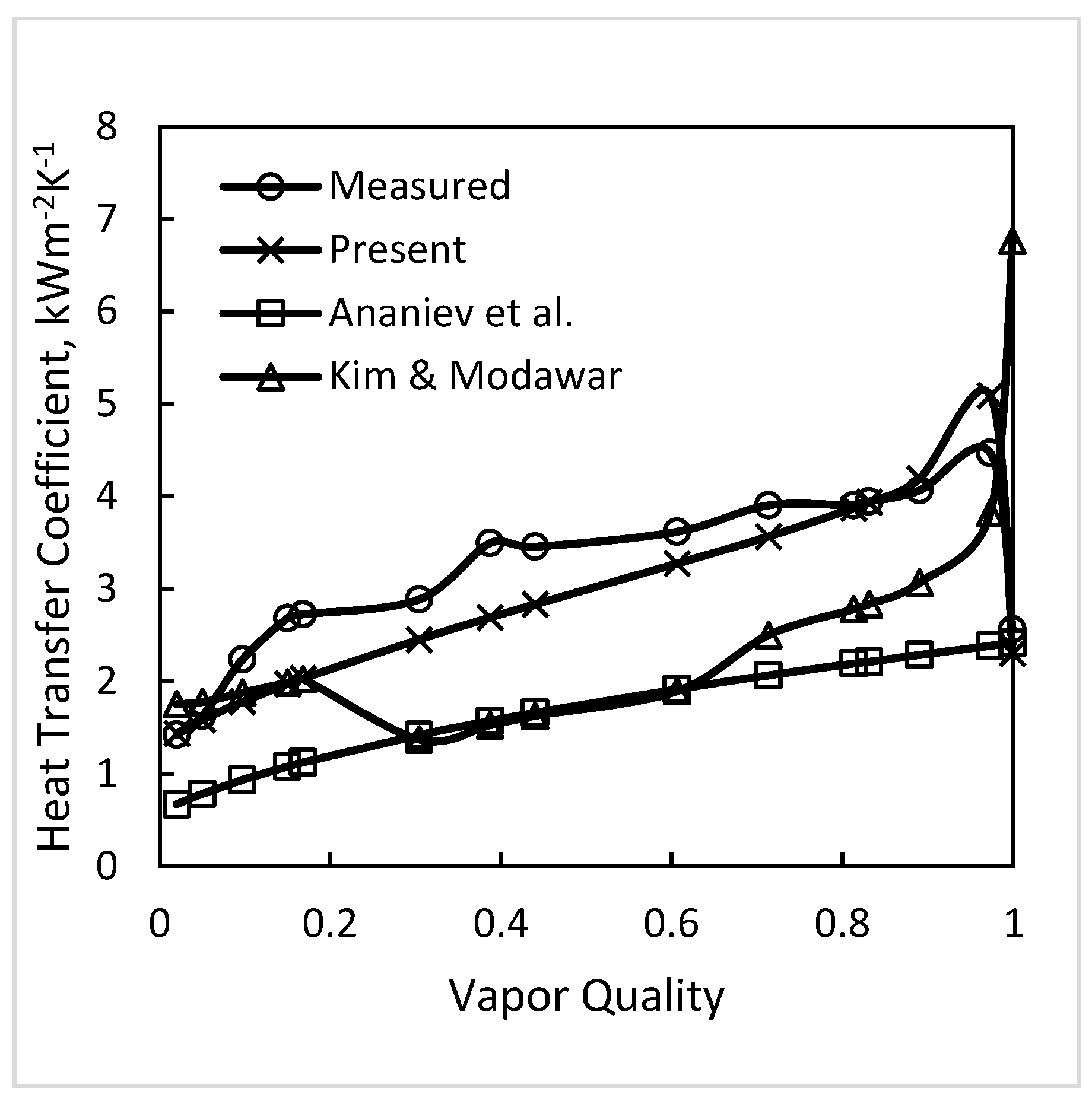

| Source | D mm | Fluid | pr | G kg·m−2s−1 | N | Shah [1] | Present | Kim and Mudawar [22] | Ananiev et al. [26] | Dorao and Fernandino [23] | Hosseini et al. [24] | Moradkhani et al. [25] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Agarwak and Hrnjak [17] | 6.1 | R-134a | 0.1889 0.3234 | 100 300 | 26 | 24.0 3.4 | 13.4 −7.1 | 37.9 −11.3 | 35.0 −34.7 | 20.3 −14.2 | 23.6 22.9 | 23.2 −10.6 |
| R-32 | 0.3321 | 100 | 29 | 31.0 15.9 | 14.6 −7.5 | 41.4 −5.7 | 45.7 −45.7 | 20.9 −10.1 | 26.0 25.5 | 23.7 −19.4 | ||
| R-1234ze | 0.1584 0.2733 | 100 200 | 39 | 29.0 6.1 | 14.9 −11.0 | 40.7 −7.3 | 38.9 −38.0 | 20.2 −17.2 | 22.3 22.3 | 23.4 −15.9 | ||
| Kondou and Hrnjak [13] | 6.1 | CO2 | 0.6756 0.9460 | 100 | 40 | 18.5 6.8 | 12.8 −2.8 | 36.8 −23.2 | 27.2 −27.2 | 20.0 12.2 | 39.8 38.7 | 29.3 −29.3 |
| R-410A | 0.5489 0.9438 | 100 200 | 60 | 23.1 14.2 | 17.2 5.7 | 36.6 −5.1 | 31.7 −19.1 | 27.0 18.1 | 20.3 20.3 | 13.5 4.4 | ||
| All sources | 6.1 | 0.1584 0.9468 | 100 300 | 194 | 24.6 9.9 | 14.9 −3.1 | 39.1 −10.7 | 34.8 −30.6 | 22.4 1.2 | 26.0 −21.5 | 21.6 −12.2 |
| Orientation | WeGt | N | Deviation, % Mean Absolute Average | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Present | Shah [1] | Kim and Mudawar [22] | Ananiev et al. [26] | Dorao and Fernandino [23] | Hosseini et al. [24] | Moradkhani et al. [25] | |||
| Horizontal | <100 | 1044 | 21.8 −0.1 | 21.9 0.0 | 38.3 −12.2 | 45.2 −42.5 | 35.9 −27.2 | 42.0 −22.6 | 30.9 −20.9 |
| >100 | 6639 | 17.1 −0.2 | 17.4 0.2 | 24.7 −17.3 | 22.6 −11.9 | 18.9 −1.1 | 26.3 1.5 | 18.8 −3.2 | |
| All | 7683 | 17.8 −0.2 | 18.0 0.2 | 26.6 −16.6 | 25.7 −15.1 | 21.2 −4.7 | 28.4 −1.8 | 20.2 −6.3 | |
| Vertical | All | 810 | 17.4 −0.7 | 17.4 −0.7 | 34.7 6.6 | 32.1 −8.3 | 28.6 1.2 | 37.9 −5.0 | 27.2 3.4 |
| Horizontal and VerticaL | All | 8492 | 17.7 −0.2 | 18.0 0.1 | 27.3 −14.4 | 26.3 −15.3 | 21.9 −4.1 | 29.3 −1.1 | 20.9 −5.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, M.M. Improved General Correlation for Condensation in Channels. Inventions 2022, 7, 114. https://doi.org/10.3390/inventions7040114
Shah MM. Improved General Correlation for Condensation in Channels. Inventions. 2022; 7(4):114. https://doi.org/10.3390/inventions7040114
Chicago/Turabian StyleShah, Mirza M. 2022. "Improved General Correlation for Condensation in Channels" Inventions 7, no. 4: 114. https://doi.org/10.3390/inventions7040114
APA StyleShah, M. M. (2022). Improved General Correlation for Condensation in Channels. Inventions, 7(4), 114. https://doi.org/10.3390/inventions7040114




