Abstract
In this paper, a new fractional-order chaotic system containing several nonlinearity terms is introduced. This new system can excite hidden chaotic attractors or self-excited chaotic attractors depending on the chosen system parameters or its fraction-order derivative value. Several dynamics of this new system, such as chaotic attractors, equilibrium points, Lyapunov exponents, and bifurcation diagrams, are analyzed analytically and numerically. Then, adaptive control laws are developed to achieve chaos synchronization in two identical new systems with uncertain parameters; one of these two new identical systems is the master, and the other is the slave. In addition, update laws for estimating the uncertain slave parameters are derived. Furthermore, in chaos application fields, these master and slave synchronized systems are applied in secure communication to act as the transmitter and receiver, respectively. Finally, the security analysis metric tests were analyzed using histograms and spectrograms to establish the communication system’s security strength. Numerical test results demonstrate the possibility of using this proposed fractional-order chaotic system in high-security communication systems. The employed communication system is also highly resistant to pirate attacks.
1. Introduction
In 1892, Henri Poincaré introduced the first understanding of the chaos possibility [1]. Nonlinear phenomena in chaos have been used extensively in engineering, science, and applied mathematics over the past few decades [2]. Chaos occurs when a deterministic system exhibits the strange phenomenon of aperiodic trajectories. When the initial conditions and system parameters have a strong influence on chaotic systems, chaotic system sensitivity is introduced; however, even minor changes in the initial conditions can have a significant impact on the final result [3]. As result, the chaotic system is considered a complex system.
Recent research has concentrated on chaotic systems with hidden attractors. Since the seminal paper by Leonov et al., attractors in dynamical systems have been classified as self-excited attractors and hidden attractors [4]. A basin of attraction is associated with an unstable equilibrium of a self-excited attractor. On the other hand, an attractor is said to be hidden if its basin of attraction does not intersect with any of the unstable equilibrium’s small neighborhoods [5]. Chaotic attractors in dynamical systems with no equilibrium, surfaces or lines of equilibria, and stable equilibria are also classified as latent attractors [6].
Chaotic complex systems with hidden attractors are very important in many application fields of science and engineering, such as induction motors for drilling [7], bridge wing design [8], chemical reactor systems [9], aircraft control systems [10], encryption [11], PLL systems [12], weather prediction systems [13], memristive circuits [14], and secure communication schemes [15].
The fractional-order derivative and fractional-order integration calculus have recently gained popularity because fractional calculus offers more accurate models than integer-order calculus [16]. The fractional-order chaotic models exhibit more complex dynamical behavior than their integer analogs and thus play an important role in the fields of secure communication applications and high-level cryptography [17]. Moreover, because the fractional-order derivative value (q) of the system can be changed in the (0, 1] range, that gives an additional system parameter as well as the original system parameters [18].
Through the development and applications of chaos theory, many fractional-order chaotic systems have been introduced, such as the fractional-order Lorenz system [19], fractional-order Rössler system [20], fractional-order Chen system [21], fractional-order Liu chaotic system [22], fractional-order financial systems [23], fractional-order Lotka–Volterra system [24], and various other systems [25]. In the past few decades, the control and synchronization of chaotic systems have attracted much attention, and chaos synchronization presents the major issue of applying chaotic systems to secure communication systems and encryption systems [26]. Various control and synchronization techniques for chaotic systems have been developed in recent years such as sliding mode control [27], adaptive control [28], the active control method based on parameter identification [29], passive control [30], impulsive control [31], and so on as in [32]. In the secure communication application field, synchronization is achieved between two chaotic systems; the first one is a master, and the second response one is a slave, where the master presents the transmitter side, and the slave acts as the receiver side [33]. The researchers employed many fractional-order chaotic systems, and they were used in secure communication and encryption [34].
In this work, a new three-dimensional fractional-order chaotic system is proposed. The proposed system displays more complex dynamic properties than an analog integer chaotic system, which can be considered the main reason for using these systems in the design of high-security communication and encryption systems [35]. In addition, the proposed system does not contain complex functions such as the hyperbolic tangent function. Thus, it can be implemented simply using an electronic circuit. The system dynamics, such as system equilibria, chaotic attractors, bifurcation diagrams, and Lyapunov exponents, are studied analytically and numerically. Because the new system is being used in a secure communication system, an adaptive synchronization mechanism is established between two identical new systems, one of which is acting as the master (transmitter) and the other as the slave (receiver). In the adaptive synchronization process, the master adaptive control laws that will drive the slave were derived based on Lyapunov theory. Consequently, the update laws that are responsible for estimating the uncertain slave parameter correspond to the equivalent master parameters. Our work, tests, and results were verified by using the MATLAB platform. Several chaotic-based safe communication schemes have been implemented in recent years. The main approaches for utilizing chaotic signals in secure communications are chaotic masking, inclusion, chaotic shift keying, and parameter modulation. The chaotic-masking approach has the benefit of being simple and straightforward to use in electronic circuits [36]. Therefore, this technique has been employed in our work.
The rest of this paper’s organization is as follows: The fundamentals of fractional-order calculus are introduced in Section 1. In Section 2, the new fractional-order chaotic system is presented, and its chaotic attracter’s classes are determined; in addition, the system equilibria and corresponding eigenvalues are investigated in this section. The system dynamics, including Lyapunov exponents, and a bifurcation diagram are considered in Section 3. In Section 4, we establish the synchronization strategy between two identical new systems, where the adaptive control laws and the update laws are derived based on Lyapunov stability. In Section 5, the achieved synchronization is applied to the construction of the secure communication scheme, where the master and slave perform the role of transmitter and receiver, respectively. In Section 7, histograms and spectrograms are examined to demonstrate the security analysis of the communication strategy in use. Finally, the conclusions are presented in Section 8.
2. Fractional Calculus Fundamentals
Fractional calculus is a mathematical extension of integer-order calculus [37]. While it incorporates the benefits of integer-order calculus, it has its own logic and laws as well. The Riemann–Liouville (RL), Caputo, and Grünwald–Letnikov (GL) concepts are generally used in the definitions of fractional calculus [38]. In 1832, Liouville introduced the first study on FOC, and in 1867, Grünwald presented his work on the fractional-order system. In the year 1892, Riemann completed the theoretical analysis and development of the fractional-order system [39]. The basic function used in fractional-order calculus known as the Gamma function is noted by the following, which is defined as in [40]:
where .
The fractional integral operator (Jq) introduced by Riemann–Liouville for order (q ≥ 0) of function (f(t)) is given by [41].
The fractional-order calculus form by Caputo is expressed as follows (3) [42]:
where m is the first integer number more than q-order.
Grünwald–Letnikov approximates the fractional derivative as described below in Equation (4) [43]:
where h is the step size.
3. New 3D Fractional-Order Chaotic System
Fractional-order chaotic systems are a special form of nonlinear chaotic systems; in addition, this form of a system has the basic characteristics of an integer-order chaotic system, and it also has other characteristics such as extra complexity and comfortable behavior [44]. Despite the fact that many novel chaotic systems have been presented in recent years, developing, discovering, and analyzing new chaotic systems is still beneficial to the subject of chaos in theoretical and practical fields. This fact is stated in numerous specialized papers, some of which are cited in this article’s sources [45,46,47,48]. The proposed new three-dimensional fractional-order chaotic system with two quadratic nonlinearity terms is described by the fractional-order dynamics in Equation (5).
In system (5), the system state variables are symbolized by x, y, and z, while a, b, c, and d are symbolized for the system parameters, whereas the q symbol represents the fraction-order derivative value. The system parameters have the main effects on the system behaviors, where these parameters can be constant and/or integer parameters [49,50,51]. The equilibria (equilibrium points) of this system can be obtained by equalizing the system Equations to zero as in the following Equation.
If the parameter a of this system is considered to be 1 (a = 1), then the equilibrium points of the system (5) are computed to be as below.
It is clear that there are two cases for the solutions of Equation (6) that are determined by the selected parameter values of the parameters b and c.
3.1. Case1: Hidden Attractors
Regarding the equilibrium points obtained by Equation (7), if (b/c) ≥ 1, that yields two sets of solutions as in the following: If b > c that results in x2 = , so x = ±i (imaginary value), so there are no equilibrium points. On the other hand, if b = c or/and c = 0, that leads to a contradiction in the solution of Equation (7); in other words, there are no solutions for Equation (7), so, there are no equilibrium points in the system (5) in this situation also. As a result of that, the suggested system (5) can excite hidden chaotic attractors in this case.
The proposed system parameters are chosen as a = 1, b = 0.05, and c = 0.05, and the fractional-order derivative value (q = 0.98) with the initial condition of (x0, y0, z0) = (0.1, 0.1, 0.1) and the corresponding hidden attractor projections are shown in Figure 1. The simulation results were obtained for a time of 500 s with a step size of h = 0.005 using the Roberto Garrappa method of solving fractional-order nonlinear systems [52].
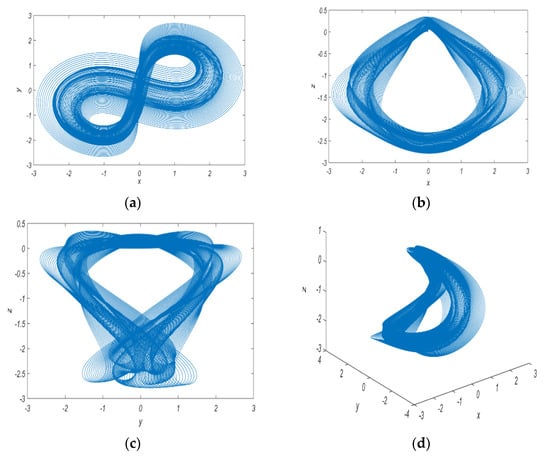
Figure 1.
Phase portraits of the hidden chaotic attractors obtained from the system (5): (a) x-y projection; (b) x-z projection; (c) y-z projection; (d) x-y-z 3D arrangement.
3.2. Case2: Self-Excited Attractor
When (b/c) < 1, the fractional chaotic system (3) has two equilibrium points.
The corresponding Jacobian matrix of the fixed points is obtained as follows.
The eigenvalues for the Jacobian matrix can be calculated using the following Equation (9) to assess the stability of the equilibrium points.
If our proposed system parameters are selected as a = 1, b = 0.05, and c = 0.1, that causes the equilibrium points to be E1,2 = (±√2, ±10√2, −20) and the corresponding eigenvalues as λ1,2,3 = (13.7781, 0.3903, −0.0263). As a result, the equilibrium points are unstable foci. When the used fractional-order derivative value is (q = 0.98) and the initial conditions are (x0, y0, z0) = (0.1, 0.1, 0.1), the corresponding self-excited attractor projections are shown in Figure 2.
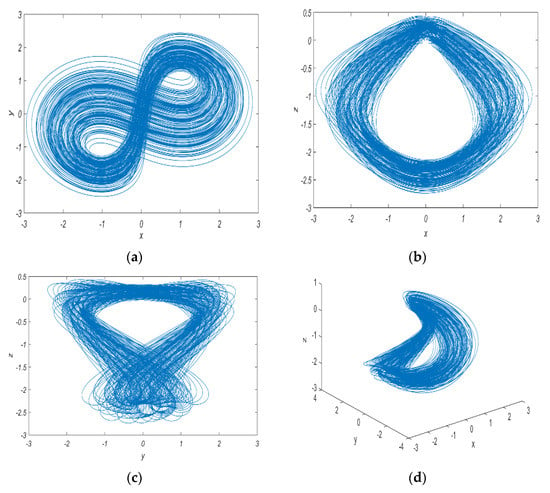
Figure 2.
Phase portraits of the self-excited chaotic attractors obtained from the system (5): (a) x-y projection; (b) x-z projection; (c) y-z projection; (d) x-y-z 3D arrangement.
4. Dynamical Behavior of New System
In this section, the system is analyzed based on Lyapunov exponents and bifurcation diagrams, where MATLAB is used to numerically explore the bifurcation diagrams and the Lyapunov exponents.
4.1. Lyapunov Exponents
In order to have an improved observation of the hidden chaotic attractor, the Lyapunov exponents were determined. The Lyapunov exponents were calculated with respect to time and to fractional-order derivative value (q) as shown in Figure 3. It can be seen from Figure 3a that the new system excites a hidden chaotic attractor without any equilibrium point because there is a positive Lyapunov exponent. The system parameters are selected as a = 1, b = 0.05, and c = 0.05, and the fractional-order derivative value is (q = 0.98) with the initial conditions as (x0, y0, z0) = (0.1, 0.1, 0.1), and then the corresponding obtained Lyapunov exponents are Le1 = 0.2643, Le2 = −0.1223, and Le3 = −0.2372. In Figure 3b, the same above-mentioned parameters of Figure 3a are used, except that the fractional-order derivative value is changing as q ∈ [0.8, 1]. The corresponding calculated Lyapunov exponents are Le1 = 0.0203, Le2 = −0.0049, and Le3 = −0.0007, which indicates that the system can excite a hidden attractor without any equilibria because a positive Lyapunov exponent is verified [53]. The Lyapunov exponents are explored according to [54].
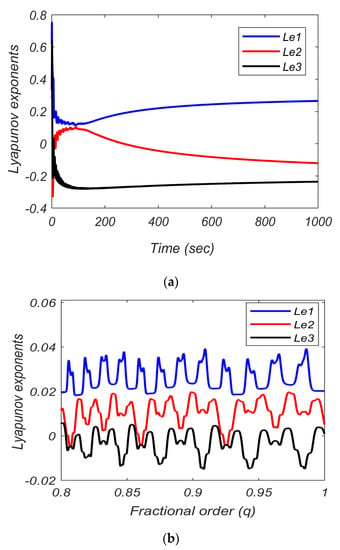
Figure 3.
Lyapunov exponents: (a) with respect to time; (b) with respect to changing fractional-order derivative value (q).
4.2. Bifurcation Diagrams
Finally, the bifurcation diagrams were numerically determined to further demonstrate that the new system exhibits chaotic behavior. The bifurcation diagrams were determined with respect to the fractional-order derivative value (q) and the system parameters (a, b, and c), where these diagrams were obtained by plotting the local maximum of state variable z(t) with the varying fractional-order derivative value (q) and the system parameters (a, b, and c). Figure 4 presents the bifurcation diagram with the selected initial conditions as (x0, y0, z0) = (0.1, 0.1, 0.1). From Figure 4a, it can be noted that the system excites a hidden chaotic attractor as the fractional-order derivative value changes as q ∈ [0.8, 1]. Further, other classes of chaotic attracter are excited when q = 0.98 and the system parameters were changed as in Figure 4b–d.
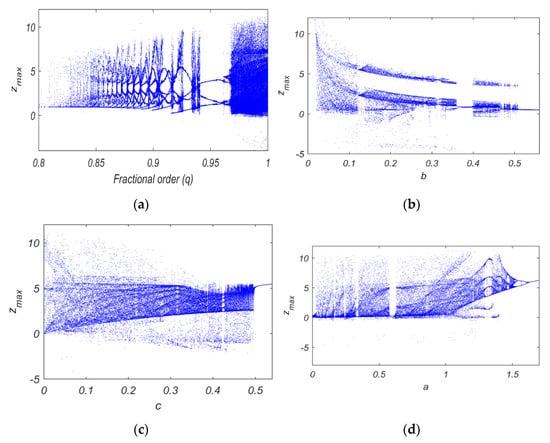
Figure 4.
The bifurcation diagram of the new system: (a) Zmax versus a for b = 0.4, c = 0.4, and q = 0.98; (b) Zmax versus b for a = 1, c = 0.4, and q = 0.98; (c) Zmax versus c for a = 1, b = 0.4, and q = 0.98; (d) Zmax versus fractional-order derivative value (q) with a = 1, b = 0.4, and c = 0.4.
5. Synchronization Strategy
The synchronization of two new fractional-order chaotic systems that are identical to one another is investigated in this section. So that the slave (response system) and master system (drive system) trajectories asymptotically match and confirm synchronization, a synchronization mechanism is explored. Chaos synchronization is commonly used in secure communication applications. Due to chaos’ unique properties, such as time-based complexity, extreme initial conditions sensitivity, and unpredictable chaos behavior, it is a particularly secure approach to hiding information in a chaotic signal, resulting in a transmission of a secure encrypted signal. On the other hand, by employing the chaotic synchronization technique at the receiver end, the original information signal can be retrieved.
With the growth of research, many control and synchronization mechanisms have been proposed in the chaos field and especially their applications in secure communication schemes [55]. In this work, an adaptive synchronization technique is developed to synchronize two identical new systems; one acts as the drive system (the master or transmitter side), and the other acts as the response system (the slave or receiver side). The design of the synchronization controller is developed based on Lyapunov theory, then the uncertain parameters on the slave side are estimated with derived updating laws to reach the master corresponding parameters. This is responsible for achieving synchronization and reducing synchronization error as much as possible to be zero in a very short time. In addition, the response system and drive system can have different sets of initial conditions. As a result, the two identical new systems can reach a perfect synchronization between their state variables and sustain it.
5.1. Fast Adaptive Controller Design
In this subsection, a controller for the synchronization of two identical new systems based on the Lyapunov method is developed, considering the consistent slave–master systems stated in Equations (10) and (11), respectively.
In Equation (11), u1, u2, and u3 present the adaptive synchronization controllers that need to be designed, and bs(t) and cs(t) are the uncertain slave system parameters that must be estimated. The master–slave synchronization errors are defined as:
Therefore, the dynamic errors are determined as in Equations (13)–(15)
where eb and ec are the master–slave parameter estimation errors as in Equations (16) and (17), respectively.
Therefore, the dynamics of the parameter estimation error can be calculated by:
To determine stable update laws for estimating the uncertain slave parameter, the Lyapunov method is used [56]. Selecting the quadratic positive definite Lyapunov function as:
it follows that:
Then, substituting Equations (13)–(18) in Equation (20) yields:
Now, the synchronization controller functions have been selected as:
where, kx, ky, and kz are positive constants. In Equation (22), the uncertain slave parameters are estimated by the following update laws:
Finally, by substituting Equations (22) and (23) in Equation (21), we obtain:
As noted in Equation (24), it is a negative definite function based on Lyapunov theory. Thus, based on Lyapunov stability [57], this ensures that the synchronization state errors and the master–slave parameter estimation error converge to zero exponentially with respect to time for any initial conditions.
5.2. Numerical Simulation Results
In this section, computer simulations are achieved to prove the efficacy of the introduced synchronization technique. These numerical simulations are performed using the MATLAB platform. In the simulation, the parameters of the systems in Equations (10) and (11) are chosen as bm = 0.4, cm = 0.4, bs(t) is uncertain, cs(t) is uncertain, and the fractional-order derivative value q = 0.9 with the initial conditions for the master and slave being (xm(0), ym(0), zm(0)) = (0.1, 0.1, 0.1) and (xs(0), ys(0), zs(0)) = (−1, 1, −0.5), respectively.
The obtained synchronized states are shown in Figure 5. Figure 6 confirms that the synchronization errors ex, ey, and ez converge to zero quickly with time (in less than 0.3 s). In addition, the accurate estimation of the uncertain slave parameters with the update laws in Equation (23) is demonstrated in Figure 7. From Figure 7, it is clear that the uncertain slave parameters bs(t) and cs(t) are estimated correctly corresponding to the master parameters bm = 0.4 and cm = 0.4, respectively. The estimation process is verified rapidly with time.
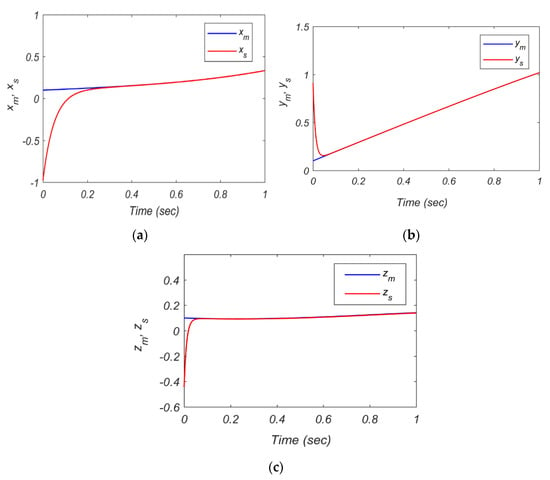
Figure 5.
State variable synchronization of systems (10) and (11): (a) xm-xs; (b) ym-ys; (c) zm-zs.
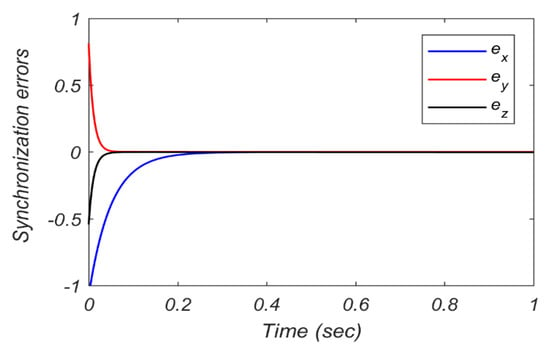
Figure 6.
Synchronization error evolution ex, ey, and ez.
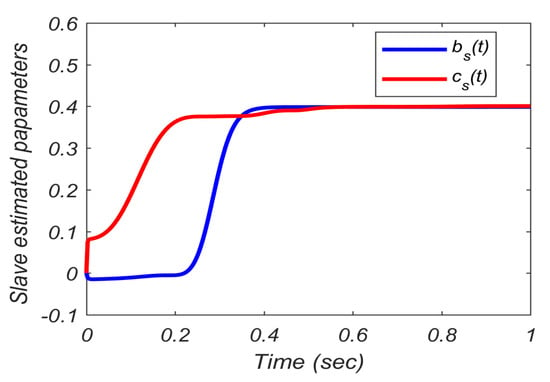
Figure 7.
Slave parameter estimation bs and cs.
6. Chaos-Based Secure Communication System
Fractional-order chaotic systems may provide more efficient secure communication when compared with traditional chaotic systems; this is because the derivative order(s) can be observed as additional system parameter(s) as well as the basic system parameter(s). Synchronization in chaotic systems has potential applications in the secure communication fields and control processing. The aforementioned introduced adaptive synchronization technique is used in secure communication arrangements. Many chaotic systems have been developed and used in a secure communication system based on different synchronization techniques as in [58,59,60,61,62]. Based on the developed adaptive synchronization technique between the two identical new fractional-order systems (10) and (11), the secure communication scheme is demonstrated by the block diagram as shown in Figure 8. In Figure 8, the main two parts of the used secure communication system are the transmitter (which presents the master or drive system) and the receiver (which presents the slave or response system).
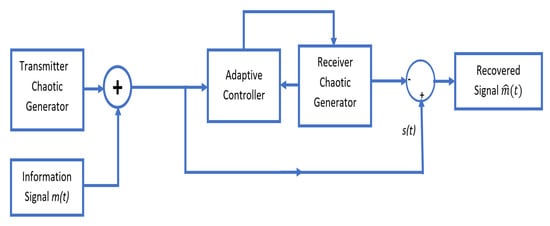
Figure 8.
Block diagram of secure-communication-system-based chaotic masking.
Many techniques, including chaotic shift keying, chaotic masking, inclusion, and parameter modulation, have been used to implement secure communication based on chaos. The most popular technique is the chaotic-masking technique, and this technique has been employed in our work.
The chaotic-masking method applied to the transmitter adds the information signal to the chaotic generator state output to produce an encrypted signal that is transmitted to the receiver [63]. To hide the information signal and achieve synchronization at the receiver, the information signal needs to be 20 to 30 dB less than the chaotic generator output signal. As a result, in order to recover the original information signal at the receiver, the matching regenerated chaotic signal is subtracted. At the transmitter side, the information signal m(t) is added to the chaotic output state signal (ym), as in the following Equation:
where s(t) denotes the acquired masked signal that will be sent to the receiver. Thus, by subtracting the output chaotic state signal (ys) from the encrypted signal as in Equation (26), the original information signal can be recovered. The information signal in the numerical simulation is given by Equation (27) as below.
In this Equation (26), the information signal is sinusoidal with amplitude A and frequency w (rad/sec). The obtained numerical simulation results of our chaos-based secure communication system are shown in Figure 9, where the parameters are selected as am = as = 1, bm = 4, and cm = 0.4, and bs and cs are estimated to correspond to the matched bm and cm, respectively, while q = 0.98 and the initial conditions are (0.1, 0.1, 0.1) and (1, 0, −0.5) for the transmitter and receiver, respectively. According to Equation (27), one can retrieve the original information signal m(t) as below.
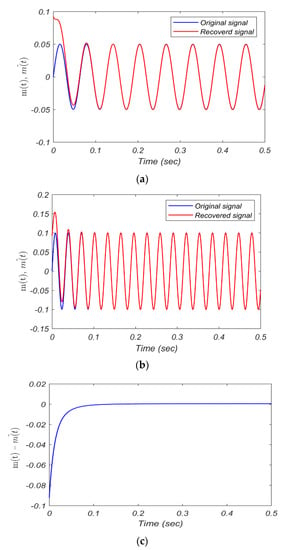
Figure 9.
The secure communication signals: (a) the original signal and recovered signal with A = 0.05 and w = 100 rad/s; (b) the original signal and recovered signal with A = 0.1 and w = 200 rad/s; (c) the error difference between the original and retrieved signal.
7. Communication System’s Security Analysis
The secure communication system is well-renowned for its resistance to pirate attacks. To illustrate the high-security performance of the applied communication system in resisting pirate attacks, histograms and spectrograms were used in this study, because the presence of noise makes identifying a signal more challenging. As a result, the applicable communication system’s security was studied, where the original signal with A = 0.05 and w = 100 rad/s was tested.
7.1. Histogram Analysis
A signal’s histogram is a graph that shows how signal intensity levels are distributed. The statistical analysis of the original data and the encrypted versions can both be evaluated using histogram analysis [64]. Because the original information signal is a sine-wave signal, it has significant intensities on the sine-wave peaks. The histogram of an encrypted signal, on the other hand, shows a wide range of intensity levels. An encrypted signal’s histogram should differ from the original signal’s histogram both statistically and visually. The original information signal, encrypted signal, and recovered signal histograms are depicted in Figure 10.
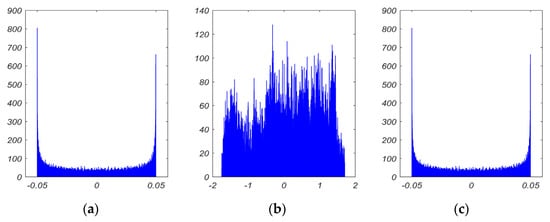
Figure 10.
Histograms: (a) the original information signal; (b) the encrypted signal; (c) the retrieved signal.
When comparing the histograms in Figure 10a,b, it is obvious that the encrypted signal histograms have a significantly different distribution than the original signal, proving the applicable communication system’s great robustness against statistical attack. Furthermore, the encrypted image’s histogram distribution in Figure 10c is identical to that of the original image in Figure 10a. As a result, the original image can be retrieved effectively.
7.2. Spectrogram Analysis
A spectrogram is yet another effective technique for calculating the spectrum of time signals that is employed in a variety of applications. A spectrogram is a plot that depicts the frequency of a signal on the vertical axis, time on the horizontal axis, and signal power on a color scale to offer information about power as a function of frequency and time [65]. The spectrograms of the original, encrypted, and recovered signals are shown in Figure 11. The spectrogram was computed using the short-time Fourier transform (STFT).
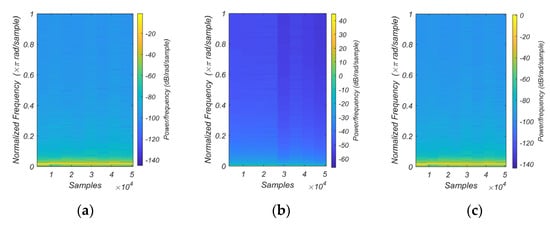
Figure 11.
The spectrogram analysis: (a) the original information signal; (b) the encrypted signal; (c) the retrieved signal.
8. Conclusions
A new fractional-order chaotic system is presented in this work. The behavior of the dynamics of this proposed system containing the chaotic attractors, the fixed points and corresponding eigenvalues, the bifurcation diagrams, and the Lyapunov exponents have been considered. As it is clear, our suggested fractional-order chaotic system is simple to implement, where the suggested system did not contain complex functions (for example, hyperbolic tangent functions). In our system, all mathematical functions are addition, subtraction, and multiplication; these functions can easily be implemented with simple analog op-amps like summer, subtracter, and multiplier, respectively. The investigated dynamics prove that the new FOCS system can excite hidden chaotic attractors or self-excited chaotic attractors. On the basis of the results of the simulation, it can be concluded that the dynamical behavior of the proposed system is very complex and extremely sensitive to the system parameters and initial conditions and to slight variations in the value of the fractional-order derivative. In addition, the proposed system is highly suited for usage in high-security communication systems because it offers nonlinear dynamical characteristics of incredible complexity.
Following this, an adaptive synchronization approach was developed. This synchronization strategy was established between two identical new systems, one of which serves as the master and the other as the slave. The adaptive control laws which are responsible for verifying the synchronization were derived on the basis of the Lyapunov stability approach. Correspondingly, the uncertain slave update parameter laws were determined to estimate these uncertain parameters. Additionally, in the chaos application field, a secure communication scheme was constructed on the basis of the developed synchronization technique. Finally, the security analysis metric tests were examined with histograms and spectrograms to determine the security strength of the employed communication system. The obtained experimental results and thorough security evaluations validate the efficiency, high security, and time efficiency of the employed cryptosystem and demonstrate a high, robust resistance to attacks.
Author Contributions
Conceptualization, Z.-A.S.A.R. and B.H.J.; methodology, Z.-A.S.A.R.; software, Z.-A.S.A.R. and B.H.J.; validation, Z.-A.S.A.R. and B.H.J.; formal analysis, Z.-A.S.A.R. and B.H.J.; investigation, Z.-A.S.A.R. and B.H.J.; resources, Z.-A.S.A.R. and B.H.J.; data curation, Z.-A.S.A.R. and B.H.J.; writing—original draft preparation, Z.-A.S.A.R. and B.H.J.; writing—review and editing, Z.-A.S.A.R. and B.H.J.; visualization, Z.-A.S.A.R. and B.H.J.; supervision, B.H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting the reported results cannot be shared at this time, as they is being used in producing more publications on this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brady, P. Chaos Theory, Control Theory, and Literary Theory or: A Story of Three Butterflies. Mod. Lang. Stud. 1990, 20, 65. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Abd-Alhameed, R.A. Efficient Colour Image Encryption Algorithm Using a New Fractional-Order Memcapacitive Hyperchaotic System. Electronics 2022, 11, 1505. [Google Scholar] [CrossRef]
- Solano, J.; Balibrea, F.; Moreno, J. Applications of the Network Simulation Method to Differential Equations with Singularities and Chaotic Behaviour. Mathematics 2021, 9, 1442. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Jasim, B.H.; Hassan, K.H.; Omran, K.M. A new 4-D hyperchaotic hidden attractor system: Its dynamics, coexisting attractors, synchronization and microcontroller implementation. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 2068–2078. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spéc. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Kiseleva, M.; Kuznetsov, N.; Leonov, G.; Neittaanmäki, P. Hidden oscillations in drilling system actuated by induction motor. IFAC Proc Vol 2013, 46, 86–89. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.C.; Li, Z.J. A Novel Four-Dimensional No-Equilibrium Hyper-Chaotic System With Grid Multiwing Hyper-Chaotic Hidden Attractors. J. Comput. Nonlinear Dyn. 2018, 13, 090908. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Global chaos synchronization of chemical chaotic reactors via novel sliding mode control method. Parameters 2015, 1, 4. [Google Scholar]
- Bi, H.; Qi, G.; Hu, J.; Faradja, P.; Chen, G. Hidden and transient chaotic attractors in the attitude system of quadrotor unmanned aerial vehicle. Chaos Solitons Fractals 2020, 138, 109815. [Google Scholar] [CrossRef]
- Yu, J.; Li, C.; Song, X.; Guo, S.; Wang, E. Parallel Mixed Image Encryption and Extraction Algorithm Based on Compressed Sensing. Entropy 2021, 23, 278. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, N.V.; Leonov, G.A.; Yuldashev, M.V.; Yuldashev, R.V. Hidden attractors in dynamical models of phase-locked loop circuits: Limitations of simulation in MATLAB and SPICE. Commun. Nonlinear. Sci. Numer. Simul. 2017, 51, 39–49. [Google Scholar]
- Lorenz, E.N.; Haman, K. The essence of chaos. Pure Appl. Geophys. 1996, 147, 598–599. [Google Scholar]
- Pham, V.-T.; Vaidyanathan, S.; Volos, C.; Tlelo-Cuautle, E.; Tahir, F.R. A memristive system with hidden attractors and its engineering application. In Advances in Memristors, Memristive Devices and Systems; Springer: New York, NY, USA, 2017; pp. 81–99. [Google Scholar]
- Pisarchik, A.; Jaimes-Reátegui, R.; Rodríguez-Flores, C.; García-López, J.; Huerta-Cuellar, G.; Martín-Pasquín, F. Secure chaotic communication based on extreme multistability. J. Frankl. Inst. 2021, 358, 2561–2575. [Google Scholar] [CrossRef]
- Vanchinathan, K.; Valluvan, K.R.; Gnanavel, C.; Gokul, C. Design methodology and experimental verification of intelligent speed controllers for sensorless permanent magnet Brushless DC motor: Intelligent speed controllers for electric motor. Electr. Energy Syst. 2021, 31, e12991. [Google Scholar] [CrossRef]
- Kamal, F.M.; Elsonbaty, A.; Elsaid, A. A novel fractional nonautonomous chaotic circuit model and its application to image encryption. Chaos Solitons Fractals 2021, 144, 110686. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Abd-Alhameed, R.A. High-Security Image Encryption Based on a Novel Simple Fractional-Order Memristive Chaotic System with a Single Unstable Equilibrium Point. Electronics 2021, 10, 3130. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Q.; He, B.; Chen, Y.; Peng, X.; Mei, R. Adaptive Predefined-Time Synchronization of Two Different Fractional-Order Chaotic Systems With Time-Delay. IEEE Access 2021, 9, 31908–31920. [Google Scholar] [CrossRef]
- Razminia, A.; Majd, V.J.; Baleanu, D. Chaotic incommensurate fractional order Rössler system: Active control and synchronization. Adv. Differ. Equ. 2011, 2011, 15. [Google Scholar] [CrossRef]
- Kayalvizhi, S.; Malarvizhi, S. A novel encrypted compressive sensing of images based on fractional order hyper chaotic Chen system and DNA operations. Multimed. Tools Appl. 2020, 79, 3957–3974. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Liu, J.; Yang, F.; Yan, H.; Zhao, X. Coexistence of multiple attractors for an incommensurate fractional-order chaotic system. Eur. Phys. J. Plus 2020, 135, 1–21. [Google Scholar] [CrossRef]
- Gupta, S.; Varshney, P.; Srivastava, S. Whale optimization based synchronization and control of two identical fractional order financial chaotic systems. J. Intell. Fuzzy Syst. 2022, 42, 929–942. [Google Scholar] [CrossRef]
- Khan, H.; Li, Y.; Khan, A.; Khan, A. Existence of solution for a fractional-order Lotka-Volterra reaction-diffusion model with Mittag-Leffler kernel. Math. Methods Appl. Sci. 2019, 42, 3377–3387. [Google Scholar] [CrossRef]
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer: New York, NY, USA, 2017. [Google Scholar]
- Rahman, Z.; AL-Kashoash, H.; Ramadhan, S.; Al-Yasir, Y. Adaptive control synchronization of a novel Menristive chaotic system for secure communication application. Inventions 2019, 10, 1–11. [Google Scholar]
- Vaseghi, B.; Pourmina, M.A.; Mobayen, S. Secure communication in wireless sensor networks based on chaos synchronization using adaptive sliding mode control. Nonlinear Dyn. 2017, 89, 1689–1704. [Google Scholar] [CrossRef]
- Jasim, B.H.; Mjily, A.H.; Al-Aaragee, A.M.J. A novel 4 dimensional hyperchaotic system with its control, Synchronization and Implementation. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 2974–2985. [Google Scholar] [CrossRef]
- Yuan, L.-G.; Yang, Q.-G. Parameter identification and synchronization of fractional-order chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 305–316. [Google Scholar] [CrossRef]
- Keyong, S.; Ruixuan, B.; Wang, G.; Qiutong, W.; Yi, Z. Passive Synchronization Control for Integer-order Chaotic Systems and Fractional-order Chaotic Systems. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 1115–1119. [Google Scholar]
- Liu, B.; Sun, Z.; Luo, Y.; Zhong, Y. Uniform synchronization for chaotic dynamical systems via event-triggered impulsive control. Phys. A: Stat. Mech. its Appl. 2019, 531, 121725. [Google Scholar] [CrossRef]
- Azar, A.T.; Vaidyanathan, S.; Ouannas, A. Fractional-Order Control and Synchronization of Chaotic Systems; Springer: New York, NY, USA, 2017; Volume 688. [Google Scholar]
- Rahman, Z.A.S.A.; Jassim, B.H.; Al-Yasir, Y.I.A. New Fractional Order Chaotic System: Analysis, Synchronization, and it’s Application. Iraqi J. Electr. Electron. Eng. 2021, 17, 116–123. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional-Order Chaotic Circuits and Applications; Springer: New York, NY, USA, 2020. [Google Scholar]
- Petrzela, J. Chaos in Analog Electronic Circuits: Comprehensive Review, Solved Problems, Open Topics and Small Example. Mathematics 2022, 10, 4108. [Google Scholar] [CrossRef]
- Hashemi, S.; Pourmina, M.A.; Mobayen, S.; Alagheband, M.R. Design of a secure communication system between base transmitter station and mobile equipment based on finite-time chaos synchronisation. Int. J. Syst. Sci. 2020, 51, 1969–1986. [Google Scholar] [CrossRef]
- Vanchinathan, K.; Selvaganesan, N. Adaptive fractional order PID controller tuning for brushless DC motor using Artificial Bee Colony algorithm. Results Control Optim. 2021, 4, 100032. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Vanchinathan, K.; Valluvan, K.R. A Metaheuristic Optimization Approach for Tuning of Fractional-Order PID Controller for Speed Control of Sensorless BLDC Motor. J. Circuits Syst. Comput. 2018, 27, 1850123. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Wen, C.; Yang, J. Complexity evolution of chaotic financial systems based on fractional calculus. Chaos Solitons Fractals 2019, 128, 242–251. [Google Scholar] [CrossRef]
- Ashpazzadeh, E.; Chu, Y.M.; Hashemi, M.S.; Moharrami, M.; Inc, M. Hermite multiwavelets representation for the sparse solution of nonlinear Abel’s integral equation. Appl. Math. Comput. 2022, 427, 127171. [Google Scholar] [CrossRef]
- Cao, Y. Chaotic synchronization based on fractional order calculus financial system. Chaos Solitons Fractals 2020, 130, 109410. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation. Inventions 2021, 6, 49. [Google Scholar] [CrossRef]
- Liu, T.; Yan, H.; Banerjee, S.; Mou, J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Solitons Fractals 2021, 145, 110791. [Google Scholar] [CrossRef]
- Gong, L.; Wu, R.; Zhou, N. A New 4D Chaotic System with Coexisting Hidden Chaotic Attractors. Int. J. Bifurc. Chaos 2020, 30, 2050142. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, C.; Xu, D.; Chen, C. Dynamic analysis and synchronisation control of a novel chaotic system with coexisting attractors. Pramana 2020, 94, 19. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K.; Fotsin, H. Coexisting attractors, circuit implementation and synchronization control of a new chaotic system evolved from the simplest memristor chaotic circuit. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105341. [Google Scholar] [CrossRef]
- Dabiri, A.; Moghaddam, B.; Machado, J.T. Optimal variable-order fractional PID controllers for dynamical systems. J. Comput. Appl. Math. 2018, 339, 40–48. [Google Scholar] [CrossRef]
- Ma, L.; Liu, X.; Moradi, Z. On the chaotic behavior of graphene-reinforced annular systems under harmonic excitation. Eng. Comput. 2022, 38, 2583–2607. [Google Scholar] [CrossRef]
- Parsa, M.B.; Dabiri, A.; Machado, J.A.T. Application of variable-order fractional calculus in solid mechanics. Appl. Eng. Life Soc. Sci. Part A 2019, 7, 207–224. [Google Scholar]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Wang, C.; Fan, C.; Ding, Q. Constructing Discrete Chaotic Systems with Positive Lyapunov Exponents. Int. J. Bifurc. Chaos 2018, 28, 1850084. [Google Scholar] [CrossRef]
- Danca, M.-F.; Kuznetsov, N. Matlab code for Lyapunov exponents of fractional-order systems. Int. J. Bifurc. Chaos 2018, 28, 1850067. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C. Advances and Applications in Chaotic Systems; Springer: Berlin, Germany, 2016; Volume 636. [Google Scholar]
- Haddad, W.M.; Bernstein, D.S. Explicit construction of quadratic Lyapunov functions for the small gain, positivity, circle, and Popov theorems and their application to robust stability. In Control of Uncertain Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2020; pp. 149–173. [Google Scholar]
- Cai, G.; Tan, Z. Chaos synchronization of a new chaotic system via nonlinear control. J. Uncertain Syst. 2007, 1, 235–240. [Google Scholar]
- Dutta, M.; Roy, B.K. A new fractional-order system displaying coexisting multiwing attractors; its synchronisation and circuit simulation. Chaos Solitons Fractals 2020, 130, 109414. [Google Scholar] [CrossRef]
- Rashidnejad, Z.; Karimaghaee, P. Synchronization of a class of uncertain chaotic systems utilizing a new finite-time fractional adaptive sliding mode control. Chaos Solitons Fractals X 2020, 5, 100042. [Google Scholar] [CrossRef]
- Martínez-Guerra, R.; Gómez-Cortés, G.C.; Pérez-Pinacho, C.A. Synchronization of Integral and Fractional Order Chaotic Systems; Springer: Berlin, Germany, 2015. [Google Scholar]
- Martínez-Guerra, R.; Pérez-Pinacho, C.A. Advances in Synchronization of Coupled Fractional Order Systems: Fundamentals and Methods; Springer: Berlin, Germany, 2018. [Google Scholar]
- Kharel, R. Design and Implementation of Secure Chaotic Communication Systems. Doctoral Dissertation, Northumbria University, Newcastle-upon-Tyne, UK, 2011. [Google Scholar]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. Phys. Rev. Lett. 1993, 71, 65. [Google Scholar] [CrossRef] [PubMed]
- Alanazi, A.S.; Munir, N.; Khan, M.; Asif, M.; Hussain, I. Cryptanalysis of Novel Image Encryption Scheme Based on Multiple Chaotic Substitution Boxes. IEEE Access 2021, 9, 93795–93802. [Google Scholar] [CrossRef]
- Kacha, A.; Grenez, F.; Orozco-Arroyave, J.R.; Schoentgen, J. Principal component analysis of the spectrogram of the speech signal: Interpretation and application to dysarthric speech. Comput. Speech Lang. 2020, 59, 114–122. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).