A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation
Abstract
:1. Introduction
2. Fundamentals of Fractional Order Systems
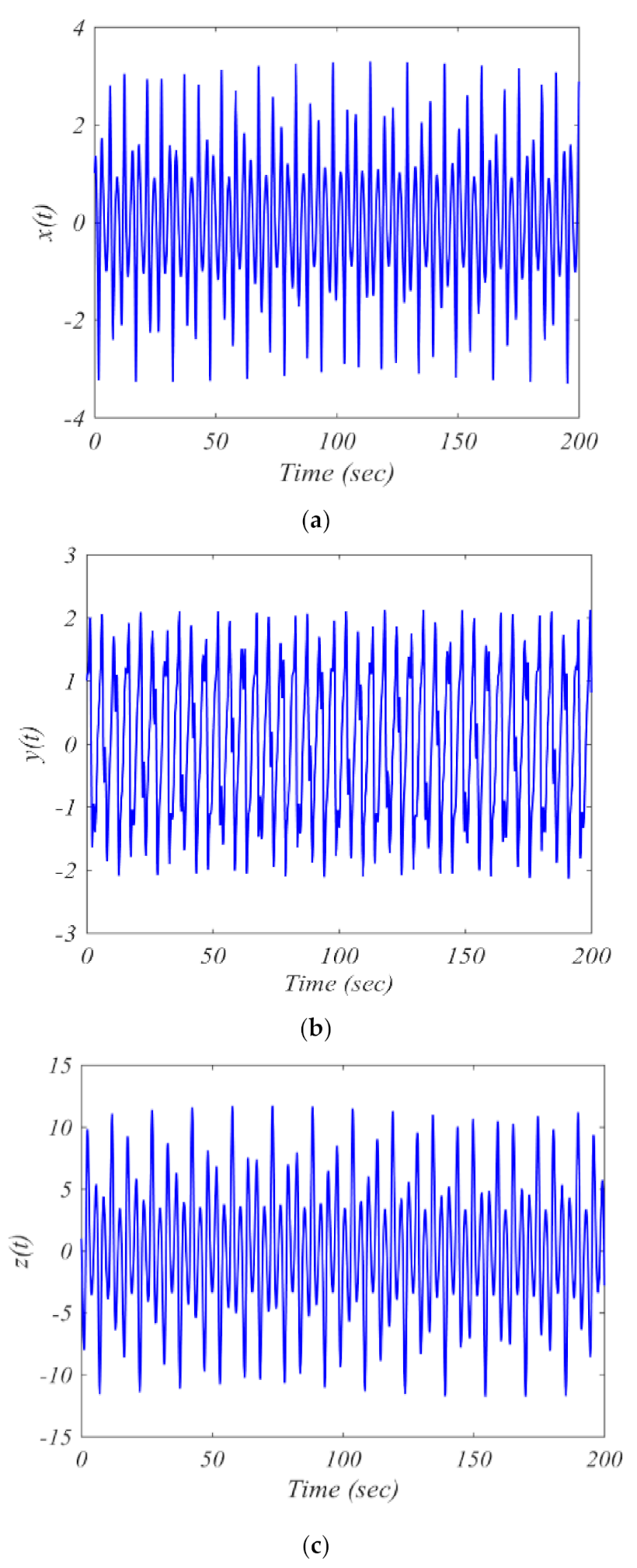
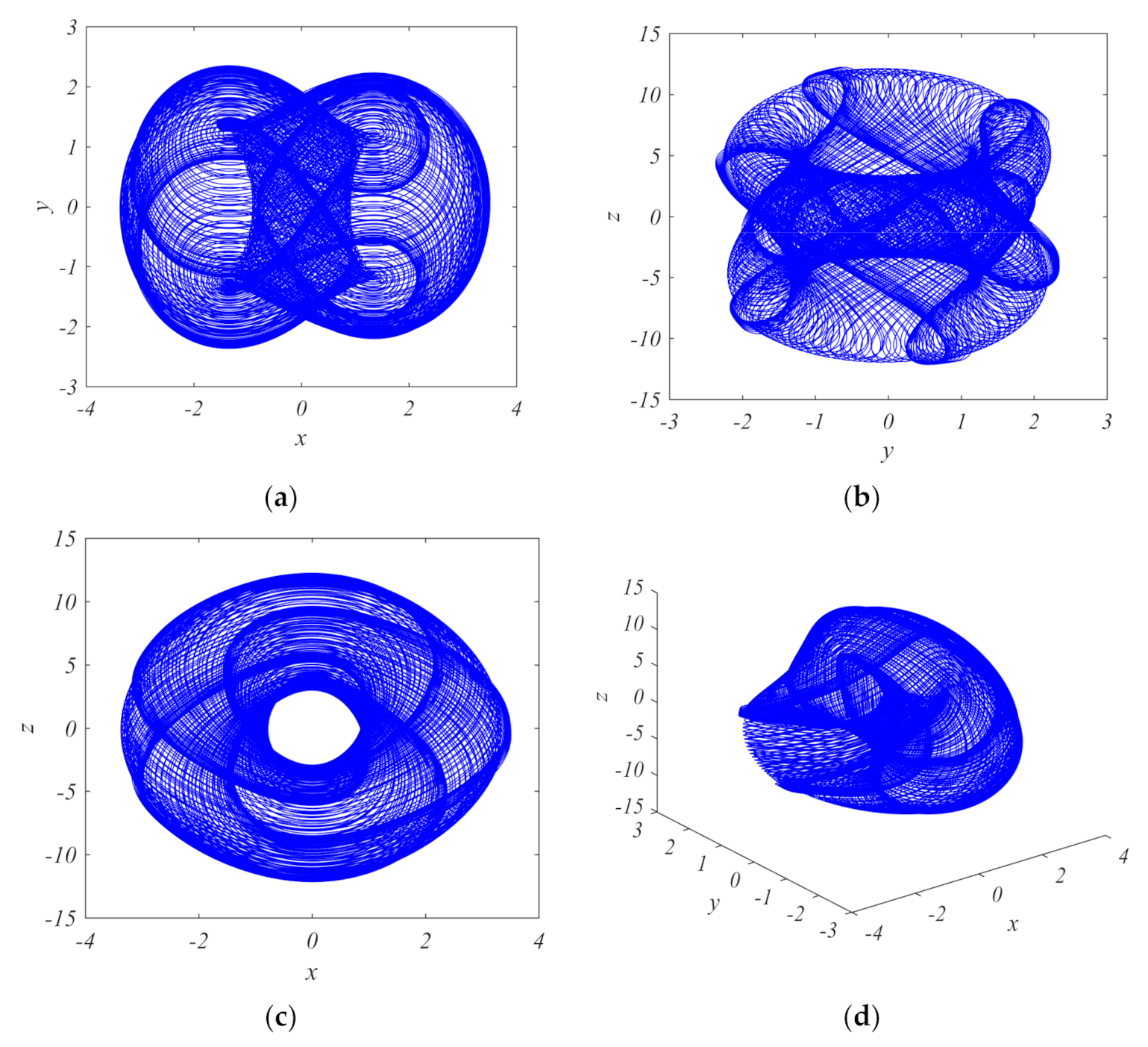
3. A New Fractional Order Chaotic Model
4. The System Dynamical Analyses
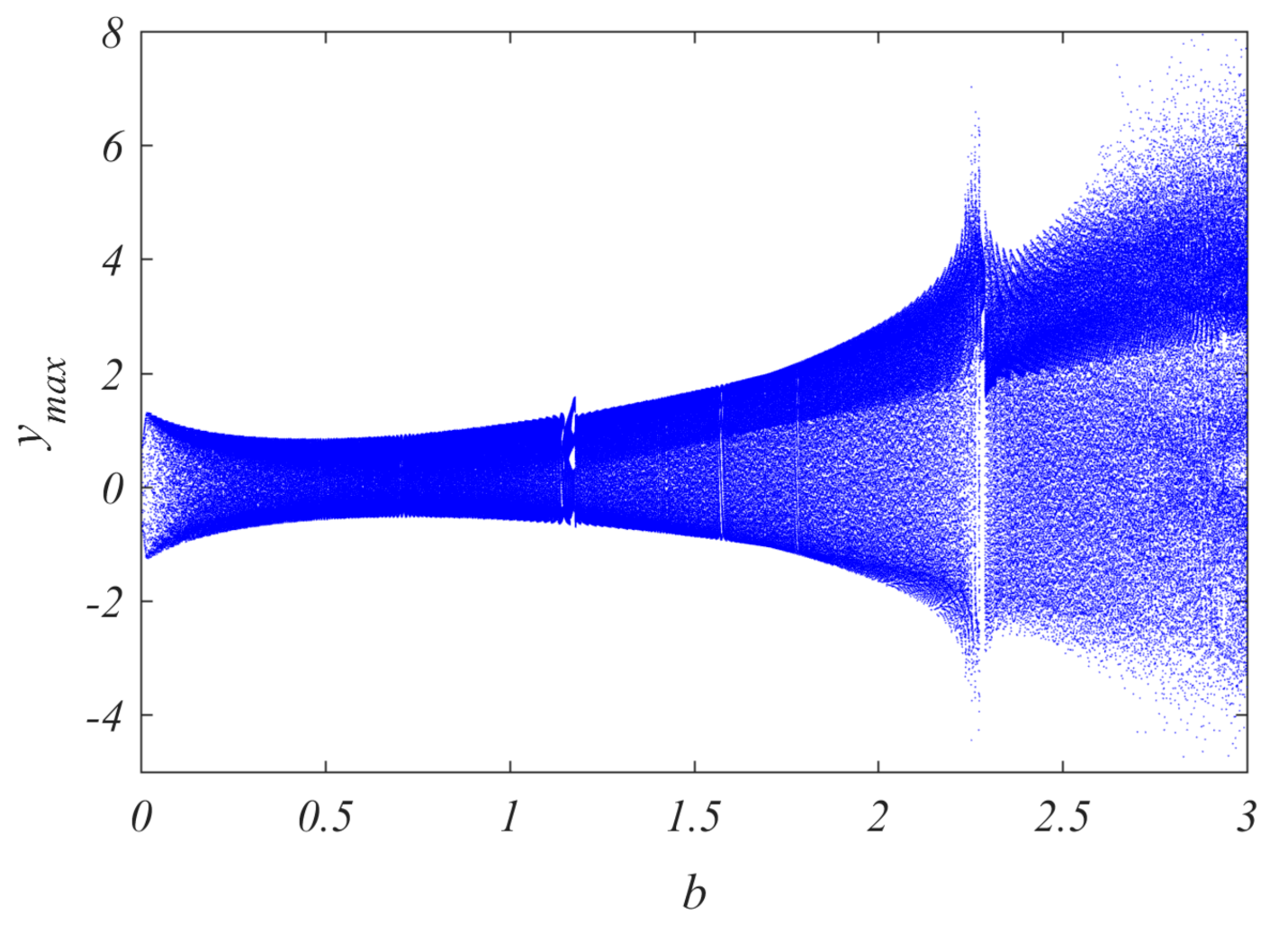
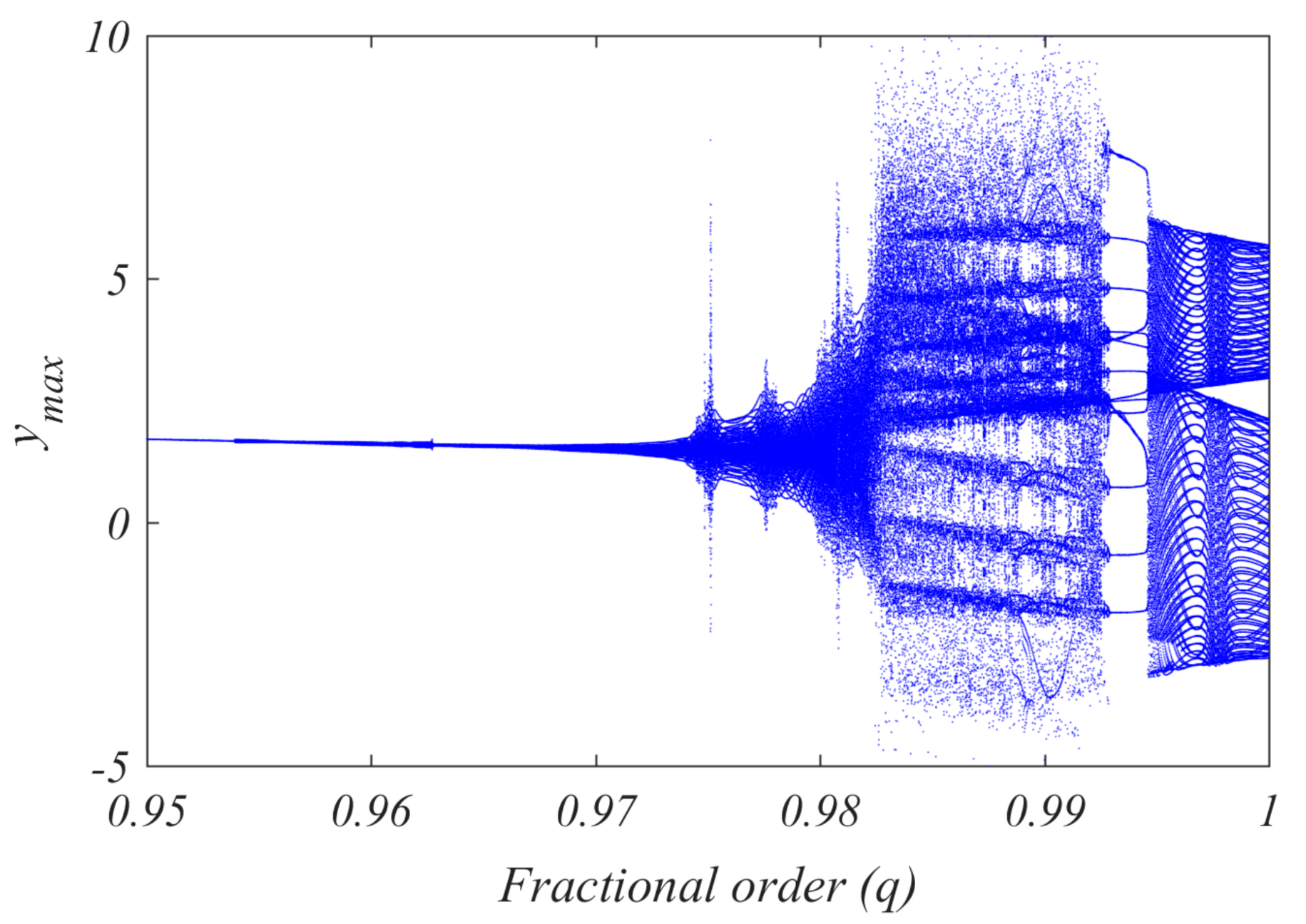
4.1. Bifurcation Diagrams
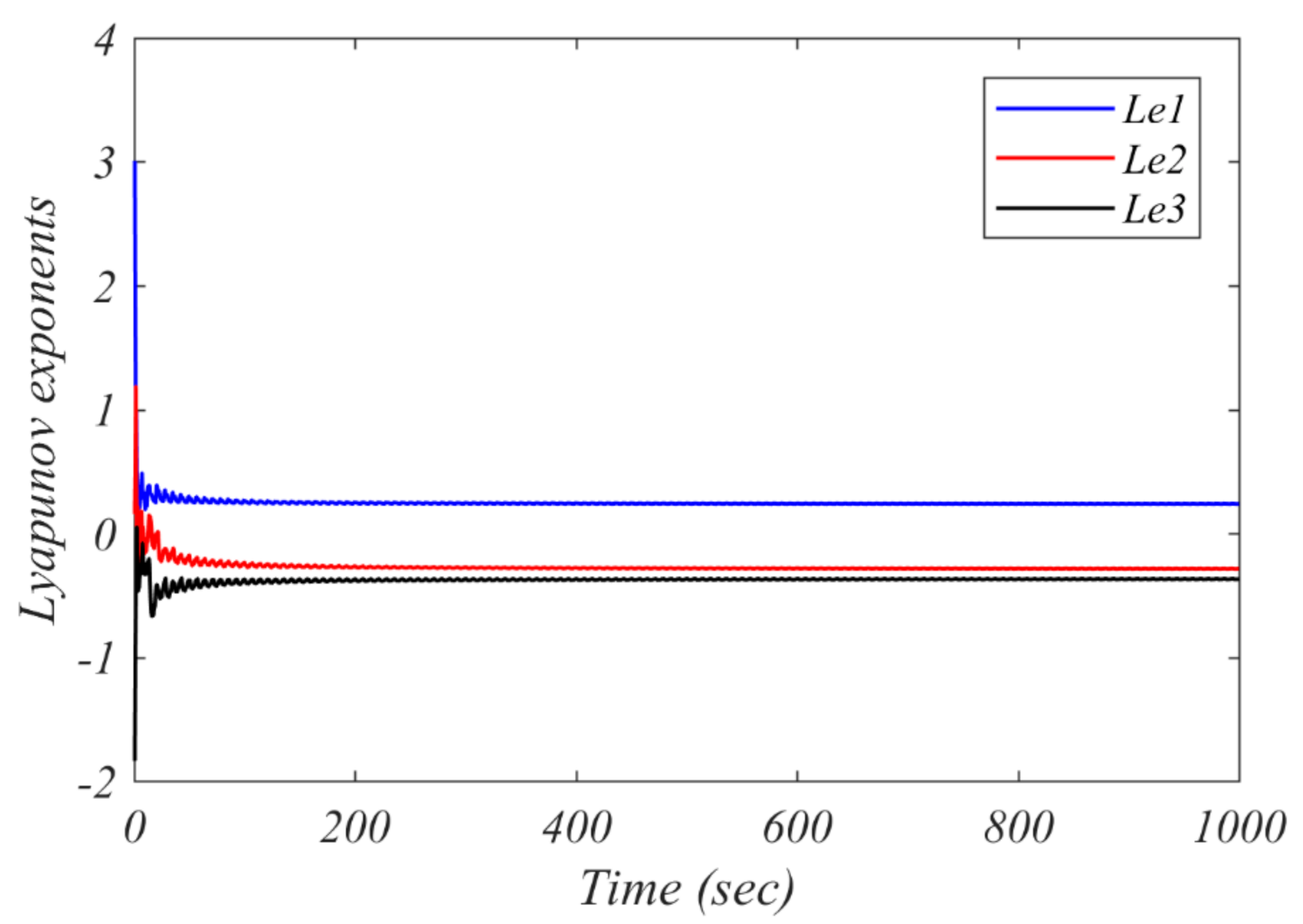
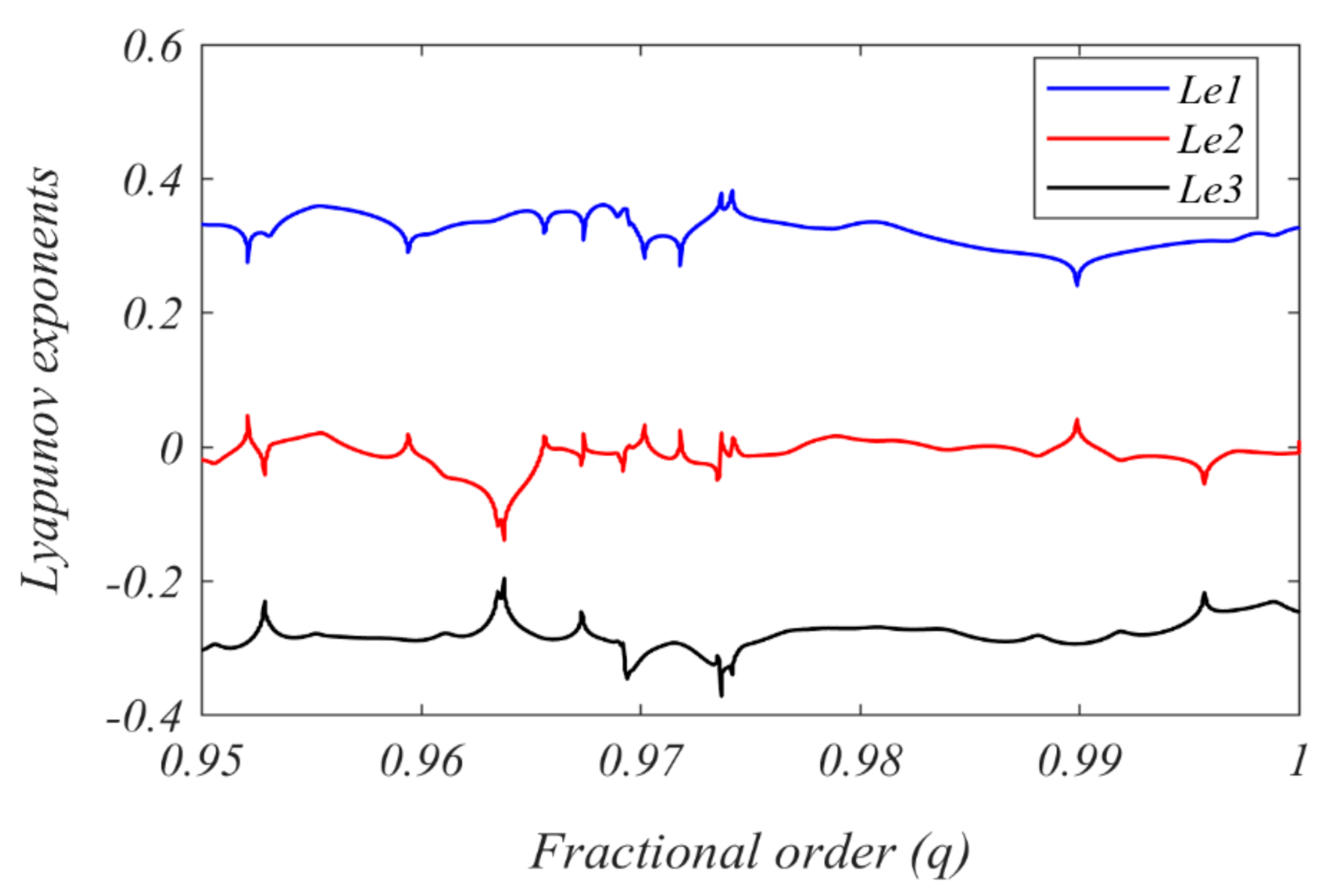
4.2. Lyapunov Exponents
5. Adaptive Synchronization of Two New Fractional Order Chaotic Systems
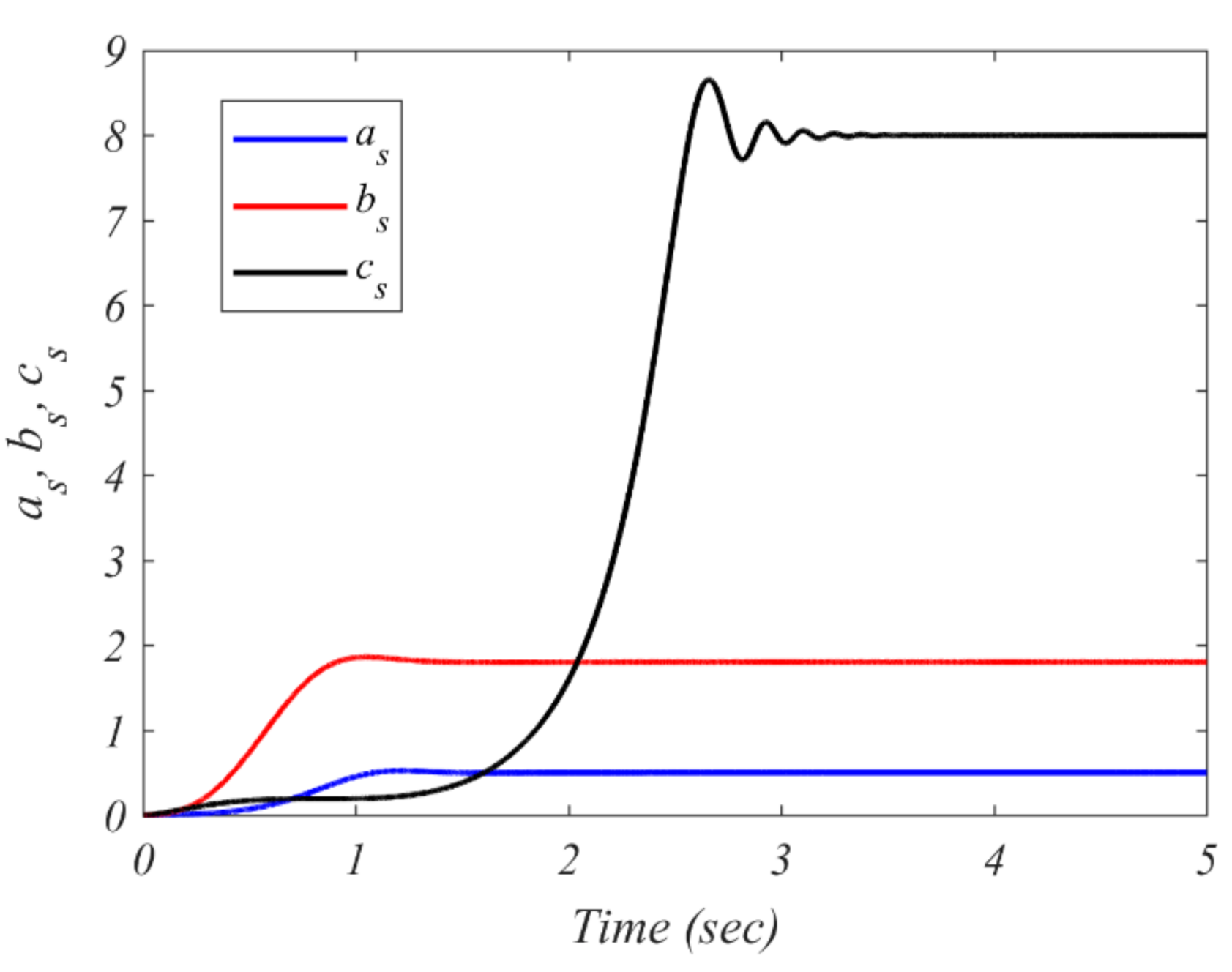
5.1. Adaptive Controller Design Process
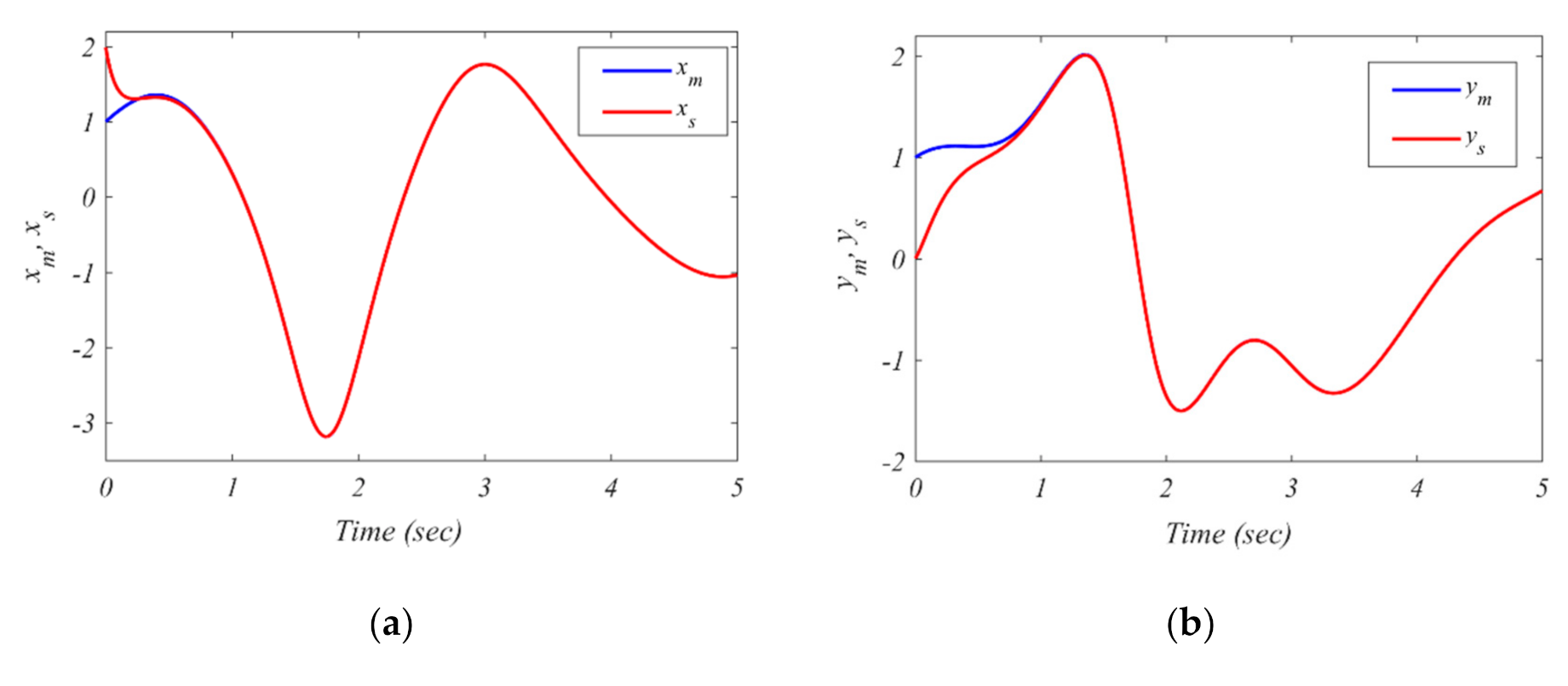
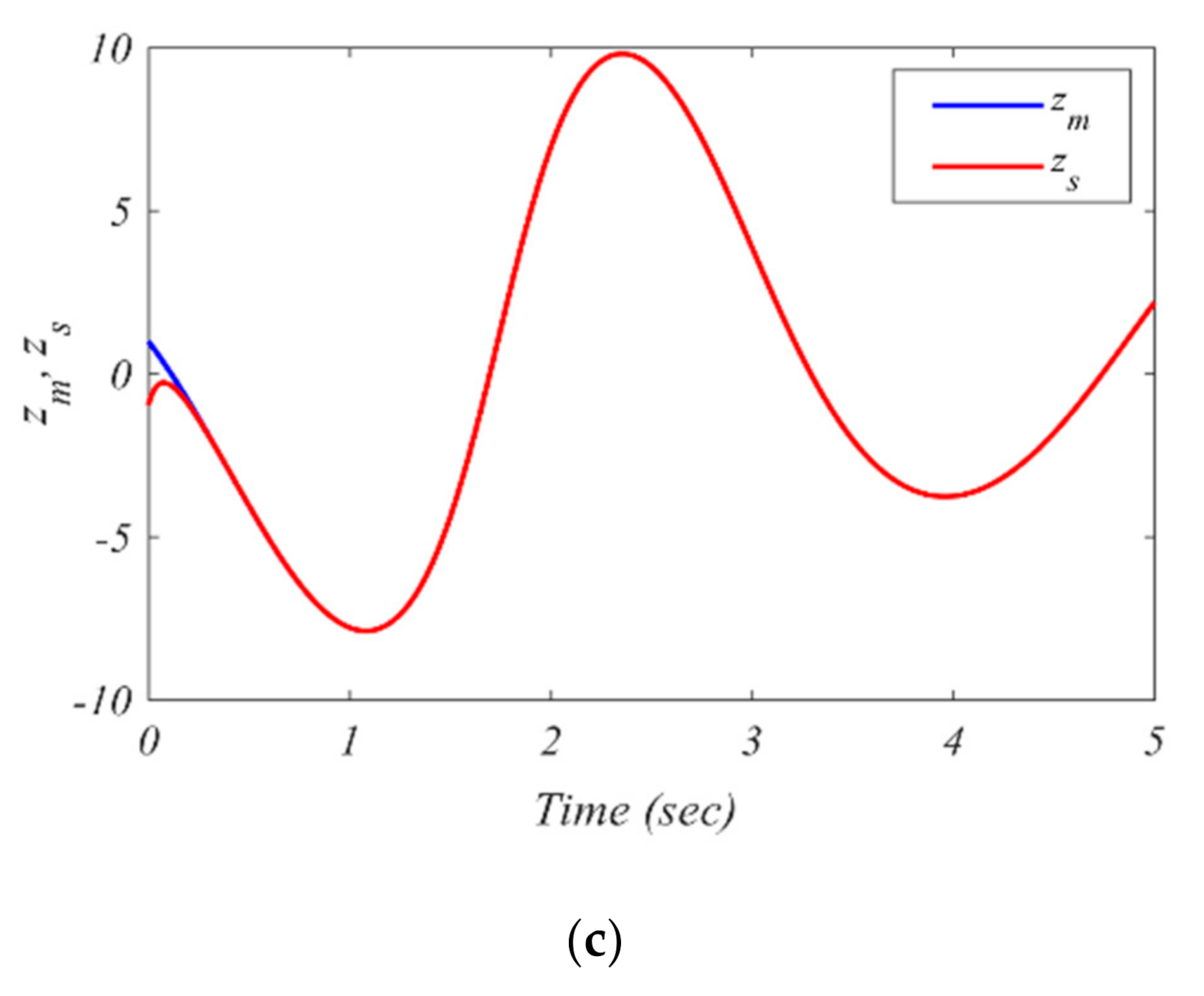
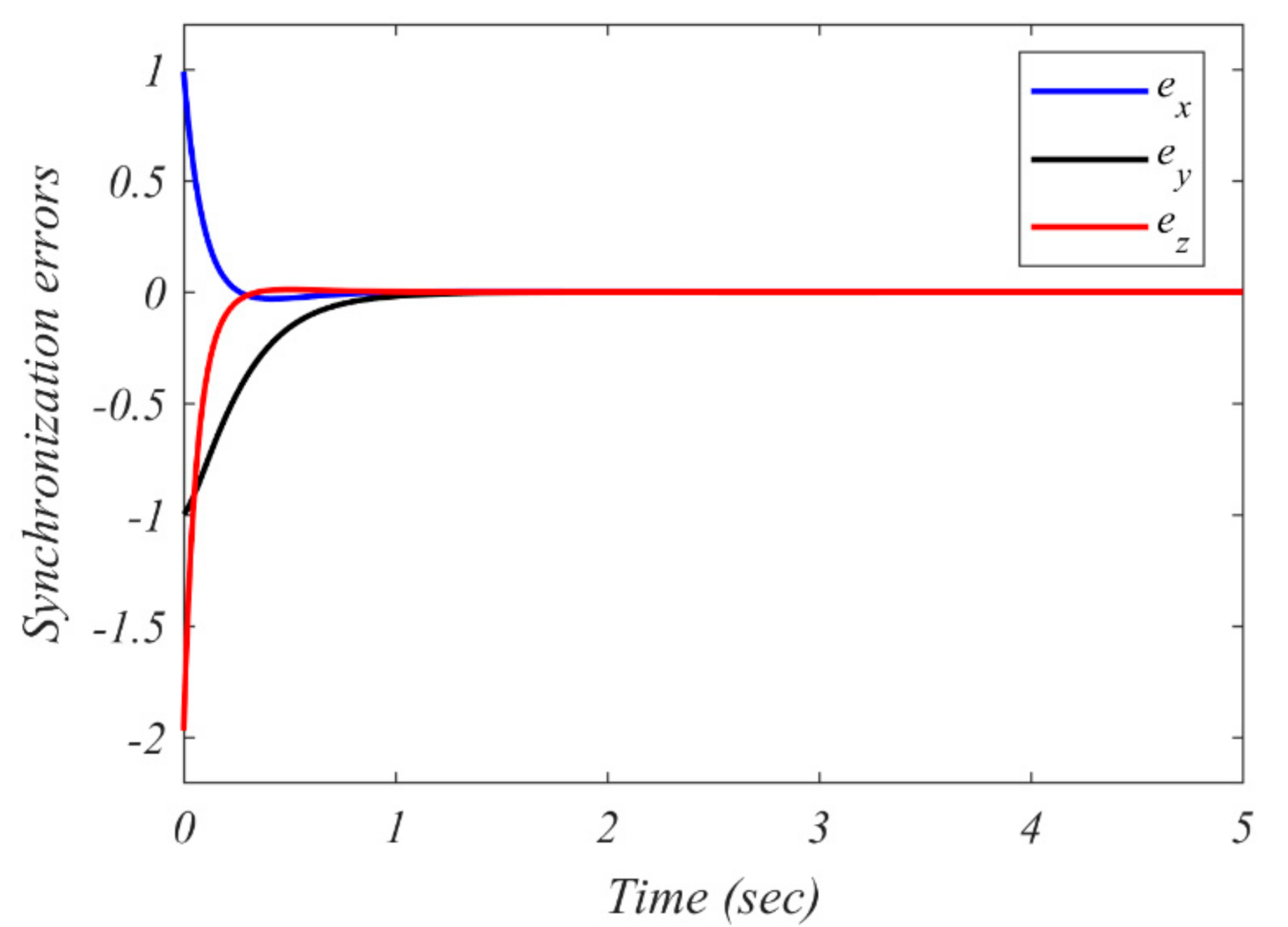
5.2. Simulation Results
6. Digital Implementation of New Fractional Order Chaotic System
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Sordi, A. Chua’s oscillator: An introductory approach to chaos theory. Rev. Bras. Ensino Física 2021, 43. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C. Advances and Applications in Chaotic Systems; Springer: Berlin/Heidelberg, Germany, 2016; Volume 636. [Google Scholar]
- Asiain, E.; Garrido, R. Anti-Chaos control of a servo system using nonlinear model reference adaptive control. Chaos Solitons Fractals 2021, 143, 110581. [Google Scholar] [CrossRef]
- Cuellar, G.H.; Jiménez-López, E.; Campos-Cantón, E.; Pisarchik, A. An approach to generate deterministic Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2740–2746. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, Y.; Wei, Z.; Zhang, L. Hidden chaotic attractors in a class of two-dimensional maps. Nonlinear Dyn. 2016, 85, 2719–2727. [Google Scholar] [CrossRef] [Green Version]
- Jasim, B.H.; Hassan, K.H.; Omran, K.M. A new 4-D hyperchaotic hidden attractor system: Its dynamics, coexisting attractors, synchronization and microcontroller implementation. Int. J. Electr. Comput. Eng. 2021, 11, 2068–2078. [Google Scholar] [CrossRef]
- Volos, C.K.; Jafari, S.; Kengne, J.; Munoz-Pacheco, J.M.; Rajagopal, K. Nonlinear dynamics and entropy of complex systems with hidden and self-excited attractors. Entropy 2019, 21, 370. [Google Scholar] [CrossRef] [Green Version]
- Azar, A.T.; Serrano, F.E. Stabilization of Port Hamiltonian Chaotic Systems with Hidden Attractors by Adaptive Terminal Sliding Mode Control. Entropy 2020, 22, 122. [Google Scholar] [CrossRef] [Green Version]
- Leonov, G.; Kuznetsov, N.V.; Mokaev, T. Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion. Eur. Phys. J. Spéc. Top. 2015, 224, 1421–1458. [Google Scholar] [CrossRef] [Green Version]
- Leonov, G.; Kuznetsov, N.V.; Kiseleva, M.; Solovyeva, E.P.; Zaretskiy, A.M. Hidden oscillations in mathematical model of drilling system actuated by induction motor with a wound rotor. Nonlinear Dyn. 2014, 77, 277–288. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Bonny, T.; Zhang, S.; Sukono; Hidayat, Y.; Gundara, G.; Mamat, M. Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-Like Curve of Equilibrium Points. Appl. Sci. 2021, 11, 788. [Google Scholar] [CrossRef]
- Andrievsky, B.; Kuznetsov, N.; Leonov, G.; Pogromsky, A. Hidden oscillations in aircraft flight control system with input saturation. IFAC Proc. Vol. 2013, 46, 75–79. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Vaidyanathan, S.; Volos, C.; Wang, X. A novel memristive neural network with hidden attractors and its circuitry implementation. Sci. China Ser. E Technol. Sci. 2015, 59, 358–363. [Google Scholar] [CrossRef]
- Kiani-B, A.; Fallahi, K.; Pariz, N.; Leung, H. A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 863–879. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Leonov, G.A.; Yuldashev, M.V.; Yuldashev, R.V. Hidden attractors in dynamical models of phase-locked loop circuits: Limitations of simulation in MATLAB and SPICE. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Vlachas, P.R.; Byeon, W.; Wan, Z.Y.; Sapsis, T.P.; Koumoutsakos, P. Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170844. [Google Scholar] [CrossRef] [Green Version]
- Velamore, A.A.; Hegde, A.; Khan, A.A.; Deb, S. Dual cascaded Fractional-order Chaotic Synchronization for Secure Communication with Analog Circuit Realisation. In Proceedings of the 2021 IEEE Second International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2021; IEEE: New York, NY, USA, 2021; pp. 30–35. [Google Scholar]
- Pham, V.-T.; Vaidyanathan, S.; Volos, C.K.; Jafari, S. Hidden attractors in a chaotic system with an exponential nonlinear term. Eur. Phys. J. Spéc. Top. 2015, 224, 1507–1517. [Google Scholar] [CrossRef]
- Tahir, F.R.; Jafari, S.; Pham, V.-T.; Volos, C.; Wang, X. A Novel No-Equilibrium Chaotic System with Multiwing Butterfly Attractors. Int. J. Bifurc. Chaos 2015, 25. [Google Scholar] [CrossRef]
- Pham, V.-T.; Vaidyanathan, S.; Volos, C.; Kapitaniak, T. Nonlinear Dynamical Systems with Self-Excited and Hidden Attractors; Springer: Berlin/Heidelberg, Germany, 2018; Volume 133. [Google Scholar]
- Bayani, A.; Rajagopal, K.; Khalaf, A.J.M.; Jafari, S.; Leutcho, G.D.; Kengne, J. Dynamical analysis of a new multistable chaotic system with hidden attractor: Antimonotonicity, coexisting multiple attractors, and offset boosting. Phys. Lett. A 2019, 383, 1450–1456. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Jassim, B.H.; Al-Yasir, Y.I.A. New Fractional Order Chaotic System: Analysis, Synchronization, and it’s Application. Iraqi J. Electr. Electron. Eng. 2021, 17. [Google Scholar] [CrossRef]
- Escalante-González, R.J.; Campos, E. Multistable systems with hidden and self-excited scroll attractors generated via piecewise linear systems. Complex. Dyn. Control Appl. Nonlinear Syst. Multistability 2020, 2020. [Google Scholar] [CrossRef] [Green Version]
- Ma, C. A Novel Computational Technique for Impulsive Fractional Differential Equations. Symmetry 2019, 11, 216. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Boubaker, O.; Jafari, S. Recent Advances in Chaotic Systems and Synchronization: From Theory to Real World Applications; Academic Press: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Abdelaty, A.M.; Azar, A.T.; Vaidyanathan, S.; Ouannas, A.; Radwan, A. Applications of Continuous-time Fractional Order Chaotic Systems. Math. Tech. Fract. Order Syst. 2018, 409–449. [Google Scholar] [CrossRef]
- Soleimanizadeh, A.; Nekoui, M.A. Optimal type-2 fuzzy synchronization of two different fractional-order chaotic systems with variable orders with an application to secure communication. Soft Comput. 2021, 25, 6415–6426. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.; Gilardi-Velázquez, H.; Jaimes-Reátegui, R.; Aboites, V.; Huerta-Cuellar, G. A physical interpretation of fractional-order-derivatives in a jerk system: Electronic approach. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105413. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K.; Fotsin, H. Coexisting attractors, circuit implementation and synchronization control of a new chaotic system evolved from the simplest memristor chaotic circuit. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105341. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Al-Kashoash, H.A.A.; Ramadhan, S.M.; Al-Yasir, Y.I.A. Adaptive Control Synchronization of a Novel Memristive Chaotic System for Secure Communication Applications. Inventions 2019, 4, 30. [Google Scholar] [CrossRef] [Green Version]
- Jasim, B.H.; Mjily, A.H.; AL-Aaragee, A.M.J. A novel 4 dimensional hyperchaotic system with its control, synchronization and implementation. Int. J. Electr. Comput. Eng. 2021, 11, 2974–2985. [Google Scholar]
- Agrawal, S.; Srivastava, M.; Das, S. Synchronization of fractional order chaotic systems using active control method. Chaos Solitons Fractals 2012, 45, 737–752. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Synchronization of chaotic fractional-order systems via active sliding mode controller. Phys. A Stat. Mech. Appl. 2008, 387, 57–70. [Google Scholar] [CrossRef]
- Kumar, S.; Matouk, A.E.; Chaudhary, H.; Kant, S. Control and synchronization of fractional-order chaotic satellite systems using feedback and adaptive control techniques. Int. J. Adapt. Control. Signal Process. 2021, 35, 484–497. [Google Scholar] [CrossRef]
- Liu, L.; Du, C.; Zhang, X.; Li, J.; Shi, S. Adaptive Synchronization Strategy between Two Autonomous Dissipative Chaotic Systems Using Fractional-Order Mittag–Leffler Stability. Entropy 2019, 21, 383. [Google Scholar] [CrossRef] [Green Version]
- Megherbi, O.; Hamiche, H.; Djennoune, S.; Bettayeb, M. A new contribution for the impulsive synchronization of fractional-order discrete-time chaotic systems. Nonlinear Dyn. 2017, 90, 1519–1533. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T.; Trujillo, J.J. Fractional derivatives and periodic functions. Int. J. Dyn. Control. 2017, 5, 72–78. [Google Scholar] [CrossRef]
- Huseynov, I.T.; Ahmadova, A.; Fernandez, A.; Mahmudov, N.I. Explicit analytical solutions of incommensurate fractional differential equation systems. Appl. Math. Comput. 2021, 390, 125590. [Google Scholar] [CrossRef]
- Wang, C.; Ding, Q. A New Two-Dimensional Map with Hidden Attractors. Entropy 2018, 20, 322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, Y.; Zhang, B. Comparative Study of Riemann–Liouville and Caputo Derivative Definitions in Time-Domain Analysis of Fractional-Order Capacitor. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2184–2188. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhao, W.; Dai, H. A new definition of fractional derivative. Int. J. Nonlinear Mech. 2019, 108, 1–6. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Banerjee, S. Dynamical properties and complexity in fractional-order diffusionless Lorenz system. Eur. Phys. J. Plus 2016, 131, 1–12. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef] [Green Version]
- Qi, G.; Xu, L.; Yang, X. Energy mechanism analysis for chaotic dynamics of gyrostat system and simulation of displacement orbit using COMSOL. Appl. Math. Model. 2021, 92, 333–348. [Google Scholar] [CrossRef]
- Stankevich, N.V.; Kuznetsov, A.P.; Seleznev, E.P. Chaos and hyperchaos arising from the destruction of multifrequency tori. Chaos Solitons Fractals 2021, 147, 110998. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, H.; Li, Y.; Pei, B. Image encryption based on synchronization of fractional chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3735–3744. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Z. A Fuzzy Lyapunov Function Method to Stability Analysis of Fractional Order T-S Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2021, PP, 1. [Google Scholar] [CrossRef]
- Nowak, R.D. Nonlinear system identification. Circuits Syst. Signal Process 2002, 21, 109–122. [Google Scholar] [CrossRef]
- Sánchez-López, C. An experimental synthesis methodology of fractional-order chaotic attractors. Nonlinear Dyn. 2020, 100, 3907–3923. [Google Scholar] [CrossRef]
- Due, A. Core ARM. Arduino Due. Retrieved 2017, 9, 2019. [Google Scholar]


| Master System | Slave System | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| am | 0.5 | as(t) | Estimated |
| bm | 1.8 | bs(t) | Estimated |
| cm | 8 | cm(t) | Estimated |
| fractional order (q) | 0.98 | fractional order (q) | 0.98 |
| Xm(0) | 1 | Xs(0) | 2 |
| ym(0) | 1 | ys(0) | 0 |
| zm(0) | 1 | zs(0) | −1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, Z.-A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation. Inventions 2021, 6, 49. https://doi.org/10.3390/inventions6030049
Rahman Z-ASA, Jasim BH, Al-Yasir YIA, Abd-Alhameed RA, Alhasnawi BN. A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation. Inventions. 2021; 6(3):49. https://doi.org/10.3390/inventions6030049
Chicago/Turabian StyleRahman, Zain-Aldeen S. A., Basil H. Jasim, Yasir I. A. Al-Yasir, Raed A. Abd-Alhameed, and Bilal Naji Alhasnawi. 2021. "A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation" Inventions 6, no. 3: 49. https://doi.org/10.3390/inventions6030049
APA StyleRahman, Z.-A. S. A., Jasim, B. H., Al-Yasir, Y. I. A., Abd-Alhameed, R. A., & Alhasnawi, B. N. (2021). A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation. Inventions, 6(3), 49. https://doi.org/10.3390/inventions6030049










