The Expected Impact of Marine Energy Farms Operating in Island Environments with Mild Wave Energy Resources—A Case Study in the Mediterranean Sea
Abstract
1. Introduction
- (a)
- What is the long-term wind and wave energy pattern in the vicinity of Giglio Island according to some state-of-the-art data (satellite and reanalysis).
- (b)
- What is the impact of a hybrid marine energy farm on the local area.
- (c)
- Hw the coastal dynamics will be affected by the presence of such a marine energy farm.
2. Materials and Methods
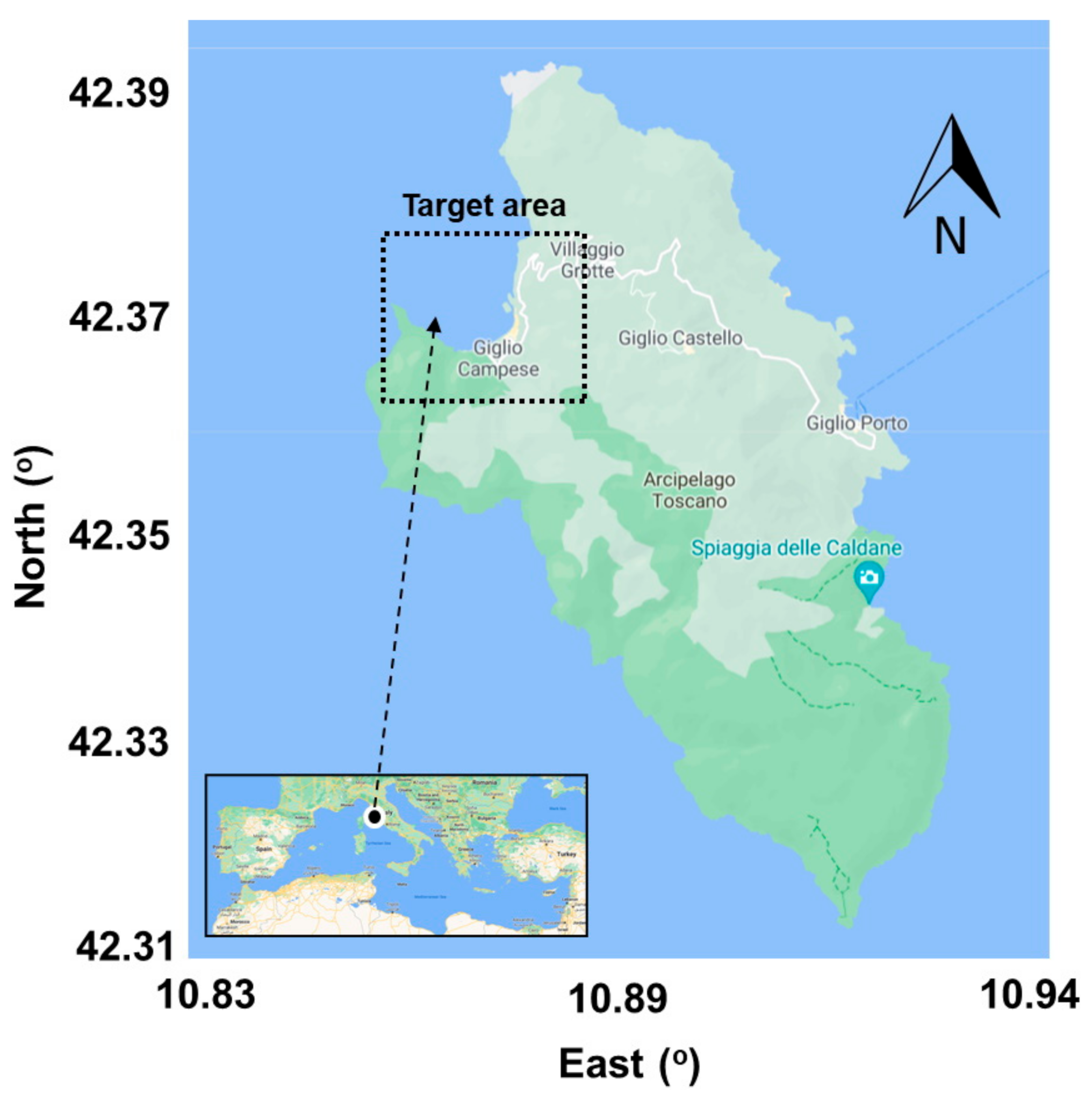
2.1. Target Area
2.2. ISSM Computational Platform and Case Studies
2.2.1. The ISSM Interface
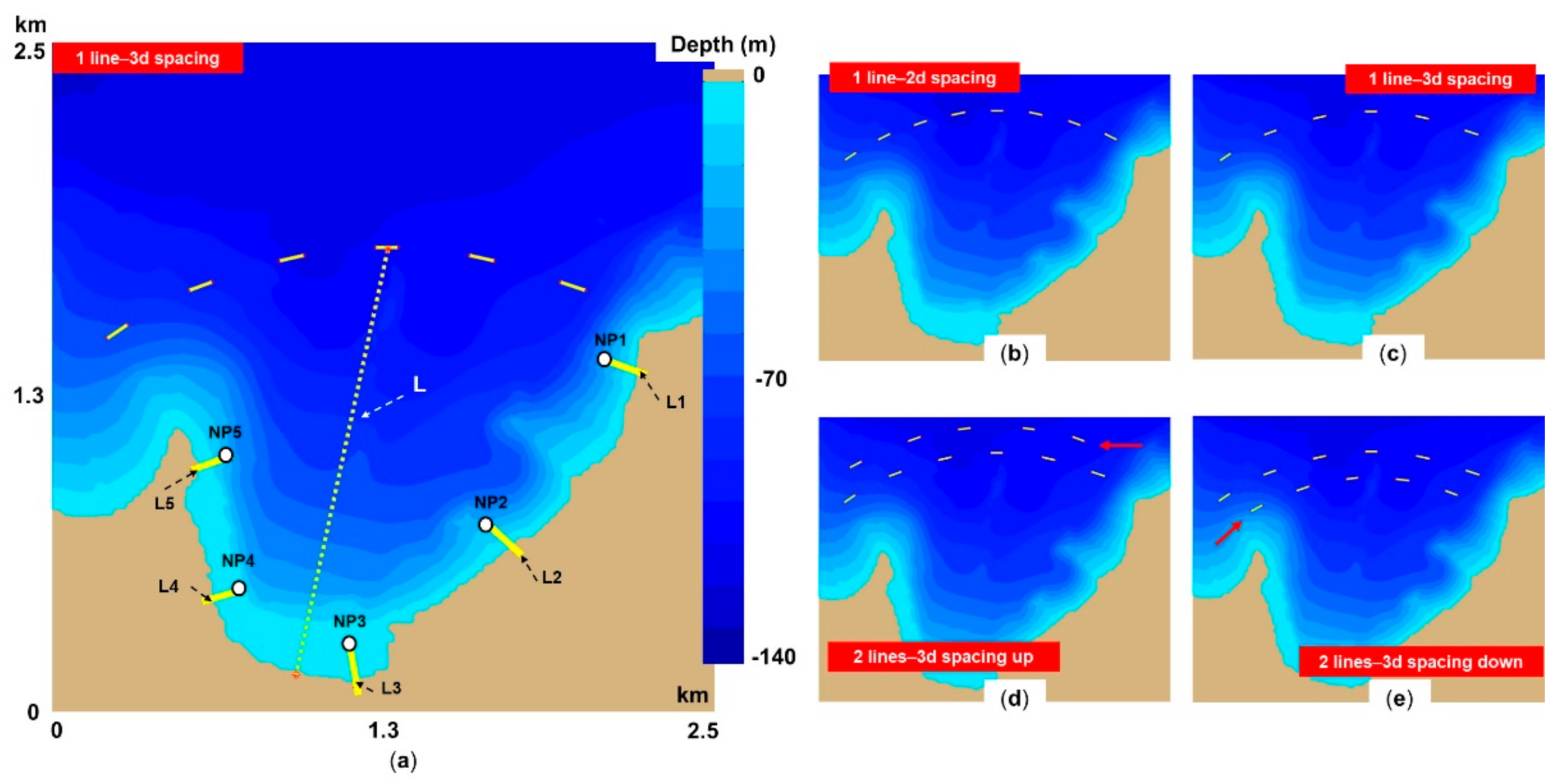
2.2.2. Case Studies
2.3. Wind and Wave-Data and Analysis
3. Results
3.1. Wind and Wave-Data and Analysis
3.2. Coastal Impact Induced by the Generic Marine Energy Farm
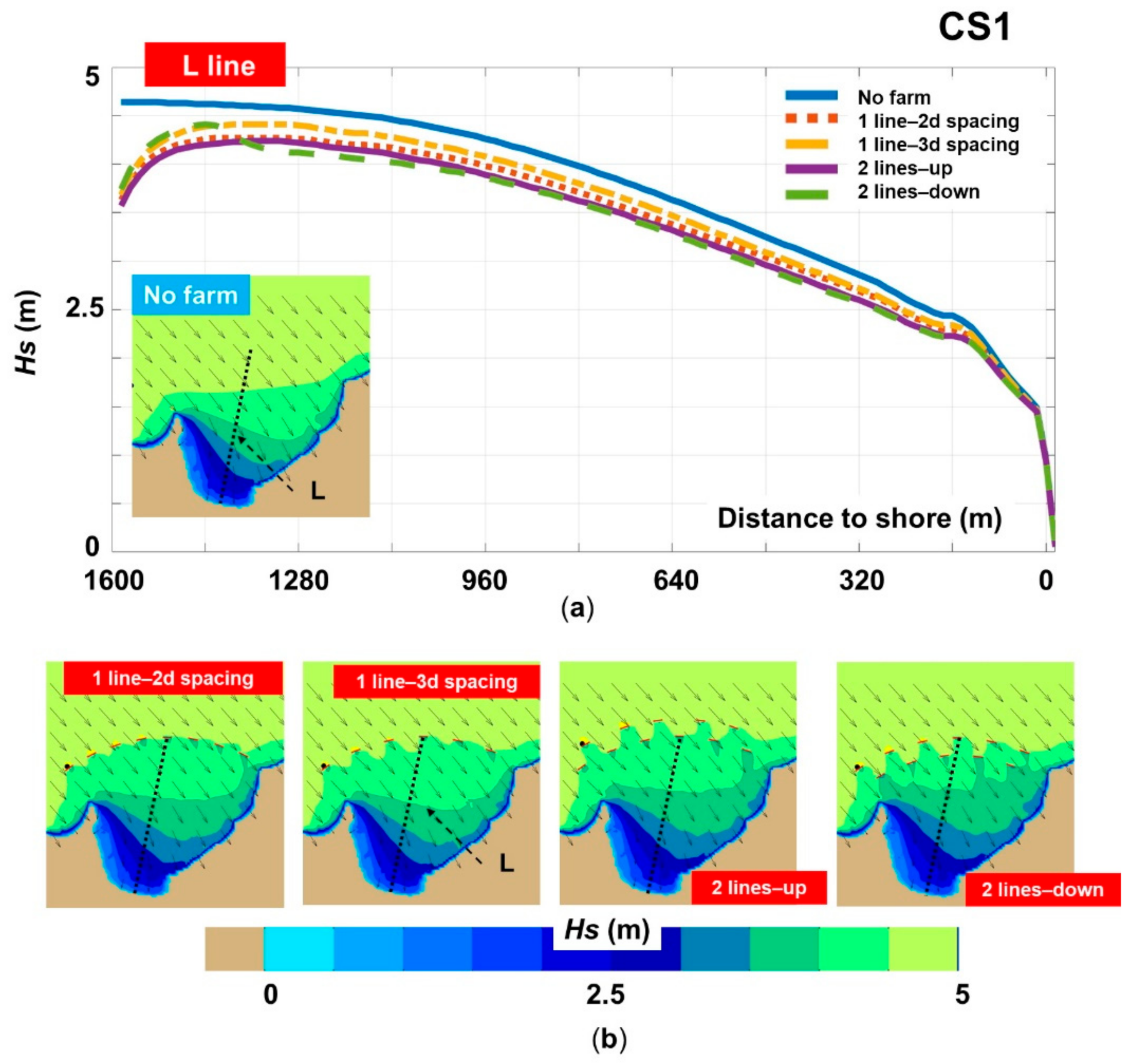
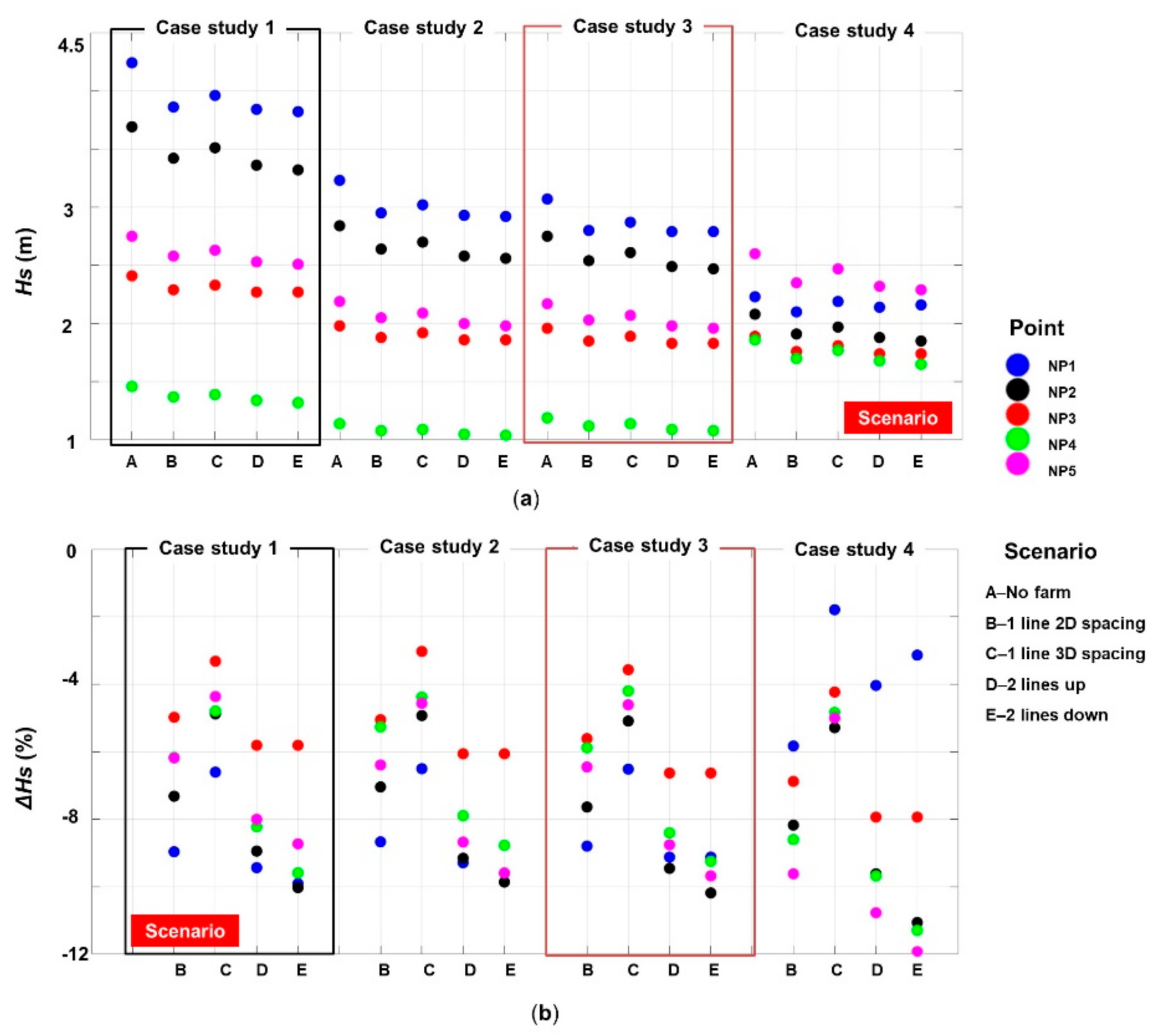
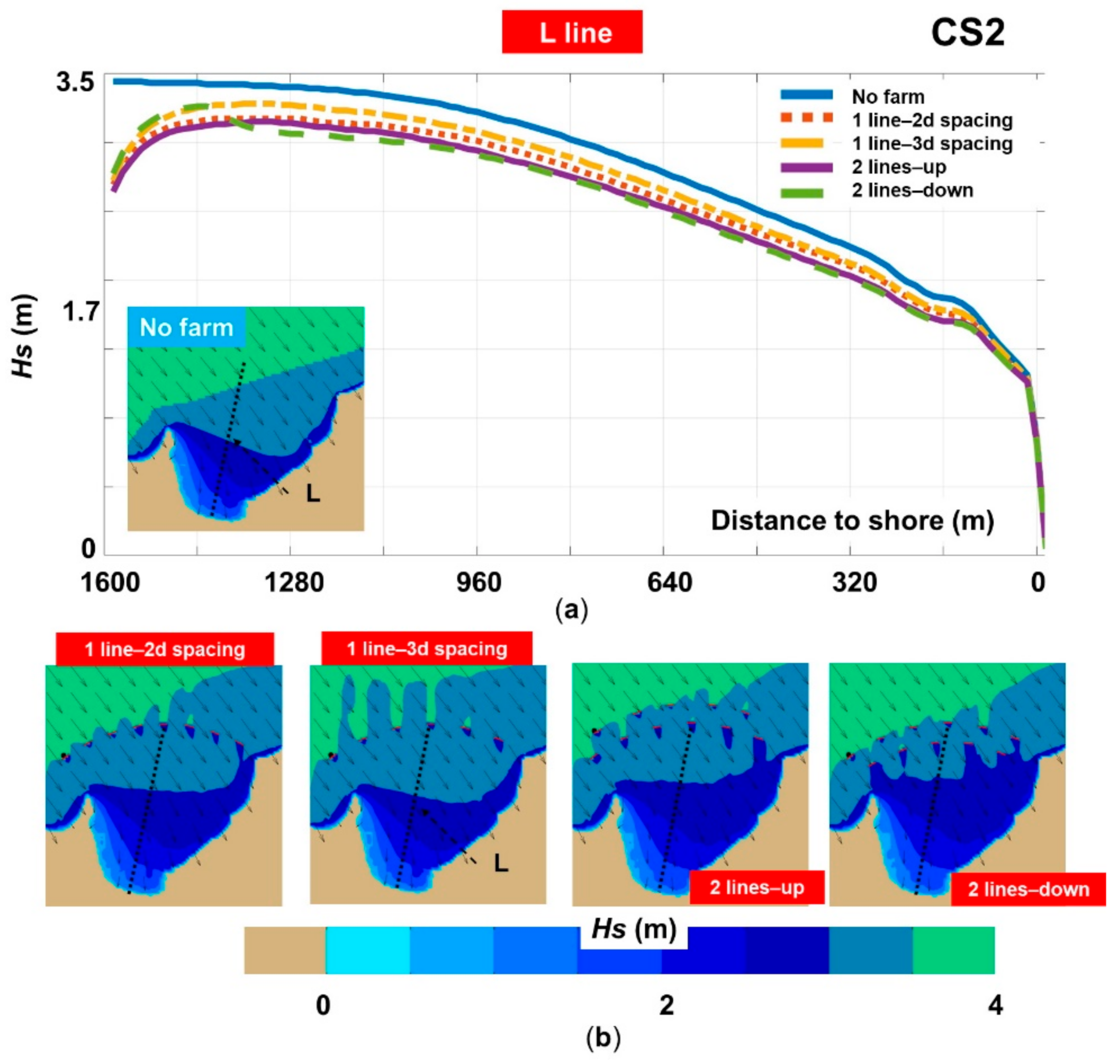
3.2.1. Analysis of the Significant Wave Heights
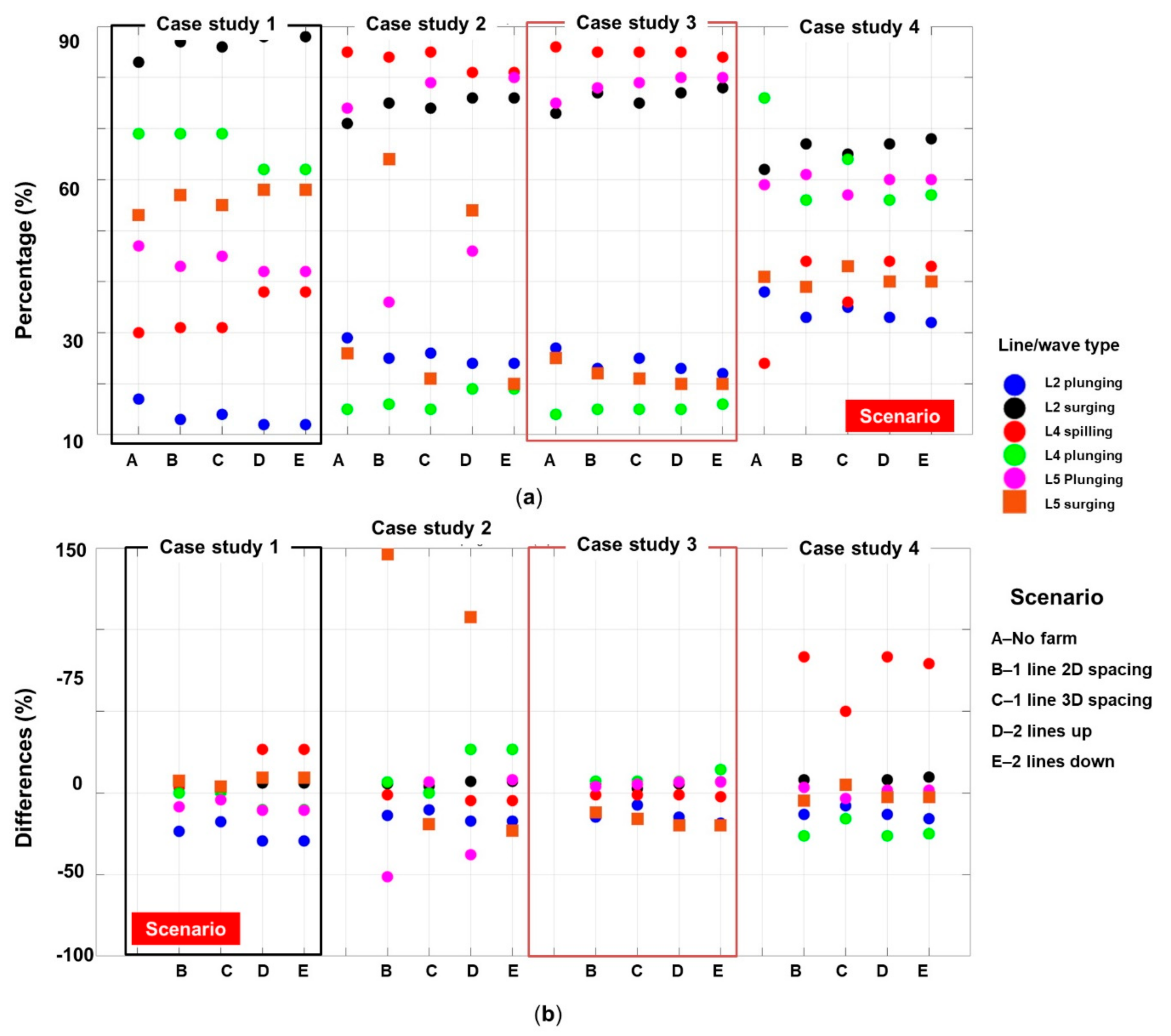
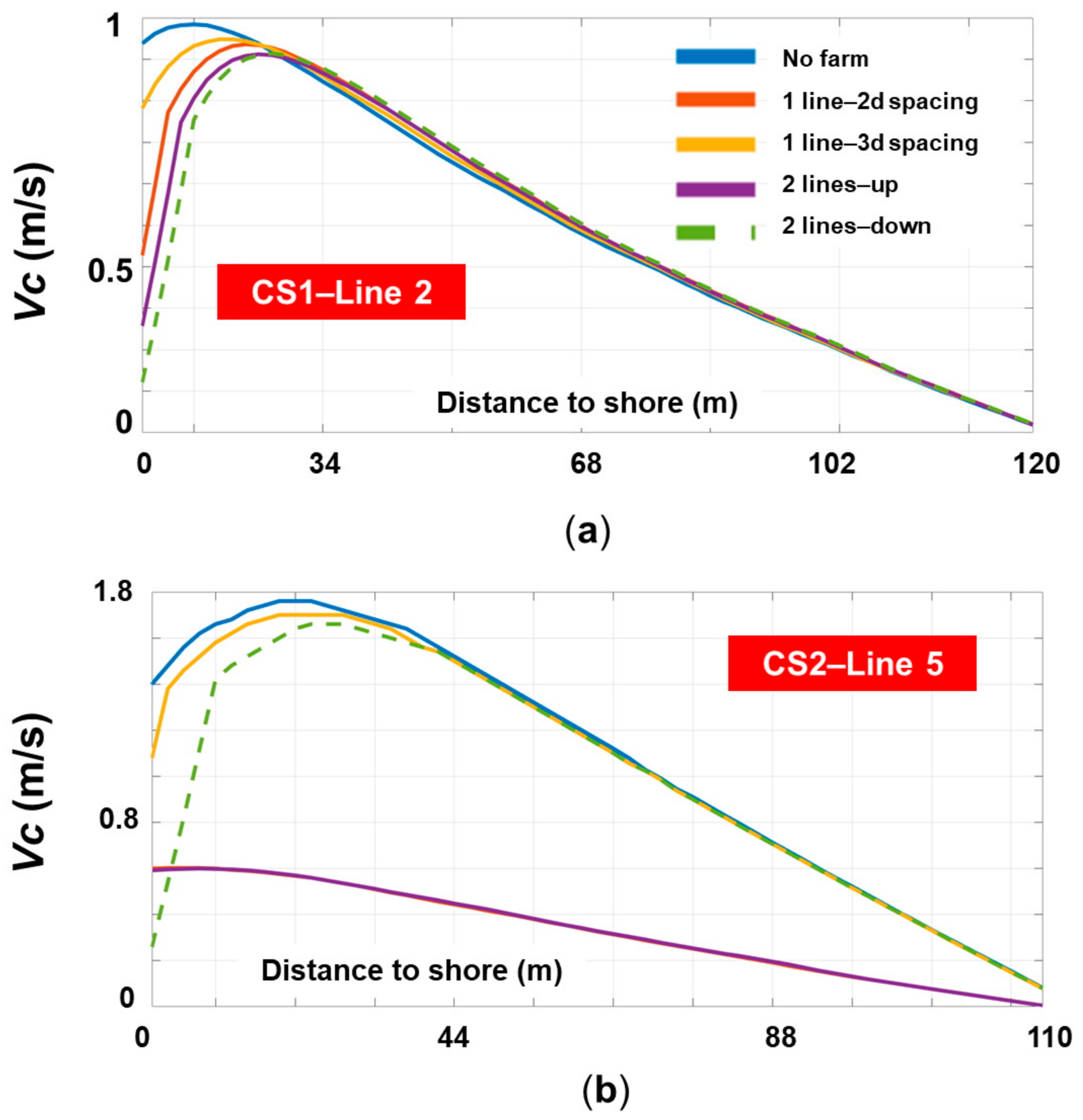
3.2.2. Additional Wave Parameters
4. Discussion
5. Conclusions
- (a)
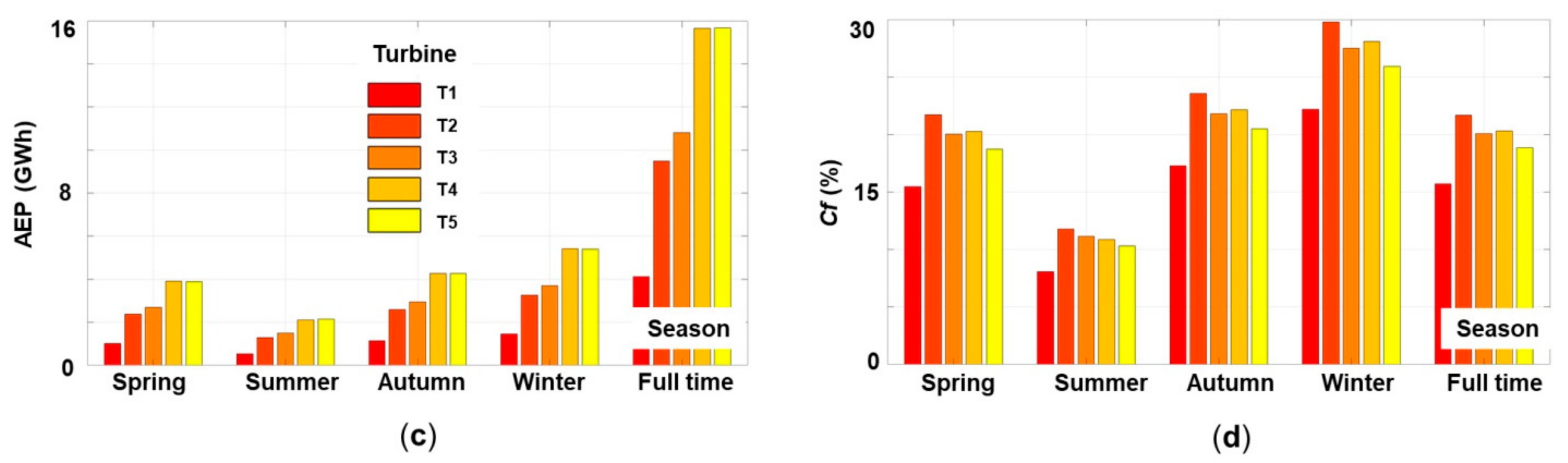
- The ERA 5 dataset indicates for the Giglio site higher extreme values than those provided by altimeter data. The accuracy of the satellite measurements in predicting the wave heights close to the shoreline area can be put into discussion, taking into account the interference problems that may occur near the land-water interface. From the analysis of the wave conditions, it was found that the target area is naturally protected by a peninsula, but there are also certain situations when the storm conditions may enter in the target area without any restriction. As for the wind conditions, a small offshore wind farm can cover a large percentage of the Giglio’s electricity demand during the touristic season.
- (b)
- The proposed wave farm made up of WaveCat systems, may reduce the wave heights close to the shore by almost 12%, a more significant effect being noticed for the two-line configuration. From the analysis of the spatial maps, it is difficult to quantify the far field effect, a short attenuation of the waves close to the WEC line followed by a quick regeneration of the wave fields being observed. It is also important to mention that the type of the breaking waves can significantly change, being possible to increase the percentage of the spilling waves (ex. Case 4—Line 4) that can carry sediments from the offshore area.
- (c)
- The impact of the wave farms on the longshore currents is minimal, being noticed however various patterns, such as the increase of the currents (up to 20%) or attenuation (up to 70%).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| σ | Relative frequency |
| θ | Wave direction |
| Velocity of the ambient current | |
| AEP | Annual Electricity Production |
| CAPEX | Capital expenditures |
| CCI-SS | European Space Agency Climate Change Initiative for Sea State |
| Dir | Wave direction |
| f(u) | Probability distribution of the wind speed |
| Hs | Significant wave height |
| ISSM | Interface for SWAN and Surf Models |
| N | Action density spectrum |
| P(u) | Power curve of a turbine |
| S | Sink and source terms |
| SWAN | Simulating Waves Nearshore |
| T | Number of hours per year |
| Tm | Wave period |
| U100 | Wind speed reported at 80 m above sea level |
| UTC | Universal Time Coordinated |
| Ubot | Orbital velocity at the bottom |
| Vcmax | Longshore currents maximum velocity |
| WECs | Wave Energy Converters |
| WT | Wind turbines |
| T1 | Vestas 90-3.0MW |
| T2 | Areva M5000-116 |
| T3 | Senvion 6.2M126 |
| T4 | Vestas 164-8.8 MW |
| T5 | Vestas 164-9.5 MW |
| CS | Case studies considered |
| CS1, CS2, CS3, CS4 | |
| Marine farm configurations | |
| Scenario A | No farm |
| Scenario B | 1 line—2d spacing |
| Scenario C | 1 line—3d spacing |
| Scenario D | 2 lines—up (the second line is up in relationship with the 1 line case) |
| Scenario E | 2 lines—down (the second line is down in relationship with the 1 line case) |
| Reference lines (L) defined in the nearshore | |
| L1, L2, L3, L4, L5 | |
| Nearshore points (NP) | NP1, NP2, NP3, NP4, NP5, reference points defined in the offshore extremity of the reference lines |
References
- Bernardino, M.; Rusu, L.; Soares, C.G. Evaluation of the wave energy resources in the cape verde islands. Renew. Energy 2017, 101, 316–326. [Google Scholar] [CrossRef]
- Mattiazzo, G. State of the art and perspectives of wave energy in the mediterranean sea: Backstage of ISWEC. Front. Energy Res. 2019, 7, 114. [Google Scholar] [CrossRef]
- Vannucchi, V.; Cappietti, L. Wave energy assessment and performance estimation of state of the art wave energy converters in italian hotspots. Sustainability 2016, 8, 1300. [Google Scholar] [CrossRef]
- Rusu, E.; Onea, F. An assessment of the wind and wave power potential in the island environment. Energy 2019, 175, 830–846. [Google Scholar] [CrossRef]
- Lavidas, G.; Venugopal, V. A 35 year high-resolution wave atlas for nearshore energy production and economics at the aegean sea. Renew. Energy 2017, 103, 401–417. [Google Scholar] [CrossRef]
- Ferrari, F.; Besio, G.; Cassola, F.; Mazzino, A. Optimized wind and wave energy resource assessment and offshore exploitability in the mediterranean sea. Energy 2020, 190, 116447. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Williams, A.T.; Anfuso, G. Hard protection structures as a principal coastal erosion management strategy along the caribbean coast of colombia. A chronicle of pitfalls. Ocean Coast. Manag. 2018, 156, 58–75. [Google Scholar] [CrossRef]
- Andre, C.; Boulet, D.; Rey-Valette, H.; Rulleau, B. Protection by hard defence structures or relocation of assets exposed to coastal risks: Contributions and drawbacks of cost-benefit analysis for long-term adaptation choices to climate change. Ocean Coast. Manag. 2016, 134, 173–182. [Google Scholar] [CrossRef]
- Veron, S.; Mouchet, M.; Govaerts, R.; Haevermans, T.; Pellens, R. Vulnerability to climate change of islands worldwide and its impact on the tree of life. Sci. Rep. 2019, 9, 14471. [Google Scholar] [CrossRef] [PubMed]
- State and Pressures of the Marine and Coastal Mediterranean Environment|Semantic Scholar. Available online: https://www.semanticscholar.org/paper/State-and-pressures-of-the-marine-and-coastal-Map/5cde8bbfa6ce871e82f450a3135231ccbaaf604a (accessed on 14 January 2021).
- Erosion of the Mediterranean Coastline: Implications for Tourism. Available online: https://assembly.coe.int/nw/xml/XRef/X2H-Xref-ViewHTML.asp?FileID=10340&lang=EN (accessed on 14 January 2021).
- Barcelona Convention-Marine-Environment-European Commission. Available online: https://ec.europa.eu/environment/marine/international-cooperation/regional-sea-conventions/barcelona-convention/index_en.htm (accessed on 14 January 2021).
- Onea, F.; Rusu, E. Sustainability of the reanalysis databases in predicting the wind and wave power along the european coasts. Sustainability 2018, 10, 193. [Google Scholar] [CrossRef]
- Rusu, E.; Onea, F. Joint evaluation of the wave and offshore wind energy resources in the developing countries. Energies 2017, 10, 1866. [Google Scholar] [CrossRef]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F. On the potential synergies and applications of wave energy converters: A review. Renew. Sustain. Energy Rev. 2021, 135, 110162. [Google Scholar] [CrossRef]
- Bergillos, R.J.; Lopez-Ruiz, A.; Medina-Lopez, E.; Monino, A.; Ortega-Sanchez, M. The role of wave energy converter farms on coastal protection in eroding deltas, guadalfeo, southern spain. J. Clean. Prod. 2018, 171, 356–367. [Google Scholar] [CrossRef]
- Abanades, J.; Flor-Blanco, G.; Flor, G.; Iglesias, G. Dual wave farms for energy production and coastal protection. Ocean Coast. Manag. 2018, 160, 18–29. [Google Scholar] [CrossRef]
- Rusu, E.; Onea, F. Study on the influence of the distance to shore for a wave energy farm operating in the central part of the portuguese nearshore. Energy Conv. Manag. 2016, 114, 209–223. [Google Scholar] [CrossRef]
- Onea, F.; Rusu, E. The expected efficiency and coastal impact of a hybrid energy farm operating in the portuguese nearshore. Energy 2016, 97, 411–423. [Google Scholar] [CrossRef]
- Zanopol, A.T.; Onea, F.; Rusu, E. Coastal impact assessment of a generic wave farm operating in the romanian nearshore. Energy 2014, 72, 652–670. [Google Scholar] [CrossRef]
- Fairley, I.; Lewis, M.; Robertson, B.; Hemer, M.; Masters, I.; Horrillo-Caraballo, J.; Karunarathna, H.; Reeve, D. Global wave resource classification and application to marine energy deployments. In Proceedings of the EGU General Assembly Conference Abstracts, Online Conference. 4–8 May 2020. [Google Scholar]
- Lavidas, G.; Blok, K. Shifting wave energy perceptions: The case for Wave Energy Converter (WEC) feasibility at milder resources. Renew. Energy 2021, 170, 1143–1155. [Google Scholar] [CrossRef]
- Bergillos, R.J.; Rodriguez-Delgado, C.; Allen, J.; Iglesias, G. Wave energy converter configuration in dual wave farms. Ocean Eng. 2019, 178, 204–214. [Google Scholar] [CrossRef]
- Rodriguez-Delgado, C.; Bergillos, R.J.; Iglesias, G. dual wave farms and coastline dynamics: The role of inter-device spacing. Sci. Total Environ. 2019, 646, 1241–1252. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, E.; Silva, R.; Zanuttigh, B.; Angelelli, E.; Andersen, T.L.; Martinelli, L.; Norgaard, J.Q.H.; Ruol, P. Beach response to wave energy converter farms acting as coastal defence. Coast. Eng. 2014, 87, 97–111. [Google Scholar] [CrossRef]
- Raileanu, A.; Onea, F.; Rusu, E. An overview of the expected shoreline impact of the marine energy farms operating in different coastal environments. J. Mar. Sci. Eng. 2020, 8, 228. [Google Scholar] [CrossRef]
- Onea, F.; Rusu, L. Coastal Impact of a Hybrid Marine Farm Operating Close to the Sardinia Island; IEEE: New York, NY, USA, 2015; ISBN 978-1-4799-8737-5. [Google Scholar]
- Piazzi, L.; Cecchi, E.; Gennaro, P.; Penna, M.; Trabucco, B.; Ceccherelli, G. Spread of non-indigenous macroalgae and disturbance: Impact assessment of the costa concordia shipwreck (Giglio island, Italy) using the ALEX index. Ocean Coast. Manag. 2020, 183, 104999. [Google Scholar] [CrossRef]
- Cutroneo, L.; Ferretti, G.; Scafidi, D.; Ardizzone, G.D.; Vagge, G.; Capello, M. Current observations from a looking down vertical V-ADCP: Interaction with winds and tide? The case of Giglio island (Tyrrhenian sea, Italy). Oceanologia 2017, 59, 139–152. [Google Scholar] [CrossRef]
- Rusu, E.; Conley, D.; Ferreira-Coelho, E. A hybrid framework for predicting waves and longshore currents. J. Mar. Syst. 2008, 69, 59–73. [Google Scholar] [CrossRef]
- Rusu, E.; Macuta, S. Numerical modelling of longshore currents in marine environment. Environ. Eng. Manag. J. 2009, 8, 147–151. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Mettlach, T.R.; Earle, M.D.; Hsu, Y.L. Software Design Document for the Navy Standard Surf Model Version 3.2; Defense Technical Information Center: Fort Belvoir, VA, USA, 2002. [Google Scholar]
- Smith, H.C.M.; Pearce, C.; Millar, D.L. Further analysis of change in nearshore wave climate due to an offshore wave farm: An enhanced case study for the wave hub site. Renew. Energy 2012, 40, 51–64. [Google Scholar] [CrossRef]
- O’Dea, A.; Haller, M.C.; Özkan-Haller, H.T. The impact of wave energy converter arrays on wave-induced forcing in the surf zone. Ocean Eng. 2018, 161, 322–336. [Google Scholar] [CrossRef]
- Rusu, E. A matlab toolbox associated with modeling coastal waves. Curr. Dev. Oceanogr. 2011, 2, 17–52. [Google Scholar]
- Goda, Y.; Takeda, H.; Moriya, Y. Laboratory Investigation of Wave Transmission over Breakwaters; 13 (from Seelig, 1979); Port and Harbour Technical Research Institute: Yokosuka, Japan, 1967. [Google Scholar]
- Bergillos, R.J.; Rodriguez-Delgado, C.; Iglesias, G. Wave farm impacts on coastal flooding under sea-level rise: A case study in southern spain. Sci. Total Environ. 2019, 653, 1522–1531. [Google Scholar] [CrossRef]
- Carballo, R.; Iglesias, G. Wave farm impact based on realistic Wave-WEC interaction. Energy 2013, 51, 216–229. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Dodet, G.; Piolle, J.-F.; Quilfen, Y.; Abdalla, S.; Accensi, M.; Ardhuin, F.; Ash, E.; Bidlot, J.-R.; Gommenginger, C.; Marechal, G.; et al. The sea state CCI dataset v1: Towards a sea state climate data record based on satellite observations. Earth Syst. Sci. Data 2020, 12, 1929–1951. [Google Scholar] [CrossRef]
- Rusu, L.; Rusu, E. Evaluation of the worldwide wave energy distribution based on ERA5 data and altimeter measurements. Energies 2021, 14, 394. [Google Scholar] [CrossRef]
- Palone, F.; Portoghese, P.; Buono, L.; Necci, A.; Gatta, F.M.; Geri, A.; Lauria, S.; Maccioni, M. Replacing diesel generators with hybrid renewable power plants: Giglio smart island project. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Onea, F.; Rusu, L. Evaluation of some state-of-the-art wind technologies in the nearshore of the black sea. Energies 2018, 11, 2452. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- CERC. Shore Protection Manual; Coastal Engineer Research Center, U.S. Army Corps of Engineers, U.S. Government Printing Office: Vicksburg, MS, USA, 1984.
- Onea, F.; Rusu, E. The expected shoreline effect of a marine energy farm operating close to sardinia island. Water 2019, 11, 2303. [Google Scholar] [CrossRef]
- Shemdin, P.; Hasselmann, K.; Hsiao, V.; Herterich, K. Non-linear and linear bottom interaction effects in shallow water. In Turbulent Fluxes through the Sea Surface, Wave Dynamics and Prediction; Springer: Boston, MA, USA, 1978; pp. 347–372. [Google Scholar]
- The SWAN Team. SWAN User Manual, SWAN Cycle III Version 41.31A; Delft University of Technology: Delft, The Netherlands, 2020. [Google Scholar]
- Ulazia, A.; Sáenz, J.; Ibarra-Berastegi, G.; González-Rojí, S.J.; Carreno-Madinabeitia, S. Global estimations of wind energy potential considering seasonal air density changes. Energy 2019, 187, 115938. [Google Scholar] [CrossRef]
- Assessment of Offshore Wind Energy Resources for the United States. Available online: https://www.energy.gov/eere/wind/downloads/assessment-offshore-wind-energy-resources-united-states (accessed on 15 February 2021).








| Input/ Process | Wave | Wind | Tide | Crt | Gen | Wcap | Quad | Triad | Diff | Bfric | Setup | Br |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | x | - | x | x | x | x | x | x | x | x | x | |
| Computational domain | Coordinates | ∆x × ∆y (m) | ∆θ (°) | Mod | nf | nθ | ngx × ngy = np | |||||
| Cartesian | 25 × 25 | 5 | Stat/BSBT | 36 | 34 | 99 × 101 = 9999 | ||||||
| Turbine | ID | Hub Height (m) | Cut-in Speed (m/s) | Rated Speed (m/s) | Cut-Out Speed (m/s) | Projects |
|---|---|---|---|---|---|---|
| V90-3.0 | T1 | 100 | 4 | 15 | 25 | Barrow (UK) |
| Areva M5000-116 | T2 | 100 | 4 | 12.5 | 25 | Global Tech I (DE) |
| Senvion 6.2 M126 | T3 | 100 | 3.5 | 13.5 | 30 | Nordsee Ost (DE) |
| V164-8.8 MW | T4 | 100 | 4 | 13 | 25 | Aberdeen (UK) |
| V164-9.5MW | T5 | 100 | 3.5 | 14 | 25 | EolMed (FR) |
| Case Study | Time Frame | Hs (m) | Tm (s) | Dir (°) |
|---|---|---|---|---|
| CS1 | 1999.12.28-h18 | 4.72 | 8.20 | 273.7 |
| CS2 | 1999.02.22-h18 | 3.49 | 6.96 | 275.6 |
| CS3 | 2018.01.17-h12 | 3.34 | 6.75 | 280.8 |
| CS4 | 2013.11.11-h12 | 3.17 | 6.32 | 353 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusu, L.; Onea, F.; Rusu, E. The Expected Impact of Marine Energy Farms Operating in Island Environments with Mild Wave Energy Resources—A Case Study in the Mediterranean Sea. Inventions 2021, 6, 33. https://doi.org/10.3390/inventions6020033
Rusu L, Onea F, Rusu E. The Expected Impact of Marine Energy Farms Operating in Island Environments with Mild Wave Energy Resources—A Case Study in the Mediterranean Sea. Inventions. 2021; 6(2):33. https://doi.org/10.3390/inventions6020033
Chicago/Turabian StyleRusu, Liliana, Florin Onea, and Eugen Rusu. 2021. "The Expected Impact of Marine Energy Farms Operating in Island Environments with Mild Wave Energy Resources—A Case Study in the Mediterranean Sea" Inventions 6, no. 2: 33. https://doi.org/10.3390/inventions6020033
APA StyleRusu, L., Onea, F., & Rusu, E. (2021). The Expected Impact of Marine Energy Farms Operating in Island Environments with Mild Wave Energy Resources—A Case Study in the Mediterranean Sea. Inventions, 6(2), 33. https://doi.org/10.3390/inventions6020033








