Simple Design Methodology for R.C. Slabs by Hybrid Reinforcing of Steel Rebars and Uniaxial or Triaxial Geogrids
Abstract
1. Introduction
2. Focused Literature Review on the Hybrid Reinforcing System of Geogrids and Steel Rebar
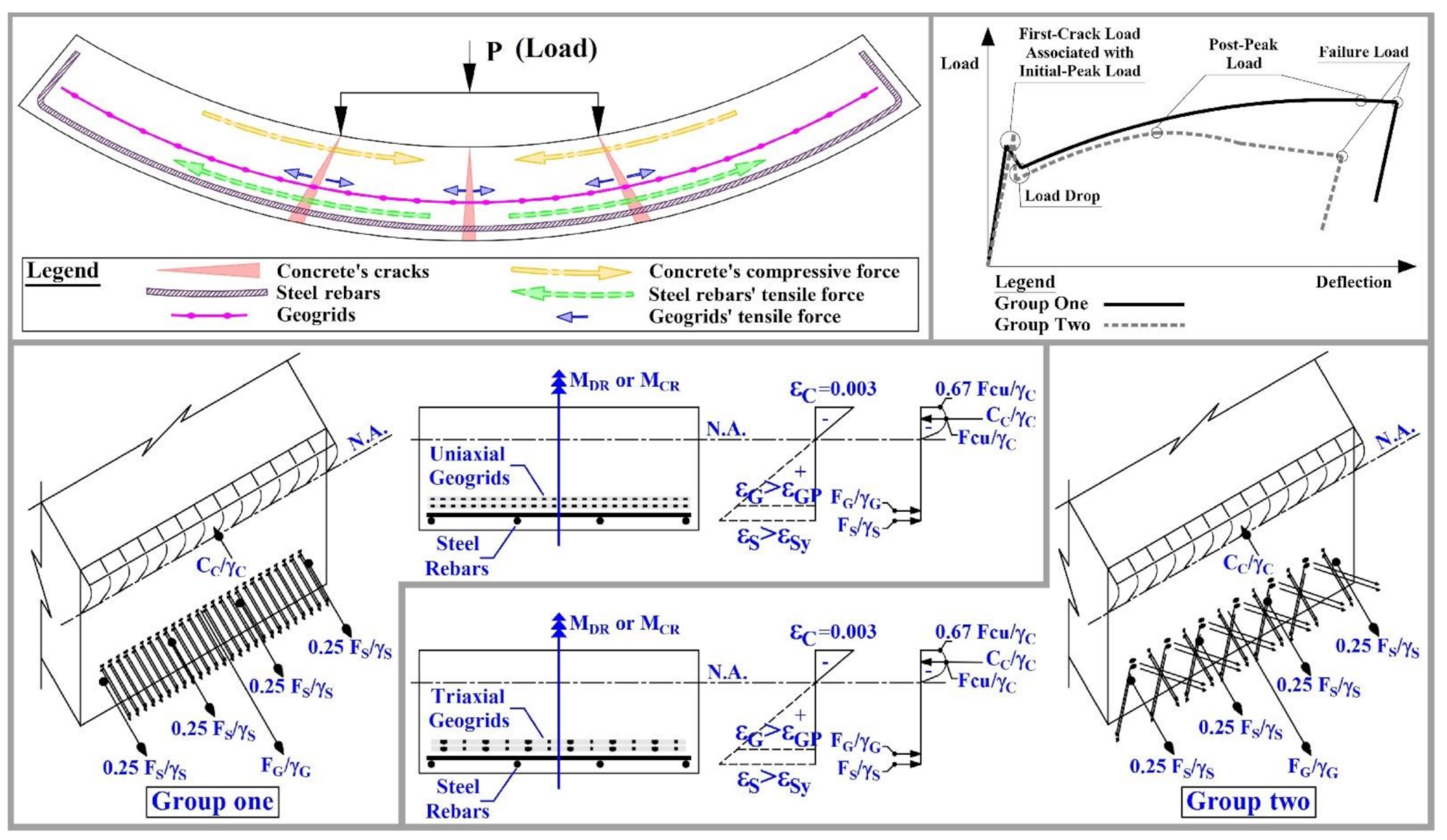
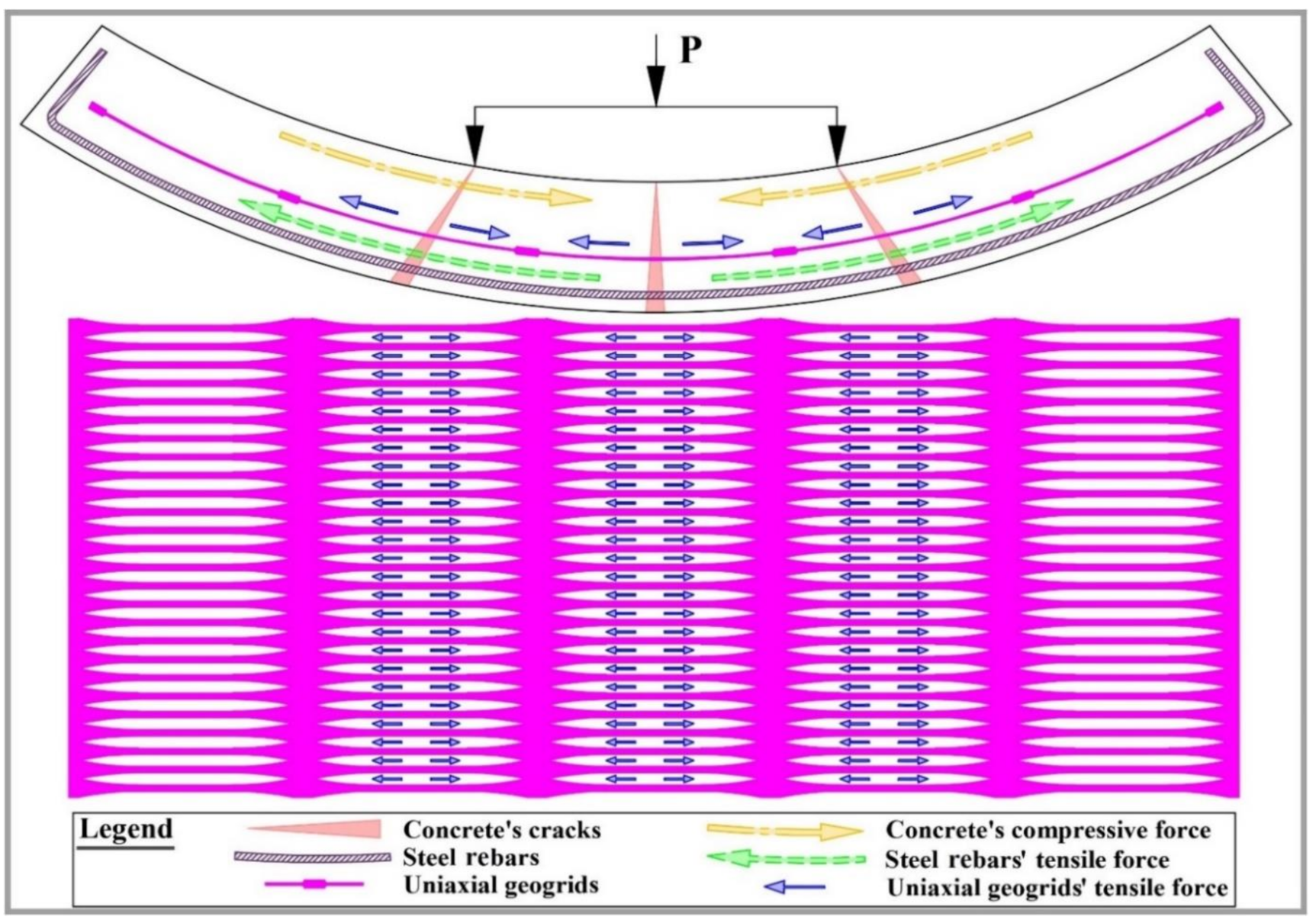
- The use of steel rebars and geogrids as a hybrid reinforcing material for concrete slabs provides a greater first-crack load and a greater ultimate load comparing to the conventional reinforcing material of steel rebars or using geogrids as the main reinforcing material. Meanwhile, it increased the deflection values.
- For the hybrid reinforcing of steel rebars and geogrids, the reduction of steel rebars’ reinforcing ratio to 0.13% led to a reduction in the geogrids’ contribution and its effectiveness as concrete slab-reinforcing material. Accordingly, it cannot be dependent on geogrids as the main reinforcing material for concrete slabs.
- The impact energy capacity and impact resistance of concrete slabs have improved by using the hybrid reinforcing steel rebars and geogrids with a positive relation to the count of the geogrids’ layers.
- The hybrid reinforcing of steel rebars and uniaxial geogrids provided efficient utilization and better performance, particularly for uniaxial geogrids with the grade of 120 kN/m and greater, as it provided greater benefits in terms of values, including and not limited to capacity of loads, capacity of energy absorption, and displacement ductility index. It also provided more effective utilization, including and not limited to better flexural performance and greater benefits in terms of cost compared to the case of using the conventional reinforcing of steel rebars using the hybrid reinforcing of steel rebars and triaxial geogrids. However, the hybrid reinforcing of steel rebars and triaxial geogrids provided smaller deflection values and greater values of first-crack load values. As a recommendation, the uniaxial geogrids is should be tension-stressed before the concrete pouring.
3. Characteristics of Used Materials
4. Summary of the Experimental Program and Results
5. Geogrids Tensile Force at the Post-Peak Load
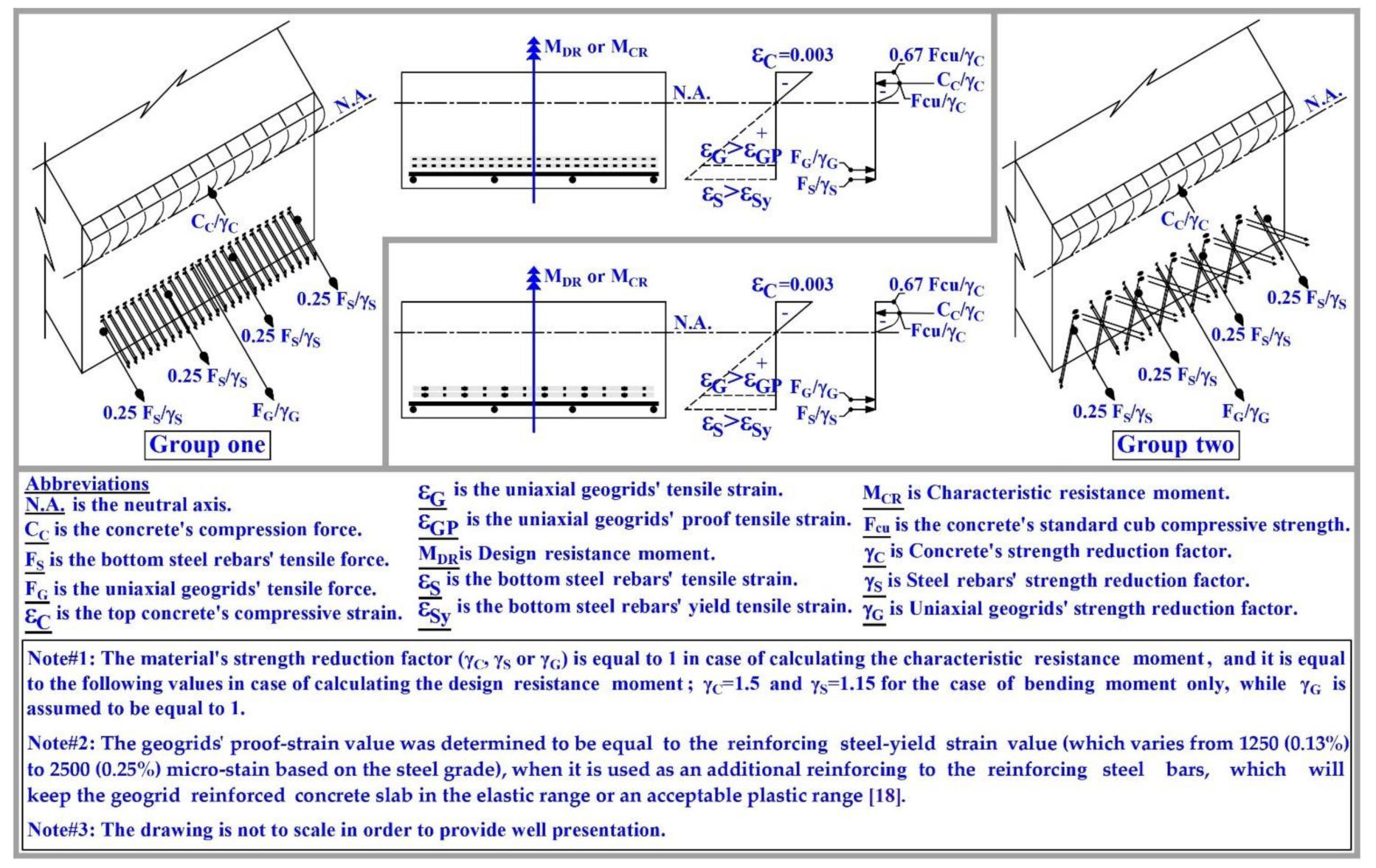
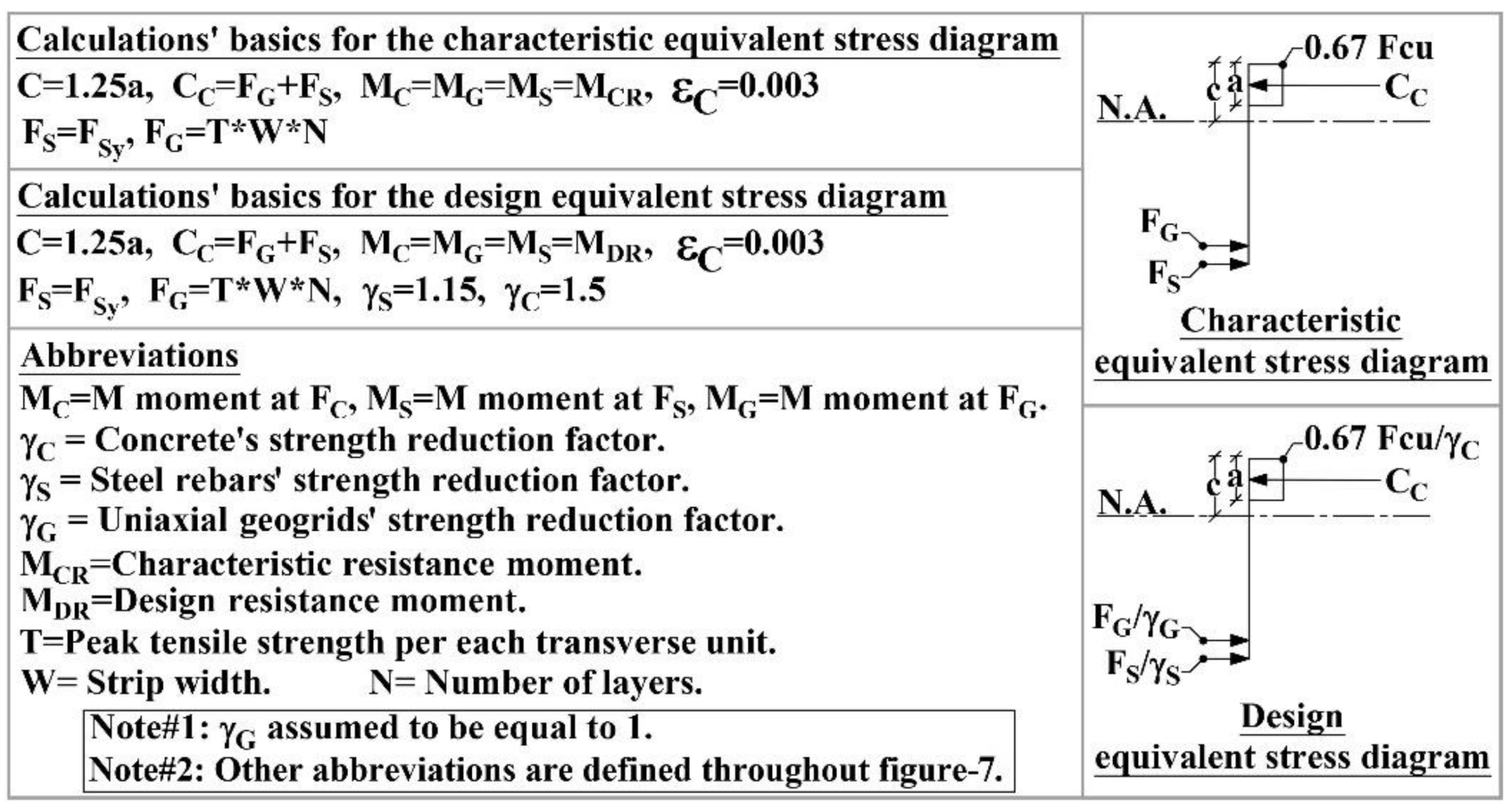
6. Experimental Moment, Characteristics Resistance Moment, and Design Resistance Moment
7. Simple Design Relation to Estimate the Desired Grade of Geogrids and Its Count of Layers
8. Conclusions and Recommendations
9. Future Studies
Author Contributions
Funding
Conflicts of Interest
References
- Saranyadevi, M.; Suresh, M.; Sivaraja, M. Strengthening of Concrete Beam by Reinforcing with Geosynthetic Materials. Int. J. Adv. Res. Educ. Technol. 2016, 3, 245–251. [Google Scholar]
- Maxwell, S.; Kim, W.-H.; Tuncer, B.E.; Benson, C.H. Effectiveness of Geo-Synthetics in Stabilizing Soft Subgrades; University of Wisconsin-Madison: Madison, WI, USA, 2005. [Google Scholar]
- Webster, S.L. Geogrid Reinforced Base Course for Flexible Pavements for Light Aircraft: Test. Section Construction, Behaviour under Traffic, Laboratory Tests, and Design Criteria; National Technical Information Service: Springfield, VA, USA, 1992. [Google Scholar]
- Sharbaf, M. Laboratory Evaluation of Geogrid-Reinforced Flexible Pavements. Master’s Thesis, University of Nevada, Las Vegas, NV, USA, May 2016. [Google Scholar]
- Al-Hedad, S.A.; Bambridge, E.; Muhammad, N.S. Influence of Geogrid on The Drying Shrinkage Performance of Concrete Pavements. Constr. Build. Mater. 2017, 146, 165–174. [Google Scholar] [CrossRef]
- Al-Hedad, A.S.A.; Farhan, N.A.; Zhang, M.; Sheikh, M.N.; Hadi, M.N.S. Effect of geogrid reinforcement on the drying shrinkage and thermal expansion of geopolymer concrete. Struct. Concr. 2020, 21, 1029–1039. [Google Scholar] [CrossRef]
- Al-Hedad, A.-A.; Hadi, M.N.S. Effect of geogrid reinforcement on the strains at compressive zone of concrete pavements. Struct. Concr. 2020, 1–11. [Google Scholar] [CrossRef]
- Al Basiouni Al Masri, Z.; Daou, A.; Haj Chhade, R.; Chehab, G. Experimental and Numerical Assessment of the Behavior of Geogrid-Reinforced Concrete and Its Application in Concrete Overlays. J. Mater. Civ. Eng. 2018, 30, 04018332. [Google Scholar] [CrossRef]
- Itani, H.; Saad, G.A.; Chehab, G.R. The use of geogrid reinforcement for enhancing the performance of concrete overlays: An experimental and numerical assessment. Constr. Build. Mater. 2016, 124, 826–837. [Google Scholar] [CrossRef]
- Khodaii, A.; Fallah, S. Effects of Geo-Synthetic Reinforcement on The Propagation of Reflection Cracking in Asphalt Overlays. Int. J. Civ. Eng. 2009, 7, 131–140. [Google Scholar]
- Walubita, L.F.; Nyamuhokya, T.P.; Komba, J.; Tanvir, H.A.; Souliman, M.; Naik, B. Comparative assessment of the interlayer shear-bond strength of geogrid reinforcements in hot-mix asphalt. Constr. Build. Mater. 2018, 191, 726–735. [Google Scholar] [CrossRef]
- Tang, X.; Chehab, G.R.; Kim, S. Laboratory study of geogrid reinforcement in Portland cement concrete. In Proceedings of the 6th RILEM International Conference on Cracking in Pavements, Chicago, IL, USA, 16–18 June 2018; pp. 769–778. [Google Scholar]
- Ahmed Shaban, A.H.G. Strengthening of Reinforced Concrete Slabs Using Different types of Geo-Grids. Int. J. Civ. Eng. Technol. 2019, 10, 1851–1861. [Google Scholar]
- Al Qadi, A.N.; Al-Kadi, Q.N.S.; Al-Zaidyeen, S.M. Impact Strength of Oil-Palm Shell on Lightweight Concrete Slabs Reinforced with a Geo-Grid. J. Mater. Civ. Eng. 2015, 27, 04014264. [Google Scholar] [CrossRef]
- Tang, X.; Mohamad, N.; Higgins, J.; Higgins, I. Concrete Slab-on-Grade Reinforced by Geogrids. In Proceedings of the Eight International Conference on Case Histories in Geotechnical Engineering, Philadelphia, PA, USA, 24–27 March 2019. [Google Scholar]
- Mohamed, R.N.A.; El Sebai, A.M.; Gabr, A.S.A.-H. Flexural Behavior Analysis and Design Approach for R.C. Beams by Hybrid Reinforcement of Steel Rebars and HDPE Uniaxial Geogrids. Lat. Am. J. Solids Struct. 2021, 18, 1–27. [Google Scholar] [CrossRef]
- El Meski, F.; Chehab, G.R. Flexural behavior of concrete beams reinforced with different types of geogrids. J. Mater. Civ. Eng. 2014, 26, 04014038. [Google Scholar] [CrossRef]
- Mohamed, R.N.A.; El Sebai, A.M.; Gabr, A.S.A.-H. Flexural Behavior of Reinforced Concrete Slabs Reinforced with Innovative Hybrid Reinforcement of Geogrids and Steel Bars. Buildings 2020, 10, 161. [Google Scholar] [CrossRef]
- Ahmed Alamli, A.S.; Yousif, M.A.; Mohammed, M.H. Reinforced Concrete Strengthening by Using Geotextile Reinforcement for Foundations and Slabs. Int. J. Civ. Struct. Environ. Infrastruct. Eng. Res. Dev. 2017, 7, 35–46. [Google Scholar] [CrossRef]
- Ali, Y.S.; Awad Waryosh, W.; Yousif, M.A. Increasing Ultimate Strength of Reinforced Concrete Slab by Using Geogrid. Glob. J. Eng. Sci. Res. Manag. 2018, 5, 83–94. [Google Scholar] [CrossRef]
- Tharani, K.; Mahendran, N.; Vijay, T.J. Experimental Investigation of Geogrid Reinforced Concrete Slab. Int. J. Eng. Adv. Technol. 2019, 8, 158–163. [Google Scholar]
- Dong, Y.-L.; Han, J.; Bai, X.-H. Numerical analysis of tensile behavior of geogrids with rectangular and triangular apertures. Geotext. Geomembr. 2011, 29, 83–91. [Google Scholar] [CrossRef]
- Egyptian Ministry of Housing; Egyptian Code Standing Committee for Design and Construction of Concrete Structures. Egyptian Code for Design and Construction of Concrete Structures (ECP:203-2018); Housing and Building National Research Center (HBRC): Dokki, Egypt, 2018.



| Concrete–Mix, WC = 0.5, 1.5% Admixture | ||||||
|---|---|---|---|---|---|---|
| Cement Grade 42.5 | Sand | Crushed Limestone | Water | Water Reducing and Super-Plasticizer Concrete Admixture | Cone Slump | Compressive Strength after 28 days |
| 400 kg/m3 | 600 kg/m3 | 1200 kg/m3 | 200 kg/m3 | 6 kg/m3 | 6.5 cm | 40 N/mm2 |
| Characteristics of the Steel Rebars | |||
|---|---|---|---|
| Diameter in mm (nominal) | 6 | Cross-Area in mm2 (nominal) | 28.29 |
| Weight in kg/m (experimental) | 0.224 | Cross-Area in mm2 (experimental) | 28.52 |
| Yield Load in kN (experimental) | 8.4 | Ultimate Load in kN (experimental) | 13.51 |
| Yield Stress in N/mm2 (experimental) | 296.97 | Tensile Resistance in N/mm2 (experimental) | 477.51 |
| Yield Strain in Micro-strain (experimental) | 1485 | Elongation After Break Down in % (experimental) | 32.7 |
| Young’s modulus in N/mm2 (experimental) 200000 | |||
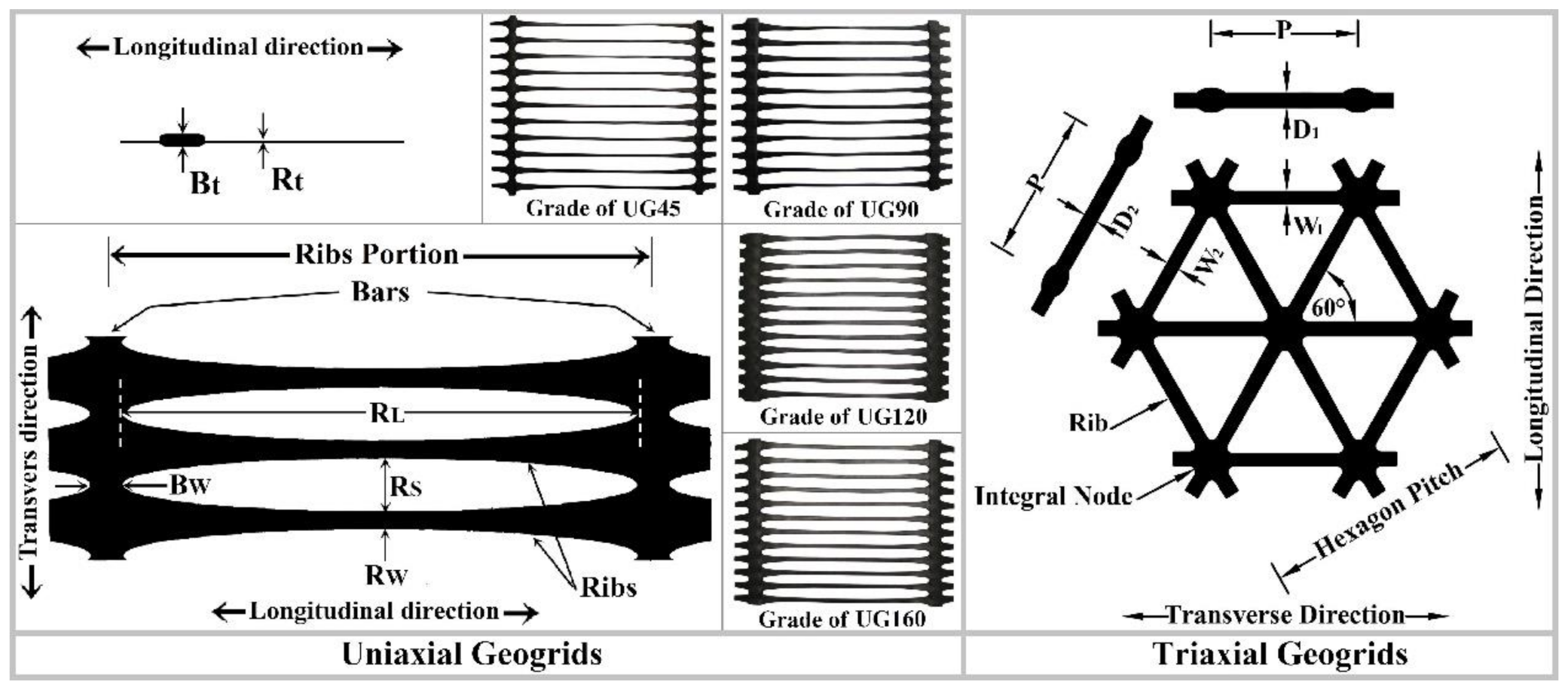
| Characteristics | Uniaxial Geogrids (UG) Grades | |||
|---|---|---|---|---|
| UG45 | UG90 | UG120 | UG160 | |
| RL in mm (physical) | 220 | 220 | 220 | 220 |
| Rs in mm (physical) | 18 | 15 | 15 | 13 |
| Bw in mm (physical) | 12.5 | 15 | 16.8 | 19.5 |
| Rw in mm (physical) | 2.7 | 3.3 | 4 | 6.1 |
| Bt in mm (physical) | 3.6 | 5.5 | 7 | 7.5 |
| Rt in mm (physical) | 1.3 | 1.7 | 2.4 | 2.3 |
| Mass per Unit Area in g/m2 | 300 | 600 | 800 | 1000 |
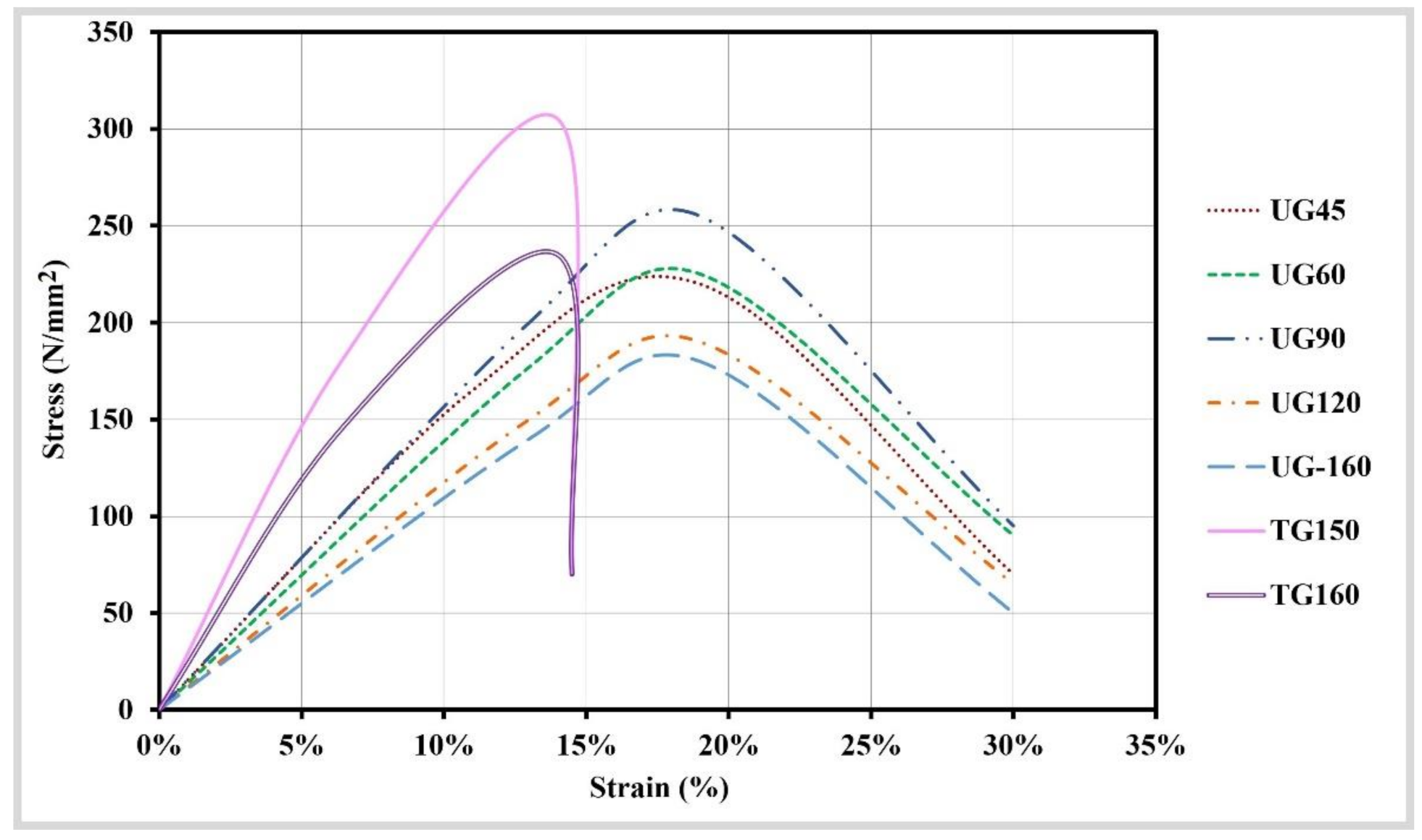
| Tensile Strength at 2% Strain in kN/m (theoretical) | 11 | 26 | 36 | 45 |
| Tensile Strength at 5% Strain in kN/m (theoretical) | 25 | 50 | 72 | 90 |
| Tensile design Strength in kN/m (theoretical) | 21.2 | 42.4 | 56.5 | 75.4 |
| Yield Point Elongation in % (theoretical) | 11.5 | 13 | 13 | 13 |
| Peak Tensile Strength in kN/m (theoretical) | 45 | 90 | 120 | 160 |
| Peak Tensile Strength in kN/m (experimental) | 45.56 | 79.36 | 103.91 | 143.46 |
| Peak Strain in % (Experimental) | 30 | 30 | 30 | 30 |
| Young’s modulus in N/mm2 (experimental) | 1500 | 1550 | 1200 | 1100 |
| Material | High-Density Polyethylene (HDPE) | |||
| Characteristics | Triaxial Geogrids (TG) Grades | |||
|---|---|---|---|---|
| TG150 | TG160 | |||
| Transverse (1) | Diagonal (2) | Transverse (1) | Diagonal (2) | |
| Mid-rib depth D in mm (physical) | 1.1 | 1.4 | 1.5 | 1.8 |
| Mid-rib width W in mm (physical) | 1.2 | 1 | 1.3 | 1.1 |
| Rib pitch P in mm (physical) | 40 | 40 | ||
| Rib shape | Rectangular | Rectangular | ||
| Aperture shape | Triangular | Triangular | ||
| Radial Secant Stiffness at 0.5% Strain in kN/m (theoretical) | 360 (–75) | 390 (−75) | ||
| Radial Secant Stiffness at 2% Strain in kN/m (theoretical) | 250 (−65) | 290 (−65) | ||
| Hexagon Pitch in mm (theoretical) | 80 (±4) | 80 (±4) | ||
| Radial Secant Stiffness Ratio (theoretical) | 0.8 | 0.8 | ||
| Peak Tensile Strength in kN/m (experimental) | 17.21 | 19.45 | ||
| Radial Secant Stiffness at 2% strain in kN/m (Experimental), according to BS EN 1SO 10319:1996 | 195 | 245 | ||
| Peak Strain in % (experimental) | 14.5 | 14.5 | ||
| Yield Strain in % (numerical) [22] | 6.4 | 6.4 | ||
| Young’s modulus in N/mm2 (experimental) | 2800 | 2350 | ||
| Material | Polypropylene with a Minimum of 2% Finely Divided Carbon Black Content | |||
| Group No. | Concrete Slab Number | Loading Period Critical Points | Experimental Moment at the Post-Peak Load (kN·m) | ||||
|---|---|---|---|---|---|---|---|
| First-Crack Load Associated with Initial-Peak Load (kN) | Load Drop (kN) | Steel-Yield Load (kN) | Post-Peak Load (kN) | Failure Load (kN) | |||
| Control Slab | S1-ST-CONT | 22.16 | 17.9 | 18.37 | 21.18 | 21.15 | 3.71 |
| Group One | S2-ST+1UG45 | 24.35 | 19.5 | 20.59 | 25.69 | 25.46 | 4.49 |
| S3-ST+1UG90 | 24.18 | 21.4 | 21.39 | 26.59 | 26.59 | 4.65 | |
| S4-ST+2UG45 | 25.92 | 18.1 | 21.84 | 27.68 | 27.39 | 4.84 | |
| S5-ST+1UG120 | 25.22 | 21.4 | 22.14 | 29.2 | 29.12 | 5.11 | |
| S6-ST+1UG160 | 27.17 | 20.3 | 22.92 | 33.82 | 33.74 | 5.91 | |
| S7-ST+2UG90 | 25.33 | 23.4 | 22.88 | 32.75 | 32.64 | 5.73 | |
| S8-ST+2UG120 | 26.33 | 22.6 | 24.22 | 36.7 | 34.59 | 6.42 | |
| S9-ST+2UG160 | 28.16 | 24.1 | 25.17 | 39.67 | 39.61 | 6.94 | |
| Group Two | S10-ST+1TG150 | 25.59 | 17.9 | 19.24 | 22.96 | 19.49 | 4.02 |
| S11-ST+1TG160 | 27.84 | 18.9 | 20.12 | 26.15 | 21.66 | 4.57 | |
| S12-ST+2TG150 | 26.59 | 19.7 | 19.91 | 25.78 | 18.05 | 4.51 | |
| S13-ST+2TG160 | 28.94 | 20 | 21.39 | 27.27 | 22.12 | 4.77 | |
| The Load-Deflection Behaviour and the Load-Loading Period Critical Points | 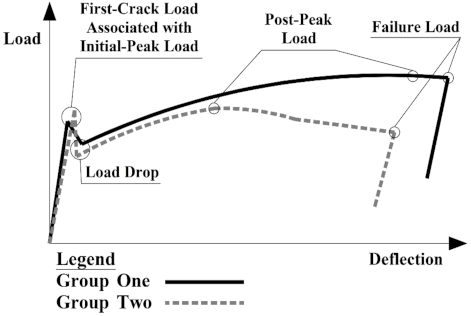 | ||||||
| Group Number | Concrete Slab No. | The Tensile Force of Geogrids (FG) at the Experimental Post-Peak Load (kN) | The Peak Tensile Strength of Geogrids (TG), Estimated by Equation-(1) (kN) | FG/TG (%) |
|---|---|---|---|---|
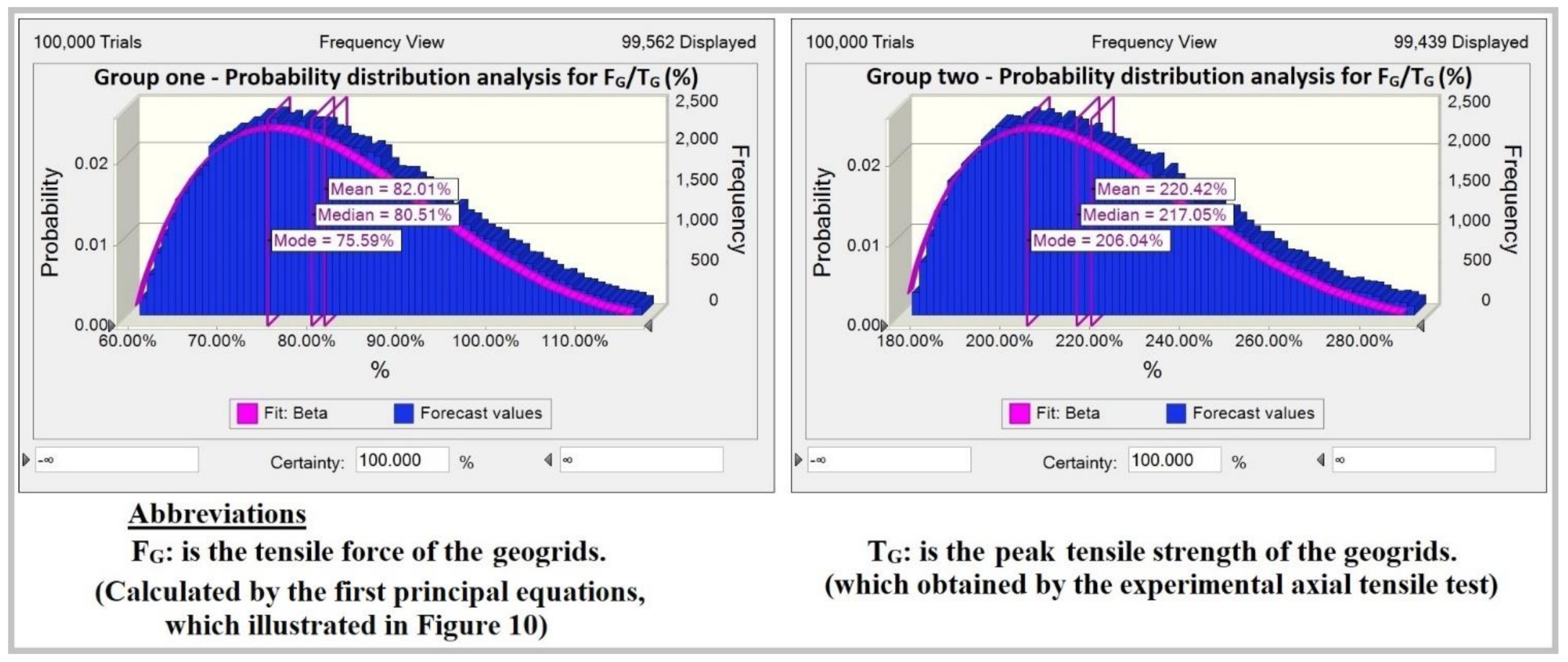
| Group one | S2-ST+1UG45 | 26.52 | 20.51 | 129.37% |
| S3-ST+1UG90 | 29.34 | 35.712 | 82.15% | |
| S4-ST+2UG45 | 32.77 | 41.004 | 79.91% | |
| S5-ST+1UG120 | 36.93 | 46.759.5 | 78.98% | |
| S6-ST+1UG160 | 50.52 | 64.557 | 78.25% | |
| S7-ST+2UG90 | 49.08 | 71.424 | 68.70% | |
| S8-ST+2UG120 | 63.97 | 93.519 | 68.40% | |
| S9-ST+2UG160 | 77.61 | 129.114 | 60.10% | |
| Group two | S10-ST+1TG150 | 19.37 | 7.75 | 250.12% |
| S11-ST+1TG160 | 28.15 | 8.76 | 321.72% | |
| S12-ST+2TG150 | 27.59 | 15.49 | 178.13% | |
| S13-ST+2TG160 | 32.14 | 17.51 | 183.65% | |
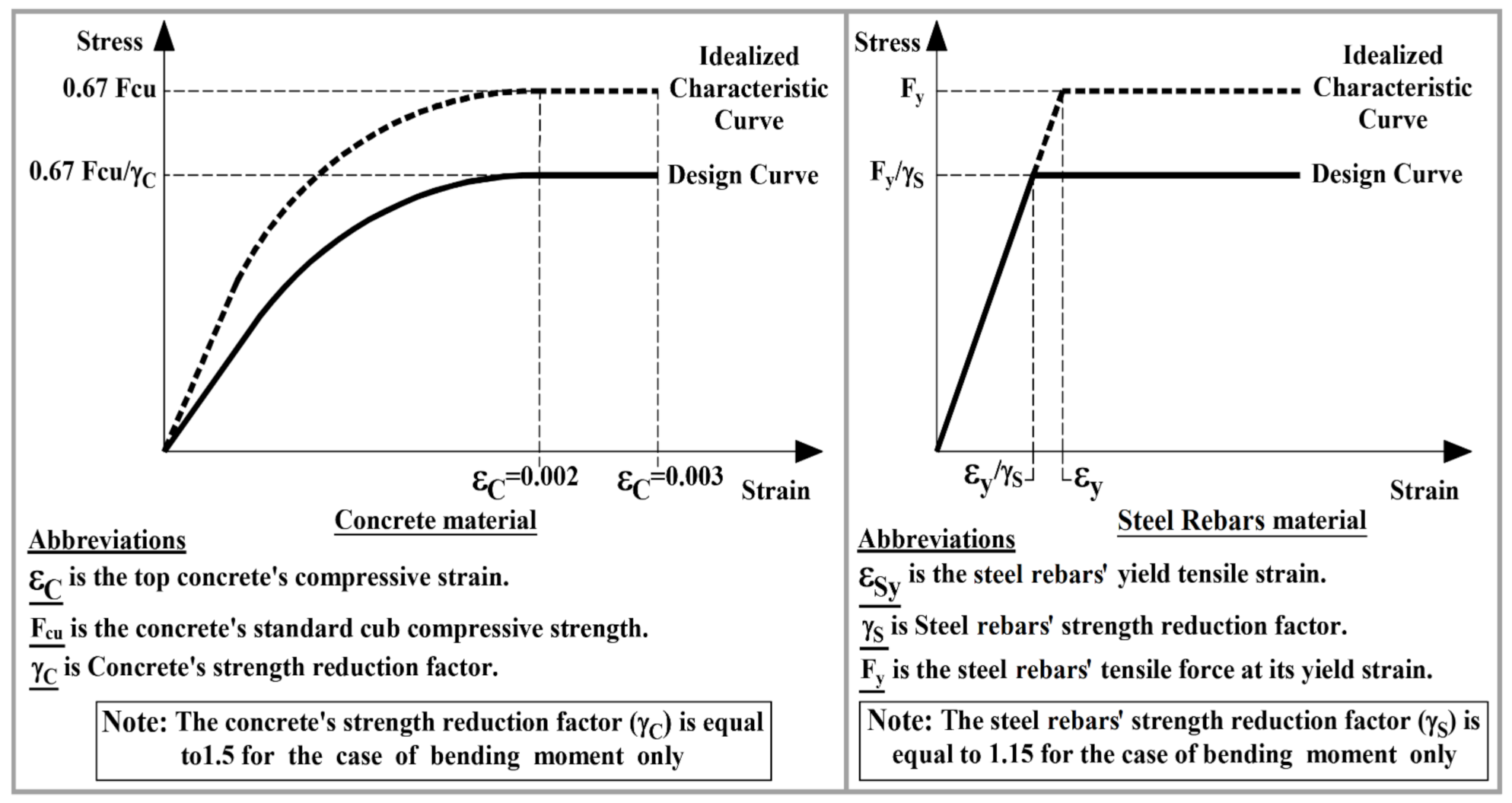
| First note: The tensile force of the geogrids was estimated based on: ● Considering the characteristic state of the concrete slabs’ material (the strength reduction factors of the concrete slabs’ materials are not considered), the top concrete’s compressive strain is equal to 0.3%, and the bottom steel rebars tensile force equal to its yield force. ● The bending moment of the concrete slabs is equal to its experimental moment at the post-peak load. Second note: The geogrids’ rib-cuttings occurred only for group two’s concrete slabs, as numerous rib-cuttings of triaxial geogrids occurred. | ||||
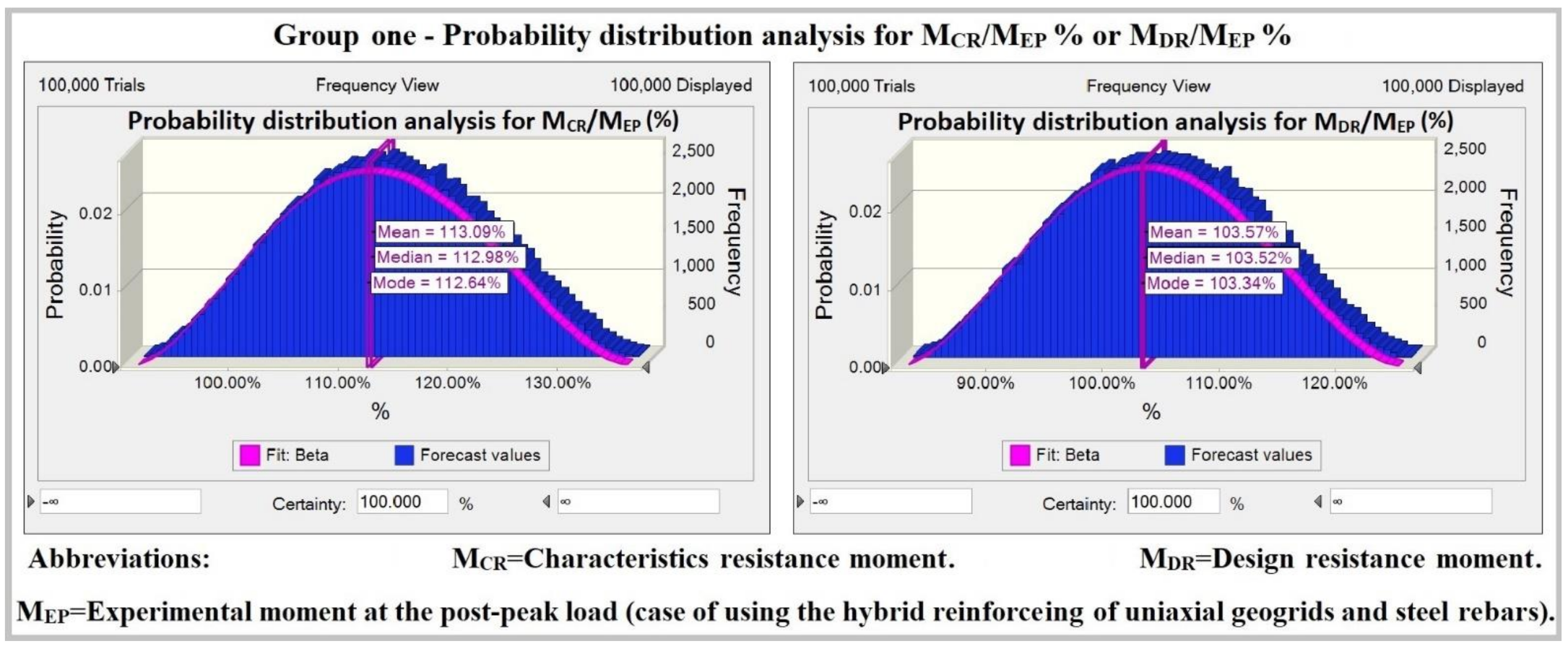
| Group No. | Concrete Slabs | MEP (kN·m) | MCR (kN·m) | MDR (kN·m) | MCR/MEP (%) | MDR/MEP (%) |
|---|---|---|---|---|---|---|
| Group one | S2-ST+1UG45 | 4.50 | 4.09 | 3.70 | 90.97% | 82.30% |
| S3-ST+1UG90 | 4.65 | 5.06 | 4.65 | 108.74% | 99.93% | |
| S4-ST+2UG45 | 4.84 | 5.36 | 4.94 | 110.65% | 101.98% | |
| S5-ST+1UG120 | 5.11 | 5.73 | 5.29 | 112.13% | 103.52% | |
| S6-ST+1UG160 | 5.92 | 6.77 | 6.28 | 114.39% | 106.11% | |
| S7-ST+2UG90 | 5.73 | 7.05 | 6.53 | 123.01% | 113.94% | |
| S8-ST+2UG120 | 6.42 | 8.03 | 7.43 | 125.03% | 115.69% | |
| S9-ST+2UG160 | 6.94 | 9.50 | 8.73 | 136.84% | 125.75% | |
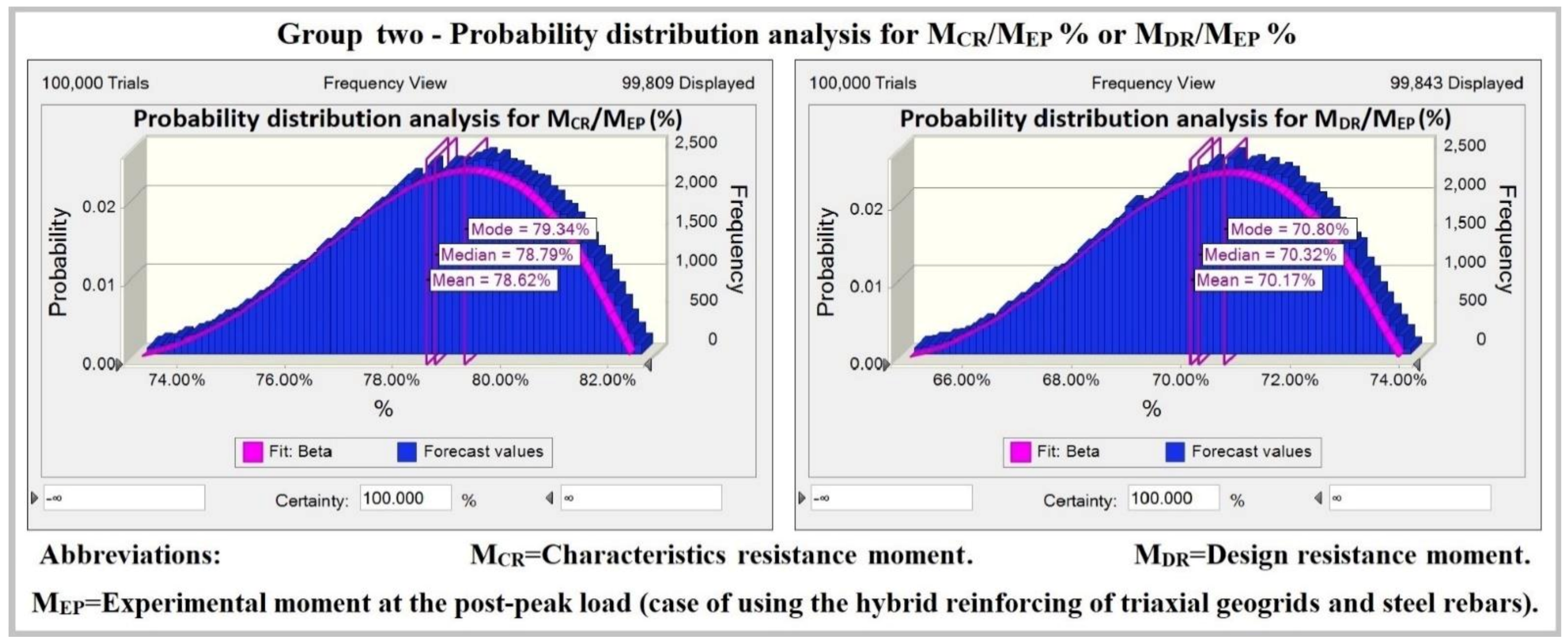
| Group two | S10-ST+1TG150 | 4.02 | 3.23 | 2.86 | 80.39% | 71.18% |
| S11-ST+1TG160 | 4.58 | 3.29 | 2.92 | 71.89% | 63.81% | |
| S12-ST+2TG150 | 4.51 | 3.72 | 3.34 | 82.46% | 74.03% | |
| S13-ST+2TG160 | 4.77 | 3.84 | 3.45 | 80.47% | 72.29% |
| Group No. | Concrete Slabs | MEP (kN·m) | MEP = 0.88 MCR (where FG = TG) (kN·m) | MEP = 0.97 MDR (where FG = TG) (kN·m) | 0.88 MCR/MEP (%) | 0.97 MDR/MEP (%) |
| Group one | S2-ST+1UG45 | 4.5 | 3.5992 | 3.589 | 79.98% | 79.76% |
| S3-ST+1UG90 | 4.65 | 4.4528 | 4.5105 | 95.76% | 97.00% | |
| S4-ST+2UG45 | 4.84 | 4.7168 | 4.7918 | 97.45% | 99.00% | |
| S5-ST+1UG120 | 5.11 | 5.0424 | 5.1313 | 98.68% | 100.42% | |
| S6-ST+1UG160 | 5.92 | 5.9576 | 6.0916 | 100.64% | 102.90% | |
| S7-ST+2UG90 | 5.73 | 6.204 | 6.3341 | 108.27% | 110.54% | |
| S8-ST+2UG120 | 6.42 | 7.0664 | 7.2071 | 110.07% | 112.26% | |
| S9-ST+2UG160 | 6.94 | 8.36 | 8.4681 | 120.46% | 122.02% | |
| Group No. | Concrete Slabs | MEP (kN·m) | MEP = 1.26 MCR (where FG = TG) (kN·m) | MEP = 1.41 MDR (where FG = TG) (kN·m) | 1.26 MCR/MEP (%) | 1.41 MDR/MEP (%) |
| Group two | S10-ST+1TG150 | 4.02 | 4.0698 | 4.0326 | 101.24% | 100.31% |
| S11-ST+1TG160 | 4.58 | 4.1454 | 4.1172 | 90.51% | 89.90% | |
| S12-ST+2TG150 | 4.51 | 4.6872 | 4.7094 | 103.93% | 104.42% | |
| S13-ST+2TG160 | 4.77 | 4.8384 | 4.8645 | 101.43% | 101.98% |
| Group number | Concrete Slabs | MEP (kN·m) | MCR (kN·m) | MCR/MEP (%) |
|---|---|---|---|---|
| Group one | S2-ST+1UG45 | 4.50 | 3.77 | 83.86% |
| S3-ST+1UG90 | 4.65 | 4.51 | 96.92% | |
| S4-ST+2UG45 | 4.84 | 4.74 | 97.85% | |
| S5-ST+1UG120 | 5.11 | 5.02 | 98.24% | |
| S6-ST+1UG160 | 5.92 | 5.83 | 98.50% | |
| S7-ST+2UG90 | 5.73 | 6.04 | 105.39% | |
| S8-ST+2UG120 | 6.42 | 6.81 | 106.03% | |
| S9-ST+2UG160 | 6.94 | 7.98 | 114.95% | |
| Group two | S10-ST+1TG150 | 4.02 | 3.79 | 94.33% |
| S11-ST+1TG160 | 4.58 | 3.91 | 85.44% | |
| S12-ST+2TG150 | 4.51 | 4.78 | 105.95% | |
| S13-ST+2TG160 | 4.77 | 5.01 | 104.98% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, R.N.A.; El Sebai, A.M.; Gabr, A.S.A.-H. Simple Design Methodology for R.C. Slabs by Hybrid Reinforcing of Steel Rebars and Uniaxial or Triaxial Geogrids. Inventions 2021, 6, 32. https://doi.org/10.3390/inventions6020032
Mohamed RNA, El Sebai AM, Gabr ASA-H. Simple Design Methodology for R.C. Slabs by Hybrid Reinforcing of Steel Rebars and Uniaxial or Triaxial Geogrids. Inventions. 2021; 6(2):32. https://doi.org/10.3390/inventions6020032
Chicago/Turabian StyleMohamed, Ramy Nasr Abdelmonem, Ahmed Mohamed El Sebai, and Ahmed Shaban Abdel-Hay Gabr. 2021. "Simple Design Methodology for R.C. Slabs by Hybrid Reinforcing of Steel Rebars and Uniaxial or Triaxial Geogrids" Inventions 6, no. 2: 32. https://doi.org/10.3390/inventions6020032
APA StyleMohamed, R. N. A., El Sebai, A. M., & Gabr, A. S. A.-H. (2021). Simple Design Methodology for R.C. Slabs by Hybrid Reinforcing of Steel Rebars and Uniaxial or Triaxial Geogrids. Inventions, 6(2), 32. https://doi.org/10.3390/inventions6020032







