Intelligent Wavelet Based Pre-Filtering Method for Ultrasonic Sensor Fusion Inverse Algorithm Performance Optimization
Abstract
1. Introduction
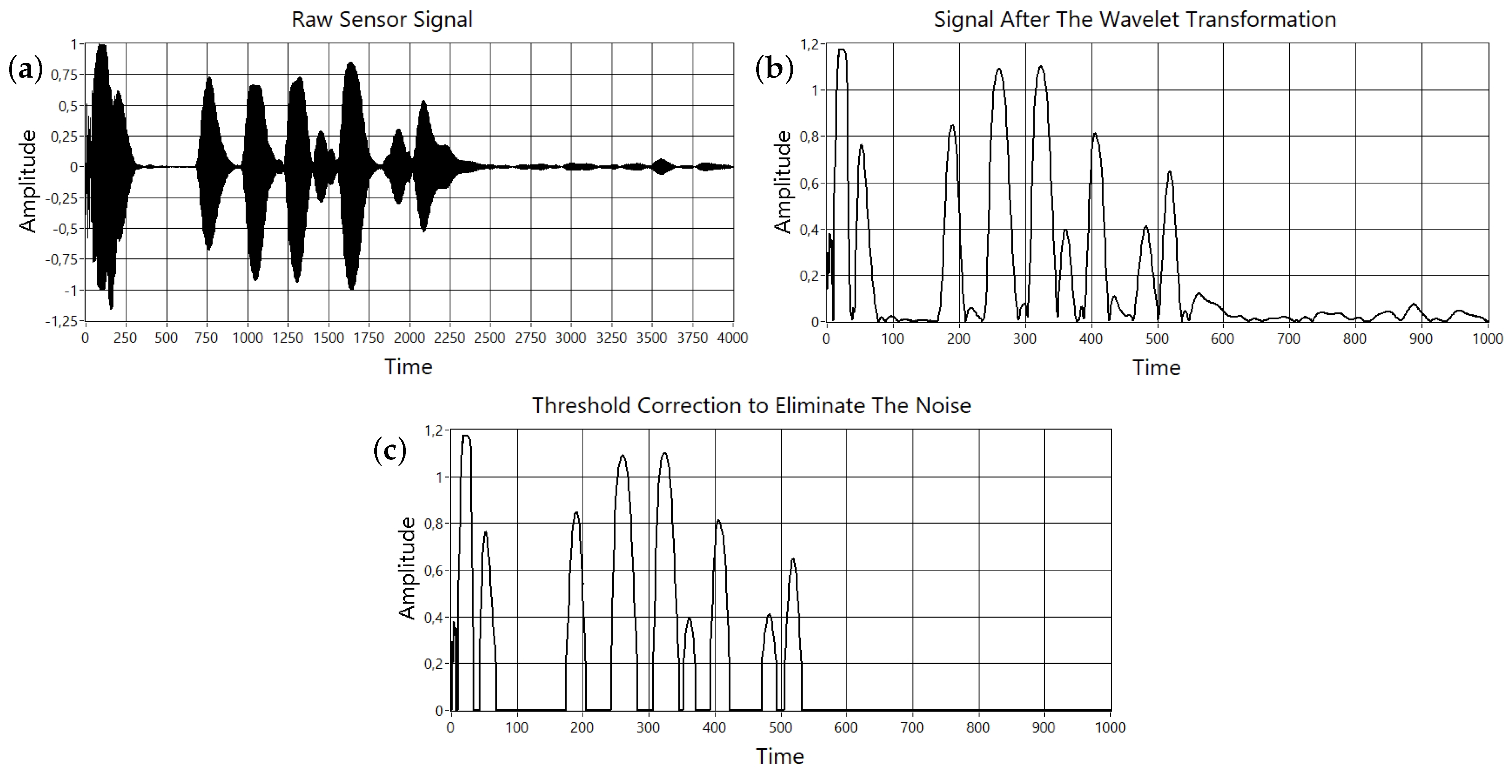
2. Mathematical Establishment of the Pre-Filter Function
Mathematical Evaluation of the Sensor Data
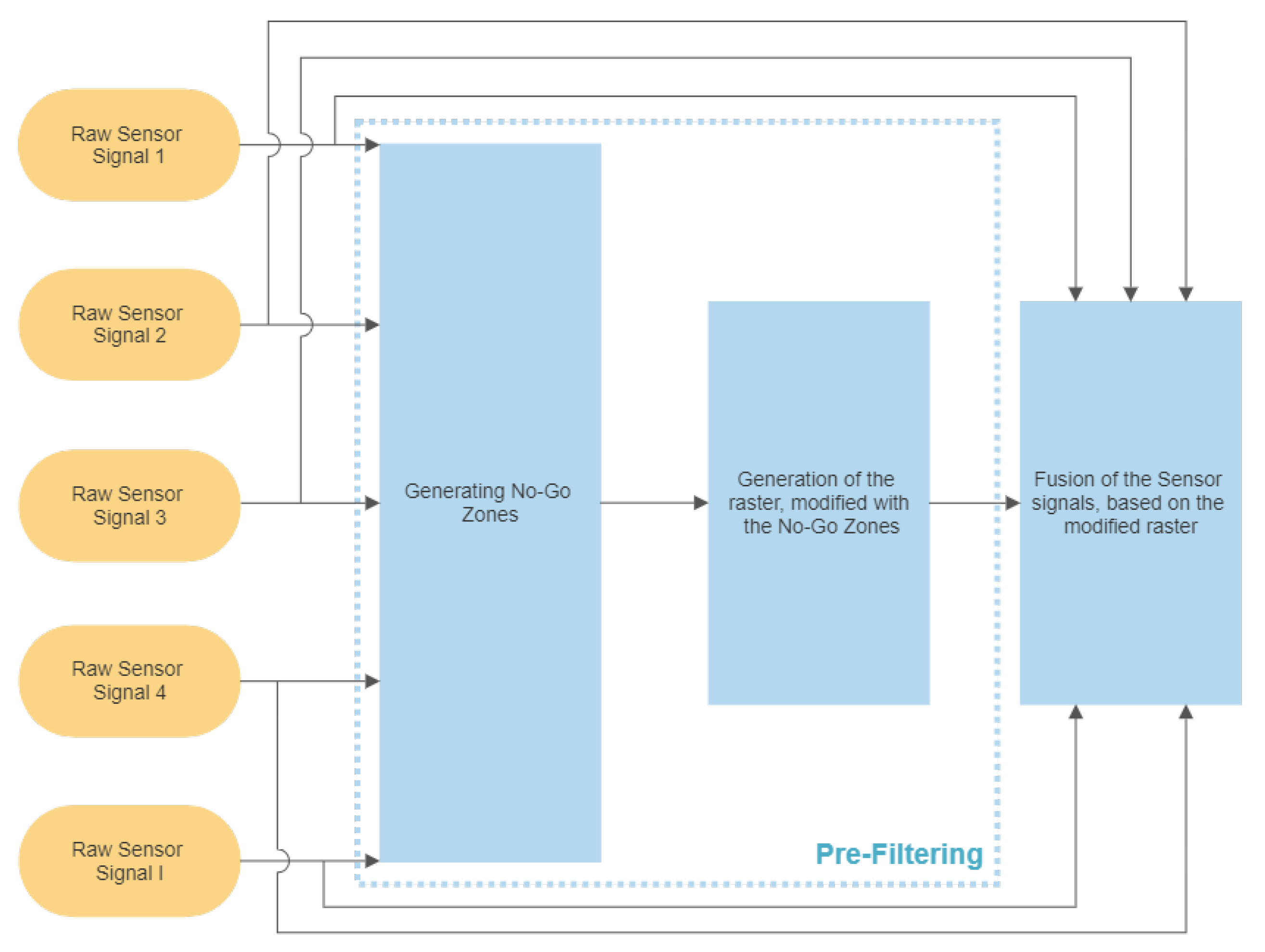
3. Calculation Optimization of the Algorithm
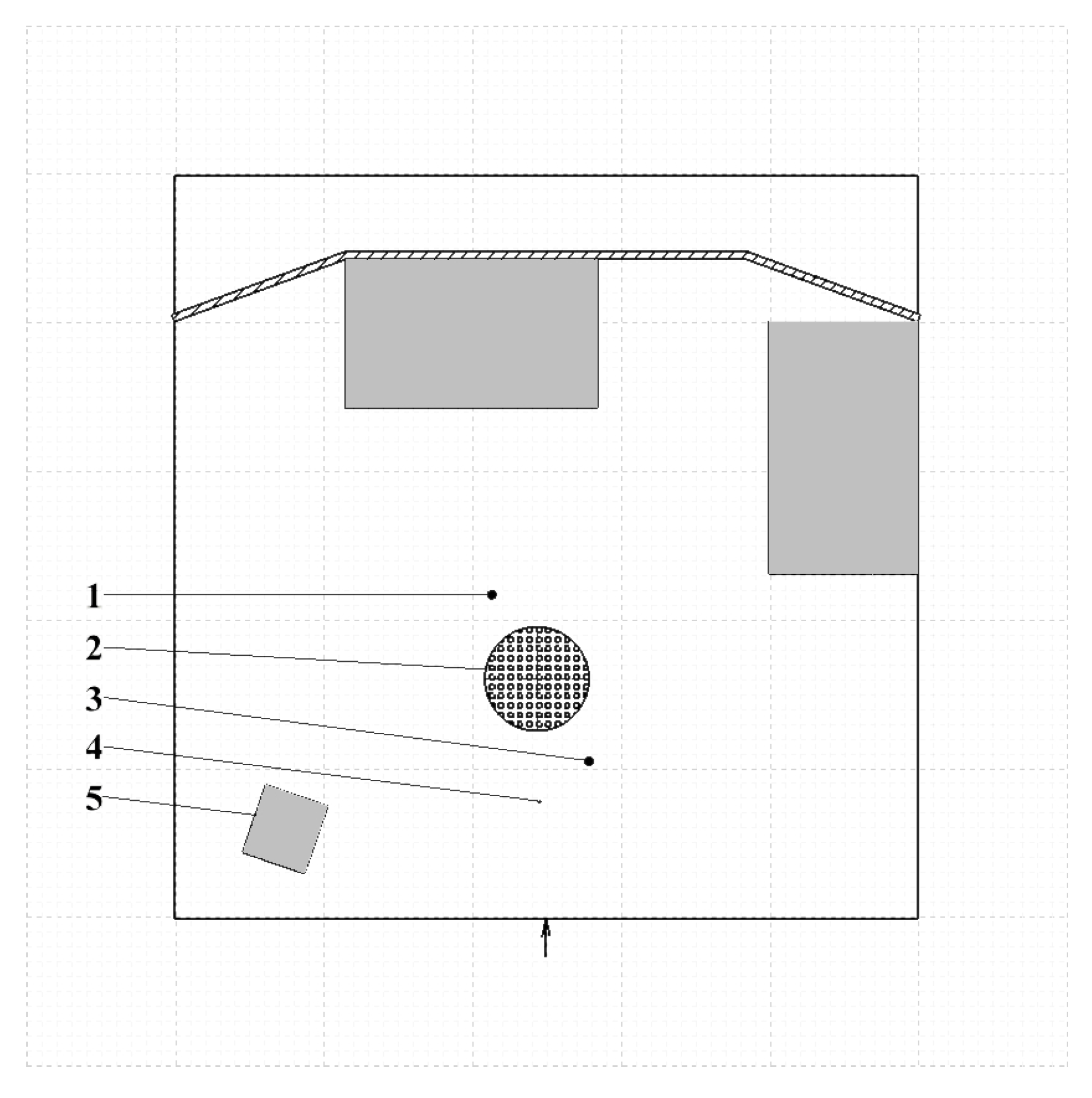
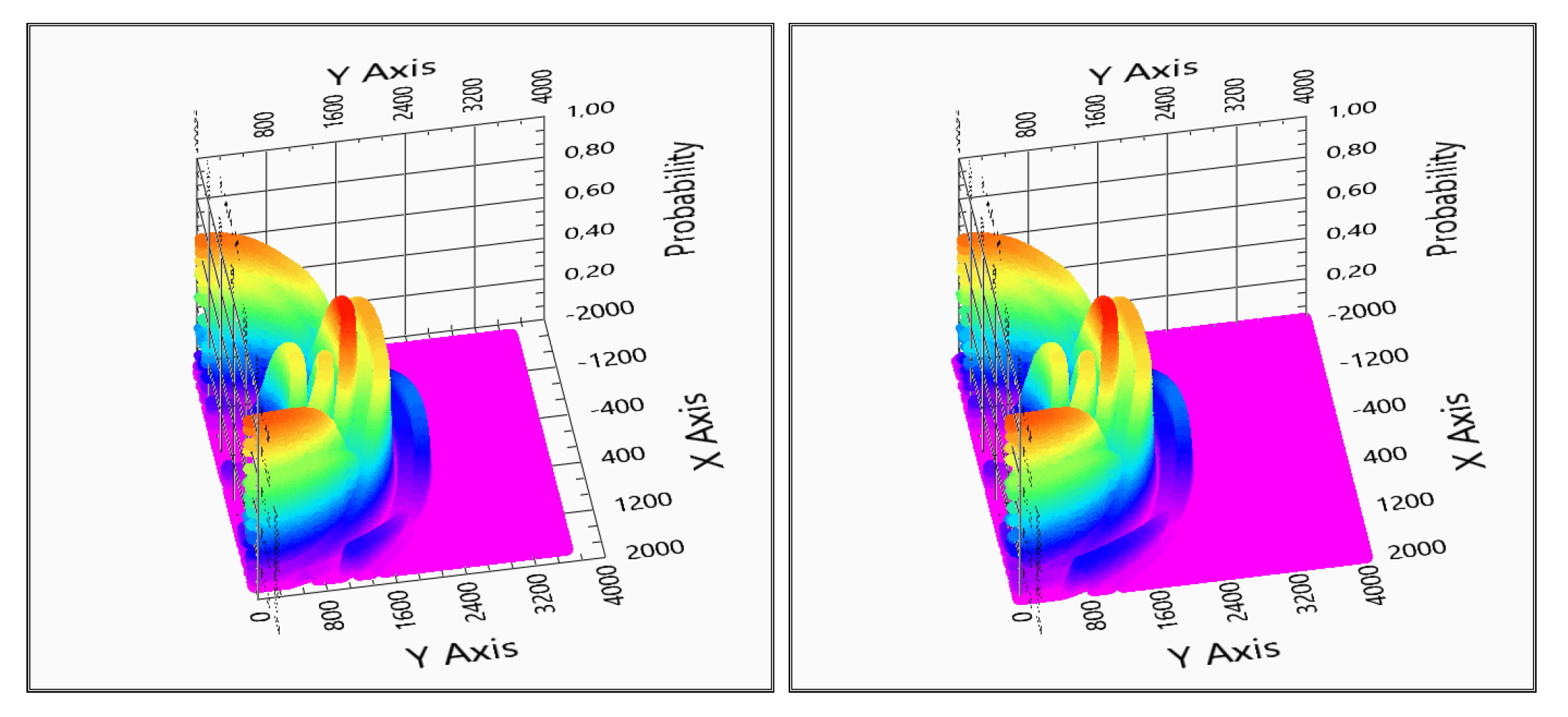
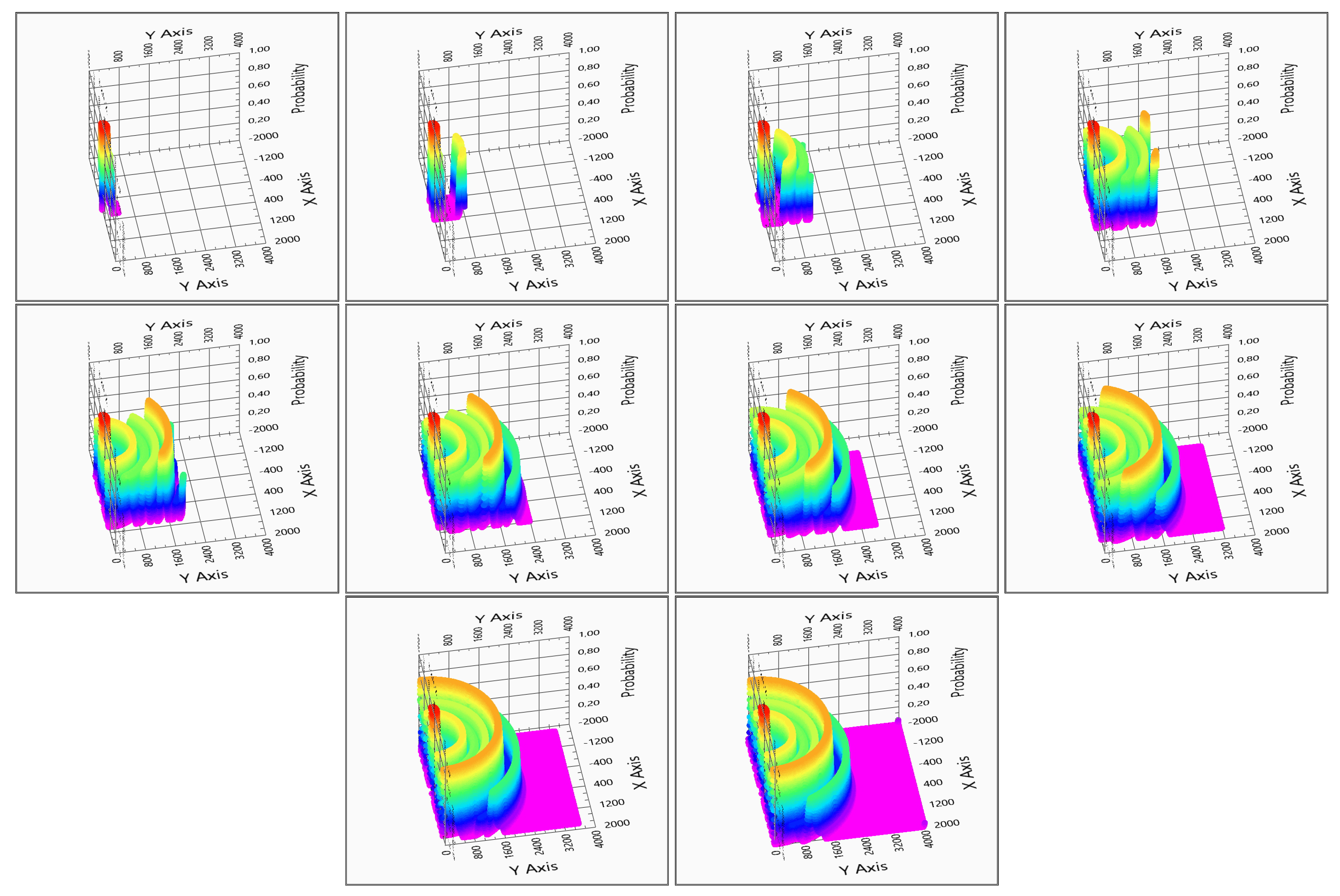
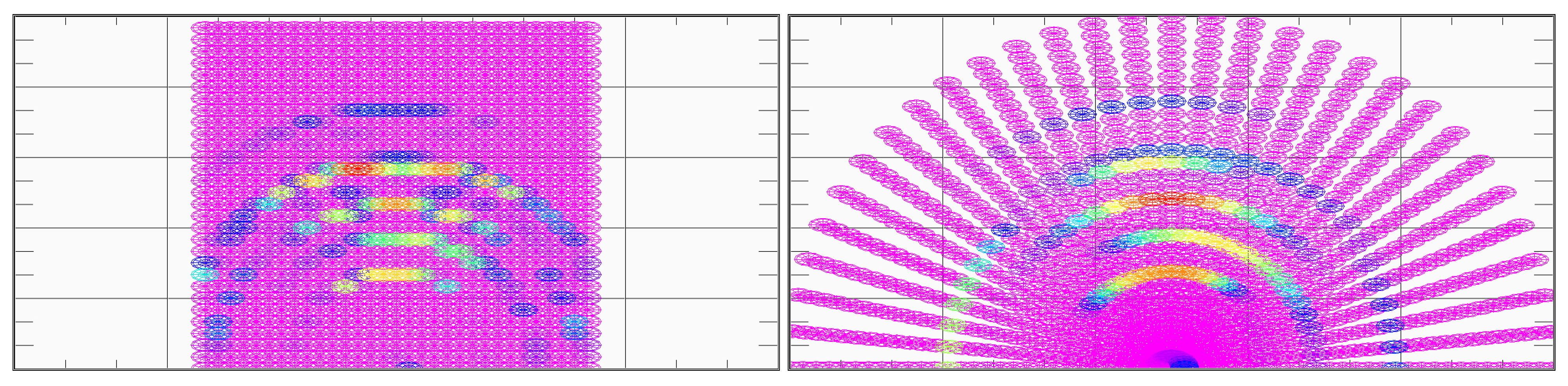
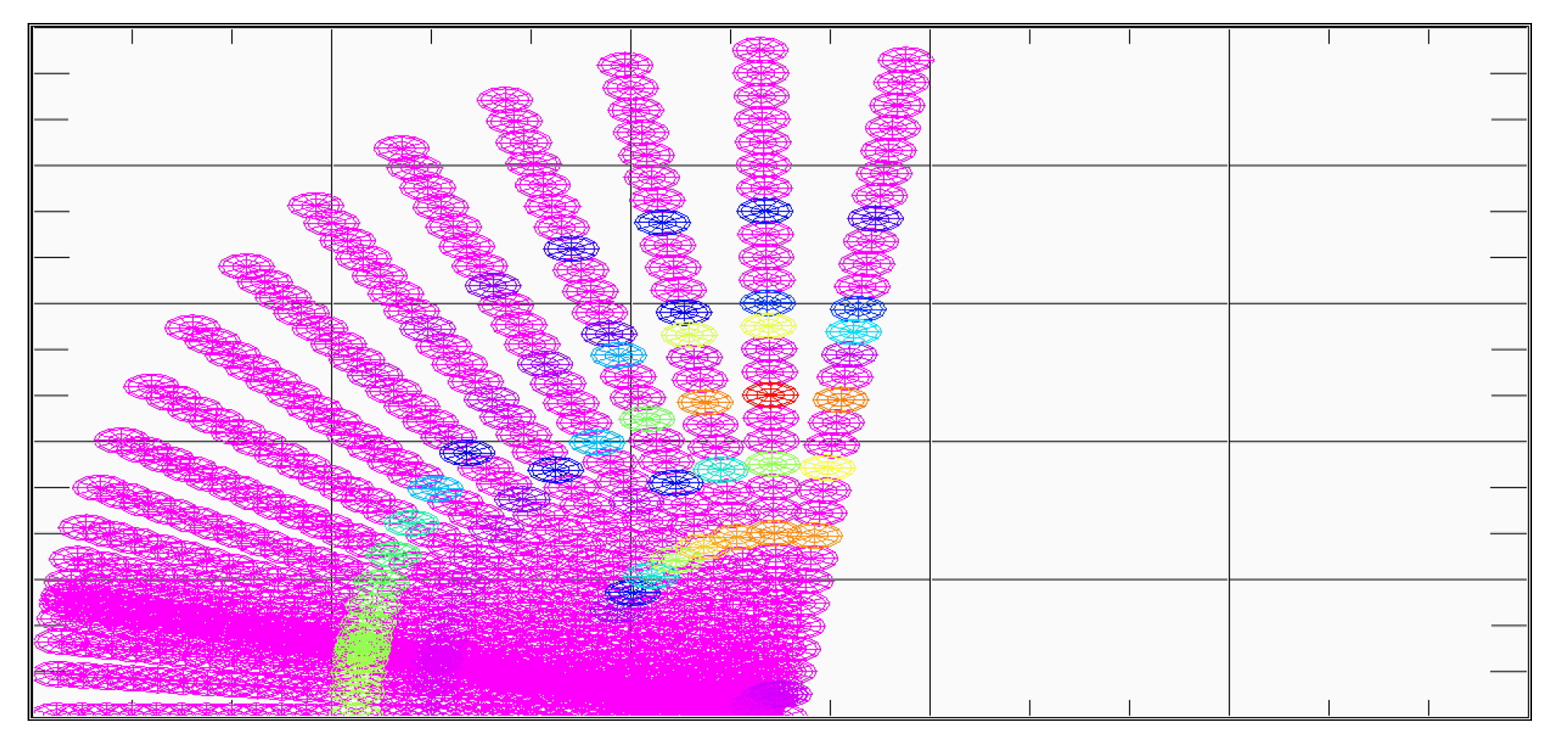
3.1. Calculation of the Possibility for a Space–Point Array
3.2. Intelligent Searching for Low Amplitude Domains to Decrease the Calculation Load
- If in a given position one sensor does not detect (i.e., ), then the possibility is 0;
- Check and store the lower and upper limits of 0 possibility domains for each sensor;
- Create no-go zones from this 0 possibility domain for each sensor;
- In no-go zones, the calculation of the possibility (8) is not carried out, and it has to be 0.
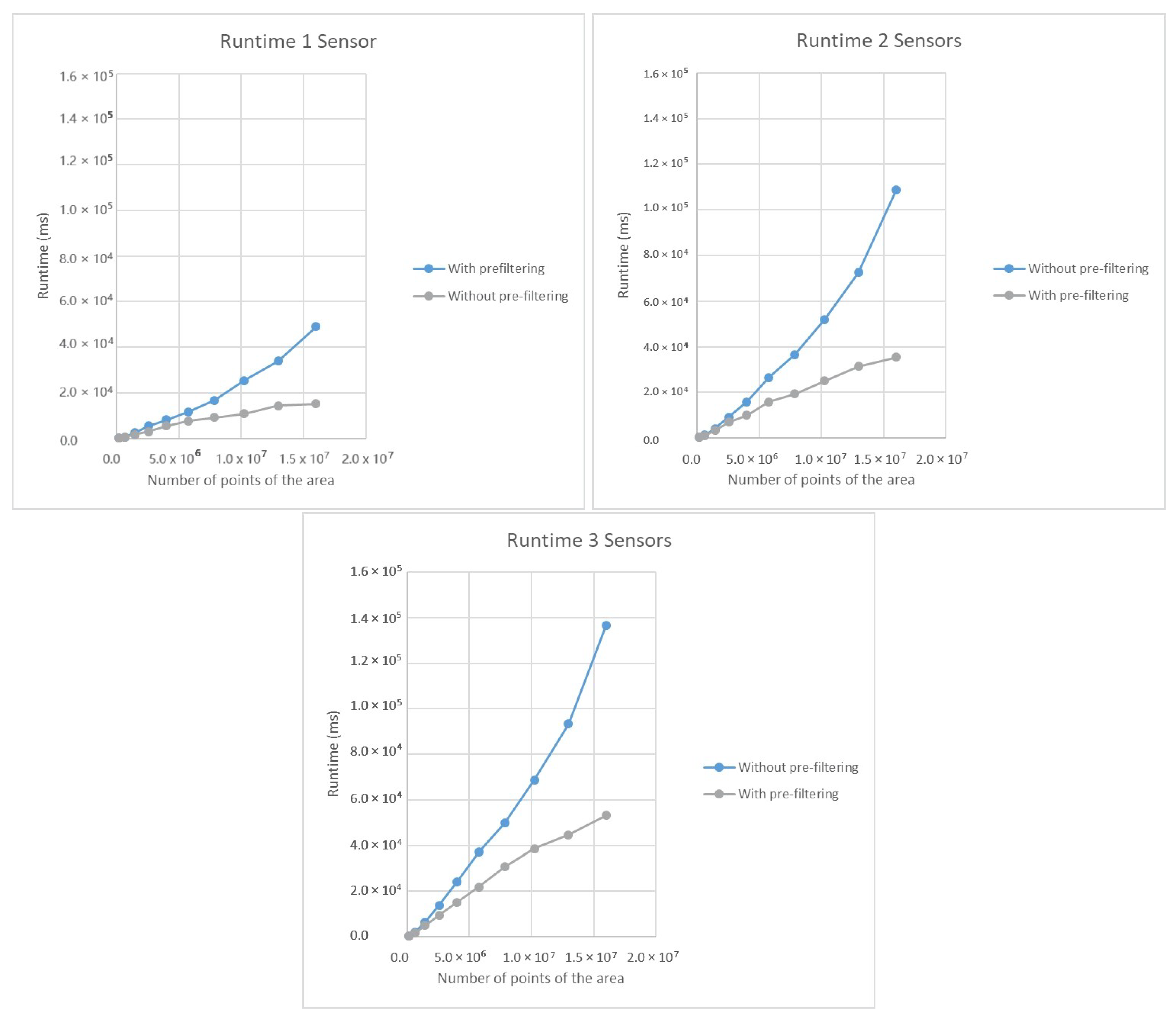
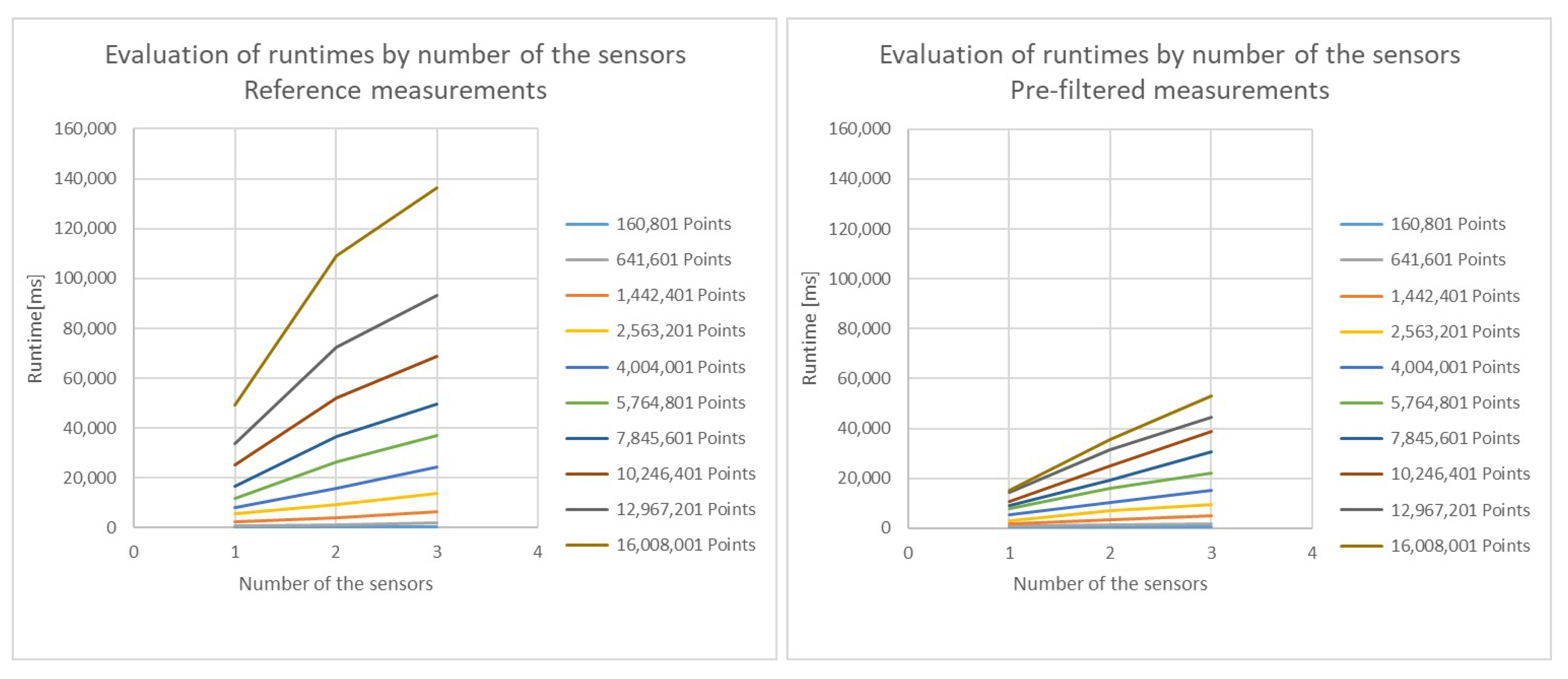
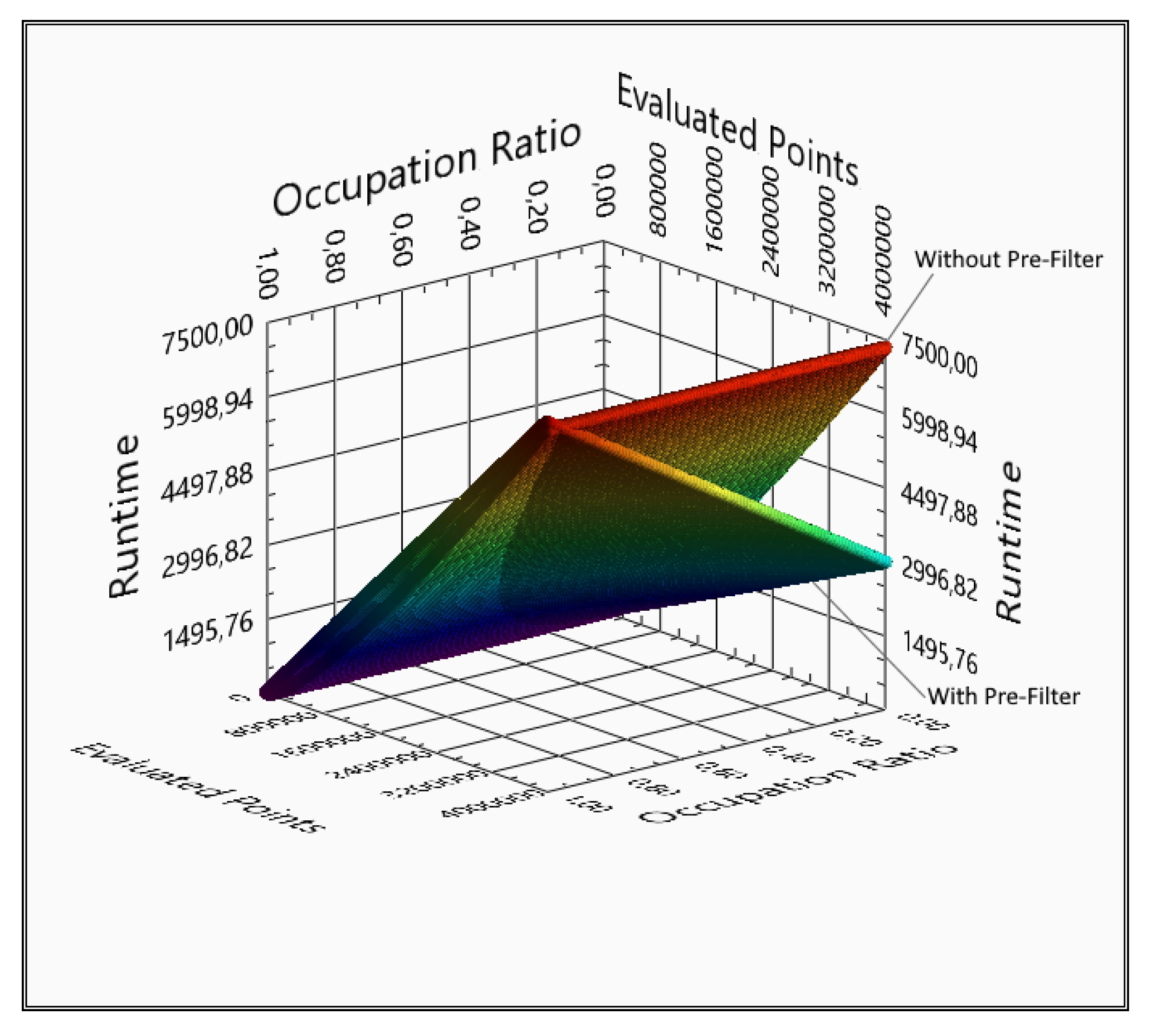
4. Comparison with and without the Pre-Filtering Regarding the Evaluated Area Size and the Number of the Sensors
4.1. Reference Runs with Different Number of Points to Be Evaluated
- The number of evaluated points was between 160,801 and 16,008,001;
- The number of sensors were 3;
- The occupation of the area was between 24.1% and 44.1%.
4.2. Pre-Filtered Runs with Different Number of Evaluated Points
4.3. Changes of the Runtime Based on the Number of the Sensors
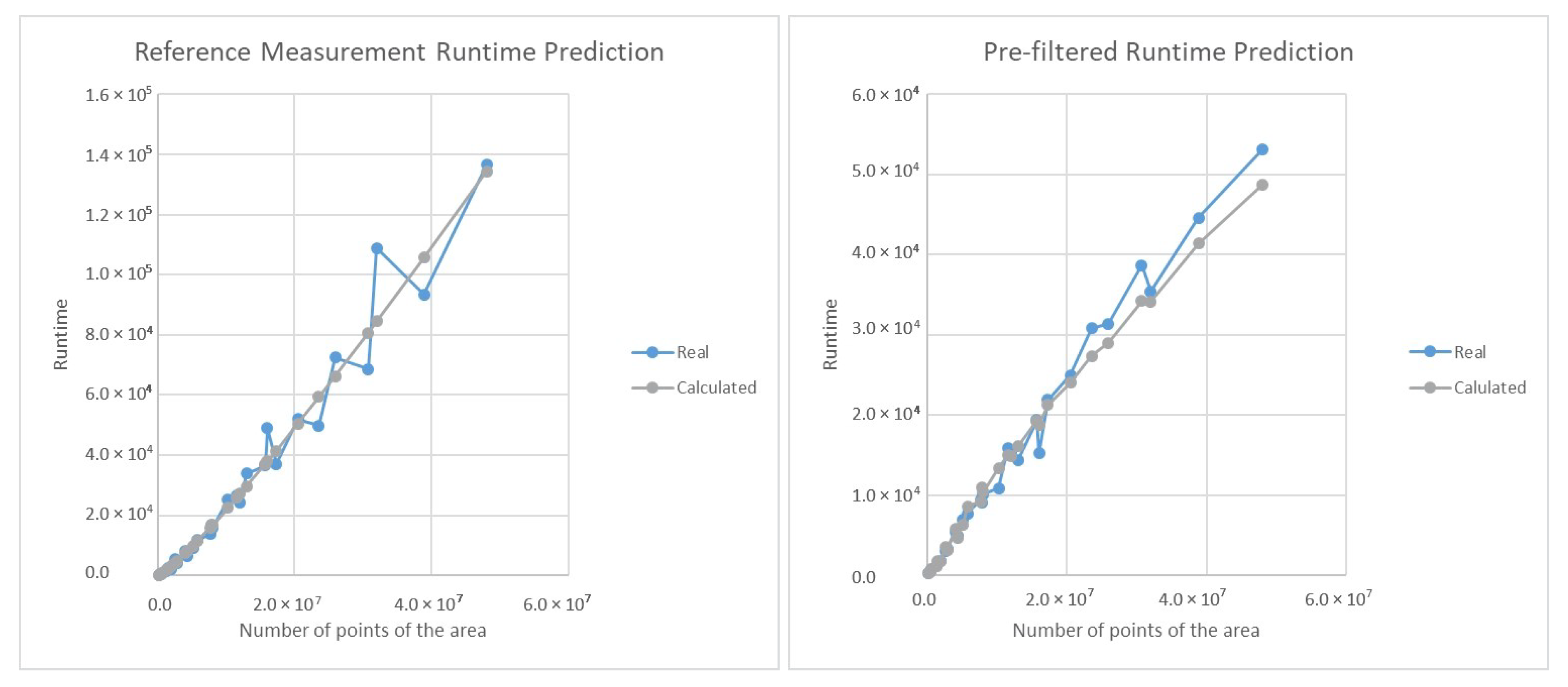
5. Prediction of the Runtime
6. Raster Modification with Prioritized Direction
7. Raster Modification with Prioritized Places
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Measurement Results in Tabular Form
Appendix A.1. Three Receivers Measurements
| Evaluated Points | Amplitude Approximation (# of Runs) | Amplitude Approximation (ms) |
|---|---|---|
| 160,801 | 482,403 | 437.5 |
| 641,601 | 1,924,803 | 2156.2 |
| 1,442,401 | 4,327,203 | 6500.0 |
| 2,563,201 | 7,689,603 | 13,812.5 |
| 4,004,001 | 12,012,003 | 24,218.8 |
| 5,764,801 | 17,294,403 | 37,140.6 |
| 7,845,601 | 23,536,803 | 49,843.8 |
| 10,246,401 | 30,739,203 | 68,703.1 |
| 12,967,201 | 38,901,603 | 93,375.0 |
| 16,008,001 | 48,024,003 | 136,578.1 |
| Evaluated Points | Amplitude Approx. (# of Runs) | Amplitude Approx. (ms) | Pre-Filter (ms) | Pre-Filter (# of Runs) | Array Integral (ms) | Array Integral (# of Runs) | Occupation (%) | SUM (ms) |
|---|---|---|---|---|---|---|---|---|
| 160,801 | 150,150 | 140.6 | 390.6 | 482,403 | 0 | 3 | 31.1 | 531.2 |
| 641,601 | 354,267 | 343.8 | 1453.1 | 1,924,803 | 0 | 3 | 18.4 | 1796.9 |
| 1,442,401 | 1,271,811 | 1453.1 | 3468.8 | 4,327,203 | 0 | 3 | 29.4 | 4921.9 |
| 2,563,201 | 3,148,599 | 3578.1 | 5890.6 | 7,689,603 | 0 | 3 | 40.9 | 9468.7 |
| 4,004,001 | 5,302,455 | 6375 | 8859.4 | 12,012,003 | 0 | 3 | 44.1 | 15,234.4 |
| 5,764,801 | 7,515,594 | 9437.5 | 12,468.8 | 17,294,403 | 0 | 3 | 43.5 | 21,906.3 |
| 7,845,601 | 8,800,671 | 10,625 | 20,171.9 | 23,536,803 | 0 | 3 | 37.4 | 30,796.9 |
| 10,246,401 | 10,152,120 | 12,187.5 | 26,500.0 | 30,739,203 | 0 | 3 | 33.0 | 38,687.5 |
| 12,967,201 | 11,125,824 | 14,406.2 | 30,187.5 | 38,901,603 | 0 | 3 | 28.6 | 44,593.7 |
| 16,008,001 | 11,670,015 | 15,296.9 | 37,875.0 | 48,024,003 | 0 | 3 | 24.3 | 53,171.9 |
Appendix A.2. Two Receivers Measurement
| Evaluated Points | Amplitude Approximation (# of Runs) | Amplitude Approximation (ms) |
|---|---|---|
| 160,801 | 321,602 | 296.9 |
| 641,601 | 1,283,202 | 1265.6 |
| 1,442,401 | 2,884,802 | 4078.1 |
| 2,563,201 | 5,126,402 | 9234.4 |
| 4,004,001 | 8,008,002 | 15,937.5 |
| 5,764,801 | 11,529,602 | 26,578.1 |
| 7,845,601 | 15,691,202 | 36,578.1 |
| 10,246,401 | 20,492,802 | 52,015.6 |
| 12,967,201 | 25,934,402 | 72,500.0 |
| 16,008,001 | 32,016,002 | 108,921.9 |
| Evaluated Points | Amplitude Approx. (# of Runs) | Amplitude Approx. (ms) | Pre-Filter (ms) | Pre-Filter (# of Runs) | Array Integral (ms) | Array Integral (# of Runs) | Occupation (%) | SUM (ms) |
|---|---|---|---|---|---|---|---|---|
| 160,801 | 100,100 | 93.8 | 250.0 | 321,602 | 0 | 2 | 31 | 343.8 |
| 641,601 | 237,100 | 265.6 | 859.4 | 1,283,202 | 0 | 2 | 18 | 1125.0 |
| 1,442,401 | 862,106 | 984.4 | 2328.1 | 2,884,802 | 0 | 2 | 30 | 3312.5 |
| 2,563,201 | 2,260,698 | 2796.9 | 4156.2 | 5,126,402 | 0 | 2 | 44 | 6953.1 |
| 4,004,001 | 4,013,918 | 4593.8 | 5500.0 | 8,008,002 | 0 | 2 | 50 | 10,093.8 |
| 5,764,801 | 5,705,024 | 6171.9 | 9703.1 | 11,529,602 | 0 | 2 | 49 | 15,875.0 |
| 7,845,601 | 6,798,012 | 7453.1 | 11,890.6 | 15,691,202 | 0 | 2 | 43 | 19,343.7 |
| 10,246,401 | 7,858,932 | 8921.9 | 16,078.1 | 20,492,802 | 0 | 2 | 38 | 25,000.0 |
| 12,967,201 | 8,665,870 | 9437.5 | 21,937.5 | 25,934,402 | 0 | 2 | 33 | 31,375.0 |
| 16,008,001 | 9,233,954 | 10,750.0 | 24,687.5 | 32,016,002 | 0 | 2 | 29 | 35,437.5 |
Appendix A.3. One Receivers Measurement
| Evaluated Points | Amplitude Approximation (# of Runs) | Amplitude Approximation (ms) |
|---|---|---|
| 160,801 | 160,801 | 140.6 |
| 641,601 | 641,601 | 734.4 |
| 1,442,401 | 1,442,401 | 2593.8 |
| 2,563,201 | 2,563,201 | 5562.5 |
| 4,004,001 | 4,004,001 | 8156.2 |
| 5,764,801 | 5,764,801 | 11,750.0 |
| 7,845,601 | 7,845,601 | 16,750.0 |
| 10,246,401 | 10,246,401 | 25,359.4 |
| 12,967,201 | 12,967,201 | 33,906.2 |
| 16,008,001 | 16,008,001 | 49,062.5 |
| Evaluated Points | Amplitude Approx. (# of Runs) | Amplitude Approx. (ms) | Pre-Filter (ms) | Pre-Filter (# of Runs) | Array Integral (ms) | Array Integral (# of Runs) | Occupation (%) | SUM (ms) |
|---|---|---|---|---|---|---|---|---|
| 160,801 | 114,302 | 203.1 | 125.0 | 160,801 | 0 | 1 | 71 | 328.1 |
| 641,601 | 231,110 | 281.2 | 437.5 | 641,601 | 0 | 1 | 36 | 718.7 |
| 1,442,401 | 653,861 | 640.6 | 984.4 | 1,442,401 | 0 | 1 | 45 | 1625.0 |
| 2,563,201 | 1,490,006 | 1390.6 | 1609.4 | 2,563,201 | 0 | 1 | 58 | 3000.0 |
| 4,004,001 | 2,498,445 | 2593.8 | 2875 | 4,004,001 | 0 | 1 | 62 | 5468.8 |
| 5,764,801 | 3,873,273 | 3656.2 | 4046.9 | 5,764,801 | 0 | 1 | 67 | 7703.1 |
| 7,845,601 | 4,541,136 | 4015.6 | 5125.0 | 7,845,601 | 0 | 1 | 58 | 9140.6 |
| 10,246,401 | 5,179,844 | 4515.6 | 6359.4 | 10,246,401 | 0 | 1 | 51 | 10,875.0 |
| 12,967,201 | 5,743,590 | 5328.1 | 8984.8 | 12,967,201 | 0 | 1 | 44 | 14,312.9 |
| 16,008,001 | 6,180,412 | 5609.4 | 9609.4 | 16,008,001 | 0 | 1 | 39 | 15,218.8 |
References
- Jimenez, J.A.; Urena, J.; Mazo, M.; Hernandez, A.; Santiso, E. Three-dimensional discrimination between planes corners and edges using ultrasonic sensors. In Proceedings of the ETFA’03, IEEE Conference, Lisbon, Portugal, 16–19 September 2003; pp. 692–699. [Google Scholar]
- Ochoa, A.; Urena, J.; Hernandez, A.; Mazo, M.; Jimenez, J.A.; Perez, M.C. Ultrasonic Multitransducer System for Classification and 3-D Location of Reflectors Based on PCA. Instrum. Meas. IEEE Trans. 2009, 58, 3031–3041. [Google Scholar] [CrossRef]
- Akbarally, H.; Kleeman, L. A sonar sensor for accurate 3D target localisation and classification. In Proceedings of the IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 3003–3008. [Google Scholar]
- Kleeman, L.; Kuc, R. An Optimal Sonar Array for Target Localization and Classification. In Proceedings of the IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3130–3135. [Google Scholar]
- Barshan, B.; Kuc, R. Differentiating sonar reflections from corners and planes by employing an intelligent sensor. IEEE PAMI 1990, 12, 560–569. [Google Scholar] [CrossRef]
- Kreczmer, B. Relations between classification criteria of objects recognizable by ultrasonic systems. In Proceedings of the Methods and Models in Automation and Robotics (MMAR) 2013 18th International Conference, Miedzyzdroje, Poland, 26–29 August 2013; pp. 806–811. [Google Scholar]
- Akbarally, H.; Kleeman, L. 3D robot sensing from sonar and vision. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; pp. 686–691. [Google Scholar]
- Kleeman, L.; Kuc, R. Mobile robot sonar for target localization and classification. Int. J. Robot. Res. 1995, 14, 295–318. [Google Scholar] [CrossRef]
- Kuc, R.; Viard, V.B. A physically based navigation strategy for sonar-guided vehicles. Int. J. Robot. Res. 1991, 10, 75–87. [Google Scholar] [CrossRef]
- Tardós, J.D.; Neira, J.; Newman, P.M.; Leonard, J.J. Robust Mapping and Localization in Indoor Environments Using Sonar Data. Int. J. Robot. Res. 2002, 21, 311–330. [Google Scholar] [CrossRef]
- Yata, T.; Kleeman, L.; Yuta, S. Wall following using angle information measured by a single ultrasonic transducer. In Proceedings of the IEEE International Conference on Robotics and Automation, Leuven, Belgium, 20 May 1998; pp. 1590–1596. [Google Scholar]
- Wijk, O.; Christensen, H.I. Triangulation-Based Fusion of Sonar Data with Application in Robot Pose Trackin. IEEE Trans. Robot. Autom. 2000, 16, 740–752. [Google Scholar] [CrossRef]
- Basha, A.; Gupta, H.; Perinbam, K.C.; Sowmya, L.; Ghosal, P.; Sameer, S.M. A Robot Controlled 3D Mapping and Communication System Using Ultrasonic Sensors. In Proceedings of the IEEE Region 10 Conference (TENCON), Penang, Malaysia, 5–8 November 2017; pp. 3078–3083. [Google Scholar]
- Borenstein, J.; Koren, Y. Obstacle avoidance with ultrasonic sensors. Robot. Autom. IEEE J. 1988, 4, 213–218. [Google Scholar] [CrossRef]
- Arshad, M.R.; Manimaran, R.M. Surface mapping using ultrasound technique for object visualisation. In Proceedings of the 2002 Student Conference on Research and Development, Shah Alam, Malaysia, 17 July 2002; pp. 484–488. [Google Scholar]
- Kovacs, G.; Nagy, S. Ultrasonic sensor fusion inverse algorithm for visually impaired aiding applications. Sensors 2020, 20, 3682. [Google Scholar] [CrossRef] [PubMed]
- Csapó, Á.; Wersényi, G.; Nagy, H.; Stockman, T. A survey of assistive technologies and applications for blind users on mobile platforms: A review and foundation for research. J. Multimodal User Interfaces 2015, 9, 275–286. [Google Scholar] [CrossRef]
- Pareja-Contreras, J.; Sotomayor-Polar, M.; Zenteno-Bolanos, E. Beamforming echo-localization system using multitone excitation signals. In Proceedings of the Instrumentation Systems Circuits and Transducers (INSCIT) 2017 2nd International Symposium, Fortaleza, Ceará, Brazil, 28 August–1 September 2017; pp. 1–5. [Google Scholar]
- Walter, C.; Schweinzer, H. An accurate compact ultrasonic 3D sensor using broadband impulses requiring no initial calibration. In Proceedings of the Instrumentation and Measurement Technology Conference (I2MTC) 2012 IEEE International, Graz, Austria, 13–16 May 2012; pp. 1571–1576. [Google Scholar]
- Orchard, G.; Etienne-Cummings, R. Discriminating Multiple Nearby Targets Using Single-Ping Ultrasonic Scene Mapping. Circuits Syst. I Regul. Pap. IEEE Trans. 2012, 57, 2915–2924. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets. In CBMS-NSF Regional Conference Series in Applied Mathematics 61; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Graham, D.; Simmons, G.; Nguyen, D.T.; Zhou, G. A Software-Based Sonar Ranging Sensor for Smart Phones. Internet Things J. IEEE 2015, 2, 479–489. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovács, G.; Nagy, S. Intelligent Wavelet Based Pre-Filtering Method for Ultrasonic Sensor Fusion Inverse Algorithm Performance Optimization. Inventions 2021, 6, 30. https://doi.org/10.3390/inventions6020030
Kovács G, Nagy S. Intelligent Wavelet Based Pre-Filtering Method for Ultrasonic Sensor Fusion Inverse Algorithm Performance Optimization. Inventions. 2021; 6(2):30. https://doi.org/10.3390/inventions6020030
Chicago/Turabian StyleKovács, György, and Szilvia Nagy. 2021. "Intelligent Wavelet Based Pre-Filtering Method for Ultrasonic Sensor Fusion Inverse Algorithm Performance Optimization" Inventions 6, no. 2: 30. https://doi.org/10.3390/inventions6020030
APA StyleKovács, G., & Nagy, S. (2021). Intelligent Wavelet Based Pre-Filtering Method for Ultrasonic Sensor Fusion Inverse Algorithm Performance Optimization. Inventions, 6(2), 30. https://doi.org/10.3390/inventions6020030






