Near-Field Simulations of Film Cooling with a Modified DES Model
Abstract
1. Introduction
2. Computational Methods
3. The Development of a Three-Directional Eddy Viscosity Modification
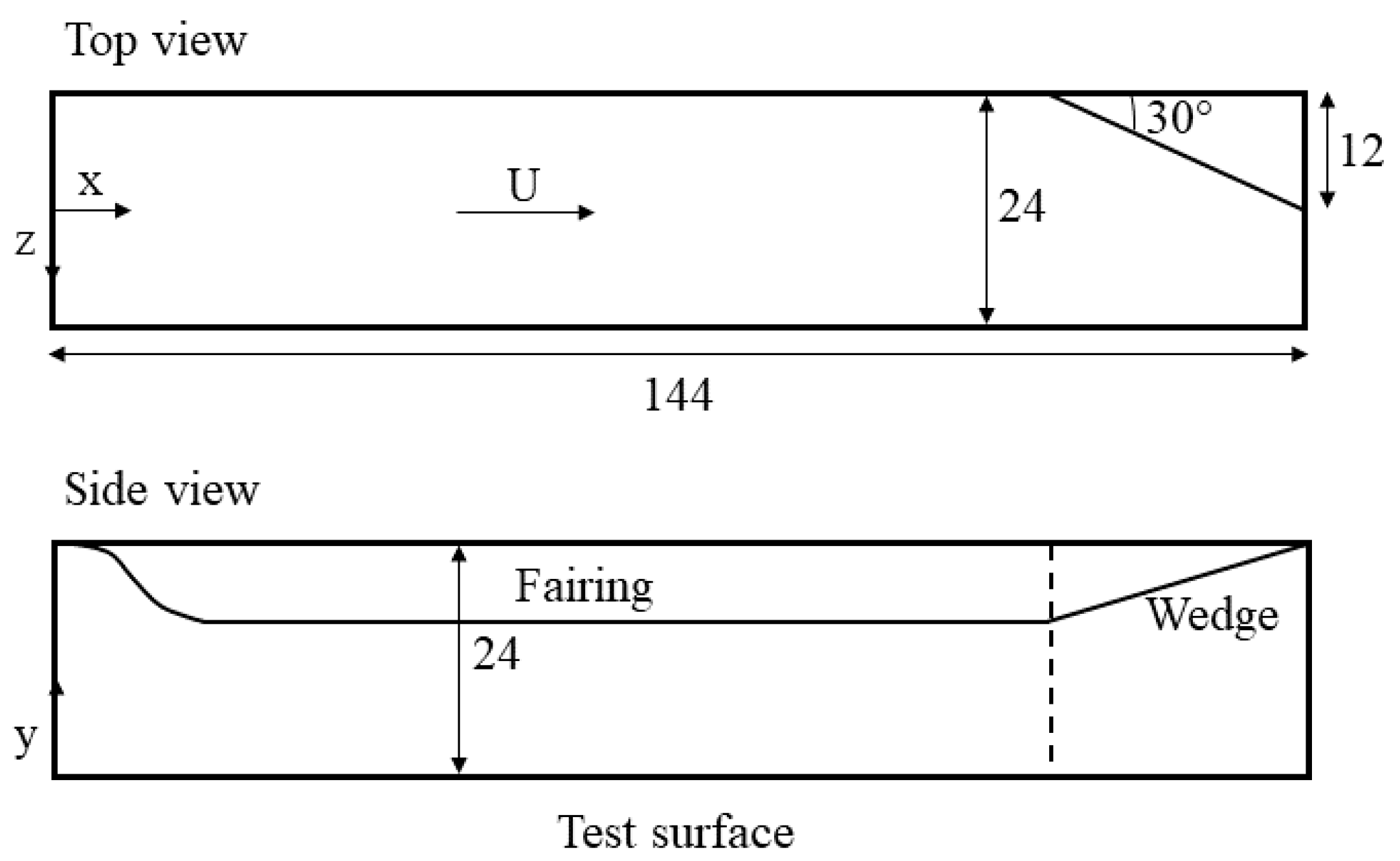
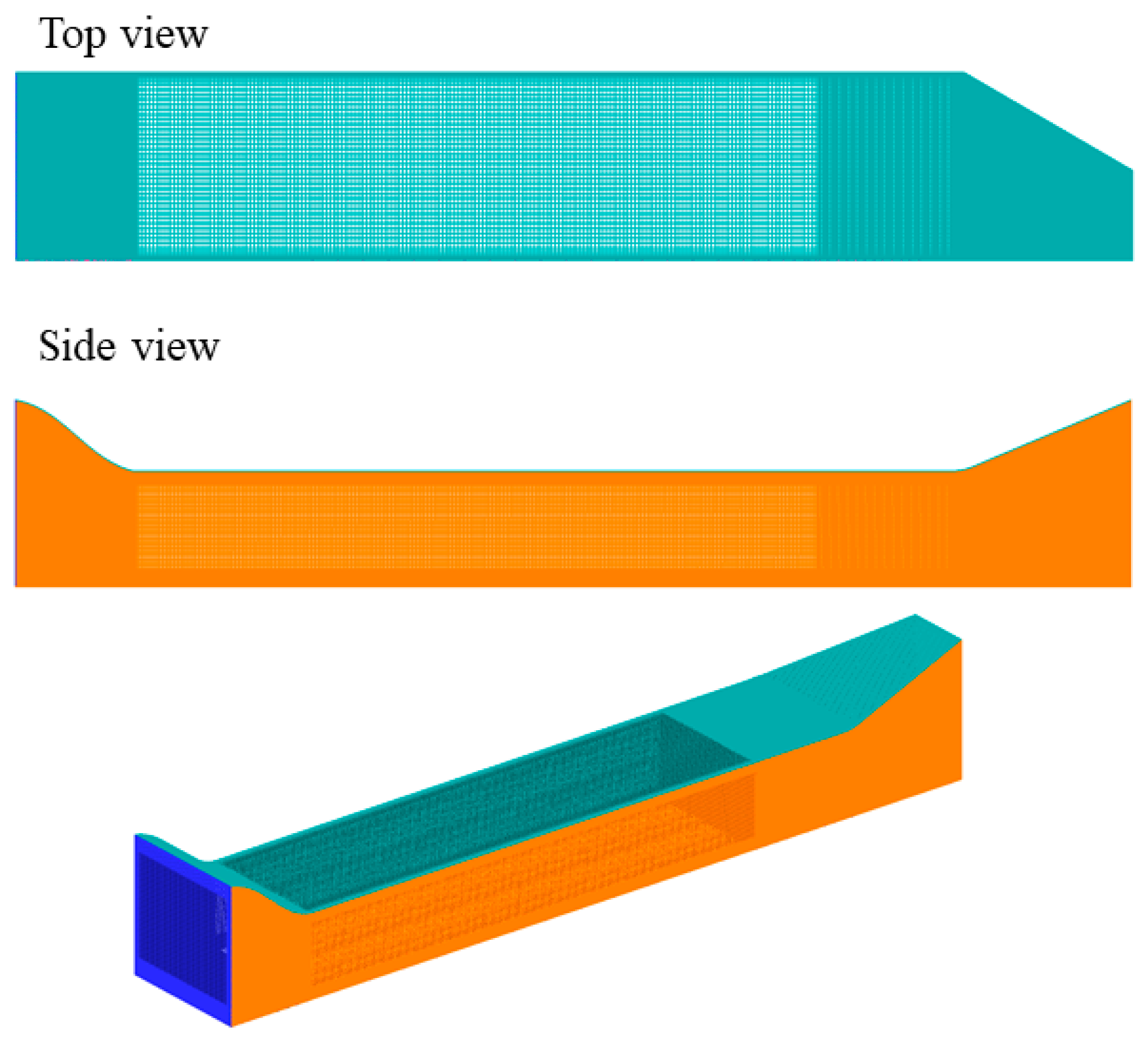
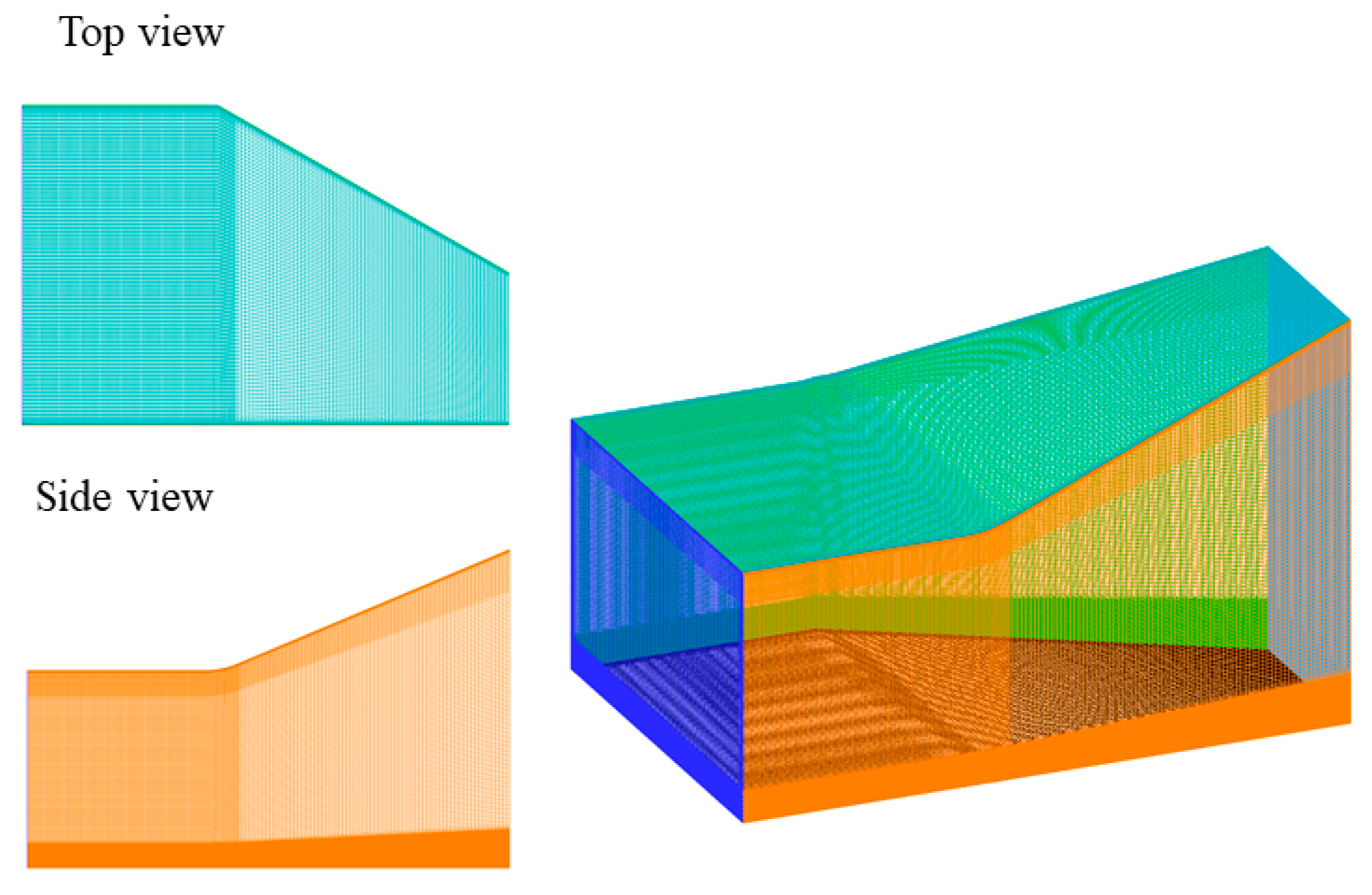
3.1. Anisotropic Eddy Viscosity Validation in a Three-Dimensional Boundary Layer Flow
3.2. Method Used for LES Data Post-Processing to Obtain Anisotropic Eddy Viscosity
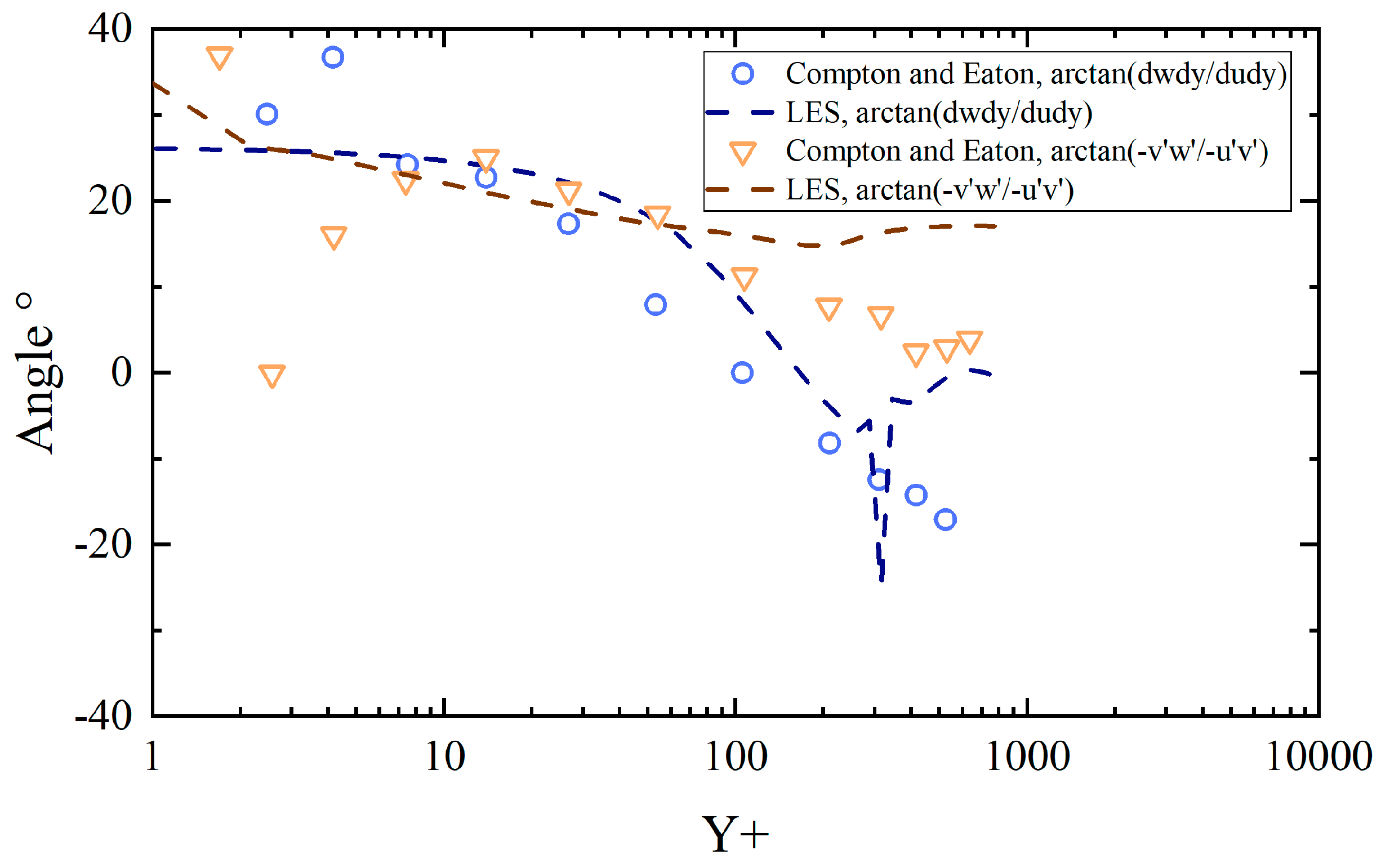
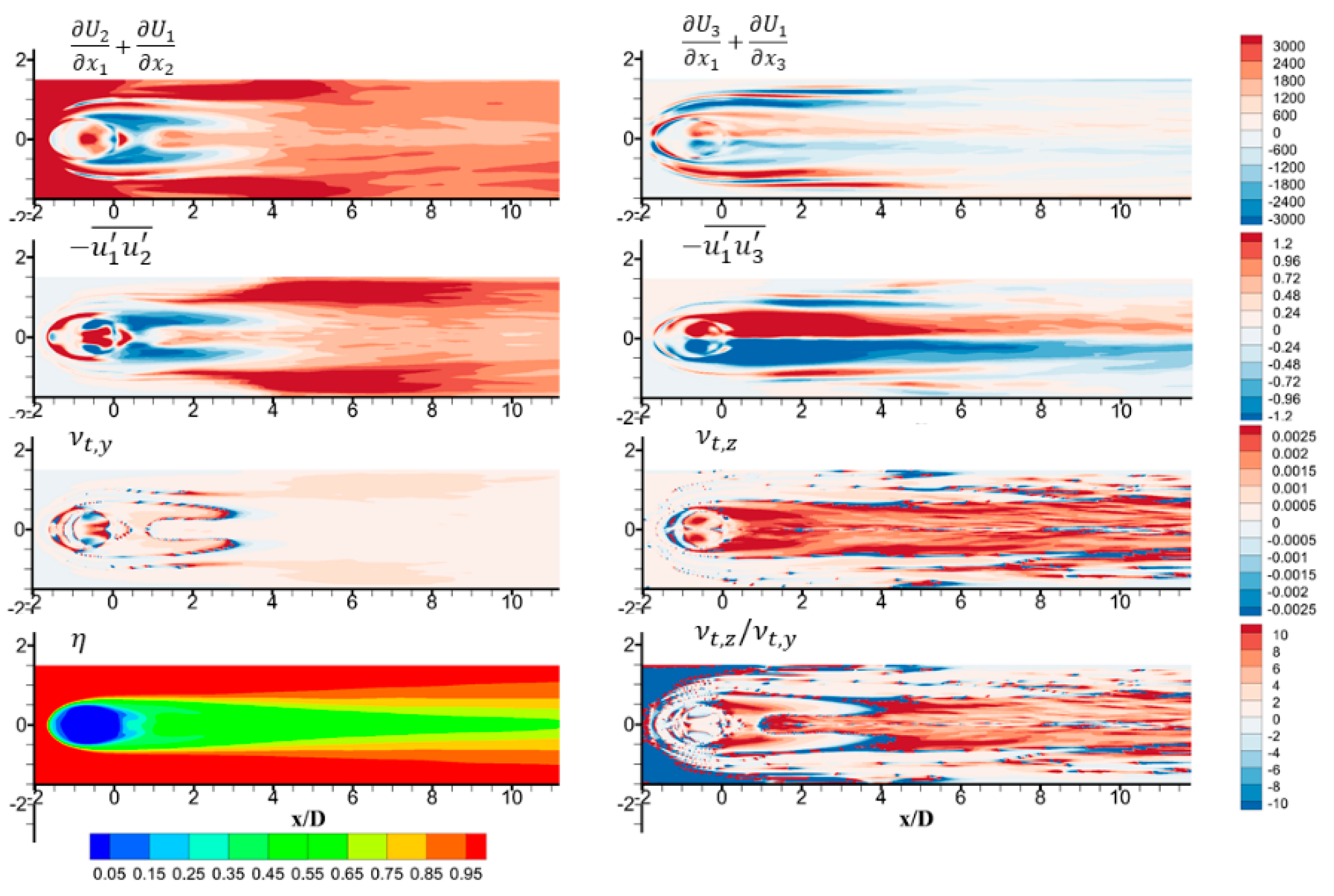
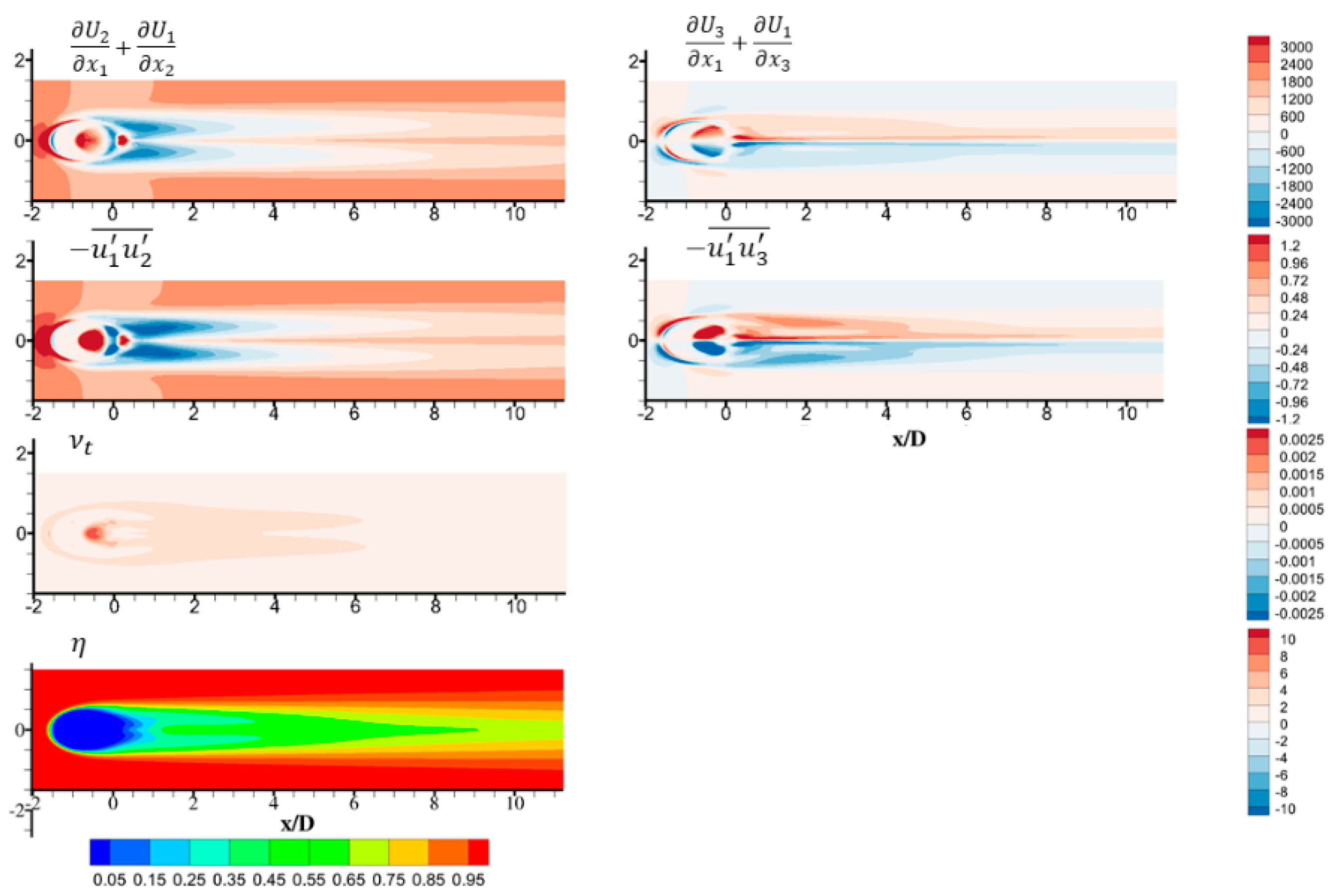
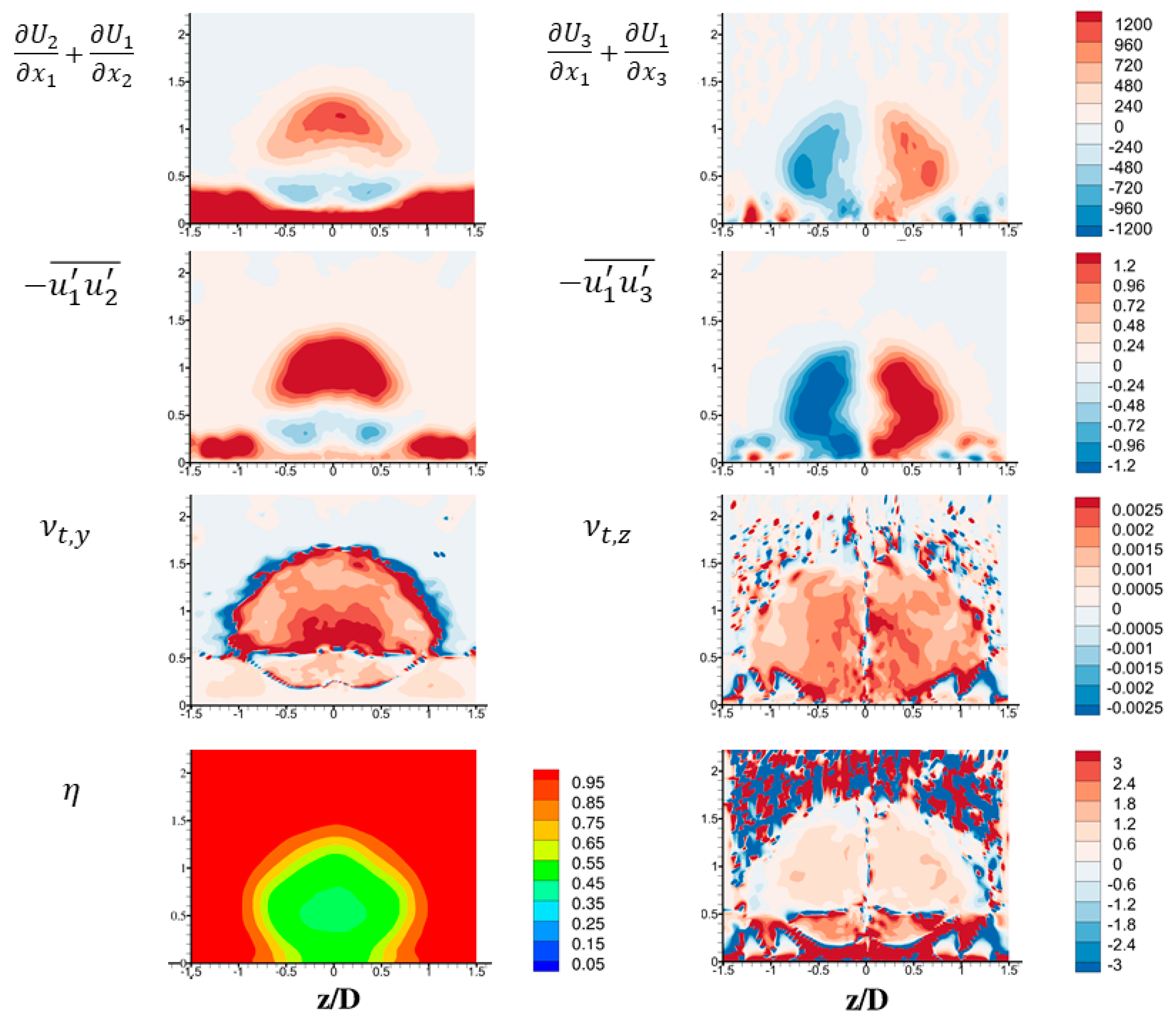
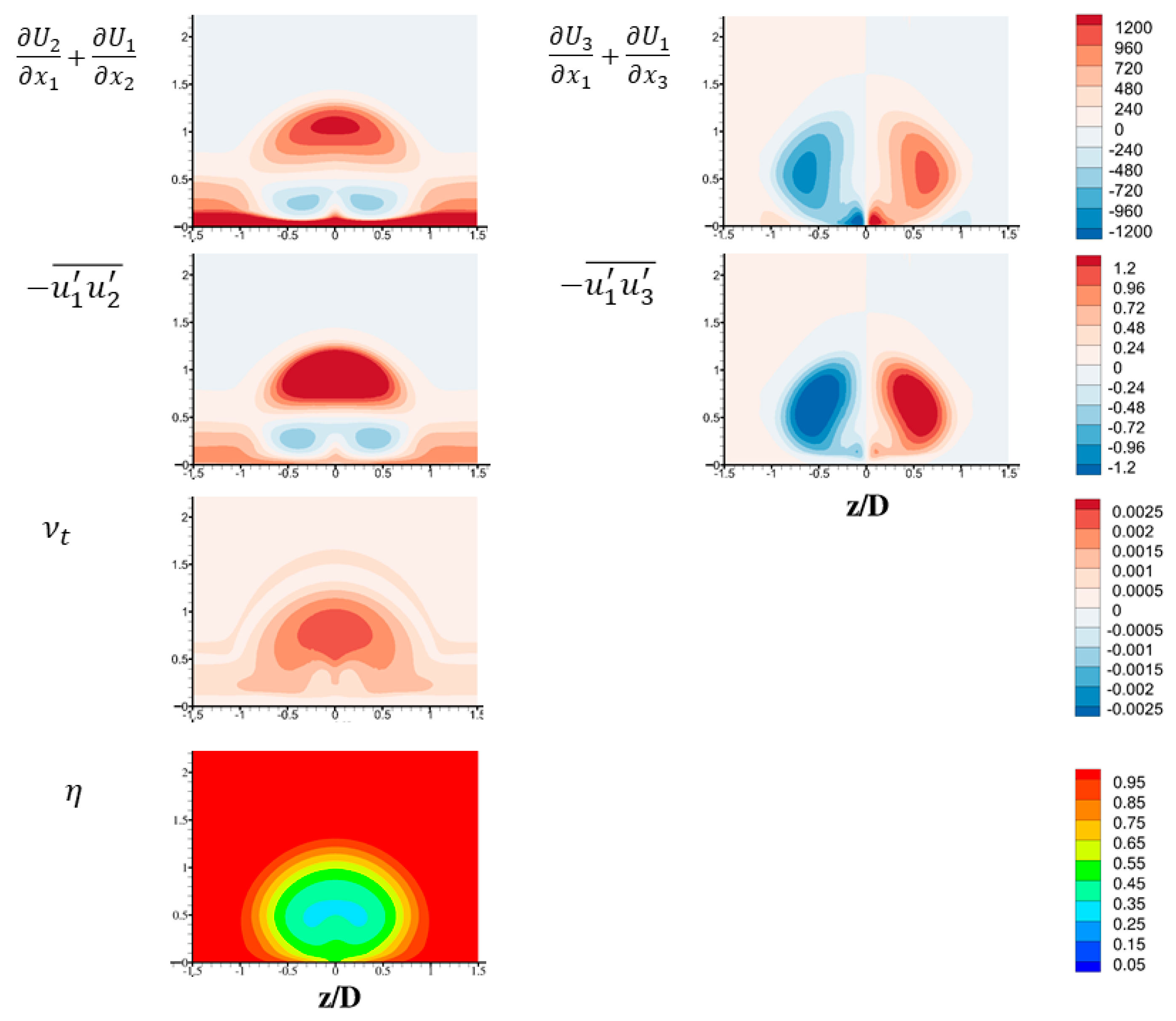
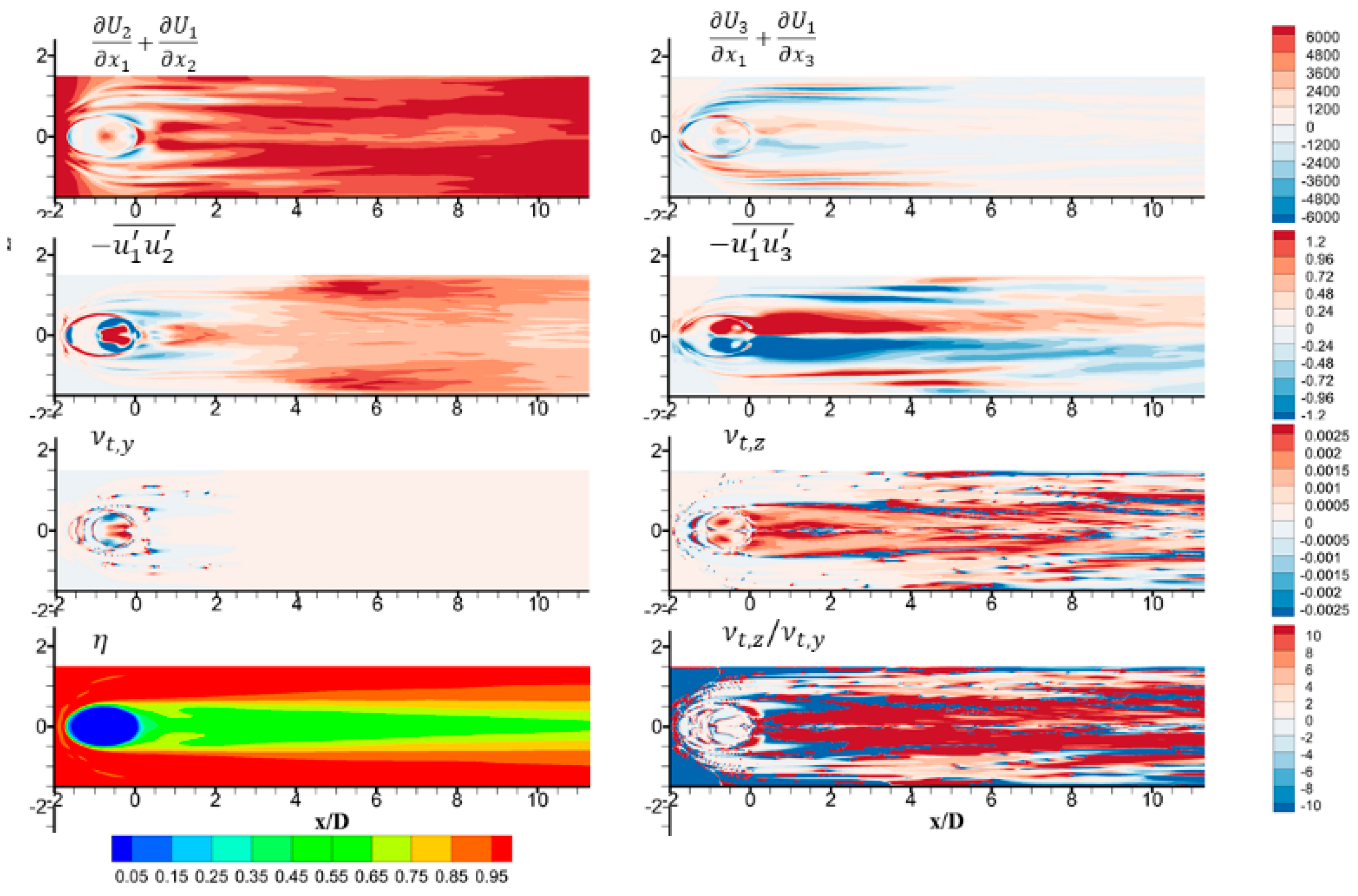
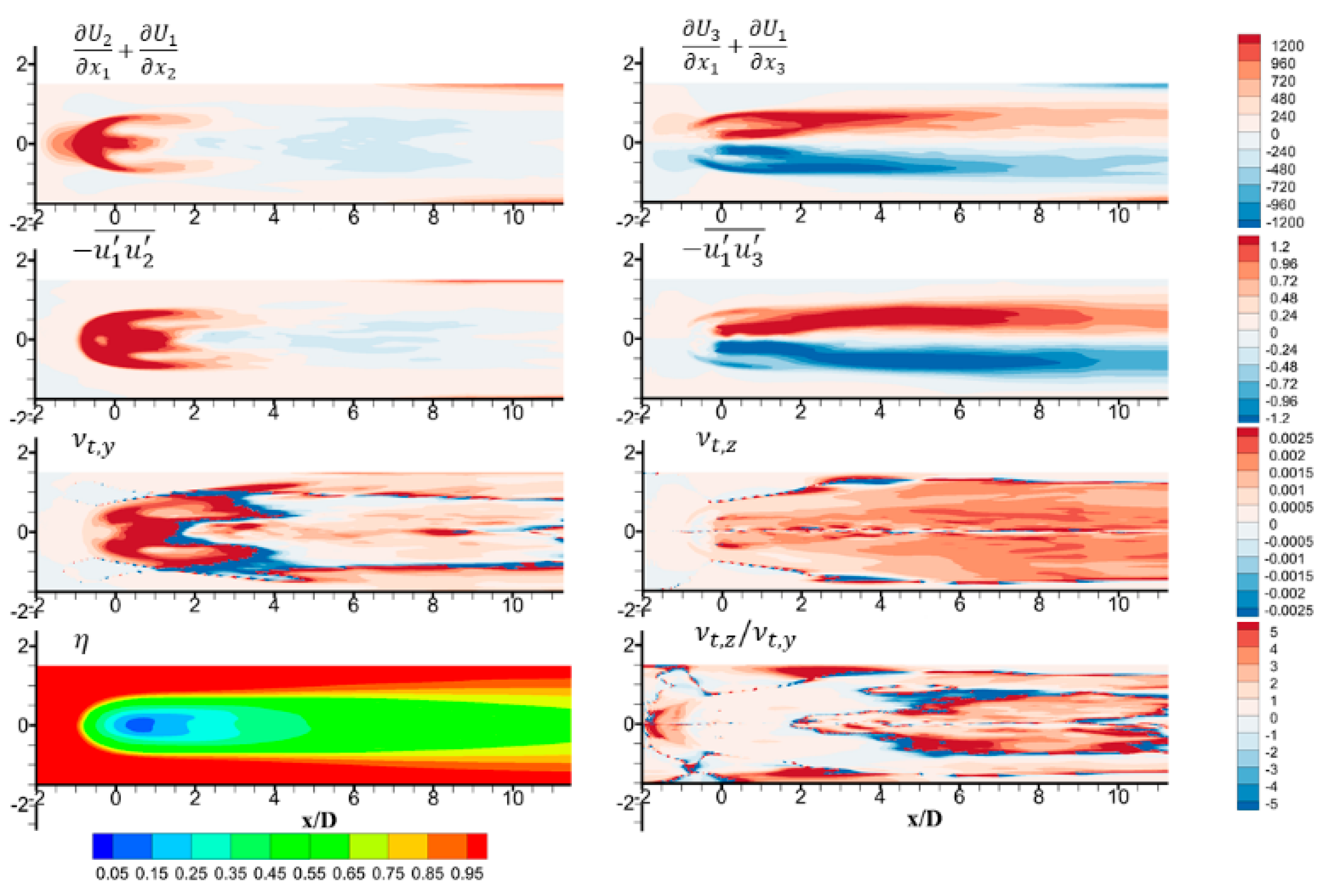
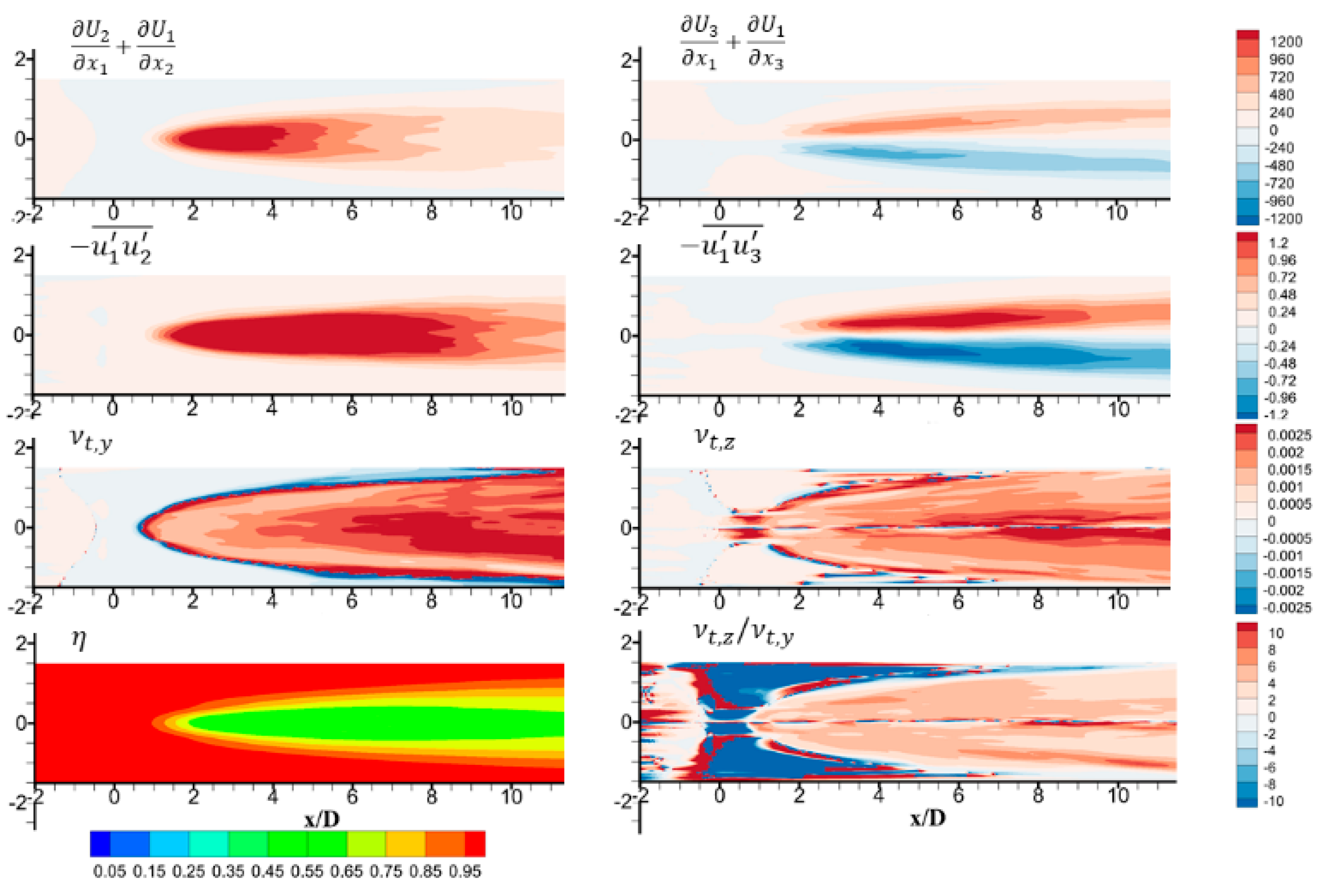
3.3. Post-Processing of LES Results and Analysis of Anisotropic Eddy Viscosity
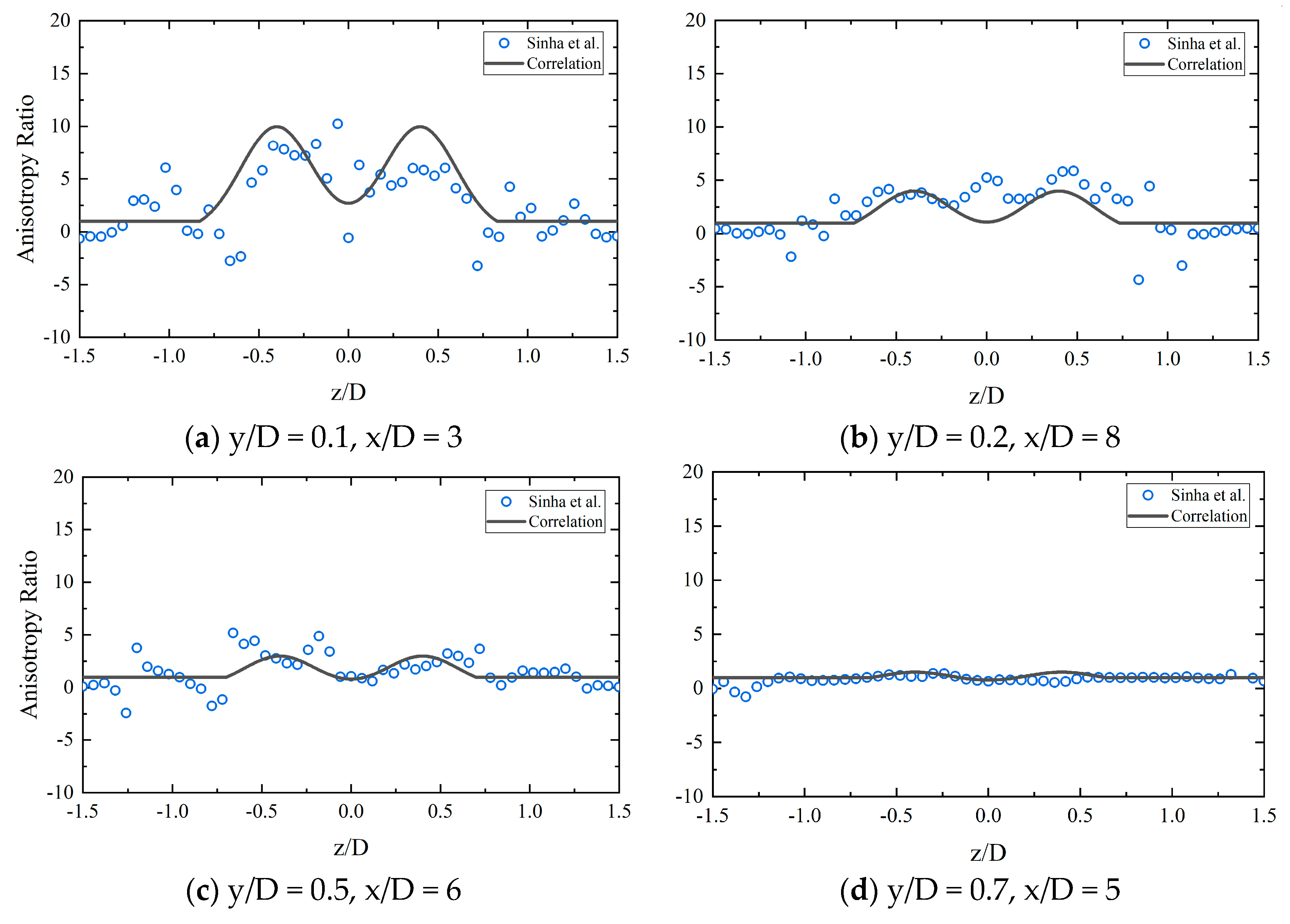
3.4. Three-Directional Anisotropy Ratio Correlation Development
4. Modeling of the Near Field of Film Cooling with Three-Directional Eddy Viscosity Using a Modified DES Model
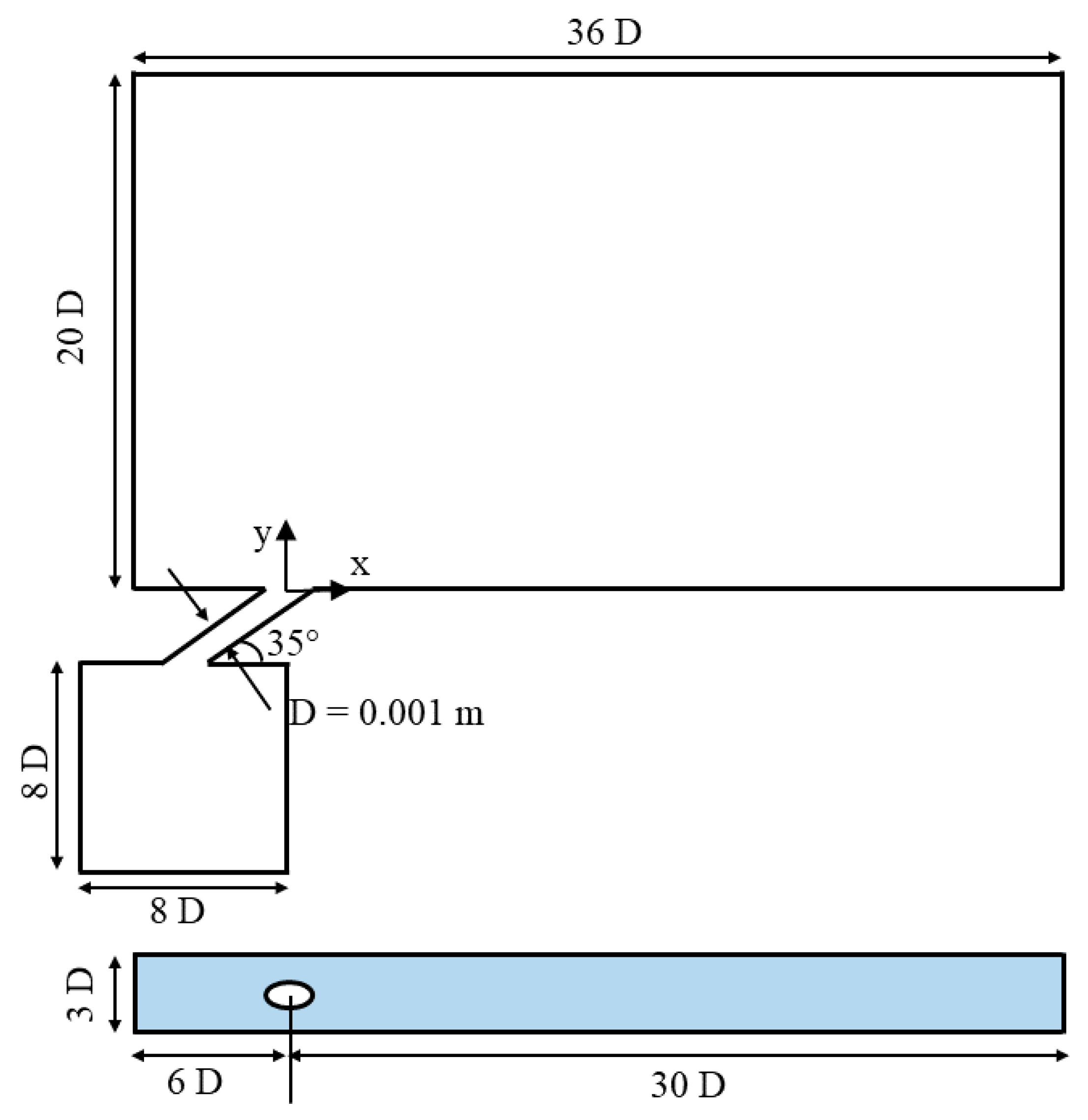
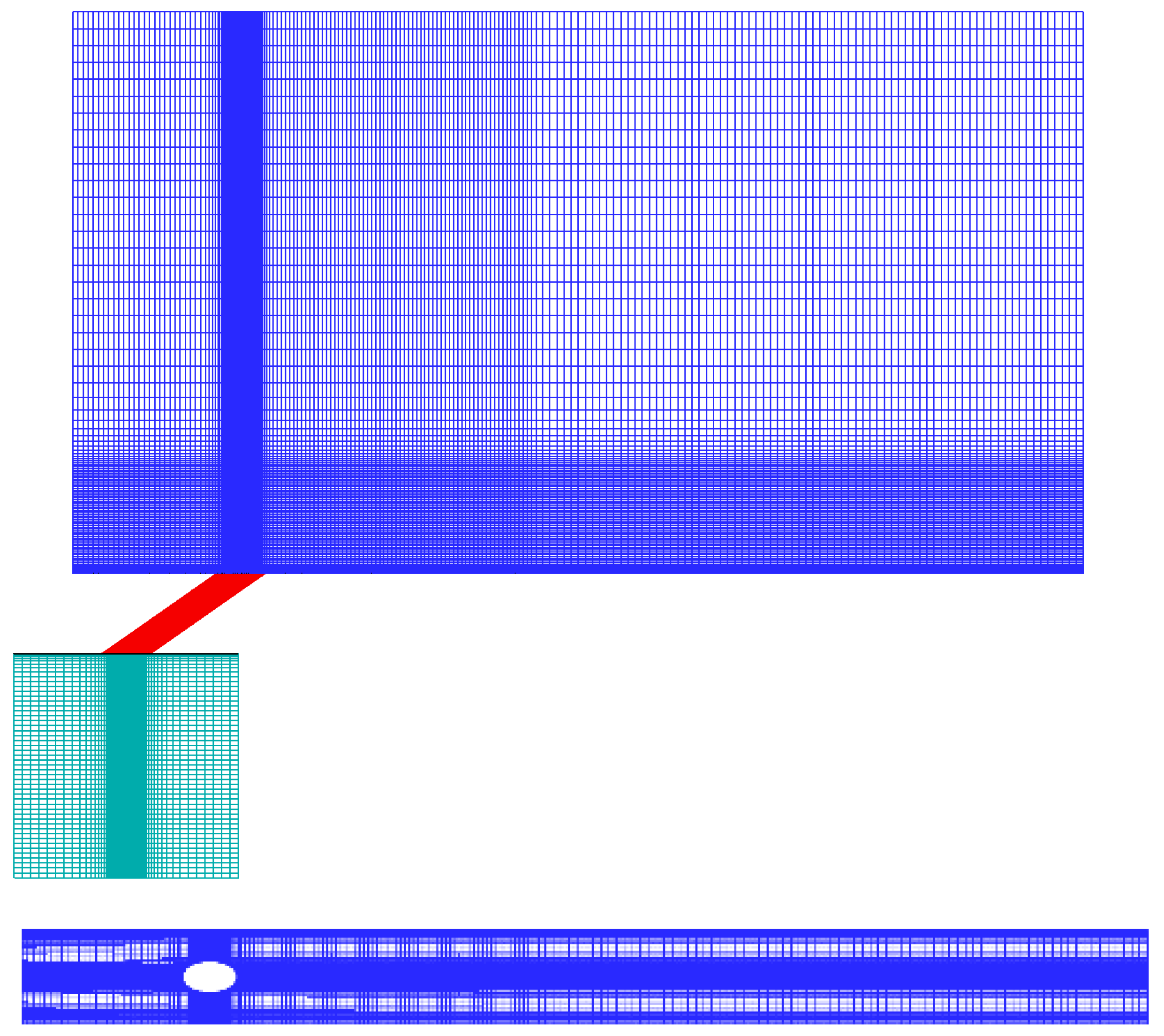
4.1. Computational Domain and Simulation Setup
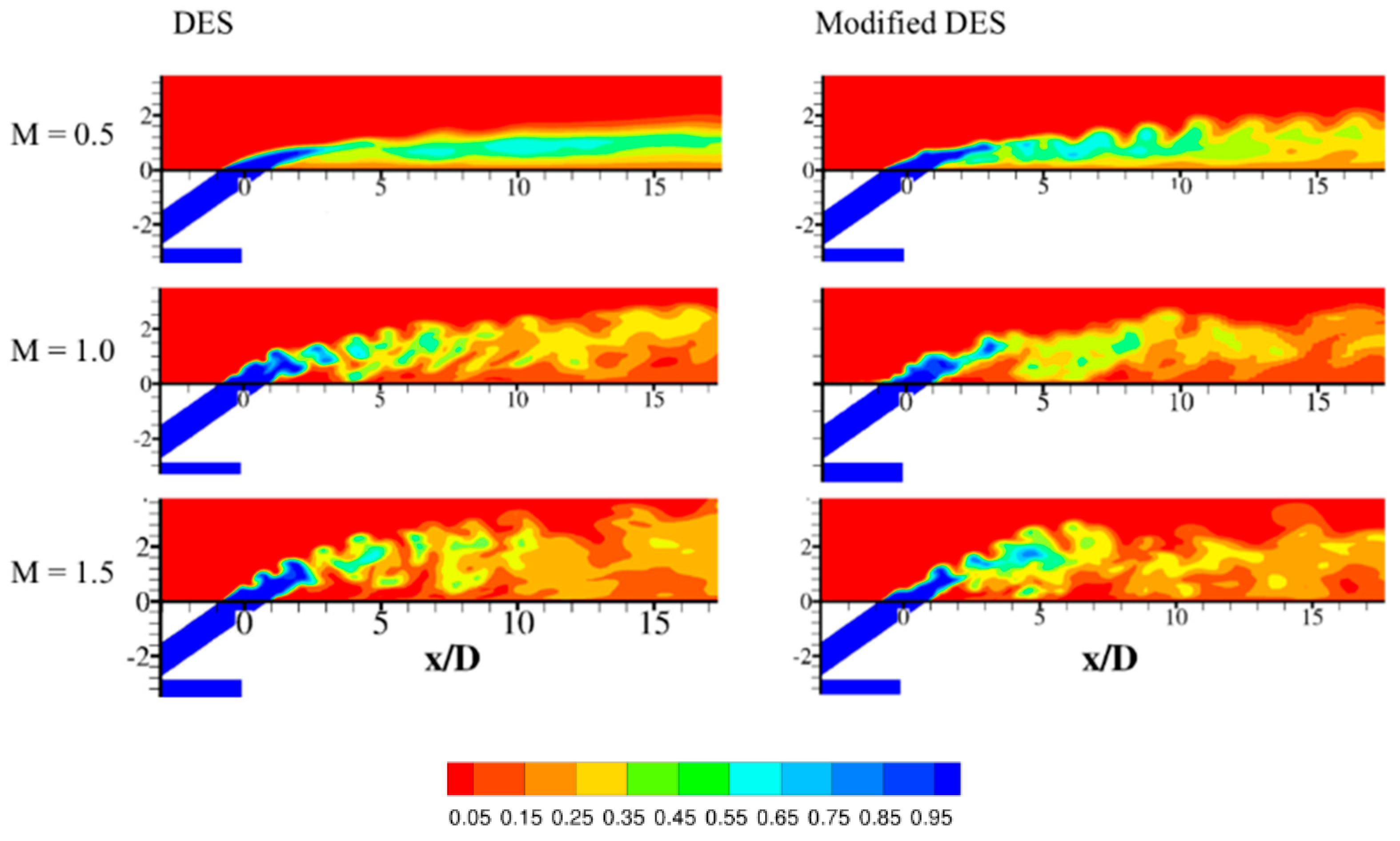
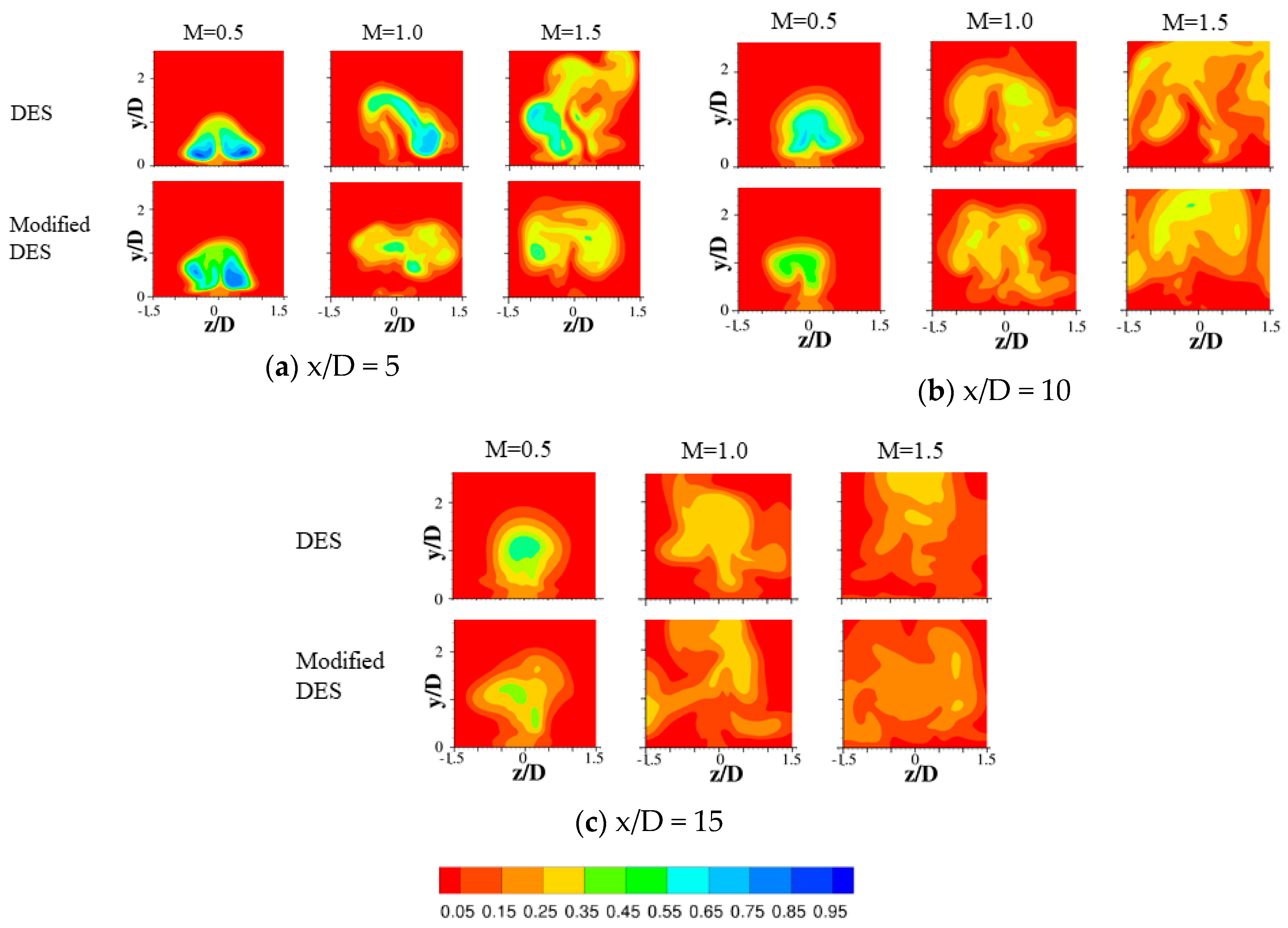
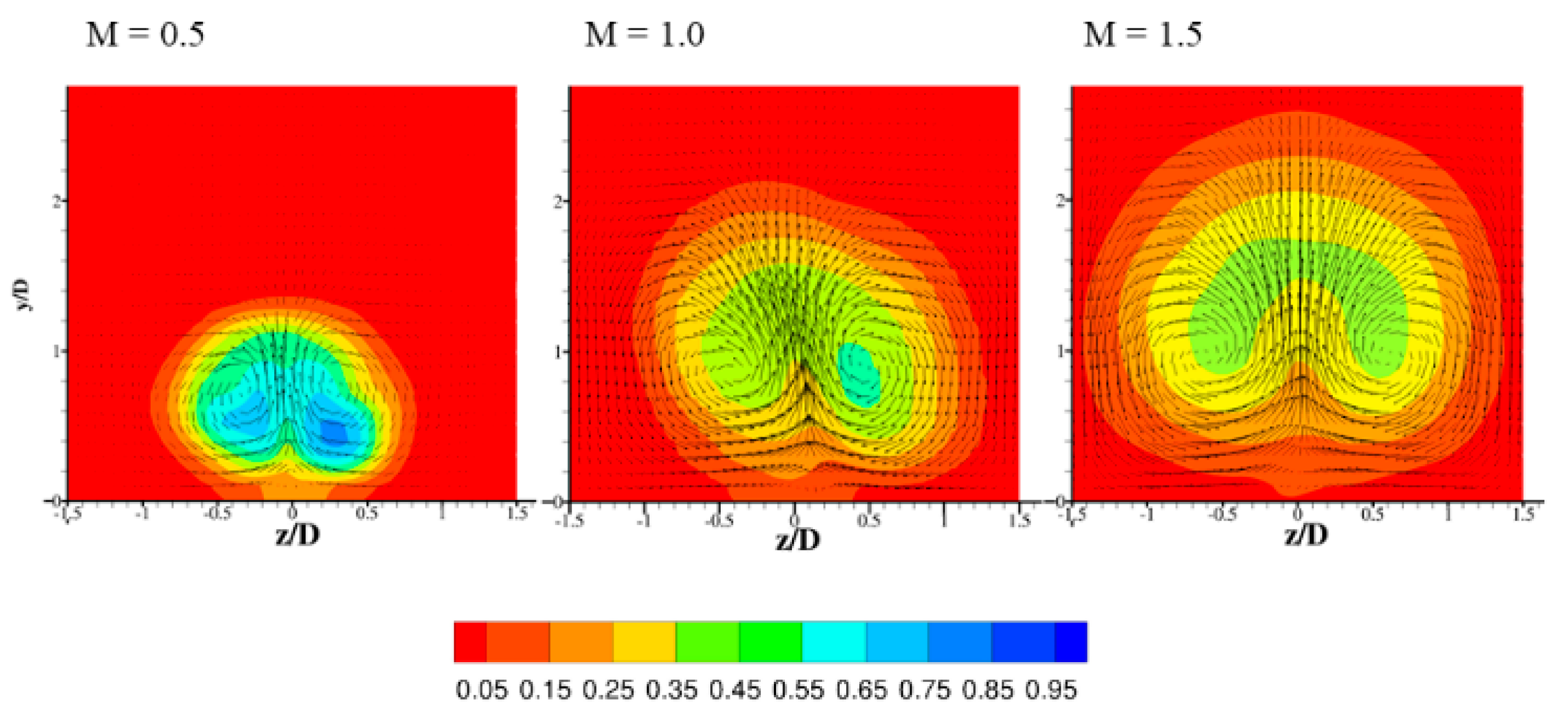
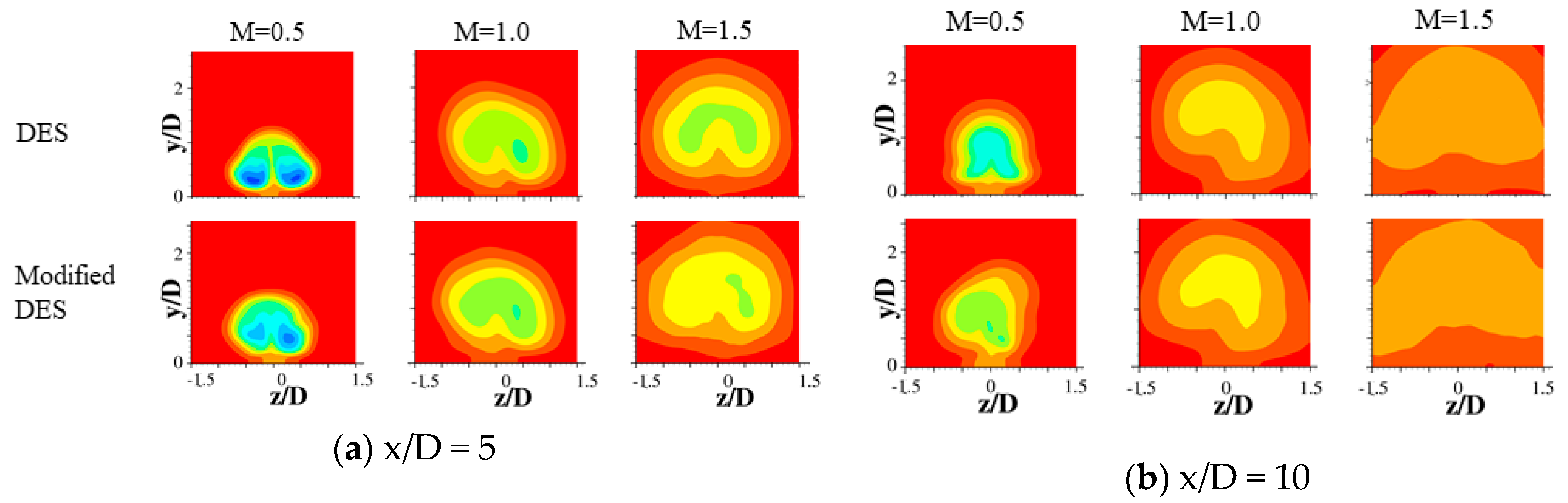
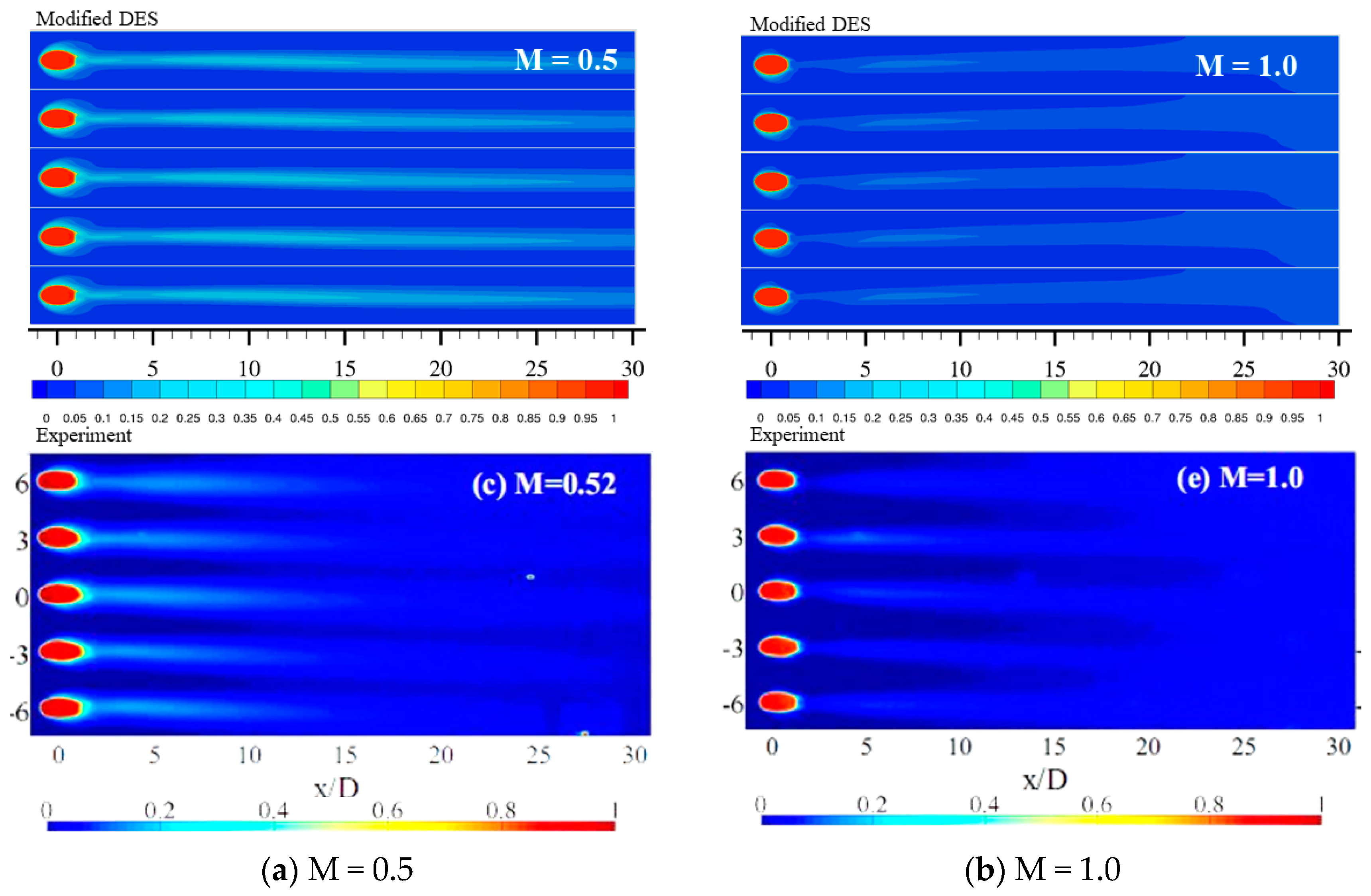
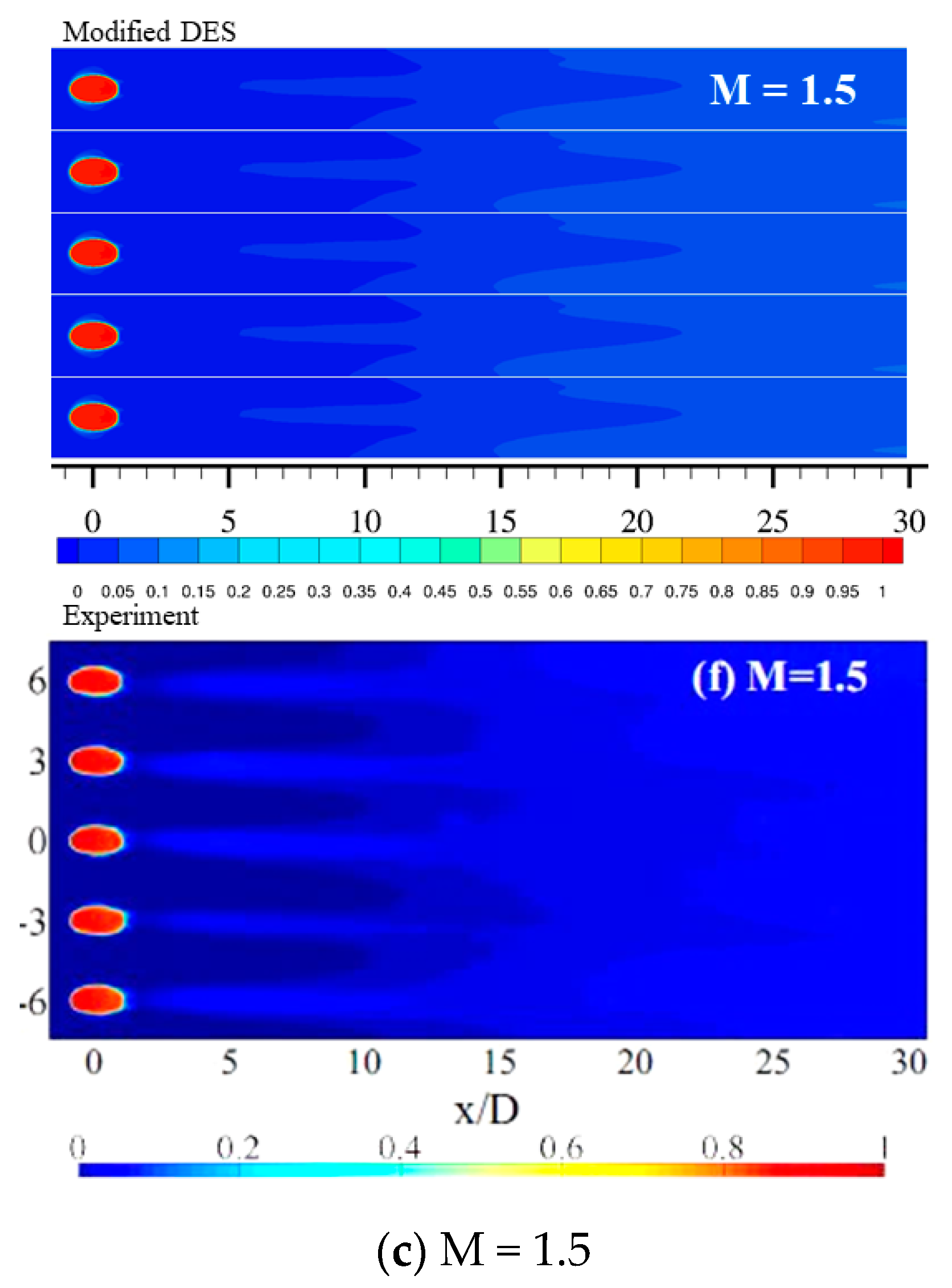
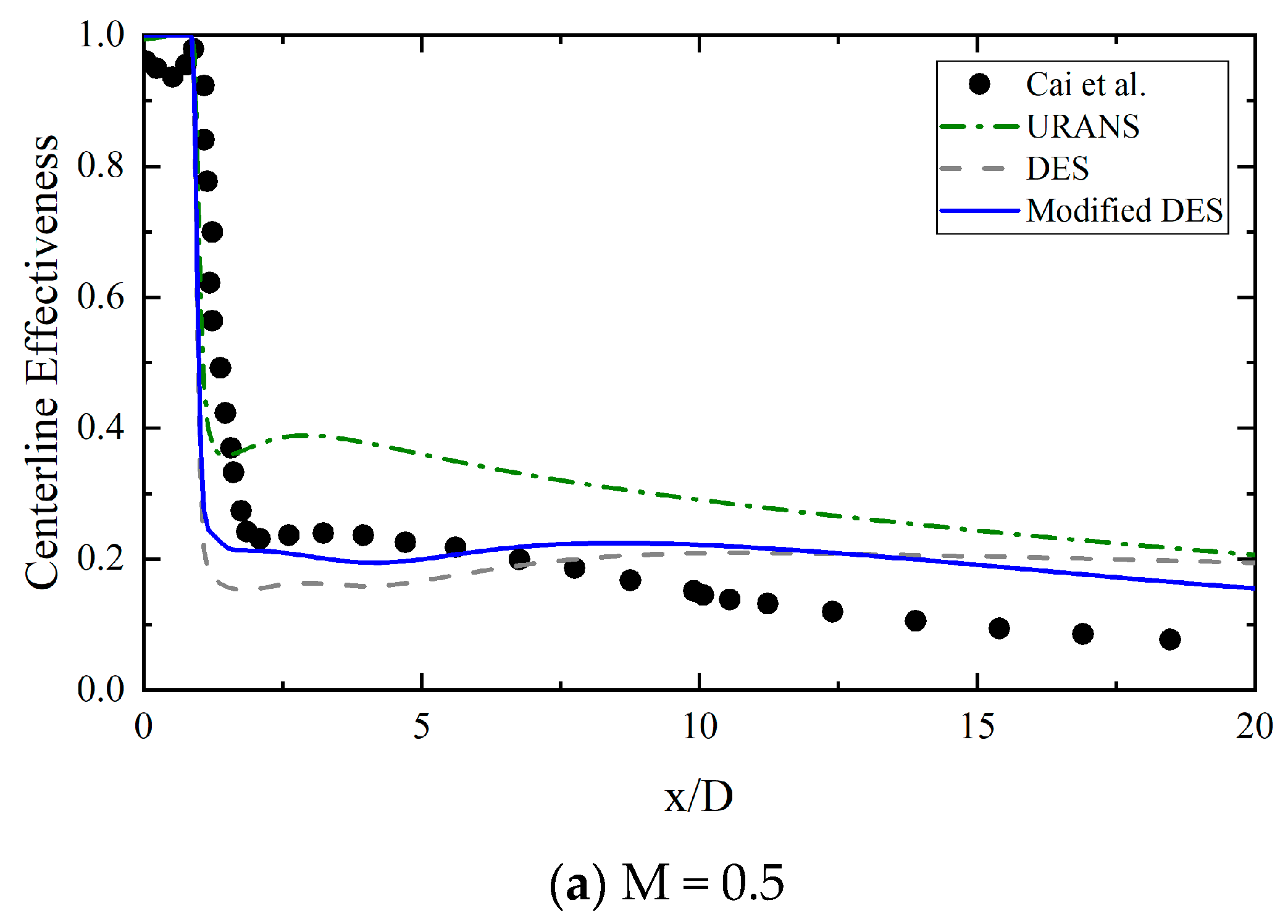
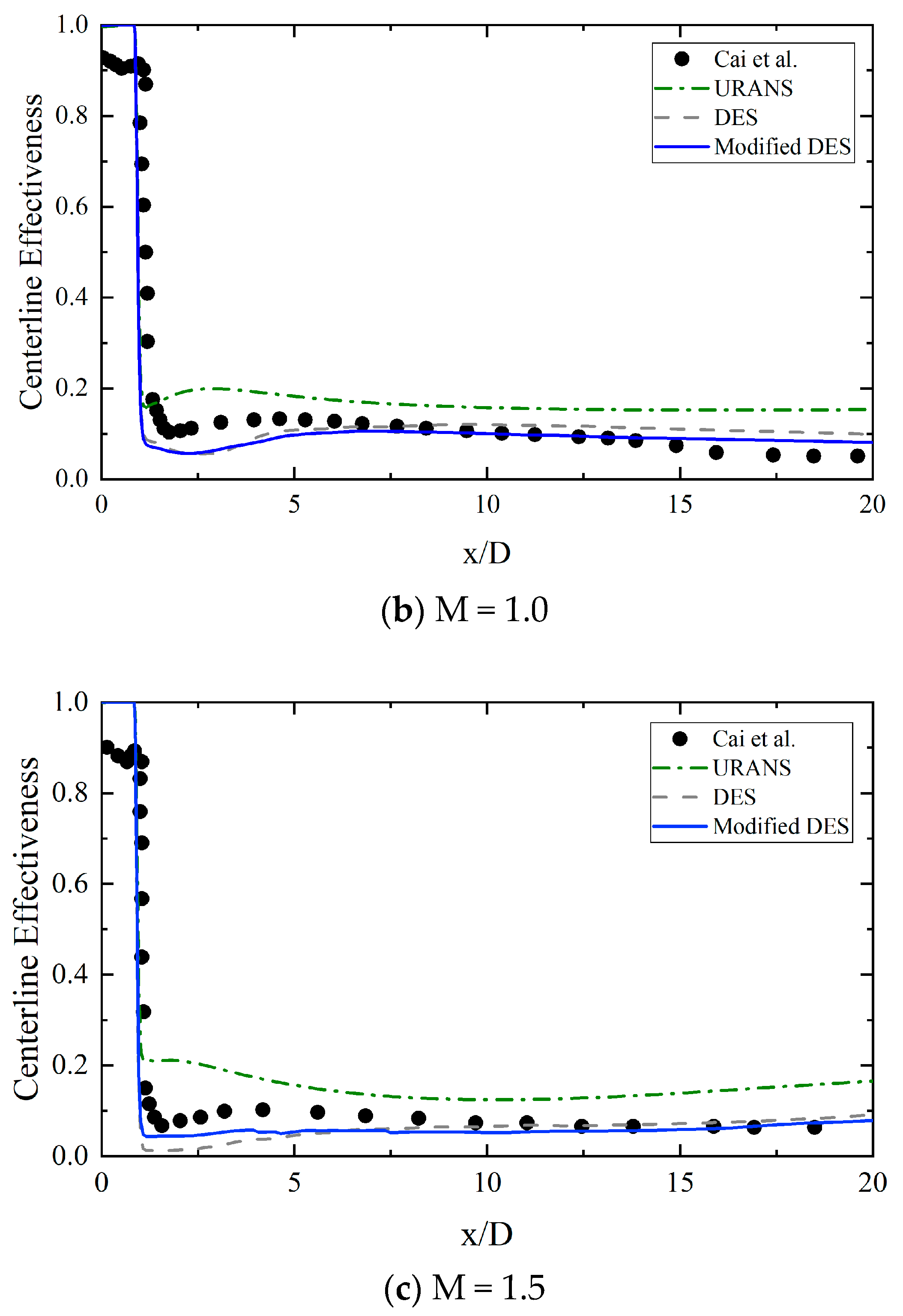
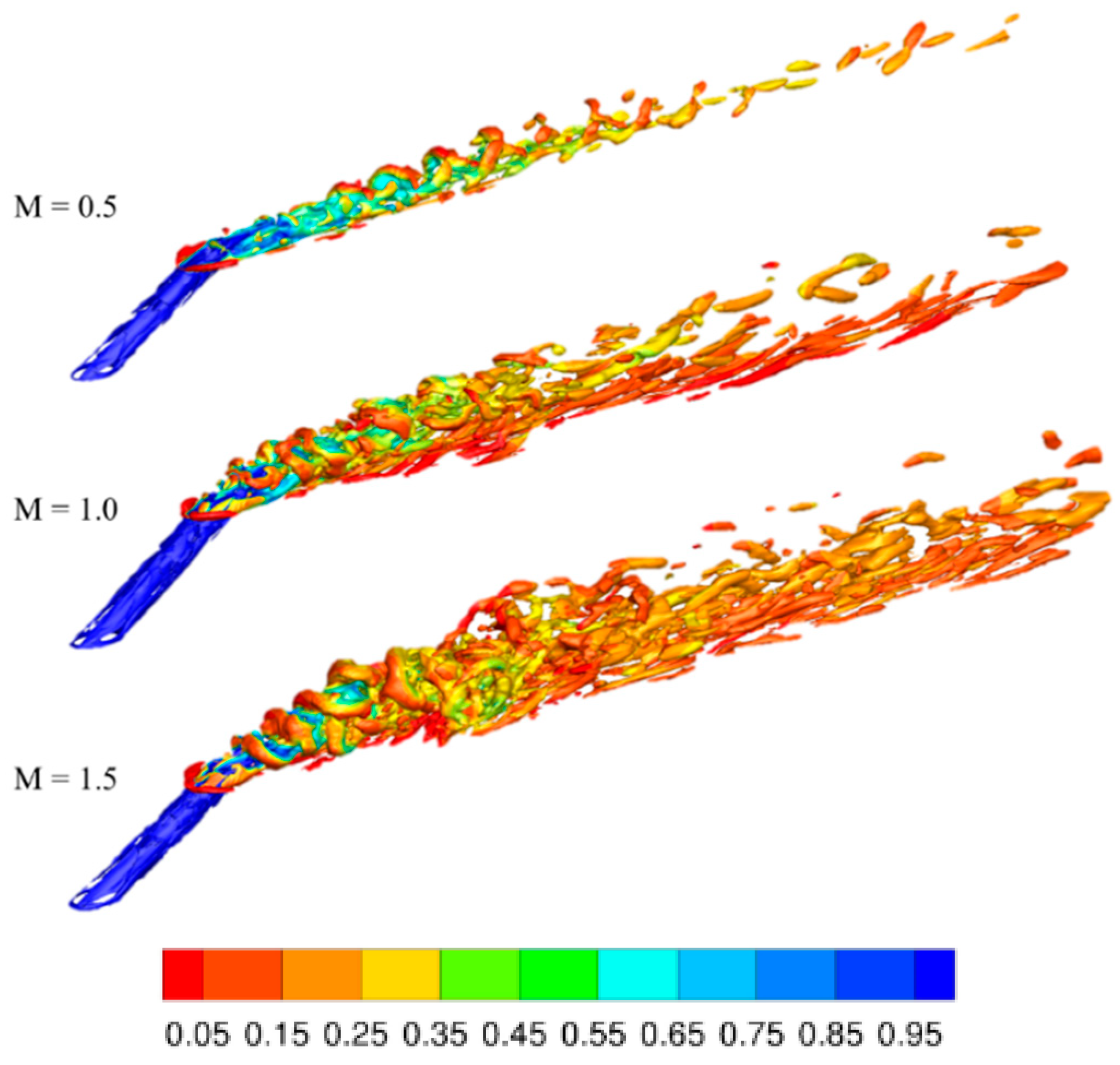
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jansohn, P. Modern Gas Turbine Systems: High Efficiency, Low Emission, Fuel Flexible Power Generation; Woodhead Publishing Limited: Cambridge, UK, 2013; pp. 21–23. [Google Scholar]
- Hada, S.; Takata, K.; Iwasaki, Y.; Yuri, M.; Masada, J. High-efficiency gas turbine development applying 1600°C class “J” technology. Mitsubishi Heavy Ind. Tech. Rev. 2015, 52, 2–9. [Google Scholar]
- Ito, E.; Okada, I.; Tsukagoshi, K.; Masada, J. Development of key technologies for the next generation high temperature gas turbine. In Proceedings of the ASME Turbo Expo, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Han, J.C.; Ekkad, S. Recent development in turbine blade film cooling. Int. J. Rotating 2001, 7, 21–40. [Google Scholar] [CrossRef]
- Baldauf, S.M.; Schulz, A.; Wittig, S. High-resolution measurements of local effectiveness from discrete hole film cooling. ASME J. Turbomach 2001, 123, 758–765. [Google Scholar] [CrossRef]
- Han, J.C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology; Taylor & Francis: Boca Raton, FL, USA, 2012; pp. 225–229. [Google Scholar]
- Goldstein, R.J.; Jin, P.; Olson, R.L. Film cooling effectiveness and mass/heat transfer coefficient downstream of one row of discrete holes. ASME J. Turbomach. 1999, 121, 225–232. [Google Scholar] [CrossRef]
- Walters, D.K.; Leylek, J.H. A systematic computational methodology applied to three-dimensional film-cooling flowfield. ASME J. Turbomach. 1997, 199, 777–785. [Google Scholar] [CrossRef]
- Walters, D.K.; Leylek, J.H.; Buck, F.A. Film cooling on a modern HP turbine blade: Part II–compound-angle round holes. In Proceedings of the ASME Turbo Expo, Amsterdam, The Netherlands, 3–6 June 2002. [Google Scholar]
- Akbarzadeh, M.; Rashidi, S.; Karimi, N.; Ellahi, R. Convection of heat and thermodynamic irreversibilities in two-phase, turbulent nanofluid flows in solar heaters by corrugated absorber plates. Adv. Powder Technol. 2018, 29, 2243–2254. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Ellahi, R.; Mirzakhanlari, S.; Mamourian, M. Enhancement of heat transfer and heat exchanger effectiveness in a double pipe heat exchanger filled with porous media: Numerical simulation and sensitivity analysis of turbulent fluid flow. Appl. Therm. Eng. 2016, 109, 761–774. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Pourmehran, O.; Yang, B.; Arjomandi, M.; Ellahi, R. Pool boiling heat transfer characteristics of iron oxide nano-suspension under constant magnetic field. Int. J. Therm. Sci. 2020, 147, 106131. [Google Scholar] [CrossRef]
- Ray, A.K.; Vasu, B.; Bég, O.A.; Gorla, R.S.; Murthy, P.V.S.N. Homotopy semi-numerical modeling of non-Newtonian nanofluid transport external to multiple geometries using a revised Buongiorno Model. Inventions 2019, 4, 54. [Google Scholar] [CrossRef]
- Compton, D.A.; Eaton, J.K. Near-wall measurements in a three-dimensional turbulent boundary layer. ASME J. Fluid Mech. 1997, 350, 189–208. [Google Scholar] [CrossRef]
- Kaszeta, R.W.; Simon, T.W. Measurement of eddy diffusivity of momentum in film cooling flows with streamwise injection. ASME J. Turbomach. 1999, 122, 178–183. [Google Scholar] [CrossRef]
- Coletti, F.; Benson, M.J.; Ling, J.; Elkins, C.J.; Eaton, J.K. Turbulent transport in an inclined jet in crossflow. Int. J. Heat Fluid Flow 2013, 43, 149–160. [Google Scholar] [CrossRef]
- Ling, J.; Templeton, J. Evaluation of machine learning algorithms for prediction of regions of high Reynolds averaged Navier Stokes uncertainty. Phys. Fluids 2015, 27, 085103. [Google Scholar] [CrossRef]
- Dow, E.; Wang, Q. Uncertainty quantification of structural uncertainties in RANS simulations of complex flows. In Proceedings of the AIAA Computational Fluid Dynamics Conference, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar]
- Acharya, S.; Tyagi, M.; Hoda, A. Flow and heat transfer predictions for film cooling. Ann. N. Y. Acad. Sci. 2001, 934, 110–125. [Google Scholar] [CrossRef] [PubMed]
- Kapadia, S.; Roy, S.; Heidmann, J. Detached eddy simulation of turbine blade cooling. In Proceedings of the 36th AIAA Thermophysics Conference, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Spalart, P.R.; Streett, C. Young-person’s guide to detached-eddy simulation grids. NASA CR-2001-211032.
- Squires, K.D.; Forsythe, J.R.; Morton, S.A.; Strang, W.Z.; Wurtzler, K.E.; Tomaro, R.F.; Grismer, M.J.; Spalart, P.R. Progress on detached-eddy simulation of massively separated flows. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Fröhlich, J.; Terzi, D.V. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Yu, F.; Yavuzkurt, S. Simulation of film cooling flow structure and heat transfer in the near field of cooling jets with a modified DES model. In Proceedings of the ASME SHTC, Bellevue, WA, USA, 12–15 July 2019. [Google Scholar]
- Roy, S.; Kapadia, S.; Heidmann, J.D. Film cooling analysis using des turbulence model. In Proceedings of the ASME Turbo Expo, Atlanta, GA, USA, 16–19 June 2003. [Google Scholar]
- Sakai, E.; Takahashi, T.; Funazaki, K.I.; Salleh, H.B.; Watanabe, K. Numerical study on flat plate and leading edge film cooling. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 8–12 June 2009. [Google Scholar]
- Ling, J.; Ryan, K.J.; Bodart, J.; Eaton, J.K. Analysis of turbulent scalar flux models for a discrete hole film cooling flow. J. Turbomach. 2016, 138, 011006. [Google Scholar] [CrossRef]
- Milani, P.M.; Ling, J.; Saez-Mischlich, G.; Bodart, J.; Eaton, J.K. A machine learning approach for determining the turbulent diffusivity in film cooling flows. J. Turbomach. 2018, 140, 021006. [Google Scholar] [CrossRef]
- Gritsch, M.; Colban, W.; Schär, H.; Döbbeling, K. Effect of hole geometry on the thermal performance of fan-shaped film cooling holes. J. Turbomach. 2005, 127, 718–725. [Google Scholar] [CrossRef]
- Schroeder, R.P.; Thole, K.A. Adiabatic effectiveness measurements for a baseline shaped film cooling hole. In Proceedings of the ASME Turbo Expo, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Zuniga, H.A.; Kapat, J.S. Effect of increasing pitch-to-diameter ratio on the film cooling effectiveness of shaped and cylindrical holes embedded in trenches. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 8–12 June 2009. [Google Scholar]
- Cai, T.; Peng, D.; Yavuzkurt, S.; Liu, Y.Z. Unsteady 2-D film-cooling effectiveness behind a single row of holes at different blowing ratios: Measurements using fast-response pressure-sensitive paint. Int. J. Heat Mass Transfer 2018, 120, 1325–1340. [Google Scholar] [CrossRef]
- Shih, T.; Liou, W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-epsilon Eddy-Viscosity Model for High Reynolds Number Turbulent Flows—Model Development and Validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Fluent, ANSYS. 12.0 Theory Guide; Ansys Inc: Canonsburg, PA, USA, 2009.
- Han, J.C.; Rallabandi, A. Turbine blade film cooling using PSP technique. FHMT 2010, 1, 013001. [Google Scholar] [CrossRef]
- Wright, L.M.; Gao, Z.; Varvel, T.A.; Han, J.C. Assessment of steady state PSP, TSP, and IR measurement techniques for flat plate film cooling. In Proceedings of the ASME Summer Heat Transfer Conference collocated with the ASME Pacific Rim Technical Conference and Exhibition on Integration and Packaging of MEMS, NEMS, and Electronic Systems, San Francisco, CA, USA, 17–22 July 2005. [Google Scholar]
- Rallabandi, A.P.; Li, S.J.; Han, J.C. Unsteady Wake and Coolant Density Effects on Turbine Blade Film Cooling Using Pressure Sensitive Paint Technique. J. Heat Transf. 2012, 134, 081701. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Sinha, A.K.; Bogard, D.G.; Crawford, M.E. Film-cooling effectiveness downstream of a single row of holes with variable density ratio. ASME J. Turbomach. 1991, 113, 442–449. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Yavuzkurt, S. Near-Field Simulations of Film Cooling with a Modified DES Model. Inventions 2020, 5, 13. https://doi.org/10.3390/inventions5010013
Yu F, Yavuzkurt S. Near-Field Simulations of Film Cooling with a Modified DES Model. Inventions. 2020; 5(1):13. https://doi.org/10.3390/inventions5010013
Chicago/Turabian StyleYu, Feiyan, and Savas Yavuzkurt. 2020. "Near-Field Simulations of Film Cooling with a Modified DES Model" Inventions 5, no. 1: 13. https://doi.org/10.3390/inventions5010013
APA StyleYu, F., & Yavuzkurt, S. (2020). Near-Field Simulations of Film Cooling with a Modified DES Model. Inventions, 5(1), 13. https://doi.org/10.3390/inventions5010013



