Statistical Analysis of the Mathematical Model of Entropy Generation of Magnetized Nanofluid
Abstract
1. Introduction
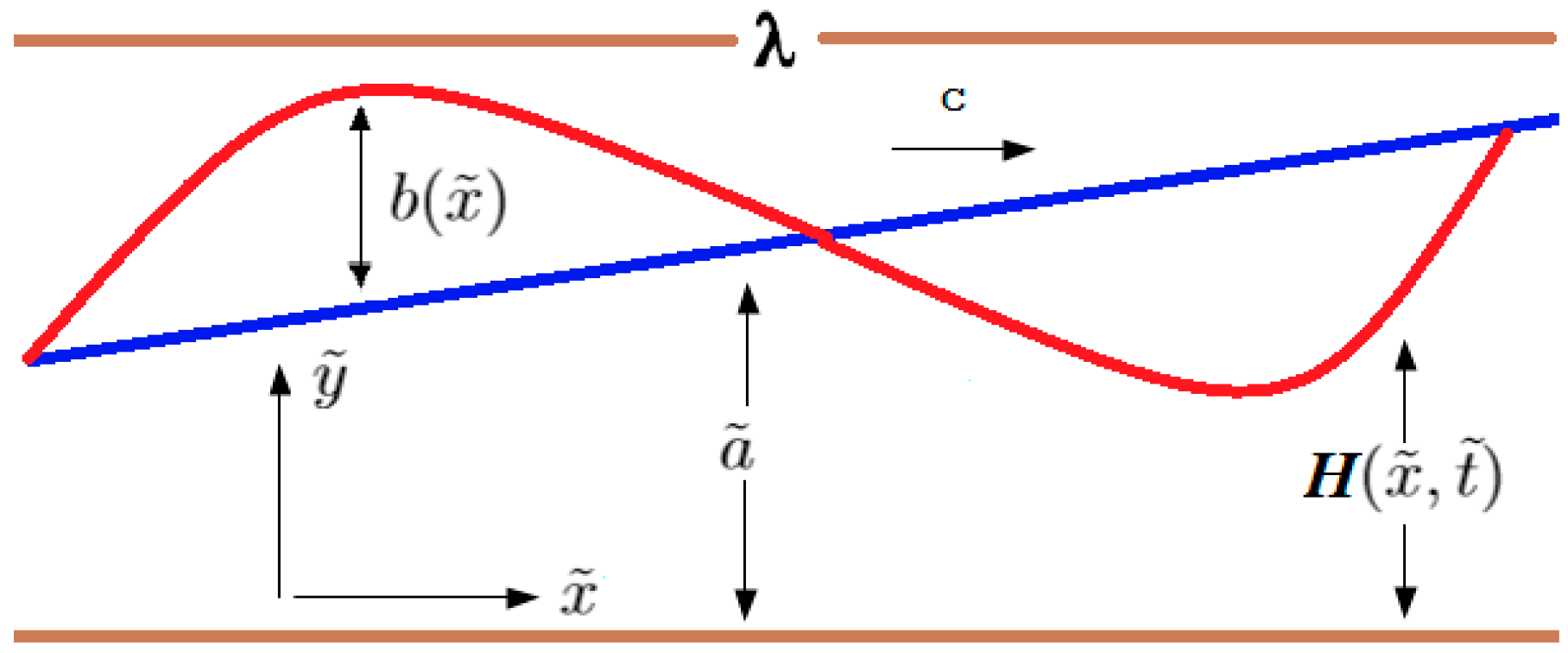
2. Mathematical Formulation
3. Solution of Problem
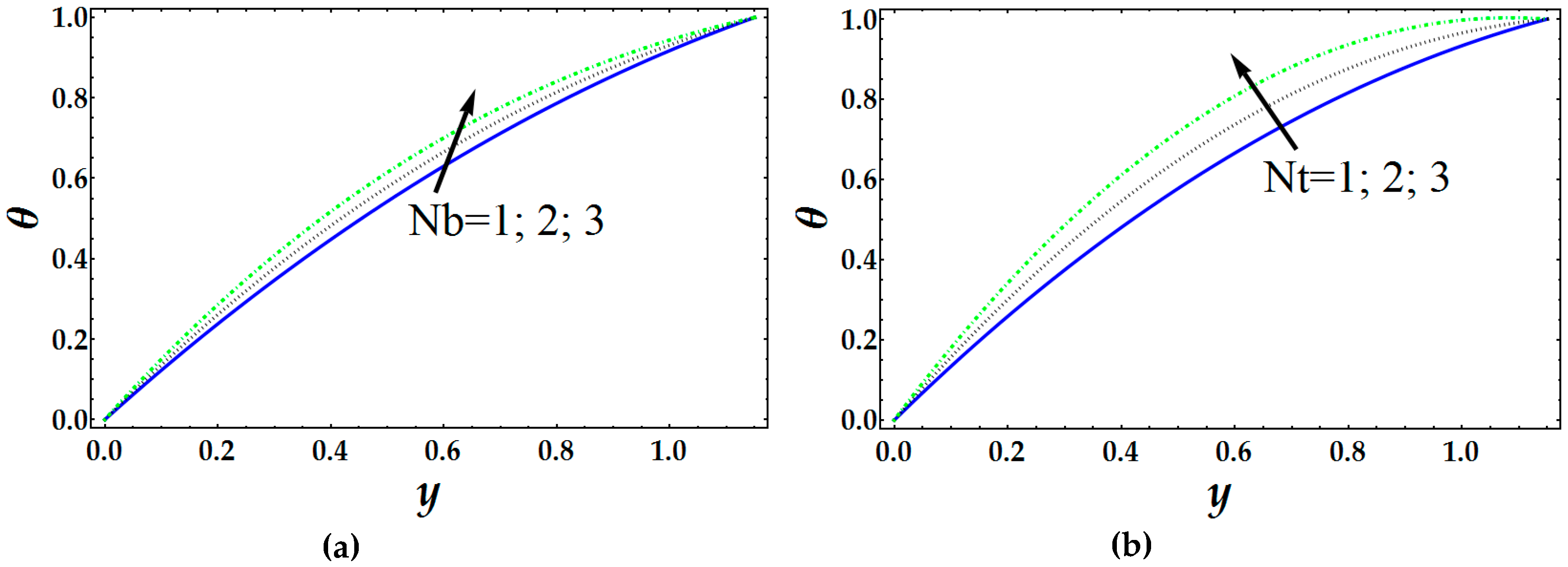
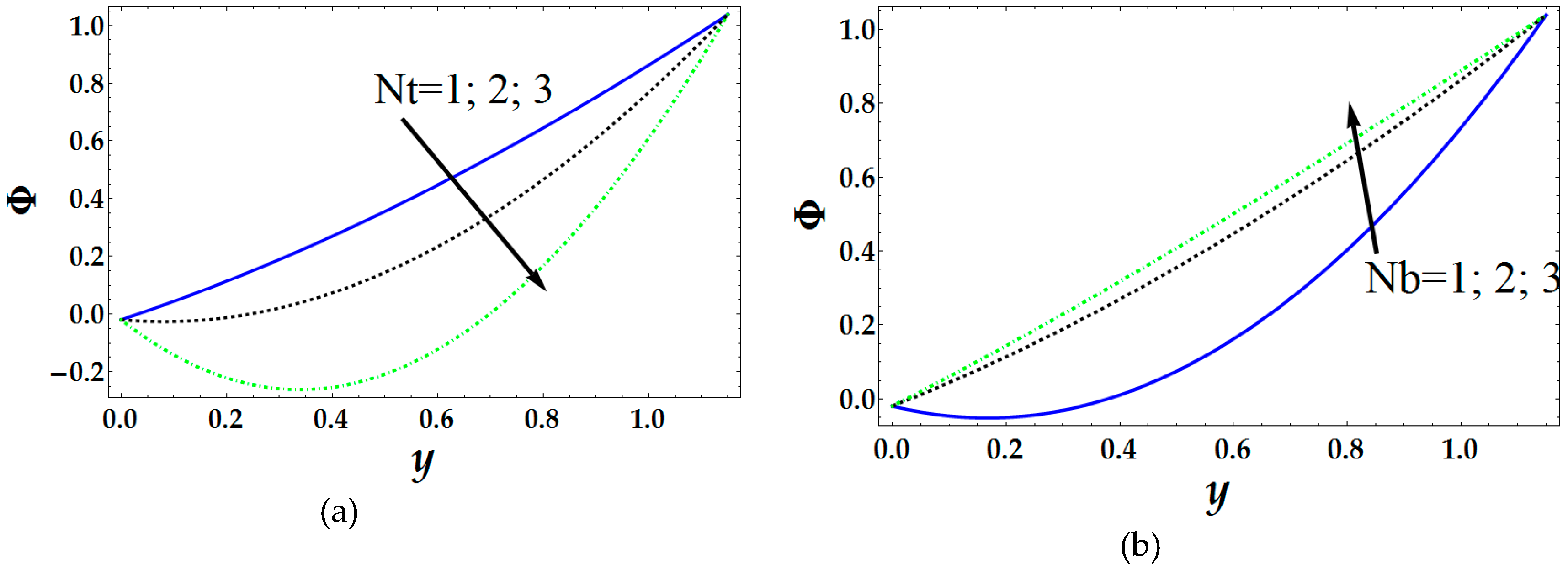
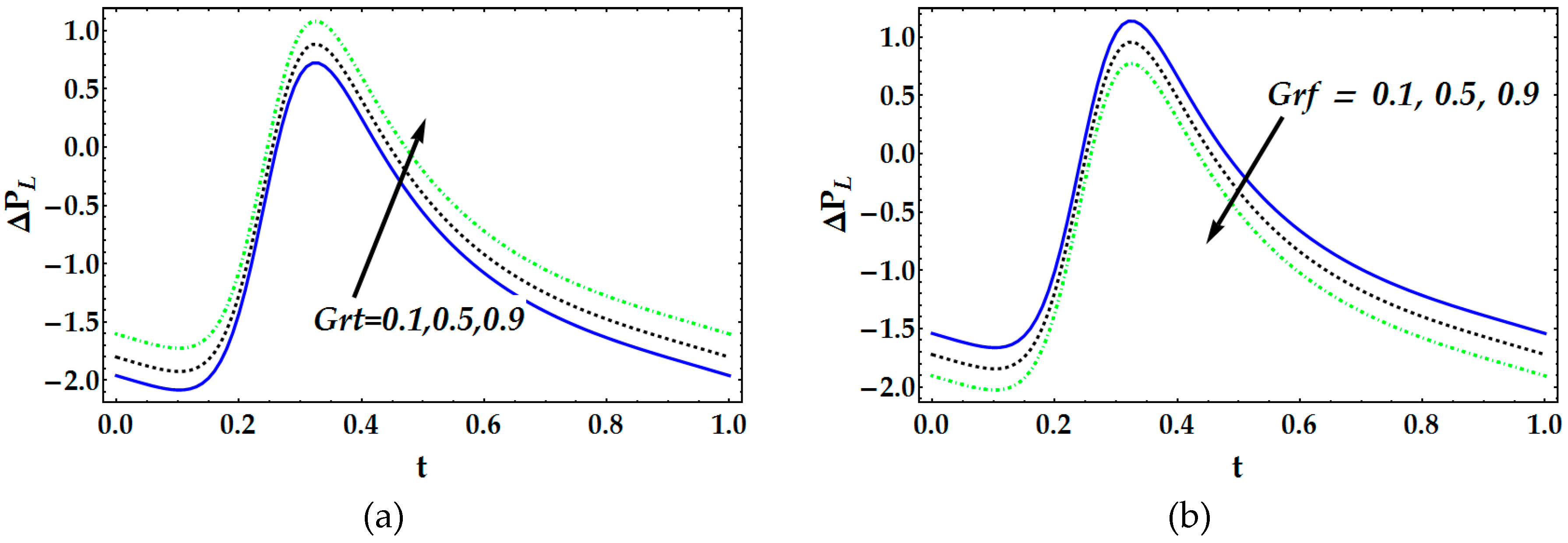
4. Results and Discussion
5. Conclusions
- Temperature profile increases with higher values of and .
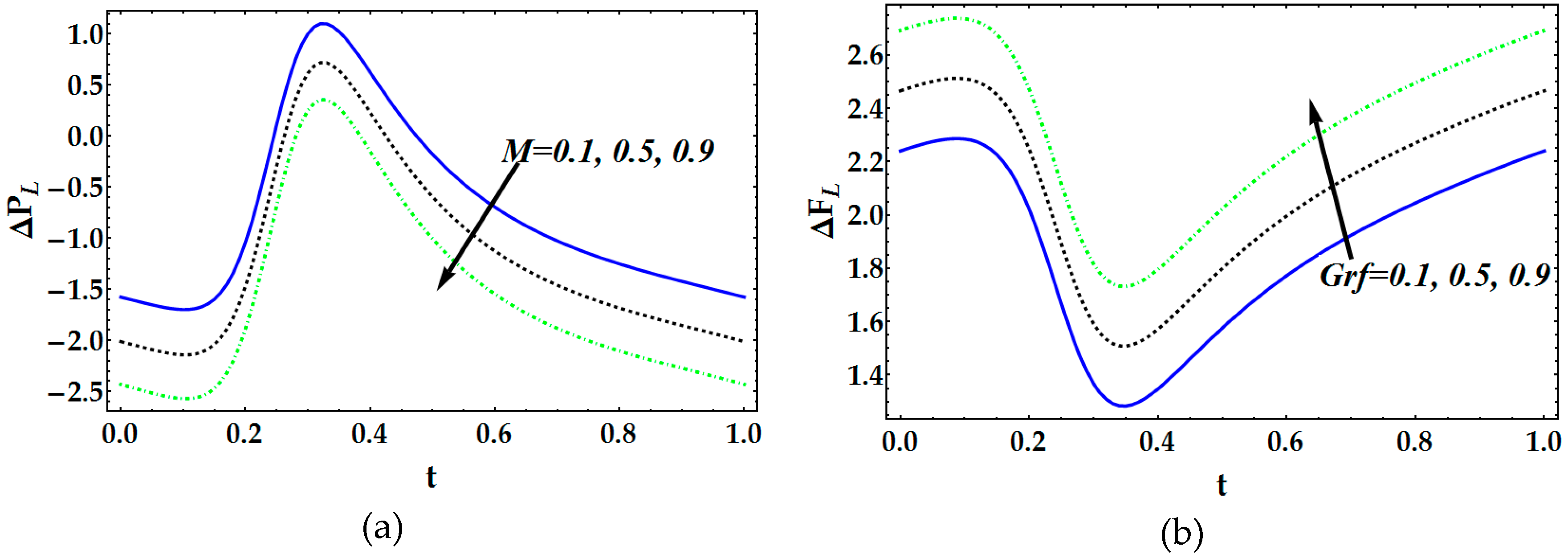
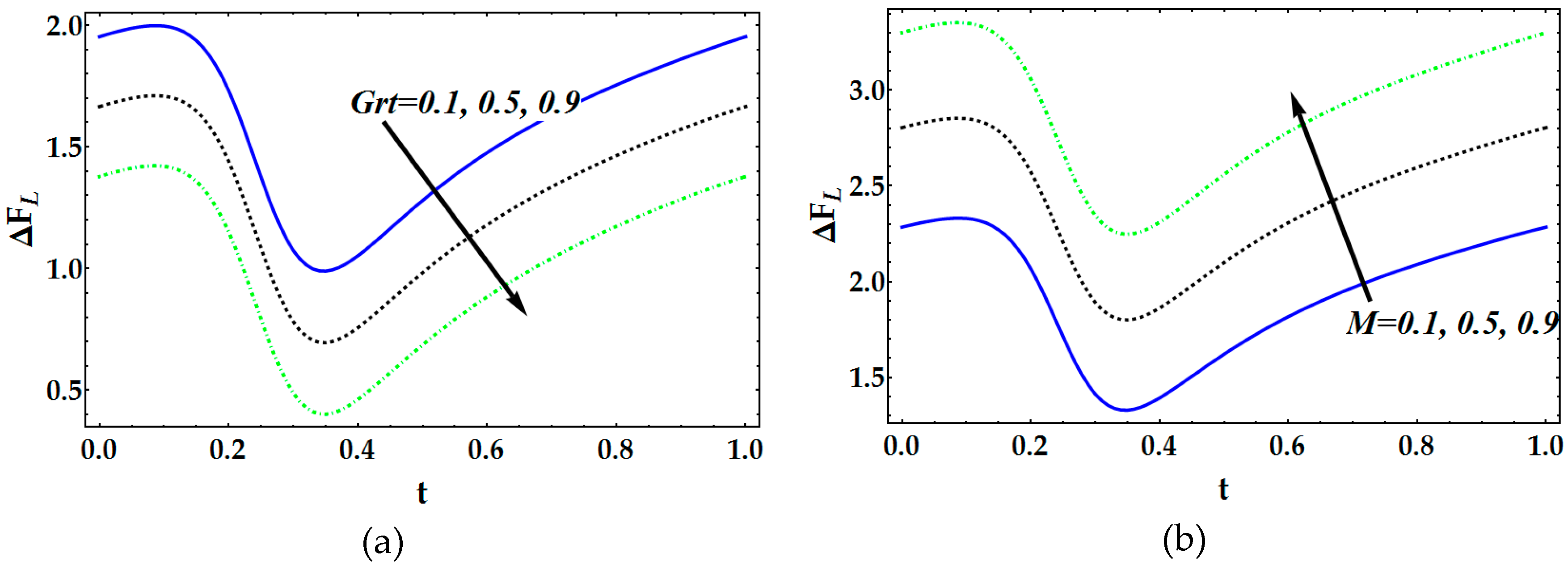
- Pressure distribution and friction have an inverse conduct for bigger estimations of the magnetic parameter, Brownian movement parameter and thermophoresis parameter.
- The variability of entropy generation is 81% for the values of M, while 99% variability for the parameter .
- The variability of entropy generation is 40% for the values of while 100% variability for the parameter .
Author Contributions
Conflicts of Interest
Nomenclature
| velocity components | |
| Cartesian coordinate | |
| pressure in fixed frame | |
| wave amplitude | |
| width of the channel | |
| wave velocity | |
| Prandtl number | |
| Reynolds number | |
| Radiation parameter | |
| time | |
| basic density Grashof number | |
| thermal Grashof number | |
| Brownian motion parameter | |
| thermophoresis parameter | |
| constant | |
| magnetic field | |
| Weissenberg number | |
| volume flow rate | |
| temperature and concentration | |
| acceleration due to gravity | |
| Brownian diffusion coefficient | |
| thermophoretic diffusion coefficient | |
| mean absorption constant | |
| Hartman number | |
| stress tensor | |
| porosity parameter |
Greek Symbols
| nanofluid thermal conductivity | |
| viscosity of the fluid | |
| nanoparticle volume fraction | |
| electrical conductivity | |
| wave number | |
| effective heat capacity of nanoparticle | |
| nanofluid kinematic viscosity | |
| nanoparticle mass density | |
| fluid density | |
| fluid density at the reference temperature | |
| volumetric expansion coefficient of the fluid | |
| heat capacity of fluid | |
| wavelength | |
| amplitude ratio | |
| viscosity of nanofluid | |
| Temperature |
References
- Villone, M.M.; Greco, F.; Hulsen, M.A.; Maffettone, P.L. Simulation of an elastic particle in Newtonian and Viscoelastic fluids subjected to confined shear flow. J. Non-Newton. Fluid Mech. 2014, 210, 47–55. [Google Scholar] [CrossRef]
- Hatami, M.; Domairry, G. Transient vertically motion of a soluble particle in a Newtonian fluid media. J. Powder Technol. 2014, 253, 481–485. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, C.; Fu, T.; Ma, Y.; Li, H. Numerical simulation of the interaction between three equal interval parallel bubbles rising in non-Newtonian fluid. Chem. Eng. Sci. 2013, 93, 55–66. [Google Scholar] [CrossRef]
- Hatami, M.; Ganji, D.D. Natural convection of sodium alginate Non-Newtonian nanofluid flow between two vertical flat plates by analytical and numerical methods. Case Stud. Therm. Eng. 2014, 2, 14–22. [Google Scholar] [CrossRef]
- Chamkha, A.J. On laminar hydromagnetic mixed convection flow in a vertical channel with symmetric and asymmetric wall heating conditions. Int. J. Heat Mass Transf. 2002, 45, 2509–2525. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Kumar, J.P.; Chamkha, A.J.; Pop, I. Mixed convection in a vertical porous channel. Transp. Porous Media 2005, 61, 315–335. [Google Scholar] [CrossRef]
- Chamkha, A.J. Unsteady laminar hydromagnetic fluid–particle flow and heat transfer in channels and circular pipes. Int. J. Heat Fluid Flow 2000, 21, 740–746. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Behseresht, A.; Behseresht, J.; Chamkha, A. Effects of nanoparticles diameter and concentration on natural convection of the Al2O3–water nanofluids considering variable thermal conductivity around a vertical cone in porous media. Adv. Powder Technol. 2015, 26, 224–235. [Google Scholar] [CrossRef]
- Reddy, P.S.; Chamkha, A.J. Soret and Dufour effects on MHD convective flow of Al2O3–water and TiO2–water nanofluids past a stretching sheet in porous media with heat generation/absorption. Adv. Powder Technol. 2016, 27, 1207–1218. [Google Scholar] [CrossRef]
- Chamkha, A. Fully developed free convection of a micropolar fluid in a vertical channel. Int. Commun. Heat Mass Transf. 2002, 29, 1119–1127. [Google Scholar] [CrossRef]
- Kumar, J.P.; Umavathi, J.C.; Chamkha, A.J.; Pop, I. Fully-developed free-convective flow of micropolar and viscous fluids in a vertical channel. Appl. Math. Model. 2010, 34, 1175–1186. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Grosan, T.; Pop, I. Fully developed mixed convection of a micropolar fluid in a vertical channel. Int. J. Fluid Mech. Res. 2003, 30, 251–263. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. Mater. Sci. 1995, 231, 99–105. [Google Scholar]
- Eastman, J.A.; Choi, U.S.; Li, S.; Soyez, G.; Thompson, L.J.; DiMelfi, R.J. Novel thermal properties of nanostructured materials. Mater. Sci. Forum 1999, 312, 629–634. [Google Scholar] [CrossRef]
- Latham, T.W. Fluid Motions in a Peristaltic Pump. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Abbas, M.A.; Bai, Y.Q.; Rashidi, M.M.; Bhatti, M.M. Application of drug delivery in magnetohydrodynamics peristaltic blood flow of nanofluid in a non-uniform channel. J. Mech. Med. Biol. 2016, 16, 1650052. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M. Combine effects of magnetohydrodynamics (MHD) and partial slip on peristaltic blood flow of Ree–Eyring fluid with wall properties. Eng. Sci. Technol. Int. J. 2016, 19, 1497–1502. [Google Scholar] [CrossRef]
- Salleh, S.; Bachok, N.; Arifin, N.; Ali, F.; Pop, I. Magnetohydrodynamics flow past a moving vertical thin needle in a nanofluid with stability analysis. Energies 2018, 11, 3297. [Google Scholar] [CrossRef]
- Cong, R.; Ozaki, Y.; Machado, B.; Das, P. Constructal Design of a Rectangular Fin in a Mixed Convective Confined Environment. Inventions 2018, 3, 27. [Google Scholar] [CrossRef]
- Sadiq, M.; Alsabery, A.; Hashim, I. MHD Mixed Convection in a Lid-Driven Cavity with a Bottom Trapezoidal Body: Two-Phase Nanofluid Model. Energies 2018, 11, 2943. [Google Scholar] [CrossRef]
- Das, P.K.; Mahmud, S.; Humaira Tasnim, S.; Sadrul Islam AK, M. Effect of surface waviness and aspect ratio on heat transfer inside a wavy enclosure. Int. J. Numer. Methods Heat Fluid Flow 2003, 13, 1097–1122. [Google Scholar] [CrossRef]
- Abbas, M.A.; Faraz, N.; Bai, Y.Q.; Khan, Y. Analytical study of the non-orthogonal stagnation point flow of a micro polar fluid. J. King Saud Univ. Sci. 2017, 29, 126–132. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Chamkha, A.J.; Sridhar KS, R. Generalized plain Couette flow and heat transfer in a composite channel. Transp. Porous Media 2010, 85, 157–169. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, M.A. Simultaneous effects of slip and MHD on peristaltic blood flow of Jeffrey fluid model through a porous medium. Alex. Eng. J. 2016, 55, 1017–1023. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.Q.; Bhatti, M.M.; Rashidi, M.M. Three-dimensional peristaltic flow of hyperbolic tangent fluid in non-uniform channel having flexible walls. Alex. Eng. J. 2016, 55, 653–662. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Al-Subaie, M.A. Hydromagnetic buoyancy-induced flow of a particulate suspension through a vertical pipe with heat generation or absorption effects. Turk. J. Eng. Environ. Sci. 2010, 33, 127–134. [Google Scholar]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Unsteady flow and heat transfer on a semi-infinite flat plate with an aligned magnetic field. Int. J. Eng. Sci. 1999, 37, 1723–1736. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Khaled, A.R.A. Hydromagnetic combined heat and mass transfer by natural convection from a permeable surface embedded in a fluid-saturated porous medium. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 455–477. [Google Scholar] [CrossRef]
- Chamkha, A.J. Flow of two-immiscible fluids in porous and nonporous channels. J. Fluids Eng. 2000, 122, 117–124. [Google Scholar] [CrossRef]
- Chamkha, A. Unsteady flow of a dusty conducting fluid through a pipe. Mech. Res. Commun. 1994, 21, 281–288. [Google Scholar] [CrossRef]
- Chamkha, A.J. Non-Darcy fully developed mixed convection in a porous medium channel with heat generation/absorption and hydromagnetic effects. Numer. Heat Transf. Part A Appl. 1997, 32, 653–675. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Chamkha, A.J.; Mateen, A.; Al-Mudhaf, A. Unsteady oscillatory flow and heat transfer in a horizontal composite porous medium channel. Nonlinear Anal. Model. Control 2009, 14, 397–415. [Google Scholar]
- Umavathi, J.C.; Chamkha, A.J.; Mateen, A.; Al-Mudhaf, A. Unsteady two-fluid flow and heat transfer in a horizontal channel. Heat Mass Transf. 2005, 42, 81. [Google Scholar] [CrossRef]
- Chamkha, A.J. Unsteady laminar hydromagnetic flow and heat transfer in porous channels with temperature-dependent properties. Int. J. Numer. Methods Heat Fluid Flow 2001, 11, 430–448. [Google Scholar] [CrossRef]
- Chamkha, A.J. Hydromagnetic two-phase flow in a channel. Int. J. Eng. Sci. 1995, 33, 437–446. [Google Scholar] [CrossRef]
- Ismael, M.A.; Pop, I.; Chamkha, A.J. Mixed convection in a lid-driven square cavity with partial slip. Int. J. Therm. Sci. 2014, 82, 47–61. [Google Scholar] [CrossRef]
- Parvin, S.; Nasrin, R.; Alim, M.A.; Hossain, N.F.; Chamkha, A.J. Thermal conductivity variation on natural convection flow of water–alumina nanofluid in an annulus. Int. J. Heat Mass Transf. 2012, 55, 5268–5274. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Doostani, A.; Izadpanahi, E.; Chamkha, A.J. Phase-change heat transfer in a cavity heated from below: The effect of utilizing single or hybrid nanoparticles as additives. J. Taiwan Inst. Chem. Eng. 2017, 72, 104–115. [Google Scholar] [CrossRef]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Zaraki, A.; Ghalambaz, M.; Chamkha, A.J.; Ghalambaz, M.; De Rossi, D. Theoretical analysis of natural convection boundary layer heat and mass transfer of nanofluids: Effects of size, shape and type of nanoparticles, type of base fluid and working temperature. Adv. Powder Technol. 2015, 26, 935–946. [Google Scholar] [CrossRef]
- Gupta, B.B.; Seshadri, V. Peristaltic pumping in non-uniform tubes. J. Biomech. 1976, 9, 105–109. [Google Scholar] [CrossRef]
- Mekheimer, K.S. Peristaltic flow of blood under effect of a magnetic field in a non-uniform channel. Appl. Math. Comput. 2004, 153, 763–777. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali ME, S. Entropy Generation on MHD Blood Flow of Nanofluid Due to Peristaltic Waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Torabi, M.; Zhang, K.; Karimi, N.; Peterson, G.P. Entropy generation in thermal systems with solid structures—A concise review. Int. J. Heat Mass Transf. 2016, 97, 917–931. [Google Scholar] [CrossRef]
- Biswal, P.; Basak, T. Entropy generation vs energy efficiency for natural convection based energy flow in enclosures and various applications: A review. Renew. Sustain. Energy Rev. 2017, 80, 1412–1457. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abbas, M.A. Effect of Slip Conditions and Entropy Generation Analysis with an Effective Prandtl Number Model on a Nanofluid Flow through a Stretching Sheet. Entropy 2017, 18, 414. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.S. Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M. Numerical study of entropy generation with nonlinear thermal radiation on magnetohydrodynamics non-newtonian nanofluid through a porous shrinking sheet. J. Magn. 2016, 21, 468–475. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of Entropy Generation in the Flow of Peristaltic Nanofluids in Channels with Compliant Walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Moh’d, A.A.N.; Pop, I.; Sahin, A.Z.; Wongwises, S. A review of entropy generation in Nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]

| Model | R | R Square | Adjusted R Square | Standard Error of the Estimate |
|---|---|---|---|---|
| 1 | 0.900 a | 0.809 | 0.799 | 0.7558884 |
| 2 | 0.999 a | 0.998 | 0.998 | 0.0550427 |
| 3 | 0.635 a | 0.403 | 0.370 | 4.6675041 |
| 4 | 1.000 a | 1.000 | 1.000 | 0.19437519 |
| Model | Unstandardized Coefficients | Standardized Coefficients | T | Significant | ||
|---|---|---|---|---|---|---|
| B | Standard Error | Beta | ||||
| 1 | (Constant) | 74.223 | 0.351 | 211.381 | 0.000 | |
| M | −2.562 | 0.293 | −0.900 | −8.739 | 0.000 | |
| 2 | (Constant) | 29.097 | 0.026 | 1137.975 | 0.000 | |
| M | 2.049 | 0.021 | 0.999 | 95.977 | 0.000 | |
| 3 | (Constant) | 65.565 | 2.168 | 30.239 | 0.000 | |
| M | 6.307 | 1.810 | 0.635 | 3.485 | 0.003 | |
| 4 | (Constant) | 1.359 | 0.090 | 15.056 | 0.000 | |
| M | 68.492 | 0.075 | 1.000 | 908.676 | 0.000 | |
| Entropy and Parameters | ||||
|---|---|---|---|---|
| Values range | 0.1 to 2.0 | 0.1 to 2.0 | 0.1 to 2.0 | 0.1 to 2.0 |
| N | 20 | 20 | 20 | 20 |
| Pearson Correlation Siganificant (2-tailed) | 1.000 ** 0.000 | 0.635 ** 0.003 | 0.999 ** 0.000 | 0.900 ** 0.000 |
| Remarks | Perfect Relation | Strong Positive Relation | Strong Positive Relation | Very Strong Negative Relations |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, M.A.; Hussain, I. Statistical Analysis of the Mathematical Model of Entropy Generation of Magnetized Nanofluid. Inventions 2019, 4, 32. https://doi.org/10.3390/inventions4020032
Abbas MA, Hussain I. Statistical Analysis of the Mathematical Model of Entropy Generation of Magnetized Nanofluid. Inventions. 2019; 4(2):32. https://doi.org/10.3390/inventions4020032
Chicago/Turabian StyleAbbas, Munawwar Ali, and Ibrahim Hussain. 2019. "Statistical Analysis of the Mathematical Model of Entropy Generation of Magnetized Nanofluid" Inventions 4, no. 2: 32. https://doi.org/10.3390/inventions4020032
APA StyleAbbas, M. A., & Hussain, I. (2019). Statistical Analysis of the Mathematical Model of Entropy Generation of Magnetized Nanofluid. Inventions, 4(2), 32. https://doi.org/10.3390/inventions4020032





