Adaptive Control Synchronization of a Novel Memristive Chaotic System for Secure Communication Applications
Abstract
1. Introduction
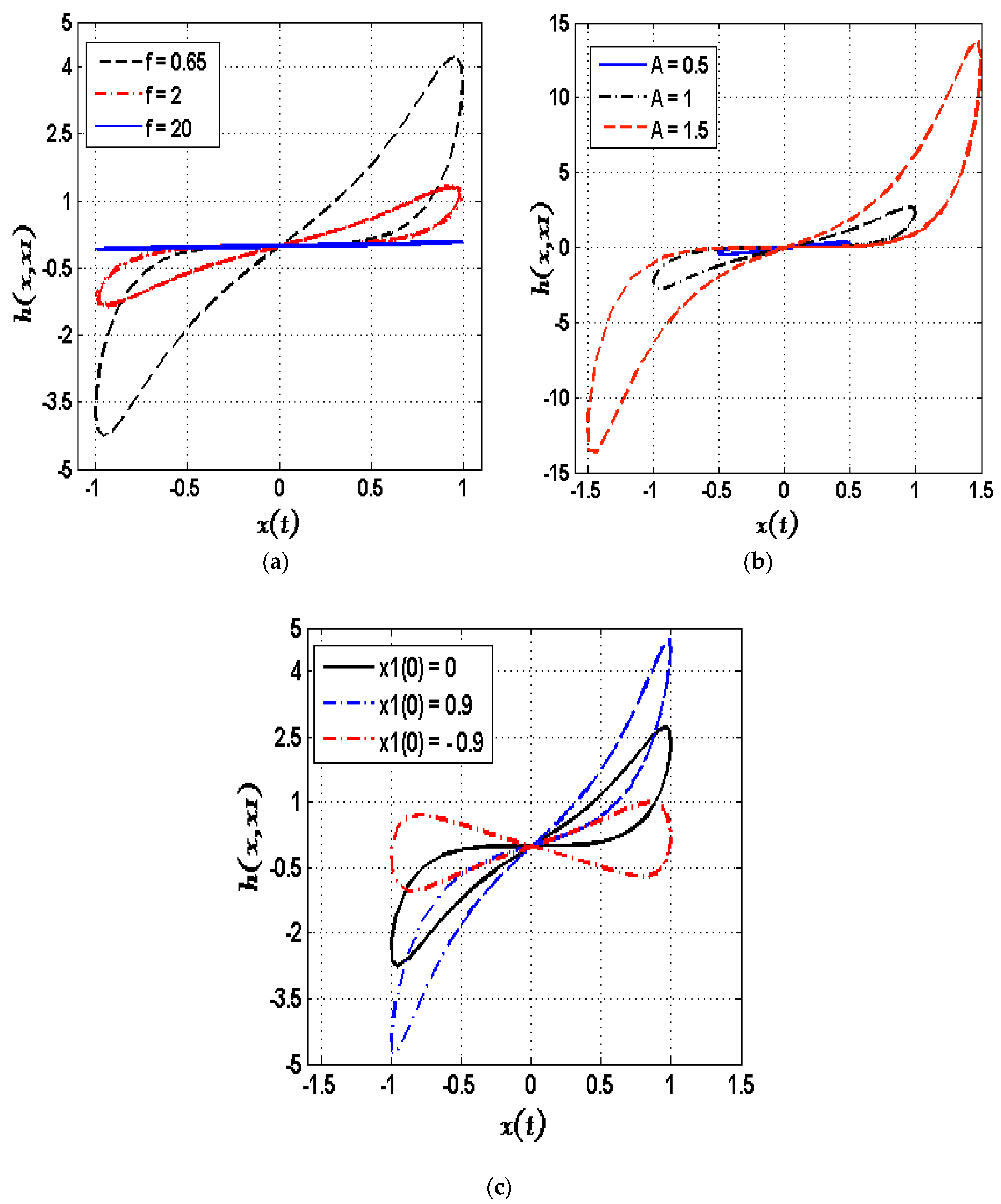
2. Memristive Model
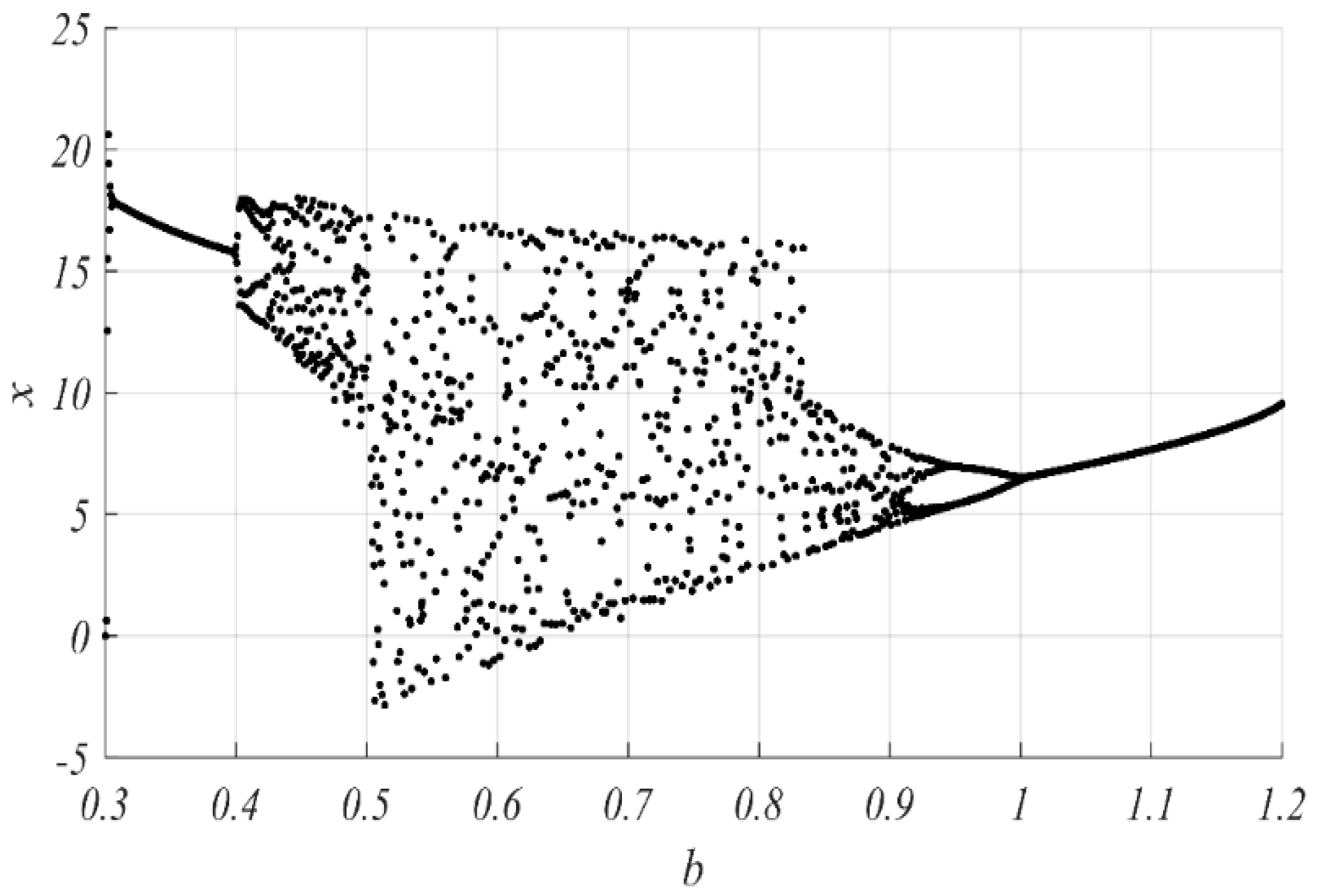
3. New Memristive Jerk System
4. Adaptive Synchronization
4.1. Controller Design
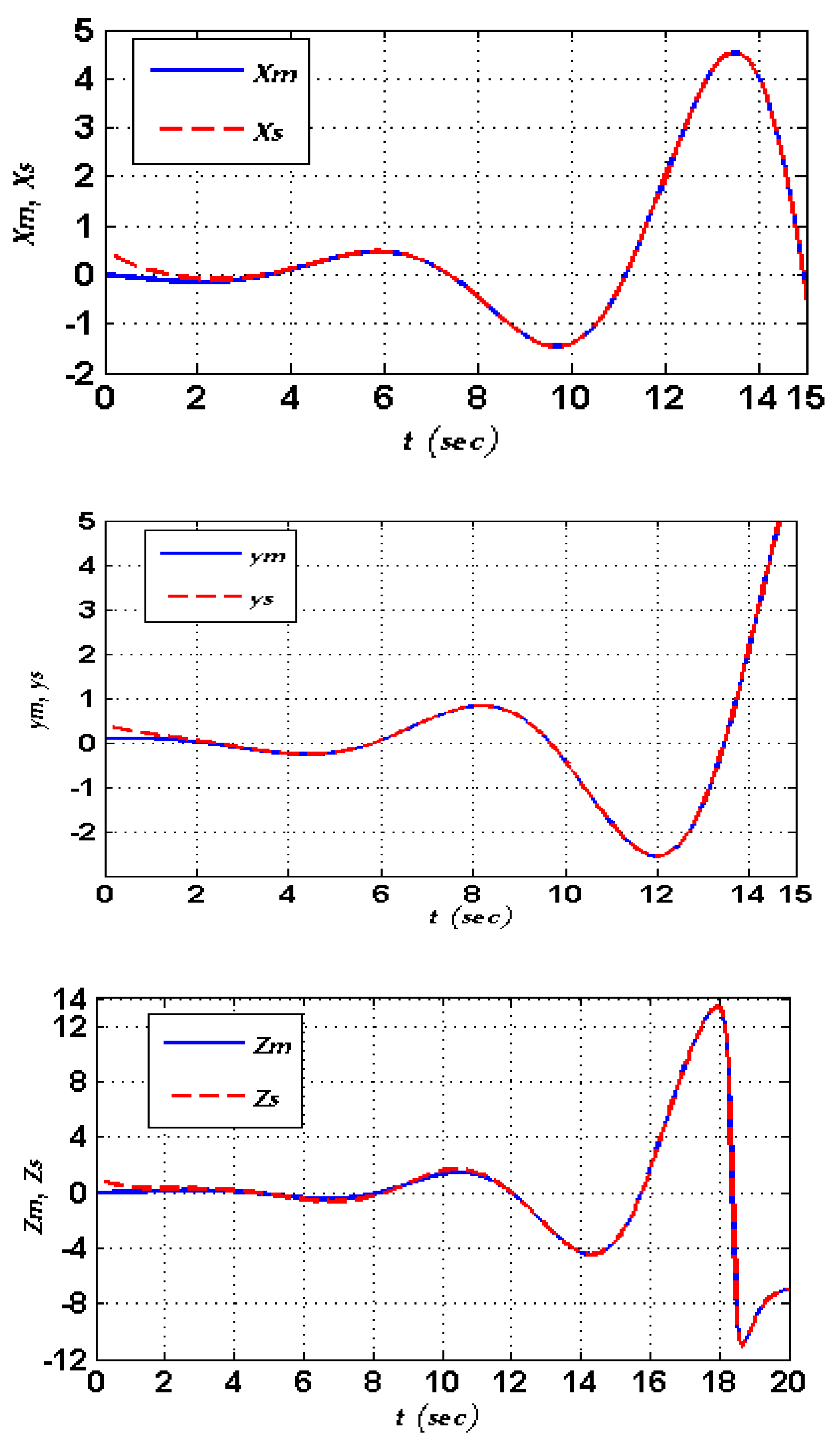
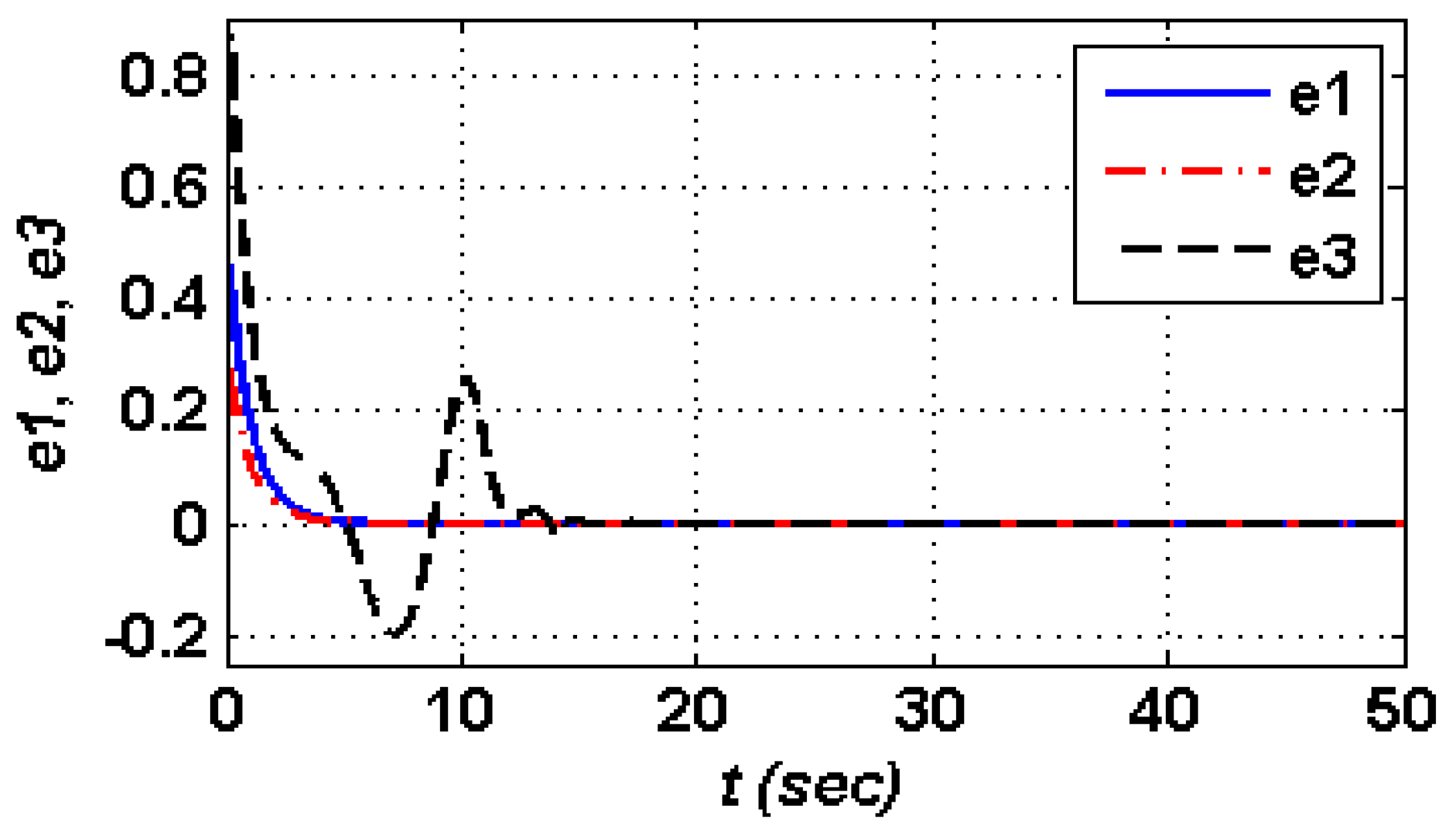
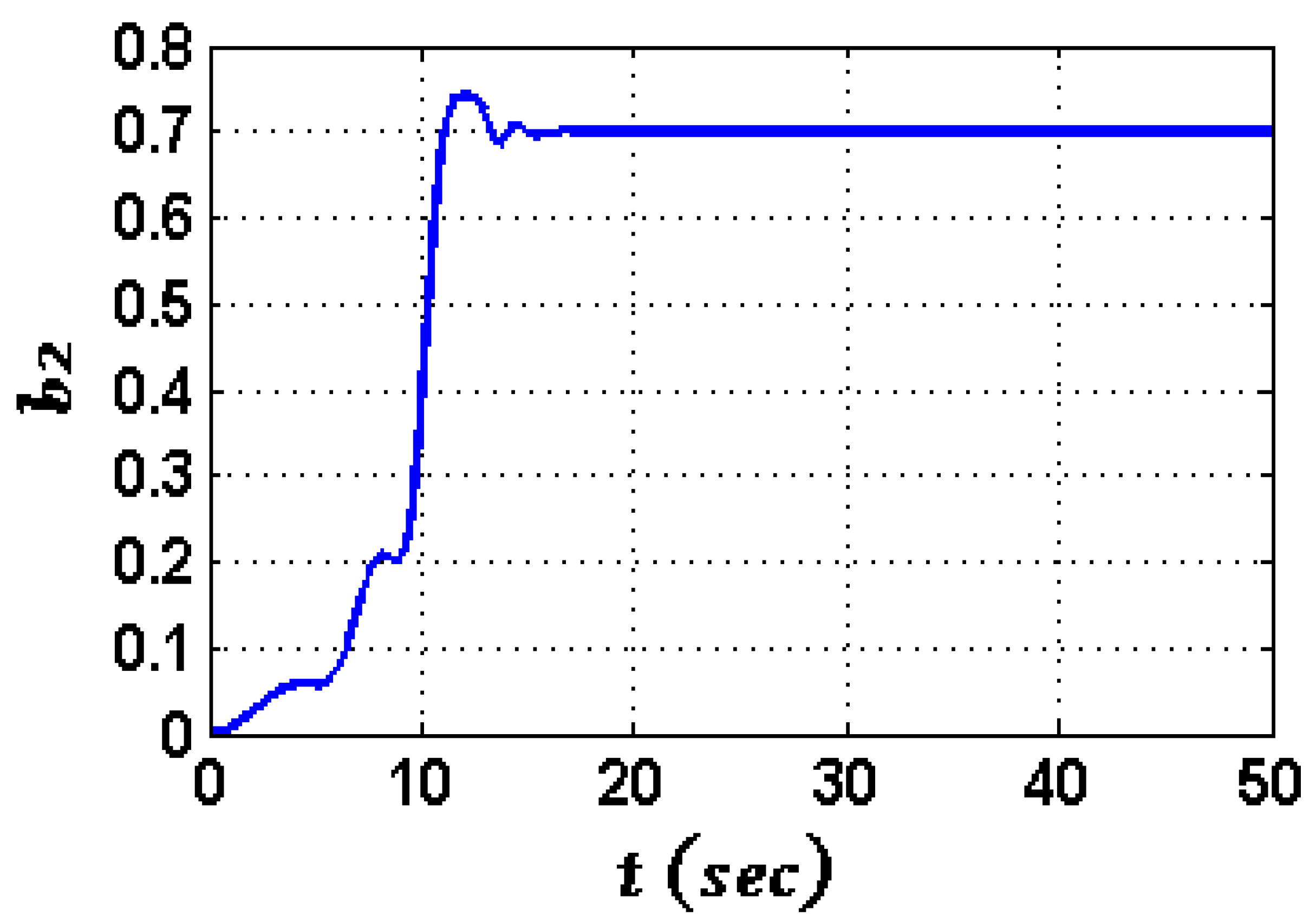
4.2. Numerical Simulation
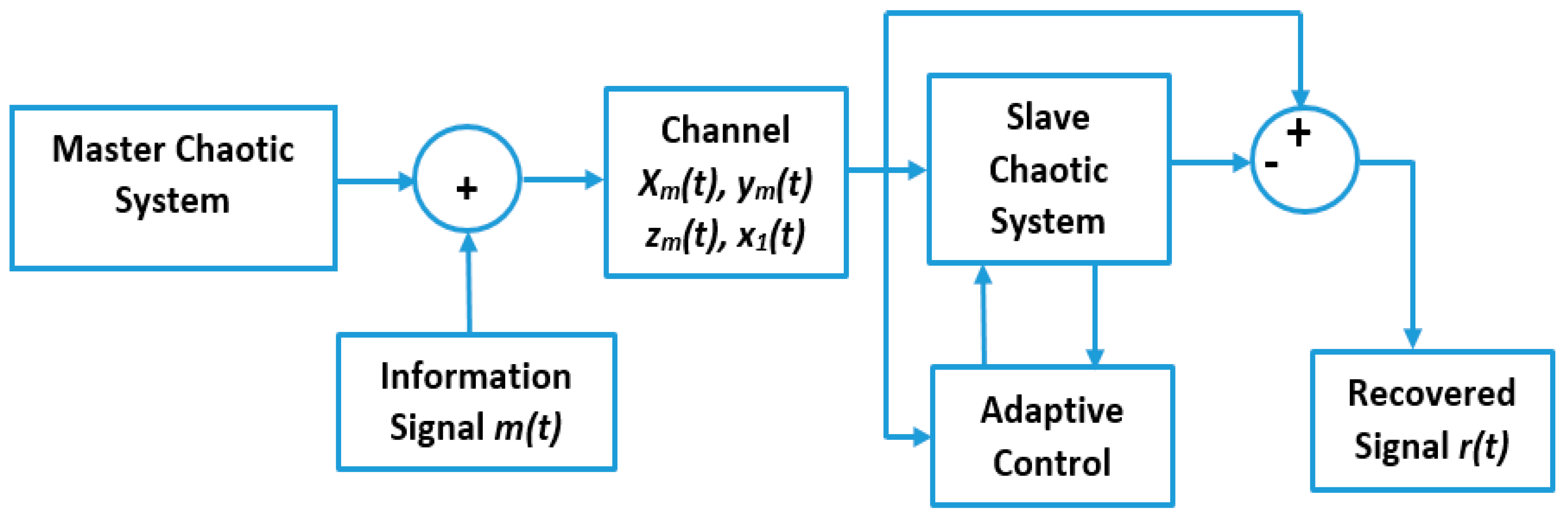
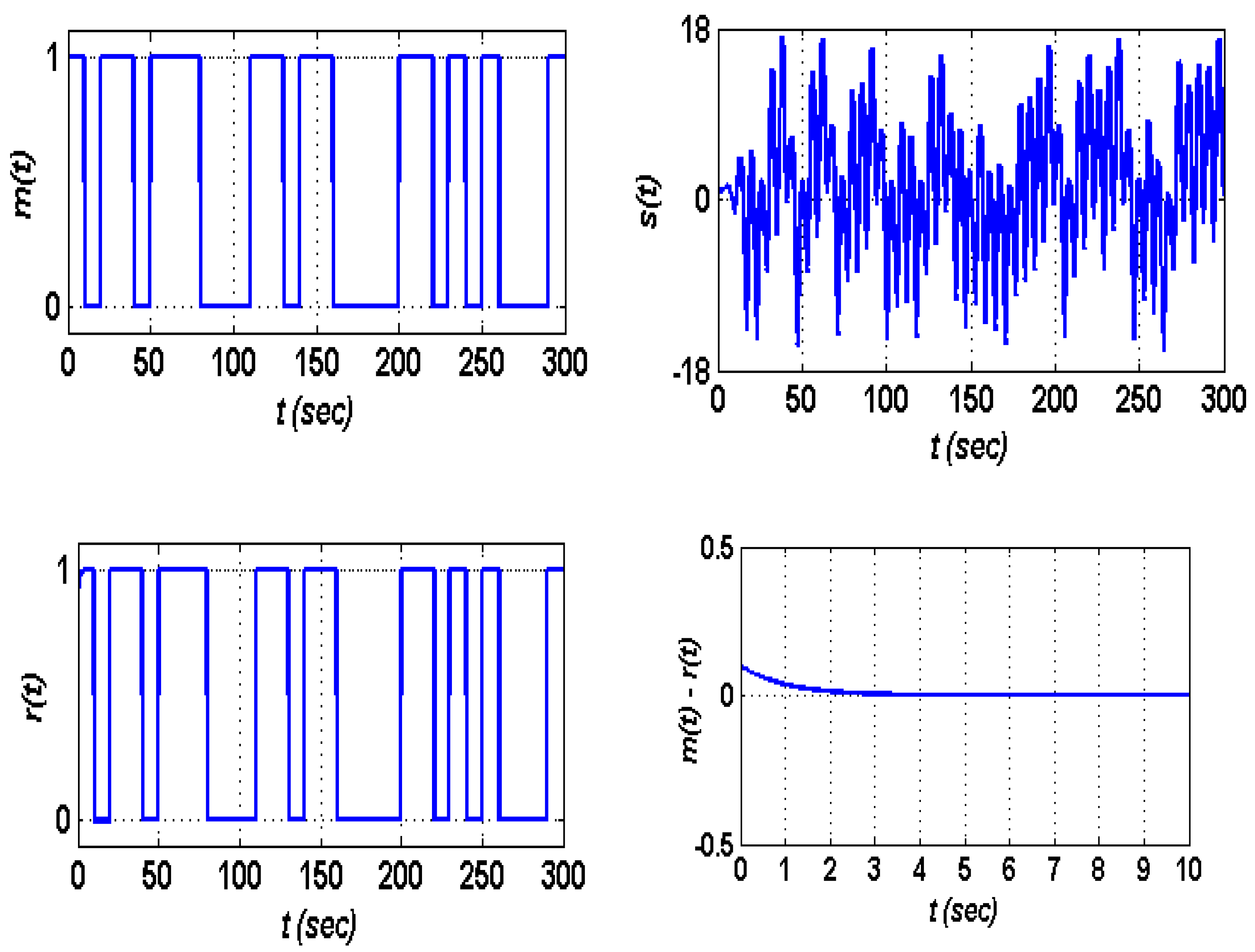
5. Application in Secure Communication
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chau, L. Memristor-The Missing Circuit Element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chau, L.; Kang, S.M. Memristive Devices and Systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The Missing Memristor Found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Ventra, M.D.; Pershin, Y.V.; Chua, L. Circuit elements with memory: Memristors, memcapacitors, and meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Bao, B.; Ma, Z.; Xu, J.; Liu, Z.; Xu, Q. A simple memristor chaotic circuit with complex dynamics. Int. J. Bifurc. Chaos 2011, 21, 2629–2645. [Google Scholar] [CrossRef]
- Wang, L.; Drakakis, E.; Duan, S.; He, P. Memristor model and its application for chaos generation. Int. J. Bifurc. Chaos 2012, 22, 1250205. [Google Scholar] [CrossRef]
- Pehlivan, I.; Glu, Y. A new chaotic attractor from general Lorenz system family and its electronic experimental implementation. Turk. J. Electr. Eng. Comp. Sci. 2010, 18, 171–184. [Google Scholar]
- Damei, L.; Junan, L.; Xiaoqun, W.; Guanrong, C. Estimating the ultimate bound and positively invariant set for the Lorenz system and a unified chaotic system. J. Math. Anal. Appl. 2006, 323, 844–853. [Google Scholar]
- Grigorenko, I.; Grigorenko, E. Chaotic Dynamics of the Fractional Lorenz System. Phys. Rev. Lett. 2003, 91, 034101. [Google Scholar] [CrossRef]
- Liao, T.; Tsai, S. Adaptive synchronization of chaotic systems and its application to secure communications. Chaos Solitons Fractals 2000, 11, 1387–1396. [Google Scholar] [CrossRef]
- L, L.Z.; Zheng, Z. Secure Communication Scheme with Hyper-Chaotic Lorenz-Stenflo System. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 1928–1931. [Google Scholar]
- Sergej, C.; Guanrong, C. Secure Synchronization of a Class of Chaotic Systems from a Nonlinear Observer Approach. IEEE Trans. Autom. Control 2005, 50, 76–82. [Google Scholar]
- Stefanskin, A.; Kapitaniak, T. Synchronization of two chaotic oscillators via a negative feedback mechanism. Int. J. Solids Struct. 2003, 40, 5175–5185. [Google Scholar] [CrossRef]
- Wang, G.; Cui, M.; Cai, M.; Wang, X.; Hu, T. A Chaotic Oscillator Based on HP Memristor Model. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Li, H.; Wang, L.; Duan, S. A memristor-based scroll chaotic system-design, analysis and circuit implementation. Int. J. Bifurc. Chaos 2014, 24, 1–13. [Google Scholar] [CrossRef]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Gambuzza, L. A chaotic circuit based on Hewlett-Packard memristor. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 023136. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.-T.; Volos, C.K.; Vaidyanathan, S.; Le, T.P.; Vu, V.Y. A Memristor Based Hyperchaotic System with Hidden Attractors: Dynamics, Synchronization and Circuital Emulating. J. Eng. Sci. Technol. Rev. 2015, 8, 205–214. [Google Scholar] [CrossRef]
- Yener, S.C.; Barbaros, C.; Mutlu, R.; Karakulak, E. Implementation of Microcontroller-Based Memristive Chaotic Circuit. Acta Phys. Pol. A 2017, 132, 1058–1061. [Google Scholar] [CrossRef]
- Zhulin, W.; Fuhong, M.; Guangya, P.; Yaoda, W.; Yi, C. Bifurcation and Chaos of the Memristor Circuit. Int. J. Comput. Inf. Eng. 2016, 10, 1976–1982. [Google Scholar]
- Pyvovar, O.S.; Polikarovskykh, O.I. A System of Secure Communication with Chaos Masking Based on Rucklidge Generators. In Proceedings of the 38th International Conference on Electronics and Nanotechnology (ELNANO), Kiev, Ukraine, 24–26 April 2018. [Google Scholar]
- Elkholy, M.M.; Hennawy, H.M.E.L.; Elkouny, A. Design and implementation of hyper chaotic masking system for secured audio transmission. In Proceedings of the 2015 Tenth International Conference on Computer Engineering & Systems (ICCES), Cairo, Egypt, 23–24 December 2015. [Google Scholar]
- Tahir, S.A. The synchronization of identical Memristors systems via Lyapunov direct method. Appl. Comput. Math. 2013, 2, 130–136. [Google Scholar] [CrossRef]
- Ma, J.; Chen, Z.; Wang, Z.; Zhang, Q. A four-wing hyper-chaotic attractor generated from a 4D memristive system with a line equilibrium. Nonlinear Dyn. 2015, 81, 1275–1288. [Google Scholar] [CrossRef]
- Kim, H.; Sah, M.; Yang, C.; Cho, S.; Chua, L. Memristor emulator for memristor circuit applications. IEEE Trans. Circuits Syst. I 2012, 59, 2422–2431. [Google Scholar]
- Corinto, F.; Forti, M. Memristor circuits: bifurcations without parameters. IEEE Trans. Circuits Syst. I 2017, 64, 1540–1551. [Google Scholar] [CrossRef]
- Junsangsri, P.; Lombardi, F. Design of a hybrid memory cell using memristance and ambipolarity. IEEE Trans. Nanotechnol. 2013, 12, 71–80. [Google Scholar] [CrossRef]
- Bao, B.; Jiang, P.; Wu, H.; Hu, F. Complex transient dynamics in periodically forced memristive Chua’s circuit. Nonlinear Dyn. 2015, 79, 2333–2343. [Google Scholar] [CrossRef]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.K.; Jafari, S.; Kuznetsov, N.V.; Hoang, T.M. A Novel memristive time-delay chaotic system without equilibrium points. Eur. Phys. J. Spec. Top. 2016, 225, 127–136. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Ahmed, M.E. Chaotic and Hyperchaotic Complex Jerk Equations. Int. J. Mod. Nonlinear Theory Appl. 2012, 1, 6–13. [Google Scholar] [CrossRef][Green Version]
- Sprott, J.C. Some simple chaotic jerk functions. Am. J. Phys. 1997, 65, 537–543. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Friedman, E.G. Memristor-Based circuit design for multilayer neural networks. IEEE Trans. Circuits Syst. I 2018, 65, 677–686. [Google Scholar] [CrossRef]
- Xu, J.; Cai, G.; Zheng, S. Adaptive Synchronization for an Uncertain New Hyperchaotic Lorenz System. Int. J. Nonlinear Sci. 2009, 8, 117–123. [Google Scholar]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Yang, T.; Chua, L. Impulsive stabilization for control and synchronization of chaotic systems: Theory and application to secure communication. IEEE Trans. Circuits Syst. I 1997, 44, 976–988. [Google Scholar] [CrossRef]
- Durdu, A.; Özcerit, A.T. A Novel Chaotic System for Secure Communication Applications. Inf. Technol. Control 2015, 44, 271–278. [Google Scholar] [CrossRef]
- Huang, T. Synchronization of Chaotic Systems with Time-Varying Coupling Delays. Discret. Contin. Dyn. Syst. Ser. B 2011, 16, 1071–1082. [Google Scholar] [CrossRef]
- Chen, S.; Lü, J. Synchronization of an uncertain unified chaotic system via adaptive control. Chaos. Solut. Fractals 2002, 14, 643–647. [Google Scholar] [CrossRef]
- Maheril, M.; Arifin, N.M. Application adaptive exponential synchronization of chaotic dynamical systems in secure communications. Adv. Differ. Equ. 2017. [Google Scholar] [CrossRef]

| Master | Slave | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| a1 | 3.846 × 10−4 | a2 | 3.846 × 10−4 |
| b1 | 0.7 | b2(t) | uncertain |
| xm(t0) | 0 | xs(t0) | 0.5 |
| ym(t0) | 0.1 | ys(t0) | 0.4 |
| zm(t0) | 0 | zs(t0) | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
A. Rahman, Z.-A.S.; Al-Kashoash, H.A.A.; Ramadhan, S.M.; Al-Yasir, Y.I.A. Adaptive Control Synchronization of a Novel Memristive Chaotic System for Secure Communication Applications. Inventions 2019, 4, 30. https://doi.org/10.3390/inventions4020030
A. Rahman Z-AS, Al-Kashoash HAA, Ramadhan SM, Al-Yasir YIA. Adaptive Control Synchronization of a Novel Memristive Chaotic System for Secure Communication Applications. Inventions. 2019; 4(2):30. https://doi.org/10.3390/inventions4020030
Chicago/Turabian StyleA. Rahman, Zain-Aldeen S., Hayder A. A. Al-Kashoash, Saif Muneam Ramadhan, and Yasir I. A. Al-Yasir. 2019. "Adaptive Control Synchronization of a Novel Memristive Chaotic System for Secure Communication Applications" Inventions 4, no. 2: 30. https://doi.org/10.3390/inventions4020030
APA StyleA. Rahman, Z.-A. S., Al-Kashoash, H. A. A., Ramadhan, S. M., & Al-Yasir, Y. I. A. (2019). Adaptive Control Synchronization of a Novel Memristive Chaotic System for Secure Communication Applications. Inventions, 4(2), 30. https://doi.org/10.3390/inventions4020030







