Abstract
Two-phase ejectors play a major role as refrigerant expansion devices in vapor compression systems and can find potential applications in many other industrial processes. As a result, they have become a focus of attention for the last few decades from the scientific community, not only for the expansion work recovery in a wide range of refrigeration and heat pump cycles but also in industrial processes as entrainment and mixing enhancement agents. This review provides relevant findings and trends, characterizing the design, operation and performance of the two-phase ejector as a component. Effects of geometry, operating conditions and the main developments in terms of theoretical and experimental approaches, rating methods and applications are discussed in detail. Ejector expansion refrigeration cycles (EERC) as well as the related theoretical and experimental research are reported. New and other relevant cycle combinations proposed in the recent literature are organized under theoretical and experimental headings by refrigerant types and/or by chronology whenever appropriate and systematically commented. This review brings out the fact that theoretical ejector and cycle studies outnumber experimental investigations and data generation. More emerging numerical studies of two-phase ejectors are a positive step, which has to be further supported by more validation work.
1. Introduction
Ejectors have been extensively studied for decades mainly for use in ejector cooling and refrigeration systems, as a potential alternative to conventional compression systems or more generally to assist conventional systems and improve their overall performance. Ejectors may be used with almost any fluid without any need for lubricants. They are simple passive components, reliable, low cost and almost maintenance-free.
Today, ejectors may be found in several fields of applications such as vacuum creation, fluid circulation, water desalination or refrigerant expansion, as reported in previous papers such as Elbel and Hrnjak [1], Kumar et al. [2] to name only two cases. In novel refrigeration systems, they can operate in single-phase mode to boost or even replace the compressor, in two-phase mode to recover the energy usually lost in the throttling valve of refrigeration or heat pump cycles. Irrespective of their type, ejectors offer good opportunities to build cycles potentially more efficient and less energy demanding than the conventional mechanical refrigeration systems [3]. In view of the many potential uses, different ejector types are available. They are categorized as single-phase or two-phase devices.
Single phase, liquid–liquid ejectors generally serve as feed pumps and flow circulators. An application example was considered by Li et al. [4] for water chillers where the ejector worked as a liquid recirculation component in a horizontal tube falling-film evaporator with R134a. Supersonic gas–gas ejectors can recover waste heat and they have been the most widely studied to date (see Part 1 of this review for details).
Two-phase ejectors refer generally to the condensing ejector (vapor stream condenses in the ejector), or to the conventional two-phase ejector (two-phase, liquid–vapor flow throughout the ejector) [5]. Two-phase ejectors where a primary liquid drives a secondary vapor are finding an increased use as expansion devices. They reduce throttling losses and recover expansion work (replacement of expansion valves) in heat pumps, air-conditioning and refrigeration systems.
Available literature reviews dedicated to two-phase ejectors and their applications focused mainly on refrigeration and heat pumps [1,3,6,7,8,9,10]. Elbel and Hrnjak [1] summarized the historical background of the ejector technology and its development in air-conditioning and refrigeration. Two-phase ejector application to CO2 heat pumps occupies an important place among the available works. Sarkar [6] compared several important such cycles with transcritical CO2 for the purpose of expansion recovery. Elbel [7], building on previous work [1], provided a detailed account of the transcritical CO2 ejector application in air-conditioning, in addition to analytical and experimental results on system performance improvements. Further work by Sumeru et al. [3] extended the investigation to issues like thermodynamic modeling and comparison with the conventional cycle, irrespective of the refrigerant type. Around the same time, Sarkar [8] also proposed a review of ejector expansion cycle including geometric parameters, refrigerant and operating considerations. This work included a good description of various cycle configurations as well as performance characteristics of both subcritical and transcritical systems. A recent paper by Besagni [11], gives a concise rundown of last two-year achievements in areas of ejector-based refrigeration, power conversion and chemical processes, with future research and development perspectives.
Colarossi and Yazdani teams [12,13] summarized the first trials for the determination of spatial fields (Mach number, pressure and quality) inside CO2 ejector passages by means of validated CFD modeling. The recent work of Elbel and Lawrence [10] provided more information on emerging CFD efforts, new control measures, alternate cycle configurations and progress towards the development of applications based on ejectors for expansion recovery in cooling-refrigeration setups.
Given the large amount of ejector material accumulated over the years and the availability of well-documented works in the literature, focus here will be put on highlighting the main characteristics of the technology and the latest development trends.
This work therefore presents updates of representative and recent progress in two-phase ejector modeling, integration in air-conditioning, refrigeration and heat pump cycles as well as in diverse potential applications.
2. Two-Phase Ejector Characteristics
Like other ejector types, two-phase ejectors are simple devices with no moving parts and similar geometric components: a primary nozzle, a mixing chamber and a diffuser. Two fluid streams, a liquid phase and a gas (or vapor phase) are involved. Generally, both phases are of the same fluid such as is the case with conventional refrigerants or water. Depending on the role of each phase, a different type of ejector is obtained with its specific design, local geometry, operation and application [14].
If the vapor is the moving agent of the liquid, the device generally represented by this configuration is the condensing ejector (often called steam injector) [15].
If on the contrary, the liquid is the moving agent of the vapor, then the device is simply called two-phase ejector [16,17,18].
2.1. Ejector Types
2.1.1. Gas–Liquid Injectors
A condensing ejector (also known as steam injector) uses vapor at high pressure as a motive stream to pump cold liquid at low pressure, and to produce an outlet pressure potentially higher than the vapor inlet pressure. Its operation relies only on thermodynamic processes of mass, momentum, and heat transfer between the two phases in order to produce the compression effect. Such a device can be used as a safety pump in light water reactors, as steam supply is generally available in power plants and a high-pressure water supply can be useful for heat removal in case of incident [14,19,20].
A schematic representation of a steam injector is shown in Figure 1a, where four zones can be distinguished. The first zone is the vapor nozzle, with a converging–diverging shape, where the vapor is accelerated to supersonic velocity through a nearly isentropic expansion. Liquid feeds into the injector by means of the liquid nozzle. Two nozzle arrangements can be found in the literature: vapor-central or liquid-central. In this figure the arrangement shown is a vapor-central nozzle and an annular outer liquid nozzle for illustration purposes.
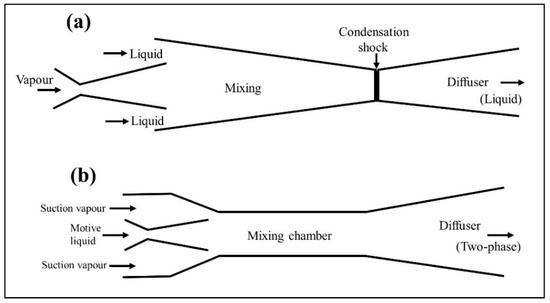
Figure 1.
Typical geometry of two-phase ejectors: (a) vapor–liquid ejector; (b) liquid–vapor ejector.
In the mixing section, vapor and liquid exchange heat, momentum and mass (due to condensation of steam on the water droplets extracted from the water cone at the exit of the water nozzle). Condensation is achieved in the shock wave occurring at the exit of the mixing section in the form of condensation shock. The major pressure rise results from this process, further liquid slow down and a low-pressure increase is obtained in the diffuser [21]. Review details on injector modeling and application may be found in [22]. In a recent paper, Miwa et al. [23] extended their previous experimental study on steam injectors with central liquid jet to widen the operating range and improve pumping performance. The conditions investigated were within 0.02–0.81 MPa for inlet steam pressure and 0.21–0.80 kg/s for inlet water flow rate, respectively. The authors considered the liquid jet break-up length to assess the injector operation mode, confirming the existence of inlet water flow rate and steam pressure limits; by using the liquid jet stability analysis, they also proposed an explanation to its operating range.
Bergander [24] used this concept to propose a modified vapor compression cycle for refrigeration with R22 where the condensing ejector was used. In such a system, the mechanical compressor pressurized the vapor to approximately 2/3 of the final pressure. The ejector device provided additional compression, therefore significantly reducing the amount of mechanical energy required by the compressor. A thermodynamic analysis of the system showed a potential efficiency improvement of 38% above the conventional vapor compression cycle and preliminary experiments on a 10 kW prototype suggested about 16% energy savings.
2.1.2. Liquid–Gas Ejectors
Additionally referred to, as two-phase ejectors, they use the potential energy of the liquid flow (primary motive stream) to entrain a secondary fluid of the same or of a different type (gas or vapor stream) and impress on it some compression effect (generally weak in comparison to single-phase supersonic ejectors). The geometry consists of a convergent or convergent–divergent nozzle, a mixing chamber and a diffuser, as shown in Figure 1b. In the commonly intended ejector-expansion refrigeration cycle application, the motive liquid stream, is provided by the condenser at high, saturated pressure, or slightly sub-cooled. Nearly isentropic expansion occurs in the primary nozzle, accelerating the liquid into the mixing chamber where a secondary vapor stream from the evaporator is drawn and entrained. In the zone of the mixing chamber with constant cross-section, sometimes called the ejector second throat, the resulting two-phase mixture is assumed to go through a process of shock wave formation before heading towards the diffuser for final compression. This mixing process is not yet well understood and due to its complexity, little confirmed information is available in the literature. Two-phase ejector modest compression is likely due, mainly to weak shocks and to the limited compressibility of the two-phase mixture [25].
2.2. Ejector Geometry
The geometrical features of an ejector have an important influence on performance, irrespective of its type. Typical parameters, commonly identified to affect optimal ejector design for maximized performance are generally the area ratio (ϕ) which is the ratio of the constant area cross-section zone or second throat to the nozzle throat cross-section area, the nozzle exit position (NXP) and the constant area cross-section zone length (Lm) as defined in Figure 2. The mixing chamber and the diffuser angles (respectively φ and η) as well as the angle of the primary nozzle divergent β, also are sometimes considered.
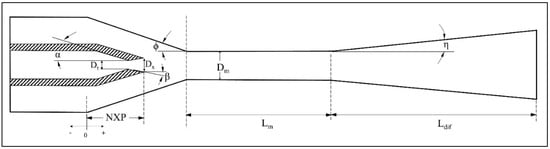
Figure 2.
Typical ejector geometry parameters.
As previously discussed (Part 1 of this review), two alternate ejector geometry concepts proposed by Keenan et al. [26] are the constant pressure mixing (CPM) and constant mixing area (CMA). In spite of the fact that the CPM concept is usually preferred for its secondary flow entrainment capability under given conditions, both concepts are equally used, depending on the ejector intended use and its environment conditions. Very recent work of Atmaca et al. [27] compared the two mixing concepts by means of thermodynamic analysis. Similar performance improvement of the expansion ejector refrigeration cycle, under both CAM and CPM configurations, was found.
In heat pump and refrigeration applications, the geometric parameters used for two-phase ejectors are essentially the same as those used to qualify single-phase ejectors. In the case of ejectors serving other purposes in industrial and process applications some slight differences in the definitions and terminology may sometimes be encountered in the literature. Geometric parameters have an effect on ejector performance and operation to various extents, depending on the ejector type, the working fluids, the application and operating conditions. The nozzle exit position, NXP is the relative nozzle distance to the mixing chamber throat inlet and sometimes reported in non-dimensional form as NXP/Dm. It generally has an effect on both the entrainment and the compression ratios of ejectors.
Liu et al. [28] investigated the effects of various ejector geometries and operating conditions on the performance of an air conditioner working with CO2 under transcritical conditions. A maximum COP value was reached when the motive nozzle exit positioned before the mixing chamber inlet was three times the diameter of the constant-area mixing section. Hu et al. [29] experimented a two-phase ejector with the refrigerant R410A, in an air-conditioning system. The distance between the nozzle outlet and the constant section mixing chamber was varied from 0 to 9 mm. An optimal position of the nozzle for system capacity and performance was found to be 3 mm. Experimental results obtained by Wang and Yu [30] with R600a two-phase ejector showed no optimal position for the nozzle. A slight increase of entrainment ratio with NXP was observed, but at 6 mm upstream of the mixing chamber, the entrainment ratio tended to remain constant. Unlike this trend, experiments of Ameur and Aidoun [31] with R134a two-phase ejector have shown an optimal position of the primary nozzle in the ejector, and this position was not very sensitive to operational conditions. The authors noticed a sharp drop in performance of the ejector when the nozzle was placed close to the inlet of the constant-area section.
Nehdi et al. [32] showed by means of thermodynamic analysis the importance of the area ratio on EERC system’s performance for several refrigerants. A maximum COP was obtained for ϕ value around 10. Along the same lines of investigations, Sarkar [33] thermodynamic analysis of EERC with ammonia, isobutane and propane confirmed the importance of the area ratio on performance. In the conditions of the study (Te = 5 °C and Tc = 40 °C), isobutane yielded maximum COP improvement of 21.6% followed by propane (17.9%) and ammonia (11.9%), for area ratios of 10, 7.7 and 5.7 respectively.
The area of the mixing chamber cross-section affects ejector performance differently, depending on inlet conditions. Small mixing areas are more favorable with low inlet pressures in terms of entrainment and compression ratios while larger cross-section areas are more suitable with high ejector pressures or low temperatures for more capacity [8].
Nakagawa et al. [34] experimentally showed 10% COP difference between smallest and largest mixing areas. As shown by Hu et al. [29] by means of thermodynamic analysis and experiments on an EERC type air-conditioning apparatus working with R410A, NXP and the area ratio ϕ sensibly affected system performance by exhibiting optimum working conditions.
The effects of the second throat length (i.e., the zone of the mixing chamber with constant cross-section) were identified to play a role in ejector performance. Nakagawa et al. [35] investigated the effects experimentally of the mixing section’s geometry on the performance of a two-phase ejector with R12. Results indicated an enhancement of the pressure recovery by increasing the length and decreasing the diameter of the mixing section. Tested Lm/Dm ratios ranged from 4 to 21. However, no significant improvement in pressure recovery was observed beyond Lm/Dm = 16.
In another paper, Nakagawa et al. [36] analyzed experimentally the effect of mixing length of a transcritical CO2 two-phase ejector with rectangular cross-section. Three mixing lengths were experimented (5 mm, 15 mm, and 25 mm); the 15 mm case yielded the highest ejector efficiency and COP in all tested conditions. Along the same lines of investigations with transcritical CO2 two-phase ejector, Banasiak et al. [37] tested three mixing section length (Lm/Dm = 5, 10 and 20); the ratio Lm/Dm = 10 was associated with the highest ejector efficiency. In a recent study, Jeon et al. [38], investigated the effects of Dt and Dm on the performance of an ejector expansion air conditioner using R410A, under various climatic conditions. Dt was varied from 1.04 to 1.21 mm, and Dm from 7 to 13 mm, while the ratio Lm/Dm was fixed at 10. At the smallest Dt, the maximum COP increase was observed. The optimum Dm was determined to be 9 mm. Dm was optimized based on the climatic conditions. The optimum Dm increased with an increase in the average annual outdoor temperature.
In general, results about mixing length indicated that an optimization procedure might be crucial for proper ejector design. Indeed, a substantial length can result in considerable friction forces with a negative impact on the mechanism of pressure recovery, whereas a shorter length may result in an inefficient mixing of the two streams. Angles φ and η do not seem to have a systematic influence despite some cases where said influence was reported [29,39,40].
Nakagawa et al. [41] investigated the effect of the divergent angle of the primary nozzle, showing that it played an important role in the decompression boiling phenomena of transcritical CO2, such that the pressure profiles did not correspond to the predictions of the isentropic homogeneous equilibrium model because the flow was in a non-equilibrium and supersaturated state.
More recently, the variable nozzle throat area was proposed and thus the area ratio, as control means to improve the operating performance of the transcritical CO2 ejector refrigeration system [42].
A further geometry concept of the two-phase ejector was introduced by Zhou et al. [43] as the dual ejector, shown in Figure 3. It is equipped with two nozzles and will be further discussed in a later Section 5.2.1.
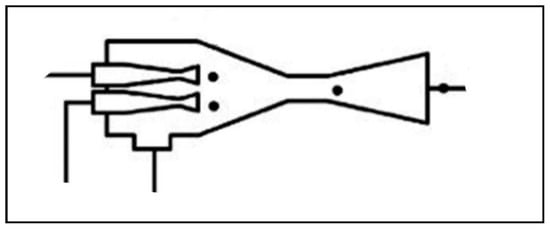
Figure 3.
Dual-nozzle ejector [43].
Recent work by Bodys et al. [44] proposed a two-phase ejector for CO2 with a bypass on the suction nozzle duct (Figure 4). The study assessed numerically the bypass positioning and its angle of incidence under several working conditions. Encouraging preliminary results in the order of 22.4% to 30.4% efficiency improvement at low-pressure conditions were obtained but more work is needed for higher pressures.
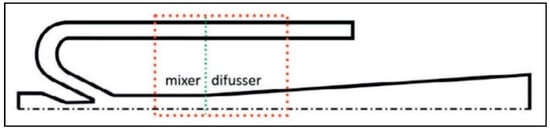
Figure 4.
Ejector with a bypass [44].
2.3. Ejector Performance
Two-phase ejector performance in the refrigeration context is defined in the same manner as for the familiar single phase, supersonic ejector. The entrainment ratio ω, characterizes the capacity of the ejector to draw secondary mass flow rate by a primary mass flow rate determined by the inlet conditions,
and the compression ratio relates the outlet to secondary inlet pressures.
In the context of EERC, primary and secondary inlet pressures are typically defined by the condenser and the evaporator temperatures, affecting both the entrainment and compression ratios.
As was shown by Disawas and Wongwises [45], the motive mass flow rate of the ejector is highly dependent on the heat sink temperature and independent of the heat source temperature. This is due to the fact that choked flow occurs at the motive nozzle, and the upstream condition has a significant effect on the mass flow rate. On the other hand, the heat source and heat sink temperatures have a significant effect on the cooling capacity. Liquid sub-cooling was shown to have an effect on performance. The entrainment ratio is generally higher for small amounts of sub-cooling [46].
2.3.1. Ejector Efficiency
The performance characterization of all ejector types requires two performance parameters, the entrainment and the compression ratios defined above, respectively as ω and τ. During ejector operations, these parameters vary in opposite direction: if ω increases, τ decreases and vice-versa, while it is generally desired that both factors be simultaneously maximized. This represents a limitation for comparing ejector design alternatives in practical conditions. As a result, ways were sought to represent ejector performance by a single characteristic factor, accounting for both aspects of entrainment and compression. Hence, various efficiency definitions were proposed, differing particularly on their interpretation of the energy accounting and the required steps for their computation.
Lawrence and Elbel [47], compared several different ejector efficiency definitions, noting that each definition resulted in a different numerical value for the same ejector operating conditions. They discussed their respective features and the requirements for their application. They concluded that the performance of ejectors from different studies were not directly comparable unless they were measured with the same efficiency. They also noted that in the case of efficiencies developed for single-phase ejectors, the large enthalpy differences between saturated liquid and vapor hinder their application in two-phase ejectors.
For these reasons, Elbel and Hrnjak [48] efficiency definition seems to be better adapted to handle two-phase situations without having recourse to assumptions on internal non-measured parameter values. They defined the ejector efficiency as the actual work recovered by the ejector, divided by the theoretical maximum amount that could be recovered by an isentropic expansion of the motive stream from motive inlet to diffuser outlet pressure, as shown in Equation (3). This efficiency was introduced by Koehler et al. [49] and was subsequently confirmed by Elbel and Hrnjak [48] with a different derivation procedure.
Thermodynamic models accuracy depends largely on ejector component efficiencies. Some studies were dedicated to assess the ejector internal efficiencies [50,51,52,53]. An analysis based on measured parameters allowed Liu et al. [28] to generate information and operational data on parameters affecting ejector performance and components efficiencies in the cycle. These results served to establish correlations for the ejector internal efficiencies. In a subsequent work, the authors found that ejector component efficiencies do not remain constant but rather vary with internal geometry and operating conditions. They further established and incorporated empirical correlations into a CO2 air-conditioning system model to estimate ejector component efficiencies at different ejector geometries and operating conditions [52].
2.3.2. Second Law Analysis of Ejectors
Analysis of irreversibility in an ejector refrigeration cycle (ERC or EERC) and its contribution to overall performance represents a further step in the evaluation process. Entropy and exergy approaches allow identifying the distribution of irreversible losses in the system, their magnitude and makes comparisons possible with other processes.
Banasiak et al. [54] numerically analyzed the contribution of the local irreversibility losses to the overall entropy increase in CO2 ejectors by introducing a new factor to evaluate performance, based on the reference entropy increase in a classic expansion valve. The parameter ςej introduced by the authors quantifies the entropy increase avoided with the use of an ejector relative to a reference process:
where ΔSej and ΔSref are the generated entropies across the ejector and reference process respectively. In the case of an EERC, ΔSref represents the throttling stage of a standard refrigeration cycle under the same operating conditions.
For an experimental EERC with CO2, Banasiak et al. [54] observed ςej in the range (−0.062; 0.223). Negative ςej values mean that more irreversibilities were generated across the ejector than the reference did. In addition, the influence of the diameter and length of the mixing chamber was shown to significantly affect performance. In the conditions considered in this study, an enlargement of the mixing cross section area by 17.4% and shortening the mixing length by 33.3% resulted in an increase of the overall entropy growth rate by 8.9% and 5.4%, respectively.
Another useful performance parameter resulting from the second law is the exergy efficiency ξχ, defined as the ratio of outlet to input exergy flow rates:
with being the exergy flow rate, that is: the maximum work rate theoretically available between the thermodynamic conditions at surface i and a reference dead state 0:
Typical reference (or dead state) choices for isolated ejector studies are the secondary inlet state or the working fluid at normal conditions (1 atm and 288 K). For refrigeration cycles, it is usual to choose the condenser inlet conditions. The value of ξχ represents the amount of potential work recovered using an ejector.
Ersoy and Bilir [50] assessed the effects of two-phase ejector internal efficiencies on performance and for a given set of these efficiencies, a comparison of the exergy destruction in the cycle components with and without ejector. The results indicated that increased ejector efficiencies enhanced cycle performance, exergy efficiency and reduced the optimum ejector area ratio.
Later, Bilir et al. [55] experimentally compared the performance of a vapor compression refrigerator using R134a and its ejector-expander equivalent under the same conditions. The ejector-expander refrigeration system’s coefficient of performance was higher than that of the basic system by 7.34–12.87%, while the exergy efficiency values were 6.6–11.24% higher. The authors measured ξej ≈ 98% for an EERC with R134a. The exergy efficiency of the whole EERC system was on average 18%, always two points over that of the standard refrigeration system without ejector tested under the same operating conditions.
2.4. Internal Flow Structure
The flow structure inside the ejector influences operation and performance. Information on flow distribution is therefore necessary to explore gas–liquid phenomena and the nature of streams interaction. Global analyses resulting from thermodynamic treatment or experimental operations hardly give access to this type of information. Theoretical and experimental studies conducted in order to establish links between the internal structure and performance are still scarce. Multi-dimensional numerical studies based CFD are emerging in two-phase ejector area but need more local validation. Visualization experiments are important in boosting numerical capabilities to reliably predict the complex flow structure inside ejectors and link it to their operation.
Most visualization experiments available in the literature are single-phase ejectors, with air, nitrogen or steam at low to moderate pressures. Visualization techniques commonly employed in theses cases are the Schlieren, Shadowgraph and laser tomography methods as discussed in Part 1 of this work. However, limited studies were conducted to illustrate the mixing process and shock patterns in two-phase ejectors.
Banasiak et al. [9] pointed out in relation to experimental methods of flow visualization in transcritical CO2 ejectors, the scarcity of experimental identification or classification of flow patterns for the two-phase CO2 ejector passages. In this respect and for two-phase ejector internal flow structures in general, visualization methods with high resolution are needed to capture shock phenomena in specially limited component sizes such as found in two-phase ejectors operating with common and natural refrigerants. Schlieren visualization and PIV techniques applied in single-phase devices are also progressively introduced to capture two-phase flow structures and velocity effects.
Experiments supported by visualization techniques in two-phase flow are performed in nozzles as they are utilized in many applications. For example, pressure drop mechanisms as well as flow choking conditions that determine mass flow rate in refrigerant expansion devices are relevant to heat pumps and refrigerators, areas where expansion work recovery is nowadays one of the privileged methods to improve refrigeration cycle performance [56].
Two-phase ejector flow visualization was first applied with water, air, steam or other gases before the conventional refrigerants and carbon dioxide.
In the development context of a suitable standard for the design of jet pumps for chemical industries, Takashima [57] conducted a theoretical and experimental study on several water–air ejector geometries. The jet-pump setup was made out of two pairs of steel plates forming the internal shape, inserted between two Perspex plates in order to allow visual observation by trans-illumination. The author did not detail his observations of the actual motion of the liquid–gas compound, which he considered as too intricate to be analyzed. However, these preliminary visualizations served as guidance to simplifying assumptions for modeling the flow.
Much later, and in order to develop a CFD application of a large-scale steam injector, Narabayashi et al. [19] conducted visualization experiments on a reduced scale injector to generate the needed information. The mixing nozzle was made of stacked heat-resisting acrylic resin annuluses to visualize water and the steam jet inside. The central nozzle introduced a water jet, while the steam jet was blown into the mixing nozzle through the annulus gap formed by water jet and the mixing nozzle. Steam velocity measurement, made by means of a Laser Doppler Velocimetry (LDV) system, consisted of 1 W laser source, transmitting optics, a fiber-optic probe, receiving optics and a high-speed signal processor (up to 150 MHz). A frequency shifting technique was used to decrease the observed Doppler frequency. The laser beam was such that mist droplets moving with the steam could be used as tracer particles.
Moreover, and considering the fact that an ejector can be viewed as a combination of an internal nozzle (motive) and an external nozzle (main body) many studies on nozzle flow are relevant to ejectors. Therefore, some visualization work on two-phase nozzle operation is worth mentioning. In this respect, Simoes-Moreira et al. [58] performed flashing liquid jet experiments in a simple convergent with iso-octane, using Shlieren images to analyze flashing jet structure and geometry. Berana et al. [59] conducted visualization experiments on two-phase flow fluid structure in a converging–diverging nozzle operating with CO2 in transcritical conditions. Images of flashing CO2 flow were captured for both under-expanded and over-expanded flow by using an analog microscope and a camera. The flows could be observed through the transparent polycarbonate wall on one side of the nozzle.
Ohira et al. [60] conducted their study on cavitation instability behavior of sub-cooled cryogenic liquid flows in a converging–diverging circular nozzle with several throat diameters (Figure 5). The working fluid was sub-cooled liquid nitrogen and the flow visualization of cavitation phenomena was undertaken at the outlet of a converging–diverging nozzle, using a high-speed video camera with imaging at a high frame rate and backlighting, so that the bubble clouds appeared as shadows.

Figure 5.
Photographs of cavitation at nozzle throat (Dt = 1.5 mm) [60].
Kim et al. [61] tested a two-phase injector to study hydrodynamic characteristics of the annular type ejector system. In contrast to Narabayashi et al. [19] device, steam was the central stream and water the annular stream. The injector module was made of acrylic materials to allow visual observation of the formation of air bubbles by PIV measurement. A high-speed camera and a 12 W LED lamp used as a continuous volume illumination light source to get bubble images were installed. Flow visualization revealed that water/air mixed flow was immediately generated in the throat region of the mixing chamber. The instantaneous shadow images of bubbles illuminated by the LED lamp showed typical characteristics of homogeneous bubbly flow. At high water flow rate, the whole section was filled with small bubbles. However, buoyant effects are partially observed at low water flow rate.
In a similar configuration as Kim et al. [61], Kwidzinski [62] investigated the condensation wave structure in a steam–water injector for validation purposes and visualized the phenomenon with a high-speed video camera. To this end, the light source was placed behind the observed flow section and the two-phase parts of the flow, which were translucent, appeared dark in the still frames (Figure 6). This recording synchronized with the measurements of pressure and temperature along the mixing chamber and diffuser walls, helped reveal the flow dynamics and the structures associated with the final stages of condensation.
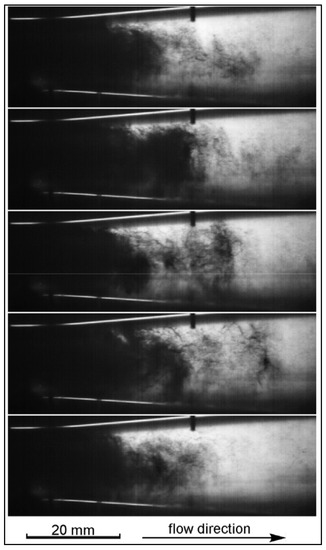
Figure 6.
Condensation wave structure [62].
Subsequently, Choi et al. [63] used the same visualization procedure for the case of recovering air pollutant generated in an oil tank into the crude oil using a gas–liquid ejector system. The flow visualization experiments were conducted on an air–water ejector, using a high speed, 60 mm lens camera. An LED lamp rated at 12 W, installed at the back of a rectangular visualization chamber made of transparent acrylic, served as the light source to obtain bubble images through a light scattering.
Relevant to refrigeration studies, Little and Garimella [64] designed a transparent ejector test section which they tested in an ejector-based chiller operating with R134a. The undistorted visual access allowed for detailed shadowgraph visualization of the motive jet in the mixing section at various degrees of condensation. They used high-speed imaging with measured temperatures and pressures at the ejector inlets for model validation purposes (Figure 7).

Figure 7.
Motive jet condensation in mixing chamber inlet [64].
The interest in the use of Carbone Dioxide in transcritical heat pump and refrigerator cycles paved the way for the first visualization works on the flow structure in these devices.
Elbel and Hrnjak [65] in their investigations on high-side pressure control of a transcritical R744 two-phase ejector system to maximize the COP, used a semi-transparent ejector on which images of the mixing section were taken through high-speed flow visualization and under realistic operating conditions. In addition, their measurements of the static wall pressure distributions along the axis of the ejector allowed them to identify the existence of mixing shock waves, confirmed by visualization.
Deng et al. [66] visual investigation of a two-phase ejector for a transcritical CO2 cycle was based on a shadowgraph visualization approach. The study concerned the mixing chamber and focused on suction and mixing processes as well as configuration variations in flow structure with operational parameters or geometry features such as primary pressure conditions, cross-section area mixing and the primary nozzle divergent length. Images of the mixing process showed that these parameters played an important role in premixed vortex formations, their size and their location in the suction chamber. The geometry features in particular, seemed to substantially influence the stream mixing and the flow homogeneity, a condition that affects performance.
More recently, Zhu et al. [67] investigated the internal structure of a CO2 two-phase ejector operating in transcritical flow conditions, relying of visualization experiments by direct photography. The method used a single lens reflex camera and a light film for uniform light and more brightness adjustment to better distinguish vapor and liquid droplets in the flow medium.
The Schlieren method was used without success to visualize the flow field, because this approach, based on the deflection of light by the refractive index gradient was very sensitive to CO2 and oil droplets in the flow. The results of the investigations have shown the influence of parameters such as the inlet pressures and the expansion angle at the nozzle exit.
2.5. Applications Potential of the Two-Phase Ejector
As early as 1858, Henri Giffard [68] patented a two-phase ejector to supply water for steam locomotives. Nowadays, significant efforts are undertaken to use the two-phase ejector in several applications such as fuel cells [69,70], desalination system [2,71], ballast water treatment [72], nuclear power plant [22], evacuation and exhaust of gases [73].
Two-phase ejectors unique feature of static devices with no moving parts, which makes them particularly reliable and requiring no or minimal maintenance is most attractive for many applications in industry. They can handle phase-changing streams and two-phase mixtures, irrespective of the fluid nature and its level of cleanliness. They are widely used as mixing devices or for pumping corrosive fluids, slurries, fumes and dust-laden gases. In chemical industries and in biochemical industry they are used in gas–liquid reactions, serve for absorption and stripping [74]. Ejectors produce high mass transfer rates by generating small bubbles/droplets, which can then be injected into a reaction vessel thereby improving the contact between phases. In this context, numerical and experimental studies were made, showing that there was an optimum area ratio, at which the liquid entrainment rate was the highest. The liquid entrainment rate increased with the pressure difference between the water surface in the suction chamber and the throat exit for a wide variety of ejector geometries and operating conditions [40,75,76,77]. For example, the Kandakure et al. [76] use of two-phase ejector as a liquid–gas contactor, relied on CFD in order to assess the hydrodynamic characteristics with reference to the ejector geometry. In this case water as the motive fluid and air as the entrained fluid were considered. It was found that there was an optimum area ratio for the maximum air entrainment rate.
Liquid–gas ejectors were studied experimentally by Choi et al. [63] to explore methods of dissolving the volatile organic compounds generated from crude oil into the oil itself, in an oil tanker. These unique features make them a potential alternative to several competing technologies for energy integration schemes in a wide range of industries.
In nuclear plants, two-phase, vapor–water ejectors serve as emergency systems [22,78].
The sector of cooling, refrigeration and heat pumps seems the most promising for the two-phase ejector. In this field, the two-phase ejector is mainly used according to two approaches: ejector as an expander (Figure 8a) and ejector as a recirculator (Figure 8b).
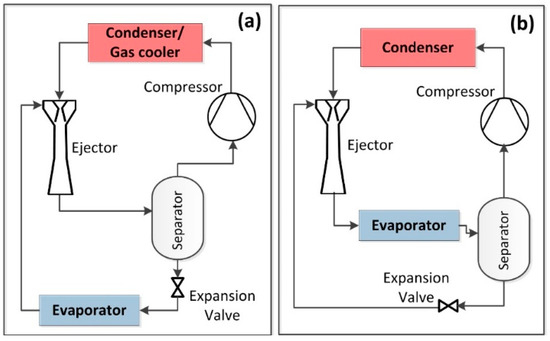
Figure 8.
Refrigeration cycles with two-phase ejector: (a) ejector-expander (EERC); (b) ejector-recirculator (ERC).
The conventional EERC (Figure 8a) was patented by Kemper in 1966 [79]. The acronym EERC refers to refrigeration, but also to air-conditioning applications and heating. Depending on the working fluid, two types of EERC cycles are reported in the published literature: subcritical cycles [30,80] and transcritical CO2 cycle [48,81]. The performances of the transcritical CO2 cycles are generally superior to the other refrigerants.
The second way to use the two-phase ejector is as a liquid recirculator (ERC) (Figure 8b). The benefit of this cycle configuration is essentially due to a more performant evaporator. Overfeeding the evaporator allows a better heat transfer [82,83].
There are several variants of the conventional cycle with two-phase ejector as an expander, such as those with two evaporators and no separator (Figure 9). More details on different cycles with two-phase ejector are presented in Section 5.2.
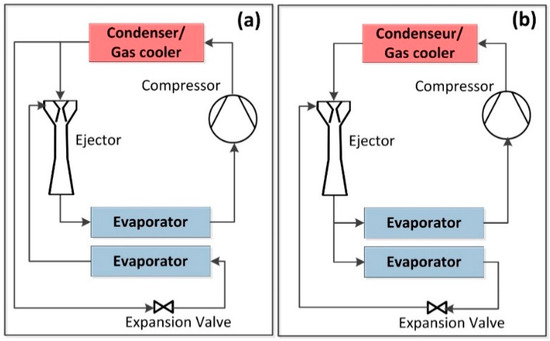
Figure 9.
Variants of the conventional EERC: (a) Condenser outlet split cycle (COS) [84]; (b) diffuser outlet split cycle (DOS) [85].
3. Two-Phase Ejector Modeling
The modeling of two-phase ejectors and cycles for heat pumps, refrigeration an air-conditioning presents a high interest for the optimization because performance can be predicted for the ejector in terms of its specific efficiency parameters and for EERC or its variants in terms of COP and other efficiency expressions discussed in previous paragraphs. The design of cycle components can be handled to ensure overall maximized performance for the system. A great deal of research and development work along this path is available in the literature.
A major part of design and simulation effort consists of one-dimensional and thermodynamic modeling, depending on the nature of the task. Typically, cycle design and simulation is based on thermodynamic, first and second law modeling. Ejector modeling is more generally handled by 1-D and thermodynamic approaches. Methods combining thermodynamic considerations and experimental based correlations were useful in specific cases [33,86,87].
Multi-dimensional CFD methods have been relatively scarce due to the flow complexity in two-phase ejectors (in comparison with the supersonic type) and the high computational cost but due to the progress in computational power becoming increasingly available, studies based on these techniques are emerging [88,89]. A good description of the progress in two-phase ejector modeling up to 2015 can be found in the review of Elbel and Lawrence [10].
3.1. Thermodynamic and Analytical Modeling
Methods of ejector analysis based on thermodynamics and the solution of the integral form of conservation equations are generally the simplest way to estimate the influence of geometry and operating conditions on performance, provided that simplifying assumptions on two-phase flow structure and conditions are adopted in different zones of the device. A key component in the development of these models is the motive nozzle which, according to experimental observations has a considerable influence on ejector operations and performance.
A great deal of research has been devoted to nozzle flow, due to its importance in many fields of applications, driven by the impetus for developing ways to convert fluid energy at high pressure and/or temperature in the form of velocity to favor momentum transfer between streams and in the case of ejectors to accurately determine the primary mass flow rate for fluid maximized entrainment and compression ratios.
Flashing nozzles have been most researched for ejector use because their conditions of moderate to low sub-cooling and low quality mixtures are the most encountered in EERC machines. Effects of inlet sub-cooling, fluid quality and flashing inception in expanding fluid flow on mass flow rates, have been among the main elements in the quest for relevant information on nozzle design criteria and mostly experimental [90,91,92,93].
Later, Liu et al. [94] modeled sub-cooled water flow in a convergent–divergent nozzle with the flashing process occurring immediately past the throat. They considered an oblique evaporation wave with a velocity direction change of the supersonic flow downstream the shock occurrence. Expansion downstream was assumed to be in Isentropic Homogeneous Equilibrium (IHE) except near the throat. In this zone, heterogeneous equilibrium conditions were considered to prevail and the length of said zone increased with the inlet degree of sub-cooling.
Further theoretical modeling of convergent–divergent nozzles was performed for CO2 by Banasiak and Hafner [95], who investigated the influence of the phase transition model on the mass flow rate prediction. The delayed equilibrium model with homogeneous nucleation, superimposed to homogeneous and heterogeneous nucleation was used for the purpose of the metastable state analysis of a transcritical flow with delayed flashing over the motive nozzle.
In two-phase ejector studies, the liquid–vapor flow mixture reaches sonic conditions at fairly low stream velocity. However, determining the choked conditions is particularly difficult since a reliable speed of sound computation still remains an open question, despite the many works available so far [25,96]. A convenient way to overcome this issue is by maximizing the mass flow rate per unit area G which, for an isentropic expansion, can be expressed as:
Local enthalpy, h and density ρ, solely depend on P and S0. At choking conditions, the mass flux G is maximized. There is therefore less need to determine the local speed of sound for this particular purpose and the mass flux approach can be easily applied in two-phase flows, where critical conditions lie mostly over the saturation line. The model of Ameur et al. [18,25] employs this approach to compute the thermodynamic properties of liquid–vapor in the primary nozzle in critical conditions. In the application to ejectors for EERCs, deviations of up to 7–14% and 6–14% were respectively observed in the primary jet critical mass flow rate and the compression ratios.
The relative simplicity, the low cost in terms of computational memory and time with the ability to rapidly generate results is an advantage of the thermodynamic approach over 1-D modeling, which remains based on the resolution of a differential form of the conservation equations.
Some representative theoretical highlights from previous work with respect to two-phase ejectors are worth mentioning first. They relate to two-phase ejector modeling proposed for flash system use in refrigeration, where a refrigerant condensate close to saturation is expanded.
Kornhauser [97] developed a thermodynamic model for two-phase ejectors, widely cited in the literature and used by many researchers, given its simplicity [98,99,100,101]. Kornhauser [97] first set up such a simple model extended to the ejector which he applied with various refrigerants, mainly halocarbons. The approach used the Homogeneous Equilibrium Model (HEM), the assumption of constant pressure mixing and isentropic efficiencies to account for friction losses. An updated version by Menegay and Kornhauser [102] accounted for under-expansion of the flow, a condition found to favor better overall ejector efficiency.
Improvements to the Kornhauser model were subsequently brought by researchers such as Nakagawa et al. [35] who proposed a hybrid approach, consisting of a combination of 1-D and thermodynamic considerations. The isentropic flow treatment was used to model the primary nozzle while a 1-D approach was applied in the remaining zones to both phases in terms of the momentum equation conservation, where a wall friction coefficient was only used in the vapor phase which was assumed to be in contact with the wall. In this way the authors could analyze the geometric characteristics of the mixing chamber.
Liu and Groll [103] computed the critical flow in the primary nozzle of the ejector by assuming choking conditions at the throat. They evaluated the sonic velocity with an equation derived by Attou and Seynhaeve [104]. Momentum exchange in the mixing chamber was accounted for by the conventional coefficient method and a recovery factor was used in the diffuser according to the recommendation of Owen et al. [105]. Later Liu and Groll [52] used this model to study performance characteristics of a transcritical CO2 EERC.
The effects of thermal and mechanical non-equilibrium taking place between vapor and liquid were modeled by Kwidziński [106] for the case of a steam–water ejector. The model simulations were compared with experiments which they predicted within 15% in terms of discharge pressure and 1 K in terms of temperature.
A similar line of development was followed by Banasiak et al. [37,95,107] in the context of expansion work recovery by means of two-phase ejectors. The authors proposed a 1-D method utilizing the Delayed Equilibrium Model along with the homogeneous nucleation theory, the treatment of the metastable state analysis for a transcritical CO2 flow with delayed flashing over the motive nozzle.
More recent analytical work regarding the treatment of CO2 expansion process in ejectors was proposed. Zhu and Jiang [87], in a study of transcritical CO2 ejector expansion refrigeration cycle proposed an analytical model taking into account non-equilibrium effects by means of a correlation based on experimental data of several case studies and capable of predicting primary and secondary mass flow rates. A further correlation simplifying computations at the ejector throat was developed for the primary mass flow rate. Accounting for non-equilibrium was to be important when the liquid mass fraction at the nozzle throat was higher than 0.65. A number of analytical and thermodynamic ejector models are reported in Table 1.

Table 1.
Ejector global models.
3.2. CFD Modeling of Two-Phase Ejectors
Computational Fluid Dynamics techniques allow the detailed study of ejector flow, based on the solution of the Navier–Stokes (NS) equations. In order to manage the otherwise prohibitive computational cost, a statistically averaged version of these equations in the form of the Favre-Averaged Navier–Stokes (FANS) or compressible Reynolds-Averaged Navier–Stokes (RANS) equations is commonly solved. In such an approach, the mean features of the flow are all preserved but extra terms for turbulent effects need to be handled by means of turbulence models in order to close the system of equation. In addition, an equation of state relating pressure, temperature and density is required. As discussed earlier for supersonic ejectors, turbulence models need to be carefully selected on a case-by-case basis and the issue is no different for two-phase ejectors. Regarding the fluid properties, NIST database for refrigerants, REFPROP is generally used.
The computational power and the simulation flexibility provided by the recent CFD platforms have resulted in the treatment of several two-phase ejectors being undertaken. The CFD modeling of two-phase flows (flashing liquid or vapor condensation) is a challenging task. Many phenomena on the local scale are not yet well understood, such as nucleation characteristics and bubble-droplet growth. The complex structure of the gas–liquid interface and the transfer mechanism require more elaborate models with empirical correlations or assumptions which are so far insufficiently tested [108,109].
3.2.1. Treatment of Two-Phase CO2 Ejectors
Bulinski et al. [110] conducted a preliminary CFD work on CO2 transonic ejector flow by using homogeneous and heterogeneous flow models in order to account for non-equilibrium effects. They then compared the predictions of both approaches in terms of pressure distribution in the mixing chamber, which were well predicted by both approaches. Unfortunately, this partial validation was insufficient since the heterogeneous approach predicted the lowest pressure by an order of magnitude right after the nozzle throat. In addition, according to the authors, entrainment ratio predictions were also different.
Colarossi et al. [13] built a multi-dimensional simulation model based on a pseudo-fluid concept where two phases mass, momentum and energy conservation equations were treated as a single fluid with combined transport equations. The flow was assumed to be in non-equilibrium state and a modified form of the homogenous relaxation model (HRM) was employed to describe the delay in nucleation. Standard k-ε turbulence model was used and the fluid properties were obtained from REFPROP database. Simulations performed with CO2 as the working fluid were based on Nakagawa et al. [36] for validation in terms of pressure recovery. Even though the trends of the results were comparable, the discrepancies between simulations and experiments were important. The authors attributed this poor concordance to the challenges of modeling two-phase, turbulent non-equilibrium flow and the selection of the turbulence model.
This paper was followed by the work of Yazdani et al. [12], consisting of a numerical model of transcritical CO2 ejector-expander applications for refrigeration and heat pumps. It is a non-homogeneous mixture model, including several sub-models for local interphase energy and mass transfer, two-phase velocity of sound formulation and real fluid properties of the refrigerant. The turbulence model formulation used was the k-ω SST type and the thermophysical properties of CO2 were obtained from the NIST-REFPROP database. The simulations indicated that the ejector performance was only slightly influenced by the inclusion of the slip model. The cavitation portion of phase change was generally small but could be dominant near the walls and at the motive nozzle throat. Compression and entrainment ratios were predicted to within 10% of experimental data and there was a threshold diameter at which performance was characterized with a gentle shock in the mixing zone. In a subsequent investigation, Yazdani et al. [111] put more focus on the flow process of transcritical and subcritical cases of CO2 in converging–diverging nozzles. This study showed that phase change is generally small but can be dominant near the walls and at the motive nozzle throat. Choking occurred downstream of the throat, where void generation promoted flow acceleration while leading to a drop in the sound speed. The nozzle configuration and the upstream operating conditions were found to shape the two-phase jet and affect the void generation rate.
Back to ejector simulation, Smolka et al. [112] three-dimensional CFD model of a transcritical CO2 ejector was developed on the assumption of homogeneous equilibrium flow. An enthalpy-based formulation, in which the specific enthalpy, instead of the temperature, as an independent variable was employed. Gas–liquid mechanical and thermal equilibrium between phases was assumed for two-phase flow and the turbulence effects were modeled by the RNG k-ε turbulence model. In addition, NIST-REFPROP database was again used for the extraction of the fluid properties. Maximum discrepancies on the prediction of primary and secondary flows were respectively 14% and 19.7%.
Lucas et al. [113] numerical model also based on the homogeneous equilibrium approach and validated by the authors’ data with and without suction in order to isolate effects of mixing and friction. High Reynolds k-ω SST turbulence model in its standard implementation in OpenFOAM was used. The numerical results were compared with experimental data previously published by the authors for validation needs. Simulations allowed for the prediction of the driving mass flux and the pressure recovery within an error margin of 10%. However, this error increased to 20% when the ejector was operated with a suction flow.
In the conditions of a supermarket application CFD modeling was applied as well in order to test the validity of HEM model for ejector transcritical CO2 operations. The comparison of the experimental and computational results showing accurate results could be obtained when operating near or above the critical point. The model accuracy decreased with the decreasing temperature and decreasing distance to the saturation line [114].
More recently, Haida et al. [115] applied the HRM model to CO2 two-phase ejectors. The predictive accuracy of the motive nozzle mass flow rate improved, in comparison to currently available numerical models for subcritical regimes. For operating regimes in transcritical conditions, comparable high accuracy to the HEM model was found. Further, the authors reported that HRM application for motive pressures above 59 bar predicted motive flow within 15% accuracy. Below 59 bar, the motive mass flow rate prediction was 5% to 10% more accurate than with HEM formulation.
The CFD approach was also employed to assess locally the ejector’s internal irreversibility. Banasiak et al. [54] analyzed numerically the overall entropy increase in CO2 ejectors by introducing a new factor to evaluate the ejector performance based on the reference entropy increase in a classic expansion valve. They found that the shock train at the primary nozzle outlet and the turbulent interaction process in the mixing chamber were a major source of irreversibility. Moreover, and based on the model predictions, the authors recommend that all ejector dimensions must be optimized simultaneously, otherwise, the irreversibility reduction in one ejector section may translate into an increase in the next section, thus neutralizing the overall gain. In addition, the influence of the diameter and length of the ejector mixing chamber was shown to significantly affect performance.
In addition to CFD investigation mainly focusing on the ejector component and the local flow characteristics, Palacz et al. [116] conducted their study on the ejector from the viewpoint of shape optimization and efficiency enhancements. More particularly, the authors applied a scheme combining CFD and a genetic algorithm to optimize CO2 ejectors for refrigeration systems. They worked on ejector geometries to adjust several parameters for maximized performance. The optimization of the results showed that the ejector efficiency could be improved by up to 6%. A recently published paper by Haida et al. [117] numerically assessed the effects of heat transfer on the wall of a CO2 ejector in the context of air-conditioning. The results indicated the reduction of the mass entrainment ratio could be as high as 13%, as a result of the non-adiabatic assumption condition.
3.2.2. Phase Change in the Motive Nozzle
Vapor condensation phenomena in convergent–divergent nozzles were well described by Mikasser [118]. Generally, superheated vapor at the nozzle inlet first expands with a decrease in temperature until the saturation condition is reached. Beyond this point the expansion process is no more in equilibrium but continues in metastable conditions (non-equilibrium) until a maximum sub-cooling is attained accompanied by a sudden appearance of a cloud of droplets (Wilson point). This spontaneous condensation releases latent heat which is absorbed by the vapor flow, elevating its temperature to near thermodynamic equilibrium. Vapor phase change reduces the specific volume, decelerating the supersonic flow and producing a local characteristic compression increase, known as a condensation shock Figure 10. Further theoretical and experimental details of this process showed that spontaneous condensation reduced the overall Mach number along the nozzle diverging section but increased the entropy generation linked to droplet nucleation, an effect found to be reduced by injecting droplets mixed with the inlet flow [119,120].
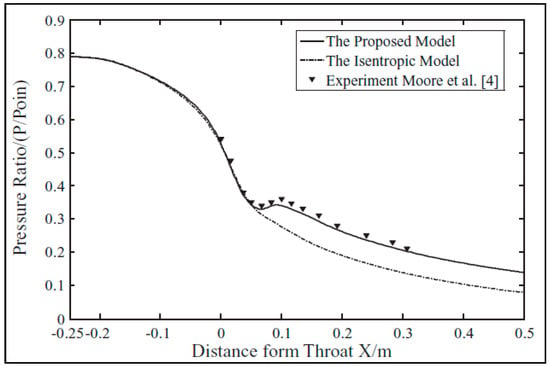
Figure 10.
Pressure distribution along the nozzle centerline with condensation shock [120].
Spontaneous condensation may produce unstable flow conditions at the nozzle exit, especially when it takes place immediately after the nozzle throat. The nozzle should be designed in such a way as to move the nucleation inception downstream of the throat in order to avoid flow oscillations across the sonic threshold. In the case of ejector design where the ideal gas assumption was commonly used, Grazzini et al. [121] undertook to check the validity of such an assumption for the condition of their refrigeration case, since high-speed flow generally prevailed in the primary nozzle, suggesting the existence of metastable conditions. Their findings indicated that the isentropic expansion of vapor through the nozzle, modeled as ideal gas was well within the metastable zone and the classic nucleation theory showed that the Wilson line was crossed at the nozzle throat.
Wang et al. [122] numerical simulations of steam spontaneous condensation in the motive nozzle, resulted in 10% higher outlet pressure than predicted by the perfect gas assumption and an equally higher temperature. The analysis demonstrated that the steam condensation would hinder the supersonic expansion process in the divergent and reduce the nozzle efficiency, which in turn would affect the pumping performance of the steam-jet pump. Similar work by Ariafar et al. [123] investigated this effect in a steam ejector and nozzles with different area ratios. Wet steam simulations showed that nozzle static pressures were higher than those predicted by the ideal gas model. Enhanced mixing between streams, which arises because primary stream condensation reduces compressibility in the mixing layer, was proposed to explain the increased entrainment ratio predicted by wet steam ejector simulations.
Little and Garimella [64,124] suggested a simple way to promote the formation of liquid droplets by adjusting the degree of superheat at the motive nozzle inlet. Depending on the time scale of this expansion and the kinetics of droplet formation, droplets may form to produce a “wet” motive jet at the nozzle exit. Information on its metastable states and sub-cooled droplet nucleation and growth, critical to understanding the mechanisms of suction flow entrainment and overall ejector performance was the focus of the numerical and visual studies undertaken by the authors on an R134a heat-driven ejector-based chiller. It was found that shadowgraph imaging combined with a numerical assessment based on k-ε RNG turbulence model that the assumption of motive flow leaving the primary nozzle in thermodynamic equilibrium was reasonable. Shock and expansion wave inceptions were observed to start at the motive nozzle throat and dissipate in the mixing section. Moreover, a decrease of enthalpy at nozzle inlet increased the amount of condensate at the outlet which in turn, expanded to span the entire width of the mixing section, steadily deteriorating in the process the ejector entrainment ratio. However, no information on the critical pressure was reported.
Another aspect that attracted the interest of researchers was the influence of droplets injection on supersonic ejector performance. The point of injection may be the inlet of the primary stream or any favorable location in the mixing chamber. The injection of droplets in the primary inlet has for main objective the reduction of the velocity mismatch at the mixing section by decelerating the motive flow while maintaining its momentum, reducing entropy generation and enhancing mixing [125]. The intensity of shocks in the constant area section may be attenuated by droplet injection before the shock wave occurrence [126]. However, the amount of research on this subject is still very limited to draw reliable conclusions.
Al-Ansary and Jeter [125] first experimented the effect of droplets on ejector performance, by introducing 17 μm droplets in the primary nozzle inlet of air ejector. Numerically, these droplets were considered as spherical, inert particles with constant size and simulated in a Lagrangian frame of reference. In off-design operation corresponding to a pressure range of 107 kPa to 446 kPa, an increase of up to 98% of suction flow was achieved experimentally in the best case, within a range of liquid injection between 4.3% and 11.2% in terms of pressure ratio. The reliability of these results may be limited, due to uncontrolled liquid–air phase-change exchanges, water accumulation in the ejector due to wall effects and the additional air from the atomizing device. Further investigations were later conducted numerically and experimentally by Hemidi et al. [127]. They indicated that with a liquid injection of 1%, the presence of water droplets had no significant effect at on-design operation but beyond the critical point (off-design operation) it reached on average 10–40% increase with some loss in back pressure. These findings somewhat disagree with the numerical findings of the same authors indicating that performance decreased by the addition of water droplets. It is worth underlining, however, that the abovementioned studies were based on an air–water ejector operation. In the refrigeration context, the working fluids are generally the phases of the same fluid with different thermophysical properties and likely significantly different overall operational behavior.
Very recent thermodynamic and CFD modeling development work of Croquer [126] concerned about the effect of droplet injection in the mixing chamber. Vapor and liquid were both of R134a and the investigation was performed in the context of refrigeration. The droplets were injected normally to the flow in the first half of the mixing chamber throat and had a negative impact on the ejector performance. No noticeable changes in the internal flow structure were observed until mass fractions of about 10% of the primary flow mass flow rate were attained. At these conditions, the shock wave intensity decreased by 8% and thus the entropy associated with these shocks but for a given entrainment condition, the compression ratio was diminished by 10%, relative to the case without injection. These negative results were attributed to the additional losses generated by the mixing interaction between the droplets and the primary stream as well as the additional entropy of the injection process. Table 2 contains a few relevant two-phase ejector CFD studies from current literature.

Table 2.
Two-phase ejector computational fluid dynamics (CFD) studies.
4. Experiments on Ejectors
Much experimental work currently available in the literature about two-phase ejectors was generated to support the theoretical developments discussed in the previous sections. A large percentage of this endeavor was intended to validate theories. Other studies were devoted to generate data as well as operational information. A good deal of the experiments was formulated in terms of characteristic performance indicators, that is the entrainment and compression ratio or accessorily thermodynamic first and second law efficiencies previously introduced. These studies are very important because they establish the link between the ejector and its application environment. Similarly, to single-phase ejectors, local experiments in two-phase ejectors are limited to wall pressure distribution.
As pointed out in the previous section, numerical work requires more local information in terms of variable distributions and flow visualization, since the effort is mainly concentrated on internal flow structure and the complex interactions between various phenomena influencing the ejector operation. Less experimental work was devoted to this aspect so far due to its cost, even though the prospects are encouraging as more focus is increasingly being put on this task. Indeed, the highly complex internal ejector flow structure has not yet fully been clarified despite a very extensive ground breaking work, and most existing experimental literature does not provide a complete picture linking ejector operation under various conditions and its internal structure.
A sample of the relevant work on nozzle flow includes the studies of Menegay and Starkman [80,90] and two consecutive papers of Nakagawa [41,59,128]. More specifically, the Starkman [90] experimental investigation had for main objective the determination of mass flow rate in nozzles under choked two-phase flow operations. The data analysis indicated that the nozzles were operating in over-expanded conditions. Shock waves were observed to occur inside the nozzles with a deleterious effect on efficiency. Menegay and Kornhauser [80] used on the other hand, flashing flow motive nozzles in tests of a refrigeration system incorporating a two-phase ejector. In later tests, the researchers attempted to improve nozzle efficiency by seeding the motive flow with small bubbles.
Nakagawa et al. [128] in a first instance carried out experiments on a rectangular converging–diverging nozzle in which CO2 was expanded. The decompression pressure profile was recorded. It was found that the optimum supersonic decompression before shock waves occurrence obeyed the homogeneous equilibrium model, while behind the shock, the pressure profile displayed no equilibrium condition as indicated by the thickness of the shock waves and the subsonic flow behind them. These measurements indicated that the decompression process in the motive nozzle divergent could not be correctly predicted by the IHE model, which hinted to a thermal and mechanical non-equilibrium state. In a subsequent work, Nakagawa et al. [41] observed and experimentally addressed the CO2 decompression phenomena in the nozzle divergent when metastable fluid flashes to low quality two-phase flow. As was previously established, the fluid in the nozzle was in temperature and pressure equilibrium, in accordance with the experimental measurements. Two-phase flow results through converging–diverging nozzles with divergence angles ranging from 0.07° and 0.612° at inlet pressure and temperature conditions of 6 to 9 MPa and about 20 to 37 °C, respectively were gathered. The authors confirmed by both calculation and experiment that optimum decompression for the largest divergent angles (>0.306°) and inlet temperature above 35 °C, was in homogeneous equilibrium condition. Similar experimental observations were reported by Berana et al. [59] who also measured the wall pressure along the nozzle divergent in an attempt to trace the shock wave occurrence.
An interesting experimental and numerical study performed by Kim et al. [61] is that of a water-driven annular type ejector loop, designed and constructed for air absorption. The application of annular ejectors can be found in the ship-building industry for the recovery of volatile organic compound which is grossly generated during crude oil shipping and transporting process [129]. Airflow rate measurement and PIV experiments were performed. Visualizations revealed that water/air mixed flow was immediately generated in the throat region of the annular ejector. Different bubble-liquid flow regimes were observed and served to guide comparative CFD simulations on air/water arrangements. Little and Garimella [64] is probably the only visualization work with R134a refrigerant, currently available for two-phase ejector in a real EERC system. The authors conducted a detailed shadowgraph visualization of the ejector motive jet at various degrees of condensation. The main intent was to clarify the effect of the condensation on momentum and heat transfer characteristics in the mixing section.
Further visualization studies are available with CO2, in view of the growing interest for this refrigerant. Berana et al. [59] investigated the two-phase flow field in a converging–diverging nozzle with transcritical pressure CO2. This work concerned a flashing flow with different lengths but with the same divergence angle and in the presence of shocks and non-equilibrium effects measurements.
Kwidzinski [62] experimentally investigated the structure of condensation waves in steam–water injectors by means of a high-speed video camera. Simultaneous recordings of pressure and temperature distributions were captured. Vapor clouds were observed to form and then disappear accompanied by pressure pulses. Simultaneous pressure fluctuations were sensed at the injector outlet. It was observed that these pressure variations had no influence on upstream conditions indicating supersonic conditions in the mixing chamber.
More recent visualization experiments were conducted on an ejector running on CO2 by Zhu et al. [67]. The flow structure was recorded by means of direct photography under various operating conditions in the zones of suction and mixing after the primary nozzle exit. Observations highlighted the effect of inlet pressures on the primary mass flow rate. The primary flow angle at the nozzle exit decreased with increasing secondary pressures. Large expansion angles of the primary flow reduced the entrainment of the secondary stream. It was also observed that both primary and the secondary flows mix over short mixing region in the chamber and the resulting stream became rapidly uniform.
Experimental studies on two-phase ejectors also concerned geometry aspects such as those presented by Butrymowicz et al. [130] with the refrigerant R123. These authors evaluated the effects of the mixing chamber geometry in terms of area ratio and the operating conditions on ejector efficiency. Their results suggested that for the operating conditions of the investigation corresponding to air-conditioning environment, the liquid to vapor density ratio was very high, resulting in a small mass entrainment ratio and isothermal compression in the ejector.
Similar investigations were also conducted in the context of a chemical process, generally as liquid–gas-contacting devices. Due to their favorable mass transfer and mixing characteristics, ejectors are being increasingly used in diverse processes of this industry. In this respect, the work of Kim et al. [75] is an example of such an application. Effects of the ejector geometry and the operating conditions on the hydraulic characteristics in a rectangular bubble column with a horizontal flow ejector were analyzed. Gas phase holdup obtained in the water column was shown to increases with increasing liquid circulating rate and decreases with increasing liquid level in the column and nozzle diameter.
Further experiments on an ejector cycle operating with R600a were generated under various conditions of operation by Wang and Yu [53]. Combining the measured data with the predictions of an ejector model, a computational procedure was devised by the authors in order to derive the efficiencies of the characteristic components for two-phase ejectors, including the motive nozzle, the mixing chamber and the diffuser. Operating conditions and geometry were shown to influence component efficiencies which vary sensibly within the range of the conditions considered. The results generated by this study were gathered to build empirical correlations for two-phase ejector design purposes.
Even more recently, Ameur et al. [46,93] reported new experiments on the operation of a two-phase ejector run on R134a with no induced flow and aimed at generating data in addition to information about the effects of the primary stream conditions and primary geometry on the flow through a converging–diverging nozzle. The intent was to develop a better understanding of the parameters and conditions influencing the critical flow, necessary for efficient and stable ejector operation, generally desirable to increase EERC overall performance. Tests conducted with two nozzles of different divergent lengths over a range of inlet pressures, inlet sub-cooling and geometry led to several observations. The inlet sub-cooling played a more important role than motive pressure in the ejector operation. The critical flow was strongly influenced by the nozzle geometry and the operating conditions. The influence of inlet sub-cooling appeared to be at least as important as the pressure in this process. Compared with an isenthalpic expansion valve, a two-phase ejector was shown to be a pseudo-isentropic device which produced less refrigerant flashing, a fact that may translate into potential efficiency improvements of the conventional refrigeration cycle.
Ejector using spindle to adjust the throat area of primary nozzle is a common solution to control the ejector performance across variable operating conditions [131]. Recently, Zhu and Elbel [132] experimentally tested a novel nozzle flow control mechanism called vortex control. Without changing the nozzle geometry, the authors showed that the strength of the nozzle inlet vortex could change the restrictiveness of the two-phase convergent–divergent nozzle with initially sub-cooled R134a. The nozzle becomes more restrictive as the strength of the vortex increases. Representative experiments on ejector are summarized in Table 3.

Table 3.
Experiments on ejector operation.
5. Two-Phase Ejector Cycles and Systems
Up to this point in the present review, the main focus was put on the study of the ejector as a key component in terms of physics, operation, design, experimentation and modeling. Modeling as shown was essentially handled by analytical or numerical methods validated by dedicated test bench experiments. However, the end purpose of ejector developments is its application in many areas of industry as previously discussed, even though the present discussion is limited to the refrigeration and heat pumping area which has been by far the most researched [5,8,10].
Research in refrigeration, air-conditioning and heat pumps has been structured around key aspects such as cycle refinement, refrigerant type, modeling approach among other things. The most basic ejector cycle is the simplest configuration to produce a cooling effect at low cost but its operating range is very limited, a fact that led to further work on hybrid cycles to extend the application range and increase efficiency with no or minor complexity and cost. Theoretical and experimental papers handling this aspect aim to go beyond air-conditioning applications and make ejector systems available for refrigeration as well. Refrigerant properties are known to impact ejector-based and hybrid cycles. Moreover, depending on the cycle configuration, refrigerant mixtures or more than one refrigerant may be used in the cycle loops for more flexibility. Several recent studies investigated refrigerants ranging from synthetic refrigerants to hydrocarbons and more recently some HFOs, due to their performance potential but the current trend demonstrated by the number of published papers leans toward CO2 as a natural refrigerant with good thermophysical properties and performance potential in transcritical cycles [133]. Relevant theoretical and experimental developments in two-phase ejector treating these aspects are briefly presented in the next subsections.
5.1. The Conventional Ejector Expansion Refrigeration Cycle
In a conventional EERC (Figure 8a), instead of an isenthalpic expansion, which results in substantial throttling losses, a two-phase ejector is used to expand the condensate in a quasi-isentropic manner, recovering part of the work that would otherwise be lost in the expansion valve. In the same process, secondary flow from the evaporator is drawn at the ejection suction port, slightly compressed and the mixture sent to a phase separator. This latter feeds vapor to the compressor to complete the cycle and liquid to the evaporator through a metering valve.
This cycle combination differs from the conventional mechanical cycle by the replacement of the isenthalpic expansion valve with a quasi-isentropic expansion ejector and a separator located between the ejector discharge and the compressor suction. The main advantages of the new configuration are the recovery of part of the energy release during the expansion to slightly compress the vapor drawn from the evaporator. In addition, a two-phase ejector cycle can improve the evaporator performance due to near liquid-feeding operation [134]. The combination of all these effects for a good system design results in a more efficient cycle than the conventional one, working in the same conditions [3,135,136,137].
Similarly to conventional refrigeration, the performance of alternative cycles such as EERC is expressed in terms of the Coefficient of Performance (COP), commonly defined as:
This equation relates the heat absorbing capacity at low temperature (cooling effect) to the energy consumed in the compression process, expressed as a ratio of the total heat extracted in the evaporator to the compressor work. It is conveniently expressed in terms of the ejector entrainment ratio. The system performance thus directly depends on the ejector drawing capacity, which in turn depends on the refrigerant type, the operating conditions and the ejector design quality. It is clear that better understanding the influence of operating conditions and design parameters on ejector performance is crucial to enhance the competitiveness of alternative refrigeration cycles.
5.1.1. EERC Theoretical Studies
Suitable models for heat pump cycle performance and efficiency analysis rely on the laws of thermodynamics. The first law is typically employed to evaluate the performance in terms of COP for the complete cycle. The second law is typically used to evaluate the entropy generation. In addition to one-dimensional considerations commonly employed in ejector treatment, both first and second laws, as well as the concept of exergy, which is a combined formulation of both laws are frequently used in cycle analysis, including at the component level.
Analysis of EERC performance by Kornhauser [97] indicated that improvements over the standard cycle depended on the refrigerant employed and for several of them, a COP value 21% above the standard COP was possible. However, COP improvements were highly sensitive to efficiency of the ejector components [138].
Nehdi et al. [32] basing their analysis on thermodynamic model considerations involving several conventional refrigerants concluded that the geometric parameters of the ejector design had considerable effects on the system’s performance. They observed, at ϕ optimal and for given operating conditions, that the best performances were obtained with R141b. Compared to the standard cycle, the COP of the EERC showed an increase in COP of about 22%.
A theoretical study by Bilir and Ersoy [139] established that the EERC performance with R134a was superior to the corresponding conventional compression refrigeration cycle (CRC), even in off-design conditions. At optimal conditions, enhancements of up to 22.3% were predicted, depending on the operating conditions.
Effects of refrigerants and optimized ejector geometry on EERC were analyzed by Sarkar [33]. Relying on thermodynamic analysis, the author compared the cycle operation with ammonia, propane and isobutene for maximized performance in terms of COP. He proposed expressions for optimum ejector geometric parameters, which offer useful guidelines for optimal design and operation. In the conditions of the study (Te = 5 °C and Tc = 40 °C) with the use of the ejector as an expansion device, isobutene yielded maximum COP improvement of 21.6% followed by propane (17.9%) and ammonia (11.9%).
Along the same lines of investigations, Li et al. [140] thermodynamic study of EERC with R134a and R1234yf confirmed the potential of this cycle over the conventional mechanical compression cycle. For air conditioning, estimates indicate that EERC is superior in terms of COP and volumetric capacity by over 13% and 11.5% respectively, depending on the suction pressure difference. In terms of geometry effects, the area ratio was shown to have an optimum value for COP and capacity. Even though R1234yf showed slightly less performance than R134a, its potential for cycle performance improvements seemed to be superior.
An investigation with R134a/R143a zeotropic mixture in EERC by Zhao et al. [141], showed that COP increased to maximum 10.47% for R134a mass fraction of 0.9 but decreased other mass fractions. The cycle exergy efficiency, on the other hand, was maximized at nearly 25% with a mass fraction of R134a of 0.7, most of the exergy losses being at ejector and compressor levels.
Luo [142] built a mathematical model to study the performance of an oil flooded compression cycle enhanced by ejector and internal heat recovery. The investigation was conducted with R32, −25 °C evaporation and 45 °C condensation respectively. The COP improvement of this cycle was found to increase up to 8.5% in comparison to the conventional cycle.
The effect of heat recovery by internal heat exchanger (IHX) was recently revisited by Rodríguez-Muñoz et al. [143] with R134a, R1234ze(E) and R290 as refrigerants. Energy and exergy analysis were employed for two locations in the cycle: at the compressor suction and at the ejector suction. Theoretical comparison suggested that both configurations reduced somewhat the cycle COP, irrespective of the refrigerant selected.
Khosravi et al. [136] conducted a theoretical study including the design, thermodynamic and technical–economic considerations for an ejector expansion cooling system in a refinery where 1631 kW of water cooling was required from 40 °C to 30 °C. The refrigerant R134a was selected after evaluation among a number of candidates and expected energy consumption reduction was estimated to be as much as 22% in comparison to the conventional system with separator.
In the last few decades, there has also been a renewed interest in the use of Carbone dioxide (CO2) due to its favorable thermophysical properties generally and more particularly as a working fluid in EERC cycles under transcritical operating conditions. In air-conditioning system applications, the use of transcritical CO2 in two-phase ejectors as expanders presents advantageous features. The pressure difference across the compressor is very high in comparison to ordinary refrigerants, thus representing a high source potential for work in ejectors which otherwise will not be recovered. Moreover, the compression ratio remains moderate, which means more reliable compressor operation and reasonable electricity consumption.
In an early theoretical study by Li and Groll [144], the effect of operating conditions on the ejector expansion transcritical CO2 cycle for air-conditioning was investigated. It was found that the COP of EERC could be improved by more than 16% over the conventional compression CO2 cycle working in the same conditions.
Ksayer and Clodic [145] employed a 1-D analysis of two-phase ejector-expander refrigeration cycle in the conditions of air-conditioning with transcritical CO2 and R134a. It was found that the COP of the ejector expansion transcritical CO2 cycle could be improved by more than 15% compared to the conventional transcritical reference. Furthermore, a comparison of R-134a and CO2 based refrigeration cycles showed a better performance with CO2.
The next investigation on two-phase ejector transcritical CO2 refrigeration application by Deng et al. [146] provided performance improvements in terms of system COP and capacity of 18.5% and 8.2% respectively over the conventional case with an internal heat exchanger and 22% and 11.5% respectively without the internal heat exchanger.
Sarkar [147] compared conventional expansion layouts for heating and cooling by means of transcritical CO2 heat pumps, showing that the use of ejector as an alternative improved the energetic and exergy performances, while significantly reducing the optimum high side system pressure. He also proposed a correlation for the optimum pressure discharge of the system. A thermodynamic analysis of transcritical CO2 refrigeration cycles performed by Perez-Garcia et al. [148] compared three configurations: with internal heat exchanger, ejector (EERC) or turbine, as alternative replacement devices to the conventional expansion valve. COP based estimations indicated that the turbine-using cycle generally outperformed the other configurations under the same conditions. However, outlet gas-cooler temperatures above 27 °C favor the ejector configuration over the internal heat exchanger one, for entrainment ratios higher than 0.5. Further, increasing the evaporation temperature from −10 °C to 0 °C results in the highest COP improvement in comparison to the IHX and turbine configurations (35.85%, 25.4%, and 24.21%, respectively).
The first and second laws of thermodynamics were also applied by Fangtian and Yitai [149] to a transcritical CO2 cycle for air-conditioning purposes. They evaluated losses in different parts of the cycle, the effect of ejector operation on overall performance and compared the EERC and the expansion valve compression cycle. It was found that for any given running condition there was a critical point for which the operating parameters corresponded to the optimized operation of the cycle. At this point, the use of ejector instead of a throttling valve could reduce by more than 25% exergy losses and increase COP by more than 30%.
The use of internal heat exchanger (IHX) in a transcritical CO2 ejector expansion cycles was studied by Zhang et al. [150]. In their paper they reported simulations on the effect of IHX on the performance of the ejector expansion refrigeration cycle. They found that unlike in a conventional throttle valve cycle, the addition of an IHX in the CO2 ejector refrigeration cycle did not always improve the system performance but rather depended on the isentropic efficiency level of the ejector.
The thermodynamic analysis was also applied by Zhang and Tian [151] for the case of the transcritical CO2 EERC performance. Results from this study indicated that maximum COP could be up to 45.1% higher than that of the conventional cycle. In addition, exergy losses of the ejector-expansion could be reduced by about 43.0% in the same conditions.
In contrast with CFD investigations, typically focused on the ejector component and the internal flow structure on its losses and its performance, Zheng et al. [152] considered the ejector as a component of a system. More specifically, Zheng et al. [152] work consisted in modeling the dynamic operational behavior of an EERC cycle for transcritical CO2. This model helps monitoring changes in the expansion valve openings or the ejector area ratio variations and understand the EERC operational characteristics. As such, this tool can serve as a guide for better system control.
Liu et al. [153] developed a dynamic optimal control strategy for energy charging of both hot and cold storages, using a transcritical CO2 ejector-expansion heat pump. Dynamic optimization control strategy by genetic algorithm was used to obtain the optimal setting points. Results indicated the overall performances during the charging process can be increased, the energy consumption and the charging time can be reduced significantly.
Typical EERC relevant theoretical studies are summarized in Table 4 (synthetic refrigerants) and Table 5 (transcritical CO2).

Table 4.
Selection of EERC relevant theoretical studies (synthetic refrigerants).

Table 5.
Selection of EERC relevant theoretical studies (transcritical CO2).
5.1.2. EERC Experimental Studies
First EERC experiments were mainly performed with synthetic refrigerants. However, in recent years, studies are related mostly to natural refrigerants, particularly CO2.
The apparatus of Menegay and Kornhauser [80,102] was a 3.5 kW capacity air-to-air-conditioning system, using R12 as the refrigeration fluid. Unfortunately, the performance improvement of the system was modest. The authors attributed this drawback firstly to the ejector inefficiency, designed for single-phase conditions and then to the non-equilibrium effects which were underestimated by the Henry and Fauske [155], approach introduced in their improved model. Building on these works, subsequent ejector designs and experiments performed by several researchers were more successful. Harrell and Kornhauser [156] tested a two-phase ejector with R134a and used its performance obtained from the test rig to estimate the COP of the refrigeration cycle, ranging from 3.9 to 7.6%.
Wongwises and his team [45,157,158,159] conducted experiments on an EERC using R134a as refrigerant and with recirculation in the evaporator. They considered the effects of the nozzle outlet size and recirculation ratio variation on overall cycle performance which they compared to a CRC system. The analysis of the experiments was reported in a series of papers in which the main conclusions were that the EERC had lower compressor pressure ratio, lower discharge temperature, higher cooling capacity and higher COP than those of the CRC. However, the authors did not report explicitly any substantial performance improvement over CRC systems.
Reddick et al. [160] built and tested an EERC with R134a. Their preliminary performance results were modest and in some cases even lower than those of a CRC in the same conditions, seemingly due to the separator’s low efficiency. The authors then provided additional heat input to the separator before the compressor suction in order to eliminate liquid droplets at suction. The additional heat input was accounted for with cooling capacity and the system showed an enhanced overall performance of up to 11%, particularly at low condenser temperatures. A similar observation made by Lawrence and Elbel [101] explained that if the separation efficiency fell below 15%, there was no advantage in using the ejector system.
Lawrence and Elbel [161] compared EERC systems with different working fluids against CO2, more specifically R134a and its potential substitute, R1234fa, showing that higher COPs were achieved with R1234fa and R134a, respectively 12% and 8% over the same cycle with CO2. Yet, the latter is more popular given its higher work recovery rate. Ersoy and Bilir [162] generated further experimental results showing that the R134a refrigeration system with an ejector as the expander could reach a COP between 6.2% and 14.5% higher than that of the conventional system.
Experiments with refrigerant R410A were conducted as well by Pottker et al. [163], on three refrigeration cycle configurations: conventional (CC), flash-gas bypass (FGB) and ejector enhanced conventional (EEC) systems. Performance comparisons CC-FGB, CC-EEC and FGB-EEC were performed at the same cooling capacity. CC-FGB comparison identifies the flash gas separation benefit, EEC-FGB comparison the work recovery benefit and CC-EEC the overall benefits (work recovery + flash-gas separation). COP improvements per case were 4.9–9.0% for CC-FGB, 1.9–8.4% for FGB-EEC and 8.2–14.8% for CC-EEC, while ejector efficiencies varied in the range 12.7–21%.
Similar work with refrigerant R410A conducted by Hu et al. [29], demonstrated that the energy efficiency ratio of the conventional cycle could be improved by 9.1%, depending on the operating conditions.
In further experiments of Pottker and Hrnjak [134] two important elements affecting the efficient operation and performance improvement of an ejector system using R410A were quantified: work recovery and liquid-fed evaporator. The ejector system was compared with a liquid-fed evaporator and a conventional system under the same conditions. The results indicated that performance improvement of 1.9% to 8.4% from work recovery and ΔCOP of 8.2% to 14.8% from simultaneous benefits of liquid-fed evaporator and work recovery. Overall, the system efficiency improved from 12.2% to 19.2%.
Popovac et al. [164] tested an ejector heat pump with butane as refrigerant. The cycle was similar to a conventional EERC system. However, the tested conditions were suitable for industrial applications: 50–80 °C on the low temperature side, and 100–130 °C on the high temperature side. The preliminary measurement showed a COP improvement of 25% compared to a heat pump without ejector. The ejector presented a pressure recovery of 1.3 with a corresponding entrainment ratio of 0.3 under the tested operating conditions.
Study undertaken by Elbel and Hrnjak [65] indicated that a transcritical CO2 EERC could increase COP by up to 22% over a conventional CRC working in similar conditions. The author confirmed that this increment in performance varied, depending on the operating temperature, ejector flow ratio, nozzle and diffuser efficiencies. Elbel and Hrnjak [48] then generated experimental data in a transcritical CO2 ejector system which they then compared to conventional expansion valve system test results. Ejector integration in the cycle indicated that both the COP and the cooling capacity were improved by up to 7% and 8%, respectively.
Nakagawa et al. [36] on the other hand focused their investigation on the size of the internal heat exchanger, its effect on system operation and performance in the context of the ejector refrigeration system (Figure 11). They tested the system without and with two heat exchanger sizes (30 cm and 60 cm). The system with the larger IHX resulted in 27% COP improvement over a similar conventional system. The internal heat exchanger provided a good control of the inlet temperature to the motive nozzle flow, which in turn had a significant effect on system performance. A lower inlet temperature in the motive nozzle influenced positively both the ejector performance and the overall system efficiency. The authors observed an excess of liquid in the vapor leaving the separator, which may be detrimental to performance and to the compressor, depending on the size of the internal heat exchanger. They then extended the experimental investigation to the effect of the ejector mixing length on the performance of the transcritical CO2 EERC with or without an IHX, which they compared to the conventional system in the same conditions. The results indicated that an optimum length existed, for which performance in terms of ejector efficiency and cycle COP was maximized irrespective of the use of IHX. In this condition, a COP improvement of up to 26% over the conventional system was attained. Away from this optimum length, COP decreased by as much as 10% [165].
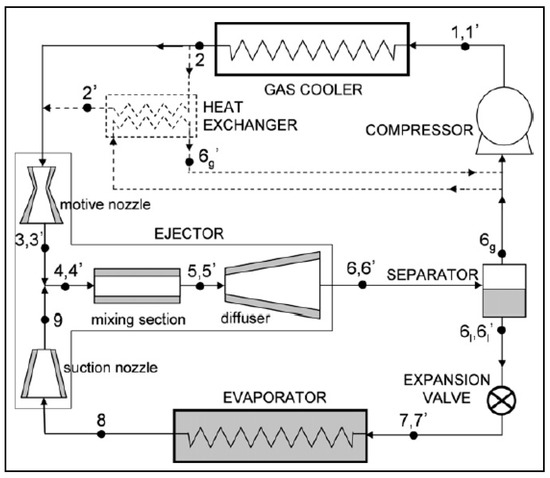
Figure 11.
EERC with internal heat recovery [36].
Lee et al. [166] experimental study focused on the system performance with respect to different ejector geometries and designs. A CO2 air-conditioning system in both expansion valve and ejector based configurations was assessed. The ejector design accounted for the non-equilibrium state in the evaluation of the sonic velocity and the critical mass flux in the motive nozzle. The variation of ejector geometry such as the motive nozzle throat and the mixing section diameters, NXP as well as the separator volume were carried out. The system configuration included an internal heat exchanger for heat recovery in all cases. Experimental results showed that there exist optimum design parameters in each test. Comparison between the conventional air-conditioning system with a throttle valve and an ejector-based configuration revealed that the COP of this latter was superior by 15% approximately.
An extension of this work [167] proposed more detailed information on system behavior with respect to various operating conditions. Experimental results were compared with various outdoor temperatures and inverter frequencies for an air-conditioning system using an ejector and a conventional system, based on experiments with the pressures and temperatures to which the system is subjected. It was found that the cooling capacity and COP of the air-conditioning system using an ejector were sensibly higher than those of the conventional system at an entrainment ratio greater than 0.76. Both cooling capacity and COP improved by approximately 2–5% and 6–9%, respectively.
Liu et al. [168] experiments on a transcritical CO2 EERC used a controllable ejector. At constant compressor speed, COP and capacity were enhanced by 60% and 40% respectively at optimum nozzle throat, Dt and NXP. The variable speed compressor was found to significantly increase COP and cooling capacity in comparison to conventional compression cycle.
Lucas and Koehler [169] conducted experiments on ejector operation with CO2 and the corresponding cycle performance which they compared to a conventional cycle with an expansion valve in terms of the ejector efficiency, the entrainment ratio, and the pressure recovery. Investigations were for constant evaporation pressures of 26 bar and 34 bar (respectively −10 °C and −1 °C), gas cooler outlet temperatures of 30 °C, 35 °C and 40 °C and nozzle inlet suction superheat about 4 °C. Maximum ejector efficiency as defined by Koehler et al. [49] was up to 22% and COP improvement over the conventional cycle with expansion valve in similar conditions was up to 17% with respect to the high side pressure.
This work was continued and reported in a second paper by the authors Lucas et al. [170]. Experimental ejector operation characteristics were validated and correlations for the ejector efficiency and the driving mass flow rate were used, based on previously generated experimental data. The correlations were used to simulate a simple CO2 ejector cycle to predict the experimental data within 10% for ejector efficiency and the mass flow rate within 5%.
Water heating and low-temperature refrigeration are among the priority interests in the use of heat pumps and refrigerators with two-phase ejector enhanced CO2 configurations, which represent an interesting performance improvement potential. In this respect, Guangming et al. [171] conducted a theoretical analysis and experimentation with CO2 on two-phase ejectors for water heating applications. Their theoretical predictions were in good agreement with the experiments. The system was tested in both on-design and off-design conditions.
Experiments on a water-to-water, off-the-shelf, CO2 heat pump equipped with an ejector, were performed by Minetto et al. [172] showing improved circulation of refrigerant in the evaporator. The heat pump was both tested for water and space heating. The comparison to a conventional heat pump employing an expansion valve was favorable according to the authors but no explicit performance comparison was provided. Recently, Zhu et al. [133] investigated the effects of working conditions on the performance of transcritical CO2 ejector-expansion heat pump water heater system. Results showed a COP = 4.6 when the tap water outlet temperature was 70 °C, corresponding to an improvement of 10.3% over the basic cycle.
The multi-ejector approach used by Hafner et al. [173] was later employed by Boccardi et al. [81] to conduct experiments on an air-to-water CO2 heat pump for space heating under partial and full-load conditions. The authors evaluated individual components and overall heat pump performance, varied the ejector area ratio and the compressor frequency to adjust to ambient conditions from −15 to 12 °C. Optimal COP was possible by varying the ejector area, regulated to match with the pressures at the inlet and outlet of the compressor. Optimal ejector performance does not necessarily match with optimal system operation.
Zhu et al. [174] investigated experimentally the issue of the oil circulation in a transcritical CO2 EERC. Significantly higher oil circulation rate was observed at the evaporator inlet of the ejector cycle than at the high-pressure side. To reduce the negative impact of evaporator oil circulation, the influence of compressor speeds, ejector motive nozzle needle positions and evaporator inlet metering valve openings were considered.
A representative sample of EERC experimental studies are summarized in Table 6 (synthetic refrigerants) and Table 7 (transcritical CO2).

Table 6.
Selection of EERC relevant experimental studies (synthetic refrigerants).

Table 7.
Selection of EERC relevant experimental studies (transcritical CO2).
5.2. Miscellaneous Two-Phase Ejector Cycles
Two-phase ejector obvious applications in refrigeration, air-conditioning and heat pump, as detailed in the previous paragraphs rely on the EERC configuration with or without internal heat recovery. However, many industrial uses of two-phase ejectors were also found in the literature and highlighted. In addition, new cycle ejector-based combinations were proposed by the researchers with the same purpose of improving efficiency and saving energy in many areas of application. The following developments will however focus more on the area of refrigeration and heat pumping, where several cycle configurations and application objectives have been explored.
5.2.1. Theoretical Studies
Boumaraf et al. [176] relied on thermodynamic modeling to study a bi-evaporator EERC based on the patent of Oshitani et al. [84] (Figure 9a). The authors used R134a and R1234yf and analyzed the effects of the area ratio on its operation and performance. The results showed COP improvements of more than 17% at Tc = 40 °C for both refrigerants. This increase in COP was higher for R1234yf, especially at high condensing temperatures.
In another instance, the concept of a two-evaporator EERC proposed by Unal and Yilmaz [177] for bus air-conditioning was similar to the case analyzed by Boumaraf et al. [176]. The theoretical evaluation of this device showed that interesting performance gains could be reached (up to 15% COP improvement), depending on the design parameters of the existing bus air-conditioning system.
Effect of refrigerants and their mixtures on a variant of a two-evaporator EERC (Figure 12) performance were the subject of the study by Liu et al. [178]. The authors worked with a zeotropic mixture of R290/R600a and demonstrated that a theoretical COP and cooling capacity improvements over a conventional cycle of 6.71% and 35%, respectively, could be reached. The exergy efficiency improved by about 6.71% and the total exergy loss diminished approximately by 24.47%.
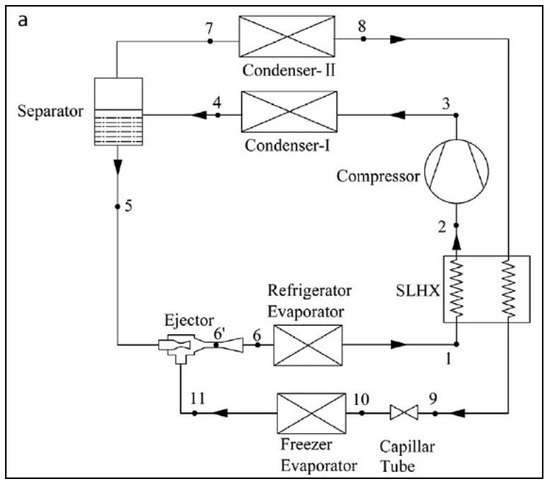
Figure 12.
Variant of EERC cycle [178].
The concept of dual-nozzle ejector represented in Figure 13a, was theoretically investigated by Zhou et al. [43], for use in a household refrigerator freezer with R134a. The ejector is equipped with two nozzles for more efficient expansion losses recovery to form a dual-nozzle which, not only may operate the heat pump with two heat sources at the same time, but also may improve heat pump performances. Simulations predicted COP improvements of 22.9–50.8% over the conventional mechanical refrigeration cycle. Compared to a conventional EERC, the cycle COP was 10.5–30.8% superior in similar conditions. The authors’ preliminary estimates predicted even higher performances with R600 refrigerant.
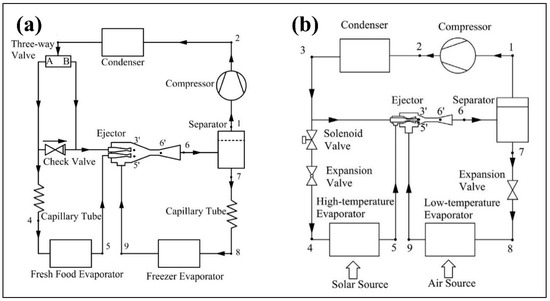
Figure 13.
Multi-evaporator cycles with dual-nozzle ejector: (a) Zhou cycle [43]; (b) Zhu cycle [179].
Zhu et al. [179] work on dual nozzle cycle shown in Figure 13b, is an extension of a previous research by the same authors [43]. It consists of a cycle integrating an ejector equipped with two nozzles. The first nozzle feeds from the condenser in liquid to draw vapor from a high-pressure evaporator, which then feeds the second nozzle as shown in Figure 3. The compound flow becomes the motive flow for drawing vapor from a second evaporator at low pressure. The cycle built on the dual ejector principle may therefore use two heat sources at different temperature levels and improve heat pump performance. Simulations conducted by the authors and based on R410A predicted approximate performance improvements in terms of COP and volumetric capacity ranges of 4.60–34% and 7.8–51.9% over conventional ejector enhanced vapor-compression cycle, respectively.
Two-phase ejector application to domestic refrigerator freezer has a good potential for cycle performance enhancement, as shown by Wang et al. [180]. Several configurations available in the literature were assessed theoretically and compared with a new, modified configuration. The authors used R600a in the proposed cycle, represented in Figure 14. Average COP and capacity improvements over the conventional cycle were respectively over 11.4% and 22%. In addition, they were generally superior to other ejector-based configurations proposed in the literature.
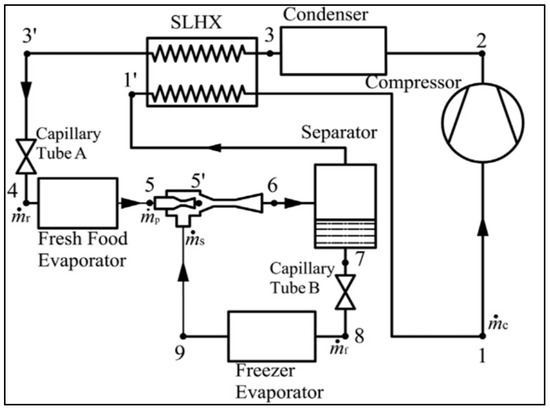
Figure 14.
Ejector application in domestic refrigeration and freezing [180].
More recently, Sarkar [181] analyzed four different cycle layouts with three evaporators and double two-phase ejectors with propane and R32. The author successively compared the new cycles to conventional, expansion valve-based two-stage compression cycle, ejector enhanced single-stage compression and conventional single-stage compression systems with three evaporators. The author reported COP enhancement of about 20% over expansion valve two-stage compression, 67% over the ejector enhanced single-stage compression and 117% over the expansion valve, single-stage compression system in the contexts of air-conditioning (5 °C), refrigeration (−20 °C) and freezing (−40 °C) applications, respectively.
As for Xing et al. [182], they modified the EERC (Figure 15) so that the ejector loop is dedicated to sub-cooling a main loop, including a flash tank, a first expansion valve, the evaporator and the compressor. The ejector loop comprises a feed pump, a second expansion valve and the ejector. The condenser is shared by both loops. The refrigerant leaving the condenser is split in two streams. The first stream is expanded to the flash tank pressure. The liquid is further expanded to the evaporator pressure, then compressed to the condenser pressure to complete the compression sub-cycle. The second liquid stream is pumped to activate the two-phase ejector, drawing the vapor from the flash tank, resulting from the first expansion. The vapor–liquid mixture leaving the ejector merges with the superheated compressor discharge vapor, which is de-superheated at the condenser inlet (Figure 15). Theoretical predictions of such a cycle with R404a and R290a at 45 °C condenser temperature and evaporator temperature range of −40 to −10 °C, improved COP by 9.5% and 7% and the refrigeration capacity by 11.7% and 7.2%, respectively.
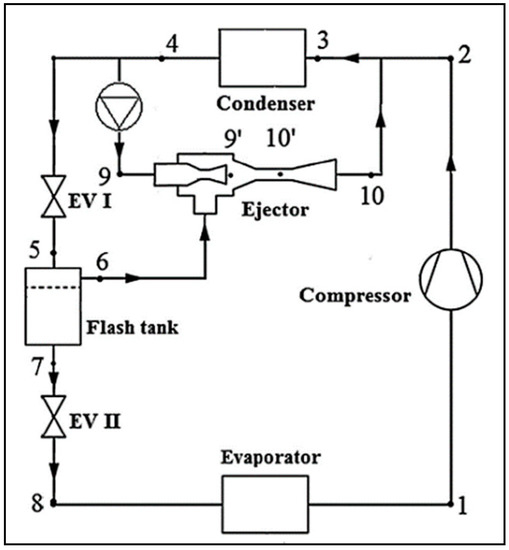
Figure 15.
Schematic diagram of ejector-sub-cooled EERC [182].
Some work was also devoted to demonstrate that it is still possible to consider using water as refrigerant. To this end, Sarevski and Sarevski [17,183] analyzed several cases of refrigeration configurations relying only on two-phase ejector to operate as water-chillers for air-conditioning and other cooling applications.
Shen et al. [184] proposed to replace the feed pump in supersonic ejector cooling cycle powered by solar energy to form a bi-ejector setup. The cycle is represented in Figure 16. The main loop is an ERS where the supersonic ejector is activated by a solar generator in order to produce a cooling effect in the evaporator. The second loop main component is a vapor–liquid two-phase ejector to drive the liquid from the condenser back to the solar generator. It is powered by the generator which feeds the primary inlets of both ejectors in high pressure and temperature vapor. The authors analyzed the feasibility of this system for different refrigerants in terms of performance.
Figure 16.
Solar-powered bi-ejector refrigeration system [184].
Research efforts were also consented in exploring ways to enhance other heating and cooling technologies thermally activated such as absorption systems, more frequently encountered in the past but limited to niche uses nowadays. As a result, ways to enhance their performance were sought through ejector integration at strategic locations within the currently available absorption cycles. For example, the integration of a two-phase ejector located at the absorber inlet to replace the solution expansion valve can benefit the overall cycle because the absorber in these conditions will work at higher pressure than the evaporator will, and reduces the energy consumed in the solution pump.
Ejector application to single effect absorption cycles was analyzed by Vereda et al. [185,186], along this path. On the basis of a thermodynamic analysis, these authors proposed the integration of a two-phase ejector with an adjustable nozzle in a single-effect absorption cycle with ammonia–lithium nitrate solution as working fluid. The purpose was to replace the solution expansion valve at the absorber inlet by an ejector and evaluate its influence. An example of such a configuration is represented in Figure 17. The influence of the ejector geometry through the variable nozzle throat area on cycle performance was first evaluated in order to determine the range of the heat source temperature where it was convenient and beneficial to use a practical ejector in the absorption cycle. Simulations indicated a decrease of the activation temperature by about 9 °C below the conventional single-effect absorption with a corresponding impact on performance. The activation temperature decreased substantially and the cooling capacity increased. This work was extended in Vereda et al. [186] by considering a combined single-effect absorption cycle coupled with a two-phase ejector simultaneously meeting the functions of pressure booster, adiabatic absorber and solution expansion valve. This configuration decreased the activation temperature by about 15 °C, for a recirculation ratio of 3 and increased the cooling capacity for a generation temperature of 80 °C.
Figure 17.
Ejector-enhanced absorption system [186].
Other ammonia/LiNO3 and ammonia/NaSCN combined ejector-absorption cycles were proposed by Garousi Farshi et al. [187]. The ejector replaced the solution expansion valves to allow for pressure recovery from the absorber and to enhance mixing of the weak solution and refrigerant vapor from the evaporator. Theoretical predictions showed that the performance potential of these cycles was higher than the single effect cycle at low generator temperatures.
Further search of new cycles and performance enhancement approaches are also available with CO2. In this respect, a transcritical CO2 two-stage refrigeration cycle integrating a two-phase ejector, an internal heat exchanger and an inter-cooler was analyzed on the basis of the first and second laws of thermodynamics by Yari and Sirousazar [188]. Compared to the conventional two-stage cycle in the same conditions, the new configuration performance’s increase in terms of COP and second law efficiency was about 55.5% and 26%, respectively for typical air-conditioning conditions (Figure 18).
Figure 18.
Modified transcritical CO2 ejector-expansion refrigeration cycle [188].
Goodarzi et al. [189] proposed a new two-stage multi-inter-cooling ejector-expansion system transcritical CO2 refrigeration cycle, shown in Figure 19. This is a modified multi-inter-cooling configuration of the previously proposed cycle by Manjili and Yavari [190] with an ejector expansion system.
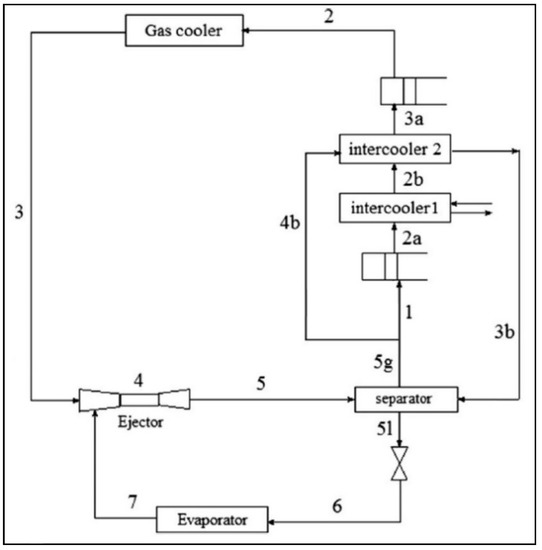
Figure 19.
Two-stage multi-inter-cooling transcritical EERC [189].
The second intercooler cools down the compressed refrigerant by extracting a saturated vapor flow from the separator. An internal heat exchanger inserted between the gas cooler and the ejector-expansion system may improve the coefficient of performance. A portion of the saturated vapor flow enters the internal heat exchanger before entering the first compressor and cools down the high-pressure liquid leaving gas cooler before entering the ejector. Theoretical analysis indicated that this configuration might operate more efficiently than the original cycle, more particularly at lower gas cooler pressures. This is an important advantage from the mechanical and metallurgical limitations point of view.
Other scenarios of two CO2 cascade layouts (Figure 20) theoretically evaluated by Yari and Mahmoudi [191], yielding COP values in the respective ranges of 10.8–17.2% and 18–31.5% compared to a reference cascade cycle.
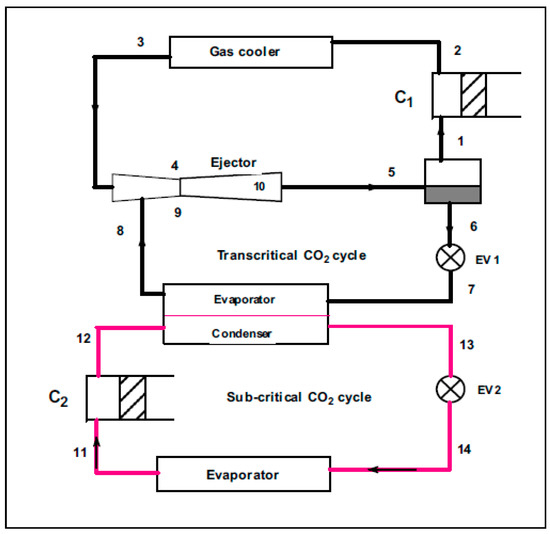
Figure 20.
Ejector-expansion based cascade refrigeration cycle layout [191].
Later studies of potentially interesting configurations with this refrigerant were proposed by Bai et al., and Dokandari et al. [192,193,194]. Energy and exergy analyses are increasingly used to theoretically investigate the effects of key parameters on the thermodynamic performance of the current and newly proposed cycles. Dokandari et al. [192] provided a detailed analysis of a CO2/NH3 cascade cycle based on the thermodynamics first and second laws. The results indicated that COP and second law efficiency of this system were found to be 5–7% higher on average than the conventional cycle and exergy destruction rates roughly 8% lower as compared to the conventional cycle.
Bai et al. [193,194] applied this approach to dual-evaporator transcritical CO2 refrigeration cycle with two-stage ejector and an ejector enhanced vapor injection transcritical CO2 heat pump cycle with sub-cooler, respectively. COP theoretical improvements over single ejector in CO2 dual-temperature refrigeration and conventional vapor injection heat pump cycles were respectively up to 37.61% and 7.7%.
A recent configuration with R290/R170 mixture for low-temperature applications was studied by Liu et al. [195] who proposed a dual ejector auto-cascade refrigeration cycle. A preliminary comparison was made with a conventional compression cascade and a single ejector cascade configuration, showing a significant potential for throttling losses recovery. More theoretical and experimental investigations need to be performed to pursue this research.
In addition to the importance of ejector design on cycle performance, evaporator design was theoretically shown to have a major importance in this respect by Lawrence and Elbel [196] in continuation of their previous experimental study. This new investigation concerned particularly the effect of microchannel heat exchangers design and operation of ejector assisted compressor refrigeration cycle in the context of the conventional EERC and the ejector recirculation cycle (ERC).
The analysis initiated by Hafner et al. [173] in the framework of supermarket applications had for objective to investigate the potential for a CO2 multi-ejector system and its comparison to a reference CO2 booster system. The analysis demonstrated that for different climatic conditions, efficiencies and capacities of a system layout with ejectors and heat recovery, relevant improvements of up to 30% could be expected (Figure 21).
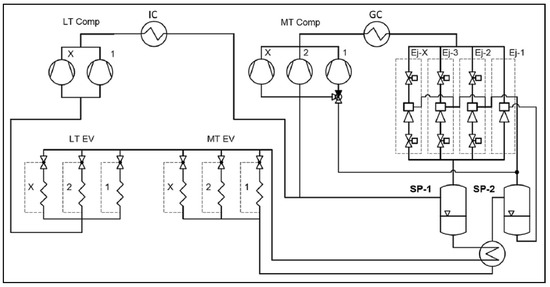
Figure 21.
Multi-ejector CO2 application in supermarkets [173].
Recently, Haida et al. [197] proposed a performance mapping of four CO2 ejectors installed in a multi-ejector module to be integrated with supermarket refrigeration systems. The proposed model was generated by use of experimental data together with CFD model results. The developed mapping allowed determining the motive nozzle mass flow rate, entrainment ratio, pressure lift and ejector efficiency at the operating conditions typical for supermarket refrigeration, air-conditioning and a heat pump system.
In order to improve performance of CO2 supermarket refrigeration systems in countries with higher ambient temperatures, Huang et al. [198] modified a conventional booster refrigeration system by means of two-phase ejector, which they simulated under various conditions. Results indicated potential efficiency improvements of up to 11% in COP when ambient temperature is high. At low ambient temperatures, performance decreased below that of the conventional booster.
Bodys et al. [199] investigated numerically different strategies to modify an existing CO2 refrigeration system for fishing vessels, to operate in warmer climates without the need for an additional compressor unit. Results showed the multi-ejector system is the only solution which ensures no necessity for an additional compressor in warmer climates while still maintaining the designed cooling capacity. In this approach, the ejectors are used as a booster for the parallel compressors. Some miscellaneous theoretical cycles of the two-phase ejector are summarized in Table 8.

Table 8.
Miscellaneous two-phase ejector applications (theoretical studies).
5.2.2. Experimental Studies
Man-O et al. [201] proposed to enhance the evaporation heat transfer in refrigeration cycle evaporators by means of two-phase ejectors. A two-phase ejector in this process plays the role of a vapour recirculator from outlet to inlet of the evaporator, increasing the vapor quality and the mass flow rate of refrigerant at the inlet. Experiments performed on plat-type evaporators with R404a increased refrigerant mass velocity, improved flow distribution and heat transfer. The authors reported more than 10% COP improvement as compared with the conventional cycle.
Dopazo and Fernández-Seara [82] considered the particular application of an ejector as a liquid circulator in an overfed NH3 plate evaporator. The system includes a liquid/vapor separator to separate the liquid and supply vapor to the compressor and saturated liquid to the evaporator by means of an ejector instead of the conventional feed pump. The liquid refrigerant fills the entire evaporator inner surface, thus improving the heat transfer coefficient with no electricity consumption associated with the pump. The experimental results obtained in this work confirm that an ejector linked to a manual expansion valve can be used as a liquid recirculator component in liquid overfeed systems with NH3, under different operating conditions and with variable refrigeration capacity. Feasibility tests on a cascade refrigeration system prototype showed recirculation rates between 2 and 4. The evaporating capacity varied from 9.48 kW to 18.37 kW, controlled by a valve located upstream of the ejector primary inlet.
Lawrence and Elbel [161] conducted an experimental investigation in which the performance of the low-pressure fluids R134a and R1234yf was compared in a two-phase ejector cycle and expansion valve cycles. To this end, an alternate two-phase ejector cycle, the condenser outlet split (COS) system configuration, in which the pressure lift provided by the ejector was utilized in order to provide multiple evaporation temperatures, was tested. Comparison was made with a single and a double evaporation temperature expansion valve cycle, respectively. The results showed that the ejector cycle maximum COP improvements were up to 12% with R1234yf and up to 8% with R134a with two valves. With one valve the comparison was 6% with R1234yf and 5% with R134a. A recent experimental investigation of Jeon et al. [202], on an R600a domestic refrigerator freezer with a COS ejector cycle, showed a COP improvement of 11.4% over the baseline cycle at an entrainment ratio of 0.18 (at similar cooling capacity condition).
Further investigations by Lawrence and Elbel [203] focused on investigating the liquid recirculation experimentally provided by using the ejector work recovery. In this way, and using R410A, liquid was recirculated through the evaporator, rather than unloading the compressor. Comparison was made with EERC and the conventional compression cycles, besides investigating the effects of evaporator geometry and ambient temperature on the performance of the cycles. The authors concluded that the ejector recirculation cycle was more favorable at lower ambient temperatures, while the standard ejector cycle is more favorable at higher ambient temperatures. In addition, performance improvement could be influenced the evaporator design as demonstrated in a further paper by the authors [204] where it was shown that COP improvement of up to 16% with the ejector recirculation cycle and 9% with the standard ejector cycle were obtained, but the COP of each cycle was very dependent on evaporator design.
Recently, Li et al. [83] tested a water chiller where the ejector worked as a liquid recirculation component in a horizontal-tube falling-film evaporator with R134a. The results showed a cooling capacity increase for the system up to 9.5%.
Bai et al. [205] tested an ejector-enhanced auto-cascade refrigeration cycle (Figure 22) with zeotropic refrigerant R134a/R23. Effects of working conditions and mass fraction ratio of the mixture on the performance were investigated. The results indicated that the cycle had more advantages in terms of lower refrigeration temperature and higher energy utilization efficiency over the conventional cycle. The COP and exergy efficiency improvements of the system over conventional cycle reached up to 9.6% and 25.1%, respectively. The mass fraction ratio of R23 significantly influences the system performance. The refrigerant R134a/R23 with the optimal mass fraction ratio of 0.70/0.30 was proposed to get the maximum system exergy efficiency.
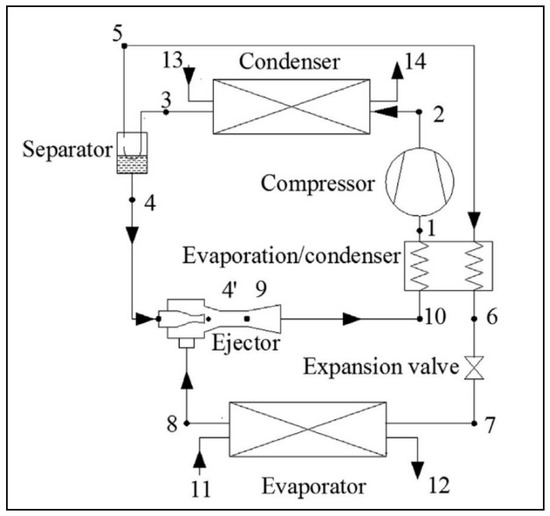
Figure 22.
Two-phase ejector auto-cascade refrigeration system [205].
Another potential use of ejectors is in the form of condensing ejector. Condensing ejectors can serve as heat transfer agents, and liquid pumps in many applications where an electric pump may be less suitable, as for example, solar activated absorption and ejection cycles. Smierciew et al. [200,206] performed experimentation on such a device represented in Figure 23, in terms of operation characteristics and internal heat transfer. Further tests and analysis with isobutane were reported in [207].
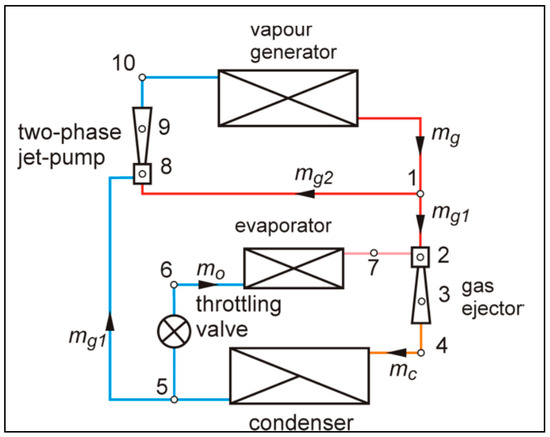
Figure 23.
Modified EERC system with two-phase injector [200].
Banasiak et al. [208] tested the concept of replacing a standard high-pressure expansion valve with a block of properly designed parallel ejectors for maintaining the discharge pressure in a R744 parallel-compression system of 70 kW at a 35 °C gas cooler outlet temperature and a 3 °C evaporation temperature. They demonstrated that the refrigeration system upgraded with the multi-ejector block fully retained its dynamic operational characteristics, and precise discharge pressure adaptations according to the variable load and ambient conditions are possible, even with the use of a simplified controlling strategy. Further details on a representative sample of these studies are given in Table 9.

Table 9.
Miscellaneous two-phase ejector applications (experimental studies).
6. General Remarks and Challenges
Previous ejector numerical investigations, irrespective of the ejector type have underlined the importance of the numerical role in ejector design and performance prediction accuracy. However, more needs to be done in this respect on two-phase ejectors.
For example, steam ejectors have until recently been treated as single-phase ejector cases and the possible condensation during the expansion and mixing process within the ejector was not taken into account, thus showing prediction discrepancies with the experimental results [125]. This particular aspect is included in the present review as a case of two-phase flow ejector for which some more recent work was devoted but more is needed, numerically to handle nucleation for a better physical approach, and experimentally with more refrigerants.
Droplet injection in the primary nozzle of an ejector is another two-phase process which should be handled as such. Al-Ansary and Jeter [125] and later Hemidi et al. [127] performed numerical and experimental studies to explore the potentially positive effects on ejector performance. The results were, however, not up to the expectations as was discussed in an earlier paragraph. Moreover, both research teams worked on air ejectors with water injection in the motive flow, a case not compatible with the refrigeration conditions. Very recently, an analytical model was developed for the purpose of injecting droplets of the same refrigerant at different locations in the mixing chamber but preliminary results seemed to reduce the compression effect [126]. This avenue thus remains an open question for future prospecting.
Numerical studies focusing on the details of local flow interactions and structure in two-phase ejectors are not yet widely available in the literature, due to the complexity of the task and the computational power required. In this context, the number of full numerical ejector studies is still very limited and the predictions often differ depending on the quality of the assumptions used and the model setup. In two-phase ejector CFD simulations, the information of the complex structure of the gas–liquid interface and the transfer mechanism require closure models. A lot of models exist in the literature, but a thorough evaluation on the effective use of these models for ejector flow, is still missing. Therefore, validation is critical. Ejector internal flow structure predictions in supersonic ejectors was shown to depend on the turbulence model used among other things even if good agreement was obtained in terms of global parameters [212,213] but no such information is yet available for two-phase case, neither numerically nor experimentally.
In addition, more investigation work is still needed to clarify the conditions under which homogeneous equilibrium model (HEM), homogeneous relaxation model (HRM) and non-equilibrium flow models can reliably be used [114,115].
The application of the second law, commonly encountered in many thermodynamic analyses of ejector-based cycles and more particularly in the assessment of carbon dioxide transcritical EERCs raises the issue of a common reference temperature, which may sometimes be different from one author to another. If not clearly stated, it makes comparisons difficult between different works [178,191].
Little numerical and experimental work is available to reflect the dynamic behavior of a system fluctuating between on-design and off-design operating conditions. This issue concerns both single-phase and two-phase ejector-based cycles where full interaction between components must be accounted for as rightly pointed out by some works [214,215]. Under these conditions component efficiencies are variable and do not correctly predict the system condition [152].
7. Conclusions
Two-phase ejectors are used for vacuum creation, fluid circulation and many other industrial applications but the refrigeration and heat pump area has been the most prominent in terms of scientific investigations on these devices. An ejector-based cycle allows for expansion work recovery, otherwise lost in the throttling valve of the conventional cycle. Such a device offers good opportunities to build new, more efficient and less energy demanding cycles than current configurations.
The proposed review updates the existing research background on the subject by discussing relevant and most recent material. Representative and recent developments in two-phase ejector modeling, integration in refrigeration cycles and in other potential applications are introduced and discussed in their particular context. Issues of the day about the different types of two-phase ejectors are reported. They include the modeling, design and experimentation of ejectors and corresponding cycles with a special focus on new developments.
The structure of the document follows approximately the format adopted in Part 1. The ejector in its different options is presented with its geometry configurations and operational characteristics in detail. Next, starting from an overview of general applications, the focus is then put on refrigeration and heat pumps with the cycle description and studies, both theoretical and experimental.
The review document organizes the information in specific paragraphs for each key aspect:
A general introduction of the context of ejector development and early work achievements is followed by a detailed description of ejector types, geometry, performance, internal flow structure and applications.
The two-phase ejector modeling in terms of analytical, thermodynamic and numerical procedures applied where appropriate, are discussed in the context of applications to refrigeration, heat pumps and accessorily other application types. To support the theoretical modeling work, experimental work about two-phase ejectors are presented.
Finally, a review of theoretical and experimental studies of two-phase ejector cycles and systems is made, followed by some comment about future works and challenges.
Funding
This research was funded by PERD, a program of Natural Resources Canada for R&D.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviation
| A | area |
| CAM | Constant Area Mixing |
| CFD | Computational Fluid Dynamics |
| COP | Coefficient of performance |
| CPM | Constant Pressure Mixing |
| D | diameter |
| EERC | Ejector Expansion Refrigeration Cycle |
| ERC | Ejector recirculation cycle |
| ERS | Ejector Refrigeration System |
| G | mass flow rate |
| h | enthalpy |
| HEM | Homogeneous Equilibrium Model |
| HRM | Homogenous Relaxation Model |
| IHE | Isentropic Homogeneous Equilibrium |
| IHX | Internal Heat Exchanger |
| L | length |
| mass flow rate | |
| NXP | nozzle exit position |
| P | pressure |
| PIV | Particle Image Velocimetry |
| Q | capacity |
| T | temperature |
| W | energy consumption |
| Greek | |
| x | vapor quality |
| α | nozzle convergent angle |
| β | nozzle divergent angle |
| Δ | difference; improvement |
| η | diffuser angle; efficiency |
| θ | nozzle area ratio |
| ξ | exergy efficiency |
| ρ | density |
| ς | entropy increase avoided |
| τ | compression ratio |
| ϕ | area ratio |
| φ | mixing convergent angle |
| ω | entrainment ratio |
| exergy flow rate | |
| Subscripts | |
| 0 | stagnation |
| amb | ambient |
| b | back |
| c | condenser |
| com | compressor |
| dif | diffuser |
| e | evaporator |
| ej | ejector |
| gc | gas cooler |
| m | mixing |
| n | nozzle |
| p | primary |
| ref | reference |
| s | secondary |
| sub | sub-cooling |
| sup | superheating |
| t | throat |
| w | water |
| x | nozzle outlet |
References
- Elbel, S.; Hrnjak, P. Ejector Refrigeration: An Overview of Historical and Present Developments with an Emphasis on Air-Conditioning Applications. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 14–17 July 2008; p. 884. [Google Scholar]
- Kumar, R.S.; Kumaraswamy, S.; Mani, A. Experimental investigations on a two-phase jet pump used in desalination systems. Desalination 2007, 204, 437–447. [Google Scholar] [CrossRef]
- Sumeru, K.; Nasution, H.; Ani, F.N. A review on two-phase ejector as an expansion device in vapor compression refrigeration cycle. Renew. Sustain. Energy Rev. 2012, 16, 4927–4937. [Google Scholar] [CrossRef]
- Li, Y.; Tan, L.; Zhang, X.; Du, K. Experimental evaluation of an ejector as liquid re-circulator in a falling-film water chiller. Int. J. Refrig. 2014, 40, 309–316. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 53, 373–407. [Google Scholar] [CrossRef]
- Sarkar, J. Review on Cycle Modifications of Transcritical CO2 Refrigeration and Heat Pump Systems. J. Adv. Res. Mech. Eng. 2010, 1, 22–29. [Google Scholar]
- Elbel, S. Historical and present developments of ejector refrigeration systems with emphasis on transcritical carbon dioxide air-conditioning applications. Int. J. Refrig. 2011, 34, 1545–1561. [Google Scholar] [CrossRef]
- Sarkar, J. Ejector enhanced vapor compression refrigeration and heat pump systems—A review. Renew. Sustain. Energy Rev. 2012, 16, 6647–6659. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A.; Palacz, M. State of the Art in Identification of Two-Phase Transonic Flow Phenomena in Transcritical CO2 Ejectors. In Proceedings of the ICR 2015, Yokohama, Japan, 16–22 August 2015. [Google Scholar]
- Elbel, S.; Lawrence, N. Review of recent developments in advanced ejector technology. Int. J. Refrig. 2016, 62, 1–18. [Google Scholar] [CrossRef]
- Besagni, G. Ejectors on the cutting edge: The past, the present and the perspective. Energy 2019, 170, 998–1003. [Google Scholar] [CrossRef]
- Yazdani, M.; Alahyari, A.A.; Radcliff, T.D. Numerical modeling of two-phase supersonic ejectors for work-recovery applications. Int. J. Heat Mass Transf. 2012, 55, 5744–5753. [Google Scholar] [CrossRef]
- Colarossi, M.; Trask, N.; Schmidt, D.P.; Bergander, M.J. Multidimensional modeling of condensing two-phase ejector flow. Int. J. Refrig. 2012, 35, 290–299. [Google Scholar] [CrossRef]
- Miwa, S.; Endo, H.; Moribe, T.; Sakashita, H.; Mori, M.; Hibiki, T. Investigation of the thermal-hydraulic characteristics of supersonic steam injector. Appl. Therm. Eng. 2016, 109, 261–271. [Google Scholar] [CrossRef]
- Butrymowicz, D.; Matysko, R.; Angielczyk, W.; Trela, M.; Bergander, M. Model of steam-water injector. In Proceedings of the International Seminar on Ejector/Jet-Pump Technology and Application, Louvain-la-Neuve, Belgium, 7–9 September 2009; p. 27. [Google Scholar]
- Lawrence, N.; Elbel, S. Mathematical modeling and thermodynamic investigation of the use of two-phase ejectors for work recovery and liquid recirculation in refrigeration cycles. Int. J. Refrig. 2015, 58, 41–52. [Google Scholar] [CrossRef]
- Sarevski, M.N.; Sarevski, V.N. Characteristics of R718 refrigeration/heat pump systems with two-phase ejectors. Int. J. Refrig. 2016, 70, 13–32. [Google Scholar] [CrossRef]
- Ameur, K.; Aidoun, Z.; Ouzzane, M. Analysis of the Critical Conditions and the Effect of Slip in Two-Phase Ejectors. JAFM 2016, 9, 213–222. [Google Scholar]
- Narabayashi, T.; Mizumachi, W.; Mori, M. Study on two-phase flow dynamics in steam injectors. Nucl. Eng. Des. 1997, 175, 147–156. [Google Scholar] [CrossRef]
- Trela, M.; Kwidzinski, R.; Butrymowicz, D.; Karwacki, J. Exergy analysis of two-phase steam-water injector. Appl. Therm. Eng. 2010, 30, 340–346. [Google Scholar] [CrossRef]
- Deberne, N.; Leone, J.F.; Duque, A.; Lallemand, A. A model for calculation of steam injector performance. Int. J. Multiph. Flow 1999, 25, 841–855. [Google Scholar] [CrossRef]
- Takeya, Y.; Miwa, S.; Hibiki, T.; Mori, M. Application of steam injector to improved safety of light water reactors. Prog. Nucl. Energy 2015, 78, 80–100. [Google Scholar] [CrossRef]
- Miwa, S.; Endo, H.; Moribe, T.; Mori, M. Investigation of the supersonic steam injector operation mode. Nucl. Eng. Des. 2018, 334, 57–65. [Google Scholar] [CrossRef]
- Bergander, M. Refrigeration cycle with two-phase condensing ejector. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 17–20 July 2006; p. 748. [Google Scholar]
- Ameur, K.; Aidoun, Z.; Ouzzane, M. Modeling and numerical approach for the design and operation of two-phase ejectors. Appl. Therm. Eng. 2016, 109, 809–818. [Google Scholar] [CrossRef]
- Keenan, J.H.; Neumann, E.P.; Lustwerk, F. An investigation of ejector design by analysis and experiment. J. Appl. Mech. 1950, 72, 299–309. [Google Scholar]
- Atmaca, A.U.; Erek, A.; Ekren, O. Impact of the mixing theories on the performance of ejector expansion refrigeration cycles for environmentally-friendly refrigerants. Int. J. Refrig. 2019, 97, 211–225. [Google Scholar] [CrossRef]
- Liu, F.; Groll, E.A.; Li, D. Investigation on performance of variable geometry ejectors for CO2 refrigeration cycles. Energy 2012, 45, 829–839. [Google Scholar] [CrossRef]
- Hu, J.; Shi, J.; Liang, Y.; Yang, Z.; Chen, J. Numerical and experimental investigation on nozzle parameters for R410A ejector air conditioning system. Int. J. Refrig. 2014, 40, 338–346. [Google Scholar] [CrossRef]
- Wang, X.; Yu, J. Experimental investigation on two-phase driven ejector performance in a novel ejector enhanced refrigeration system. Energy Convers. Manag. 2016, 111, 391–400. [Google Scholar] [CrossRef]
- Ameur, K.; Aidoun, Z. Nozzle displacement effects on two-phase ejector performance: An experimental study. JAFM 2018, 11, 1–8. [Google Scholar] [CrossRef]
- Nehdi, E.; Kairouani, L.; Bouzaina, M. Performance analysis of the vapour compression cycle using ejector as an expander. Int. J. Energy Res. 2007, 31, 364–375. [Google Scholar] [CrossRef]
- Sarkar, J. Geometric parameter optimization of ejector-expansion refrigeration cycle with natural refrigerants. Int. J. Energy Res. 2010, 34, 84–94. [Google Scholar] [CrossRef]
- Nakagawa, M.; Marasigan, A.R.; Matsukawa, T. Experimental analysis of two-phase ejector system with varying mixing cross-sectional area using natural refrigerant CO2. Int. J. Air-Cond. Refrig. 2010, 18, 297–307. [Google Scholar] [CrossRef]
- Nakagawa, M.; Matumi, T.; Takeuchi, H.; Kokubo, N. Mixing of the Confined Jet of Mist Flow. JSME Int. J. 1996, 39, 381–386. [Google Scholar] [CrossRef]
- Nakagawa, M.; Marasigan, A.R.; Matsukawa, T.; Kurashina, A. Experimental investigation on the effect of mixing length on the performance of two-phase ejector for CO2 refrigeration cycle with and without heat exchanger. Int. J. Refrig. 2011, 34, 1604–1613. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A.; Andresen, T. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump. Int. J. Refrig. 2012, 35, 1617–1625. [Google Scholar] [CrossRef]
- Jeon, Y.; Jung, J.; Kim, D.; Kim, S.; Kim, Y. Effects of ejector geometries on performance of ejector-expansion R410A air conditioner considering cooling seasonal performance factor. Appl. Energy 2017, 205, 761–768. [Google Scholar] [CrossRef]
- Randheer, Y.L.; Patwardhan, A.W. Design aspects of ejectors: Effects of suction chamber geometry. Chem. Eng. Sci. 2008, 63, 3886–3897. [Google Scholar]
- Li, C.; Li, Y.; Wang, L. Configuration dependence and optimization of the entrainment performance for gas-gas and gas-liquid ejectors. Appl. Therm. Eng. 2012, 48, 237–248. [Google Scholar] [CrossRef]
- Nakagawa, M.; Berana, M.S.; Kishine, A. Supersonic two-phase flow of CO2 through converging–diverging nozzles for the ejector refrigeration cycle. Int. J. Refrig. 2009, 32, 1195–1202. [Google Scholar] [CrossRef]
- He, Y.; Deng, J.; Zheng, L.; Zhang, Z. Performance optimization of a transcritical CO2 refrigeration system using a controlled ejector. Int. J. Refrig. 2017, 75, 250–261. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, X.; Yu, J. Theoretical study on a novel dual-nozzle ejector enhanced refrigeration cycle for household refrigerator-freezers. Energy Convers. Manag. 2013, 73, 278–284. [Google Scholar] [CrossRef]
- Bodys, J.; Smolka, J.; Banasiak, K.; Palacz, M.; Haida, M.; Nowak, A.J. Performance improvement of the R744 two-phase ejector with an implemented suction nozzle bypass. Int. J. Refrig. 2018, 90, 216–228. [Google Scholar] [CrossRef]
- Disawas, S.; Wongwises, S. Experimental investigation on the performance of the refrigeration cycle using a two-phase ejector as an expansion device. Int. J. Refrig. 2004, 27, 587–594. [Google Scholar] [CrossRef]
- Ameur, K.; Aidoun, Z.; Ouzzane, M. Experimental performances of a two-phase R134a ejector. Exp. Therm. Fluid Sci. 2018, 97, 12–20. [Google Scholar] [CrossRef]
- Lawrence, N.; Elbel, S. Analysis of two-phase ejector performance metrics and comparison of R134a and CO2 ejector performance. Sci. Technol. Built Environ. 2015, 21, 515–525. [Google Scholar] [CrossRef]
- Elbel, S.; Hrnjak, P. Experimental validation of a prototype ejector designed to reduce throttling losses encountered in transcritical R744 system operation. Int. J. Refrig. 2008, 31, 411–422. [Google Scholar] [CrossRef]
- Koehler, J.; Richter, C.; Tegethoff, W.; Tischendorf, C. Experimental and theoretical study of a CO2 ejector refrigeration cycle. In Proceedings of the VDA Alternative Refrigerant Winter Meeting, Saalfelden, Austria, 13–14 February 2007. [Google Scholar]
- Ersoy, H.K.; Bilir, N. The influence of ejector component efficiencies on performance of ejector expander refrigeration cycle and exergy analysis. Int. J. Exergy 2010, 7, 425–438. [Google Scholar] [CrossRef]
- Liu, F.; Groll, E.A.; Li, D. Modeling study of an ejector expansion residential CO2 air conditioning system. Energy Build. 2012, 53, 127–136. [Google Scholar] [CrossRef]
- Liu, F.; Groll, E.A. Study of ejector efficiencies in refrigeration cycles. Appl. Therm. Eng. 2013, 52, 360–370. [Google Scholar] [CrossRef]
- Wang, X.; Yu, J. An investigation on the component efficiencies of a small two-phase ejector. Int. J. Refrig. 2016, 71, 26–38. [Google Scholar] [CrossRef]
- Banasiak, K.; Palacz, M.; Hafner, A.; Bulinski, Z.; Smołka, J.; Nowak, A.J.; Fic, A. A CFD-based investigation of the energy performance of two-phase R744 ejectors to recover the expansion work in refrigeration systems: An irreversibility analysis. Int. J. Refrig. 2014, 40, 328–337. [Google Scholar] [CrossRef]
- Bilir Sag, N.; Ersoy, H.K.; Hepbasli, A.; Halkaci, H.S. Energetic and exergetic comparison of basic and ejector expander refrigeration systems operating under the same external conditions and cooling capacities. Energy Convers. Manag. 2015, 90, 184–194. [Google Scholar] [CrossRef]
- Bullard, C.W. Internal heat exchange, expanders and intercooling in trans-critical CO2 cycles. In Proceedings of the 6 th IIR Gustav Lorentzen Conference on Natural Refrigerants, Glasgow, UK, 2004. [Google Scholar]
- Takashima, Y. Studies on liquid-jet gas pumps. J. Sci. Res. Inst. 1952, 46, 230–246. [Google Scholar]
- Simoes-Moreira, J.R.; Vieira, M.M.; Angelo, E. Highly Expanded Flashing Liquid Jets. J. Thermophys. Heat Transf. 2002, 16, 415–424. [Google Scholar]
- Berana, M.S.; Nakagawa, M.; Harada, A. Shock waves in supersonic two-phase flow of CO2 in Converging-Diverging Nozzles. HVAC R Res. 2009, 15, 1081–1098. [Google Scholar] [CrossRef]
- Ohira, K.; Nakayama, T.; Nagai, T. Cavitation flow instability of subcooled liquid nitrogen in converging–diverging nozzles. Cryogenics 2012, 52, 35–44. [Google Scholar] [CrossRef]
- Kim, Y.K.; Lee, D.Y.; Kim, H.D.; Ahn, J.H.; Kim, K.C. An experimental and numerical study on hydrodynamic characteristics of horizontal annular type water-air ejector. J. Mech. Sci. Technol. 2012, 26, 2773–2781. [Google Scholar] [CrossRef]
- Kwidzinski, R. Experimental investigation of condensation wave structure in steam-water injector. Int. J. Heat Mass Transf. 2015, 91, 594–601. [Google Scholar] [CrossRef]
- Choi, S.H.; Ji, H.S.; Kim, K.C. Comparative study of hydrodynamic characteristics with respect to direction of installation of gas-liquid ejector system. J. Mech. Sci. Technol. 2015, 29, 3267–3276. [Google Scholar] [CrossRef]
- Little, A.B.; Garimella, S. Shadowgraph visualization of condensing R134a flow through ejectors. Int. J. Refrig. 2016, 68, 118–129. [Google Scholar] [CrossRef]
- Elbel, S.; Hrnjak, P. Experimental validation of a CO2 prototype ejector with integrated high-side pressure control. In Proceedings of the VDA Alternative Refrigerant Winter Meeting, Saalfelden, Austria, 13–14 February 2007. [Google Scholar]
- Deng, J.; Zhang, Y.; He, Y.; Zheng, L. Visual investigation on effect of structural parameters and operation condition of two-phase ejector. In Proceedings of the International Compressor Engineering, Refrigeration and Air Conditioning, and High Performance Buildings Conferences, West Lafayette, IN, USA, 11–14 July 2016; p. 1632. [Google Scholar]
- Zhu, Y.; Wang, Z.; Yang, Y.; Jiang, P. Flow visualization of supersonic two-phase transcritical flow of CO2 in an ejector of a refrigeration system. Int. J. Refrig. 2017, 74, 354–361. [Google Scholar] [CrossRef]
- Barrault, É. Histoire d’une grande invention, l’éjecteur Giffard. In La Nature; Masson, G., Ed.; La Nature: Paris, France, 1882; pp. 65–70. [Google Scholar]
- Kim, M.; Sohn, Y.; Cho, C.; Lee, W.; Kim, C. Customized design for the ejector to recirculate a humidified hydrogen fuel in a submarine PEMFC. J. Power Sources 2008, 176, 529–533. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Zhou, D.; Zhang, H.; Weng, S. Control strategy design for a SOFC-GT hybrid system equipped with anode and cathode recirculation ejectors. Appl. Therm. Eng. 2018, 132, 67–79. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, L.; Zhang, H.; Wang, Z. Numerical and experimental investigation of performance of the liquid-gas and liquid jet pumps in desalination systems. Desalination 2011, 276, 89–95. [Google Scholar] [CrossRef]
- Song, X.; Cao, M.; Shin, W.; Cao, W.; Kang, S.; Park, Y. Numerical investigation of a liquid-gas ejector used for shipping ballast water treatment. Math. Probl. Eng. 2014, 2014, 259593. [Google Scholar] [CrossRef]
- Borovykh, A.E. Calculation of the parameters of evacuation systems for tanks with a liquid-gas ejector. Chem. Pet. Eng. 1993, 29, 269–270. [Google Scholar] [CrossRef]
- Opletal, M.; Novotný, P.; Linek, V.; Moucha, T.; Kordač, M. Gas suction and mass transfer in gas-liquid up-flow ejector loop reactors. Effect of nozzle and ejector geometry. Chem. Eng. J. 2018, 353, 436–452. [Google Scholar] [CrossRef]
- Kim, M.I.; Sin Kim, O.; Lee, D.H.; Done Kim, S. Numerical and experimental investigations of gas-liquid dispersion in an ejector. Chem. Eng. Sci. 2007, 62, 7133–7139. [Google Scholar] [CrossRef]
- Kandakure, M.T.; Gaikar, V.G.; Patwardhan, A.W. Hydrodynamic aspects of ejectors. Chem. Eng. Sci. 2005, 60, 6391–6402. [Google Scholar] [CrossRef]
- Balamurugan, S.; Gaikar, V.G.; Patwardhan, A.W. Effect of ejector configuration on hydrodynamic characteristics of gas-liquid ejectors. Chem. Eng. Sci. 2008, 63, 721–731. [Google Scholar] [CrossRef]
- Abe, Y.; Shibayama, S. Study on the characteristics of the supersonic steam injector. Nucl. Eng. Des. 2014, 268, 191–202. [Google Scholar] [CrossRef]
- Kemper, C.A.; Harper, G.F.; Brown, G.A. Multiple-Phase Ejectors Refrigerating System. U.S. Patent 3,277,660, 11 October 1966. [Google Scholar]
- Menegay, P.; Kornhauser, A.A. Improvements to the ejector expansion refrigeration cycle. In Proceedings of the 31st Intersociety Energy Conversion Engineering Conference, IECEC 96, Washington, DC, USA, 11–16 August 1996. [Google Scholar]
- Boccardi, G.; Botticella, F.; Lillo, G.; Mastrullo, R.; Mauro, A.W.; Trinchieri, R. Experimental investigation on the performance of a transcritical CO2 heat pump with multi-ejector expansion system. Int. J. Refrig. 2017, 82, 389–400. [Google Scholar] [CrossRef]
- Dopazo, J.A.; Fernández-Seara, J. Experimental evaluation of an ejector as liquid re-circulator in an overfeed NH3 system with a plate evaporator. Int. J. Refrig. 2011, 34, 1676–1683. [Google Scholar] [CrossRef]
- Li, Y.L.; Wang, K.; Wu, W.; Xia, X.Y.; Niu, B.L.; Zhang, Z. Bin Investigation on the effect of ejector liquid recirculation system on the performance of falling-film water chiller with R134a. Int. J. Refrig. 2017, 74, 333–344. [Google Scholar] [CrossRef]
- Oshitani, H.; Oshitani, H.; Yamanaka, Y.; Takeuchi, H.; Kusano, K.; Ikegami, M.; Aikawa, Y. Ejector Cycle Having Multiple Evaporators. U.S. Patent 20050178150A1, 18 August 2005. [Google Scholar]
- Burk, R.; Dürr, G.; Feuerecker, G.; Feuerecker, G.; Kohl, M.; Manski, R.; Strauss, T. Device for Automotive Air Conditioning. European Patent EP1719650A1, 8 November 2006. [Google Scholar]
- Hassanain, M.; Elgendy, E.; Fatouh, M. Ejector expansion refrigeration system: Ejector design and performance evaluation. Int. J. Refrig. 2015, 58, 1–13. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Theoretical model of transcritical CO2 ejector with non-equilibrium phase change correlation. Int. J. Refrig. 2018, 86, 218–227. [Google Scholar] [CrossRef]
- Baek, S.; Ko, S.; Song, S.; Ryu, S. Numerical study of high-speed two-phase ejector performance with R134a refrigerant. Int. J. Heat Mass Transf. 2018, 126, 1071–1082. [Google Scholar] [CrossRef]
- Zheng, P.; Li, B.; Qin, J. CFD simulation of two-phase ejector performance influenced by different operation conditions. Energy 2018, 155, 1129–1145. [Google Scholar] [CrossRef]
- Starkman, E.S.; Schrock, V.E.; Neusen, K.F.; Maneely, D.J. Expansion of a Very Low Quality Two-Phase Fluid Through a Convergent-Divergent Nozzle. J. Basic Eng. 1964, 86, 247–254. [Google Scholar] [CrossRef]
- Abuaf, N.; Jones, O.C.; Wu, B.J.C. Critical Flashing Flows in Nozzles with Subcooled Inlet Conditions. J. Heat Transf. 1983, 105, 379–383. [Google Scholar] [CrossRef]
- Kim, Y.S. Overview of geometrical effects on the critical flow rate of sub-cooled and saturated water. Ann. Nucl. Energy 2015, 76, 12–18. [Google Scholar] [CrossRef]
- Ameur, K.; Aidoun, Z.; Ouzzane, M. Expansion of subcooled refrigerant in two-phase ejectors with no flux induction. Exp. Therm. Fluid Sci. 2017, 82, 424–432. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Chen, Z. Critical flashing flow in convergent-divergent nozzles with initially subcooled liquid. Int. J. Therm. Sci. 2008, 47, 1069–1076. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A. Mathematical modelling of supersonic two-phase R744 fl ows through converging e diverging nozzles: The effects of phase transition models. Appl. Therm. Eng. 2013, 51, 635–643. [Google Scholar] [CrossRef]
- Kong, N.; Qi, Z. Influence of speed of sound in two-phase region on 1-D ejector performance modelling. Appl. Therm. Eng. 2018, 139, 352–355. [Google Scholar] [CrossRef]
- Kornhauser, A.A. The Use of an Ejector as a Refrigerant Expander. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 17–20 July 1990; p. 82. [Google Scholar]
- Al-Ansary, H.; Jeter, S. Development of a simple homogeneous flow model of a two-phase ejector. In Proceedings of the 34th Intersociety Energy Conversion Engineering Conference, Vancouver, BC, Canada, 2–5 August 1999; p. 2698. [Google Scholar]
- Elbel, S.; Hrnjak, P.S. Effect of Internal Heat Exchanger on Performance of Transcritical CO2 Systems with Ejector. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 12–15 July 2004; p. 708. [Google Scholar]
- Li, D.; Groll, E.A. Transcritical CO2 Refrigeration Cycle with Ejector-Expansion Device. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 12–15 July 2004; p. 707. [Google Scholar]
- Lawrence, N.; Elbel, S. Experimental and Analytical Investigation of Automotive Ejector Air-Conditioning Cycles Using Low-Pressure Refrigerants. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 16–19 July 2012; p. 116. [Google Scholar]
- Menegay, P.; Kornhauser, A. Ejector expansion refrigeration cycle with underexpanded motive nozzle. In Proceedings of the Intersociety Energy Conversion Engineering Conference, Monterey, CA, USA, 7–12 August 1994; pp. 915–920. [Google Scholar]
- Liu, F.; Groll, E.A. Analysis of a Two Phase Flow Ejector For Transcritical CO2 Cycle. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 14–17 July 2008; p. 924. [Google Scholar]
- Attou, A.; Seynhaeve, J.M. Steady-state critical two-phase flashing flow with possible multiple choking phenomenon Part 1: Physical modelling and numerical procedure. J. Loss Prev. Process Ind. 1999, 12, 335–345. [Google Scholar] [CrossRef]
- Owen, I.; Abdul-Ghani, A.; Amini, A.M. Diffusing a Homogenized Two-Phase. Int. J. Multiph. Flow 1992, 18, 531–540. [Google Scholar] [CrossRef]
- Kwidziński, R. Control-volume-based model of the steam-water injector flow. Arch. Thermodyn. 2010, 31, 45–59. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A. 1D Computational model of a two-phase R744 ejector for expansion work recovery. Int. J. Therm. Sci. 2011, 50, 2235–2247. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. Possibilities and limitations of CFD simulation for flashing flow scenarios in nuclear applications. Energies 2017, 10, 139. [Google Scholar] [CrossRef]
- Mazzelli, F.; Giacomelli, F.; Milazzo, A. CFD modelling of the condensation inside a Supersonic Nozzle: Implementing customized wet-steam model in commercial codes. Energy Procedia 2017, 126, 34–41. [Google Scholar]
- Bulinski, Z.; Smolka, J.; Fic, A.; Banasiak, K.; Nowak, A.J. A comparison of heterogenous and homogenous models of two-phase transonic compressible CO2 flow through a heat pump ejector. IOP Conf. Ser. Mater. Sci. Eng. 2010, 10, 012019. [Google Scholar] [CrossRef]
- Yazdani, M.; Alahyari, A.A.; Radcliff, T.D. Numerical Modeling and Validation of Supersonic Two-Phase Flow of CO2 in Converging-Diverging Nozzles. J. Fluids Eng. 2014, 136, 14503. [Google Scholar] [CrossRef]
- Smolka, J.; Bulinski, Z.; Fic, A.; Nowak, A.J.; Banasiak, K.; Hafner, A. A computational model of a transcritical R744 ejector based on a homogeneous real fluid approach. Appl. Math. Model. 2013, 37, 1208–1224. [Google Scholar] [CrossRef]
- Lucas, C.; Rusche, H.; Schroeder, A.; Koehler, J. Numerical investigation of a two-phase CO2 ejector. Int. J. Refrig. 2014, 43, 154–166. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Fic, A.; Bulinski, Z.; Nowak, A.J.; Banasiak, K.; Hafner, A. Application range of the HEM approach for CO2 expansion inside two-phase ejectors for supermarket refrigeration systems. Int. J. Refrig. 2015, 59, 251–258. [Google Scholar] [CrossRef]
- Haida, M.; Smolka, J.; Hafner, A.; Palacz, M.; Banasiak, K.; Nowak, A.J. Modified homogeneous relaxation model for the R744 trans-critical flow in a two-phase ejector. Int. J. Refrig. 2018, 85, 314–333. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Nowak, A.J.; Banasiak, K.; Hafner, A. Shape optimisation of a two-phase ejector for CO2 refrigeration systems. Int. J. Refrig. 2017, 74, 212–223. [Google Scholar] [CrossRef]
- Haida, M.; Smolka, J.; Hafner, A.; Mastrowski, M.; Palacz, M.; Madsen, K.B.; Nowak, A.J.; Banasiak, K. Numerical investigation of heat transfer in a CO2 two-phase ejector. Energy 2018, 163, 682–698. [Google Scholar] [CrossRef]
- Mikasser, S. Transfert de Masse et de Chaleur dans les Injecteurs-Condenseurs. Ph.D. Thesis, Institut National des Sciences Appliquées de Lyon, Villeurbanne, France, 2004. [Google Scholar]
- Teymourtash, A.R.; Esfahani, J.A.; Mousavi Shaegh, S.A. The effects of rate of expansion and injection of water droplets on the entropy generation of nucleating steam flow in a Laval nozzle. Heat Mass Transf. 2009, 45, 1185–1198. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, S.; Kong, T.; Zhang, K. Numerical investigation of homogeneous nucleation and shock effect in high-speed transonic steam flow. Heat Transf. Eng. 2010, 31, 1007–1014. [Google Scholar] [CrossRef]
- Grazzini, G.; Milazzo, A.; Piazzini, S. Prediction of condensation in steam ejector for a refrigeration system. Int. J. Refrig. 2011, 34, 1641–1648. [Google Scholar] [CrossRef]
- Wang, X.D.; Dong, J.L.; Wang, T.; Tu, J.Y. Numerical analysis of spontaneously condensing phenomena in nozzle of steam-jet vacuum pump. Vacuum 2012, 86, 861–866. [Google Scholar] [CrossRef]
- Ariafar, K.; Buttsworth, D.; Sharifi, N.; Malpress, R. Ejector primary nozzle steam condensation: Area ratio effects and mixing layer development. Appl. Therm. Eng. 2014, 71, 519–527. [Google Scholar] [CrossRef]
- Little, A.B.; Garimella, S. A critical review linking ejector flow phenomena with component- and system-level performance. Int. J. Refrig. 2016, 70, 243–268. [Google Scholar] [CrossRef]
- Al-Ansary, H.A.M.; Jeter, S.M. Numerical and experimental analysis of single-phase and two-phase flow in ejectors. HVAC&R Res. 2004, 10, 521–538. [Google Scholar]
- Croquer, S. Combined CFD and Thermodynamic Analysis of a Supersonic Ejector with Liquid Droplets. Ph.D. Thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, 2018. [Google Scholar]
- Hemidi, A.; Henry, F.; Leclaire, S.; Seynhaeve, J.-M.; Bartosiewicz, Y. CFD analysis of a supersonic air ejector. Part I: Experimental validation of single-phase and two-phase operation. Appl. Therm. Eng. 2009, 29, 1523–1531. [Google Scholar] [CrossRef]
- Nakagawa, M.; Berana, M.S.; Harada, A. Shock Waves in Supersonic Two-Phase Flow of CO2 in Converging-Diverging Nozzles. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 14–17 July 2008; p. 926. [Google Scholar]
- Kim, K.C.; Kim, H.D.; Kim, Y.K.; Ahn, J.H. Numerical simulation and experimental study on a water-air ejector system for VOC recovery. In Proceedings of the 12th International Conference on Multiphase Flow in Industrial Plants, Napoli, Italy, 21–23 September 2011. [Google Scholar]
- Butrymowicz, D.; Karwacki, J.; Miaskowska, D.; Trela, M. Performance of two-phase ejector of various geometries. In Proceedings of the International Congress of Refrigeration, Beijing, China, 21–26 August 2007. [Google Scholar]
- Smolka, J.; Palacz, M.; Bodys, J.; Banasiak, K.; Fic, A.; Bulinski, Z.; Nowak, A.J.; Hafner, A. Performance comparison of fixed- and controllable-geometry ejectors in a CO2 refrigeration system. Int. J. Refrig. 2016, 65, 172–182. [Google Scholar] [CrossRef]
- Zhu, J.; Elbel, S. Experimental investigation of a novel expansion device control mechanism: Vortex control of initially subcooled flashing R134a flow expanded through convergent-divergent nozzles. Int. J. Refrig. 2018, 85, 167–183. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, Y.; Li, C.; Zhang, F.; Jiang, P.X. Experimental investigation on the performance of transcritical CO2 ejector-expansion heat pump water heater system. Energy Convers. Manag. 2018, 167, 147–155. [Google Scholar] [CrossRef]
- Pottker, G.; Hrnjak, P. Ejector in R410A vapor compression systems with experimental quantification of two major mechanisms of performance improvement: Work recovery and liquid feeding. Int. J. Refrig. 2015, 50, 184–192. [Google Scholar] [CrossRef]
- Lawrence, N.; Elbel, S. Theoretical and practical comparison of two-phase ejector refrigeration cycles including First and Second Law analysis. Int. J. Refrig. 2013, 36, 1220–1232. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.N.N.; Machado, L. Thermo-economic analysis and sizing of the components of an ejector expansion refrigeration system. Int. J. Refrig. 2018, 86, 463–479. [Google Scholar] [CrossRef]
- Sarkar, J. Performance characteristics of natural-refrigerants-based ejector expansion refrigeration cycles. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 543–550. [Google Scholar] [CrossRef]
- Domanski, P.A. Minimizing Throttling Losses in the Refrigeration Cycle. In Proceedings of the 19th International Congress of Refrigeration, The Hague, The Netherlands, 20–25 August 1995. [Google Scholar]
- Bilir, N.; Ersoy, H.K. Performance improvement of the vapour compression refrigeration cycle by a two-phase constant area ejector. Int. J. Energy Res. 2009, 33, 469–480. [Google Scholar] [CrossRef]
- Li, H.; Cao, F.; Bu, X.; Wang, L.; Wang, X. Performance characteristics of R1234yf ejector-expansion refrigeration cycle. Appl. Energy 2014, 121, 96–103. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, X.; Deng, S.; Li, H.; Yu, Z. Performance analysis of the ejector-expansion refrigeration cycle using zeotropic mixtures. Int. J. Refrig. 2015, 57, 197–207. [Google Scholar] [CrossRef]
- Luo, B. Theoretical assessment of an ejector enhanced oil flooded compression cycle. Int. J. Refrig. 2017, 73, 154–162. [Google Scholar] [CrossRef]
- Rodríguez-Muñoz, J.L.; Pérez-García, V.; Belman-Flores, J.M.; Ituna-Yudonago, J.F.; Gallegos-Muñoz, A. Energy and exergy performance of the IHX position in ejector expansion refrigeration systems. Int. J. Refrig. 2018, 93, 122–131. [Google Scholar] [CrossRef]
- Li, D.; Groll, E.A. Transcritical CO2 refrigeration cycle with ejector-expansion device. Int. J. Refrig. 2005, 28, 766–773. [Google Scholar] [CrossRef]
- Ksayer, E.B.; Clodic, D. Enhancement of CO2 Refrigeration Cycle Using an Ejector: 1D Analysis. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 17–20 July 2006; p. 790. [Google Scholar]
- Deng, J.; Jiang, P.; Lu, T.; Lu, W. Particular characteristics of transcritical CO2 refrigeration cycle with an ejector. Appl. Therm. Eng. 2007, 27, 381–388. [Google Scholar] [CrossRef]
- Sarkar, J. Optimization of ejector-expansion transcritical CO2 heat pump cycle. Energy 2008, 33, 1399–1406. [Google Scholar] [CrossRef]
- Pérez-García, V.; Rodríguez-Muñoz, J.L.; Ramírez-Minguela, J.J.; Belman-Flores, J.M.; Méndez-Díaz, S. Comparative analysis of energy improvements in single transcritical cycle in refrigeration mode. Appl. Therm. Eng. 2016, 99, 866–872. [Google Scholar] [CrossRef]
- Fangtian, S.; Yitai, M. Thermodynamic analysis of transcritical CO2 refrigeration cycle with an ejector. Appl. Therm. Eng. 2011, 31, 1184–1189. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Y.; Wang, H.; Li, M. Theoretical evaluation on effect of internal heat exchanger in ejector expansion transcritical CO2 refrigeration cycle. Appl. Therm. Eng. 2013, 50, 932–938. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, L. Effect of suction nozzle pressure drop on the performance of an ejector-expansion transcritical CO2 refrigeration cycle. Entropy 2014, 16, 4309–4321. [Google Scholar] [CrossRef]
- Zheng, L.; Deng, J.; He, Y.; Jiang, P. Dynamic model of a transcritical CO2 ejector expansion refrigeration system. Int. J. Refrig. 2015, 60, 247–260. [Google Scholar] [CrossRef]
- Liu, F.; Deng, J.; Pan, W. Model-based Dynamic Optimal Control of an Ejector Expansion CO2 Heat Pump Coupled with Thermal Storages. Energy Procedia 2018, 152, 156–161. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S. Operating characteristics of transcritical CO2 heat pump for simultaneous water cooling and heating. Arch. Thermodyn. 2012, 33, 23–40. [Google Scholar] [CrossRef]
- Henry, R.E.; Fauske, H.K. The Two-Phase Critical flow of One-Component Mixtures in Nozzles, Orifice, and Short Tubes. J. Heat Transf. 1971, 93, 179–187. [Google Scholar] [CrossRef]
- Harrell, G.S.; Kornhauser, A.A. Performance tests of a two phase ejector. In Proceedings of the 30th Intersociety Energy Conversion Engineering Conference, Orlando, FL, USA, 30 July–4 August 1995. [Google Scholar]
- Wongwises, S.; Disawas, S. Performance of the two-phase ejector expansion refrigeration cycle. Int. J. Heat Mass Transf. 2005, 48, 4282–4286. [Google Scholar] [CrossRef]
- Chaiwongsa, P.; Wongwises, S. Effect of throat diameters of the ejector on the performance of the refrigeration cycle using a two-phase ejector as an expansion device. Int. J. Refrig. 2007, 30, 601–608. [Google Scholar] [CrossRef]
- Chaiwongsa, P.; Wongwises, S. Experimental study on R-134a refrigeration system using a two-phase ejector as an expansion device. Appl. Therm. Eng. 2008, 28, 467–477. [Google Scholar] [CrossRef]
- Reddick, C.; Mercadier, Y.; Ouzzane, M. Experimental study of an ejector refrigeration system. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 16–19 July 2012; p. 2136. [Google Scholar]
- Lawrence, N.; Elbel, S. Experimental investigation of a two-phase ejector cycle suitable for use with low-pressure refrigerants R134a and R1234yf. Int. J. Refrig. 2014, 38, 310–322. [Google Scholar] [CrossRef]
- Ersoy, H.K.; Bilir Sag, N. Preliminary experimental results on the R134a refrigeration system using a two-phase ejector as an expander. Int. J. Refrig. 2014, 43, 97–110. [Google Scholar] [CrossRef]
- Pottker, G.; Guo, B.; Hrnjak, P.S. Experimental Investigation of an R410A Vapor Compression System Working With an Ejector. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 12–15 July 2010; p. 1135. [Google Scholar]
- Popovac, M.; Lauermann, M.; Baumhakel, A.; Drexler-, G. Performance analysis of a high-temperature heat pump with ejector based on butane as the refrigerant. In Proceedings of the 12th IEA Heat Pump Conference 2017, Rotterdam, The Netherlands, 15–18 May 2017; pp. 1–8. [Google Scholar]
- Nakagawa, M.; Marasigan, A.R.; Matsukawa, T. Experimental analysis on the effect of internal heat exchanger in transcritical CO2 refrigeration cycle with two-phase ejector. Int. J. Refrig. 2011, 34, 1577–1586. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, M.S.; Kim, M.S. Experimental study on the improvement of CO2 air conditioning system performance using an ejector. Int. J. Refrig. 2011, 34, 1614–1625. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, M.S.; Kim, M.S. Studies on the performance of a CO2 air conditioning system using an ejector as an expansion device. Int. J. Refrig. 2014, 38, 140–152. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y.; Groll, E.A. Performance enhancement of CO2 air conditioner with a controllable ejector. Int. J. Refrig. 2012, 35, 1604–1616. [Google Scholar] [CrossRef]
- Lucas, C.; Koehler, J. Experimental investigation of the COP improvement of a refrigeration cycle by use of an ejector. Int. J. Refrig. 2012, 35, 1595–1603. [Google Scholar] [CrossRef]
- Lucas, C.; Koehler, J.; Schroeder, A.; Tischendorf, C. Experimentally validated CO2 ejector operation characteristic used in a numerical investigation of ejector cycle. Int. J. Refrig. 2013, 36, 881–891. [Google Scholar] [CrossRef]
- Guangming, C.; Xiaoxiao, X.; Shuang, L.; Lixia, L.; Liming, T. An experimental and theoretical study of a CO2 ejector. Int. J. Refrig. 2010, 33, 915–921. [Google Scholar] [CrossRef]
- Minetto, S.; Brignoli, R.; Banasiak, K.; Hafner, A.; Zilio, C. Performance assessment of an off-the-shelf R744 heat pump equipped with an ejector. Appl. Therm. Eng. 2013, 59, 568–575. [Google Scholar] [CrossRef]
- Hafner, A.; Forsterling, S.; Banasiak, K. Multi-ejector concept for R-744 supermarket refrigeration. Int. J. Refrig. 2014, 43, 1–13. [Google Scholar] [CrossRef]
- Zhu, J.; Botticella, F.; Elbel, S. Experimental investigation and theoretical analysis of oil circulation rates in ejector cooling cycles. Energy 2018, 157, 718–733. [Google Scholar] [CrossRef]
- Haida, M.; Banasiak, K.; Smolka, J.; Hafner, A.; Eikevik, T.M. Experimental analysis of the R744 vapour compression rack equipped with the multi-ejector expansion work recovery module. Int. J. Refrig. 2016, 64, 93–107. [Google Scholar] [CrossRef]
- Boumaraf, L.; Haberschill, P.; Lallemand, A. Investigation of a novel ejector expansion refrigeration system using the working fluid R134a and its potential substitute R1234yf. Int. J. Refrig. 2014, 45, 148–159. [Google Scholar] [CrossRef]
- Unal, Ş.; Yilmaz, T. Thermodynamic analysis of the two-phase ejector air-conditioning system for buses. Appl. Therm. Eng. 2015, 79, 108–116. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J.; Yan, G. Theoretical investigation on an ejector-expansion refrigeration cycle using zeotropic mixture R290/R600a for applications in domestic refrigerator/freezers. Appl. Therm. Eng. 2015, 90, 703–710. [Google Scholar] [CrossRef]
- Zhu, L.; Yu, J.; Zhou, M.; Wang, X. Performance analysis of a novel dual-nozzle ejector enhanced cycle for solar assisted air-source heat pump systems. Renew. Energy 2014, 63, 735–740. [Google Scholar] [CrossRef]
- Wang, X.; Yu, J.; Zhou, M.; Lv, X. Comparative studies of ejector-expansion vapor compression refrigeration cycles for applications in domestic refrigerator-freezers. Energy 2014, 70, 635–642. [Google Scholar] [CrossRef]
- Sarkar, J. Performance analyses of novel two-phase ejector enhanced multi-evaporator refrigeration systems. Appl. Therm. Eng. 2017, 110, 1635–1642. [Google Scholar] [CrossRef]
- Xing, M.; Yan, G.; Yu, J. Performance evaluation of an ejector subcooled vapor-compression refrigeration cycle. Energy Convers. Manag. 2015, 92, 431–436. [Google Scholar] [CrossRef]
- Sarevski, M.N.; Sarevski, V.N. Preliminary study of a novel R718 refrigeration cycle with single stage centrifugal compressor and two-phase ejector. Int. J. Refrig. 2014, 40, 435–449. [Google Scholar] [CrossRef]
- Shen, S.; Qu, X.; Zhang, B.; Riffat, S.; Gillott, M. Study of a gas-liquid ejector and its application to a solar-powered bi-ejector refrigeration system. Appl. Therm. Eng. 2005, 25, 2891–2902. [Google Scholar] [CrossRef]
- Vereda, C.; Ventas, R.; Lecuona, A.; Venegas, M. Study of an ejector-absorption refrigeration cycle with an adaptable ejector nozzle for different working conditions. Appl. Energy 2012, 97, 305–312. [Google Scholar] [CrossRef]
- Vereda, C.; Ventas, R.; Lecuona, A.; López, R. Single-effect absorption refrigeration cycle boosted with an ejector-adiabatic absorber using a single solution pump. Int. J. Refrig. 2014, 38, 22–29. [Google Scholar] [CrossRef]
- Garousi Farshi, L.; Mosaffa, A.H.; Infante Ferreira, C.A.; Rosen, M.A. Thermodynamic analysis and comparison of combined ejector-absorption and single effect absorption refrigeration systems. Appl. Energy 2014, 133, 335–346. [Google Scholar] [CrossRef]
- Yari, M.; Sirousazar, M. Cycle improvements to ejector-expansion transcritical CO2 two-stage refrigeration cycle. Int. J. Energy Res. 2008, 32, 677–687. [Google Scholar] [CrossRef]
- Goodarzi, M.; Gheibi, A.; Motamedian, M. Comparative analysis of an improved two-stage multi-inter-cooling ejector-expansion trans-critical CO2 refrigeration cycle. Appl. Therm. Eng. 2015, 81, 58–65. [Google Scholar] [CrossRef]
- Manjili, F.E.; Yavari, M.A. Performance of a new two-stage multi-intercooling transcritical CO2 ejector refrigeration cycle. Appl. Therm. Eng. 2012, 40, 202–209. [Google Scholar] [CrossRef]
- Yari, M.; Mahmoudi, S.M.S. Thermodynamic analysis and optimization of novel ejector-expansion TRCC (transcritical CO2) cascade refrigeration cycles (Novel transcritical CO2 cycle). Energy 2011, 36, 6839–6850. [Google Scholar] [CrossRef]
- Dokandari, D.A.; Hagh, A.; Mahmoudi, S.M.S. Thermodynamic investigation and optimization of novel ejector-expansion CO2/NH3 cascade refrigeration cycles (novel CO2/NH3 cycle). Int. J. Refrig. 2014, 46, 26–36. [Google Scholar] [CrossRef]
- Bai, T.; Yan, G.; Yu, J. Thermodynamic analyses on an ejector enhanced CO2 transcritical heat pump cycle with vapor-injection. Int. J. Refrig. 2015, 58, 22–34. [Google Scholar] [CrossRef]
- Bai, T.; Yan, G.; Yu, J. Thermodynamics analysis of a modified dual-evaporator CO2 transcritical refrigeration cycle with two-stage ejector. Energy 2015, 84, 325–335. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, J.; Yan, G. Theoretical analysis of a double ejector-expansion autocascade refrigeration cycle using hydrocarbon mixture R290/R170. Int. J. Refrig. 2018, 94, 33–39. [Google Scholar] [CrossRef]
- Lawrence, N.; Elbel, S. Numerical investigation of the effect of microchannel evaporator design and operation on the improvement potential of ejector refrigeration cycles. Energy 2018, 164, 21–34. [Google Scholar] [CrossRef]
- Haida, M.; Smolka, J.; Hafner, A.; Ostrowski, Z.; Palacz, M.; Madsen, K.B.; Försterling, S.; Nowak, A.J.; Banasiak, K. Performance mapping of the R744 ejectors for refrigeration and air conditioning supermarket application: A hybrid reduced-order model. Energy 2018, 153, 933–948. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, H.; Yu, Z.; Han, J. Simulation and optimization of a R744 two-temperature supermarket refrigeration system with an ejector. Int. J. Refrig. 2018, 90, 73–82. [Google Scholar] [CrossRef]
- Bodys, J.; Hafner, A.; Banasiak, K.; Smolka, J.; Ladam, Y. Design and simulations of refrigerated sea water chillers with CO2 ejector pumps for marine applications in hot climates. Energy 2018, 161, 90–103. [Google Scholar] [CrossRef]
- Smierciew, K.; Butrymowicz, D.; Kwidziński, R.; Przybyliński, T. Analysis of application of two-phase injector in ejector refrigeration systems for isobutane. Appl. Therm. Eng. 2015, 78, 630–639. [Google Scholar] [CrossRef]
- Man-O, T.; Tanino, M.; Okazaki, T.; Koyama, S. The enhanced heat transfer in the plate-type evaporator by using an ejector for recirculation. In Proceedings of the International Congress of Refrigeration, Beijing, China, 21–26 August 2007. [Google Scholar]
- Jeon, Y.; Kim, D.; Jung, J.; Jang, D.S.; Kim, Y. Comparative performance evaluation of conventional and condenser outlet split ejector-based domestic refrigerator-freezers using R600a. Energy 2018, 161, 1085–1095. [Google Scholar] [CrossRef]
- Lawrence, N.; Elbel, S. Experimental Investigation of Two-Phase Ejector Liquid Recirculation Cycles With R410a. In Proceedings of the ICR 2015, Yokohama, Japan, 16–22 August 2015; p. 194. [Google Scholar]
- Lawrence, N.; Elbel, S. Experimental investigation on the effect of evaporator design and application of work recovery on the performance of two-phase ejector liquid recirculation cycles with R410A. Appl. Therm. Eng. 2016, 100, 398–411. [Google Scholar] [CrossRef]
- Bai, T.; Yan, G.; Yu, J. Experimental investigation of an ejector-enhanced auto-cascade refrigeration system. Appl. Therm. Eng. 2018, 129, 792–801. [Google Scholar] [CrossRef]
- Smierciew, K.; Butrymowicz, D. Investigations of Two-Phase Injector Operating With Isobutane. In Proceedings of the ICR 2015, Yokohama, Japan, 16–22 August 2015; p. 506. [Google Scholar]
- Smierciew, K.; Butrymowicz, D.; Przybylinski, T. Investigations of Heat and Momentum Transfer in Vapor-Liquid Isobutane Injector. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 11–14 July 2016; p. 1823. [Google Scholar]
- Banasiak, K.; Hafner, A.; Kriezi, E.E.; Madsen, K.B.; Birkelund, M.; Fredslund, K.; Olsson, R. Development and performance mapping of a multi-ejector expansion work recovery pack for R744 vapour compression units. Int. J. Refrig. 2015, 57, 265–276. [Google Scholar] [CrossRef]
- Minetto, S.; Brignoli, R.; Zilio, C.; Marinetti, S. Experimental analysis of a new method for overfeeding multiple evaporators in refrigeration systems. Int. J. Refrig. 2014, 38, 1–9. [Google Scholar] [CrossRef]
- Jeon, Y.; Kim, S.; Kim, D.; Chung, H.J.; Kim, Y. Performance characteristics of an R600a household refrigeration cycle with a modified two-phase ejector for various ejector geometries and operating conditions. Appl. Energy 2017, 205, 1059–1067. [Google Scholar] [CrossRef]
- Kim, S.; Jeon, Y.; Joon Chung, H.; Kim, Y. Performance optimization of an R410A air-conditioner with a dual evaporator ejector cycle based on cooling seasonal performance factor. Appl. Therm. Eng. Accept. Manuscr. 2018, 131, 988–997. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Mercadier, Y. Numerical assessment of ejector operation for refrigeration applications based on CFD. Appl. Therm. Eng. 2006, 26, 604–612. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Turbulence modeling of a single-phase R134a supersonic ejector. Part 2: Local flow structure and exergy analysis. Int. J. Refrig. 2016, 61, 153–165. [Google Scholar] [CrossRef]
- Zegenhagen, M.T.; Ziegler, F. Experimental investigation of the characteristics of a jet-ejector and a jet-ejector cooling system operating with R134a as a refrigerant. Int. J. Refrig. 2015, 56, 173–185. [Google Scholar] [CrossRef]
- Hamzaoui, M.; Nesreddine, H.; Aidoun, Z.; Balistrou, M. Experimental study of a low grade heat driven ejector cooling system using the working fluid R245fa. Int. J. Refrig. 2018, 86, 388–400. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).