Current Advances in Ejector Modeling, Experimentation and Applications for Refrigeration and Heat Pumps. Part 1: Single-Phase Ejectors
Abstract
1. Introduction
- Ejector fundamentals’ discussion of conventional ejector types and extension to more recent concepts employing complex geometries for the nozzles and the mixing chambers.
- Treatment of single-phase and two-phase ejector variants in separate developments for a full account and analysis of their progress.
- Inclusion of ejector operational features, conditions affecting stability and performance, such as external constraints, internal geometry, flow regimes as well as many other considerations, which are thoroughly described and discussed in detail.
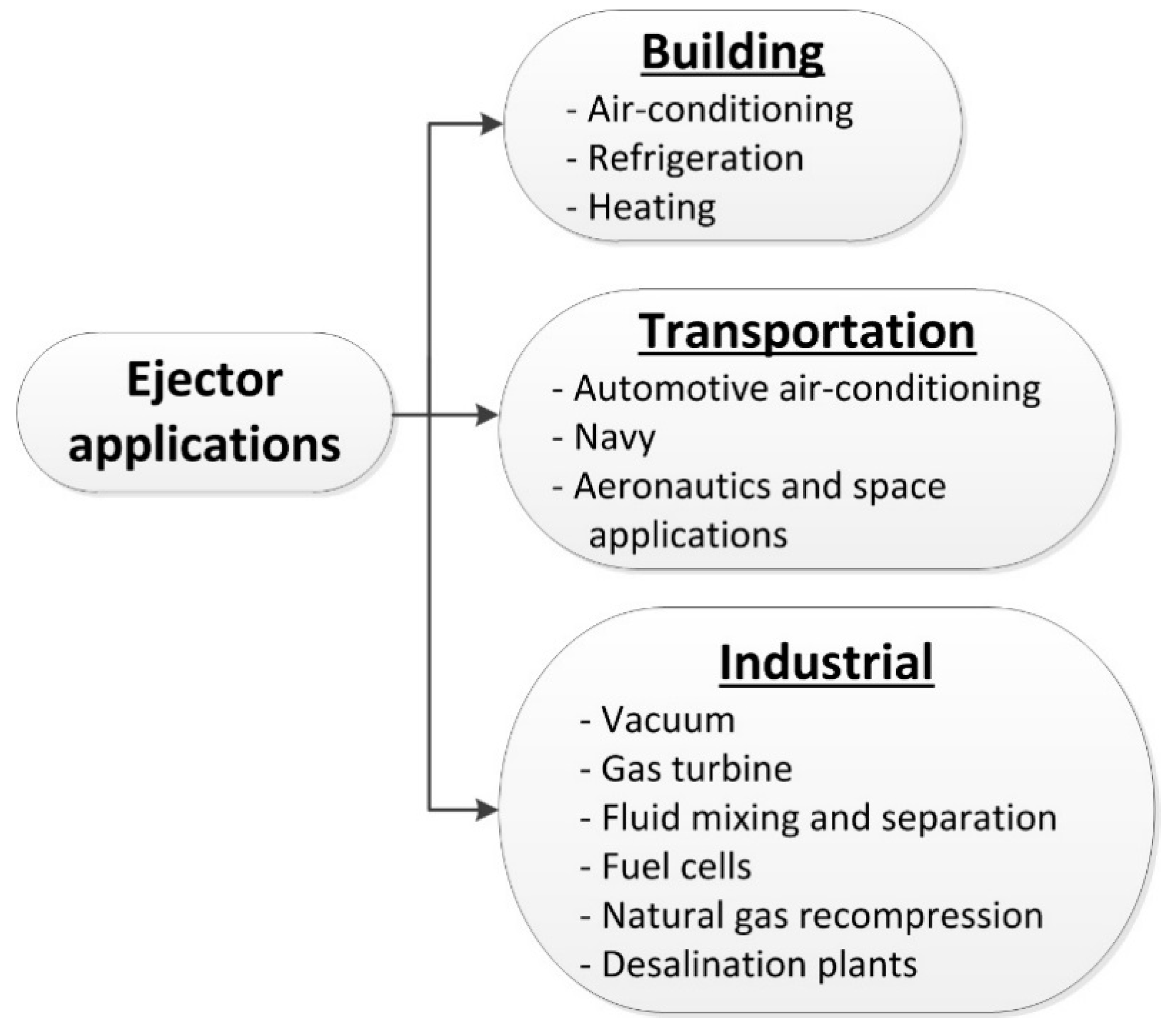
- Existing and potential ejector applications, beyond conventional refrigeration systems and selected from different areas of specialties (buildings, transportation, industry and several other domains). Their discussion aims to trigger a better exchange of information and bridge between professionals of different backgrounds and objectives.
- Modeling methods, their types and particularities thoroughly dissected to provide guidance, depending on the research objectives pursued. Typical analytical and numerical (computational fluid dynamics, CFD) models to serve as a common basis for the vast majority of similar research are proposed.
- Provision of very detailed, abundantly discussed information on the fundamental elements serving as building blocks to help structure such models. Further, a thorough discussion of the modeling works available in the literature supported by visualization and experiments complements this information.
2. Ejector Fundamentals
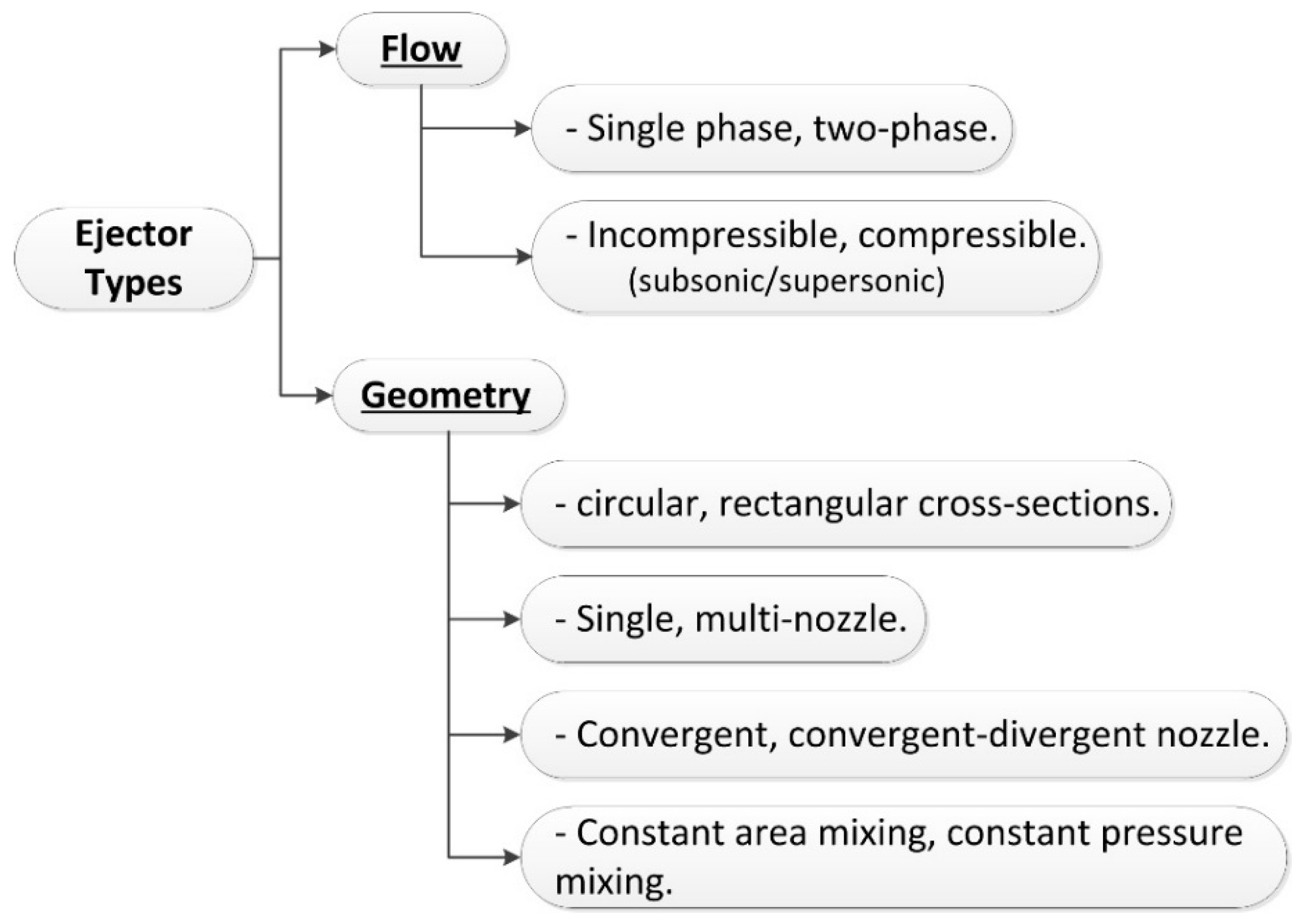
2.1. Ejector Types
2.2. Ejector Geometry
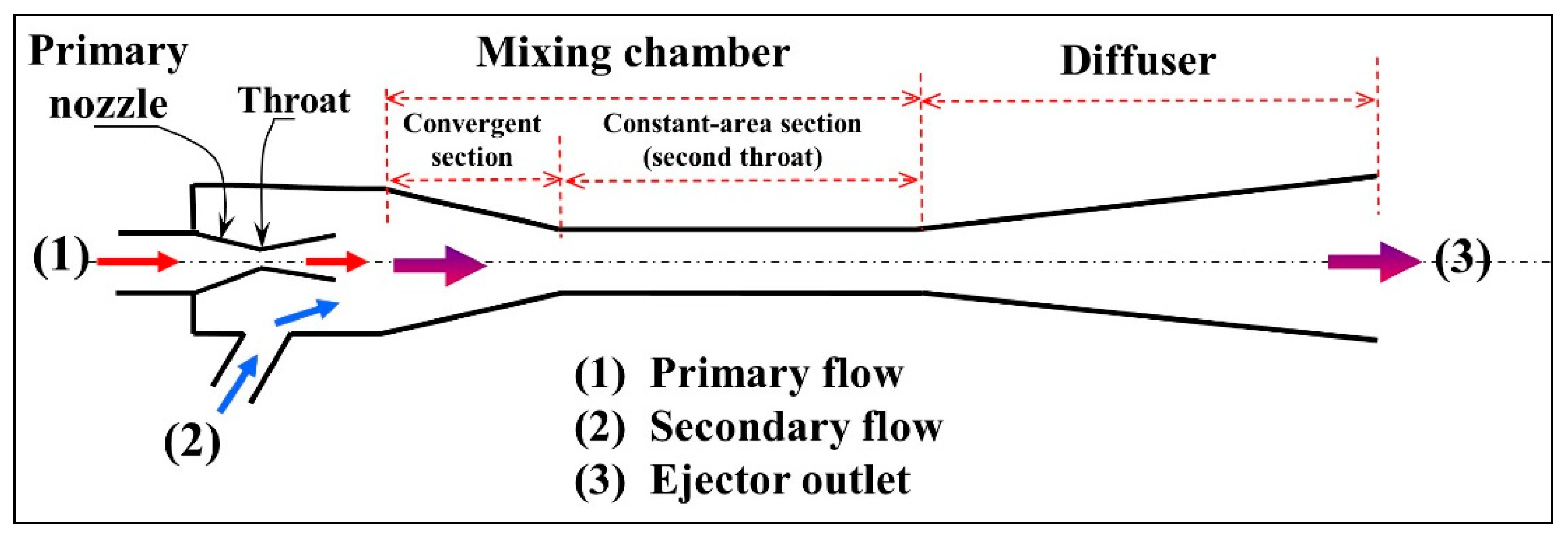
2.2.1. Conventional Ejector
2.2.2. Other Geometry Concepts
3. Ejector Operation
3.1. Performance Coefficients
3.2. Operational Factors
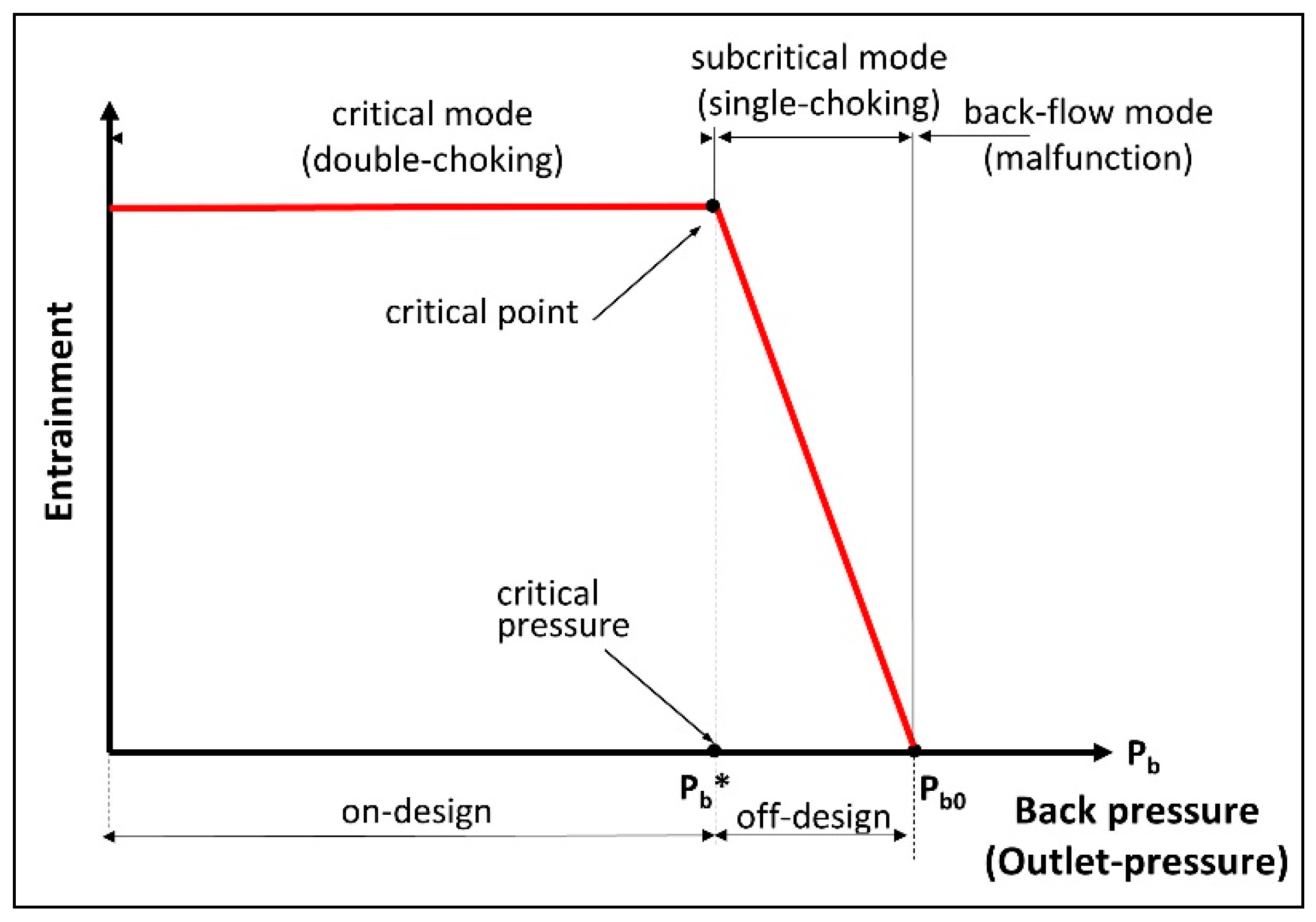
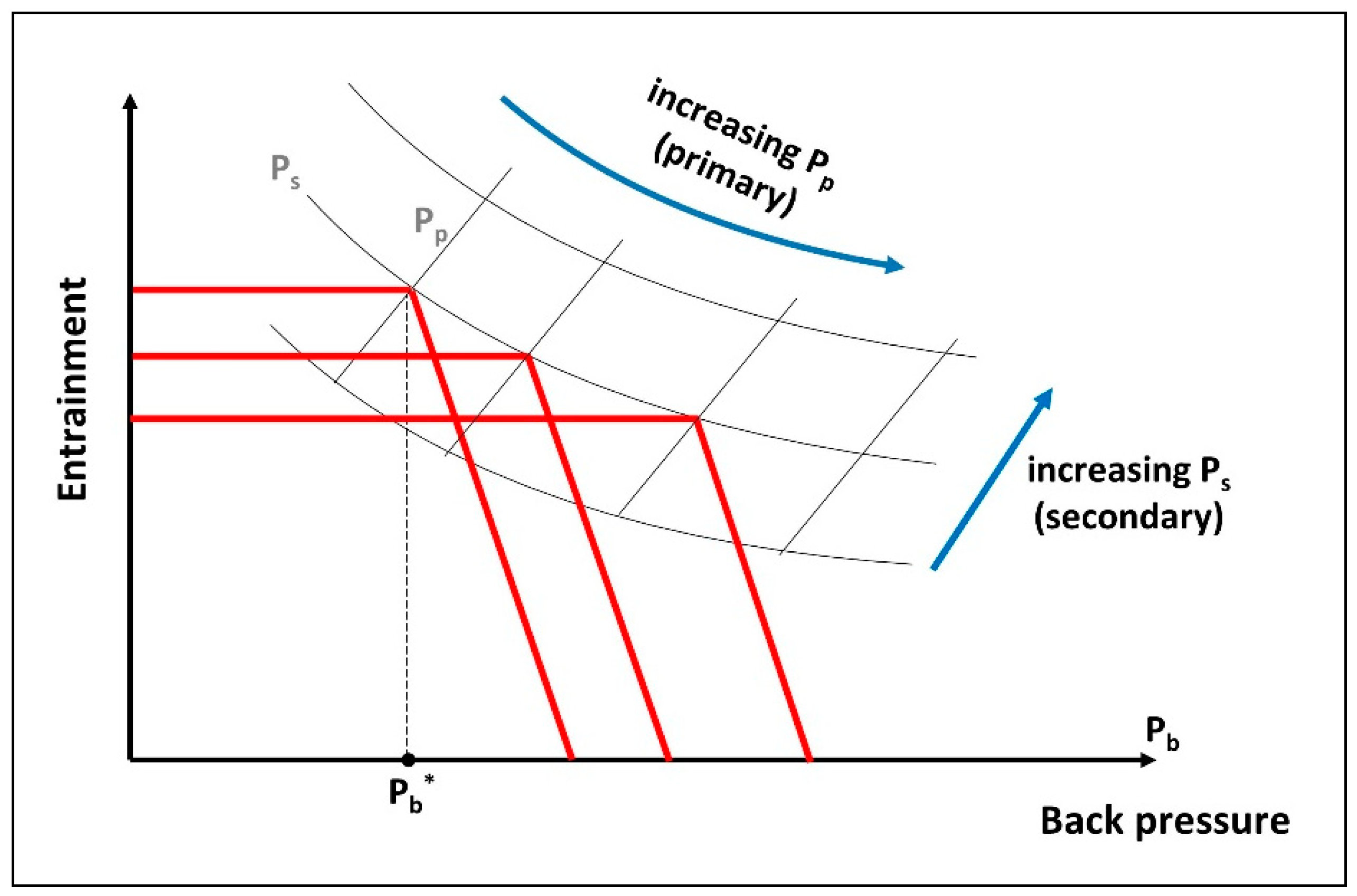
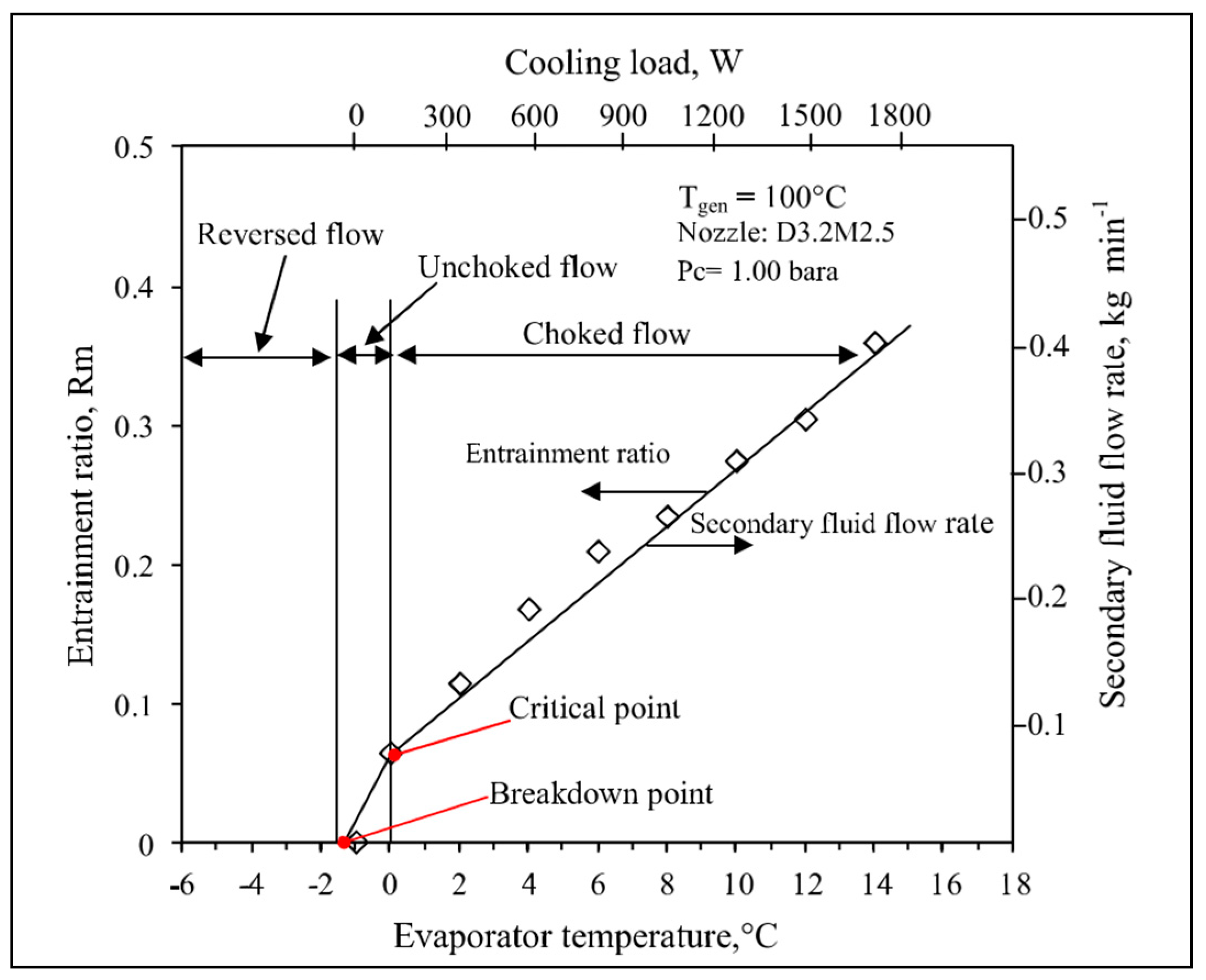
3.2.1. Ejector Operation Curve
3.2.2. Effect of Inlet Pressures
3.3. Geometry Factors
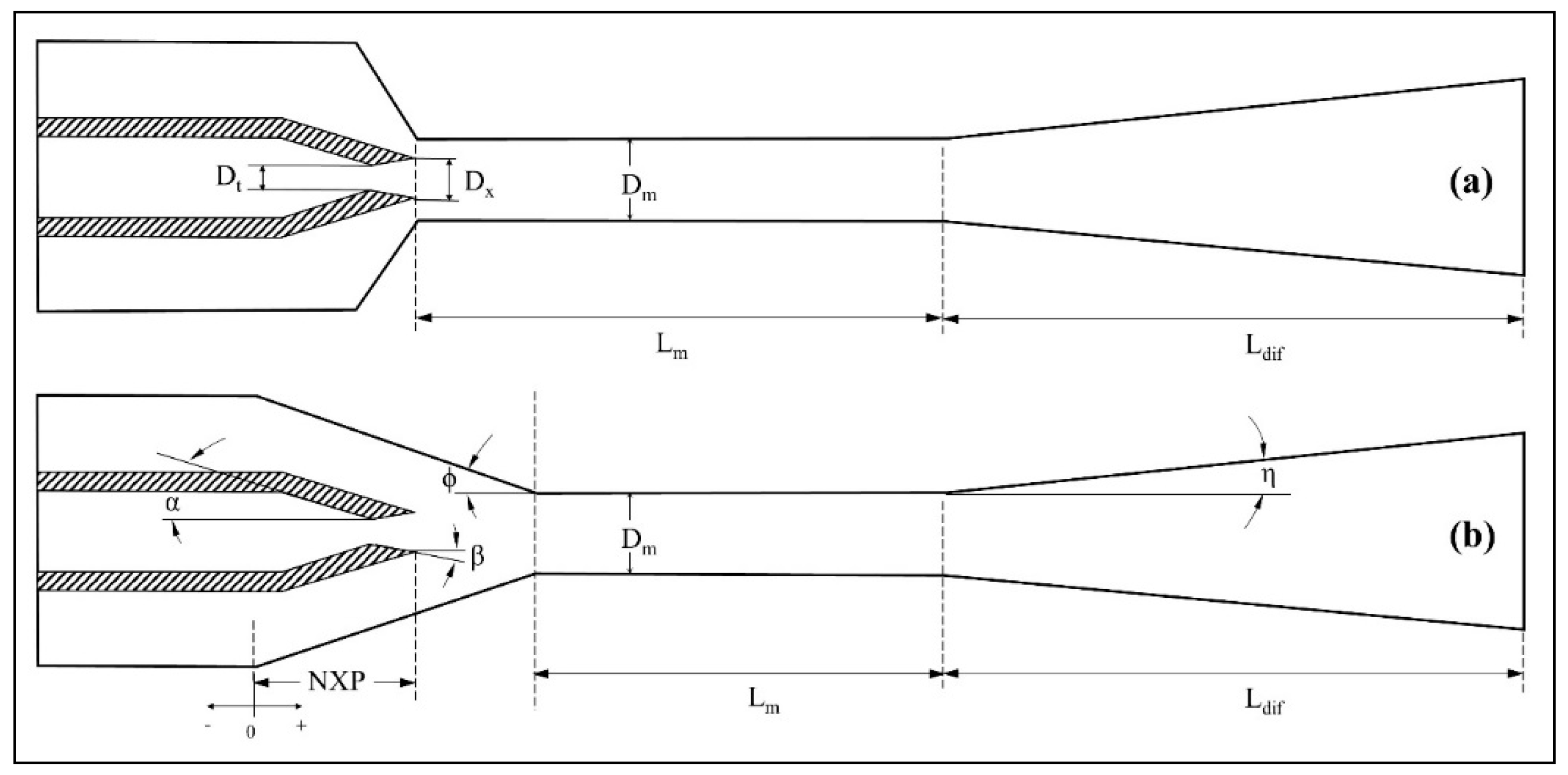
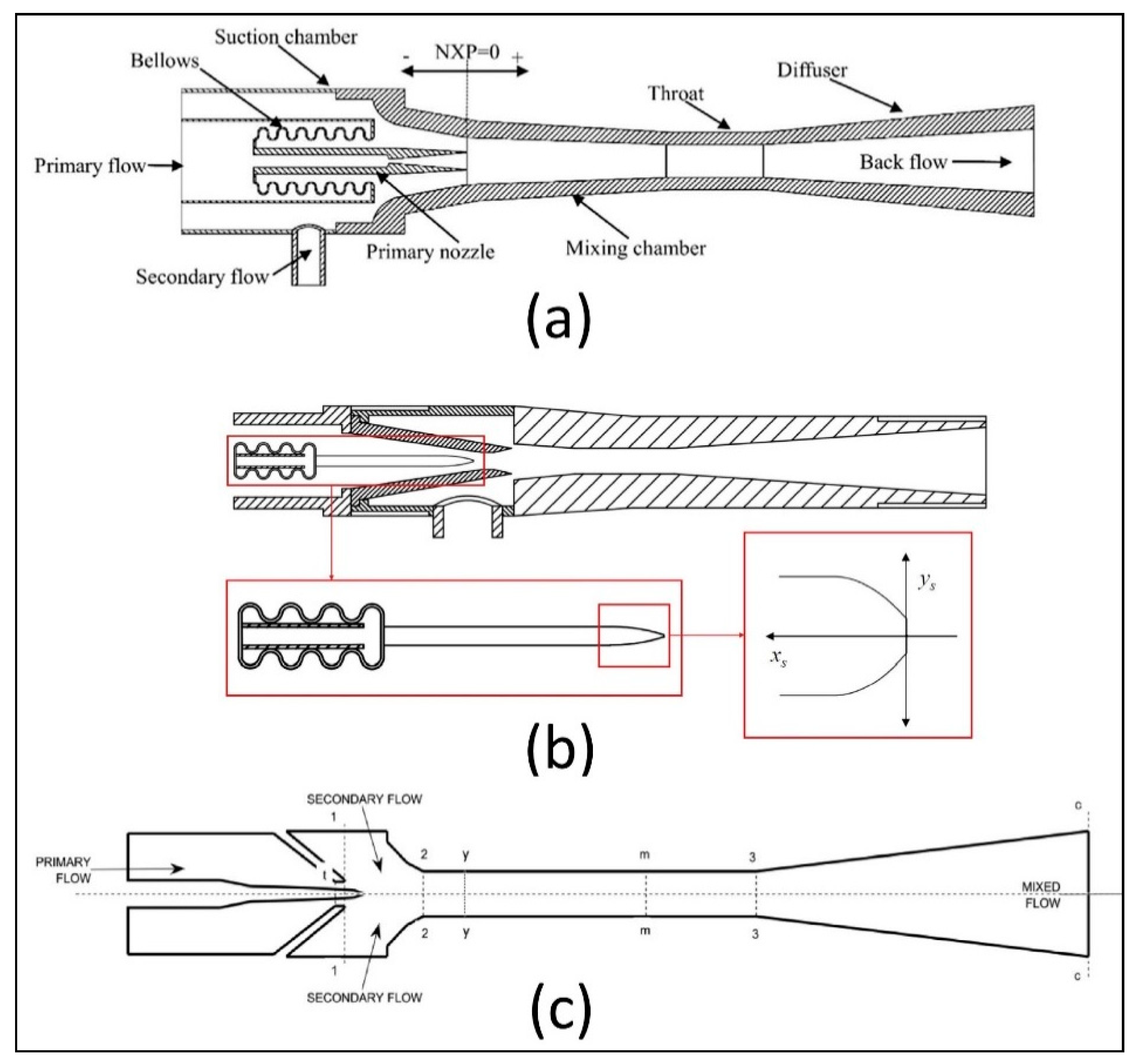
3.3.1. The Nozzle Exit Position (NXP)
3.3.2. Primary Nozzle Exit Area Ratio
3.3.3. The Mixing Chamber Shape Effects
The Mixing Chamber Throat Ratio
The Mixing Chamber Throat Length
The Mixing Chamber Inlet Angle
3.3.4. Variable Geometry Ejector (VGE)
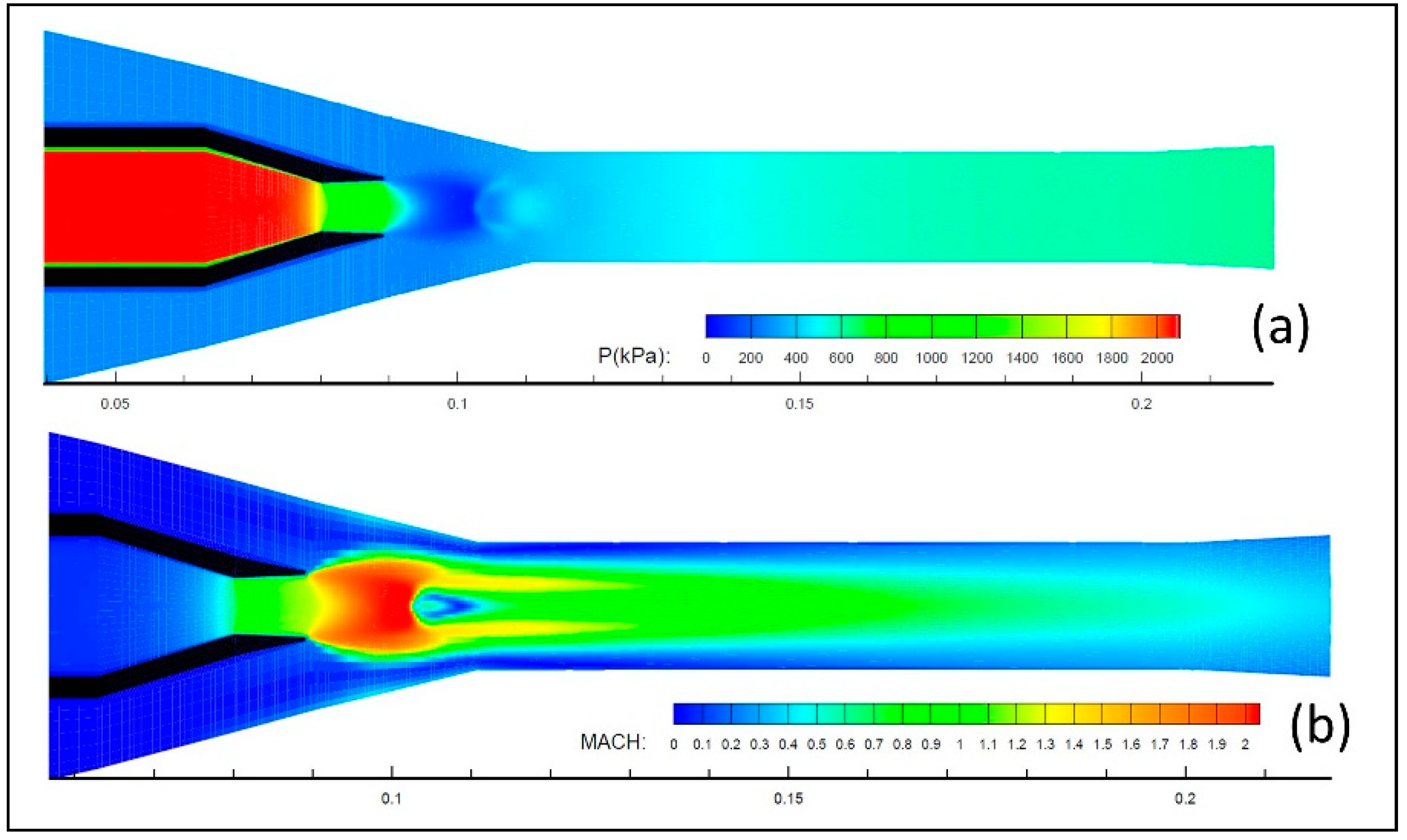
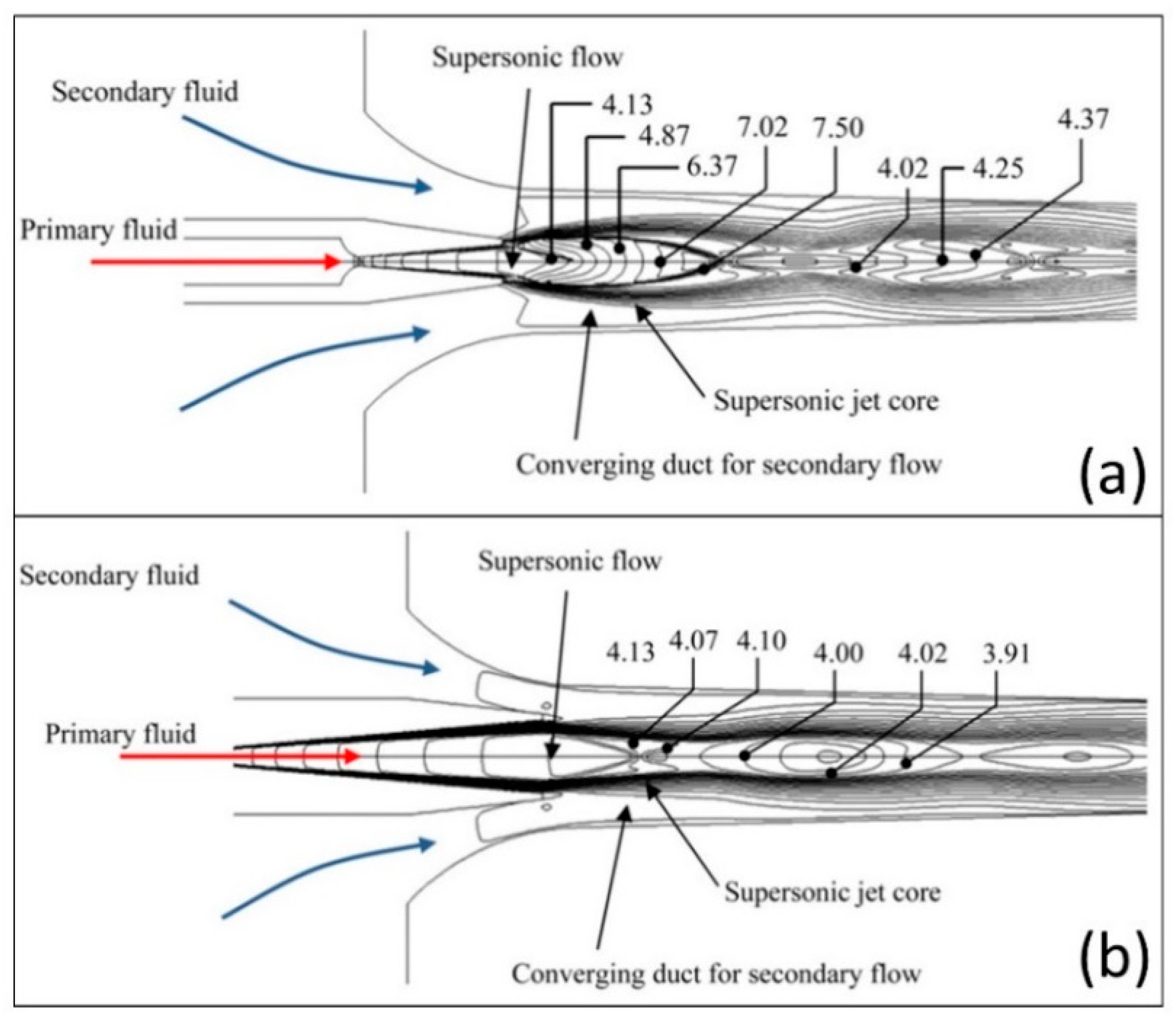
4. Flow Regimes and Internal Structure
4.1. Primary Nozzle Flow Regimes
- If the primary inlet pressure is insufficient, the jet will be supersonic in part of the divergent but leaves the nozzle in subsonic conditions due to a normal shock wave formation inside the divergent. This occurrence is a particular case of an over-expanded flow.
- When the primary pressure increases, the flow becomes an over-expanded jet of conic form with a succession of oblique shocks, generally occurring when the nozzle exit pressure is lower than the reigning ambient.
- If the primary pressure further increases, then the jet becomes under-expanded and will continue to expand past the nozzle to reach the ambient condition.
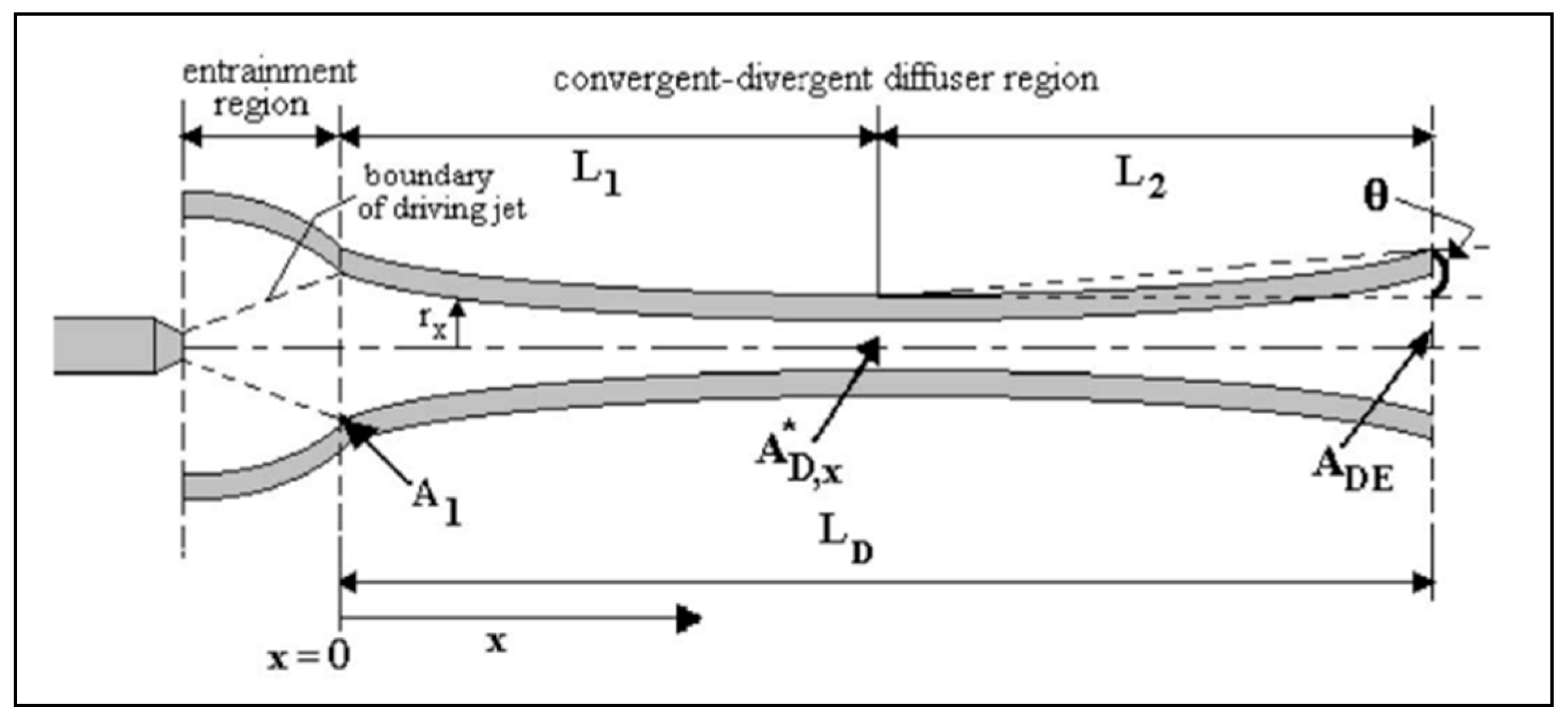
4.2. Ejector Internal Flow Structure
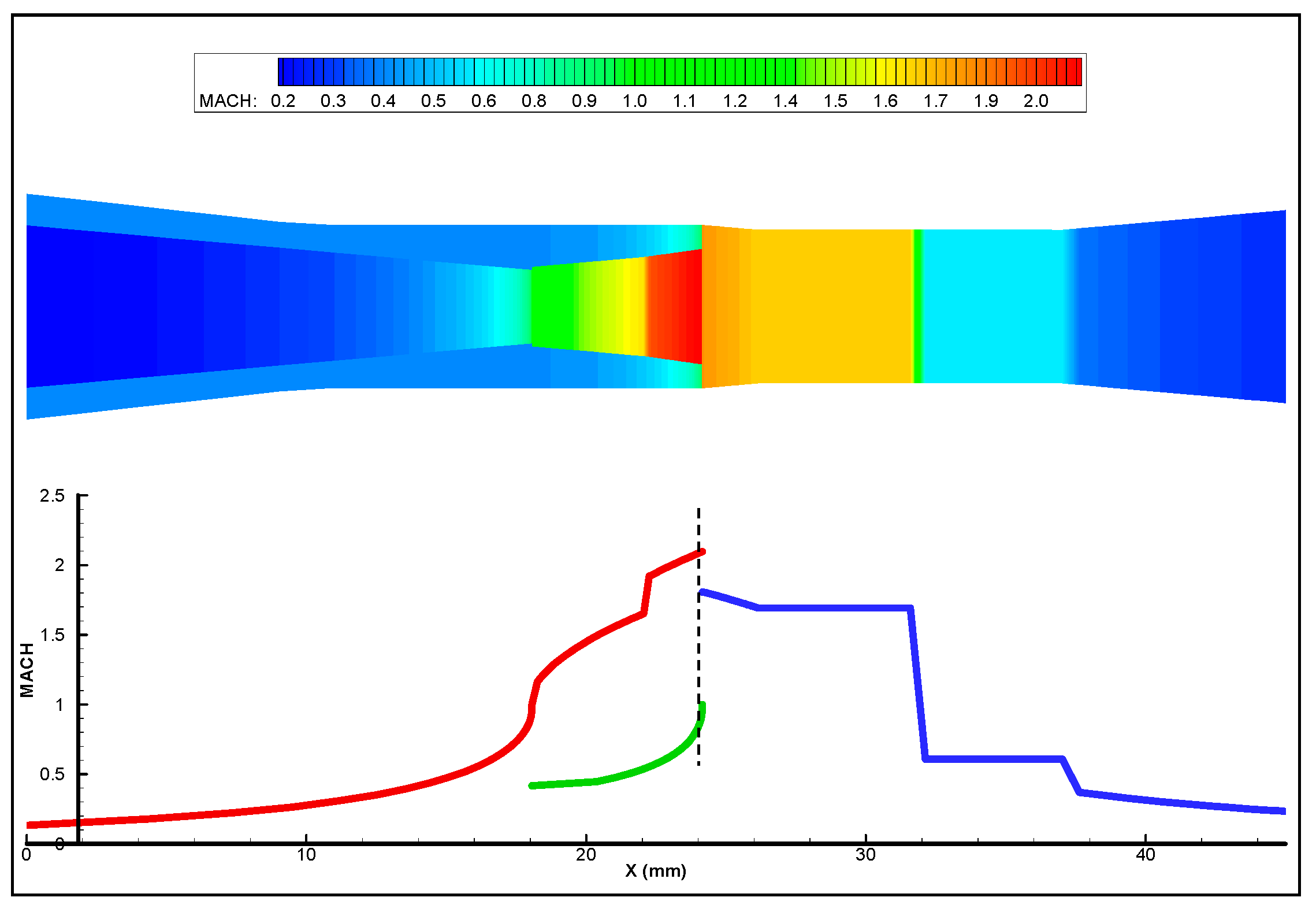
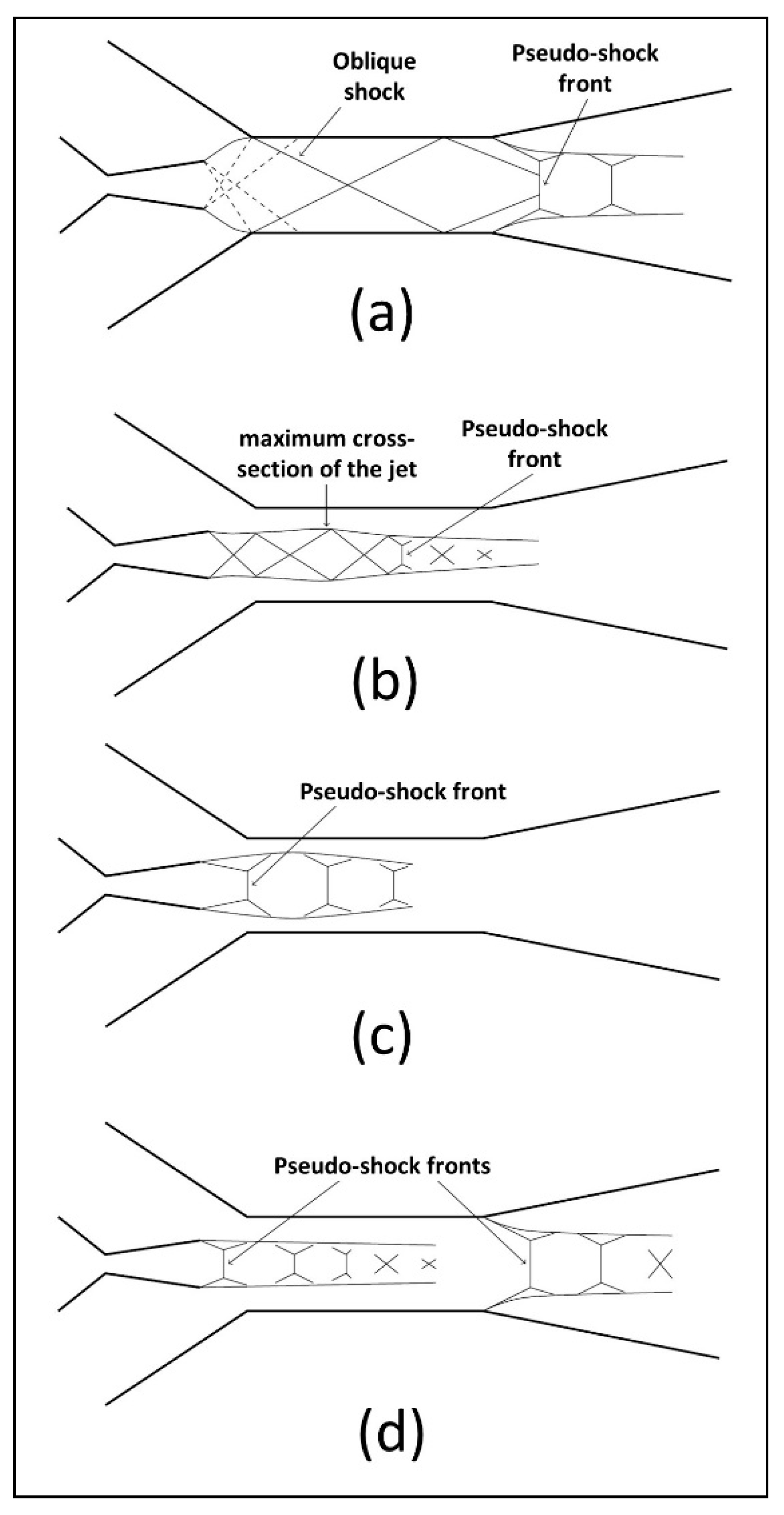
- Fully developed supersonic flow (Figure 17a): occurs for high inlet pressures and low induced flows. The primary jet is fully expanded in the mixing chamber and the induced flow is equally supersonic.
- Supersonic flow with secondary sonic throat (Figure 17b): the primary jet expansion is less important than in the preceding regime and the induced flow is higher, reaching sonic conditions in the mixing chamber at a location where the effective cross-section is minimum. Downstream of this point, both flows are supersonic.
- Supersonic saturated regime (Figure 17c): the primary jet is supersonic with moderately low pressure and the induced flow remains subsonic. A pseudo-shock front sets somewhere between the primary nozzle outlet and the mixing throat inlet.
- Supersonic regime with double choking (Figure 17d): characterized by double choking, this flow exhibits two distinct pseudo-shocks, the first behind the primary nozzle and the second before the diffuser inlet. This regime occurs for low geometric ratios, corresponding to small mixing chamber sections.
5. Application Potential of Ejectors
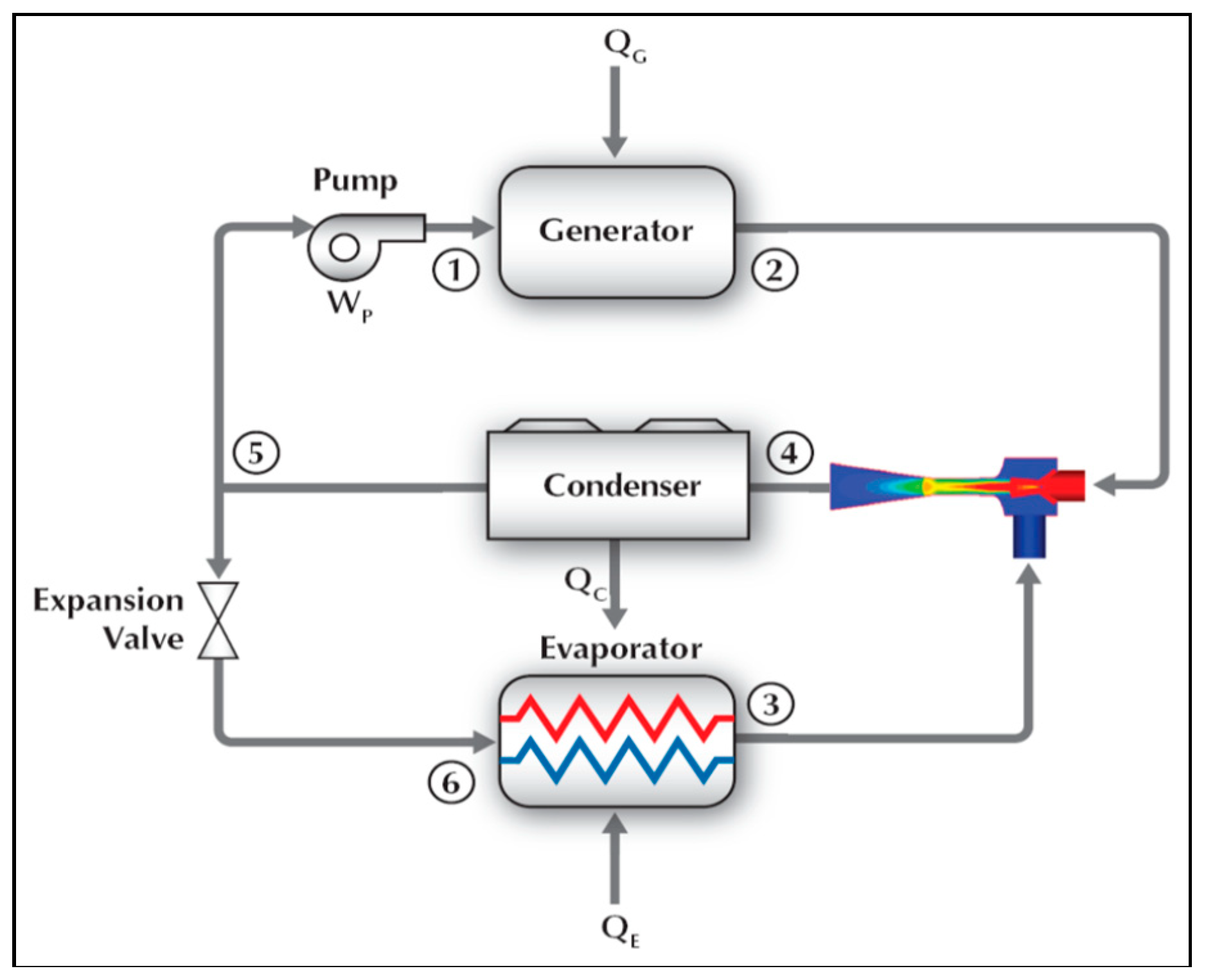
5.1. Air-Conditioning, Refrigeration and Heating
5.2. Automotive Air-Conditioning
5.3. Aeronautics and Space Applications
5.4. Vacuum Creation
5.5. Gas Turbine Performance Enhancement
5.6. Fluid Mixing and Separation
5.7. Fuel Cell Applications
5.8. Natural Gas Recompression Stations
5.9. Desalination Plants
5.10. Other Industrial Applications
6. Ejector Modeling Methods
6.1. Analytical Modeling
6.2. Numerical Ejector Modeling
6.2.1. Equations of Conservation
6.2.2. Parameters Selection
Mesh Sensitivity
Solvers
Computation and Discretization Schemes
Turbulence Modeling
7. Experimentation on Ejectors
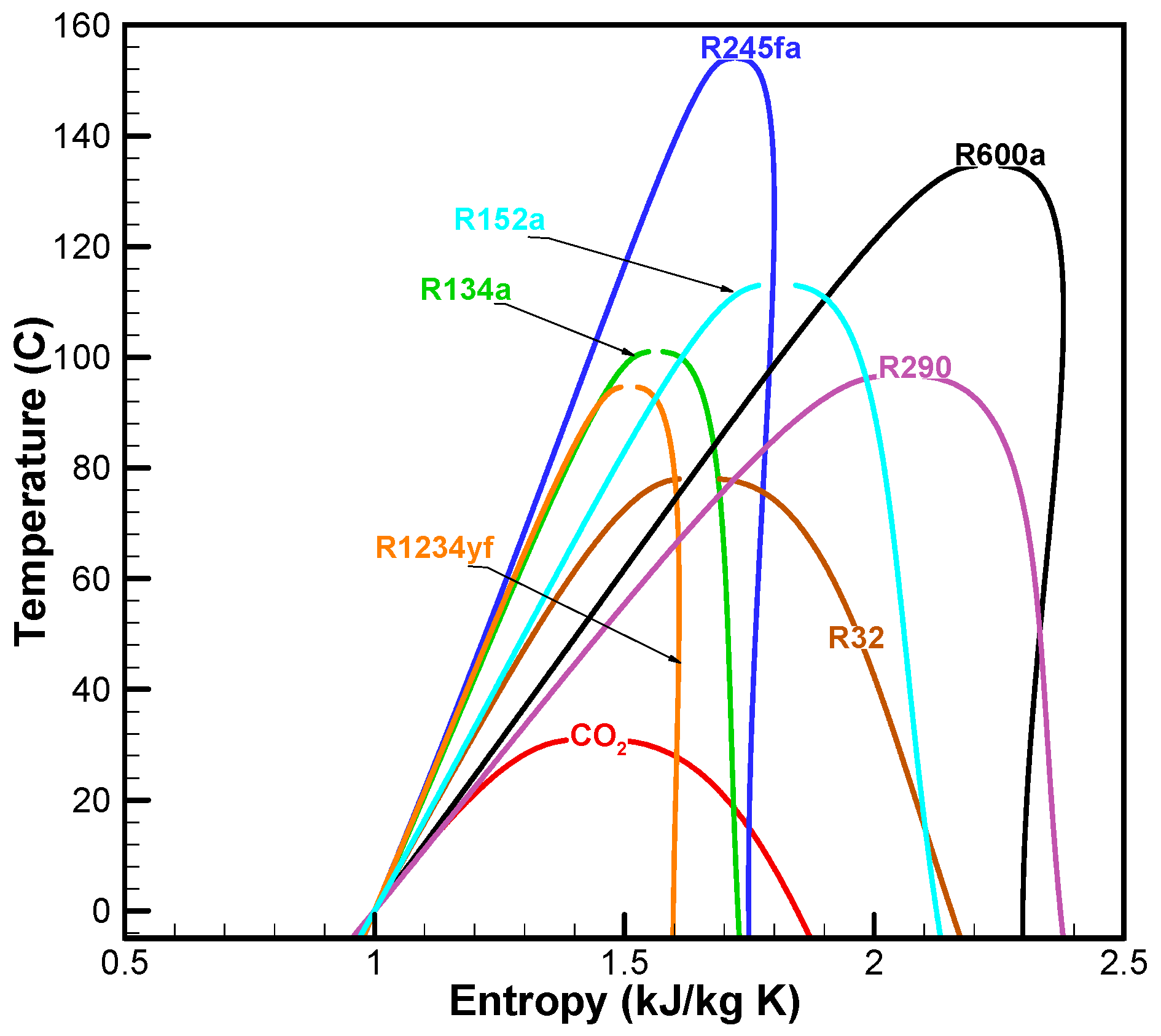
7.1. Working Fluids
7.2. Parameters Measurements
7.3. Data for Model Validations
7.3.1. Global Validation
7.3.2. Local Validation
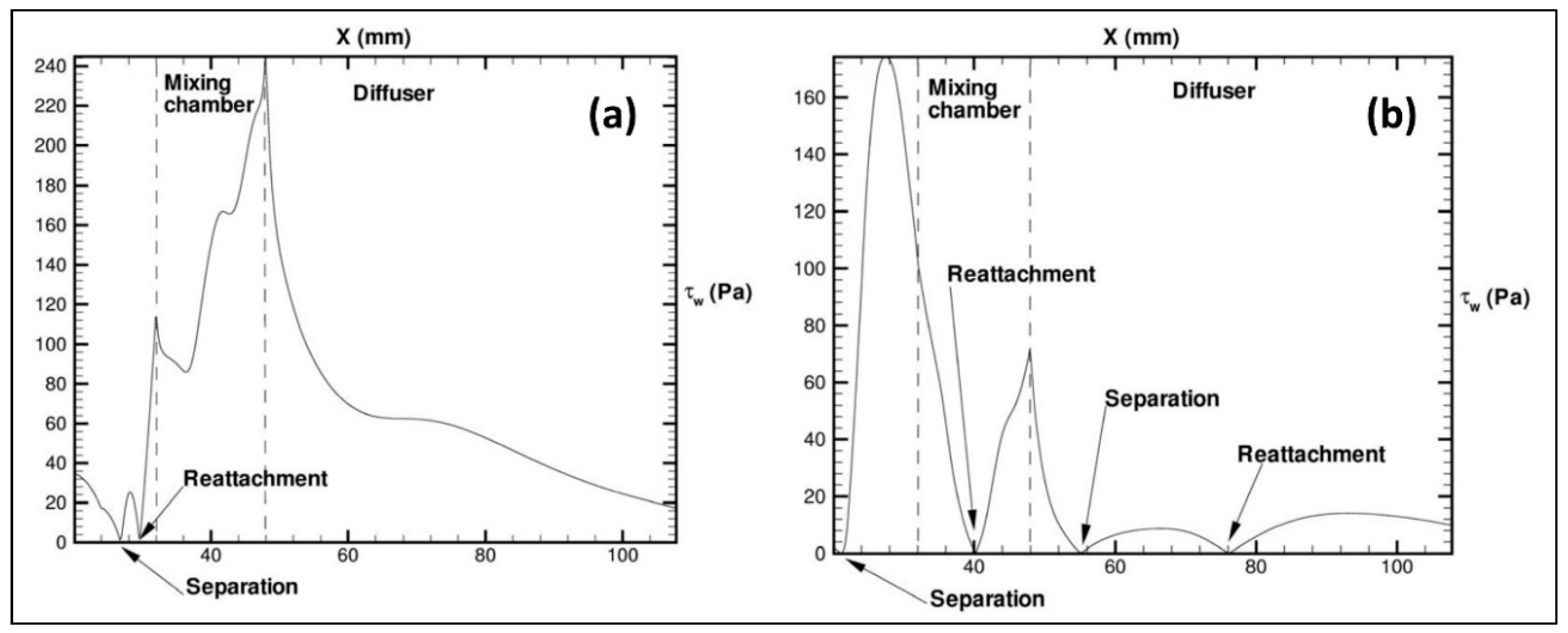
Pressure Distribution
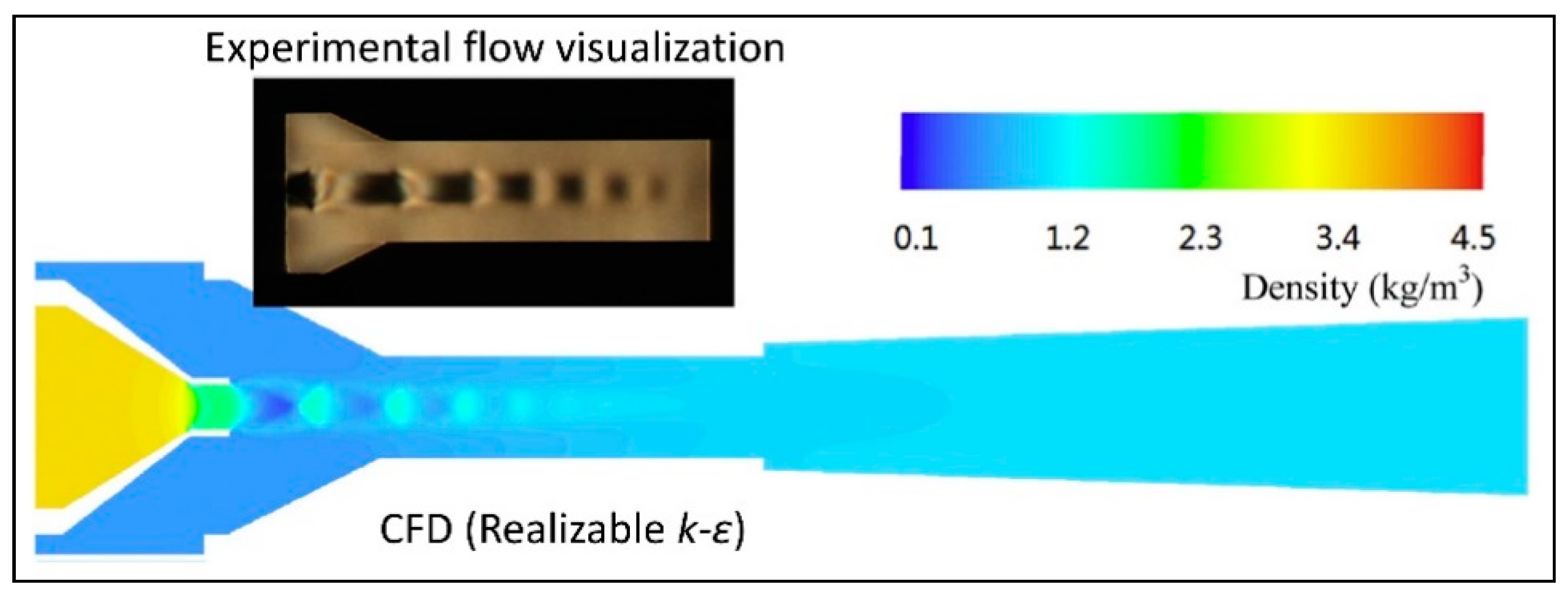
Flow Visualization
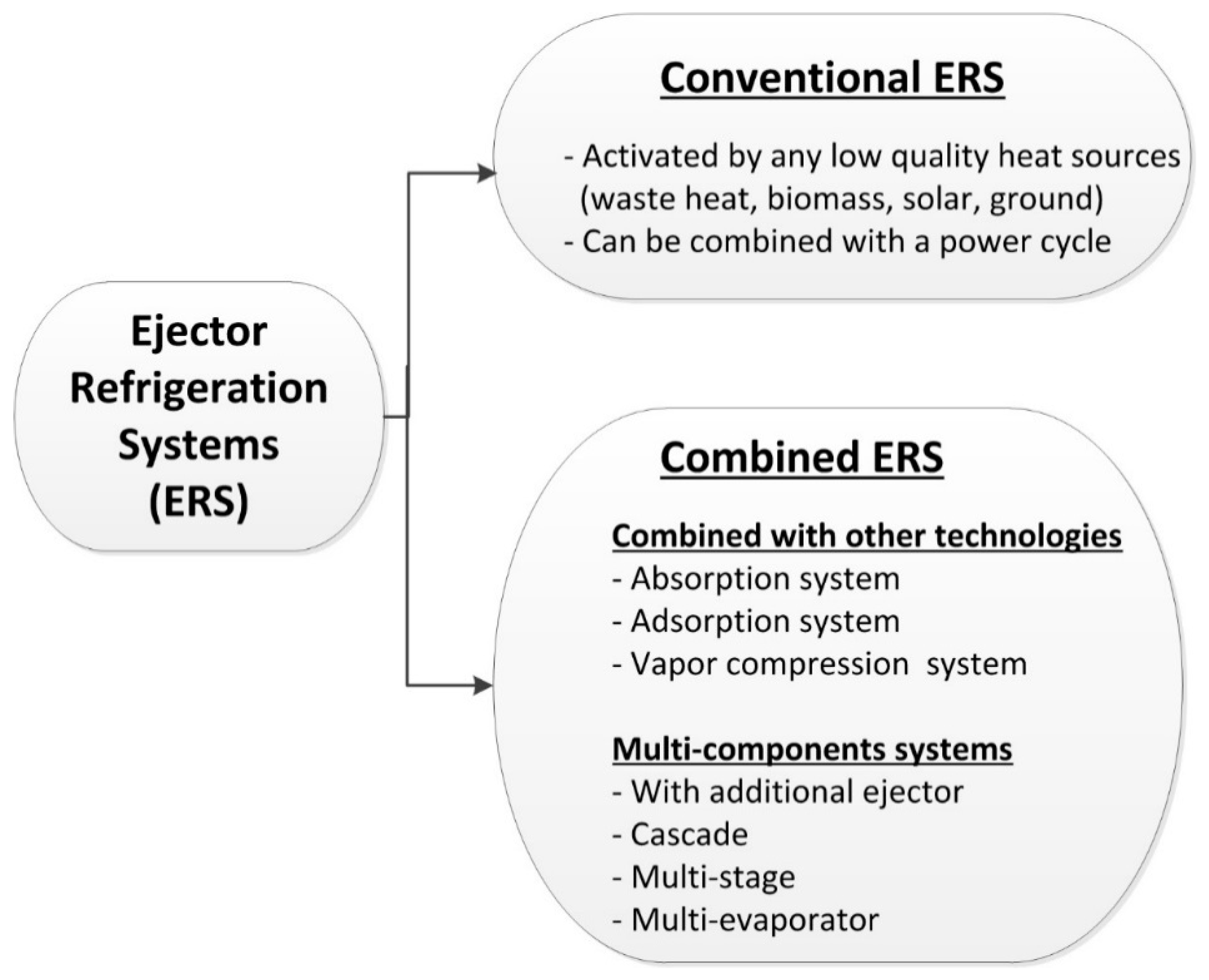
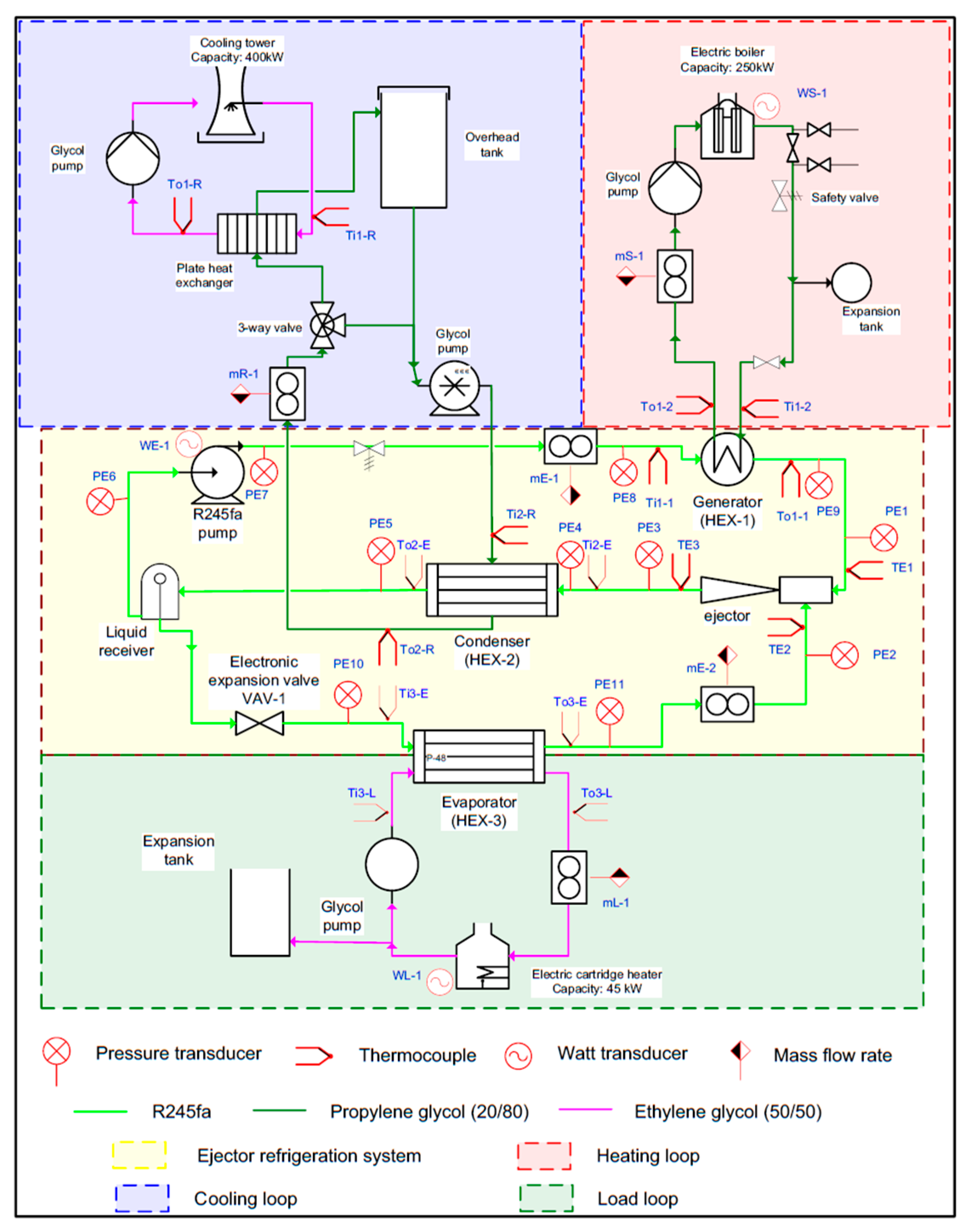
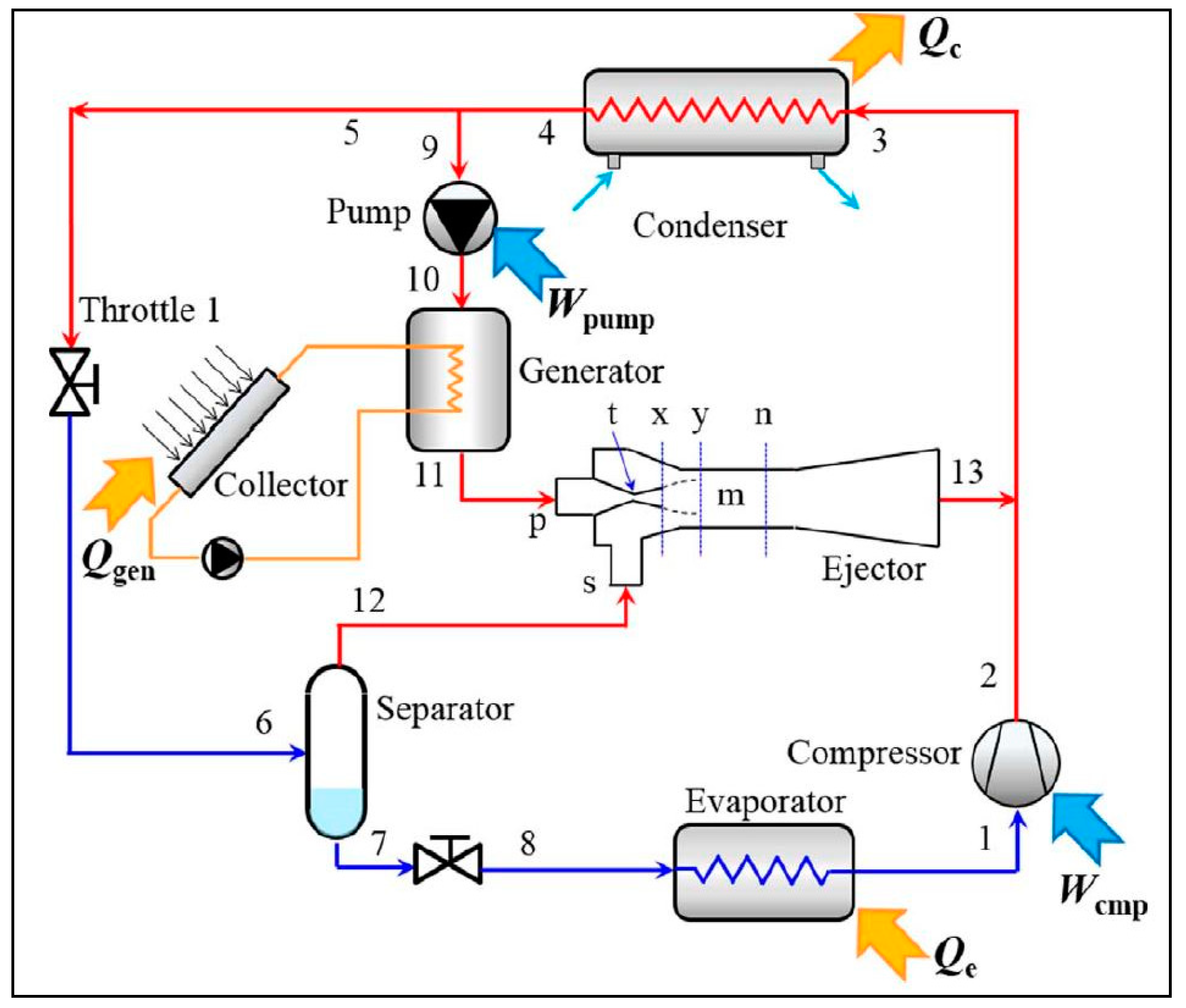
8. Recent Ejector Refrigeration Systems (ERS) Studies
8.1. Conventional ERS
8.1.1. Conventional ERS Theoretical Studies
8.1.2. Conventional ERS Experimental Studies
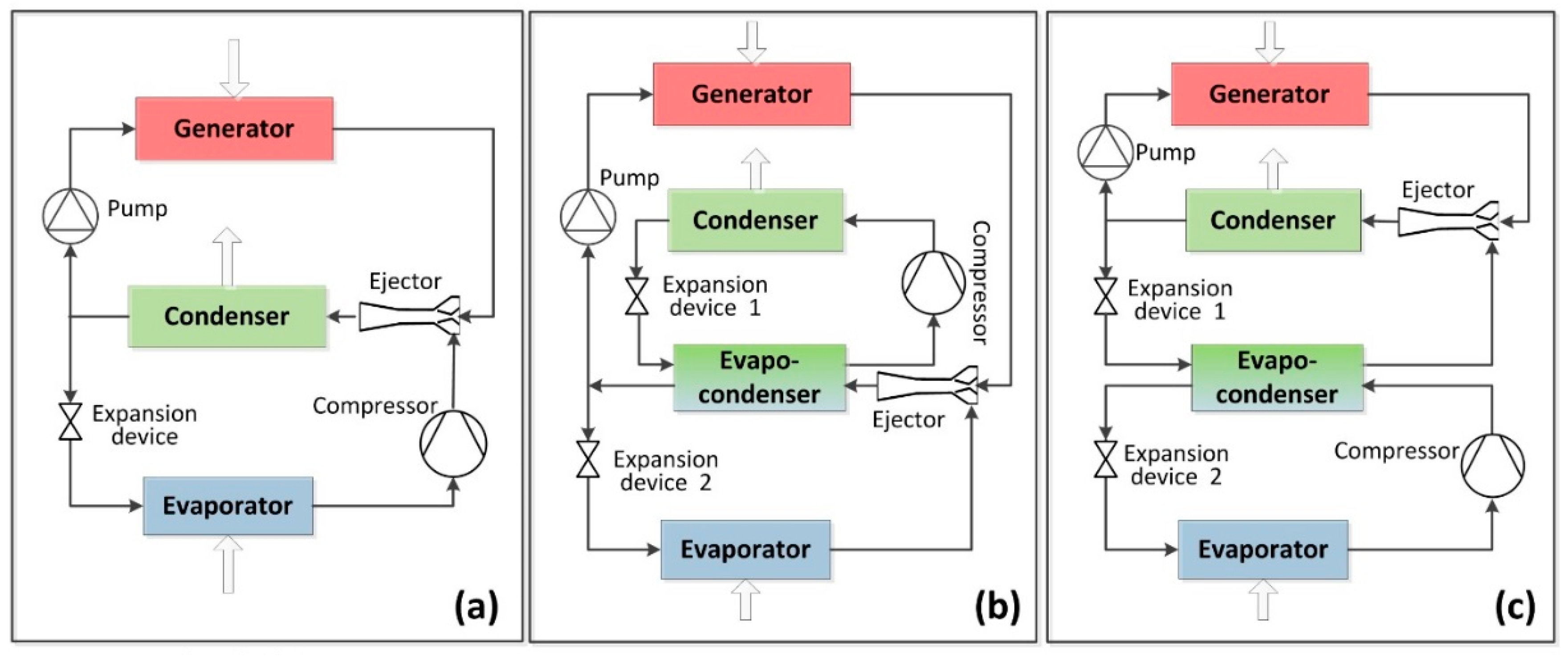
8.2. Ejector Combinations with Conventional Technologies
8.2.1. Combined ERS Theoretical Studies
8.2.2. Combined ERS Experimental Studies
9. Conclusions
- The ejector as a component is presented as theoretically and experimentally tested in terms of performance and operation under a controlled environment in which inlet and outlet conditions are imposed.
- The conventional ERS tested and analysed in the context of refrigeration and air-conditioning.
- More complex combined systems integrating ejectors and other technologies to work in complementarity.
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |||
| A | area | L | length |
| CAM | Constant Area Mixing | M | Mach number |
| CFD | Computational Fluid Dynamics | mass flow rate | |
| COP | Coefficient of performance | NXP | nozzle exit position |
| Cp | Specific heat | P | pressure |
| CPM | Constant Pressure Mixing | Q | capacity |
| CRMC | Constant Rate of Momentum Change | R, r | ideal gas constant |
| D | diameter | T | temperature |
| E | total energy | t | time |
| ERS | Ejector Refrigeration Systems | V, u, v | velocity components |
| ESDU | Engineering Sciences Data Unit | VGE | Variable Geometry Ejector |
| h | enthalpy | W | energy consumption |
| k | conductivity | xi | Cartesian coordinate |
| Greek symbols | |||
| α | nozzle convergent angle | μ | dynamic viscosity |
| β | nozzle divergent angle | ρ | density |
| δ | mixing length ratio | τ | compression ratio, stress tensor |
| η | diffuser angle, efficiency | ϕ | area ratio |
| θ | nozzle area ratio | φ | mixing convergent angle (degree) |
| κ | gas constant | ω | entrainment ratio |
| Subscripts/superscripts | |||
| 0 | stagnation | m | mixing |
| * | critical | me | mechanical |
| b | back | n | nozzle |
| c | condenser | p | primary |
| dif | diffuser | pu | pump |
| e | evaporator | s | secondary |
| f | effective | t | throat, turbulent |
| g | generator | th | thermal |
| is | isentropic | x | nozzle outlet |
References
- ASHRAE Steam-Jet Refrigeration Equipment. In ASHRAE Equipment Handbook; ASHRAE: Atlanta, GA, USA, 1983; pp. 13.1–13.6.
- Decker, L.O. Consider the cold facts about steam-jet vacuum cooling. Chem. Eng. Prog. 1993, 89, 1. [Google Scholar]
- Sun, D.W.; Eames, I. Recent developments in the design theories and applications of ejectors-a review. J. Inst. Energy 1995, 68, 65–79. [Google Scholar]
- He, S.; Li, Y.; Wang, R.Z. Progress of mathematical modeling on ejectors. Renew. Sustain. Energy Rev. 2009, 13, 1760–1780. [Google Scholar] [CrossRef]
- Abdulateef, J.M.; Sopian, K.; Alghoul, M.A.; Sulaiman, M.Y. Review on solar-driven ejector refrigeration technologies. Renew. Sustain. Energy Rev. 2009, 13, 1338–1349. [Google Scholar] [CrossRef]
- Rahamathullah, M.R.; Palani, K.; Venkatakrishnan, P. A Review On Historical And Present Developments In Ejector Systems. Int. J. Eng. Res. Appl. 2013, 3, 10–34. [Google Scholar]
- Chen, X.; Omer, S.; Worall, M.; Riffat, S. Recent developments in ejector refrigeration technologies. Renew. Sustain. Energy Rev. 2013, 19, 629–651. [Google Scholar] [CrossRef]
- Chen, J.; Jarall, S.; Havtun, H.; Palm, B. A review on versatile ejector applications in refrigeration systems. Renew. Sustain. Energy Rev. 2015, 49, 67–90. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 53, 373–407. [Google Scholar] [CrossRef]
- Little, A.B.; Garimella, S. A critical review linking ejector flow phenomena with component- and system-level performance. Int. J. Refrig. 2016, 70, 243–268. [Google Scholar] [CrossRef]
- Keenan, J.; Neumann, E.; Lustwerk, F. A simple air ejector. J. Appl. Mech. Trans. ASME 1942, 64, 75–81. [Google Scholar]
- Keenan, J.H.; Neumann, E.P.; Lustwerk, F. An investigation of ejector design by analysis and experiment. J. Appl. Mech. 1950, 72, 299–309. [Google Scholar]
- Aphornratana, S.; Chungpaibulpatana, S.; Srikhirin, P. Experimental investigation of an ejector refrigerator: Effect of mixing chamber geometry on system performance. Int. J. Energy Res. 2001, 25, 397–411. [Google Scholar] [CrossRef]
- Yapici, R.; Ersoy, H.K. Performance characteristics of the ejector refrigeration system based on the constant area ejector flow model. Energy Convers. Manag. 2005, 46, 3117–3135. [Google Scholar] [CrossRef]
- Pianthong, K.; Seehanam, W.; Behnia, M.; Sriveerakul, T.; Aphornratana, S. Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique. Energy Convers. Manag. 2007, 48, 2556–2564. [Google Scholar] [CrossRef]
- Cao, Y.; Ling, J. Performance evaluation and CFD analysis of a new jet ejector employing a conical porous duct. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Honolulu, HI, USA, 6–10 July 2003; pp. 139–145. [Google Scholar]
- Grazzini, G.; Mariani, A. A simple program to design a multi-stagejet-pump for refrigeration cycles. Energy Convers. Manag. 1998, 39, 1827–1834. [Google Scholar] [CrossRef]
- Grazzini, G.; Rocchetti, A. Numerical optimisation of a two-stage ejector refrigeration plant. Int. J. Refrig. 2002, 25, 621–633. [Google Scholar] [CrossRef]
- Kong, F.; Kim, H.D. Analytical and computational studies on the performance of a two-stage ejector-diffuser system. Int. J. Heat Mass Transf. 2015, 85, 71–87. [Google Scholar] [CrossRef]
- Eames, I.W. A new prescription for the design of supersonic jet-pumps: The constant rate of momentum change method. Appl. Therm. Eng. 2002, 22, 121–131. [Google Scholar] [CrossRef]
- Eames, I.W.; Petrenko, V.; Ablwaifa, A. Design and experimental investigation of a jet pump refrigerator. In Proceedings of the HPC 2004 3rd International Conference on Heat Powered Cycles, Larnaca, Cyprus, 10–13 October 2004. [Google Scholar]
- Ablwaifa, A. A Theoretical and Experimental Investigation of Jet Pump Refrigeration; University of Nottingham: Nottingham, UK, 2006. [Google Scholar]
- Kitrattana, B.; Aphornratana, S.; Thongtip, T.; Ruangtrakoon, N. Comparison of traditional and CRMC ejector performance used in a steam ejector refrigeration. Energy Procedia 2017, 138, 476–481. [Google Scholar] [CrossRef]
- Kumar, V.; Singhal, G.; Subbarao, P.M.V. Realization of novel constant rate of kinetic energy change (CRKEC) supersonic ejector. Energy 2018, 164, 694–706. [Google Scholar] [CrossRef]
- Chang, Y.J.; Chen, Y.M. Enhancement of a steam-driven ejector using a novel application of the petal nozzle. J. Chin. Inst. Eng. Trans. Chin. Inst. Eng. Ser. A 2000, 23, 677–686. [Google Scholar] [CrossRef]
- Garris, C.A. Pressure Exchanging Ejector and Refrigeration Apparatus and Method. U.S. Patent 5647221A, 1997. [Google Scholar]
- Garris, C.A.; Hong, W.J.; Mavriplis, C.M.; Shipman, J. The Pressure-Exchange Ejector Heat Pump. In Proceedings of the ASME International Mechanical Engineering Conference and Exposition, Anaheim, CA, USA, 15–20 November 1998; pp. 15–20. [Google Scholar]
- Alhussan, K.; Garris, C.A. Non-Steady Three-Dimensional Flow Field Analysis in Supersonic Flow Induction. In Proceedings of the ASME 2002 Joint US-European Fluids Engineering Division Conference, Montreal, QC, Canada, 14–18 July 2002. [Google Scholar]
- Hong, W.J.; Alhussan, K.; Zhang, H.; Garris, C.A. A novel thermally driven rotor-vane/pressure-exchange ejector refrigeration system with environmental benefits and energy efficiency. Energy 2004, 29, 2331–2345. [Google Scholar] [CrossRef]
- Alhussan, K.; Garris, C.A. Effect of Changing Throat Diameter Ratio on a Steam Supersonic Pressure Exchange Ejector. Mod. Phys. Lett. B 2005, 19, 1715–1718. [Google Scholar] [CrossRef]
- Pietrowicz, S.; Kasperski, J. The numerical modeling of thermo-flow processes in high-speed rotation ejector used in refrigerating system. In Proceedings of the 22nd International Congress of Refrigeration, Beijing, China, 21–26 August 2007. [Google Scholar]
- Yang, X.; Long, X.; Yao, X. Numerical investigation on the mixing process in a steam ejector with different nozzle structures. Int. J. Therm. Sci. 2012, 56, 95–106. [Google Scholar] [CrossRef]
- Opgenorth, M.J.; Sederstrom, D.; McDermott, W.; Lengsfeld, C.S. Maximizing pressure recovery using lobed nozzles in a supersonic ejector. Appl. Therm. Eng. 2012, 37, 396–402. [Google Scholar] [CrossRef]
- Kong, F.S.; Kim, H.D.; Jin, Y.; Setoguchi, T. Application of Chevron nozzle to a supersonic ejector-diffuser system. Procedia Eng. 2013, 56, 193–200. [Google Scholar] [CrossRef]
- Rao, S.; Jagadeesh, G. Novel supersonic nozzles for mixing enhancement in supersonic ejectors. Appl. Therm. Eng. 2014, 71, 62–71. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Bypass ejector with an annular cavity in the nozzle wall to increase the entrainment: Experimental and numerical validation. Energy 2014, 68, 174–181. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Z.; Li, Y.; Shi, C. Combined auxiliary entrainment and structure optimization for performance improvement of steam ejector with consideration of back pressure variation. Energy Convers. Manag. 2018, 166, 163–173. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Z.; Shi, C.; Li, Y. A novel steam ejector with pressure regulation to optimize the entrained flow passage for performance improvement in MED-TVC desalination system. Energy 2018, 158, 305–316. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Z.; Shi, C.; Li, Y. A novel steam ejector with pressure regulation to dredge the blocked entrained flow for performance improvement in MED-TVC desalination system. Energy Convers. Manag. 2018, 172, 237–247. [Google Scholar] [CrossRef]
- Vermeulen, P.J.; Ramesh, V.; Meng, G.C.; Miller, D.N.; Domel, N. Air Ejector Pumping Enhancement through Pulsing Primary Flow. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, Oregon, 28 June–1 July 2004. [Google Scholar]
- Ouzzane, M.; Aidoun, Z. Model development and numerical procedure for detailed ejector analysis and design. Appl. Therm. Eng. 2003, 23, 2337–2351. [Google Scholar] [CrossRef]
- Dvorak, V.; Vit, T. Experimental And Numerical Study Of Constant Area Mixing. In Proceedings of the 16th International Symposium on Transport Phenomena, Prague, Czech Republic, 29 August–1 September 2005; pp. 1–7. [Google Scholar]
- Elbel, S. Predrag Hrnjak Ejector Refrigeration: An Overview of Historical and Present Developments with an Emphasis on Air-Conditioning Applications. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 14–17 July 2008; 884p. [Google Scholar]
- Aidoun, Z.; Ouzzane, M. The effect of operating conditions on the performance of a supersonic ejector for refrigeration. Int. J. Refrig. 2004, 27, 974–984. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. Ejectors: applications in refrigeration technology. Renew. Sustain. Energy Rev. 2004, 8, 129–155. [Google Scholar] [CrossRef]
- Boumaraf, L.; Lallemand, A. Comportement d’un éjecteur dans des conditions de fonctionnement nominales et non nominales. In Proceedings of the 12th JITH, Tanger, Morocco, 15–17 November 2005. [Google Scholar]
- Khalil, A.; Fatouh, M.; Elgendy, E. Ejector design and theoretical study of R134a ejector refrigeration cycle. Int. J. Refrig. 2011, 34, 1684–1698. [Google Scholar] [CrossRef]
- García Del Valle, J.; Saíz Jabardo, J.M.; Castro Ruiz, F.; San José Alonso, J.F. An experimental investigation of a R-134a ejector refrigeration system. Int. J. Refrig. 2014, 46, 105–113. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. An experimental investigation of a steam ejector refrigerator: The analysis of the pressure profile along the ejector. Appl. Therm. Eng. 2004, 24, 311–322. [Google Scholar] [CrossRef]
- Huang, B.J.; Jiang, C.B.; Hu, F.L. Ejector performance characteristics and design analysis of jet refrigeration system. J. Eng. Gas. Turbine Power 1985, 107, 792–802. [Google Scholar] [CrossRef]
- Eames, I.; Aphornratana, S.; Haider, H. A theoretical and experimental study of a small-scale steam jet refrigerator. Int. J. Refrig. 1995, 18, 378–386. [Google Scholar] [CrossRef]
- Huang, M.C.; Chen, S.L. An experimental investigation of ejector performance characteristics in a jet refrigeration system. Journal of the Chinese Institute of Chemical Engineers 1996, 27, 91–100. [Google Scholar]
- Yapici, R.; Yetişen, C.C. Experimental study on ejector refrigeration system powered by low grade heat. Energy Convers. Manag. 2007, 48, 1560–1568. [Google Scholar] [CrossRef]
- Ablwaifa, A.; Eames, I.W.; Petrenko, V.O. Experimental validation of CFD model used to design jet-pumps. In Proceedings of the International Seminar on Ejector/jet- Pump Technology and Application, Louvain, Belgium, 7–9 September 2009. [Google Scholar]
- Shestopalov, K.O.; Huang, B.J.; Petrenko, V.O.; Volovyk, O.S. Investigation of an experimental ejector refrigeration machine operating with refrigerant R245fa at design and off-design working conditions. Part 2. Theoretical and experimental results. Int. J. Refrig. 2015, 55, 212–223. [Google Scholar] [CrossRef]
- Shestopalov, K.O.; Huang, B.J.; Petrenko, V.O.; Volovyk, O.S. Investigation of an experimental ejector refrigeration machine operating with refrigerant R245fa at design and off-design working conditions. Part 1. Theoretical analysis. Int. J. Refrig. 2015, 55, 201–211. [Google Scholar] [CrossRef]
- Yan, J.; Chen, G.; Liu, C.; Tang, L.; Chen, Q. Experimental investigations on a R134a ejector applied in a refrigeration system. Appl. Therm. Eng. 2017, 110, 1061–1065. [Google Scholar] [CrossRef]
- Sun, D.W. Geometry ejectors and their applications in ejector refrigeration systems. Energy 1996, 21, 919–929. [Google Scholar] [CrossRef]
- Selvaraju, A.; Mani, A. Experimental investigation on R134a vapour ejector refrigeration system. Int. J. Refrig. 2006, 29, 1160–1166. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Sun, C.-Y. Experimental study of the performance characteristics of a steam-ejector refrigeration system. Exp. Therm. Fluid Sci. 1997, 15, 384–394. [Google Scholar] [CrossRef]
- Yapici, R. Experimental investigation of performance of vapor ejector refrigeration system using refrigerant R123. Energy Convers. Manag. 2008, 49, 953–961. [Google Scholar] [CrossRef]
- Thongtip, T.; Aphornratana, S. An alternative analysis applied to investigate the ejector performance used in R141b jet-pump refrigeration system. Int. J. Refrig. 2015, 53, 20–33. [Google Scholar] [CrossRef]
- Nahdi, E.; Champoussin, J.C.; Hostache, G.; Chéron, J. Optimal geometric parameters of a cooling ejector-compresso. Int. J. Refrig. 1993, 16, 67–72. [Google Scholar] [CrossRef]
- Eames, I.W.; Wu, S.; Worral, M.; Aphornratana, S. An experimental investigation of steam ejectors for applications in jet-pump refrigerators powered by low-grade heat. J. Power Energy 1999, 213, 351–361. [Google Scholar] [CrossRef]
- Huang, B.J.; Chang, J.M. Empirical correlation for ejector design. Int. J. Refrig. 1999, 22, 379–388. [Google Scholar] [CrossRef]
- Aphornratana, S.; Eames, I.W. A small capacity steam-ejector refrigerator: experimental investigation of a system using ejector with movable primary nozzle. Int. J. Refrig. 1997, 20, 352–358. [Google Scholar] [CrossRef]
- Yapici, R.; Ersoy, H.K.; Aktoprakoǧlu, A.; Halkaci, H.S.; Yiǧit, O. Experimental determination of the optimum performance of ejector refrigeration system depending on ejector area ratio. Int. J. Refrig. 2008, 31, 1183–1189. [Google Scholar] [CrossRef]
- Varga, S.; Oliveira, A.C.; Diaconu, B. Influence of geometrical factors on steam ejector performance—A numerical assessment. Int. J. Refrig. 2009, 32, 1694–1701. [Google Scholar] [CrossRef]
- Chong, D.; Hu, M.; Chen, W.; Wang, J.; Liu, J.; Yan, J. Experimental and numerical analysis of supersonic air ejector. Appl. Energy 2014, 130, 679–684. [Google Scholar] [CrossRef]
- Huang, B.J.; Chang, J.M.; Wang, C.P.; Petrenko, V.A. 1-D analysis of ejector performance. Int. J. Refrig. 1999, 22, 354–364. [Google Scholar] [CrossRef]
- Riffat, S.B.; Omer, S.A. CFD modelling and experimental investigation of an ejector refrigeration system using methanol as the working fluid. Int. J. Energy Res. 2001, 25, 115–128. [Google Scholar] [CrossRef]
- Rusly, E.; Aye, L.; Charters, W.W.S.; Ooi, A. CFD analysis of ejector in a combined ejector cooling system. Int. J. Refrig. 2005, 28, 1092–1101. [Google Scholar] [CrossRef]
- Eames, I.W.; Ablwaifa, A.E.; Petrenko, V. Results of an experimental study of an advanced jet-pump refrigerator operating with R245fa. Appl. Therm. Eng. 2007, 27, 2833–2840. [Google Scholar] [CrossRef]
- Chen, W.; Chong, D.; Yan, J.; Liu, J. The numerical analysis of the effect of geometrical factors on natural gas ejector performance. Appl. Therm. Eng. 2013, 59, 21–29. [Google Scholar] [CrossRef]
- Sriveerakul, T.; Aphornratana, S. Performance prediction of steam ejector using computational fluid dynamics: Part 2. Flow structure of a steam ejector influenced by operating pressures and geometries. Int. J. Therm. Sci. 2007, 46, 823–833. [Google Scholar] [CrossRef]
- Ablwaifa, A.; Eames, I.W.; Petrenko, V. Use of CFD in prediction of jet-pump performances with R141b as refrigerant. In Proceedings of the XIXth National Congress of Thermodynamicists, Sopot, Poland, 5–8 September 2005. [Google Scholar]
- Wang, J.; Tao, L.; Wang, Y.; Guo, J. CFD analysis of ejector in an ejector cooling system. In Proceedings of the International Congress of Refrigeration, Beijing, China, 21–26 August 2007. [Google Scholar]
- Zhu, Y.; Cai, W.; Wen, C.; Li, Y. Numerical investigation of geometry parameters for design of high performance ejectors. Appl. Therm. Eng. 2009, 29, 898–905. [Google Scholar] [CrossRef]
- Lin, C.; Cai, W.; Li, Y.; Yan, J.; Hu, Y.; Giridharan, K. Numerical investigation of geometry parameters for pressure recovery of an adjustable ejector in multi-evaporator refrigeration system. Appl. Therm. Eng. 2013, 61, 649–656. [Google Scholar] [CrossRef]
- Yan, J.; Lin, C.; Cai, W.; Chen, H.; Wang, H. Experimental study on key geometric parameters of an R134A ejector cooling system. Int. J. Refrig. 2016, 67, 102–108. [Google Scholar] [CrossRef]
- Ariafar, K. Performance evaluation of a model thermocompressor using computational fluid dynamics. Int. J. Mech. 2012, 6, 35–42. [Google Scholar]
- Ruangtrakoon, N.; Thongtip, T.; Aphornratana, S.; Sriveerakul, T. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle. Int. J. Therm. Sci. 2013, 63, 133–145. [Google Scholar] [CrossRef]
- Yan, J.; Cai, W.; Lin, C.; Li, C.; Li, Y. Experimental study on performance of a hybrid ejector-vapor compression cycle. Energy Convers. Manag. 2016, 113, 36–43. [Google Scholar] [CrossRef]
- Thongtip, T.; Aphornratana, S. An experimental analysis of the impact of primary nozzle geometries on the ejector performance used in R141b ejector refrigerator. Appl. Therm. Eng. 2017, 110, 89–101. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Zou, T.; Zhang, H. Influences of area ratio and surface roughness on homogeneous condensation in ejector primary nozzle. Energy Convers. Manag. 2017, 149, 168–174. [Google Scholar] [CrossRef]
- Chen, J.; Havtun, H.; Palm, B. Parametric analysis of ejector working characteristics in the refrigeration system. Appl. Therm. Eng. 2014, 69, 130–142. [Google Scholar] [CrossRef]
- Boumaraf, L.; Lallemand, A. Modeling of an ejector refrigerating system operating in dimensioning and off-dimensioning conditions with the working fluids R142b and R600a. Appl. Therm. Eng. 2009, 29, 265–274. [Google Scholar] [CrossRef]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results. Int. J. Therm. Sci. 2007, 46, 812–822. [Google Scholar] [CrossRef]
- Jia, Y.; Wenjian, C. Area ratio effects to the performance of air-cooled ejector refrigeration cycle with R134a refrigerant. Energy Convers. Manag. 2012, 53, 240–246. [Google Scholar] [CrossRef]
- Mohamed, S.; Shatilla, Y.; Zhang, T. CFD-based design and simulation of hydrocarbon ejector for cooling. Energy 2019, 167, 346–358. [Google Scholar] [CrossRef]
- Varga, S.; Lebre, P.M.S.; Oliveira, A.C. CFD study of a variable area ratio ejector using R600a and R152a refrigerants. Int. J. Refrig. 2013, 36, 157–165. [Google Scholar] [CrossRef]
- Chong, D.T.; Yan, J.J.; Wu, G.S.; Liu, J.P. Structural optimization and experimental investigation of supersonic ejectors for boosting low pressure natural gas. Appl. Therm. Eng. 2009, 29, 2799–2807. [Google Scholar] [CrossRef]
- Karthick, S.K.; Rao, S.M.V.; Jagadeesh, G.; Reddy, K.P.J. Experimental parametric studies on the performance and mixing characteristics of a low area ratio rectangular supersonic gaseous ejector by varying the secondary flow rate. Energy 2018, 161, 832–845. [Google Scholar] [CrossRef]
- Ji, M.K.; Utomo, T.; Woo, J.S.; Lee, Y.H.; Jeong, H.M.; Chung, H.S. CFD investigation on the flow structure inside thermo vapor compressor. Energy 2010, 35, 2694–2702. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, W.; Omer, S.A.; Riffat, S.B. Experimental investigation of a novel steam ejector refrigerator suitable for solar energy applications. Appl. Therm. Eng. 2010, 30, 1320–1325. [Google Scholar] [CrossRef]
- Varga, S.; Oliviera, A.C.; Ma, X.; Omer, S.A.; Zhang, W.; Riffat, S.B. Experimental and numerical analysis of a variable area ratio steam ejector. Int. J. Refrig. 2011, 34, 1668–1675. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, S.; Yang, Y.; Tian, X. Experimental Investigation of Adjustable Ejector Performance. J. Energy Eng. 2012, 138, 125–129. [Google Scholar] [CrossRef]
- Pereira, P.R.; Varga, S.; Oliveira, A.C.; Soares, J. Development and Performance of an Advanced Ejector Cooling System for a Sustainable Built Environment. Front. Mech. Eng. 2015, 1, 1–12. [Google Scholar] [CrossRef]
- Chen, W.; Shi, C.; Zhang, S.; Chen, H.; Chong, D.; Yan, J. Theoretical analysis of ejector refrigeration system performance under overall modes. Appl. Energy 2017, 185, 2074–2084. [Google Scholar] [CrossRef]
- Varga, S.; Oliveira, A.C.; Diaconu, B. Numerical assessment of steam ejector efficiencies using CFD. Int. J. Refrig. 2009, 32, 1203–1211. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Cai, W.; Hu, Y.; Chen, H.; Yan, J. Analysis on performance characteristics of ejector with variable area-ratio for multi-evaporator refrigeration system based on experimental data. Appl. Therm. Eng. 2014, 68, 125–132. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, X.; Dang, C.; Hihara, E. Ejector performance analysis under overall operating conditions considering adjustable nozzle structure. Int. J. Refrig. 2017, 84, 274–286. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, X.; Shimizu, A.; Hihara, E.; Dang, C. Effects of the nozzle configuration on solar-powered variable geometry ejectors. Sol. Energy 2017, 150, 275–286. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Wang, X.; Zhao, H. Design and numerical investigation of an adaptive nozzle exit position ejector in multi-effect distillation desalination system. Energy 2017, 140, 673–681. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Zou, T.; Du, J.; Jia, F. Auto-tuning ejector for refrigeration system. Energy 2018, 161, 536–543. [Google Scholar] [CrossRef]
- Petrovic, A.; Jovanovic, M.Z.; Genic, S.; Bugaric, U.; Delibasic, B. Evaluating performances of 1-D models to predict variable area supersonic gas ejector performances. Energy 2018, 163, 270–289. [Google Scholar] [CrossRef]
- Bouhanguel, A. Etude Numérique et Expérimentale de l’interaction Entre deux Écoulements Compressibles dans un Éjecteur Supersonique; Université de Franche-Comté: Besançon, France, 2013. [Google Scholar]
- Matsuo, K.; Miyazato, Y.; Kim, H. Shock train and pseudo-shock phenomena in internal gas flows. Prog. Aerosp. Sci. 1999, 35, 33–100. [Google Scholar] [CrossRef]
- Rao, S.M.V.; Jagadeesh, G. Observations on the non-mixed length and unsteady shock motion in a two dimensional supersonic ejector. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Zegenhagen, M.T.; Ziegler, F. A one-dimensional model of a jet-ejector in critical double choking operation with R134a as a refrigerant including real gas effects. Int. J. Refrig. 2015, 55, 72–84. [Google Scholar] [CrossRef]
- Lamberts, O.; Chatelain, P.; Bartosiewicz, Y. Numerical and experimental evidence of the Fabri-choking in a supersonic ejector. Int. J. Heat Fluid Flow 2018, 69, 194–209. [Google Scholar] [CrossRef]
- Fabri, J.; Siestrunck, R. Supersonic Air Ejectors. Adv. Appl. Mech. 1958, 5, 1–34. [Google Scholar]
- Munday, J.T.; Bagster, D.F. A New Ejector Theory Applied to Steam Jet Refrigeration. Ind. Eng. Chem. Process. Des. Dev. 1977, 16, 442–449. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Turbulence modeling of a single-phase R134a supersonic ejector. Part 2: Local flow structure and exergy analysis. Int. J. Refrig. 2016, 61, 153–165. [Google Scholar] [CrossRef]
- Singhal, G.; Dawar, A.L.; Subbarao, P.M.V. Application of profiled ejector in chemical lasers. Appl. Therm. Eng. 2008, 28, 1333–1341. [Google Scholar] [CrossRef]
- Sun, D.-W.; Eames, I.W. Performance characteristics of HCFC-123 ejector refrigeration cycles. Int. J. Energy Res. 1996, 20, 871–885. [Google Scholar] [CrossRef]
- Alexis, G.K.; Karayiannis, E.K. A solar ejector cooling system using refrigerant R134a in the Athens area. Renew. Energy 2005, 30, 1457–1469. [Google Scholar] [CrossRef]
- Butrymowicz, D.; Śmierciew, K.; Karwacki, J.; Gagan, J. Experimental investigations of low-temperature driven ejection refrigeration cycle operating with isobutane. Int. J. Refrig. 2014, 39, 196–209. [Google Scholar] [CrossRef]
- Butrymowicz, D.; Śmierciew, K.; Karwacki, J. Investigation of internal heat transfer in ejection refrigeration systems. Int. J. Refrig. 2014, 40, 131–139. [Google Scholar] [CrossRef]
- Ruangtrakoon, N.; Aphornratana, S. Development and performance of steam ejector refrigeration system operated in real application in Thailand. Int. J. Refrig. 2014, 48, 142–152. [Google Scholar] [CrossRef]
- Chandra, V.V.; Ahmed, M.R. Experimental and computational studies on a steam jet refrigeration system with constant area and variable area ejectors. Energy Convers. Manag. 2014, 79, 377–386. [Google Scholar] [CrossRef]
- Nguyen, V.M.; Riffat, S.B.; Doherty, P.S. Development of a solar-powered passive ejector cooling system. Appl. Therm. Eng. 2001, 21, 157–168. [Google Scholar] [CrossRef]
- Thongtip, T.; Aphornratana, S. Development and performance of a heat driven R141b ejector air conditioner: Application in hot climate country. Energy 2018, 160, 556–572. [Google Scholar] [CrossRef]
- Chen, L.T. A heat driven mobile refrigeration cycle analysis. Energy Convers. 1978, 18, 25–29. [Google Scholar] [CrossRef]
- Salim, M. Thermally activated mobile ejector refrigeration system analysis. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2004, 218, 1055–1061. [Google Scholar] [CrossRef]
- Wang, L.; Cai, W.; Zhao, H.; Lin, C.; Yan, J. Experimentation and cycle performance prediction of hybrid A/C system using automobile exhaust waste heat. Appl. Therm. Eng. 2016, 94, 314–323. [Google Scholar] [CrossRef]
- Jaruwongwittaya, T.; Chen, G. Energy Procedia Application of Two Stage Ejector Cooling System in a Bus. Energy Procedia 2012, 14, 187–197. [Google Scholar] [CrossRef]
- Choutapalli, I.M.; Anjaneyulu, K.; Alkislar, M.B. Pulsed-Jet Ejector Thrust Augumentor Characteristics. J. Propuls. Power 2012, 28, 293–306. [Google Scholar] [CrossRef]
- Lijo, V.; Kim, H.D.; Matsuo, S.; Setoguchi, T. A study of the supersonic ejector-diffuser system with an inlet orifice. Aerosp. Sci. Technol. 2012, 23, 321–329. [Google Scholar] [CrossRef]
- Shan, Y.; Zhang, J.-Z.; Ren, X.W. Numerical modeling on pumping performance of piccolo-tube multi-nozzles supersonic ejector in an oil radiator passage. Energy 2018, 158, 216–227. [Google Scholar] [CrossRef]
- Choi, Y.H.; Soh, W.Y. Computational Analysis of the Flowfield Ejector Nozzle of a Two-Dimensional Ejector Nozzle; NASA: Washington, DC, USA, 1990.
- Gauthier, J.E.D.; Birk, A.M. Optimization of an Ejector Using Computational Fluid Dynamics. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, FEDSM97-3416, Vancouver, BC, Canada, 22–26 June 1997. [Google Scholar]
- Wang, J.; Chen, F. On the start condition of a second throat ejector diffuser. Aeronaut. J. 1996, 100, 321–326. [Google Scholar]
- Desevaux, P.; Lanzetta, F.; Bailly, Y. CFD modelling of shock train inside a supersonic ejector: Validation against flow visualizations and pressure measurements in the case of zero-secondary flow. In Proceedings of the 10th International Symposium on Flow Visualization, Kyoto, Japan, 26–29 August 2002. [Google Scholar]
- Desevaux, P.; Lanzetta, F. Computational Fluid Dynamic Modelling of Pseudoshock Inside a Zero-Secondary Flow Ejector. AIAA J. 2004, 42, 1480–1483. [Google Scholar] [CrossRef]
- Desevaux, P.; Marynowski, T.; Khan, M. CFD Prediction of Supersonic Ejectors Performance. Int. J. Turbo. Jet-Engines 2006, 23, 173–181. [Google Scholar] [CrossRef]
- Chen, F.; Liu, C.F.; Yang, J.Y. Supersonic flow in the second-throat ejector-diffuser system. J. Spacecr. Rockets 1994, 31, 123–129. [Google Scholar] [CrossRef]
- Dvorak, V. Shape optimization of supersonic ejector for supersonic wind tunnel. Appl. Comput. Mech. 2010, 4, 15–24. [Google Scholar]
- Dong, T.Z.; Mankbadi, R.R. Simulation of Unsteady Flow in Nozzle-Ejector Mixer. J. Propuls. Power 1999, 15, 539–543. [Google Scholar] [CrossRef]
- Presz, W.; Reynolds, G.; Hunter, C. Thrust Augmentation with Mixer/Ejector Systems. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, Nevada, 14–17 January 2002. [Google Scholar]
- Matsuo, K.; Sasaguchi, K.; Tasaki, K.; Mochizuki, H. Investigation of Supersonic Air Ejectors: Part 1. Performance in the Case of Zero-Secondary Flow. Bull. JSME 1981, 24, 2090–2097. [Google Scholar] [CrossRef]
- Akteriana, S. Improving the energy efficiency of traditional multi-stage steam-jet-ejector vacuum systems for deodorizing edible oils. Procedia Food Sci. 2011, 1, 1785–1791. [Google Scholar] [CrossRef]
- Reddick, C.; Sorin, M.; Sapoundjiev, H.; Aidoun, Z. Carbon capture simulation using ejectors for waste heat upgrading. Energy 2016, 100, 251–261. [Google Scholar] [CrossRef]
- Reddick, C.; Sorin, M.; Sapoundjiev, H.; Aidoun, Z. Effect of a mixture of carbon dioxide and steam on ejector performance: An experimental parametric investigation. Exp. Therm. Fluid Sci. 2018, 92, 353–365. [Google Scholar] [CrossRef]
- Bowrey, R.G.; Dang, V.B.; Sergeant, G.D. An energy model to minimize energy consumption in a low- temperature operation, steam ejector-cooling system. J. Energy Inst. 1986, 45, 45–48. [Google Scholar]
- Shaozhi, Z.; Luo, J.; Wang, Q.; Chen, G. Step utilization of energy with ejector in a heat driven freeze drying system. Energy 2018, 164, 734–744. [Google Scholar]
- Al-ansary, H.A.M. The Use of Ejector Refrigeration Systems for Turbine Inlet Air Cooling: A Thermodynamic and CFD Study. In Proceedings of the Energy Sustainability Conference, Long Beach, CA, USA, 27–30 July 2007. [Google Scholar]
- Petrenko, V. Application of innovative ejector chillers and air conditioners operating with low boiling refrigerants in tri-generation systems. In Proceedings of the International Seminar on Ejector/jet- Pump Technology and Application, Louvain, Belgium, 7–9 September 2009. [Google Scholar]
- Daubert-Deleris, I.; Hoffmann, P.A.; Fonade, C.; Maranges, C. Hydrodynamic and mass transfer performance of a new aero-ejector with its application to VOC abatement. Chem. Eng. Sci. 2006, 61, 4982–4993. [Google Scholar] [CrossRef]
- Fahmy, A.; Mewes, D.; Ohlrogge, K. On the integration of jet ejectors into hybrid dehydration processes. J. Memb. Sci. 2002, 196, 79–84. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Cai, W. Control oriented modeling of ejector in anode gas recirculation solid oxygen fuel cell systems. Energy Convers. Manag. 2011, 52, 1881–1889. [Google Scholar] [CrossRef]
- Hwang, J.J. Passive hydrogen recovery schemes using a vacuum ejector in a proton exchange membrane fuel cell system. J. Power Sources 2014, 247, 256–263. [Google Scholar] [CrossRef]
- Rao, S.M.V.; Jagadeesh, G. Studies on the effects of varying secondary gas properties in a low entrainment ratio supersonic ejector. Appl. Therm. Eng. 2015, 78, 289–302. [Google Scholar] [CrossRef]
- Maghsoodi, A.; Afshari, E.; Ahmadikia, H. Optimization of geometric parameters for design a high-performance ejector in the proton exchange membrane fuel cell system using artificial neural network and genetic algorithm. Appl. Therm. Eng. 2014, 71, 410–418. [Google Scholar] [CrossRef]
- Yan, J.; Cai, W.; Zhao, L.; Li, Y.; Lin, C. Performance evaluation of a combined ejector-vapor compression cycle. Renew. Energy 2013, 55, 331–337. [Google Scholar] [CrossRef]
- Alasfour, F.N.; Darwish, M.A.; Bin Amer, A.O. Thermal analysis of ME-TVC+MEE desalination systems. Desalination 2005, 174, 39–61. [Google Scholar] [CrossRef]
- Sharifi, N.; Boroomand, M.; Sharifi, M. Numerical assessment of steam nucleation on thermodynamic performance of steam ejectors. Appl. Therm. Eng. 2013, 52, 449–459. [Google Scholar] [CrossRef]
- Sharifi, N.; Boroomand, M. An investigation of thermo-compressor design by analysis and experiment: Part 1. Validation of the numerical method. Energy Convers. Manag. 2013, 69, 217–227. [Google Scholar] [CrossRef]
- Samaké, O.; Galanis, N.; Sorin, M. Thermodynamic study of multi-effect thermal vapour-compression desalination systems. Energy 2014, 72, 69–79. [Google Scholar] [CrossRef]
- Wu, H.; Liu, Z.; Han, B.; Li, Y. Numerical investigation of the influences of mixing chamber geometries on steam ejector performance. Desalination 2014, 353, 15–20. [Google Scholar] [CrossRef]
- Samaké, O.; Galanis, N.; Sorin, M. Thermo-economic analysis of a multiple-effect desalination system with ejector vapour compression. Energy 2018, 144, 1037–1051. [Google Scholar] [CrossRef]
- Cai, L.; He, M. A Numerical Study on the Supersonic Steam Ejector Use in Steam Turbine System. Math. Probl. Eng. 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Sharifi, N.; Sharifi, M. Reducing energy consumption of a steam ejector through experimental optimization of the nozzle geometry. Energy 2014, 66, 860–867. [Google Scholar] [CrossRef]
- Tirmizi, S.A.; Siddiqui, O.K.; Gandhidasan, P.; Zubair, S.M. Performance analysis of an ejector cooling system with a conventional chilled water system. Appl. Therm. Eng. 2014, 66, 113–121. [Google Scholar] [CrossRef]
- Mazzelli, F.; Milazzo, A. Performance analysis of a supersonic ejector cycle working with R245fa. Int. J. Refrig. 2015, 49, 79–92. [Google Scholar] [CrossRef]
- Genc, O.; Toros, S.; Timurkutluk, B. Determination of optimum ejector operating pressures for anodic recirculation in SOFC systems. Int. J. Hydrogen Energy 2017, 42, 20249–20259. [Google Scholar] [CrossRef]
- Chen, W.; Li, B.; Zhang, S.; Liu, M.; Liu, J. Simulation investigation on the design and operation strategy of a 660 MW coal-fired power plant coupled with a steam ejector to ensure NOx reduction ability. Appl. Therm. Eng. 2017, 124, 1103–1111. [Google Scholar] [CrossRef]
- Sadeghi, M.; Yari, M.; Mahmoudi, S.M.S.; Jafari, M. Thermodynamic analysis and optimization of a novel combined power and ejector refrigeration cycle—Desalination system. Appl. Energy 2017, 208, 239–251. [Google Scholar] [CrossRef]
- Alexis, G.K. Estimation of ejector’s main cross sections in steam-ejector refrigeration system. Appl. Therm. Eng. 2004, 24, 2657–2663. [Google Scholar] [CrossRef]
- Khattab, N.M.; Barakat, M.H. Modeling the design and performance characteristics of solar steam-jet cooling for comfort air conditioning. Sol. Energy 2002, 73, 257–267. [Google Scholar] [CrossRef]
- Tarantsev, K.V.; Korosteleva, A.V. Optimization of design of ejector-type mixer for producing fuel emulsions in an electric field. Chem. Pet. Eng. 2013, 49, 173–177. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, J.; Lu, W. Optimized selection of one- and two-stage ejectors under design and off-design conditions. Energy Convers. Manag. 2018, 173, 743–752. [Google Scholar] [CrossRef]
- Riffat, S.B.; Gan, G.; Smith, S. Computational fluid dynamics applied to ejector heat pumps. Appl. Therm. Eng. 1996, 16, 291–297. [Google Scholar] [CrossRef]
- Work, L.T.; Haedrich, V.W. Performance of Ejectors As a Function of the Molecular Weights of Vapors. Ind. Eng. Chem. 1939, 31, 464–477. [Google Scholar] [CrossRef]
- Work, L.T.; Miller, A. Factor C in the Performance of Ejectors As a Function of Molecular Weights of Vapors. Ind. Eng. Chem. 1940, 32, 1241–1243. [Google Scholar] [CrossRef]
- Holton, W.C. Effect of molecular weight of entrained fluid on the performance of steam ejectors. ASME Trans. 1951, 73, 905–910. [Google Scholar]
- DeFrate, L.A.; Hoerl, A.E. Optimum design of ejectors using digital computers. Chem. Eng. Prog. Symp. Ser. 1959, 55, 43–51. [Google Scholar]
- Khoury, F.; Heyman, M.; Resnick, W. Performance Characteristics of Self-Entrainment Ejectors. Ind. Eng. Chem. Process. Des. Dev. 1967, 6, 331–340. [Google Scholar] [CrossRef]
- Lallemand, A.; Dorantès, R.; Staader, J. Performances d’une machine de réfrigération à éjecteur à deux fluides de masses molaires différentes. In Proceedings of the 19th International Congress Refrigeration, Hague, The Netherlands, 20–25 August 1995. [Google Scholar]
- Chou, S.K.; Yang, P.R.; Yap, C. Maximum mass flow ratio due to secondary flow choking in an ejector refrigeration system. Int. J. Refrig. 2001, 24, 486–499. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Chen, W.; Luo, X.; Chen, Y.; Yang, Z.; Eames, I.W. Investigation of the ejector nozzle in refrigeration system. Energy 2018, 157, 571–587. [Google Scholar] [CrossRef]
- Chen, S.; Chen, G.; Fang, L. An experimental study and 1-D analysis of an ejector with a movable primary nozzle that operates with R236fa. Int. J. Refrig. 2015, 60, 19–25. [Google Scholar] [CrossRef]
- Ma, Z.; Bao, H.; Roskilly, A.P. Thermodynamic modelling and parameter determination of ejector for ejection refrigeration systems. Int. J. Refrig. 2017, 75, 117–128. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Jia, L.; Wang, X. Thermodynamic model for all modes performance analysis of supersonic ejector considering non-uniform distribution of flow field. Accepted for publication in. Int. J. Refrig. 2018, 96. [Google Scholar] [CrossRef]
- Alexis, G.K.; Rogdakis, E.D. A verification study of steam-ejector refrigeration model. Appl. Therm. Eng. 2003, 23, 29–36. [Google Scholar] [CrossRef]
- El-Dessouky, H.; Ettouney, H.; Alatiqi, I.; Al-Nuwaibit, G. Evaluation of steam jet ejectors. Chem. Eng. Process. 2002, 41, 551–561. [Google Scholar] [CrossRef]
- Selvaraju, A.; Mani, A. Analysis of an ejector with environment friendly refrigerants. Appl. Therm. Eng. 2004, 24, 827–838. [Google Scholar] [CrossRef]
- Zhu, Y.; Cai, W.; Wen, C.; Li, Y. Shock circle model for ejector performance evaluation. Energy Convers. Manag. 2007, 48, 2533–2541. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y. Novel ejector model for performance evaluation on both dry and wet vapors ejectors. Int. J. Refrig. 2009, 32, 21–31. [Google Scholar] [CrossRef]
- Cardemil, J.M.; Colle, S. A general model for evaluation of vapor ejectors performance for application in refrigeration. Energy Convers. Manag. 2012, 64, 79–86. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Thermodynamic modelling of supersonic gas ejector with droplets. Entropy 2017, 19, 579. [Google Scholar] [CrossRef]
- Galanis, N.; Faucher, G.; Nguyen, M.P. The effects of fluid entry conditions on the performance of vapour-jet compressors. Trans. Can. Soc. Mech. Eng. 1979, 9–14. [Google Scholar] [CrossRef]
- Boumaraf, L.; Lallemand, A. Performances d’une machine tritherme à éjecteur utilisant des mélanges de fluides frigorigènes. Int. J. Refrig. 1999, 22, 580–589. [Google Scholar] [CrossRef]
- Alexis, G.K.; Rogdakis, E.D. Performance characteristics of two combined ejector-absorption cycles. Appl. Therm. Eng. 2002, 22, 97–106. [Google Scholar] [CrossRef]
- Zhu, Y.; Cai, W.; Wen, C.; Li, Y. Simplified ejector model for control and optimization. Energy Convers. Manag. 2008, 49, 1424–1432. [Google Scholar] [CrossRef]
- Elakhdar, M.; Nehdi, E.; Kairouani, L.; Tounsi, N. Simulation of an ejector used in refrigeration systems. Int. J. Refrig. 2011, 34, 1657–1667. [Google Scholar] [CrossRef]
- Tashtoush, B.; Alshare, A.; Al-Rifai, S. Performance study of ejector cooling cycle at critical mode under superheated primary flow. Energy Convers. Manag. 2015, 94, 300–310. [Google Scholar] [CrossRef]
- Samaké, O.; Galanis, N.; Sorin, M. On the design and corresponding performance of steam jet ejectors. Desalination 2016, 381, 15–25. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Hou, W.; Zhao, H.; Zhang, H. Experimental investigation on ejector performance near critical back pressure. Int. J. Refrig. 2017, 80, 158–168. [Google Scholar] [CrossRef]
- Li, F.; Li, R.; Li, X.; Tian, Q. Experimental investigation on a R134a ejector refrigeration system under overall modes. Appl. Therm. Eng. 2018, 137, 784–791. [Google Scholar] [CrossRef]
- Dvorak, V.; Safarik, P. Supersonic flow structure in the entrance part of a mixing chamber of 2d model ejector. J. Therm. Sci. 2003, 12, 344–349. [Google Scholar] [CrossRef]
- Randheer, Y.L.; Patwardhan, A.W. Design aspects of ejectors: Effects of suction chamber geometry. Chem. Eng. Sci. 2008, 63, 3886–3897. [Google Scholar]
- García Del Valle, J.; Sierra-Pallares, J.; Garcia Carrascal, P.; Castro Ruiz, F. An experimental and computational study of the flow pattern in a refrigerant ejector. Validation of turbulence models and real-gas effects. Appl. Therm. Eng. 2015, 89, 795–811. [Google Scholar] [CrossRef]
- Lamberts, O.; Chatelain, P.; Bartosiewicz, Y. New methods for analyzing transport phenomena in supersonic ejectors. Int. J. Heat Fluid Flow 2017, 64, 23–40. [Google Scholar] [CrossRef]
- Croquer, S. Combined CFD and Thermodynamic Analysis of a Supersonic Ejector with Liquid Droplets. Ph.D. Thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, 2018. [Google Scholar]
- Yan, J.; Wen, N.; Wang, L.; Li, X.; Liu, Z.; Li, S. Optimization on ejector key geometries of a two-stage ejector-based multi-evaporator refrigeration system. Energy Convers. Manag. 2018, 175, 142–150. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Desevaux, P.; Mercadier, Y. CFD-experiments integration in the evaluation of six turbulence models for supersonic ejector modeling. In Proceedings of the Integrating CFD and Experiments, Glasgow, UK, 8–9 September 2003. [Google Scholar]
- Hemidi, A.; Henry, F.; Leclaire, S.; Seynhaeve, J.M.; Bartosiewicz, Y. CFD analysis of a supersonic air ejector. Part II: Relation between global operation and local flow features. Appl. Therm. Eng. 2009, 29, 2990–2998. [Google Scholar] [CrossRef]
- Mazzelli, F.; Little, A.B.; Garimella, S.; Bartosiewicz, Y. Computational and experimental analysis of supersonic air ejector: Turbulence modeling and assessment of 3D effects. Int. J. Heat Fluid Flow 2015, 56, 305–316. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Desevaux, P.; Mercadier, Y. Numerical and experimental investigations on supersonic ejectors. Int. J. Heat Fluid Flow 2005, 26, 56–70. [Google Scholar] [CrossRef]
- Hakkaki-Fard, A.; Aidoun, Z.; Ouzzane, M. A computational methodology for ejector design and performance maximisation. Energy Convers. Manag. 2015, 105, 1291–1302. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Computational fluid-dynamics modeling of supersonic ejectors: Screening of turbulence modeling approaches. Appl. Therm. Eng. 2017, 117, 122–144. [Google Scholar] [CrossRef]
- Falsafioon, M.; Aidoun, Z.; Poirier, M. A Numerical and Experimental Study of Ejector Internal Flow Structure and Geometry Modification for Maximized Performance. In Proceedings of the IOP Conference Series: 3rd International Conference Mechanical Engineering and Automation Science, Birmingham, UK, 13–15 October 2017. [Google Scholar]
- Bernstein, A.; Heiser, W.H.; Hevenor, C. Compound-Compressible Nozzle Flow. J. Appl. Mech. 1967, 34, 548–554. [Google Scholar] [CrossRef]
- Li, H.; Shen, S. Analysis of Flow Field in an Ejector With Steam as Working Fluid. In Proceedings of the ASME/JSME 2004 Pressure Vessels and Piping Conference, San Diego, CA, USA, 25–29 JuIy 2004; pp. 227–234. [Google Scholar]
- Al-ansary, H.A.M.; Jeter, S.M. Numerical and Experimental Analysis of Single-Phase and Two-Phase Flow in Ejectors Numerical and Experimental Analysis of Single-Phase and Two-Phase Flow in Ejectors. HVAC R Res. 2004, 10, 521–538. [Google Scholar] [CrossRef]
- Desevaux, P.; Aeschbacher, O. Numerical and Experimental Flow Visualizations of the Mixing Process Inside an Induced Air Ejector. Int. J. Turbo. Jet-Engines 2002, 19, 71–78. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Mercadier, Y. Numerical assessment of ejector operation for refrigeration applications based on CFD. Appl. Therm. Eng. 2006, 26, 604–612. [Google Scholar] [CrossRef]
- Wang, X.D.; Dong, J.L. Numerical study on the performances of steam-jet vacuum pump at different operating conditions. Vacuum 2010, 84, 1341–1346. [Google Scholar] [CrossRef]
- Chen, G.; Zhelezny, V.; Khliyeva, O.; Shestopalov, K.; Ierin, V. Ecological and energy efficiency analysis of ejector and vapor compression air conditioners. Int. J. Refrig. 2017, 74, 127–135. [Google Scholar] [CrossRef]
- Allouche, Y.; Bouden, C.; Varga, S. A CFD analysis of the flow structure inside a steam ejector to identify the suitable experimental operating conditions for a solar-driven refrigeration system. Int. J. Refrig. 2014, 39, 186–195. [Google Scholar] [CrossRef]
- Yen, R.H.; Huang, B.J.; Chen, C.Y.; Shiu, T.Y.; Cheng, C.W.; Chen, S.S.; Shestopalov, K. Performance optimization for a variable throat ejector in a solar refrigeration system. Int. J. Refrig. 2013, 36, 1512–1520. [Google Scholar] [CrossRef]
- Zhang, B.; Song, X.; Lv, J.; Zuo, J. Study on the key ejector structures of the waste heat-driven ejector air conditioning system with R236fa as working fluid. Energy Build. 2012, 49, 209–215. [Google Scholar] [CrossRef]
- Wang, L.; Yan, J.; Wang, C.; Li, X. Numerical study on optimization of ejector primary nozzle geometries. Int. J. Refrig. 2017, 76, 219–229. [Google Scholar] [CrossRef]
- Lin, C.; Cai, W.; Li, Y.; Yan, J.; Hu, Y. Pressure recovery ratio in a variable cooling loads ejector-based multi-evaporator refrigeration system. Energy 2012, 44, 649–656. [Google Scholar] [CrossRef]
- Brezgin, D.V.; Aronson, K.E.; Mazzelli, F.; Milazzo, A. The surface roughness effect on the performance of supersonic ejectors. Thermophys. Aeromech. 2017, 24, 553–561. [Google Scholar] [CrossRef]
- Expósito Carrillo, J.A.; Sánchez de La Flor, F.J.; Salmerón Lissén, J.M. Single-phase ejector geometry optimisation by means of a multi-objective evolutionary algorithm and a surrogate CFD model. Energy 2018, 164, 46–64. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Experimental and analytical studies on the shock wave length in convergent and convergent-divergent nozzle ejectors. Energy Convers. Manag. 2014, 88, 907–914. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Experimental and numerical investigation of the effect of shock wave characteristics on the ejector performance. Int. J. Refrig. 2014, 40, 31–42. [Google Scholar] [CrossRef]
- Scott, D.; Aidoun, Z.; Ouzzane, M. An experimental investigation of an ejector for validating numerical simulations. Int. J. Refrig. 2011, 34, 1717–1723. [Google Scholar] [CrossRef]
- Dvorak, V.; Safarik, P. Transonic Instability in Entrance Part of Mixing Chamber of High-Speed Ejector. J. Therm. Sci. 2005, 14, 258–271. [Google Scholar] [CrossRef]
- Selvaraju, A.; Mani, A. CFD analysis of an ejector in vapor ejector refrigeration system with environment friendly refrigerant. In Proceedings of the EUROTHERM Seminar 85, Louvain-la-Neuve, Belgium, 7–9 September 2009. [Google Scholar]
- Smolka, J.; Bulinski, Z.; Fic, A.; Nowak, A.J.; Banasiak, K.; Hafner, A. A computational model of a transcritical R744 ejector based on a homogeneous real fluid approach. Appl. Math. Model. 2013, 37, 1208–1224. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Inzoli, F. CFD study of ejector flow behavior in a blast furnace gas galvanizing plant. J. Therm. Sci. 2015, 24, 58–66. [Google Scholar] [CrossRef]
- Riffat, S.B.; Everitt, P. Experimental and cfd modelling of an ejector system for vehicle air conditioning. J. Inst. Energy 1999, 72, 41–47. [Google Scholar]
- Neve, R.S. Computational fluid dynamics analysis of diffuser performance in gas-powered jet pumps. Int. J. Heat Fluid Flow 1993, 14, 401–407. [Google Scholar] [CrossRef]
- Desevaux, P.; Hostache, G.; Jacquet, P. Static pressure measurement along the centerline of an induced flow ejector. Exp. Fluids 1994, 16, 289–291. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Etude Numerique d’un Ejecteur Monophasique utilisant le Fluid Frigorigene R-134A. In Proceedings of the XIIème Colloque Interuniversitaire Franco-Québécois sur la Thermique des Systèmes, Sherbrooke, QC, Canada, 8–10 June 2015. [Google Scholar]
- Kazlauskas, M. Parametric Study of An Ejector-Cooled Turbine Engine Compartment Using CFD; Rensselaer Polytechnic Institute: Troy, NY, USA, 2009. [Google Scholar]
- Fan, J.; Eves, J.; Thompson, H.M.; Toropov, V.V.; Kapur, N.; Copley, D.; Mincher, A. Computational fluid dynamic analysis and design optimization of jet pumps. Comput. Fluids 2011, 46, 212–217. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Galanis, N. Comparison of ejector predicted performance by thermodynamic and CFD models. Int. J. Refrig. 2016, 68, 28–36. [Google Scholar] [CrossRef]
- Hemidi, A.; Henry, F.; Leclaire, S.; Seynhaeve, J.-M.; Bartosiewicz, Y. CFD analysis of a supersonic air ejector. Part I: Experimental validation of single-phase and two-phase operation. Appl. Therm. Eng. 2009, 29, 1523–1531. [Google Scholar] [CrossRef]
- Gawehn, T.; Gülhan, A.; Al-Hasan, N.S.; Schnerr, G.H. Experimental and numerical analysis of the structure of pseudo-shock systems in laval nozzles with parallel side walls. Shock Waves 2010, 20, 297–306. [Google Scholar] [CrossRef]
- Yu, Y.; Shademan, M.; Barron, R.M.; Balachandar, R. CFD study of effects of geometry variations on flow in a nozzle. Eng. Appl. Comput. Fluid Mech. 2012, 6, 412–425. [Google Scholar] [CrossRef]
- Gagan, J.; Smierciew, K.; Butrymowicz, D.; Karwacki, J. Comparative study of turbulence models in application to gas ejectors. Int. J. Therm. Sci. 2014, 78, 9–15. [Google Scholar] [CrossRef]
- Bouhanguel, A.; Desevaux, P.; Gavignet, E. Visualization of flow instabilities in supersonic ejectors using Large Eddy Simulation. J. Vis. 2015, 18, 17–19. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Turbulence modeling of a single-phase R134a supersonic ejector. Part 1: Numerical benchmark. Int. J. Refrig. 2016, 61, 140–152. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Jia, L.; Wang, X. Assessment and prediction of component efficiencies in supersonic ejector with friction losses. Appl. Therm. Eng. 2018, 129, 618–627. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Sun, H.; Zhang, G.; Guo, L.; Tu, J. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance. Energy 2019, 167, 469–483. [Google Scholar] [CrossRef]
- Menter, F.; Ferreira, J.C.; Esch, T.; Konno, B. The SST Turbulence Model with Improved Wall Treatment for Heat Transfer Predictions in Gas Turbines. In Proceedings of the International Gas Turbine Congress, Tokyo, Japan, 2–7 November 2003. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Desevaux, P.; Prenel, J.P.; Hostache, G. Flow visualization methods for investigating an induced flow ejector. J. Flow Vis. Image Process. 1995, 2, 61–74. [Google Scholar] [CrossRef]
- Little, A.B.; Bartosiewicz, Y.; Garimella, S. Optical Validation of Ejector Flow Characteristics Predicted By. In Proceedings of the ASME 2012, International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 1–12. [Google Scholar]
- Little, A.B.; Garimella, S. Shadowgraph visualization of condensing R134a flow through ejectors. Int. J. Refrig. 2016, 68, 118–129. [Google Scholar] [CrossRef]
- Zegenhagen, M.T.; Ziegler, F. Experimental investigation of the characteristics of a jet-ejector and a jet-ejector cooling system operating with R134a as a refrigerant. Int. J. Refrig. 2015, 56, 173–185. [Google Scholar] [CrossRef]
- Hamzaoui, M.; Nesreddine, H.; Aidoun, Z.; Balistrou, M. Experimental study of a low grade heat driven ejector cooling system using the working fluid R245fa. Int. J. Refrig. 2018, 86, 388–400. [Google Scholar] [CrossRef]
- Sun, D.W. Comparative study of the performance of an ejector refrigeration cycle operating with various refrigerants. Energy Convers. Manag. 1999, 40, 873–884. [Google Scholar] [CrossRef]
- Dorantès, R.; Lallemand, A. Influence de la nature des fluides, purs ou en mélanges non-azéotropiques, sur les performances d’une machine de climatisation à éjecto-compresseur. Int. J. Refrig. 1995, 18, 21–30. [Google Scholar] [CrossRef]
- Cizungu, K.; Mani, A.; Groll, M. Performance comparison of vapour jet refrigeration system with environment friendly working fluids. Appl. Therm. Eng. 2001, 21, 585–598. [Google Scholar] [CrossRef]
- Selvaraju, A.; Mani, A. Analysis of a vapour ejector refrigeration system with environment friendly refrigerants. Int. J. Therm. Sci. 2004, 43, 915–921. [Google Scholar] [CrossRef]
- Al-Khalidy, N.; Zayonia, A. Design and experimental investigation of an ejector in an air-conditioning and refrigeration system. ASHRAE Trans. 1995, 101, 383–391. [Google Scholar]
- Al-Khalidy, N. Performance of solar refrigeration ejector refrigerating machine. ASHRAE Trans. 1997, 103, 56–64. [Google Scholar]
- Al-Khalidy, N. An experimental study of an ejector cycle refrigeration machine operating on R113. Int. J. Refrig. 1998, 21, 617–625. [Google Scholar] [CrossRef]
- Pereira, P.R.; Varga, S.; Soares, J.; Oliveira, A.C.; Lopes, A.M.; De Almeida, F.G.; Carneiro, J.F. Experimental results with a variable geometry ejector using R600a as working fluid. Int. J. Refrig. 2014, 46, 77–85. [Google Scholar] [CrossRef]
- Shi, M.H.; Wang, X.C.; Cai, H. Numerical Simulation of the Performance of a Capillary Thermal Driven Ejector Refrigerator. Heat Transf. Eng. 2006, 27, 23–28. [Google Scholar] [CrossRef]
- Pridasawas, W.; Lundqvist, P. A year-round dynamic simulation of a solar-driven ejector refrigeration system with iso-butane as a refrigerant. Int. J. Refrig. 2007, 30, 840–850. [Google Scholar] [CrossRef]
- Roman, R.; Hernandez, J.I. Performance of ejector cooling systems using low ecological impact refrigerants. Int. J. Refrig. 2011, 34, 1707–1716. [Google Scholar] [CrossRef]
- Śmierciew, K.; Gagan, J.; Butrymowicz, D.; Karwacki, J. Experimental investigations of solar driven ejector air-conditioning system. Energy Build. 2014, 80, 260–267. [Google Scholar] [CrossRef]
- Chen, J.; Havtun, H.; Palm, B. Screening of working fluids for the ejector refrigeration system. Int. J. Refrig. 2014, 47, 1–14. [Google Scholar] [CrossRef]
- Kasperski, J.; Gil, B. Performance estimation of ejector cycles using heavier hydrocarbon refrigerants. Appl. Therm. Eng. 2014, 71, 197–203. [Google Scholar] [CrossRef]
- Fang, Y.; Croquer, S.; Poncet, S.; Aidoun, Z.; Bartosiewicz, Y. Drop-in replacement in a R134 ejector refrigeration cycle by HFO refrigerants. Int. J. Refrig. 2017, 77, 87–98. [Google Scholar] [CrossRef]
- Śmierciew, K.; Gagan, J.; Butrymowicz, D.; Łukaszuk, M.; Kubiczek, H. Experimental investigation of the first prototype ejector refrigeration system with HFO-1234ze(E). Appl. Therm. Eng. 2017, 110, 115–125. [Google Scholar] [CrossRef]
- He, S.; Li, Y.; Wang, R.Z. A new approach to performance analysis of ejector refrigeration system using grey system theory. Appl. Therm. Eng. 2009, 29, 1592–1597. [Google Scholar] [CrossRef]
- Gagan, J.; Śmierciew, K.; Butrymowicz, D. Performance of ejection refrigeration system operating with R-1234ze(E) driven by ultra-low grade heat source. Int. J. Refrig. 2018, 88, 458–471. [Google Scholar] [CrossRef]
- Tashtoush, B.M.; Al-Nimr, M.A.; Khasawneh, M.A. Investigation of the use of nano-refrigerants to enhance the performance of an ejector refrigeration system. Appl. Energy 2017, 206, 1446–1463. [Google Scholar] [CrossRef]
- Domel, N.; Miller, D.; Vermeulen, P.J. Computational Simulations of a Pulsed Ejector Actuation System. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 11–13 July 2005. [Google Scholar]
- Kumar, V.; Singhal, G.; Subbarao, P.M.V. Study of supersonic flow in a constant rate of momentum change (CRMC) ejector with frictional effects. Appl. Therm. Eng. 2013, 60, 61–71. [Google Scholar] [CrossRef]
- García Del Valle, J.; Sáiz Jabardo, J.M.; Castro Ruiz, F.; San José Alonso, J. A one dimensional model for the determination of an ejector entrainment ratio. Int. J. Refrig. 2012, 35, 772–784. [Google Scholar] [CrossRef]
- Al-Doori, G.F. Investigation of Refrigeration System Steam Ejector Performance through Experiments and Computational Simulations; University of Southern Queensland: Toowoomba, Queensland, Australia, 2013. [Google Scholar]
- Matsuo, K.; Sasaguchi, K.; Kiyotoki, Y.; Mochizuki, H. Investigation of Supersonic Air Performance (Part 2, Effects of Throat-Area-Ratio on Ejector Performance). Bull. JSME 1982, 25, 1898–1905. [Google Scholar] [CrossRef]
- Zare-Behtash, H.; Gongora-Orozco, N.; Kontis, K. Effect of primary jet geometry on ejector performance: A cold-flow investigation. Int. J. Heat Fluid Flow 2011, 32, 596–607. [Google Scholar] [CrossRef]
- Bouhanguel, A.; Desevaux, P.; Gavignet, E. Flow visualization in supersonic ejectors using laser tomography techniques. Int. J. Refrig. 2011, 34, 1633–1640. [Google Scholar] [CrossRef]
- Bouhanguel, A.; Desevaux, P.; Gavignet, E. Flow visualization in supersonic ejectors using laser tomography technique. In Proceedings of the EUROTHERM Seminar 85, Louvain-la-Neuve, Belgium, 7–9 September 2009. [Google Scholar]
- Bouhanguel, A.; Desevaux, P.; Bailly, Y.; Girardot, L. Flow Velocity Investigation by Particle Image Velocimetry in Supersonic Air Ejector. Appl. Mech. Mater. 2012, 232, 256–260. [Google Scholar] [CrossRef]
- Dvorak, V.; Kotek, M. Experimental measurement and numerical modeling of cavitating flow in converging-diverging nozzle. Eur. Phys. J. Conf. 2012, 25, 1081. [Google Scholar] [CrossRef]
- Bravo, H.E.G.; Rodriguez, R.D.; Gutierrez, J.H.; Brown, R.B.Y.; Aguila, R.R.; Pena, H.T. State of art of simple and hybrid jet compression refrigeration systems and the working fluid influence. Int. J. Refrig. 2012, 35, 386–396. [Google Scholar] [CrossRef]
- Khaliq, A.; Agrawal, B.K.; Kumar, R. First and second law investigation of waste heat based combined power and ejector-absorption refrigeration cycle. Int. J. Refrig. 2012, 35, 88–97. [Google Scholar] [CrossRef]
- Sadeghi, M.; Mahmoudi, S.M.S.; Khoshbakhti Saray, R. Exergoeconomic analysis and multi-objective optimization of an ejector refrigeration cycle powered by an internal combustion (HCCI) engine. Energy Convers. Manag. 2015, 96, 403–417. [Google Scholar] [CrossRef]
- Ahmadzadeh, A.; Salimpour, M.R.; Sedaghat, A. Thermal and exergoeconomic analysis of a novel solar driven combined power and ejector refrigeration (CPER) system. Int. J. Refrig. 2017, 83, 143–156. [Google Scholar] [CrossRef]
- Grazzini, G.; Rocchetti, A. Influence of the objective function on the optimisation of a steam ejector cycle. Int. J. Refrig. 2008, 31, 510–515. [Google Scholar] [CrossRef]
- Dahmani, A.; Aidoun, Z.; Galanis, N. Optimum design of ejector refrigeration systems with environmentally benign fluids. Int. J. Therm. Sci. 2011, 50, 1562–1572. [Google Scholar] [CrossRef]
- Chen, J.; Havtun, H.; Palm, B. Conventional and advanced exergy analysis of an ejector refrigeration system. Appl. Energy 2015, 144, 139–151. [Google Scholar] [CrossRef]
- Hernandez, J.I.; Roman, R.; Best, R.; Dorantes, R.; Gonzalez, H.E. The behavior of an ejector cooling system operating with refrigerant blends 410A and 507. Energy Procedia 2014, 57, 3021–3030. [Google Scholar] [CrossRef]
- Buyadgie, D.; Buyadgie, O.; Artemenko, S.; Chamchine, A.; Drakhnia, O. Conceptual design of binary/multicomponent fluid ejector refrigeration systems. Int. J. Low-Carbon Technol. 2012, 7, 120–127. [Google Scholar] [CrossRef]
- Sokolov, M.; Hershgal, D. Optimal coupling and feasibility of a solar-powered year-round ejector air conditioner. Sol. Energy 1993, 50, 507–516. [Google Scholar] [CrossRef]
- Huang, B.J.; Chang, J.M.; Petrenko, V.A.; Zhuk, K.B. A solar ejector cooling system using refrigerant R141b. Sol. Energy 1998, 64, 223–226. [Google Scholar] [CrossRef]
- Diaconu, B.M.; Varga, S.; Oliveira, A.C. Numerical simulation of a solar-assisted ejector air conditioning system with cold storage. Energy 2011, 36, 1280–1291. [Google Scholar] [CrossRef]
- Diaconu, B.M. Energy analysis of a solar-assisted ejector cycle air conditioning system with low temperature thermal energy storage. Renew. Energy 2012, 37, 266–276. [Google Scholar] [CrossRef]
- Redo, M.A.B.; Berana, M.S. Geothermal-driven ejector refrigeration system. In Proceedings of the ASME 2013, International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013; pp. 1–10. [Google Scholar]
- Du, Y.; Han, P.; Qiang, X.; Hao, M.; Long, Y.; Zhao, P.; Dai, Y. Off-design performance analysis of a combined cooling and power system driven by low-grade heat source. Energy Convers. Manag. 2018, 159, 327–341. [Google Scholar] [CrossRef]
- Allouche, Y.; Bouden, C.; Riffat, S. A solar-driven ejector refrigeration system for Mediterranean climate: Experience improvement and new results performed. Energy Procedia 2012, 18, 1115–1124. [Google Scholar] [CrossRef]
- Milazzo, A.; Rocchetti, A. Modelling of ejector chillers with steam and other working fluids. Int. J. Refrig. 2015, 57, 277–287. [Google Scholar] [CrossRef]
- Riffat, S.B.; Jiang, L.; Gan, G. Recent development in ejector technology-a review. Int. J. Ambient Energy 2005, 26, 13–26. [Google Scholar] [CrossRef]
- Habibzadeh, A.; Rashidi, M.M.; Galanis, N. Analysis of a combined power and ejector-refrigeration cycle using low temperature heat. Energy Convers. Manag. 2013, 65, 381–391. [Google Scholar] [CrossRef]
- Zhang, T.; Mohamed, S. Conceptual Design and Analysis of Hydrocarbon-Based Solar Thermal Power and Ejector Cooling Systems in Hot Climates. J. Sol. Energy Eng. 2014, 137, 21001. [Google Scholar] [CrossRef]
- Landoulsi, H.; Elakhdar, M.; Nehdi, E.; Kairouani, L. Performance analysis of a combined system for cold and power. Int. J. Refrig. 2015, 60, 297–308. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, N.; Zhao, L.; Deng, S.; Li, H.; Yu, Z. Analysis of a novel combined power and ejector-refrigeration cycle. Energy Convers. Manag. 2016, 108, 266–274. [Google Scholar] [CrossRef]
- Bao, J.; Lin, Y.; He, G. Working fluids comparison and thermodynamic analysis of a transcritical power and ejector refrigeration cycle (TPERC). Int. J. Refrig. 2017, 82, 262–272. [Google Scholar] [CrossRef]
- Sokolov, M.; Hershgal, D. Enhanced ejector refrigeration cycles powered by low grade heat. Part 1. Systems characterization. Int. J. Refrig. 1990, 13, 351–356. [Google Scholar] [CrossRef]
- Sokolov, M.; Hershgal, D. Enhanced ejector refrigeration cycles powered by low grade heat. Part 2. Design procedures. Int. J. Refrig. 1990, 13, 357–363. [Google Scholar] [CrossRef]
- Sokolov, M.; Hershgal, D. Solar-powered compression enhanced ejector air conditioner. Sol. Energy 1993, 51, 183–194. [Google Scholar] [CrossRef]
- Sun, D.W. Solar powered combined ejector-vapour compression cycle for air conditioning and refrigeration. Energy Convers. Manag. 1997, 38, 479–491. [Google Scholar] [CrossRef]
- Dennis, M.; Cochrane, T.; Marina, A. A prescription for primary nozzle diameters for solar driven ejectors. Sol. Energy 2015, 115, 405–412. [Google Scholar] [CrossRef]
- Allouche, Y.; Varga, S.; Bouden, C.; Oliveira, A.C. Dynamic simulation of an integrated solar-driven ejector based air conditioning system with PCM cold storage. Appl. Energy 2017, 190, 600–611. [Google Scholar] [CrossRef]
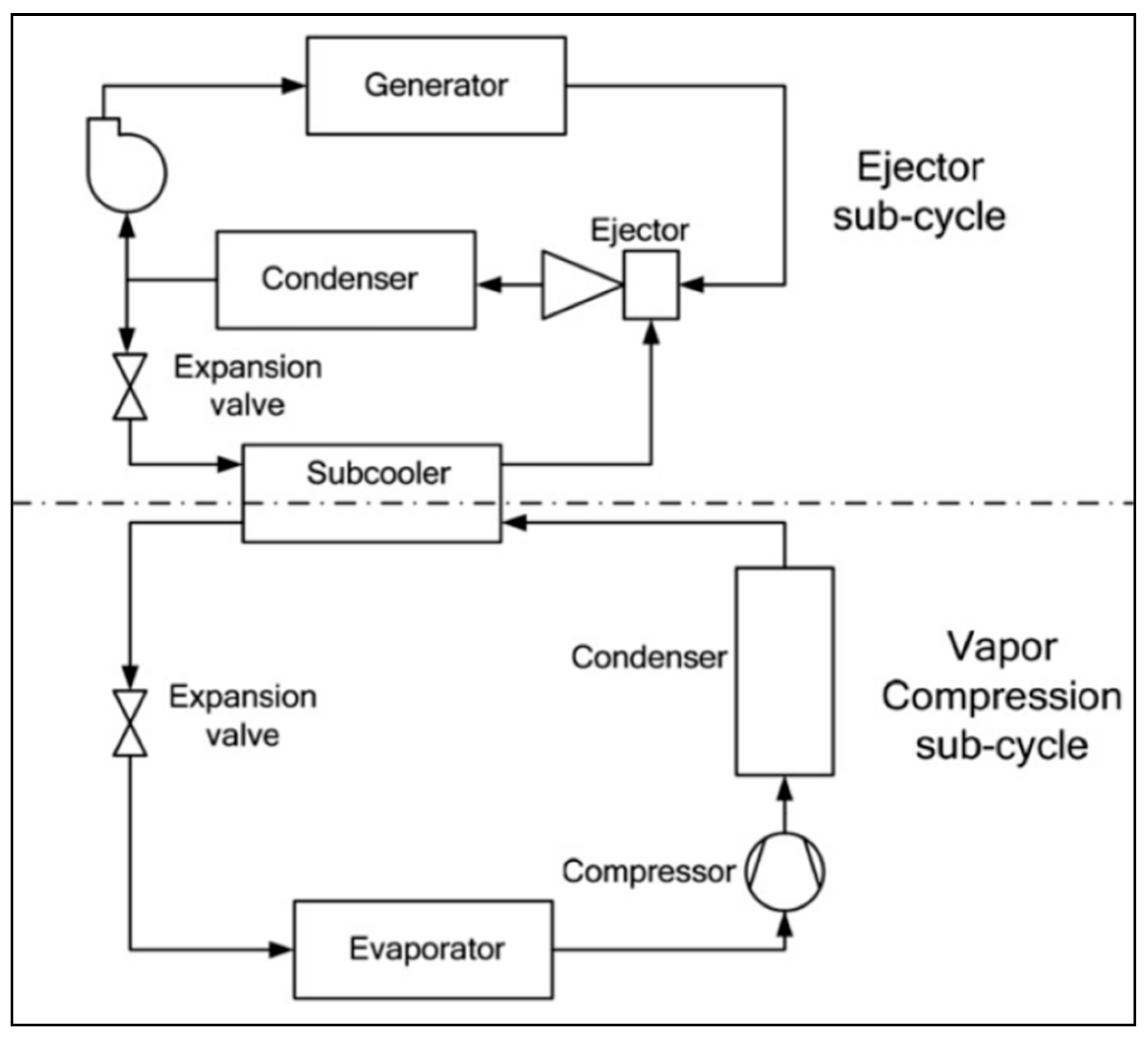
- Ben Mansour, R.; Ouzzane, M.; Aidoun, Z. Numerical evaluation of ejector-assisted mechanical compression systems for refrigeration applications. Int. J. Refrig. 2014, 43, 36–49. [Google Scholar] [CrossRef]
- Xue, B.; Cai, W.; Wang, X. State-space modelling for the ejector-based refrigeration system driven by low grade energy. Appl. Therm. Eng. 2015, 75, 430–444. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, N.; Wang, Q.; Mao, N.; Chen, G.; Gao, Z. Refrigerant evaluation and performance comparison for a novel hybrid solar-assisted ejection-compression refrigeration cycle. Sol. Energy 2018, 160, 344–352. [Google Scholar] [CrossRef]
- Expósito Carrillo, J.A.; Sánchez de La Flor, F.J.; Salmerón Lissén, J.M. Thermodynamic comparaison of ejector cooling cycles. Ejector characterisation by means of entrainment ratio and compression efficiency. Int. J. Refrig. 2017, 74, 369–382. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, L.; Liang, K. Thermodynamic performance of an auto-cascade ejector refrigeration cycle with mixed refrigerant R32 + R236fa. Appl. Therm. Eng. 2015, 84, 268–275. [Google Scholar] [CrossRef]
- Aphornratana, S.; Eames, I.W. Experimental investigation of a combined ejector-absorption refrigerator. Int. J. Energy Res. 1998, 22, 198–207. [Google Scholar] [CrossRef]
- Wu, S.; Eames, I.W. A novel absorption-recompression refrigeration cycle. Appl. Therm. Eng. 1998, 18, 1149–1157. [Google Scholar] [CrossRef]
- Eames, I.W.; Wu, S. Experimental proof-of-concept testing of an innovative heat-powered vapour recompression-absorption refrigerator cycle. Appl. Therm. Eng. 2000, 20, 721–736. [Google Scholar] [CrossRef]
- Hong, D.; Chen, G.; Tang, L.; He, Y. A novel ejector-absorption combined refrigeration cycle. Int. J. Refrig. 2011, 34, 1596–1603. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Thermodynamic analysis of a novel compact power generation and waste heat operated absorption, ejector-jet pump refrigeration cycle. J. Mech. Sci. Technol. 2014, 28, 3895–3902. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Parametric analysis and optimization of a cooling system with ejector-absorption chiller powered by solar parabolic trough collectors. Energy Convers. Manag. 2018, 168, 329–342. [Google Scholar] [CrossRef]
- Sirwan, R.; Alghoul, M.A.; Sopian, K.; Ali, Y.; Abdulateef, J. Evaluation of adding flash tank to solar combined ejector-absorption refrigeration system. Sol. Energy 2013, 91, 283–296. [Google Scholar] [CrossRef]
- Abed, A.M.; Alghoul, M.A.; Sirawn, R.; Al-Shamani, A.N.; Sopian, K. Performance enhancement of ejector-absorption cooling cycle by re-arrangement of solution streamlines and adding RHE. Appl. Therm. Eng. 2015, 77, 65–75. [Google Scholar] [CrossRef]
- Petrenko, V.O.; Huang, B.J.; Ierin, V.O. Design-theoretical study of cascade CO2 sub-critical mechanical compression/butane ejector cooling cycle. Int. J. Refrig. 2011, 34, 1649–1656. [Google Scholar] [CrossRef]
- Sun, F.; Fu, L.; Sun, J.; Zhang, S. A new waste heat district heating system with combined heat and power (CHP) based on ejector heat exchangers and absorption heat pumps. Energy 2014, 69, 516–524. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Proposal and assessment of a novel geothermal combined cooling and power cycle based on Kalina and ejector refrigeration cycles. Appl. Therm. Eng. 2018, 130, 767–781. [Google Scholar] [CrossRef]
- Seckin, C. Thermodynamic analysis of a combined power/refrigeration cycle: Combination of Kalina cycle and ejector refrigeration cycle. Energy Convers. Manag. 2018, 157, 631–643. [Google Scholar] [CrossRef]
- Alexis, G.K. Performance parameters for the design of a combined refrigeration and electrical power cogeneration system. Int. J. Refrig. 2007, 30, 1097–1103. [Google Scholar] [CrossRef]
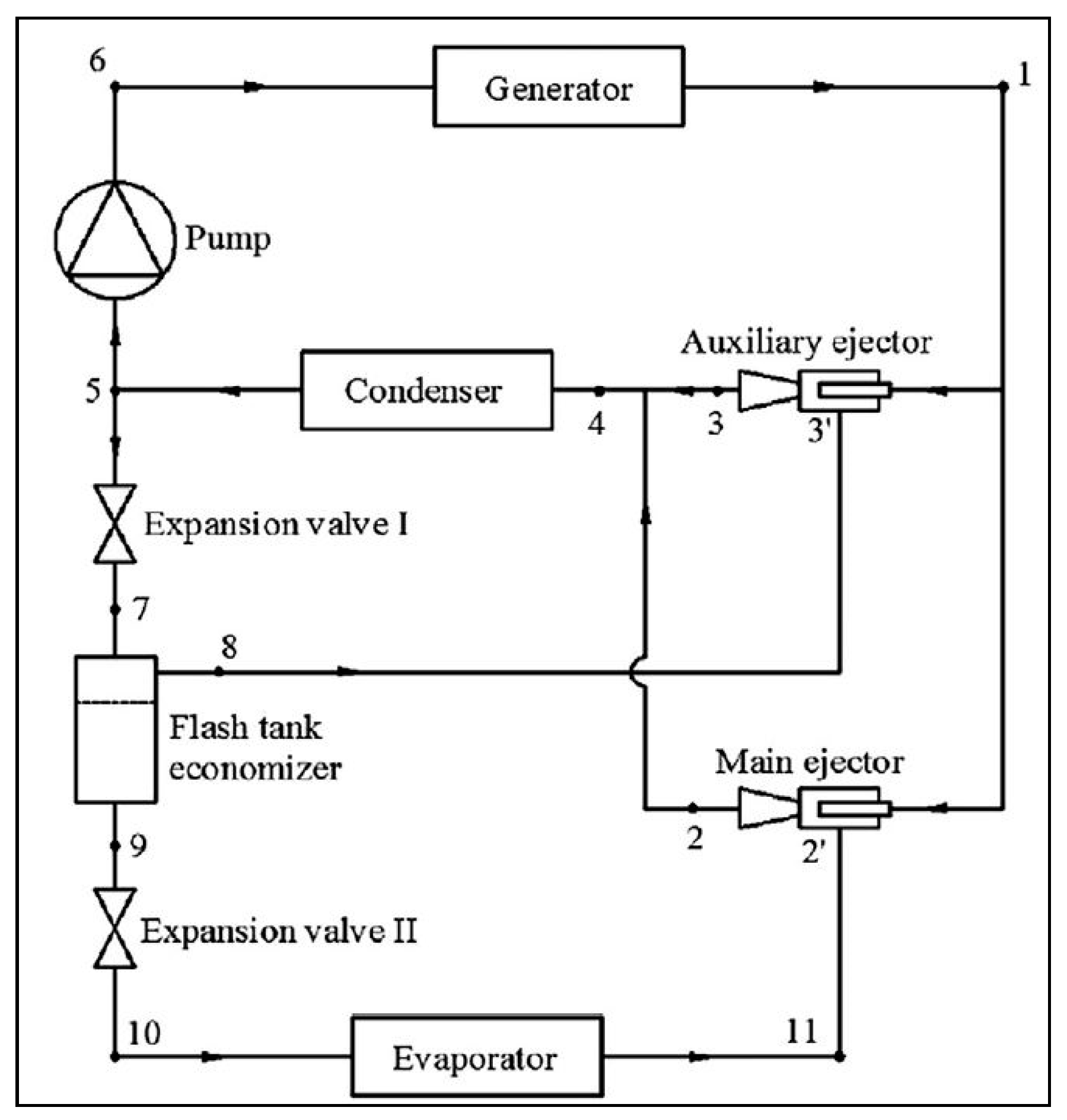
- Liu, Y.; Fu, H.; Yu, J. Performance study of an enhanced ejector refrigeration cycle with flash tank economizer for low-grade heat utilization. Appl. Therm. Eng. 2018, 140, 43–50. [Google Scholar] [CrossRef]
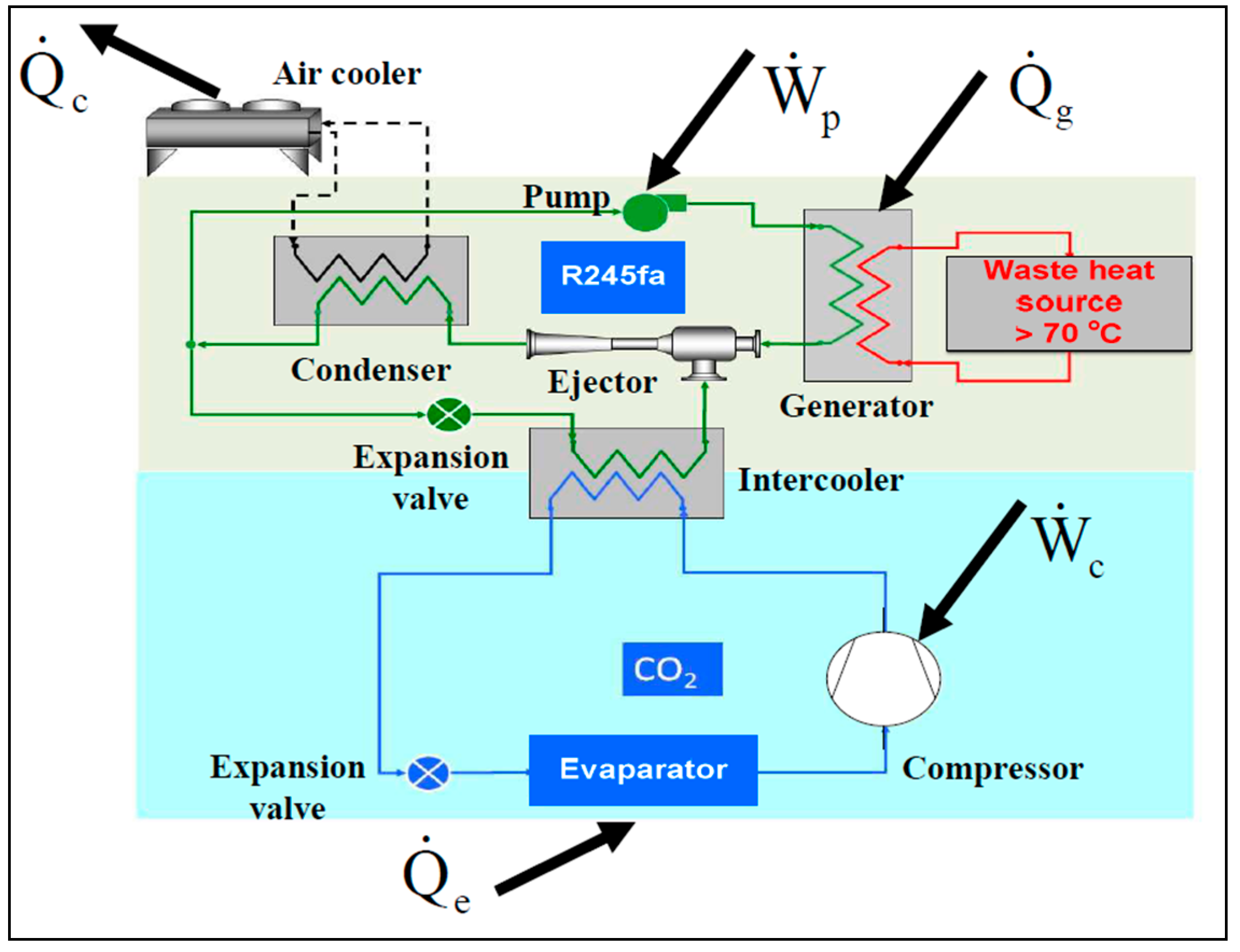
- Chen, X.; Worall, M.; Omer, S.; Su, Y.; Riffat, S. Theoretical studies of a hybrid ejector CO2 compression cooling system for vehicles and preliminary experimental investigations of an ejector cycle. Appl. Energy 2013, 102, 931–942. [Google Scholar] [CrossRef]
- Hao, X.; Wang, L.; Wang, Z.; Tan, Y.; Yan, X. Hybrid auto-cascade refrigeration system coupled with a heat-driven ejector cooling cycle. Energy 2018, 161, 988–998. [Google Scholar] [CrossRef]
- Subramanian, G.; Natarajan, S.K.; Adhimoulame, K.; Natarajan, A. Comparison of numerical and experimental investigations of jet ejector with blower. Int. J. Therm. Sci. 2014, 84, 134–142. [Google Scholar] [CrossRef]
- Huang, B.J.; Petrenko, V.A.; Chang, J.M.; Lin, C.P.; Hu, S.S. A combined-cycle refrigeration system using ejector-cooling cycle as the bottom cycle. Int. J. Refrig. 2001, 24, 391–399. [Google Scholar] [CrossRef]
- Huang, B.J.; Ton, W.Z.; Wu, C.C.; Ko, H.W.; Chang, H.S.; Hsu, H.Y.; Liu, J.H.; Wu, J.H.; Yen, R.H. Performance test of solar-assisted ejector cooling system. Int. J. Refrig. 2014, 39, 172–182. [Google Scholar] [CrossRef]
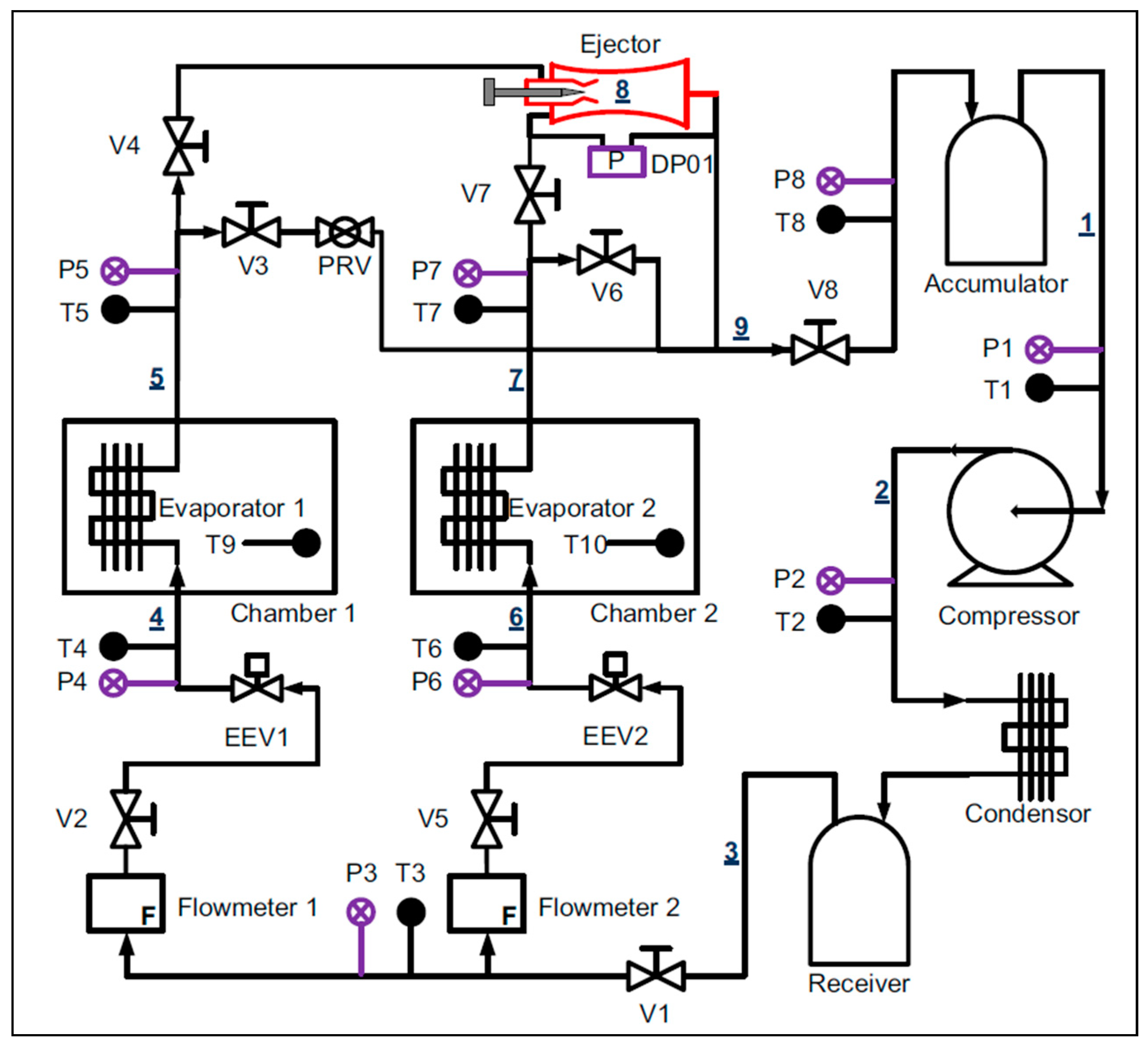
- Nesreddine, H.; Bendaoud, A.; Aidoun, Z.; Ouzzane, M. Experimental Investigation of an Ejector-Compression. In Proceedings of the ICR 2015, Yokohama, Japan, 16–22 August 2015; pp. 1051–1054. [Google Scholar]
- He, Y.; Chen, Z.; Tang, L.; Chen, G. Investigation on a two-stage ejection refrigeration system. Appl. Therm. Eng. 2015, 86, 49–59. [Google Scholar] [CrossRef]
- Zegenhagen, M.T.; Ziegler, F. Feasibility analysis of an exhaust gas waste heat driven jet-ejector cooling system for charge air cooling of turbocharged gasoline engines. Appl. Energy 2015, 160, 221–230. [Google Scholar] [CrossRef]
- Wang, H.; Cai, W.; Wang, Y.; Yan, J.; Wang, L. Experimental study of the behavior of a hybrid ejector-based air-conditioning system with R134a. Energy Convers. Manag. 2016, 112, 31–40. [Google Scholar] [CrossRef]
- Li, C.; Yan, J.; Li, Y.; Cai, W.; Lin, C.; Chen, H. Experimental study on a multi-evaporator refrigeration system with variable area ratio ejector. Appl. Therm. Eng. 2016, 102, 196–203. [Google Scholar] [CrossRef]
- Abed, A.M.; Sopian, K.; Alghoul, M.A.; Sh, H.; Al-shamani, A.N. Experimental evaluation of single stage ejector-absorption cooling cycle under different design configurations. Sol. Energy 2017, 155, 130–141. [Google Scholar] [CrossRef]
- Shi, Y.; Li, F.; Hong, D.; Wang, Q.; Chen, G. Experimental study of a new ejector-absorption refrigeration cycle driven by multi-heat sources. Appl. Therm. Eng. 2018, 133, 604–612. [Google Scholar] [CrossRef]

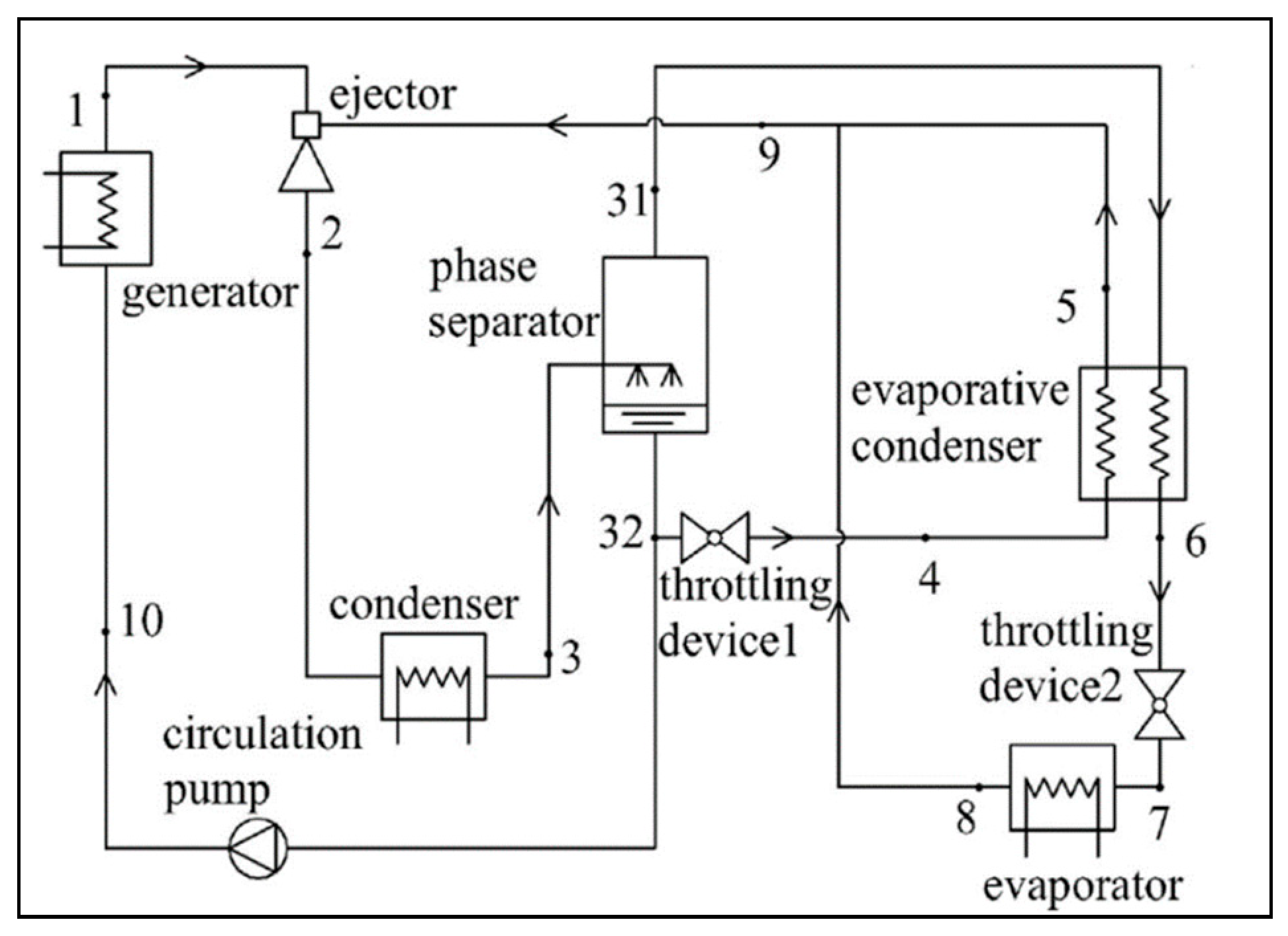
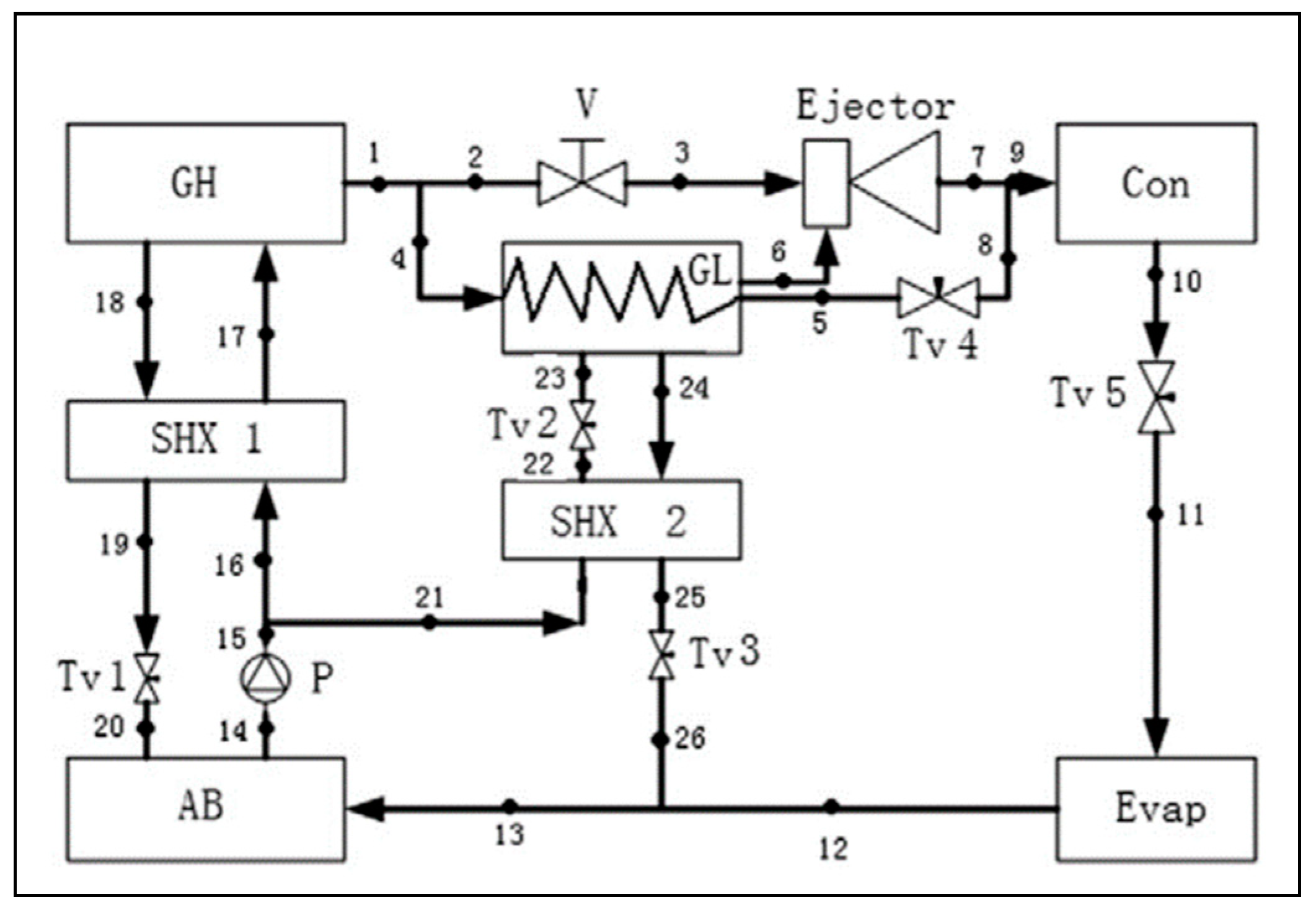
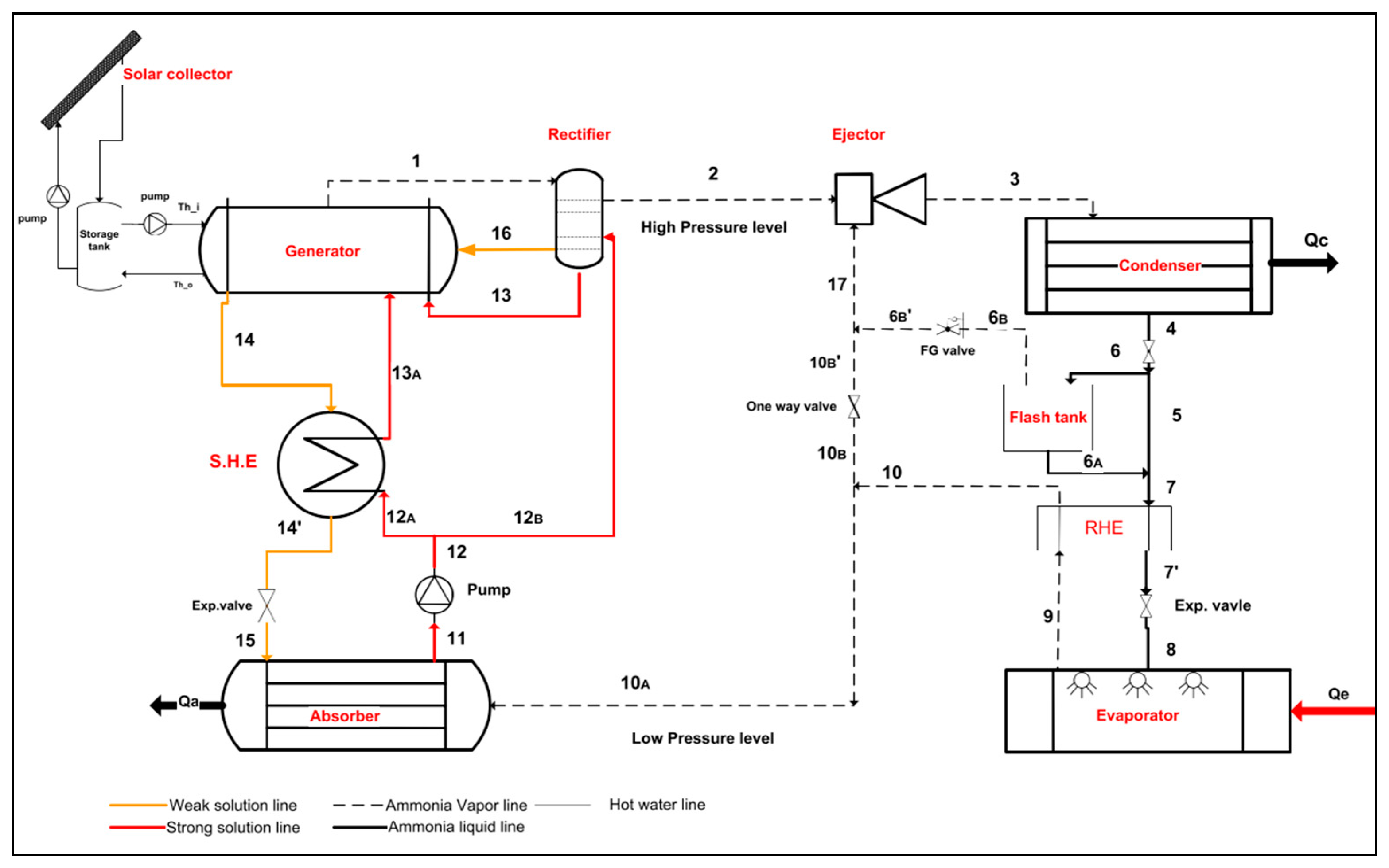
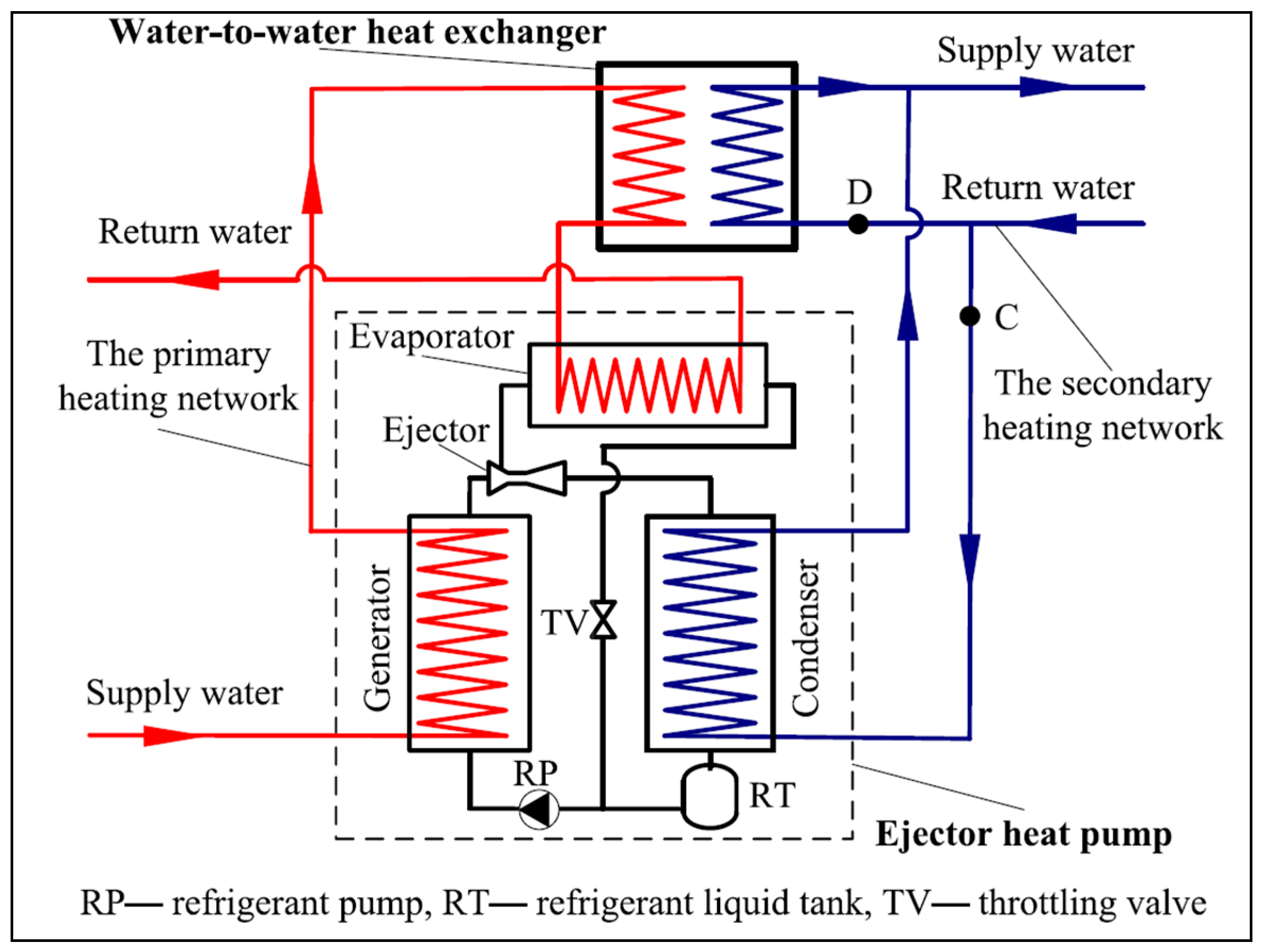
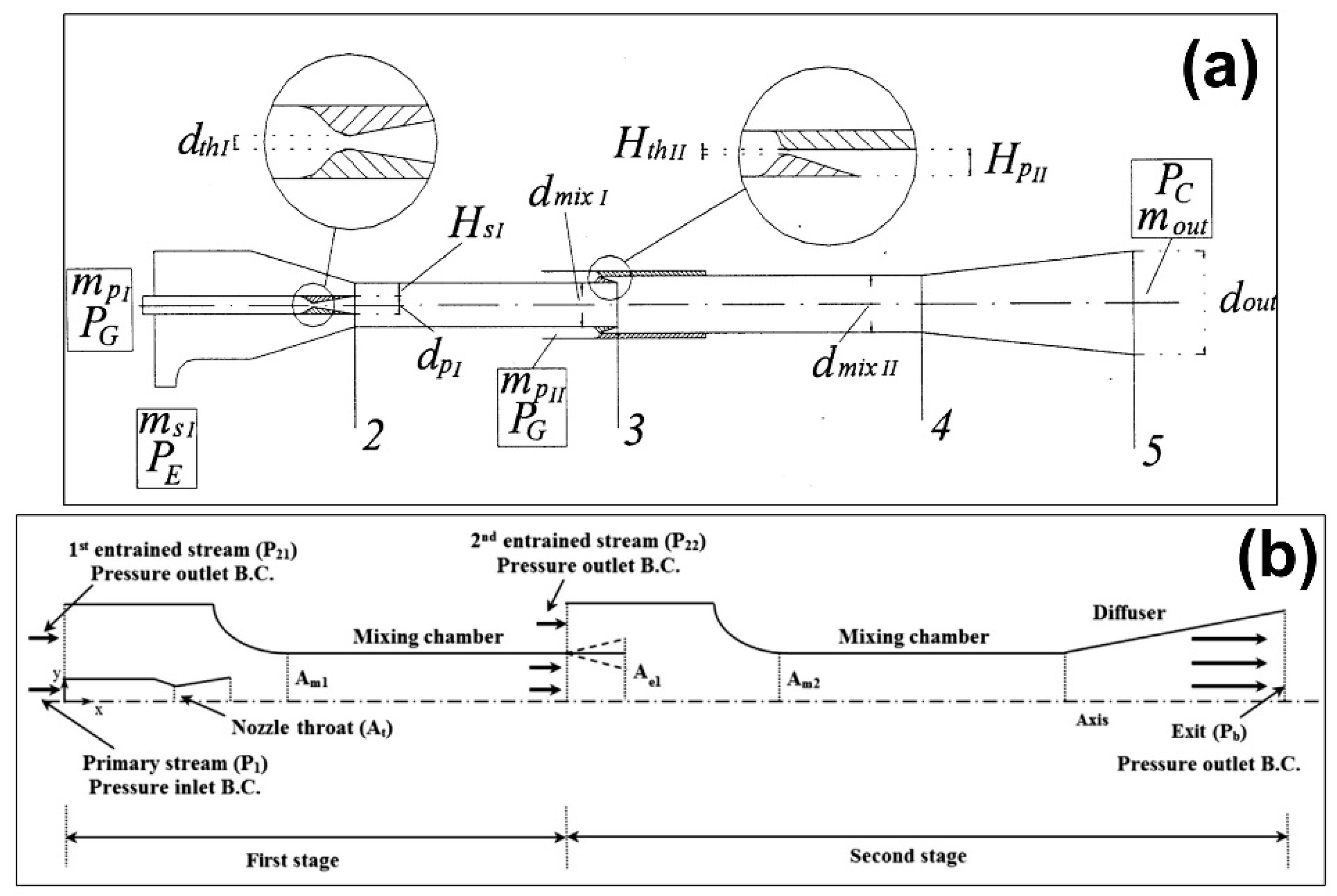
| References | Ejector Geometry | Application | Analysis | Remarks |
|---|---|---|---|---|
| [13,14,15] | CAM/CPM | Refrigeration | Theor./Exp. | CAM offers higher entrainment but lower compression than CPM. |
| [20,21,22,23] | CRMC | Refrigeration | Theor./Exp. | CRMC concept takes advantage of both CAM and CPM. Δω ≈ 37–40% than CPM. |
| [17,18,19] | Two-stage | Refrigeration | Theor. | Higher performance than CAM (Δτ ≈ 13%). |
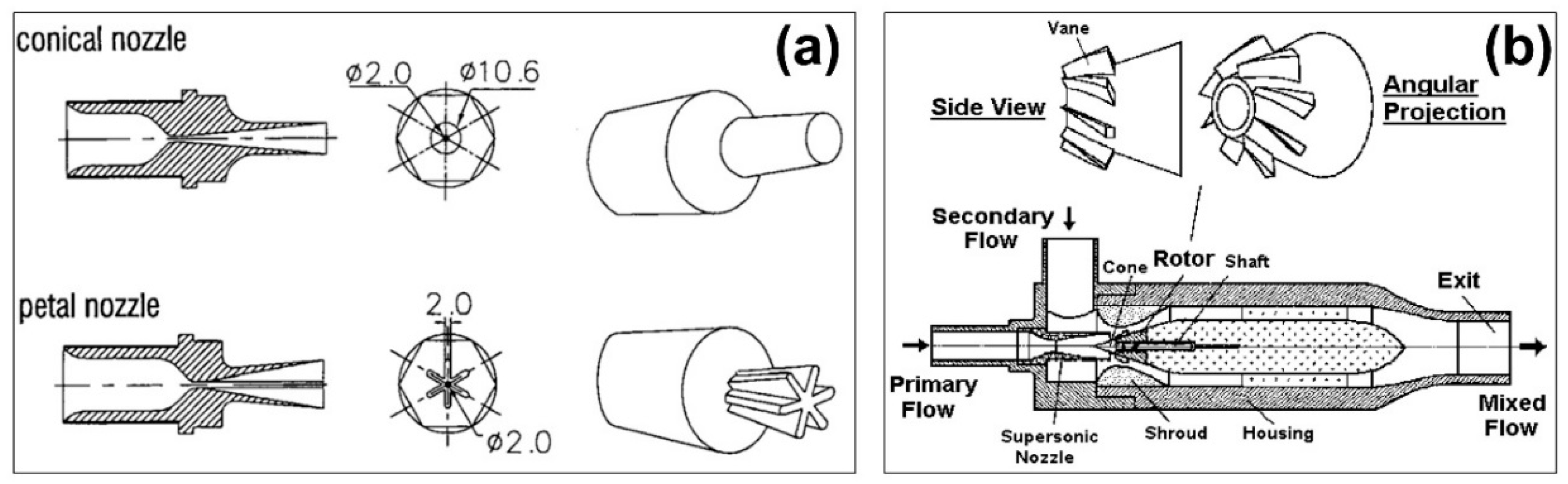
| [25] | Petal nozzle | Refrigerator | Exp. | Higher compression ratio than conical nozzle, especially for large aspect ratio. |
| [33] | Lobed nozzle | Refrigeration | Theor. | Pressure recovery improved (≈60%) |
| [35] | Tip ring version | - | Exp. | Δω ≈ 30% and Δτ ≈ -50% higher than conical nozzle. |
| [34] | Chevron nozzle | Solar desalination | Theor. | Δω ≈ 14–22% and Δτ ≈ 8.5% higher than conical nozzle. |
| [26,27,28,29,30] | Spinning rotor | Refrigeration | Theor./Exp. | Enhanced flow induction and mixing. -Increased cost and complex manufacturing of the ejector. |
| [31] | Rotating ejector | Refrigeration | Theor. | Lower secondary pressure for the rotating ejector than static ejector |
| [36] | Bypass ejector | - | Theor./Exp. | Entrainment ratio increased by up to 31.5%. |
| [37,38,39] | Ejector with auxiliary suction | Desalination | Theor./Exp. | Enhanced entrainment ratio (Δω ≈ 11–27%) |
| [40] | Pulsed ejector | - | Theor./Exp. | Mixing is enhanced and entrainment is improved |
| Author(s) | Working Fluid | Gas Properties | Mixing Model | Remarks | |
|---|---|---|---|---|---|
| Perfect | Real | ||||
| Keenan et al. [11] | Air | ✓ | - | CAM | —Neglecting losses. —Without diffuser. |
| Keenan et al. [12] | Air | ✓ | - | CPM | —Neglecting losses. —Diffuser included. |
| Khoury et al. [178] | Hexane, n-Butane | ✓ | - | CAM | —Account molecular weights. |
| Munday and Bagster [113] | steam | ✓ | - | CPM | —Effective area concept introduced. |
| Eames et al. [51] | steam | ✓ | - | CPM | —Losses in nozzle, mixing and diffuser considered. |
| Lallemand et al. [179] | R11-R114 R113-R142b | ✓ | - | CPM | —2 fluids in one ejector. |
| Grazzini and Mariani [17] | steam | ✓ | - | CAM | —Two-stage ejector configuration included. |
| Huang et al. [70] | R141b | ✓ | - | CPM | —Loss coefficients calibrated with experimental data. |
| Eames [20] | steam | ✓ | - | - | —New design method (CRMC). —Neglecting losses. |
| Ouzzane and Aidoun [41] | R142b | - | ✓ | CPM | —1D, incremental approach. |
| Selvaraju and Mani [187] | R134a, R152a, R290, R600a, R717 | - | ✓ | CPM | —Friction factor considered in mixing chamber. |
| Zhu et al. [188] | R141b, R11 | ✓ | - | CPM | —Shock circle model: boundary layer near wall considered. |
| Zhu and Li [189] | steam, R11, R141b | ✓ | - | - | —Radial velocity function imposed in mixing chamber. —Model for both wet and dry vapor fluids working. |
| Cardemil and Colle [190] | steam, R141b, CO2 | ✓ | ✓ | CPM | —Model for both wet and dry vapor fluids working. —Speed of sound in 2 phase mixture evaluated. |
| Chen et al. [182] | R236fa | - | ✓ | CAM | —NXP considered. |
| Ma et al. [183] | steam, R141b, R134a | - | ✓ | CAM | —Empirical correlation for the hypothetical throat is used. |
| Chen et al. [102] | R141b, R134a | ✓ | - | CAM | —2D. —Characteristics method used. —Account for VGE. |
| Croquer et al. [191] | CO2, air, R141b, R134a, R245fa, | - | ✓ | CAM | —Droplet injection in mixing section. |
| Author(s) | Working Fluid | Solver | Turbulence Model | Remarks |
|---|---|---|---|---|
| Riffat et al. [173] | R717, R134a, R290 | Commercial software | k-ε | —Various nozzle geometries analyzed. |
| Riffat and Omer [71] | methanol | Fluent | k-ε, RNG k-ε | —3D. |
| Bartosiewicz et al. [207] | air | Fluent | k-ε realizable, RNG k-ε, k-ω, k-ω SST, RSM | —An axial capillary probe was introduced in the ejector. |
| Al-ansary [147] | R134a | Fluent 6.2 | RNG k-ε | —Ejector for cooling turbine inlet. |
| Gawehn et al. [243] | air | ANSYS-CFX CATUM | RSM | —Laval nozzles with parallel side walls. —CATUM: a CFD tool of Technical University of Munich. |
| Yang et al. [32] | steam | Fluent V6.3.26 | k-ε, k-ε realizable, RNG k-ε | —Conical, elliptical, square, rectangular and cross-shaped nozzles tested. |
| Yu et al. [244] | air | Fluent V6.3.26 | Spalart-Allmaras, k-ε, k-ε realizable, RNG k-ε, k-ω, k-ω SST, RSM | —RSM predicts more accurately the turbulent fluctuations. |
| Zhu and Jiang [229] | N2 | ANSYS Fluent v13 | k-ε, RNG k-ε, k-ω SST | —Bypass ejector with an annular cavity in the nozzle wall. |
| Gagan et al. [245] | air | ANSYS Fluent v12 | k-ε, k-ε realizable, RNG k-ε, k-ω, k-ω SST, RSM | —2D-axi and 3D. |
| Bouhanguel et al. [246] | air | ANSYS Fluent | k-ω SST | —RANS vs. LES. |
| Mazzelli et al. [209] | R245fa | ANSYS Fluent v14.5 | k-ω SST | —Surface roughness investigated. |
| García Del Valle et al. [203] | R134a | ANSYS Fluent v14.5 | k-ε, k-ε realizable, RNG k-ε, k-ω SST | —Both k-ε and the k-ω SST turbulence models show good results. |
| Besagni et al. [234] | air, exhaust gases | ANSYS Fluent v14.5.7 | k-ε realizable, k-ω SST, RSM | —Ejector in blast furnace gas. |
| Hakkaki-Fard et al. [211] | R134a | PHOENICS | k-ε | —Design Optimization of ejector. |
| Croquer et al. [247] | R134a | ANSYS Fluent v.15 | k-ε, k-ε realizable, RNG k-ε, k-ω SST, RSM | —k-ω SST model with low-Reynolds formulation appears very promising. |
| Berzin et al. [226] | R245fa | Star-CCM+ Fluent | k-ω SST | —Surface roughness effect. |
| Wang et al. [85] | steam | ANSYS Fluent | RNG k-ε | —Surface roughness and area ratio effects on condensation primary nozzle. |
| Zhang et al. [248] | R134a | Fluent | RNG k-ε | —Surface roughness effect. |
| Expósito Carrillo et al. [227] | air, CO2 | ANSYS Fluent v.17.1 | k-ω SST | —Performance optimization by multi-objective algorithm. |
| Han et al. [249] | steam | ANSYS Fluent v.17.1 | k-ε, k-ε realizable, RNG k-ε, k-ω SST | —Influence of boundary layer separation on ejector performance. |
| Author(s) | Load (kW) | Te or Pe | Tc or Pc | Tg or Pg | COP or (ω) | Comments |
|---|---|---|---|---|---|---|
| Eames et al. [51] | 1 | 5–10 °C | 26–37 °C | 120–140 °C | 0.1–0.37 | —Fixed geometry suitable for cooling. |
| Chen and Sun [60] | - | 7–14 torr | 10–50 torr | 83–187 torr | (0.1–1.3) | —Effects of nozzle exit Mach. —Operation map and correlation. |
| Eames et al. [64] | 2 | 0–10 °C | 20–50 °C | 100–132 °C | (0.3–0.8) | —3 nozzles and 3 diffusers tested. —NXP effects. |
| Chang and Chen [25] | 6 | 12–24 °C | 12–27 °C | 54–58 °C | (0.6–2.6) | —Different area ratios and nozzle geometries. |
| Chunnanond and Aphornratana [49] | 3 | 5–15 °C | 29–40 °C | 120–140 °C | 0.25–0.5 | —Test on 3 nozzles. —Internal pressure measurements. |
| Zhang et al. [97] | - | 0.08 MPa | 0.11–0.3 MPa | 0.4–0.6 MPa | (0.1–0.6) | —VGE experiments with 3 spindle positions. |
| Reddick et al. [144] | - | 50–90 kPa | 100–170 kPa | 350–550 kPa | (0.1–.65) | —Tests on steam-CO2 mixture at the secondary. |
| Kitrattana et al. [23] | 1 | 7.5 °C | 35–70 mbar | 130–140 °C | (0.15–0.4) | —CPM vs. CRMC ejectors. |
| Author(s) | Fluid | Load (kW) | Te (°C) | Tc (°C) | Tg (°C) | ω | Comments |
|---|---|---|---|---|---|---|---|
| Huang et al. [50] | R113 | Up to 2 | 5–15 | 35–47 | 65–80 | 0.05– 0.27 | —On and off-design results —Performance map for design. |
| Huang and Chen [52] | R113 | - | 15–25 | 22–50 | 70–90 | 0.1–1.2 | —5 ejector geometries (NXP, throat area, mixing throat length variable). |
| Al-Khalidy and Zayonia [261,262,263] | R113 | Up to 0.7 | 6.7 | 42.3 | 87.8 | 0.2–0.31 | —Solar activated ejector. —Effect of boiler, condenser and evaporator on performance. |
| Aphornratana et al. [13] | R11 | Up to 1.7 | –5–12 | 35–41 | 100–110 | - | —2 mixing chambers tested —COP = 0.1–0.5. |
| Eames et al. [21] | R236fa | 1.5 | 4–12 | 27–33 | 60–100 | 0.3–0.6 | —At design condition, COP = 0.35. |
| Selvaraju and Mani [59] | R134a | 0.5 | 2–13.5 | 26–38 | 65–90 | 0.1–0.4 | —6 ejector geometries tested. —Optimal ω exists for each ejector. —COP = 0.1–0.5. |
| Eames et al. [73] | R245fa | 2 | 10–15 | 32–47 | 100–120 | 0.32–0.95 | —CRMC based —Effect of nozzle size and NXP. —Performance maps, (COP = 0.25–0.7). |
| Yapici and Yetişen [53] | R11 | ≤ 1 | 0–16 | 27–34 | 88–102 | - | —Fixed geometry ejector. —Effects of operating parameters on performance (COP = 0.02–0.35). |
| Yapici et al. [67] | R123 | - | 10 | 34 | 83–103 | - | —6 ejector geometries (area ratios 6.5–11.5) —COP = 0.29–0.41. |
| Ablwaifa et al. [54] | R245fa | 2 | 8–15 | 34–44 | 100–120 | 0.2–0.65 | —Validation data for CFD. —NXP variation. |
| Pereira et al. [264] | R600a | 2 | 9 | 12–30 | 83 | 0.55–1 | —VGE study (NXP, spindle control). —COP = 0.2–0.9. |
| Butrymowicz et al. [118] | R600a | - | 3.5–7 | 24–34 | 50–64 | 0.05–0.24 | —On and off-design results. —NXP: 5–7 mm. |
| García Del Valle et al. [48] | R134a | - | 10 | 26–36 | 84.39 | 0.02–0.5 | —Data for 3 mixing chambers. —Variable NXP. |
| Thongtip and Aphornratana [62] | R141b | 2 | –6–15 | 30–33 | 70–130 | 0–0.5 | —3 nozzle sizes tested. —Analysis based on Pe* |
| Shestopalov et al. [56] | R245fa | 12 | 8–16 | 30–39 | 80–105 | 0–0.7 | —3 nozzles and 3 mixing chambers tested. —On and off-design results —Performance maps. |
| Thongtip and Aphornratana [84] | R141b | 2 | –6–20 | 24–36 | 70–140 | 0–0.27 | —6 nozzles tested. —Analysis on nozzle exit Mach |
| Yan et al. [57] | R134a | 1.5 | 1.5–24 | 12–24 | 72–90 | 0.03–0.85 | —A correlation for Pb* was derived. |
| Hamzaoui et al. [256] | R245fa | 35 | 10–20.5 | 33– 41 | 74–90 | 0.1–0.27 | —COP = 0.1–0.6. |
| Author(s) | Analysis | Fluid(s) | Capacity [kW] | Activation Source | General Remarks |
|---|---|---|---|---|---|
| Buyadgie et al. [294] | Theoretical | binary, multicomponent | - | - |
|
| Fang et al. [271] | R1234yf R1234ze | 3 | - | ||
| Diaconu [298] | Water | 5 | Solar | ||
| Du et al. [300] | R245fa | 153 | Geothermal | ||
| Sadeghi et al. [288] | R141b | 6 | Automotive | ||
| Yan et al. [57] | Experiment | R134a | 1.5 | - | |
| Allouche et al. [301] | Water | 5 | solar | ||
| Smierciew et al. [268] | Isobutane | 2 | solar | ||
| Mazzelli and Milazzo [165] | R245fa | 40 | Industrial | ||
| Zegenhagen and Ziegler [255] | R134a | 6 | Automotive | ||
| Smierciew et al. [272] | HFO-1234ze | 30 | Any heat source below 70 °C | ||
| Hamzaoui et al. [256] | R245fa | 6 | Waste heat |
| Author(s) | Analysis | Fluid(s) | Capacity [kW] | Application | General Remarks |
|---|---|---|---|---|---|
| Ben Mansour et al. [315] | Theoretical | R134a | 5 | hybrid, cascades systems |
|
| Xu et al. [317] | R152a | 100 | hybrid solar-ejection-mechanical compression | ||
| Expósito et al. [318] | R134a, R1234yf, R600a | 5 | hybrid, multi-stage compression systems | ||
| Bellos and Tzivanidis [325] | LiBr-H2O | 100 | Solar-absorption-ejector system | ||
| Petrenko et al. [328] | R600 | 10 | Micro-trigeneration system | ||
| Ghaebi et al. [330] | ammonia-water | 1133 | Kalina cycle-ejector refrigeration | ||
| Chen et al. [172] | R141b | - | two-stage ejector refrigeration system | ||
| Hao et al. [335] | zeotropic mixture R170/R600a | 2.6 | Hybrid auto-cascade-ejector refrigeration system | ||
| Yan et al. [155] | Experiment | R134a | 8 | Combined ejector-vapor compression cycle | |
| Huang et al. [338] | R245fa | 5.6 | Solar-assisted ejector-vapor compression cycle | ||
| Nesreddine et al. [339] | R245fa | 15 | Ejector-compression cascade system | ||
| He et al. [340] | R718 | 1 | Two-stage ejector refrigeration system | ||
| Wang et al. [342] | R134a | 1.5 | Hybrid ejector-compressor air-conditioning system | ||
| Li et al. [343] | R134a | 2.5 | Multi-evaporator-ejector refrigeration system | ||
| Abed et al. [344] | Ammonia-water | 3-5 | Solar ejector-absorption cooling cycle | ||
| Shi et al. [345] | LiBr-H2O | 10 | Ejector-absorption refrigeration |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aidoun, Z.; Ameur, K.; Falsafioon, M.; Badache, M. Current Advances in Ejector Modeling, Experimentation and Applications for Refrigeration and Heat Pumps. Part 1: Single-Phase Ejectors. Inventions 2019, 4, 15. https://doi.org/10.3390/inventions4010015
Aidoun Z, Ameur K, Falsafioon M, Badache M. Current Advances in Ejector Modeling, Experimentation and Applications for Refrigeration and Heat Pumps. Part 1: Single-Phase Ejectors. Inventions. 2019; 4(1):15. https://doi.org/10.3390/inventions4010015
Chicago/Turabian StyleAidoun, Zine, Khaled Ameur, Mehdi Falsafioon, and Messaoud Badache. 2019. "Current Advances in Ejector Modeling, Experimentation and Applications for Refrigeration and Heat Pumps. Part 1: Single-Phase Ejectors" Inventions 4, no. 1: 15. https://doi.org/10.3390/inventions4010015
APA StyleAidoun, Z., Ameur, K., Falsafioon, M., & Badache, M. (2019). Current Advances in Ejector Modeling, Experimentation and Applications for Refrigeration and Heat Pumps. Part 1: Single-Phase Ejectors. Inventions, 4(1), 15. https://doi.org/10.3390/inventions4010015