A Remote Controlled Robotic Arm That Reads Barcodes and Handles Products
Abstract
:1. Introduction
2. Methods and Design
2.1. The Design of a 6-Axis Robotic Arm
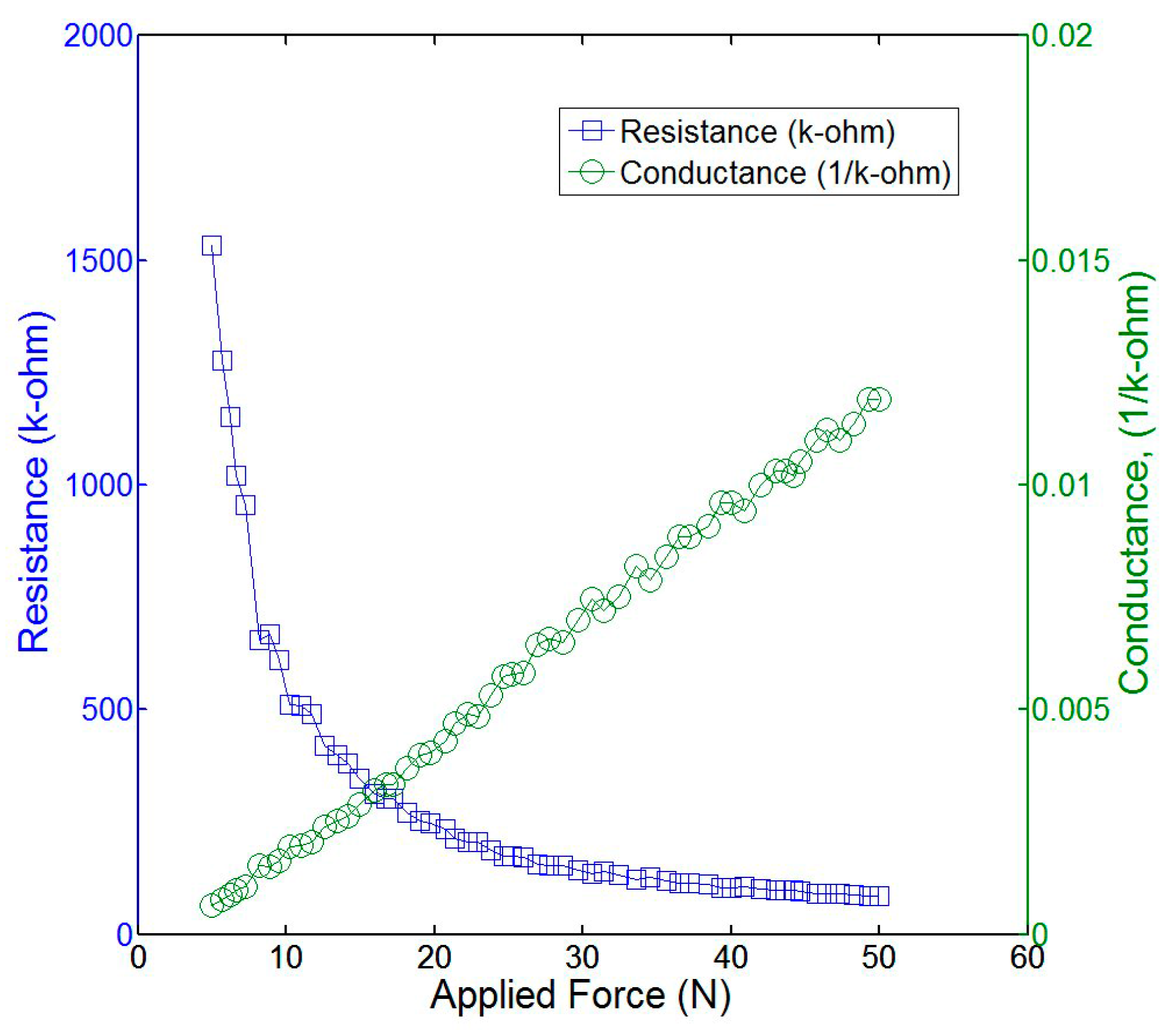
2.2. Mechanical Design of the Gripper
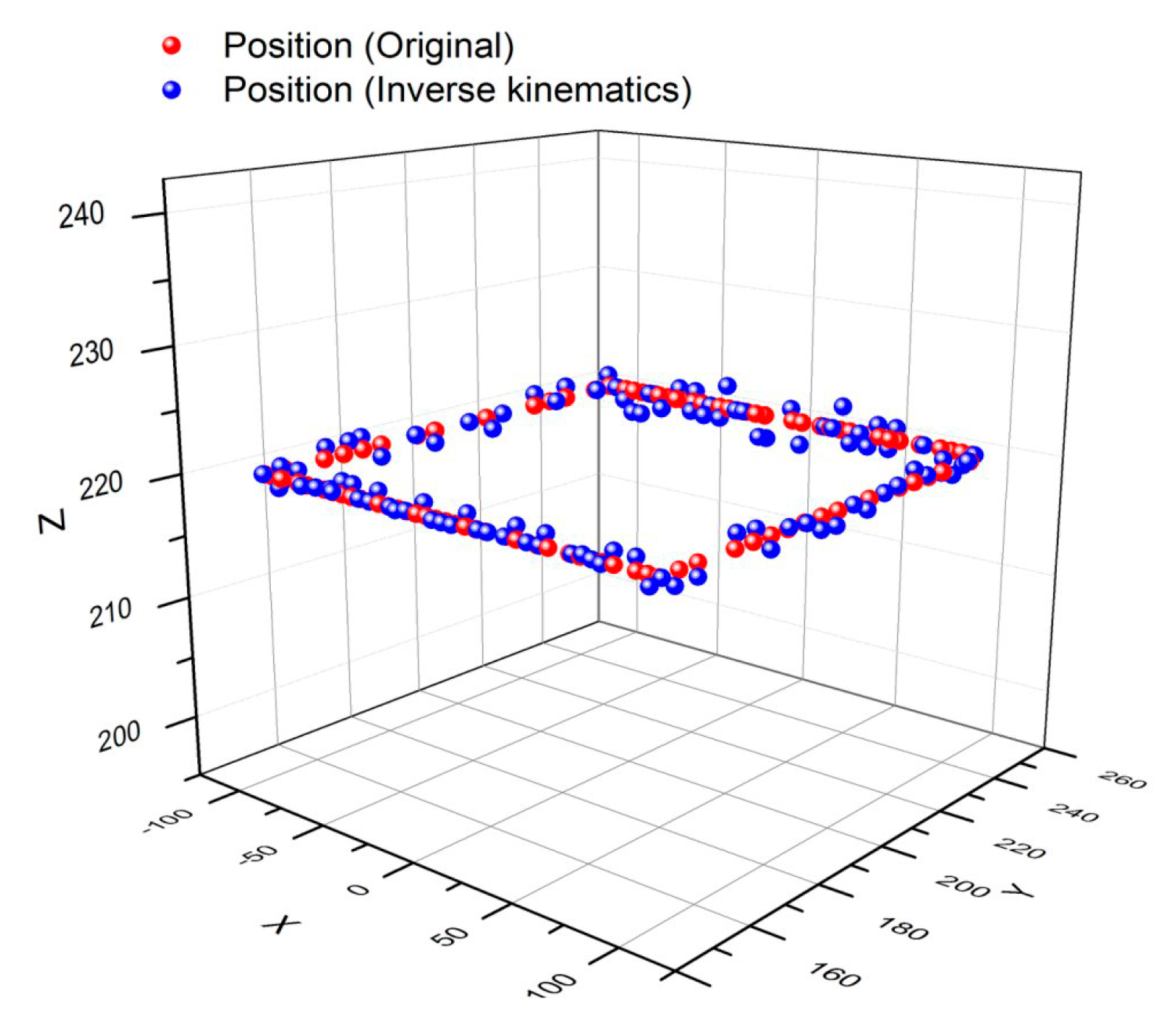
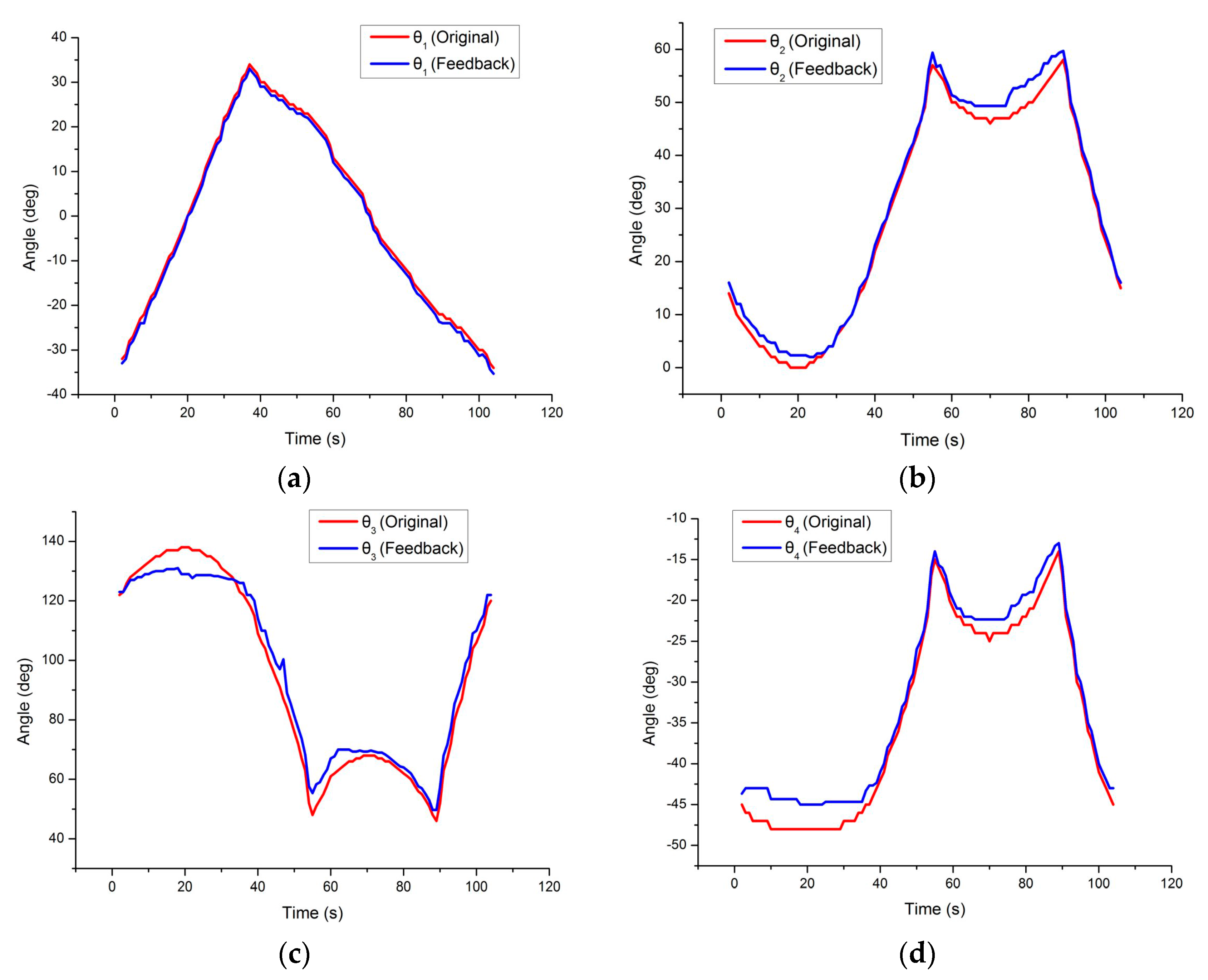
2.3. Kinematics
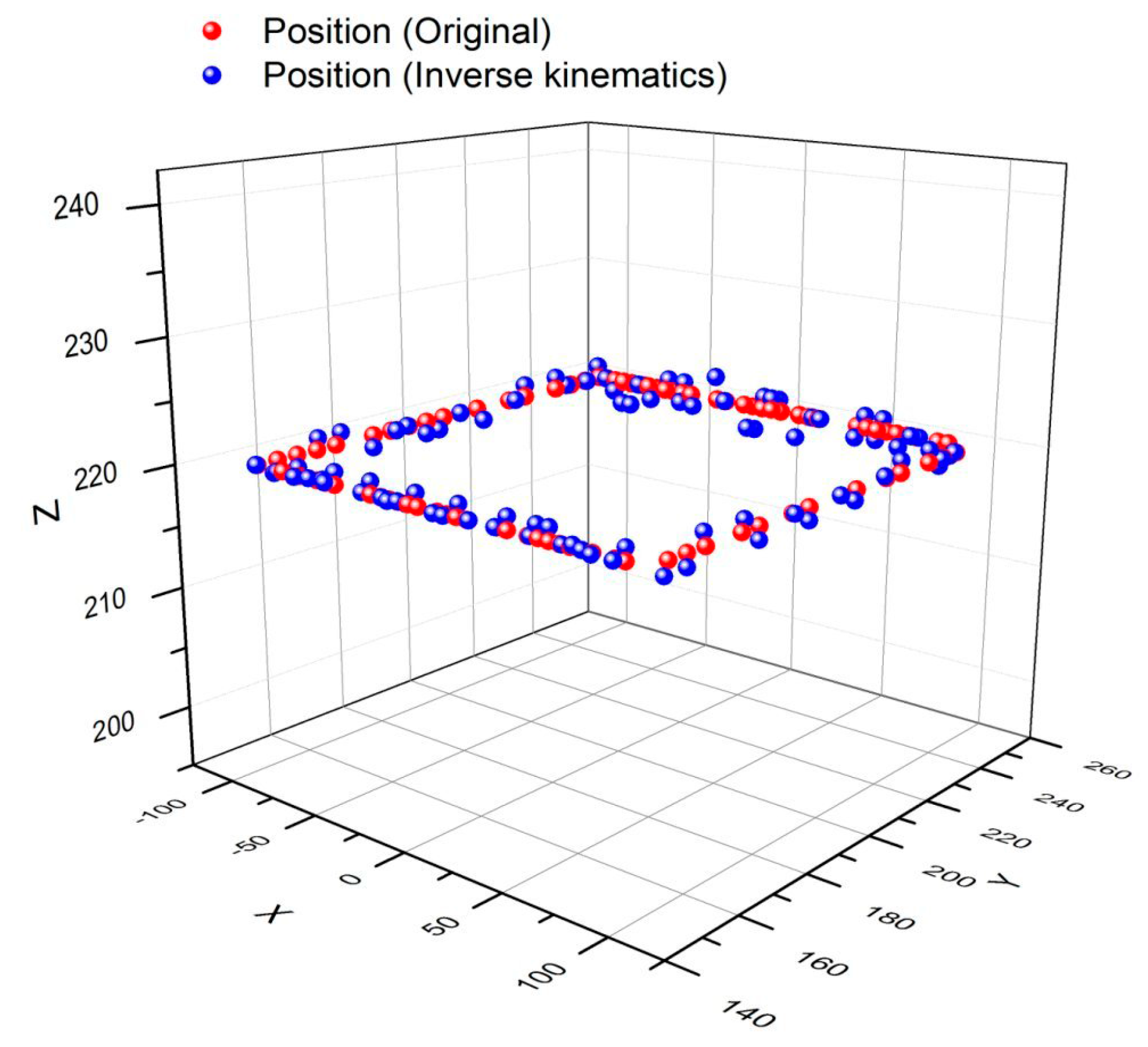
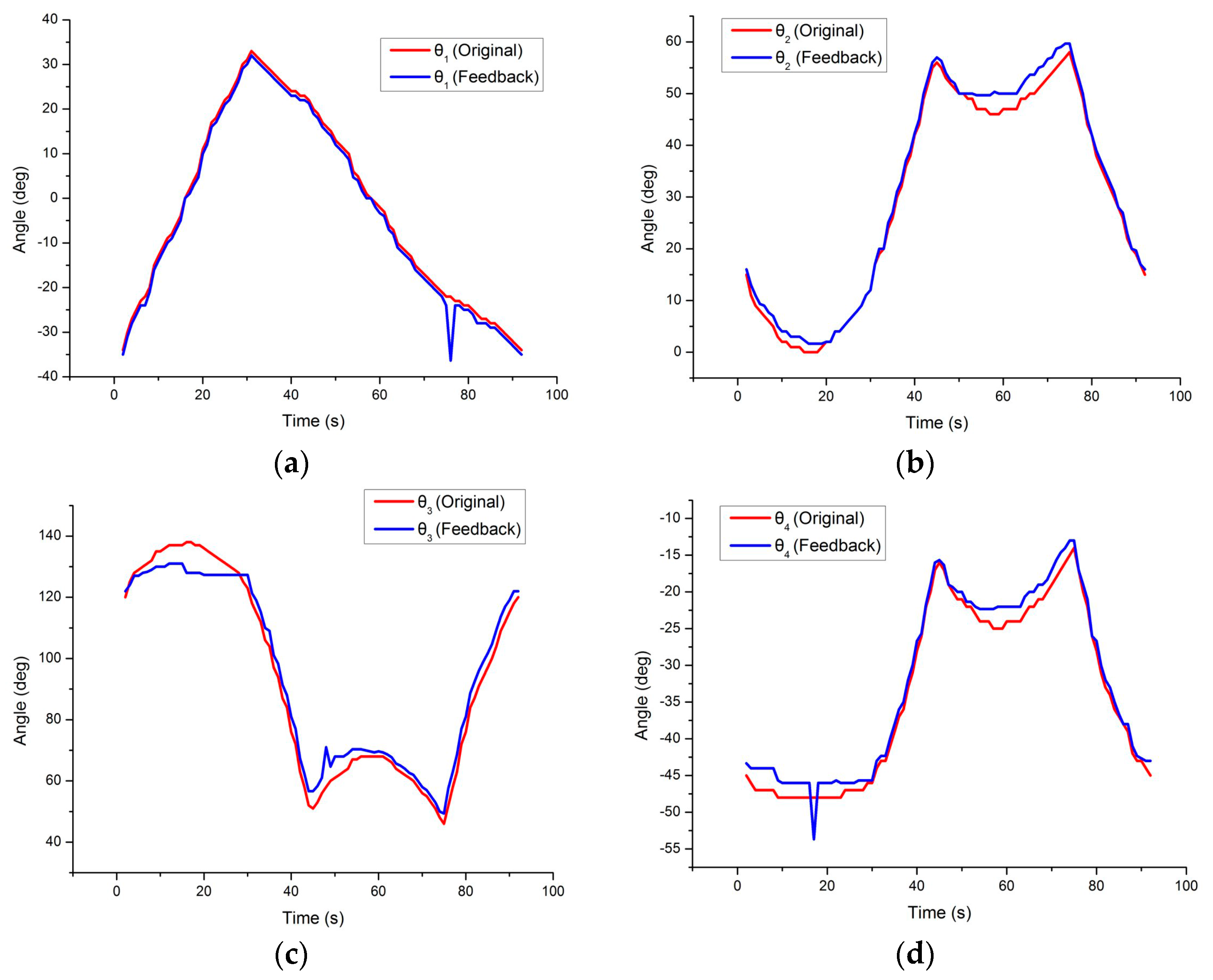
3. Results and Discussion
3.1. Robotic Control
3.2. Clamping Force and Barcode Identification
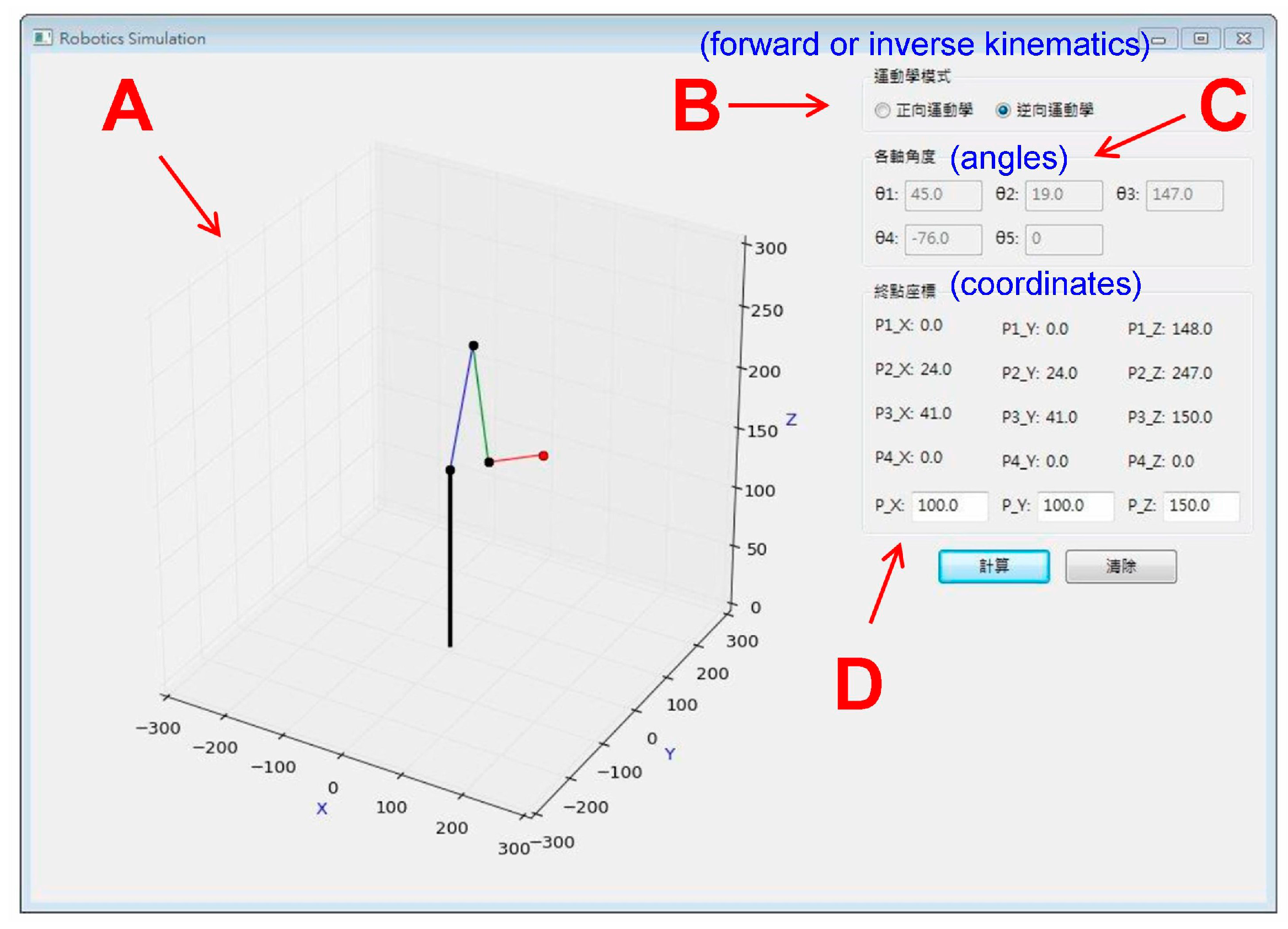
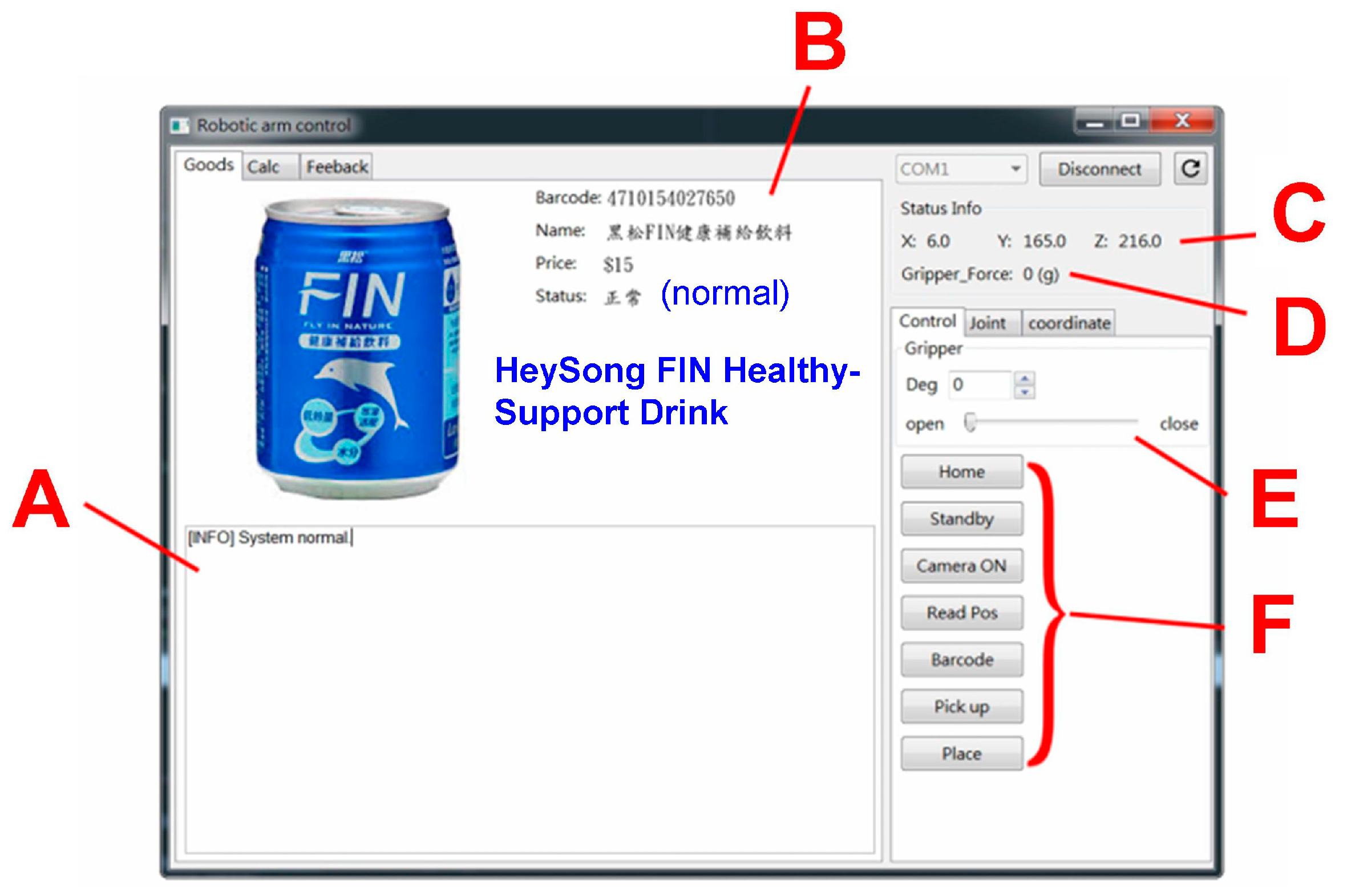
3.3. AGraphic User Interface (GUI) with an Embedded Computer
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Borgia, E. The internet of things: Key features, applications and open issues. Comput. Commmun. 2014, 54, 1–31. [Google Scholar] [CrossRef]
- McEvoy, M.A.; Correll, N. Materials that couple sensing, actuation, computation communication. Science 2015, 347, 1261689. [Google Scholar] [CrossRef] [PubMed]
- Manzoor, S.; Islam, R.U.; Khalid, A.; Samad, A.; Iqbal, J. An open-source multi-DOF articulated robotic educational platform for autonomous object manipulation. Robot. Comput. Integr. Manuf. 2014, 30, 351–362. [Google Scholar] [CrossRef]
- Lin, C.H. Vision servo based delta robot to pick-and-place moving parts. In Proceedings of the International Conference on Industrial Technology, Taipei, Taiwan, 14–17 March 2016. [Google Scholar]
- Kamei, K.; Shinozawa, K.; Ikeda, T.; Utsumi, A.; Miyashita, T.; Hagita, N. Recommendation from robots in a real-world retail shop. In Proceedings of the International Conference on Multimodal Interfaces, Beijing, China, 8–10 November 2010. [Google Scholar]
- Gruen, T.W.; Corsten, D. A Comprehensive Guide to Retail Out-Of-Stock Reduction in the Fast-Moving Consumer Goods Industry; Grocery Manufacturers of America: Arlington, VA, USA, 2007. [Google Scholar]
- Kejriwal, N.; Garg, S.; Kumar, S. Product counting using images with application to robot-based retail stock assessment. In Proceedings of the IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 11–12 May 2015. [Google Scholar]
- Corsten, D.; Gruen, T. Desperately seeking shelf availability: An examination of the extent, the causes, and the efforts to address retail out-of-stocks. Int. J. Retail Distrib. Manag. 2003, 31, 605–617. [Google Scholar] [CrossRef]
- Zhang, J.; Lyu, Y.; Roppel, T.; Patton, J.; Senthilkumar, C.P. Mobile Robot for Retail Inventory Using RFID. In Proceedings of the IEEE International Conference on Industrial Technology, Taipei, Taiwan, 14–17 March 2016. [Google Scholar]
- McFarland, M. Why This Robot May Soon Be Cruising down Your Grocery Store’s Aisles. In the Washington Post. Available online: https://www.washingtonpost.com/news/innovations/wp/2015/11/10 (accessed on 10 November 2015).
- Youssef, S.M.; Salem, R.M. Automated barcode recognition for smart identification and inspection automation. Expert Syst. Appl. 2007, 33, 968–977. [Google Scholar] [CrossRef]
- Wakaumi, H.; Nagasawa, C. A ternary barcode detection system with a pattern-adaptable dual threshold. Sens. Actuators A Phys. 2006, 130–131, 176–183. [Google Scholar] [CrossRef]
- Bockenkamp, A.; Weichert, F.; Rudall, Y.; Prasse, C. Automatic robot-based unloading of goods out of dynamic AGVs within logistic environments. In Commercial Transport; Clausen, U., Friedrich, H., Thaller, C., Geiger, C., Eds.; Springer: New York, NY, USA, 2016; pp. 397–412. [Google Scholar]
- Zwicker, C.; Reinhart, G. Human-robot-collaboration System for a universal packaging cell for heavy goods. In Enabling Manufacturing Competitiveness and Economic Sustainability; Zaeh, M., Ed.; Springer: New York, NY, USA, 2014; pp. 195–199. [Google Scholar]
- Wilf, P.; Zhang, S.; Chikkerur, S.; Little, S.A. Computer vision cracks the leaf code. Proc. Natl. Acad. Sci. USA 2016, 113, 3305–3310. [Google Scholar] [CrossRef] [PubMed]
- Do, H.N.; Vo, M.T.; Vuong, B.Q.; Pham, H.T.; Nguyen, A.H.; Luong, H.Q. Automatic license plate recognition using mobile device. In Proceedings of the IEEE International Conference on Advanced Technologies for Communications, Hanoi, Vietnam, 12–14 October 2016. [Google Scholar]
- Choi, H.; Koç, M. Design and feasibility tests of a flexible gripper based on inflatable rubber pockets. Int. J. Mach. Tools Manuf. 2006, 1350–1361. [Google Scholar] [CrossRef]
- Russo, M.; Ceccarelli, M.; Corves, B.; Hüsing, M.; Lorenz, M.; Cafolla, D.; Carbone, G. Design and test of a gripper prototype for horticulture products. Robot. Comput. Integr. Manuf. 2017, 44, 266–275. [Google Scholar] [CrossRef]
- Rodriguez, F.; Moreno, J.C.; Sánchez, J.A.; Berenguel, M. Grasping in agriculture: State-of-the-art and main characteristics. In Grasping in Robotics; Carbone, G., Ed.; Springer: New York, NY, USA, 2013; pp. 385–409. [Google Scholar]
- Hartenberg, R.S.; Denavit, J. A kinematic notation for lower pair mechanisms based on matrices. J. Appl. Mech. 1955, 77, 215–221. [Google Scholar]
- Chai, D.; Hock, F. Locating and decoding EAN-13 barcodes from images captured by digital cameras. In Proceedings of the IEEE Fifth International Conference on Information, Communications and Signal Processing, Bangkok, Thailand, 6–9 December 2005. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]



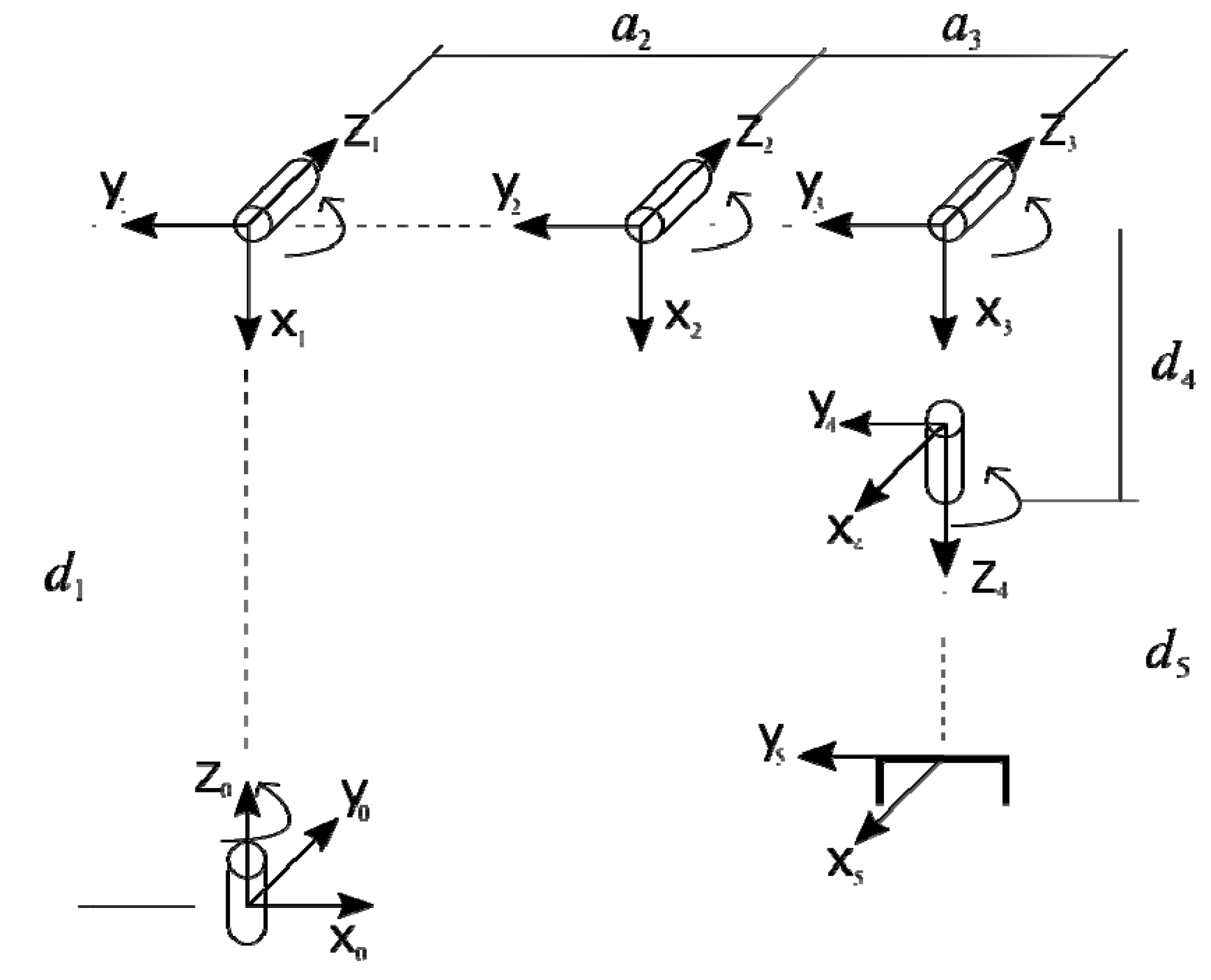


| Axis | èi (deg) | di (mm) | ai (mm) | ái (deg) |
|---|---|---|---|---|
| 0 | è1 | 0 | 0 | 90° |
| 1 | è2 | 196.25 | 0 | 0° |
| 2 | è3 − 90° | 0 | 105.5 | 0° |
| 3 | è4 − 90° | 0 | 100.4 | 0° |
| 4 | 0° | 98 | 0 | 0° |
| 5 | 0° | 165 | 0 | 0° |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.-Y.; Chen, C.-T. A Remote Controlled Robotic Arm That Reads Barcodes and Handles Products. Inventions 2018, 3, 17. https://doi.org/10.3390/inventions3010017
Chen Z-Y, Chen C-T. A Remote Controlled Robotic Arm That Reads Barcodes and Handles Products. Inventions. 2018; 3(1):17. https://doi.org/10.3390/inventions3010017
Chicago/Turabian StyleChen, Zhi-Ying, and Chin-Tai Chen. 2018. "A Remote Controlled Robotic Arm That Reads Barcodes and Handles Products" Inventions 3, no. 1: 17. https://doi.org/10.3390/inventions3010017
APA StyleChen, Z.-Y., & Chen, C.-T. (2018). A Remote Controlled Robotic Arm That Reads Barcodes and Handles Products. Inventions, 3(1), 17. https://doi.org/10.3390/inventions3010017




