Heat Transfer Enhancement and Flow Resistance Characteristics in a Tube with Alternating Corrugated-Smooth Segments

Abstract

To mitigate the inherent high flow resistance of conventional corrugated tubes, a novel design with alternating clockwise/counterclockwise corrugated segments separated by smooth sections is proposed. A 3D numerical model was developed to systematically evaluate the thermal-hydraulic performance of the novel tube against smooth and conventional corrugated tubes, with simulations conducted at Reynolds number (Re) = 9952–35,827. Results show both corrugated configurations enhanced heat transfer significantly relative to the smooth tube: the conventional tube had the highest Nusselt number (Nu) (1.76–1.79 times that of the smooth tube), while the novel tube achieved Nu = 1.61–1.65 times that of the smooth tube. Notably, the novel tube reduced flow resistance substantially—at Re = 35,827, its friction factor (f) was only 65.2% of the conventional tube’s. Parametric studies revealed that more corrugated segments improved heat transfer but increased pressure drop: the 72-12 configuration exhibited the best heat transfer, while the 72-2 configuration reduced f by 40.7%. The novel tube showed superior overall performance (Performance Evaluation Criterion (PEC) > 1.24 for all Re), as corrugated segments generated periodic vortices to disrupt the thermal boundary layer, while smooth segments enabled flow redevelopment and pressure recovery. This study provides valuable guidance for designing high-efficiency, low-resistance heat exchange elements.

1. Introduction

Heat exchangers are essential components for transferring thermal energy between fluids at different temperatures, with the primary goal of efficiently conveying heat from high-temperature to low-temperature fluids. With the escalating global demands for energy conservation, emission reduction, and industrial efficiency improvement, research on enhancing the thermal performance of heat exchangers has evolved into a long-term and critical focus in thermal engineering. Research on enhancing their thermal performance remains active, and relevant techniques are broadly categorized into active and passive methods [1]. Active methods require direct external energy input, such as vibration, surface agitation, or electric/magnetic fields [2,3]; in contrast, passive methods improve heat transfer by modifying surface geometry or fluid properties without additional energy input, rendering them more suitable for widespread industrial applications. Common passive strategies include extended surfaces (e.g., threaded [4], corrugated [5], and coiled tubes [6]), inserts [7], and nanofluids—their effectiveness in heat transfer enhancement has been well-documented in the literature [8,9,10,11].

Corrugated tubes are widely employed in industrial scenarios due to their superior thermal performance: their structured inner walls promote flow disturbance, enhance fluid turbulence, and thereby improve convective heat transfer. The development of corrugated tube technology can be traced back to the mid-20th century, when pioneering studies by Bergles and Webb (founders of enhanced heat transfer research) first experimentally validated that corrugated surfaces could disrupt the laminar sublayer and intensify fluid mixing, achieving 30–50% higher heat transfer efficiency than smooth tubes [5]. This foundational discovery laid the groundwork for subsequent decades of research. Extensive studies have explored the influence of geometric variations on their performance. Using the realizable k-ε turbulence model, Córcoles et al. (2020) demonstrated that corrugated tubes consistently outperformed smooth tubes in terms of heat transfer rate (Q), heat transfer effectiveness (ε), and number of transfer units (NTU) [12]. A numerical investigation by Kirkar et al. (2023) showed that the Nusselt number (Nu) of corrugated tubes was approximately 1.2–7.6 times higher than that of smooth tubes, albeit with a corresponding increase in friction factor (f) [13]. Similarly, Kumar et al. (2022) analyzed different corrugation patterns and found that an outward–inward structure yielded the highest heat transfer enhancement, though at the cost of a significant pressure drop [14].

Moreover, the geometric parameters of corrugated tubes play a pivotal role in determining their thermal performance, and research on parameter optimization has progressed from single-factor exploration to multi-parameter coupled analysis. Early studies in the 2010s primarily focused on single geometric parameters (e.g., pitch or depth) through orthogonal experiments, while recent years have witnessed the integration of advanced numerical methods and optimization algorithms to achieve comprehensive performance improvement. Variations in corrugation width and depth have been shown to significantly affect heat transfer behavior. Using the realizable k-ε model, Liao and Lian (2023) evaluated the influence of corrugation width (W₂) and depth (H₂) on performance, reporting that increasing both parameters improved Nu, with optimal results observed at W₂/D = 0.3 and H₂/D = 0.05 (where D denotes tube diameter) [15]. In another study, Shi et al. (2022) applied B-spline curve modeling and surrogate-based optimization to design advanced corrugated geometries, pinpointing a double-grooved structure as the most effective configuration [16]. Furthermore, Akbarzadeh and Valipour (2020) examined nine corrugated tube profiles and found that increased surface roughness and reduced pitch length significantly enhance thermal performance, as indicated by higher Performance Evaluation Criterion (PEC) values [17].

According to prior research, numerous studies have explored the influence of structural parameters (e.g., corrugation pitch and height) on the thermal-hydraulic performance of corrugated tubes, using metrics such as Nu, f, and PEC. Optimization methods have been applied to refine tube geometries, while research focus has shifted from “performance characterization” to “mechanism elucidation” in recent years, driven by advances in high-precision numerical simulation (e.g., large-eddy simulation) and experimental measurement techniques (e.g., particle image velocimetry). Wang et al. (2021) numerically examined two corrugated tube types by evaluating global entropy generation in relation to Nu and f, revealing that increased corrugation angles lead to greater pressure drops and weakened vortex separation, with the poorest performance occurring under strong turbulent pulsation [18]. Using large-eddy simulation, Hu et al. (2025) analyzed an intermediate heat exchanger (IHX) comprising smooth and helically corrugated tubes—such as single-pattern corrugations (outward–inward [13], double-grooved [16], or helical [19])—which inherently sacrifice either heat transfer efficiency or flow resistance control. A critical gap persists in developing novel configurations that achieve balanced thermal-hydraulic performance by addressing the trade-off between boundary layer disruption (for heat transfer) and excessive flow resistance (a common limitation of existing corrugated structures).

For industrial heat exchangers, two core operational demands are often mutually constrained: high heat transfer efficiency is required to improve energy utilization, while low flow resistance is critical to reduce operating costs (e.g., pumping power). However, existing corrugated tube designs fail to reconcile these needs: conventional continuous corrugated structures enhance heat transfer via persistent flow disturbance but induce excessive pressure drops, while simplified structures (e.g., reduced corrugation density) lower resistance only at the expense of significant heat transfer degradation. This unresolved trade-off, paired with the urgent industrial need for high-efficiency, low-resistance heat exchange components, constitutes the key motivation for the present study. Therefore, this study introduces a novel corrugated tube design—characterized by alternating clockwise and counterclockwise corrugated segments connected via smooth sections—to address this limitation: the corrugated segments periodically disrupt the thermal boundary layer (for heat transfer enhancement), while the smooth sections enable flow redevelopment (for resistance reduction). To advance this design, the study pursued three core objectives: (1) verify whether this innovative alternating structure can achieve superior balanced thermal-hydraulic performance compared to conventional corrugated tubes; (2) construct a three-dimensional mathematical model grounded in fluid mechanics and heat transfer fundamentals, and employ computational fluid dynamics (CFD) simulations to systematically evaluate the thermal-hydraulic behaviors (including Nu, f, and pressure drop) of the novel tube; (3) conduct in-depth performance analyses to elucidate the mechanism by which the proposed structure balances heat transfer and resistance control, thus providing a theoretical foundation for the optimization of low-resistance, high-efficiency corrugated tubes.

2. Materials and Methods

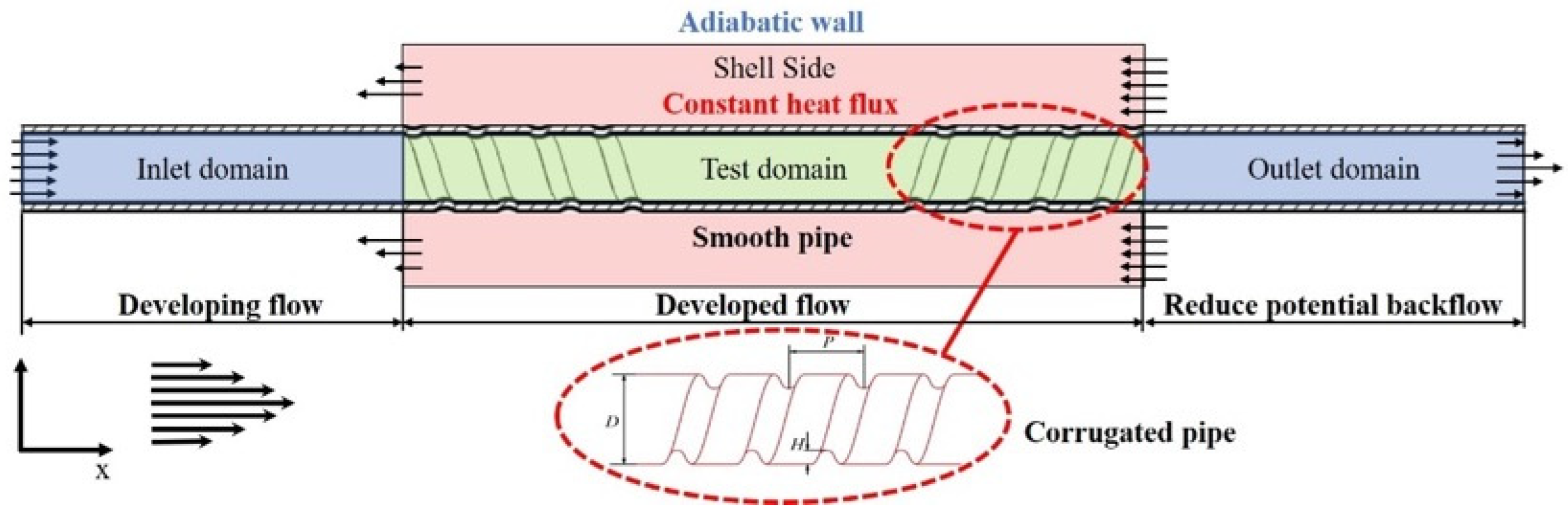
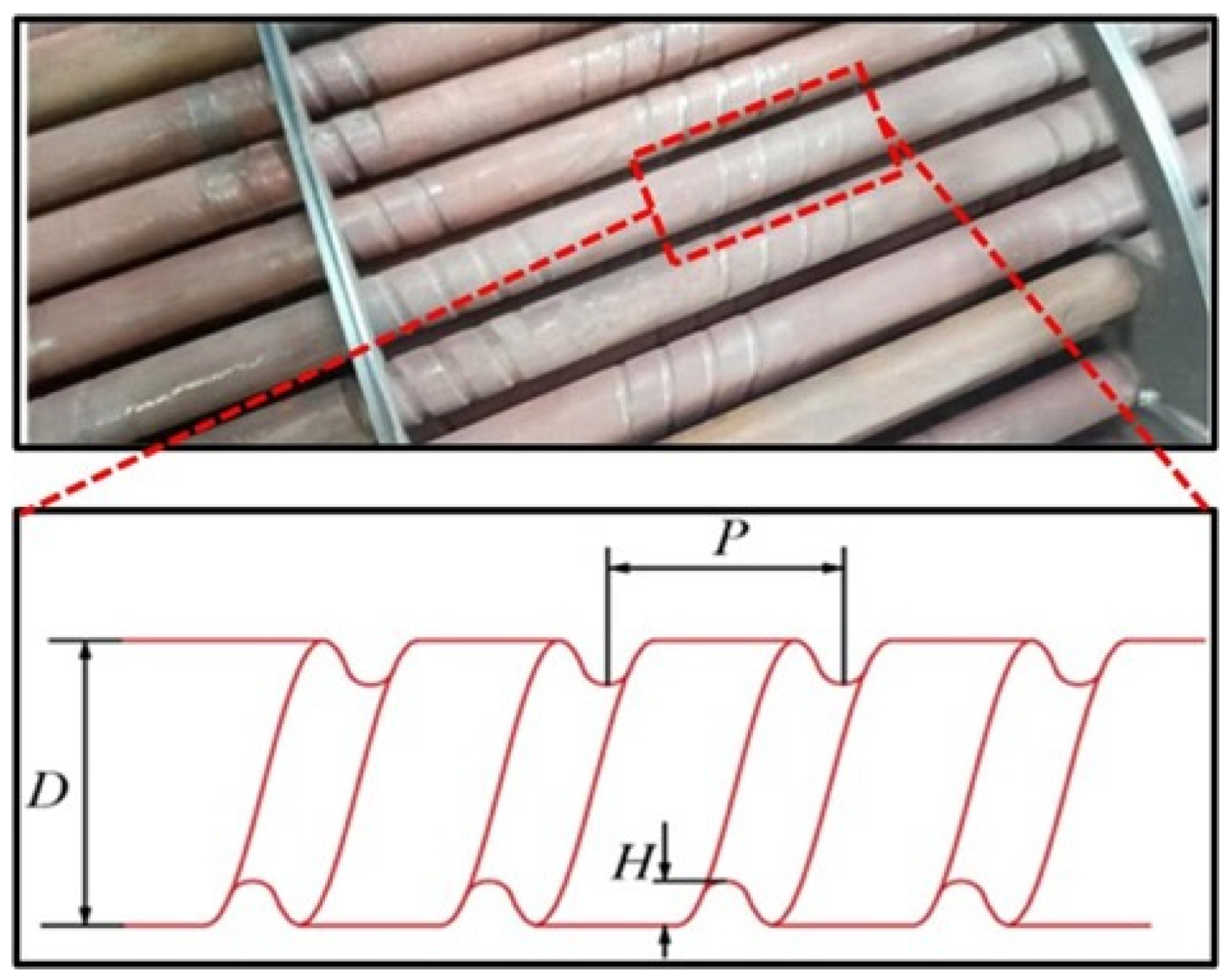
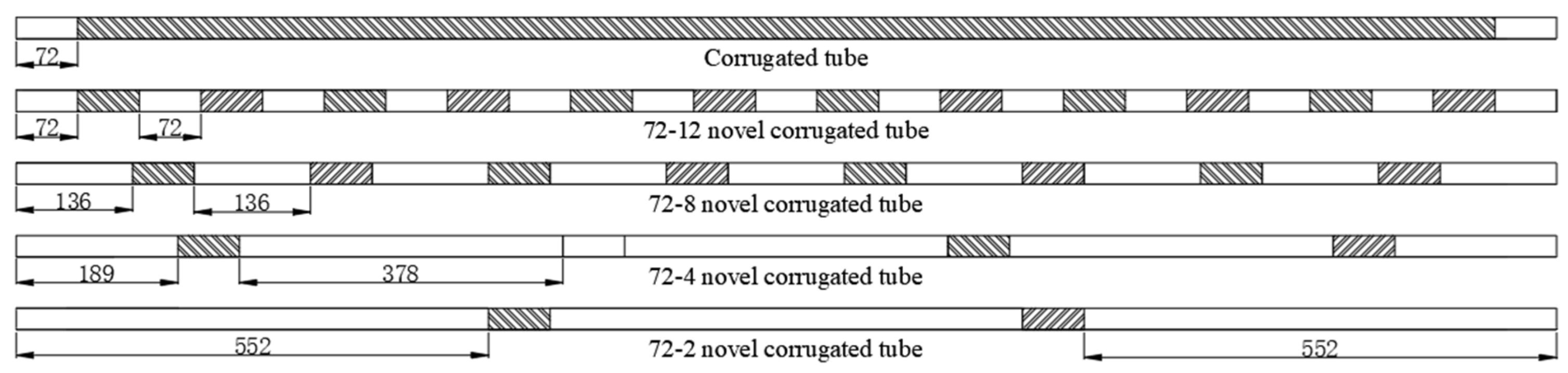
2.1. Physical Models and Boundary Conditions

To investigate the heat transfer and flow characteristics of different novel corrugated tube designs, this study adopted computational fluid dynamics (CFD) for numerical simulation. The numerical model of the single-tube heat exchanger, as illustrated in Figure 1, consists of two distinct flow regions—the tube-side inner channel (flow path of the core working fluid) and the shell-side annular gap (flow path of the heat exchange fluid). Specifically, the tube side numerical model comprises an inlet section, an 1800 mm test section (the core segment for experimental investigation), and an outlet section, with a total length of 2400 mm; a schematic diagram of the novel corrugated tube is provided in Figure 2. The inlet section was designed with a length of 400 mm—equivalent to twenty times the hydraulic diameter (20D) [20]—to ensure fully developed flow entered the test section, while a 200 mm outlet section was incorporated to reduce the impact of backflow at the exit. The tube had an inner diameter (D) of 20 mm and a wall thickness of 2 mm; within the test section, each corrugated segment measured 72 mm in length, with the corrugation height (H) and corrugation pitch (P) fixed at 1 mm and 18 mm, respectively. The shell side refers to the simplified heat exchanger shell, which wraps around the test section of the tube side, with a total length of 1800 mm (matching the length of the test section) and an inner diameter of 132 mm. Water was selected as the working medium and treated as an incompressible fluid, and the simulation was performed under steady-state assumptions.

2.2. Governing Equations and Data Reduction

Specifically, the fluid flow in the present study features a high Reynolds number and involves rotation and curvature effects. The realizable k-ε model, originally proposed for high Reynolds number turbulent flows [21], is well-suited for such flow conditions due to its superior performance in simulating flows with rotation, curvature, and moderate separation [21]. Moreover, comparative studies on turbulent flow simulation in corrugated pipes (consistent with the present study’s geometry) have demonstrated that the realizable k-ε model offers a more balanced trade-off between prediction accuracy and computational cost compared to the Reynolds Stress Model (RSM) and Large Eddy Simulation (LES) [22]. RSM and LES, while potentially more accurate in some cases, incur substantially higher computational costs that are not justified for the engineering-scale simulation objectives of this study [22]. These factors collectively justify the selection of this model.

While the model is well-adapted to the current flow conditions, it should be noted that it has inherent limitations in strongly separated flows—for instance, potential inaccuracies in predicting recirculation zone lengths and vortex intensities. Thus, the realizable k-ε model was selected for the present investigation. We utilized ANSYS Fluent 2021R2 for the numerical simulations; the governing equations employed (Equations (1) and (2)) are based on the classic formulation of the realizable k-ε model [21], and their numerical discretization and solution procedures refer to the guidelines in the ANSYS Fluent Theory Guide [23]. The governing equations are as follows:

$${\displaystyle \frac{𝜕}{𝜕x_j}}(\rho k{u}_j)={\displaystyle \frac{𝜕}{𝜕x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{𝜕k}{𝜕x_j}}\right]+P_k+P_b-\rho \epsilon -Y_M+S_k$$

(1)

$${\displaystyle \frac{𝜕}{𝜕x_j}}(\rho \epsilon u_j)={\displaystyle \frac{𝜕}{𝜕x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\right){\displaystyle \frac{𝜕\epsilon }{𝜕x_j}}\right]+\rho C_{1}S\epsilon -\rho C_2{\displaystyle \frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}}+C_1{\displaystyle \frac{\epsilon }{k}}{C}_{3\epsilon }{P}_b+S_{\epsilon }$$

(2)

where P_k and P_b represent the turbulent kinetic energy (TKE) generated by the mean velocity gradient and buoyancy, respectively; σ_k and σ_ε denote the inverse effective Prandtl numbers for k and ε; Y_M accounts for the contribution of compressible dissipation to TKE; and S_k, S_ε are user-defined source terms. Detailed definitions and derivations of these parameters can be found in the ANSYS Fluent Theory Guide.

$$C_1=\max \left[0.43,{\displaystyle \frac{\eta }{\eta +5}}\right]$$

(3)

$$\eta =S{\displaystyle \frac{k}{\epsilon }}$$

(4)

$$S=\sqrt{2S_{ij}{S}_{ij}}$$

(5)

The model coefficients employed in the investigation are as listed below:

$$C_{1\epsilon }=1.44, C_2=1.9, {\sigma }_k=1.0, {\sigma }_{\epsilon }=1.2$$

(6)

The pressure–velocity coupling is addressed using the Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) algorithm, which facilitates the accurate determination of pressure field distribution. To guarantee numerical stability and solution precision, the residual convergence criteria for the continuity, velocity, and energy equations were set to 10⁻⁵. This stringent threshold ensures stable convergence of the iterative solution and enables consistent representation of fluid flow behavior within the computational domain.

The parameters required for the numerical analysis, such as mass flow rate (q_m), Nu, f, heat transfer coefficient, and Re are determined using the following governing equations.

$$q_m=\rho u\pi D^2/4$$

(7)

$$T_a=(T_{in}+T_{out})/2=T_{in}+\Delta T/2$$

(8)

$$Re=\rho VD/\mu$$

(9)

$$Q=q_m{c}_p\Delta T$$

(10)

$$h=Q/[A(T_w-T_a)]$$

(11)

$$N_u=hD/\lambda$$

(12)

$$f=2\Delta PD/(\rho L{V}^2)$$

(13)

The overall thermal-hydraulic performance of the novel corrugated tube was evaluated using the Performance Evaluation Criterion (PEC), defined by Equation (14):

$$PEC={\displaystyle \frac{Nu}{N{u}_s}}/{\left({\displaystyle \frac{f}{f_s}}\right)}^{1/3}$$

(14)

where Nu and f are the Nusselt number and friction factor of the novel corrugated tube, respectively, and Nu_s and f_s are the corresponding values for the smooth tube at the same Reynolds number. A PEC value exceeding 1 signifies that the overall performance surpasses the reference baseline.

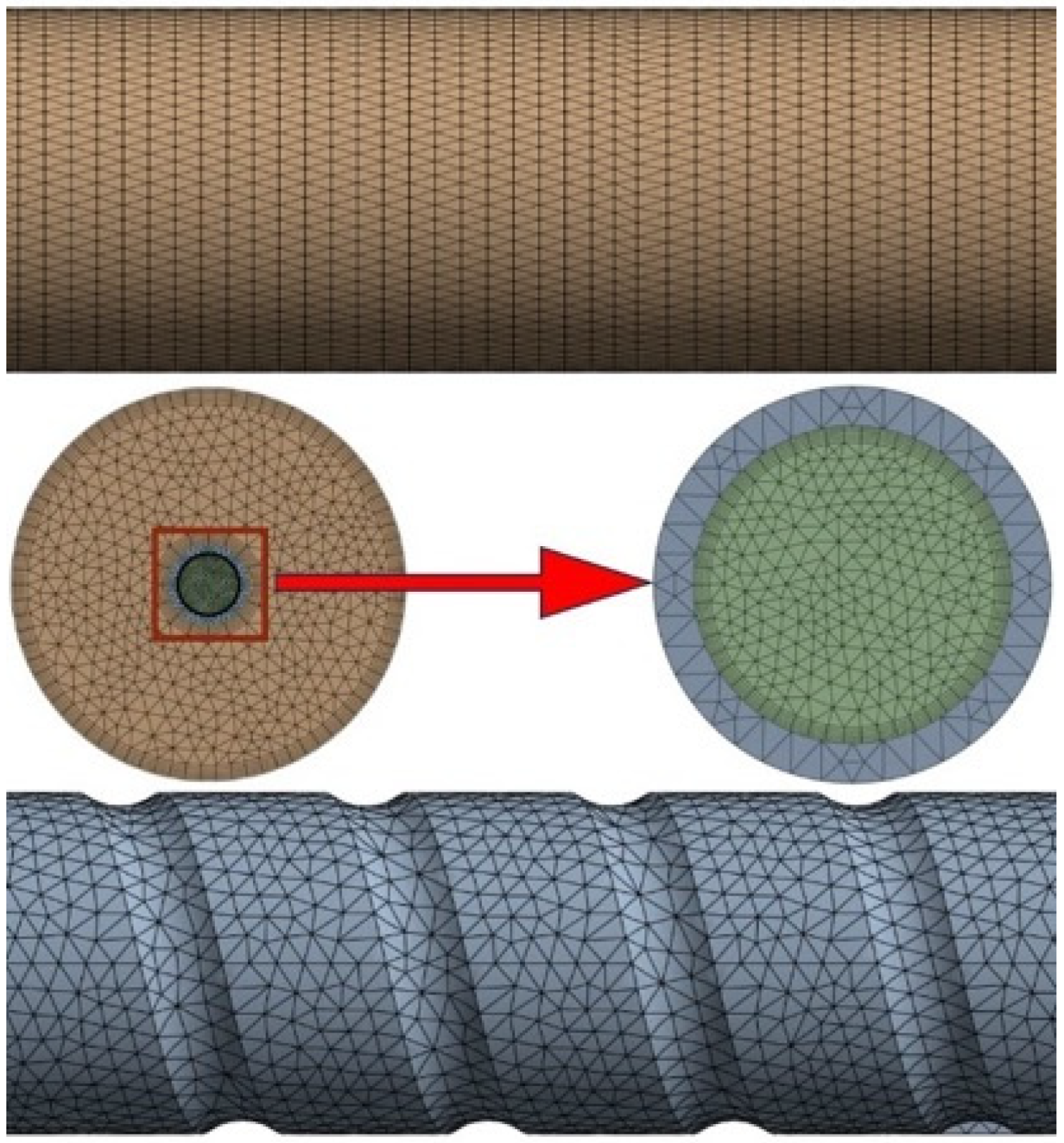
2.3. Grid Independence Analysis

A tetrahedral mesh was adopted for the entire computational domain, with local mesh refinement implemented in the near-wall boundary layers. The mesh structure of the single-tube heat exchanger is illustrated in Figure 3. Due to the geometric complexity of the novel corrugated tube, structured meshes are prone to distortion—a problem that may compromise simulation accuracy [24]. To resolve this issue, unstructured meshes were generated using tools within ANSYS Workbench.

A velocity-inlet boundary condition was imposed at the inlets of both the tube side and shell side, with a velocity magnitude of 1 m/s. The inlet temperatures for the tube-side and shell-side fluids were set to 300 K and 350 K, respectively. Water was adopted as the working fluid for both sides, where heat transfer took place through the tube wall.

To validate the numerical approach, the average Nu and f were obtained from simulations under each condition. Convergence was deemed achieved when all scaled residuals dropped below 10⁻⁶. A grid independence study was conducted on the novel corrugated tube model. As summarized in

Table 1. Grid independence.

Number of Grids (Size-NO.)	Re = 12,000
	Nu	f
3.6-125,000	92.8826	0.08256
2.9-240,000	86.2161	0.07615
2.3-480,000	83.4533	0.07221
1.8-1,000,000	82.5619	0.07113
1.4-2,140,000	81.4728	0.07005
1.2-3,360,000	81.0276	0.07010
1.1-4,290,000	81.2601	0.07003
0.9-7,660,000	81.1047	0.07008

—wherein the “Number of grids” column presents the element size on the left and the corresponding grid count under that element size on the right—the results became virtually independent of grid density once the cell count exceeded 1.8 million. Thus, a mesh with approximately 2.14 million cells was adopted for final simulations. The near-wall mesh was configured with a first-layer thickness of 0.02 mm (to ensure y⁺ < 5) and a growth rate of 1.1. For both the core fluid region and primary heat transfer surfaces, the characteristic element size was set to 1.4 mm.

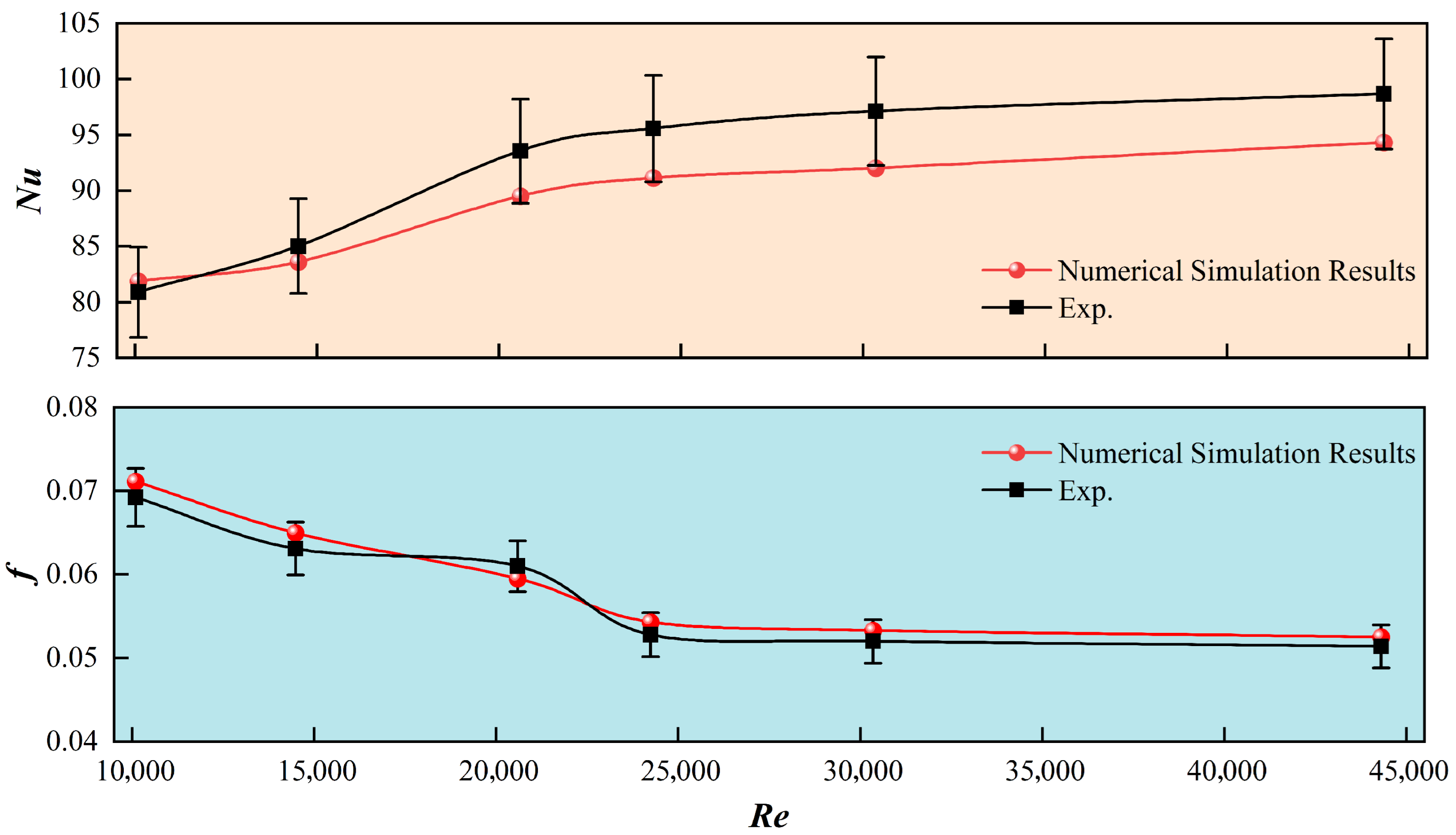
2.4. Model Validation

To validate the numerical simulations, the results were compared against experimental data obtained from a custom-built test platform. The heat exchanger employed in the experiment—shown in Figure 4—was custom-fabricated according to the requirements of the experimental heat transfer measurement, with a tube length of 2000 mm to match the research objectives, and the heat transfer section length was 1800 mm. Deionized water was used as the working fluid, and under the experimental conditions, deionized water was treated as an incompressible fluid; its physical properties (such as density, thermal conductivity, and dynamic viscosity) were referenced from standard thermophysical property tables. A 72-12 novel corrugated tube, wherein “72” denotes the length of each corrugated segment (72 mm) and “12” indicates the total number of corrugated segments, geometrically identical to the numerical model, was installed in the test section for performance evaluation. The controlled experimental parameters are summarized in

Table 2. Test conditions.

	Numerical Simulation		EXP.
	Tube Side	Shell Side	Tube Side	Shell Side
Velocity (m/s)	0.5~1.8	0.5	0.5~1.8	0.5
Inlet temperature (°C)	20	50	20	50

.

Inlet and outlet temperatures, pressures, and pressure differentials of the tube side were monitored. For the calculation of core parameters (e.g., Reynolds number, Nusselt number) involved in this study, the hydraulic diameter of the corrugated tube was determined following the method proposed by Mahmoud Abdelmagied [25]. These measured data were used to calculate the experimental Nu and f for comparison with the numerical results. To obtain data over a range of Re, the tube-side inlet velocity was adjusted systematically. For each operating condition, five replicate measurements were performed, and the averaged values were adopted for subsequent analysis. In response to the comment on measurement uncertainty, the A-type uncertainty analysis was conducted for the experimental data following the method proposed by Moffat [26]. The A-type standard uncertainty was derived from the statistical analysis of the replicate measurements, where the standard deviation (s) of the five repeated readings for each parameter (temperature, pressure, velocity) was calculated. The calculated expanded uncertainties for Nu and f were ±2.3% and ±1.8%, respectively, which were within the acceptable range for heat transfer and flow resistance measurements, confirming the reliability of the experimental data. The comparison results are presented in Figure 5.

The results indicate that the maximum deviation between the simulated and experimental Nu was less than 5%, while the maximum deviation for f was also below 5%. Notably, the discrepancy in f diminishes as Re increases, indicating better predictive accuracy of the model at higher flow rates. These findings verify the validity of the numerical model—an outcome attributable to the high accuracy of the realizable k-ε turbulence model and the strong robustness of the simulation setup.

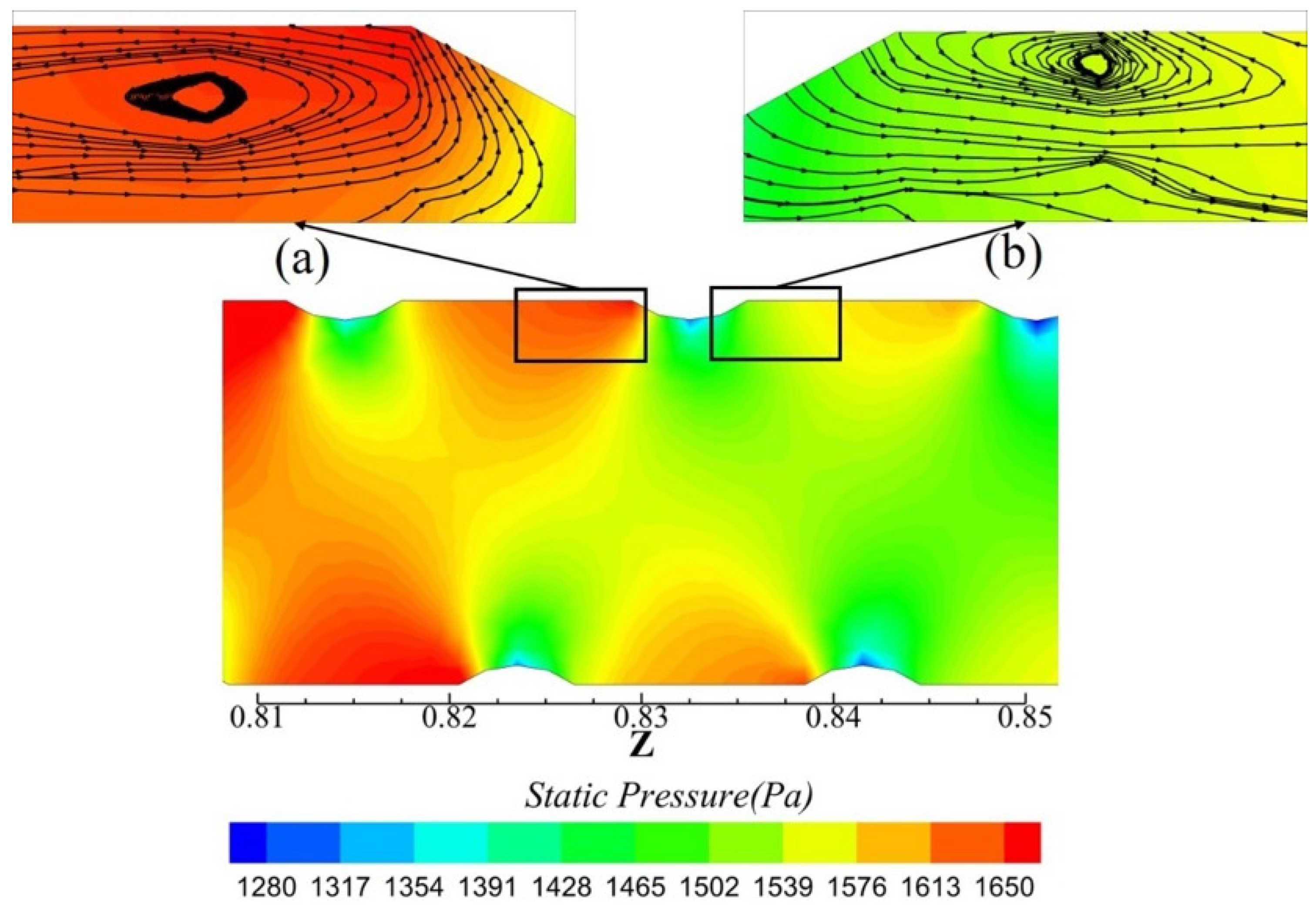
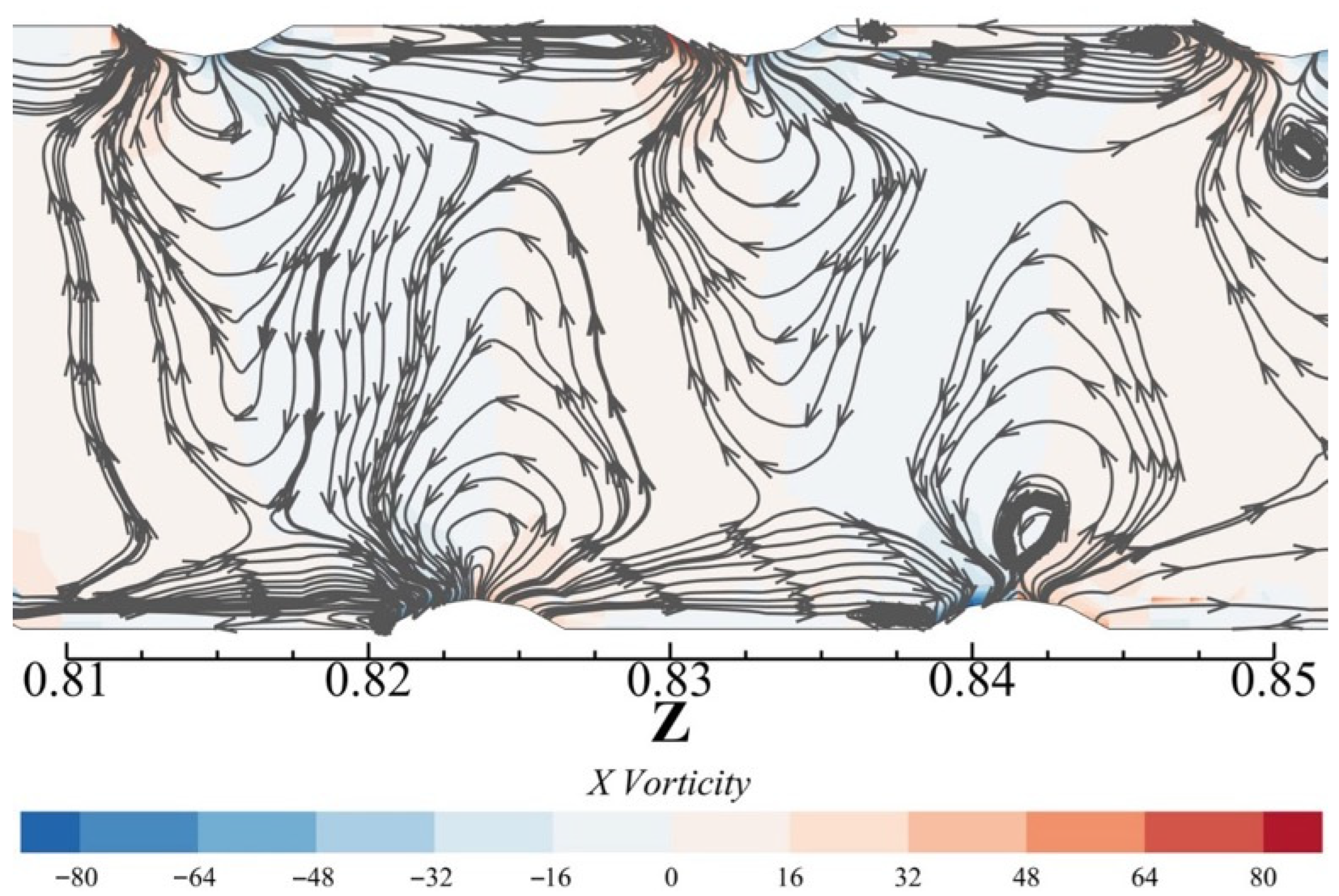
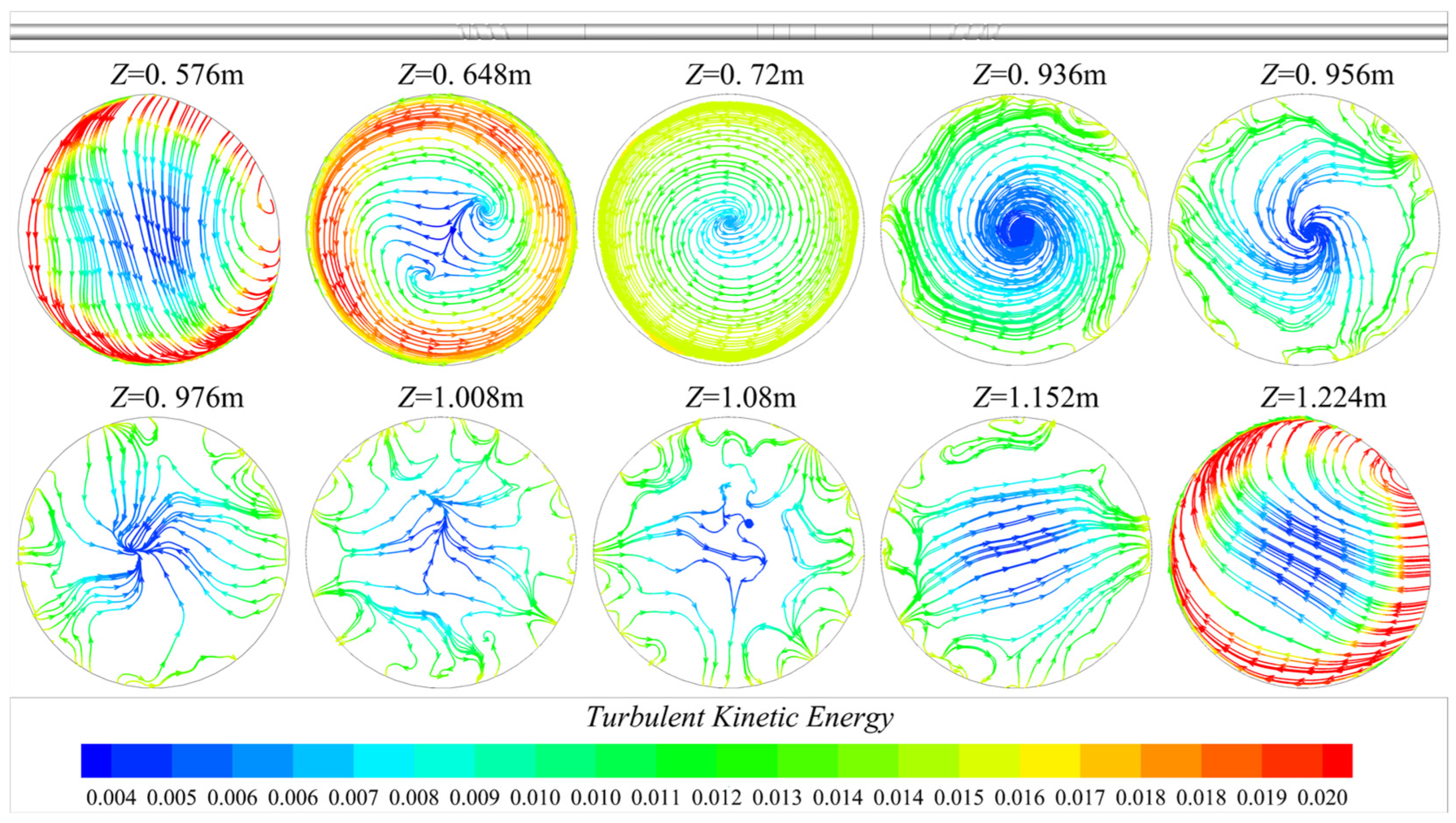
3. Results

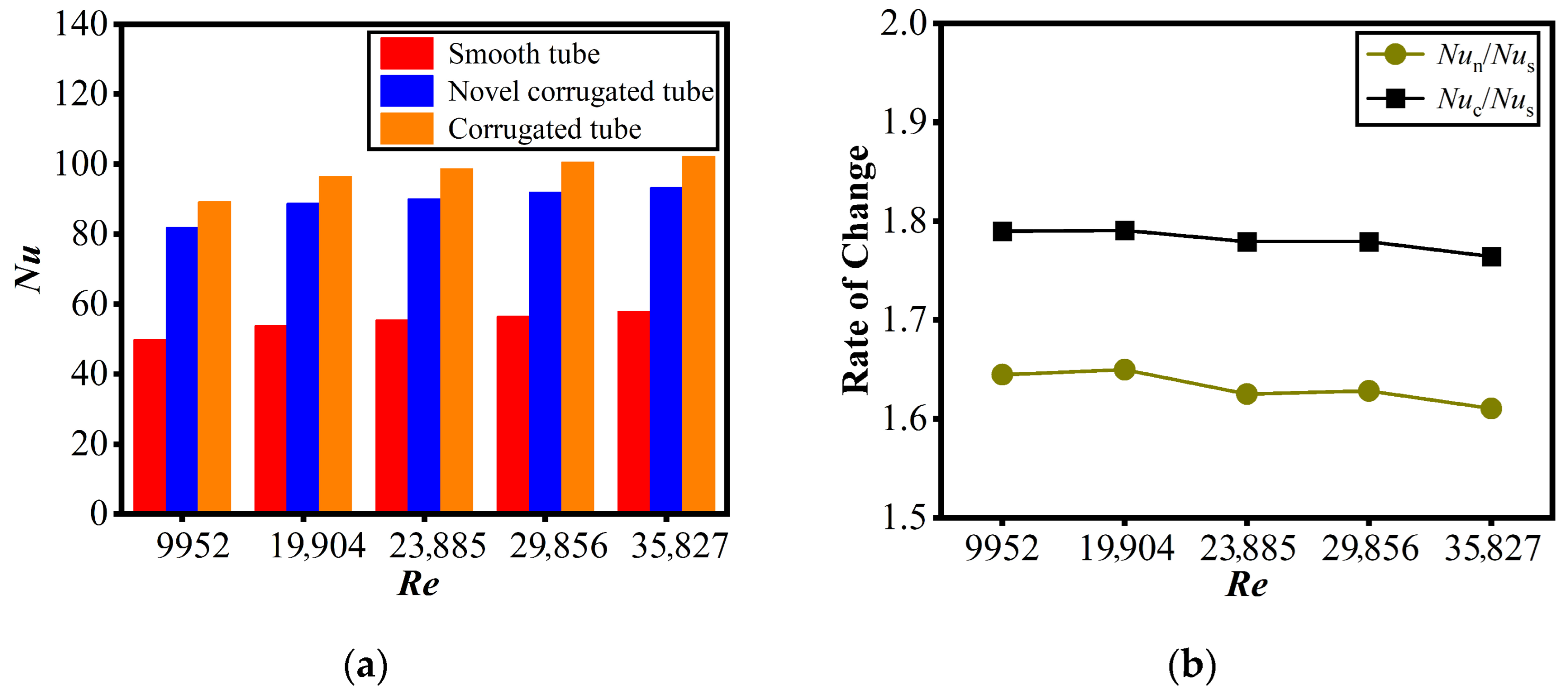
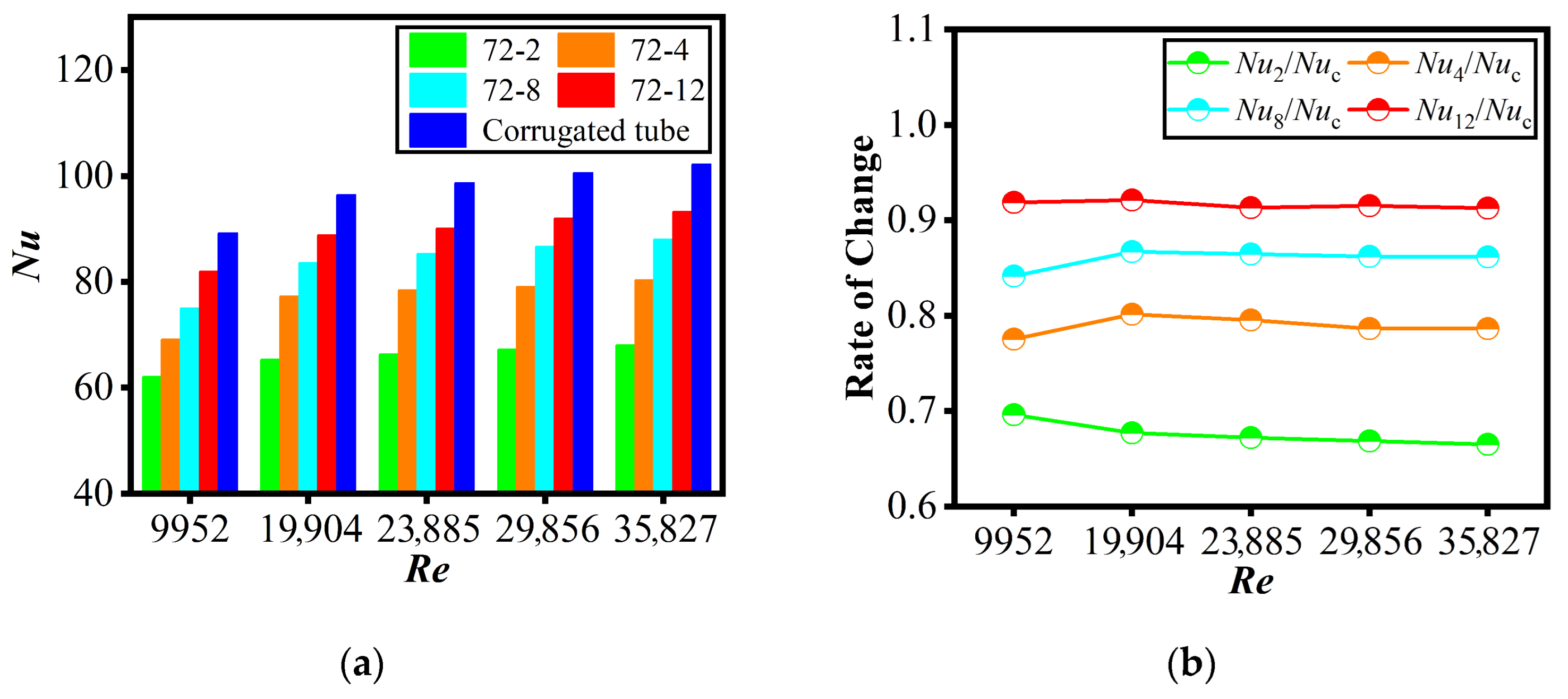
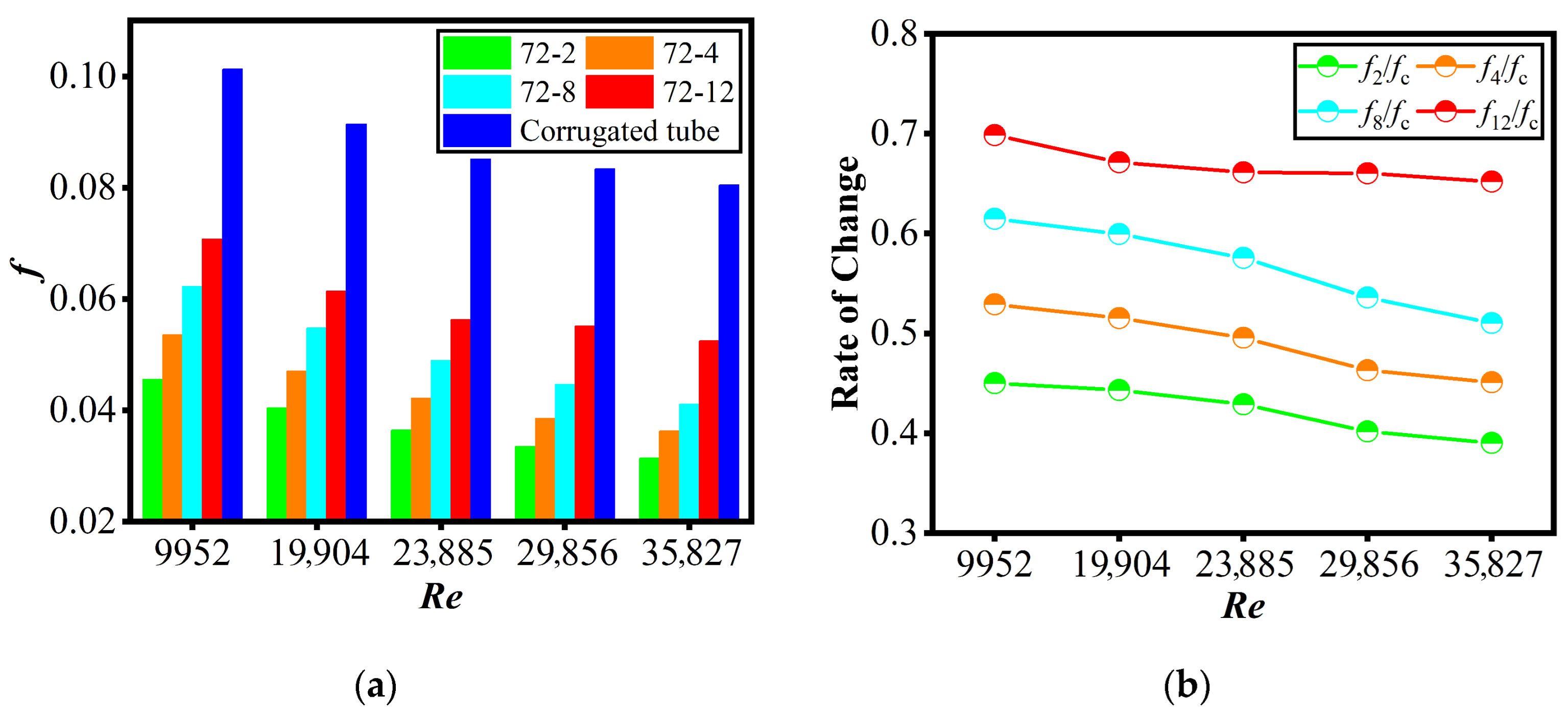
3.1. Heat Transfer Characteristics

Figure 6 presents the distribution of TKE along the flow direction in the longitudinal sections of three types of heat exchanger tube configurations: smooth tube, conventional corrugated tube, and the 72-12 novel corrugated tube. TKE quantifies the intensity of turbulent fluctuations and the chaotic kinetic energy of fluid micro-elements; higher TKE values indicate stronger turbulence and enhanced fluid mixing—effects that lead to thinner thermal boundary layers, reduced thermal resistance, and improved convective heat transfer.

The longitudinal contours reveal that TKE was minimized at the tube center, increased radially outward, and peaked near the tube wall. Compared with the smooth tube, both the conventional corrugated tube and the 72-12 novel corrugated tube exhibited significantly higher TKE in the near-wall region—an enhancement driven by their surface irregularities. This strengthened near-wall turbulence enables more efficient thermal energy transfer from high-temperature to low-temperature regions, ultimately boosting the overall heat transfer performance of the tubes.

Figure 7 illustrates the cross-sectional flow patterns of three heat exchanger tube types—smooth, conventional corrugated, and novel corrugated—at the same axial position. Streamlines are color-coded to indicate varying levels of TKE. In Figure 7a, the smooth tube exhibited symmetric, uniform streamline distribution about the centerline, a consequence of its geometrically consistent circular cross-section. Its velocity field remained evenly distributed, with negligible secondary flow or vortex generation, resulting in relatively low turbulence intensity.

In contrast, Figure 7b demonstrates that the conventional corrugated tube induced a more complex flow structure. Due to its spiral wall geometry, streamlines formed arcuate paths, concentrating toward the section center where velocity peaks were observed. Fully developed flow in this configuration exhibited markedly elevated TKE in the near-wall region, enhancing fluid mixing and heat transfer—though at the cost of increased flow resistance.

Figure 7c shows the novel corrugated tube’s cross-sectional flow structure, which exhibited distinct characteristics compared to both the smooth and conventional corrugated designs. Due to its alternating clockwise and counterclockwise corrugations separated by smooth segments, flow does not develop spiral-induced turbulence. Instead, large coherent vortices form within the smooth segments, while streamlines in the corrugated segments align along vertical and 30° oblique directions. This creates a more uniformly distributed flow field without localized high-velocity zones, suggesting an effective balance between heat transfer enhancement and flow resistance control.

The interface flow patterns in Figure 7 illustrate that the traditional corrugated tube exhibited the highest concentration and broadest distribution of TKE. Specifically, a high concentration of TKE was observed in the central region of this tube, while lower TKE levels were detected in other areas. This distinct TKE stratification—higher near the tube boundary and lower at the center—coupled with significant near-wall flow disturbances, facilitates vigorous fluid mixing inside the tube. However, this enhanced turbulence also results in higher energy dissipation and larger pressure drop in the traditional corrugated tube.

In contrast, both the novel corrugated tube and the smooth tube exhibited more uniform TKE distribution, with no obvious stratification. Notably, within the corrugated segments of the novel design, near-wall TKE was slightly higher than that in the smooth tube. When the fluid transitions from the corrugated segments to the smooth segments of the novel tube, however, TKE grows more uniform and overall lower—an effect that reduces fluid resistance. This flow characteristic enables the novel corrugated tube to improve heat transfer performance while maintaining a lower pressure drop compared to the traditional corrugated tube.

An analysis was performed on the heat transfer performance of three tube types—novel corrugated tube, conventional corrugated tube, and smooth tube—with a focus on the variation of Nu over the Re range of 9952 to 35,827. Figure 8 and Figure 9 present the variations of Nu and f with Re for the three tubes using bar charts, while line graphs quantify the performance ratios of the conventional and novel corrugated tubes relative to the smooth tube (i.e., Nu_c/Nu_s, Nu_n/Nu_s, f_c/f_s, f_n/f_s).

Numerical results indicate that the Nu of all three tube types increases significantly with rising Re, confirming that increased flow turbulence intensity effectively enhances heat transfer efficiency (Figure 8). Across the entire tested Re range, the Nu of both the novel and conventional corrugated tubes remained substantially higher than that of the smooth tube—demonstrating their superior heat transfer enhancement capabilities. To evaluate the heat transfer enhancement effect more precisely, the Nu ratios relative to the smooth tube (Nu_n/Nu_s and Nu_c/Nu_s) were calculated. For the conventional corrugated tube, the Nu_c/Nu_s ranged from 1.76 to 1.79, indicating that its heat transfer capacity was approximately 1.76 times or higher than that of the smooth tube. For the novel corrugated tube, the Nu_n/Nu_s remained stable between 1.61 and 1.65, corresponding to a heat transfer capacity roughly 1.61 times that of the smooth tube.

Across the entire testing range, the conventional corrugated tube exhibited superior heat transfer performance compared to the novel corrugated tube, with its Nu being approximately 8.8% to 10.2% higher. Such findings confirm that a greater number of corrugated structures can induce more intense fluid turbulence, thereby further enhancing heat transfer.

A further comparison of friction characteristics—illustrated in Figure 9—revealed that the f of all three heat exchanger tubes decreased gradually with increasing Re. The maximum f values were observed at Re = 9952: 0.1013 for the conventional corrugated tube, 0.0708 for the novel corrugated tube, and 0.0454 for the smooth tube.

The f of the conventional corrugated tube was consistently and significantly higher than that of the smooth tube. Its resistance ratio (f_c/f_s) increased continuously with Re over the tested range, rising from 2.23 at Re = 9952 to 2.96 at Re = 35,827. This trend indicates that the flow disturbances induced by its corrugated structure become more pronounced at higher flow velocities.

In contrast, the novel corrugated tube—incorporating smooth transition sections between corrugations—exhibited a more moderate rise in flow resistance. Its resistance ratio (f_n/f_s) ranged from 1.56 to 1.93 with a relatively stable trend, indicating that the growth of flow resistance was well-managed across the entire investigated Re range.

When combined with the heat transfer performance data (Nu_n/Nu_s = 1.610–1.650, Nu_c/Nu_s = 1.764–1.791), it becomes evident that the novel corrugated tube sustains substantial heat transfer enhancement while demonstrating a notably smaller increase in flow resistance compared to the conventional corrugated tube. At Re = 35,827, the resistance ratio (f_c/f_s) of the conventional corrugated tube reached 2.96, whereas that of the novel corrugated tube was only 1.93. This means that the resistance increase in the novel tube was approximately 65.2% of that of the conventional corrugated tube.

Notably, a similar trend supporting this thermal-hydraulic performance balance was also observed in the study by Gomaa [27], which focused on double concentric tubes with an inner twisted spiral tube. By optimizing the pitch and depth parameters of the twisted spiral structure, their experimental results revealed that the Nusselt number could be enhanced by up to 44.9% relative to a smooth tube, while only accompanying a moderate 36.4% increase in the friction factor.

These findings confirm that the novel corrugated tube achieves a superior balance between heat transfer enhancement and pressure drop control. Its structural design effectively mitigates flow separation and vortex generation, thus delivering better engineering applicability under high-Re conditions. The results of this study offer specific data support and a theoretical basis for further research on the structural optimization of low-resistance, high-efficiency heat exchange tubes.

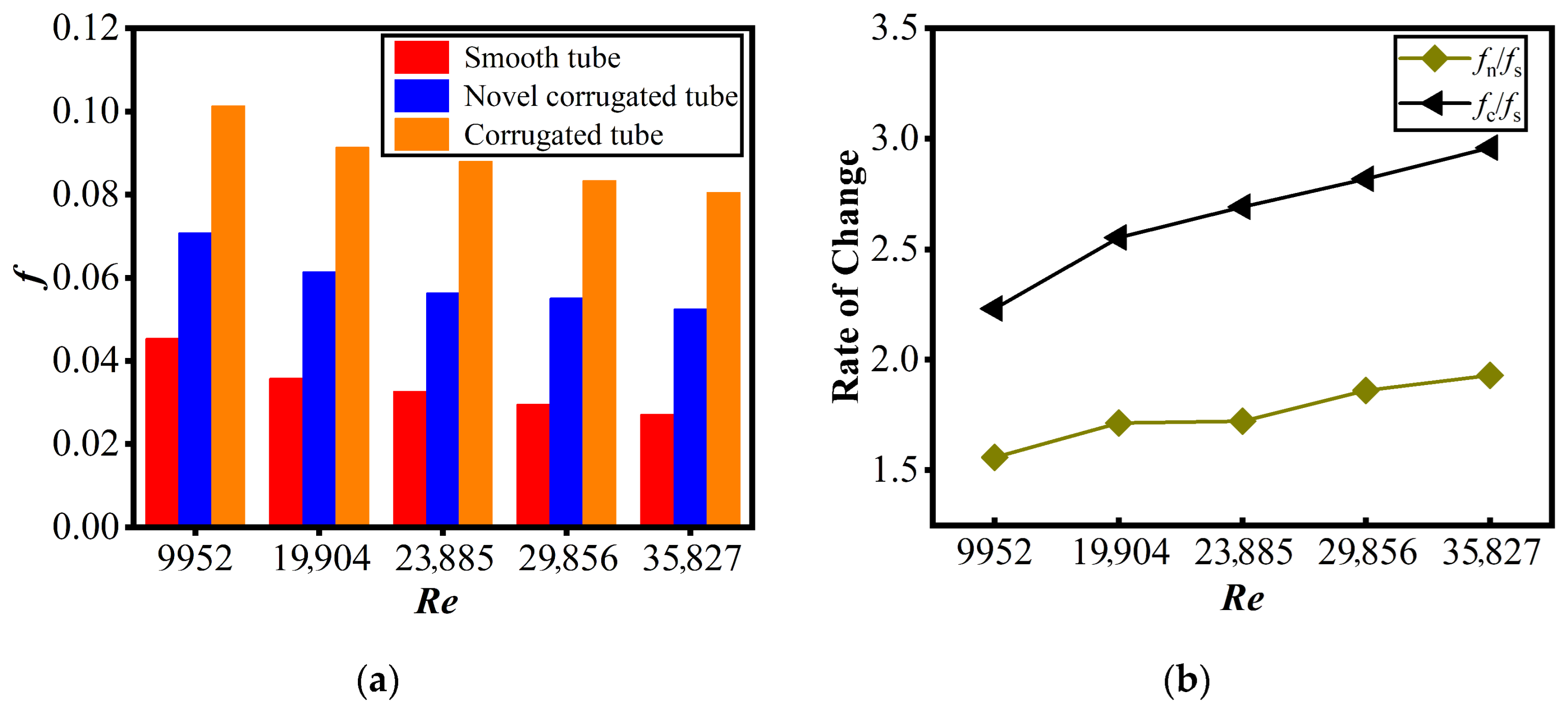
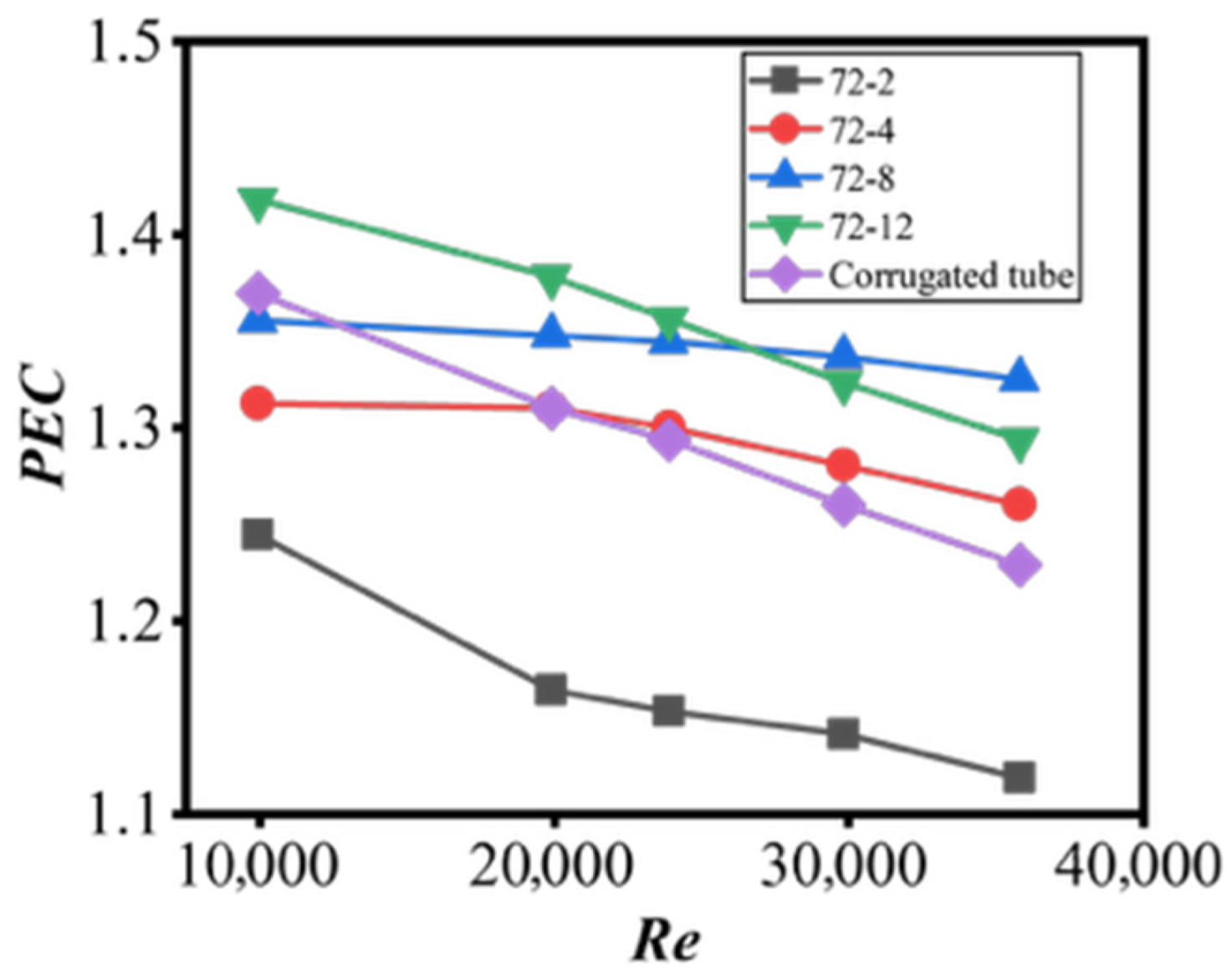
3.2. Performance Study

To determine the optimal configuration of corrugated segments, this study investigated the effect of various uniform arrangements of such segments on heat transfer performance. A 1.8-m-long smooth tube was outfitted with uniformly spaced corrugated segments along its length, which alternate between clockwise and counterclockwise orientations. Each smooth segment of the tube had an equal length, as illustrated in Figure 10. Specifically, the 1800 mm tube length was divided into 25 equal parts (each 72 mm in length); the blank parts in the figure represent smooth tube segments, while the shaded parts represent corrugated segments. For example, the notation “72-2” denotes a tube with two corrugated segments, with the specific distribution positions of the corrugated segments shown in the figure. The shaded segments represent the corrugated grooves: odd-numbered segments (from left to right) form a clockwise spiral, while even-numbered segments form a counterclockwise spiral. The corrugated segments are arranged in pairs, where each pair alternates between clockwise and counterclockwise orientations.

Figure 11 and Figure 12 presents the variations of Nu and f with Re for four novel corrugated tube configurations. Latest computational results show that as the number of corrugated segments decreases, the heat transfer performance of the novel corrugated tubes decreases accordingly, whereas the pressure drop inside the tubes is significantly reduced. As shown in Figure 11a, the Nu values of all novel corrugated tubes increase as Re increases. Specifically, the 72-12 corrugated tube exhibited the highest heat transfer performance—with a maximum Nu (Nu_max) of 93.34 at Re = 35,827—while the 72-2 type showed the lowest heat transfer capacity, with a Nu_max of 68.02 at Re = 35,827.

Compared with the conventional corrugated tube (Figure 11b), the Nusselt number ratios (i.e., Nu/Nu_c) for the 72-2, 72-4, 72-8, and 72-12 novel corrugated tubes at Re = 35,827 were 0.665, 0.786, 0.862, and 0.913, respectively. These results confirm that increasing the number of corrugated segments enhances heat transfer performance, though the rate of enhancement diminishes gradually.

Notably, a similar variation trend was also observed in the study by Mahmoud Abdelmagied [28], which focused on the thermo-fluid characteristics of a twisted tube helical coil. In his research, smaller pitch ratios (corresponding to more intensive twisted structures, analogous to the increased number of corrugated segments in our work) boosted the Nusselt number, while the friction factor also increased accordingly. This aligns with the trade-off relationship we observed: enhanced heat transfer performance was accompanied by a corresponding rise in flow resistance, echoing the consistent trend across different enhanced heat transfer structures.

The variation trend of the f in Figure 12a further validates the positive correlation between pressure drop and the number of corrugated segments.

When the number of segments was reduced from 12 to 2, the f decreased from 0.0484 to 0.0287 at Re = 35,827, representing a reduction of 40.7%.

Considering both heat transfer and flow resistance performance, although the 72-2 novel corrugated tube exhibited relatively lower heat transfer efficiency, its f was 40.7% lower than that of the 72-12 type. This highlights its significant advantage in applications where low flow resistance is critical.

Figure 13 presents a comparison of the PEC for four types of novel corrugated tubes and one conventional corrugated tube. Analysis of the PEC data revealed that over the Re range of approximately 9952–35,827, all tube types exhibited PEC values greater than 1, indicating that their overall thermal-hydraulic performance outperformed that of the smooth tube. Notably, the PEC values showed a decreasing trend with rising Re, suggesting that the negative impact of flow resistance on comprehensive thermal-hydraulic performance becomes more pronounced at higher flow velocities.

Specifically, the 72-12 tube exhibited the highest PEC value (1.418) at a low Re (Re = 9952), highlighting that its notable heat transfer enhancement outweighs the additional pressure drop under this condition. However, with increasing Re, its PEC value declines most significantly—dropping to 1.293 at Re = 35,827—which reflects that a sharp increase in flow resistance at higher velocities limits its applicability in high-Re scenarios.

In contrast, the 72-2 tube demonstrated the lowest PEC value (1.244) at low Re, but its PEC decrease with rising Re was the smallest—indicating more stable comprehensive performance. According to prior calculations, although the conventional corrugated tube delivered superior Nu values compared to the novel tubes over the entire tested Re range, its PEC values were intermediate and consistently lower than those of the 72-12 and 72-8 tubes. This finding confirms that while the conventional tube offers stronger heat transfer performance, its sharply increased flow resistance exerts a negative impact on its overall thermal-hydraulic performance, rendering it less efficient than the structurally optimized novel corrugated tubes under most operating conditions.

These findings highlight the importance of balancing heat transfer enhancement and pressure drop control in the design of novel heat exchange tubes. Via structural optimization, the novel corrugated tubes achieved a better trade-off between these two competing factors—resulting in higher overall efficiency even with marginally lower heat transfer coefficients in certain scenarios.

As shown in the velocity distribution diagram in Figure 14a, under constant inlet velocity, the fluid in the 72-12 novel corrugated tube is disturbed multiple times by the corrugated segments—leading to more pronounced velocity fluctuations relative to the overall bulk flow. By comparing velocity variation curves at different positions, it was found that after passing the first central corrugated segment, the fluid in the 72-12 tube alternated between smooth and corrugated segments, with velocity fluctuating periodically: a maximum velocity of 1.45 m/s and a minimum of 1.38 m/s, values that remained essentially consistent across each cycle. Near-wall velocity also fluctuated periodically, but with larger amplitudes at both ends of the tube and smaller ones in the middle, reaching an amplitude of 1.08 m/s.

In the 72-2 novel corrugated tube, fluid velocity also changed periodically. Before passing the first corrugated segment, the fluid velocity remained relatively stable; upon entering the corrugated segment, the central velocity surged while near-wall velocity started to fluctuate. The maximum central velocity was 1.43 m/s—close to that of the 72-12 tube—while the maximum near-wall velocity was 1.11 m/s, exceeding that of the 72-12 tube. After exiting the corrugated segment, the central velocity gradually returned to its pre-surge value of 1.29 m/s, and near-wall velocity first decreased then rose back to its pre-fluctuation level, completing one velocity cycle.

Notably, TKE within the tube exhibited an inverse relationship with local fluid velocity: higher TKE corresponds to lower velocity. As shown in Figure 14b, the TKE fluctuation trend at the tube center matched the velocity variation pattern. Near the wall of the 72-12 tube, TKE showed distinct periodic fluctuations, with clear peaks (0.022) and troughs (0.012). Within each corrugated segment, the magnitude and rate of TKE increase/decrease were nearly identical—evidence of a consistent periodic flow structure.

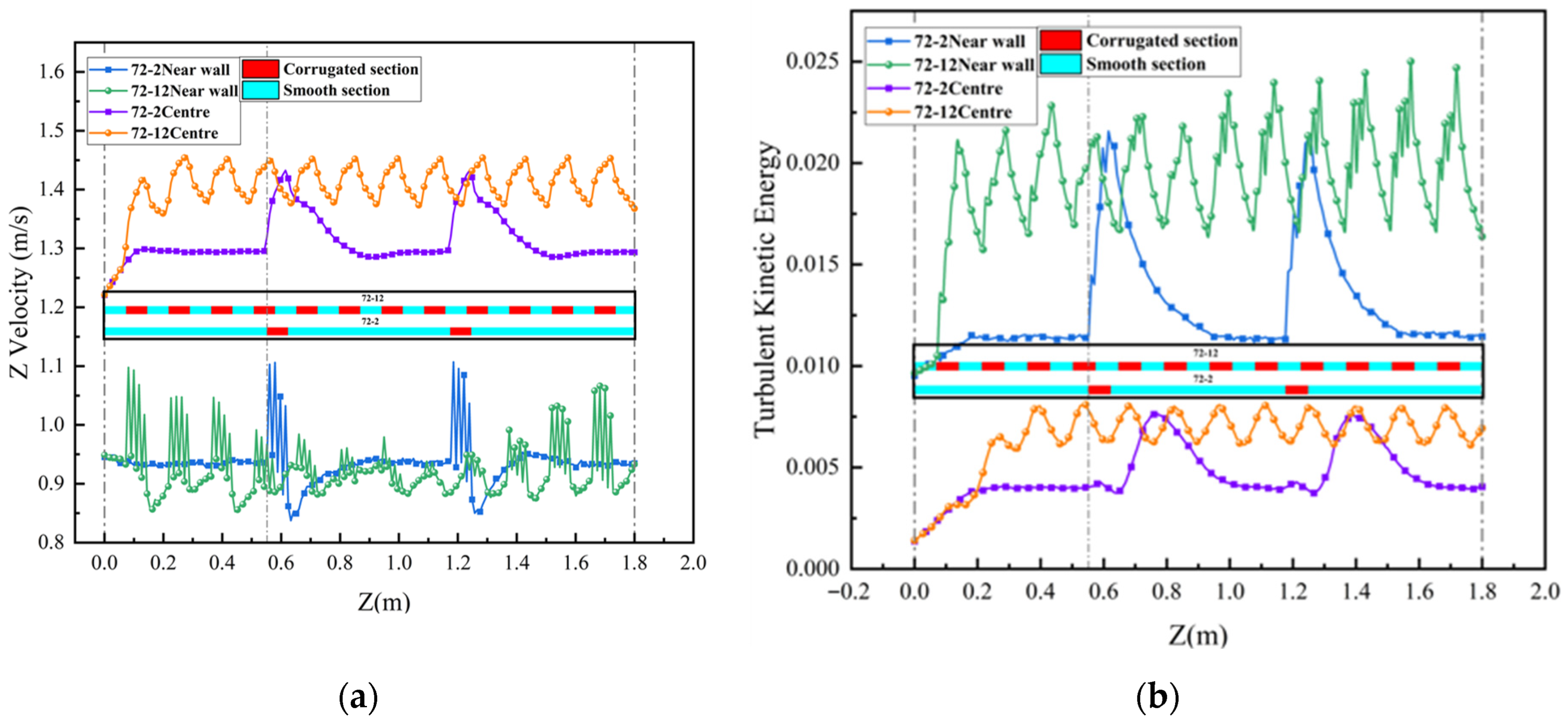
4. Discussion

The aforementioned analysis confirms that the corrugated groove structures in the heat exchange tube exerted a significant enhancement effect on heat transfer performance. Convection, particularly forced convection driven by fluid flow, is the dominant heat transfer mechanism in this system, and the corrugated structures primarily enhance this process through targeted modulation of flow dynamics. As the fluid flows through the tube’s undulating wall geometry, Bernoulli’s principle dictates that when the fluid passes over the crest of a corrugation, its near-wall velocity increases, with a corresponding decrease in static pressure. Conversely, prior to reaching the corrugation crest, the fluid experiences flow resistance—resulting in reduced velocity and elevated static pressure.

These pressure and velocity variations induce the generation of high-vorticity vortices in the region near the corrugation crest (as illustrated in Figure 15a). This vortex motion intensifies forced convection by disrupting the thermal boundary layer—a thin region adjacent to the wall where heat transfer is dominated by conduction due to low fluid mixing. By breaking up this boundary layer, the vortices increase the temperature gradient between the fluid core and the wall, while enhancing the relative velocity between the fluid and the wall, thereby accelerating convective heat transfer. After passing the corrugation crest, the fluid undergoes sudden expansion and contraction due to the tube’s wall geometric variations, which generates adverse pressure gradients along the wall downstream of the groove. This facilitates the development of a low-velocity recirculation zone, which in turn triggers the generation of another vortex (Figure 15b).

The vorticity distribution within the corrugated segment typically exhibits a complex yet periodic structure (Figure 16). In the longitudinal section of the novel corrugated tube, the vorticity field alternates periodically between positive and negative values in magnitude along the flow direction. These alternating zones are bounded by the geometric bounds of the corrugated grooves, forming distinct vorticity partitions. Ultimately, as a result of this distribution pattern, large-scale vortices emerge near the tube wall—markedly enhancing local turbulence and fluid mixing. Notably, this turbulence augmentation further amplifies forced convection: turbulent eddies transport high-temperature fluid from the core to the wall and low-temperature fluid from the wall to the core, effectively reducing thermal resistance and boosting convective heat transfer efficiency. This vortex-dominated flow behavior effectively disrupts the thermal boundary layer and intensifies convective heat transfer within the corrugated segment, thereby boosting the overall thermal performance of the segment.

However, the PEC of heat exchange tubes is not directly proportional to the length of their corrugated groove structures. For instance, the novel corrugated tube exhibited superior PEC performance relative to the conventional corrugated tube. This phenomenon can be attributed to the internal fluid dynamics within the grooves (Figure 14b): as fluid flows through the corrugated regions, the disturbance effect induced by the grooves drives a significant increase in TKE; upon exiting the corrugated segment, TKE begins to decay. However, after passing through a smooth segment, TKE is restrengthened—enabling it to remain at a relatively high level. In the smooth segments, residual turbulence from upstream corrugations sustains enhanced convection by maintaining a thinner thermal boundary layer compared to a fully smooth tube, while avoiding excessive flow resistance. This balance between sustained convective enhancement and reduced resistance is key to the superior PEC of the novel design. Consequently, the novel corrugated tube not only enhances TKE generation but also reduces flow resistance due to the integration of smooth segments. This dual effect results in a higher PEC than that of conventional corrugated tubes.

Figure 17 presents the flow distributions at ten cross-sections of the 72-2 novel corrugated tube, encompassing two corrugated segments and the smooth segment between them. At Z = 0.576 (inside the first corrugated segment), the streamline patterns and color distributions revealed significant TKE generation and intense fluid mixing. This intense mixing directly enhances convective heat transfer by maximizing fluid-wall contact and temperature exchange. In the smooth segment downstream of this corrugated segment (at Z = 0.648, 0.72, and 0.936 m), swirling flow patterns persisted as a residual outcome of upstream disturbances induced by the corrugations. These residual swirls continue to disrupt the thermal boundary layer, sustaining higher convective efficiency than a fully smooth tube without additional energy loss from corrugations. Approximately 0.4 m from the inlet of the first corrugated segment—specifically at Z = 0.956 m and 0.976 m—the vortex structures dissipated over a flow distance of 0.02 m. From Z = 0.976 to 1.08 m, the flow gradually regained a state that closely resembles fully developed flow in a smooth tube. Upstream of the second corrugated segment (at Z = 1.152 m and 1.224 m), the streamline distributions started to deviate once more—signaling the start of a new disturbance cycle.

This flow behavior confirms that the alternating arrangement of clockwise and counterclockwise corrugated segments (separated by smooth segments) not only enhances local turbulence and disrupts the thermal boundary layer within the corrugated regions but also modulates the flow characteristics in the downstream smooth segments. The TKE distribution in Figure 15b further validates this conclusion, revealing that each corrugated segment induces periodic flow disturbances. By rationally using smooth segments to separate and alternately arrange clockwise and counterclockwise corrugated segments, the novel heat exchange tube can attain the maximum achievable PEC.

5. Conclusions

This study numerically investigated the thermal-hydraulic characteristics (plus structural optimization and mechanism analysis) of a novel corrugated tube, benchmarked against smooth and conventional corrugated tubes; the key conclusions are as follows:

• Performance balance: The novel tube achieved a superior trade-off: it maintained substantial heat transfer enhancement (Nu_n/Nu_s ≈ 1.61–1.65) while limiting flow resistance growth (f_n/f_s ≈ 1.56–1.93). In contrast, the conventional corrugated tube (though achieving higher heat transfer, Nu_c/Nu_s ≈ 1.76–1.79) incurred a steep pressure penalty (f_c/f_s = 2.96)—making the novel tube well-suited for pump-power-constrained scenarios.
• Structural parameter effect: Corrugated segment count is a critical tunable parameter: more segments (e.g., 72-12, 72-8 configurations) boost heat transfer performance, fitting applications prioritizing high thermal efficiency; fewer segments (e.g., 72-2 configuration) reduce the friction factor by up to 40.7%, ideal for low-flow-resistance requirements.
• Heat transfer mechanism: Corrugated segments act as vortex generators, periodically disrupting the thermal boundary layer, inducing secondary flows, and intensifying fluid mixing to enhance heat transfer. The novel tube’s defining innovation (smooth segments between corrugated sections) allows turbulent kinetic energy (TKE) from corrugated zones to decay and redevelop—sustaining enhanced heat transfer while avoiding the excessive, continuous pressure rise of fully corrugated conventional tubes.

Furthermore, to further advance this design, future research will explore alternative combinations of corrugation parameters (e.g., height, pitch, and spiral angle) with smooth segment lengths for scenario-specific optimization, extend investigations to complex flow conditions such as two-phase flow, transient thermal loads, or inclined tube operation, and conduct comprehensive experimental validation of full-scale prototypes to confirm long-term operational reliability (e.g., fouling resistance) and expand its industrial application scope. In summary, the novel corrugated tube with alternating corrugated and smooth segments provides a promising approach for efficient heat exchanger design, enabling customizable balancing between thermal performance and energy consumption tailored to specific operational requirements.