Comparative Study of Neuroevolution and Deep Reinforcement Learning for Voltage Regulation in Power Systems

Abstract

The regulation of voltage in transmission networks is becoming increasingly complex due to the dynamic behavior of modern power systems and the growing penetration of renewable generation. This study presents a comparative analysis of three artificial intelligence approaches—Deep Q-Learning (DQL), Genetic Algorithms (GAs), and Particle Swarm Optimization (PSO)—for training agents capable of performing autonomous voltage control. A unified neural architecture was implemented and tested on the IEEE 30-bus system, where the agent was tasked with adjusting reactive power set points and transformer tap positions to maintain voltages within secure operating limits under a range of load conditions and contingencies. The experiments were carried out using the GridCal simulation environment, and performance was assessed through multiple indicators, including convergence rate, action efficiency, and cumulative reward. Quantitative results demonstrate that PSO achieved 3% higher cumulative rewards compared to GA and 5% higher than DQL, while requiring 8% fewer actions to stabilize the system. GA showed intermediate performance with 6% faster initial convergence than DQL but 4% more variable results than PSO. DQL demonstrated consistent learning progression throughout training, though it required approximately 12% more episodes to achieve similar performance levels. The quasi-dynamic validation confirmed PSO’s advantages over conventional AVR-based strategies, achieving voltage stabilization approximately 15% faster. These findings underscore the potential of neuroevolutionary algorithms as competitive alternatives for advanced voltage regulation in smart grids and point to promising research avenues such as topology optimization, hybrid metaheuristics, and federated learning for scalable deployment in distributed power systems.

1. Introduction

Voltage regulation in power systems, particularly in transmission and distribution networks, has become one of the most pressing operational challenges in the context of the ongoing energy transition. The rapid growth of distributed renewable generation, especially photovoltaic production during daylight hours, often produces significant voltage rises in certain areas of the grid. Conversely, during nighttime periods of low demand and minimal generation, transmission lines often carry limited active power but considerable reactive current, resulting in potential overvoltage conditions. This day–night duality places increasing stress on conventional regulation mechanisms and highlights the need for more dynamic, adaptive, and resilient control schemes [1,2,3].

The literature reveals a growing interest in algorithmic techniques capable of handling high-dimensional optimization problems while accounting for various operational uncertainties inherent to modern power systems. Metaheuristic approaches such as Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Artificial Bee Colony (ABC) techniques have demonstrated effectiveness in solving optimal power flow (OPF) problems, each carrying its own strengths and limitations [1]; while ABC demonstrates higher adoption rates in certain publications, GA registers fewer practical applications, often attributed to its sensitivity to parameter tuning and slower convergence in complex scenarios [4]. These limitations have prompted calls for improved frameworks capable of systematically tuning hyperparameters, standardizing performance metrics, and reporting experimental configurations transparently. Metaheuristic strategies are employed across a wide range of electrical engineering challenges beyond OPF, including voltage regulation, reactive power dispatch, and network expansion planning [5,6]. To effectively apply these techniques, a model of the considered power system is usually required to guide the evaluation of candidate solutions, with iterative refinement based on objective functions allowing operators to manage efficiency trade-offs while balancing cost minimization with system stability.

In this context, artificial intelligence (AI) has attracted growing attention in the scientific community as a promising pathway to address these operational limitations. Among AI techniques, deep reinforcement learning (DRL) has demonstrated strong potential for designing intelligent agents that can learn control policies directly through interaction with the system, without relying on precise mathematical models [7,8,9]. Recent comprehensive reviews have highlighted the effectiveness of DRL approaches in modern renewable power system control applications [10]. Multiple studies suggest DRL architectures contribute valuable capabilities in multi-objective contexts such as renewable integration in distribution networks, where action-state spaces are encoded into Markov decision processes to align with stochastic training paradigms [11]. Multi-task reinforcement learning approaches have shown particular effectiveness in handling topology changes during system operation [12]. Physics-informed graphical representations have enabled more robust deep reinforcement learning for distribution system voltage control [13]. These approaches handle diverse operational goals, from minimizing line construction and voltage deviations to maximizing subsidy utilization [14].

Nevertheless, recent studies also emphasize the limitations of DRL in real-world applications, including the high dimensionality of the state space, sensitivity to extreme operating conditions, and the stringent requirements for real-time execution [15,16,17]. Research on robust voltage control under uncertainties has shown that these limitations require careful consideration in practical implementations [18]. Despite these limitations, evidence indicates that DRL-based controllers can surpass traditional strategies in nonlinear and non-stationary environments [13].

Among the various DRL paradigms, Deep Q-Learning (DQL) represents one of the foundational approaches that learns an action-value function to estimate expected future rewards for optimal decision-making [19]. Recent advances have introduced variants such as Multi-Task SAC and Human-in-the-Loop approaches that incorporate expert knowledge for operational safety [12,20]. Modern implementations including Soft Actor–Critic (SAC) and Twin Delayed Deep Deterministic Policy Gradient (TD3) have demonstrated superior performance in voltage regulation tasks, with multi-agent formulations addressing scalability concerns through distributed control while maintaining coordination [14,21,22]. However, DRL approaches face critical limitations including training instability, poor sample efficiency, and concerns about interpretability in safety-critical applications [10,18].

In contrast to deep learning approaches, Genetic Algorithms represent a well-established metaheuristic approach that mimics biological evolution processes to solve optimization problems in power systems. GA operates through selection, crossover, and mutation operations on a population of candidate solutions, gradually improving solution quality over successive generations [23]. In voltage regulation contexts, GA has been successfully applied to optimize reactive power dispatch, transformer tap settings, and capacitor switching schedules. The strengths of GA include its global search capability, robustness to local optima, and ability to handle discrete, continuous, and mixed-variable optimization problems without gradient information [1]. GA demonstrates particular effectiveness in multi-objective optimization scenarios where trade-offs between conflicting objectives must be explored. The algorithm’s population-based nature provides inherent parallelization opportunities and maintains solution diversity throughout the optimization process. Nevertheless, GA suffers from several drawbacks that limit its practical application. Convergence speed is typically slow, particularly for high-dimensional problems, and the algorithm requires careful tuning of hyperparameters such as population size, crossover rate, and mutation probability [4]. The stochastic nature of genetic operations can lead to inconsistent results across multiple runs, and the method lacks theoretical convergence guarantees for finite-time execution.

Similarly, Particle Swarm Optimization emerges as a swarm intelligence technique inspired by the collective behavior of bird flocks and fish schools. PSO maintains a population of particles that explore the solution space by adjusting their velocities based on personal best positions and global best discoveries [3]. In power systems, PSO has found extensive application in optimal power flow problems, economic dispatch, and reactive power optimization. PSO’s advantages include faster convergence compared to Genetic Algorithms, simpler implementation with fewer parameters to tune, and effective performance in continuous optimization landscapes [24]. The algorithm demonstrates good exploration-exploitation balance through its velocity update mechanism and maintains computational efficiency even for moderately high-dimensional problems. PSO’s deterministic update rules provide more predictable behavior compared to the stochastic nature of Genetic Algorithms. However, PSO exhibits susceptibility to premature convergence, particularly in multi-modal optimization landscapes where local optima may trap particle swarms [5]. The algorithm’s performance degrades significantly with increasing problem dimensionality, and it lacks inherent mechanisms for handling discrete variables or constraint satisfaction. Additionally, PSO requires careful initialization and parameter selection to achieve optimal performance, with velocity clamping and inertia weight strategies critically affecting convergence behavior.

The interplay between metaheuristic optimization methods and DRL strategies remains a promising theme. DRL may handle temporal decision-making efficiently under uncertainty, while metaheuristics offer heuristic search potential when exact models or gradients are unavailable. This duality underscores the need for hybrid approaches combining both algorithmic families in appropriate stages of planning or control cycles [10]. Neuroevolutionary techniques, including EvoNN [25] and methods such as NEAT [26], make it possible to evolve both the structure and the weights of neural networks, paving the way for more robust and adaptable control agents. These approaches have proven effective in parameter tuning under varying operating conditions [23,24]. Graph-based multi-agent reinforcement learning approaches have also shown promise for inverter-based active voltage control [27].

Despite these individual advances in each paradigm, the literature reveals a notable gap in comprehensive comparative studies that systematically evaluate different AI paradigms under identical operational conditions; while individual studies demonstrate the effectiveness of specific approaches, the absence of standardized evaluation frameworks prevents objective assessment of relative strengths and weaknesses [21,22,28]. This limitation is particularly pronounced in power systems applications where safety, reliability, and real-time performance requirements demand rigorous validation. Most existing studies focus on single algorithmic families, with DRL-based approaches typically emphasizing learning efficiency and adaptation capability, while metaheuristic studies concentrate on global optimization performance [12,14,20,23,24]. The lack of cross-paradigm comparisons limits understanding of when each approach provides optimal performance and under what operational conditions trade-offs between different methodologies become critical. Furthermore, the lack of standardized datasets for DRL research in power distribution applications hinders reproducibility and objective comparison of results, compounded by the absence of homogeneous evaluation metrics that consider not only final performance but also convergence speed, training stability, and the quality of resulting control actions [15].

Following these advances, the present work contributes a comparative study that integrates three distinct AI paradigms for voltage regulation in the IEEE 30-bus test system. Unlike previous studies, which typically investigate DRL or evolutionary techniques in isolation, this research performs a rigorous comparison of Deep Q-Learning, Genetic Algorithms, and Particle Swarm Optimization as training strategies for a common neural agent. The study makes several significant contributions to the field by developing a unified evaluation framework that establishes a standardized experimental protocol, enabling direct comparison between different AI paradigms under identical operational conditions. Additionally, the research provides a multidimensional analysis that encompasses not only final performance metrics but also convergence rate, training stability, and the quality of the resulting control actions. The work ensures reproducibility through the provision of detailed parameters and experimental configurations that facilitate replication and extension of results by other researchers. Most importantly, the study offers practical insights by identifying the most effective approach for training an autonomous agent to regulate generator reactive power outputs and transformer tap positions, ensuring that bus voltages remain within operational limits under diverse load and generation scenarios.

To contextualize the scope and novelty of this research,

Table 1. Comprehensive comparison with previous works.

Reference	Method(s)	Test System	Evaluated Metrics	Key Limitations
Pei et al. [12]	MT-SAC	IEEE 123-bus	Voltage violations, PV curtailment	Single DRL approach, topology-specific
Sun et al. [20]	HL-SAC	IEEE 123-bus	Power losses, voltage unbalance	Human-in-the-Loop dependency, limited scalability
Bao et al. [19]	Emotional Lazy Q-Learning	Single-machine system	Rotor deviation, convergence speed	Limited to stability control, simple system
Hou et al. [21]	DF-SRL (TD3-based)	CIGRE LV network	Constraint violation, operational costs	Safety layer complexity, QP computation overhead
Zhang et al. [28]	GT-MADDPG	IEEE 33/141-bus	Voltage deviation, power losses	Multi-agent complexity, communication requirements
Hossain et al. [29]	GCN-SAC/MASAC	Distribution network	Voltage fluctuation, power losses	Topology-aware but single algorithm family
Feng et al. [22]	Stable-DDPG	IEEE 13/123-bus	Stability guarantee, control cost	Monotonicity constraint limits flexibility
Petrusev et al. [18]	TD3PG, PPO	Distribution grid	Voltage performance index	Parameter uncertainty focus, limited comparison
Su et al. [14]	MASAC	IEEE 33/141-bus	Voltage deviations, reactive losses	Multi-agent partitioning complexity
Li et al. [10]	DRL Review	Various systems	Control performance	Review paper, no experimental comparison
This work	DRL vs. GA vs. PSO	IEEE 30-bus	Voltage deviation, training efficiency	First comprehensive cross-paradigm comparison framework

presents a comprehensive comparison with previous studies in the field, highlighting the unique contributions and distinguishing characteristics of the present work.

The main objective is to identify the most effective approach for training an autonomous agent to regulate generator reactive power outputs and transformer tap positions, ensuring that bus voltages remain within operational limits under diverse load and generation scenarios.

The remainder of this article is structured as follows: Section 2 introduces the methodology and the simulation environment employed, including recent literature supporting the choice of algorithms. Section 3 presents the main results, including learning curves and performance indicators. Finally, Section 4 discusses the technical and practical implications of the findings, summarizes the key contributions, and outlines potential future directions such as interpretability, hybrid metaheuristics, and federated learning for distributed grid applications [30].

1.1. Problem Formulation

The aim of this work is to develop a reinforcement-learning-based agent [15] capable of keeping bus voltages within nominal ranges [7,8], thereby supporting the stable operation of the power system. The agent is implemented as a neural network that regulates generator reactive power and transformer tap positions.

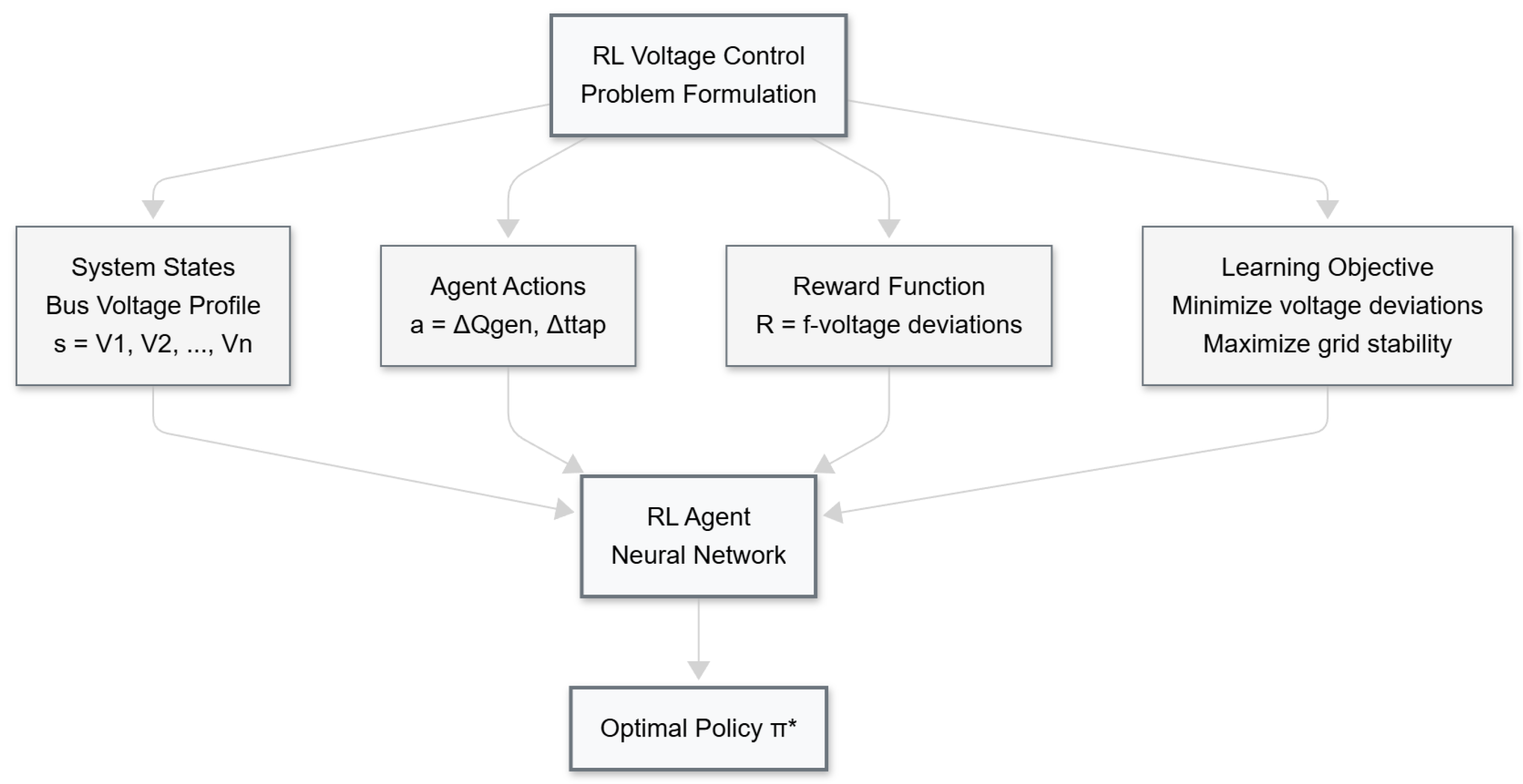
To clearly define the reinforcement learning environment, the problem is described in terms of its fundamental components. Specifically, the formulation requires the definition of the system states observed by the agent, the set of admissible actions it can take, the reward function that evaluates its performance, and the overall learning objective that guides the optimization process. These elements jointly establish the framework within which the agent interacts with the power system to achieve effective voltage regulation. Figure 1 illustrates the conceptual structure of this reinforcement learning problem formulation.

1.1.1. Mathematical System Formulation

The voltage control problem is mathematically formulated as a continuous-time optimal control problem that can be discretized for algorithmic implementation. The power system state at time t is defined by the voltage magnitude and phase angle vectors:

$${\mathbf{s}}_t={[{\mathbf{V}}_t,{\mathit{\theta }}_t]}^T={[V_1,V_2,\dots ,V_n,{\theta }_1,{\theta }_2,\dots ,{\theta }_n]}^T\in {\mathbb{R}}^{2n}$$

(1)

where $V_i$ and ${\theta }_i$ represent the voltage magnitude and phase angle at bus i, respectively, and n is the total number of buses in the system.

The admissible action space consists of continuous reactive power adjustments and discrete transformer tap positions:

$${\mathbf{a}}_t={[{\mathbf{Q}}_G,\mathbf{T}]}^T={[Q_{G1},Q_{G2},\dots ,Q_{Gm},T_1,T_2,\dots ,T_k]}^T$$

(2)

where $Q_{Gi}\in [Q_{Gi}^{min},Q_{Gi}^{max}]$ represents the reactive power output of generator i, and $T_j\in \{1,2,\dots ,N_{tap}\}$ represents the discrete tap position of transformer j.

The system dynamics are governed by the power flow equations:

$$\begin{array}{cc}\hfill P_i& =V_i\sum _{j=1}^n{V}_j[G_{ij}cos({\theta }_i-{\theta }_j)+B_{ij}sin({\theta }_i-{\theta }_j)]\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill Q_i& =V_i\sum _{j=1}^n{V}_j[G_{ij}sin({\theta }_i-{\theta }_j)-B_{ij}cos({\theta }_i-{\theta }_j)]\hfill \end{array}$$

(4)

where $G_{ij}$ and $B_{ij}$ are the conductance and susceptance elements of the admittance matrix, respectively.

The state transition function can be expressed as follows:

$${\mathbf{s}}_{t+1}=f({\mathbf{s}}_t,{\mathbf{a}}_t,{\mathbf{d}}_t,{\mathit{\xi }}_t)$$

(5)

where ${\mathbf{d}}_t$ represents external disturbances (load variations, generation changes) and ${\mathit{\xi }}_t$ represents system uncertainties.

1.1.2. System States

In this study, the system state is defined by the voltage profile across all network buses. Each bus must maintain its voltage magnitude within a nominal range to prevent overvoltage or undervoltage conditions that could jeopardize system stability. The voltage constraints are mathematically expressed as follows:

$$V_i^{min}\le V_i\le V_i^{max},\forall i\in \{1,2,\dots ,n\}$$

(6)

These voltage values serve as inputs to the agent, enabling it to evaluate the system’s operating state and determine appropriate control actions. The voltage profile is therefore essential, as it allows the agent to adapt system operation to keep bus voltages within acceptable limits [9].

1.1.3. Agent Actions

The agent’s actions target two main elements of the voltage control system: generator reactive power and transformer tap positions. The action constraints are formulated as follows:

$$\begin{array}{cc}\hfill Q_{Gi}^{min}& \le Q_{Gi}\le Q_{Gi}^{max},\forall i\in \{1,2,\dots ,m\}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill T_j& \in \{1,2,\dots ,N_{tap}\},\forall j\in \{1,2,\dots ,k\}\hfill \end{array}$$

(8)

The relationship between transformer tap positions and voltage regulation is expressed through the tap ratio:

$$t_j=t_{j,nominal}+(T_j-T_{j,nominal})·\Delta t$$

(9)

where $t_{j,nominal}$ is the nominal tap ratio, $T_{j,nominal}$ is the nominal tap position, and $\Delta t$ is the tap step size.

1.1.4. Agent Reward

The reward function is mathematically designed to minimize voltage deviations from reference values while penalizing constraint violations:

$$R_t=-\sum _{i=1}^n{w}_i{(V_i-V_{ref,i})}^2-{\lambda }_1\sum _{i=1}^{n}max{(0,V_i-V_i^{max})}^2-{\lambda }_2\sum _{i=1}^{n}max{(0,V_i^{min}-V_i)}^2$$

(10)

where $w_i$ are weighting factors for different buses, $V_{ref,i}$ are the reference voltages, and ${\lambda }_1,{\lambda }_2$ are penalty coefficients for constraint violations.

1.1.5. Learning Objective

The primary objective is to learn an optimal policy ${\pi }^{*}:\mathcal{S}\to \mathcal{A}$ that maximizes the expected cumulative reward:

$${\pi }^{*}=arg\underset{\pi }{max}\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{R}_t\mid \pi \right]$$

(11)

where $\gamma \in [0,1)$ is the discount factor that balances immediate and future rewards.

1.1.6. Algorithm Selection and Theoretical Alignment Analysis

The selection of Deep Q-Learning, Genetic Algorithms, and Particle Swarm Optimization for this comparative study is grounded in a systematic analysis of how each algorithm’s fundamental computational principles align with the specific mathematical and operational characteristics of the voltage control problem. This theoretical alignment analysis provides the foundation for understanding why these particular algorithms are theoretically suited for addressing the challenges inherent in power system voltage regulation [10,15].

Deep Q-Learning Mathematical Framework and Theoretical Suitability

The voltage control problem exhibits several characteristics that make Deep Q-Learning theoretically well-suited for this application. The Q-function for the voltage control problem is mathematically formulated as follows:

$$Q^{\pi }({\mathbf{s}}_t,{\mathbf{a}}_t)={\mathbb{E}}^{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\mid {\mathbf{s}}_t,{\mathbf{a}}_t\right]$$

(12)

The optimal Q-function satisfies the Bellman equation:

$$Q^{*}(\mathbf{s},\mathbf{a})=\mathbb{E}\left[R_{t+1}+\gamma \underset{{\mathbf{a}}^{\prime }}{max}{Q}^{*}({\mathbf{s}}^{\prime },{\mathbf{a}}^{\prime })\mid {\mathbf{s}}_t=\mathbf{s},{\mathbf{a}}_t=\mathbf{a}\right]$$

(13)

For the voltage control application, the neural network approximation is defined as follows:

$$Q_{\theta }(\mathbf{s},\mathbf{a})=N{N}_{\theta }\left([\mathbf{V},\mathit{\theta },{\mathbf{Q}}_G,\mathbf{T}]\right)$$

(14)

where $\theta$ represents the neural network parameters. The loss function for training is as follows:

$$L\left(\theta \right)=\mathbb{E}\left[{\left(y_t-Q_{\theta }({\mathbf{s}}_t,{\mathbf{a}}_t)\right)}^2\right]$$

(15)

where $y_t=R_{t+1}+\gamma {max}_{{\mathbf{a}}^{\prime }}{Q}_{{\theta }^{-}}({\mathbf{s}}_{t+1},{\mathbf{a}}^{\prime })$ and ${\theta }^{-}$ represents the target network parameters.

The continuous nature of the state space, defined by voltage magnitudes across all network buses, aligns with DQL’s capability to handle high-dimensional continuous observations through deep neural network approximation [7,8]. The temporal coupling in power systems, where control actions have cascading effects on future voltage profiles, directly corresponds to DQL’s temporal difference learning framework [9].

Genetic Algorithm Mathematical Framework and Theoretical Justification

For the voltage control optimization problem, each individual (chromosome) in the GA population represents a complete control strategy:

$${\mathbf{x}}_i={[Q_{G1},Q_{G2},\dots ,Q_{Gm},T_1,T_2,\dots ,T_k]}^T\in \mathcal{X}$$

(16)

The fitness function is formulated to minimize voltage deviations:

$$f\left({\mathbf{x}}_i\right)=-\left[\sum _{j=1}^n{w}_j|V_j\left({\mathbf{x}}_i\right)-V_{ref,j}|+\alpha \sum _{j=1}^n\mathbb{I}(V_j\left({\mathbf{x}}_i\right)\notin [V_j^{min},V_j^{max}])\right]$$

(17)

where $\mathbb{I}(·)$ is an indicator function that penalizes constraint violations, and $\alpha$ is a penalty coefficient.

The selection operator is based on fitness proportional selection:

$$P\left({\mathbf{x}}_i\right)={\displaystyle \frac{f\left({\mathbf{x}}_i\right)}{{\sum }_{j=1}^{N_{pop}}f\left({\mathbf{x}}_j\right)}}$$

(18)

The crossover operator for mixed-variable optimization is defined as follows:

$${\mathbf{x}}_{child}^{\left(k\right)}=\left\{\begin{array}{cc}\beta {\mathbf{x}}_{parent1}^{\left(k\right)}+(1-\beta ){\mathbf{x}}_{parent2}^{\left(k\right)}\hfill & \mathrm{if}k\in \left\{Q_G\right\}\hfill \\ \mathrm{random}({\mathbf{x}}_{parent1}^{\left(k\right)},{\mathbf{x}}_{parent2}^{\left(k\right)})\hfill & \mathrm{if}k\in \left\{T\right\}\hfill \end{array}\right.$$

(19)

where $\beta \sim U(0,1)$ for continuous variables and discrete selection for tap positions.

The mutation operator handles the mixed-variable nature:

$${\mathbf{x}}_{mutated}^{\left(k\right)}=\left\{\begin{array}{cc}{\mathbf{x}}^{\left(k\right)}+\mathcal{N}(0,{\sigma }^2)\hfill & \mathrm{if}k\in \left\{Q_G\right\}\mathrm{and}U(0,1)<p_m\hfill \\ \mathrm{random}\mathrm{tap}\mathrm{position}\hfill & \mathrm{if}k\in \left\{T\right\}\mathrm{and}U(0,1)<p_m\hfill \\ {\mathbf{x}}^{\left(k\right)}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(20)

The multi-modal optimization landscape created by redundancy in reactive power control theoretically favors GA’s population-based search mechanism [1,23]. The discrete nature of transformer tap positions aligns with GA’s natural handling of mixed-variable optimization problems without requiring specialized constraint handling techniques [25].

Particle Swarm Optimization Mathematical Framework and Theoretical Appropriateness

In PSO, each particle represents a potential solution in the control space:

$${\mathbf{x}}_i\left(t\right)={[Q_{G1,i}\left(t\right),Q_{G2,i}\left(t\right),\dots ,Q_{Gm,i}\left(t\right),T_{1,i}\left(t\right),T_{2,i}\left(t\right),\dots ,T_{k,i}\left(t\right)]}^T$$

(21)

The velocity update equation for continuous variables is as follows:

$$v_{i,j}(t+1)=w·v_{i,j}\left(t\right)+c_1·r_1·(p_{best,i,j}-x_{i,j}\left(t\right))+c_2·r_2·(g_{best,j}-x_{i,j}\left(t\right))$$

(22)

For discrete tap positions, a modified update rule is employed:

$$T_{i,j}(t+1)=\left\{\begin{array}{cc}{p}_{best,i,j}\hfill & \mathrm{if}{r}_3<{\displaystyle \frac{1}{1+e^{-v_{i,j}(t+1)}}}\hfill \\ g_{best,j}\hfill & \mathrm{if}{r}_4<{\displaystyle \frac{1}{1+e^{-v_{i,j}(t+1)}}}\hfill \\ T_{i,j}\left(t\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(23)

where $r_3,r_4\sim U(0,1)$ are random numbers.

The fitness function for PSO is formulated as follows:

$$fit\left({\mathbf{x}}_i\right)={\displaystyle \frac{1}{1+{\sum }_{j=1}^n{w}_j{(V_j\left({\mathbf{x}}_i\right)-V_{ref,j})}^2+\beta {\sum }_{j=1}^{n}max(0,|V_j\left({\mathbf{x}}_i\right){|-V_j^{max})}^2}}$$

(24)

The constraint handling for reactive power limits is implemented through boundary enforcement:

$$Q_{Gi}(t+1)=\left\{\begin{array}{cc}{Q}_{Gi}^{min}\hfill & \mathrm{if}{Q}_{Gi}(t+1)<Q_{Gi}^{min}\hfill \\ Q_{Gi}^{max}\hfill & \mathrm{if}{Q}_{Gi}(t+1)>Q_{Gi}^{max}\hfill \\ Q_{Gi}(t+1)\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(25)

PSO’s rapid convergence characteristics align well with the real-time requirements of voltage control applications [5]. The deterministic nature of PSO updates provides more predictable convergence behavior compared to stochastic operations in GA, which is advantageous for time-critical power system applications [3,24].

Comparative Mathematical Analysis and Theoretical Alignment

The theoretical comparison of the three algorithms reveals distinct mathematical advantages for different aspects of the voltage control problem.

State Space Dimensionality: The problem state space has dimension $\left|\mathcal{S}\right|={\mathbb{R}}^{2n}$, while the action space has dimension $\left|\mathcal{A}\right|={\mathbb{R}}^m\times {\mathbb{Z}}^k$. DQL handles this through function approximation with complexity $O\left(\right|\theta \left|\right)$, where $\left|\theta \right|$ is the number of neural network parameters. GA maintains population diversity with complexity $O(N_{pop}\times (m+k))$, while PSO operates with complexity $O(N_{particles}\times (m+k))$.

Convergence Properties: The convergence analysis shows: - DQL: ${lim}_{t\to \infty }\left|\right|Q_t-Q^{*}{\left|\right|}_{\infty }=0$ under appropriate conditions. - GA: Convergence to global optimum with probability approaching 1 as generations increase. - PSO: Guaranteed convergence to local optimum with properly chosen parameters.

Constraint Handling Mechanisms: Each algorithm addresses the constraint set $\mathcal{C}=\{\mathbf{x}:V_i^{min}\le V_i\le V_i^{max},Q_{Gi}^{min}\le Q_{Gi}\le Q_{Gi}^{max}\}$ differently: - DQL: Penalty-based reward shaping with constraint violations embedded in $R_t$. - GA: Natural boundary enforcement through genetic operators. - PSO: Explicit boundary conditions and velocity clamping.

The mathematical formulation demonstrates that DQL’s temporal reasoning capabilities make it theoretically superior for sequential decision-making scenarios, GA’s population diversity provides advantages for multi-modal optimization landscapes, and PSO’s deterministic updates offer benefits for real-time applications with strict computational constraints [10,14,22].

This comprehensive mathematical analysis establishes the theoretical foundation for comparing these algorithms’ performance in power system voltage control, providing rigorous justification for their selection and expected behavior in the experimental evaluation [30].

2. Methodology

2.1. System Description

The IEEE 30-bus test system, is a widely used benchmark electrical network for studies on stability, control, and optimization in power systems. This system represents a medium-sized transmission network comprising 30 nodes (buses), 41 transmission lines, 6 generators, and 4 on-load tap-changing (OLTC) transformers. It includes both load and generation buses, arranged in a topology that realistically simulates power flow behavior and voltage control conditions. Furthermore, the system incorporates operational constraints such as generation limits, load demands, and transmission capacities, making it an ideal test case for evaluating optimization methods and advanced control strategies.

From a voltage control perspective, the IEEE 30-bus system poses challenges due to demand variability and operational constraints on generators and transformers. The generators located at buses 1, 2, 5, 8, 11, and 13 are capable of regulating voltage by adjusting their reactive power output. Meanwhile, the transformers connecting buses 6–9, 6–10, 4–12, and 27–28 allow for voltage adjustments through tap ratio modifications. The presence of these devices makes the system an excellent test bed for assessing control strategies based on artificial intelligence and reinforcement learning, including methods such as Deep Q-Learning (DQL), Genetic Algorithms (GAs), and Particle Swarm Optimization (PSO).

2.2. Neural Network

The proposed neural network is designed to act as the agent responsible for voltage control in the IEEE 30-bus test power system. The inputs to the agent—or neural network—consist of 30 values representing the voltage magnitudes at each of the system’s 30 buses. These input values are normalized between 0 and 1. The voltage magnitudes are used to inform decisions regarding reactive power control and transformer tap settings across the network.

Within the neural network, the input data is processed through three hidden layers with 128, 256, and 128 units, respectively. The activation functions employed in the hidden layers are Rectified Linear Units (ReLU), which enable the network to learn complex nonlinear representations and effectively manage gradient propagation during training. This architecture allows the network to capture intricate interactions among the system buses, thereby supporting the learning of efficient control policies aimed at maintaining bus voltages within desired limits [7,8,9,31,32,33,34,35,36].

The agent produces two groups of outputs: six continuous outputs and four discrete outputs. The six continuous outputs correspond to the reactive power set points of the generators. These outputs are normalized in the range [0, 1] using a sigmoid activation function and represent the target reactive power levels that the generators should supply or absorb in order to maintain appropriate voltage levels in the system.

The four discrete outputs control the tap positions of the on-load tap-changing transformers. Each discrete output can take one of three values: −1 (tap down), 0 (no action), or 1 (tap up). A softmax activation function is applied independently to each of these four outputs, enabling the network to assign a probability distribution over the three possible actions for each transformer. The final action is selected based on the highest probability, and each decision is made independently of the others. This design allows the agent to learn and control each transformer independently. By combining continuous and discrete outputs within a single neural network, the agent is capable of simultaneously managing both reactive power dispatch and transformer configuration, thereby contributing to improved voltage regulation and enhanced system stability [33].

2.3. Training Algorithms

The agent is trained using a reinforcement learning framework in which the agent interacts with the system through a sequence of episodes. Each episode consists of up to 500 possible actions, which correspond to the agent’s decisions for controlling bus voltages in the IEEE 30-bus power system. During each episode, the agent observes the current state of the system—determined by bus voltage magnitudes—and selects an action involving adjustments to the reactive power of generators or the tap positions of on-load tap-changing (OLTC) transformers. Each action directly impacts the system, affecting bus voltage levels and, consequently, the overall stability of the electrical grid [1,7,8,9,15,16].

To simulate the 30-bus power system used in this study, the GridCal library was employed. GridCal is an advanced tool for the analysis and simulation of electric power networks. It enables the modeling and study of power system behavior, including power flow analysis, network stability, and the operational conditions of various components such as generators, transformers, and transmission lines. This library provides detailed simulations and accurate calculations, allowing observation of how the system responds to different operating conditions and how voltages evolve across the network. During the training process, a power flow calculation is executed in GridCal after each action performed by the agent. This calculation is essential for determining the resulting bus voltages. Therefore, for every action taken—such as modifying generator reactive power or changing transformer tap positions—GridCal simulates the resulting electrical flow and computes the corresponding voltage values. These voltages are then used to compute the reward assigned to the agent based on how closely the voltages match the nominal or desired values. This feedback is critical for guiding the agent’s learning process, as it enables the agent to determine whether its actions are improving or worsening voltage control. Throughout each episode, the agent adjusts its decisions to optimize the system’s voltage stability [37].

In this work, the simulation strategy adopted by [8] is used to introduce variability into the power system at the beginning of each episode. Specifically, the load levels at each bus are randomly varied within a range of 80% to 120% of their nominal values, while maintaining a constant power factor. Furthermore, both line contingency and non-contingency scenarios are considered under the N-1 security criterion. These initial modifications allow the evaluation of the deep reinforcement learning agent’s ability to regulate bus voltages and restore them to their nominal values within the operational range, i.e., $[0.95,1.05]$ p.u. The episode ends either when this objective is achieved, when the power flow does not converge, or when the agent reaches the 500-action limit. This approach ensures that the agent faces diverse and challenging scenarios, encouraging the development of optimal voltage control strategies in transmission networks.

The agent’s reward is calculated based on how its actions affect bus voltages relative to their nominal values. The reward function is designed to incentivize the agent to keep the voltages within desired bounds by minimizing deviations from the nominal set points. It is essential that the agent learns to take actions that not only stabilize the system but also maintain it within optimal operating margins, which is critical for ensuring the efficiency and security of the power grid [9,33].

If the agent successfully maintains all bus voltages within the target range, the episode ends prematurely, even before the 500-action limit, and the agent receives an additional reward of +50. This bonus serves as an incentive, rewarding efficient voltage regulation and compliance with the ideal operational parameters. If the episode continues to the full action limit without achieving the voltage regulation objective, the reward is computed based on the cumulative deviation of bus voltages from their nominal values. This reward structure is designed to guide the agent toward minimizing voltage deviations throughout training, gradually improving its control policy to bring bus voltages closer to the desired values. The agent’s continuous feedback loop is crucial, as it enables performance evaluation and iterative improvement of its decision-making strategies in response to the dynamic conditions of the power network [8].

A total of 3000 episodes were considered for training, with each episode consisting of a maximum of 500 actions. Each action represents a decision made by the agent, such as adjusting the reactive power output of a generator or modifying the tap position of a transformer. For every action, an individual reward is calculated for each bus in the system based on its post-action voltage magnitude $V_m\left(i\right)$, obtained after the power flow computation. The reward $R_i\left(V_m\left(i\right)\right)$ for each bus i is computed using the following expression:

$$R_i\left(V_m\left(i\right)\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}0.95\le V_m\left(i\right)\le 1.05\hfill \\ 0.05\times (V_m\left(i\right)-0.9),\hfill & \mathrm{if}0.90\le V_m\left(i\right)<0.95\hfill \\ -1,\hfill & \mathrm{if}{V}_m\left(i\right)<0.90\hfill \\ -1+0.05\times (1.1-V_m\left(i\right)),\hfill & \mathrm{if}1.05<V_m\left(i\right)\le 1.10\hfill \\ -1,\hfill & \mathrm{if}{V}_m\left(i\right)>1.10\hfill \end{array}\right.$$

(26)

Here, $V_m\left(i\right)$ represents the voltage magnitude at bus i, and N is the total number of buses in the system. The function is designed to penalize voltages that fall outside the nominal range $0.95\le V_m\left(i\right)\le 1.05$ with increasing penalties as the voltage deviates further from this ideal interval.

The reward for each action is computed as the average reward across all buses according to the following equation:

$$R_t={\displaystyle \frac{1}{N}}\sum _{i=1}^N{R}_i\left(V_m\left(i\right)\right),$$

(27)

where

• $R_i\left(V_m\left(i\right)\right)$: reward calculated for each bus;
• N: total number of buses in the system;
• $R_t$: normalized average reward for a given action.

Then, the total reward of the episode is obtained by summing the individual rewards of each action and applying a temporal discount factor throughout the episode. The formula for calculating the total reward is as follows:

$$R_{\mathrm{total}}=\sum _{t=1}^T{\gamma }^{t-1}{R}_t+B,$$

(28)

where

• $\gamma$ is the discount factor, which determines the importance of future rewards relative to immediate ones. In this case, a value of $\gamma$ = 0.9995 is used.
• $R_t$ is the reward obtained at time step t.
• T is the total number of steps or actions within an episode.
• B is the bonus assigned when the agent succeeds in keeping all voltage levels within the desired limits before reaching the maximum number of actions. This bonus, B = +50, is granted as an incentive when the agent manages to stabilize the system quickly, that is, before completing the maximum allowed actions (500).

The selection of the discount factor $\gamma$ = 0.9995 is based on the specific characteristics of voltage control problems in power systems and standard practices reported in specialized literature [8,9,17]. This value, very close to unity, reflects the long-term nature of voltage control decisions, where actions taken at a given instant have sustained effects on system stability over extended periods, requiring a broad planning horizon to ensure safe operation against future load variations and possible contingencies [7,15]. The selection aligns with previous studies in similar reinforcement learning applications for power system control, where values in the range [0.999, 0.9999] have demonstrated effectiveness in balancing immediate and future rewards. This specific value corresponds to an effective horizon of approximately 2000 time steps (1/($1-\gamma$)), which is appropriate considering that each episode can contain up to 500 actions, and encourages the agent to consider long-term consequences of its actions while avoiding myopic strategies that could generate subsequent instabilities.

This approach enables the agent to evaluate the long-term consequences of its actions, prioritizing those decisions that keep the system within ideal operating parameters across multiple episodes. Therefore, the total reward depends not only on the decisions taken at each step, but also on the agent’s ability to achieve the control objectives quickly, as reflected in the additional bonus granted when the system is stabilized efficiently.

The agent will be trained using a neural network architecture previously described in Section 2.2, implemented in the Python v3.11 programming language with the PyTorch v2.9.0 library, which provides the flexibility and computational efficiency required for the development of deep learning models. For this training process, three different algorithms will be employed to optimize the agent’s learning.

First, the standard Deep Q-Learning (DQL) algorithm will be used. It relies on two neural networks (a main network and a target network) to update Q-values in a stable and efficient manner. Additionally, two neuroevolution algorithms will be incorporated: Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO). These evolutionary methods will be used to search for and optimize the weights of the neural network, leveraging their global search capabilities to efficiently explore the solution space. By combining the strengths of deep learning and evolutionary optimization, the agent is expected to adapt more effectively to the complexities of the voltage control problem. The following section provides a detailed explanation of the training algorithms and their implementation.

To ensure reproducibility and provide a clear overview of the experimental setup,

Table 2. Simulation and training configuration parameters.

Category	Parameter	Value/Description
Simulation Setup	Test system	IEEE 30-bus transmission network
	Load variation range	80–120% of nominal demand (constant power factor)
	Security criterion	N-1 contingency and non-contingency scenarios
	Power flow simulator	GridCal (Python-based)
Neural Network Architecture	Input dimension	30 (bus voltage magnitudes)
	Hidden layers	[128, 256, 128]
	Hidden activation	ReLU
	Output types	6 continuous (generator reactive power), 4 discrete (OLTC taps)
	Output activation	Sigmoid (continuous), Softmax (discrete)
	Framework	PyTorch
	Programming language	Python
Training Configuration	Training algorithms	Deep Q-Learning (DQL), Genetic Algorithm (GA), Particle Swarm Optimization (PSO)
	Number of episodes	3000
	Maximum steps per episode	500
	Discount factor ($\gamma$)	0.9995
	Reward bonus (B)	+50 (for early stabilization)
	Learning rate ($\alpha$)	0.001 (for DQL)
	Batch size	64
	Replay buffer size	10,000

summarizes the main parameters used in the simulation and training stages, including the characteristics of the IEEE 30-bus system, neural network architecture, and algorithmic configurations.

2.3.1. Deep Q-Learning (DQL) Algorithm

Deep Q-Learning (DQL) is the first algorithm used to train the agent, extending classical Q-Learning by employing deep neural networks to approximate the Q-value function; while traditional Q-Learning relies on a tabular method to assign values to each state–action pair, this approach becomes impractical in environments with large or continuous state–action spaces, such as voltage control in power networks. Deep Q-Learning (DQL) overcomes this limitation by using a neural network to generalize Q-values based on system state features, thus avoiding the need to explicitly store all combinations. To stabilize learning, Deep Q-Learning (DQL) incorporates two networks: the main Q-network, updated continuously, and the target network, a frozen copy that is updated periodically to provide stable learning targets and prevent divergence [9,15,17].

The DQL algorithm is based on the Bellman equation for updating Q-values:

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha \left[r_{t+1}+\gamma \underset{a^{\prime }}{max}Q(s_{t+1},a^{\prime })-Q(s_t,a_t)\right]$$

(29)

where $\alpha$ is the learning rate, $\gamma$ is the discount factor, $s_t$ is the current state, $a_t$ is the action taken, and $r_{t+1}$ is the reward obtained [8,9].

The loss function used to train the main neural network is defined as follows:

$$L\left(\theta \right)={\mathbb{E}}_{(s,a,r,s^{\prime })\sim D}\left[{\left(r+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime };{\theta }^{-})-Q(s,a;\theta )\right)}^2\right]$$

(30)

where $\theta$ are the parameters of the main network, ${\theta }^{-}$ are the parameters of the target network, and D is the experience replay buffer [15,17].

In voltage control applications, such as the IEEE 30-bus system, Deep Q-Learning (DQL) enables the agent to learn policies that adjust reactive power or transformer taps to regulate bus voltages. The Q-function evaluates the quality of each action based on how closely resulting voltages align with nominal targets. Experience replay further enhances performance by allowing the agent to learn from past interactions, improving both training stability and convergence speed. This is especially important in highly variable power systems, where the agent must generalize across a range of operating conditions [7,8].

2.3.2. Genetic Algorithm

In this approach, the Genetic Algorithm (GA) is employed to optimize the weights and biases of the neural network that constitutes the control agent. Each solution in the population is represented as a chromosome encoding a specific configuration of weights and biases. The algorithm evolves these solutions over generations using genetic operators such as selection, crossover, and mutation. Chromosomes are evaluated based on their performance in voltage control, and the best candidates are selected to generate the next generation. This iterative process enables the agent to gradually discover configurations that improve its ability to maintain bus voltages within desired limits [4,5,23,38,39].

The Boltzmann-based selection function used in this work is defined as follows:

$$P_i={\displaystyle \frac{e^{f_i/T}}{{\sum }_{j=1}^N{e}^{f_j/T}}}$$

(31)

where $P_i$ is the selection probability of individual i, $f_i$ is its fitness value, T is the temperature parameter, and N is the population size [25,40].

The arithmetic crossover operator is implemented as follows:

$$\begin{array}{cc}\hfill x_1^{new}& =\alpha x_1+(1-\alpha )x_2\hfill \\ \hfill x_2^{new}& =(1-\alpha )x_1+\alpha x_2\hfill \end{array}$$

(32)

where $x_1$ and $x_2$ are the selected parents, $\alpha \in [0,1]$ is the crossover parameter, and $x_1^{new}$, $x_2^{new}$ are the offspring [4,5].

Gaussian mutation is applied according to the following:

$$x_i^{new}=x_i+\mathcal{N}(0,{\sigma }^2)$$

(33)

where $\mathcal{N}(0,{\sigma }^2)$ is a normal distribution with zero mean and variance ${\sigma }^2$ [38,39].

A key feature of this GA implementation is the use of a Boltzmann-based selection function, which balances exploration and exploitation during optimization. At high initial temperatures, selection probabilities are more uniform, encouraging exploration of diverse solutions. As the temperature decreases, the algorithm increasingly favors high-performing individuals, shifting focus toward exploitation. This simulated annealing mechanism allows the algorithm to avoid local optima early on and converge more effectively to an optimal solution. By combining evolutionary optimization with neural network training, the agent can adapt to varying operating conditions and enhance system stability and control performance [25,30,40,41].

2.3.3. Particle Swarm Optimization (PSO) Algorithm

In this approach, the Particle Swarm Optimization (PSO) algorithm is used to optimize the weights and biases of the neural network that forms the control agent. Inspired by the collective behavior of swarms in nature, PSO treats each particle as a candidate solution that represents a specific neural configuration. These particles move through the search space by adjusting, based on both their own historical best position (cognitive component) and the best-known positions of their neighbors (social component). This balance enables an effective exploration of the solution space to find optimal configurations [2,5,42,43].

The velocity equation for each particle is updated according to the following:

$$v_{i,d}^{t+1}=W·v_{i,d}^t+C_1·r_1·(p_{i,d}^t-x_{i,d}^t)+C_2·r_2·(g_d^t-x_{i,d}^t)$$

(34)

and the position is updated as follows:

$$x_{i,d}^{t+1}=x_{i,d}^t+v_{i,d}^{t+1}$$

(35)

where $v_{i,d}^t$ is the velocity of particle i in dimension d at time t, $x_{i,d}^t$ is its position, $p_{i,d}^t$ is the personal best position, $g_d^t$ is the global best position, and $r_1$, $r_2$ are random numbers in $[0,1]$ [24,43].

To enhance this capability, three key parameters are dynamically adjusted during optimization: inertia weight W, cognitive acceleration coefficient $C_1$, and social acceleration coefficient $C_2$. These parameters are updated according to the following:

$$\begin{array}{cc}\hfill W^t& =W_{max}-{\displaystyle \frac{t}{T_{max}}}·(W_{max}-W_{min})\hfill \\ \hfill C_1^t& =C_{1f}+{\displaystyle \frac{t}{T_{max}}}·(C_{1i}-C_{1f})\hfill \\ \hfill C_2^t& =C_{2i}+{\displaystyle \frac{t}{T_{max}}}·(C_{2f}-C_{2i})\hfill \end{array}$$

(36)

where t is the current iteration, $T_{max}$ is the maximum number of iterations, and subscripts i and f denote initial and final values, respectively [3,37].

This progressive adjustment of coefficients is guided by the current iteration and total number of iterations. Toward the beginning of the process, higher values of W allow a larger exploration of the search space, while $C_1$ and $C_2$ are set to favor diversity. As iterations progress, W is gradually reduced to slow particle movement and promote convergence, while the acceleration coefficients increase to focus search around promising regions. This dynamic strategy ensures that particles search widely at the beginning and refine good solutions near the end, maintaining a balance between exploration and exploitation. As a result, PSO efficiently guides the neural network toward optimal parameter configurations, improving the agent’s ability to adapt to voltage control challenges in the power system and enhancing overall performance [4,24].

2.4. Enhanced Experimental Scenario Design

This section provides comprehensive specifications for the experimental scenarios designed to evaluate voltage control performance under diverse and challenging conditions. As detailed in

Table 3. Detailed experimental scenario configuration parameters.

Category	Parameter	Value/Specification	Justification
Load Variation	Distribution type	Uniform U(0.8, 1.2)	Maximum uncertainty coverage
	Variation range	80–120% nominal	Realistic operational bounds
	Power factor	Constant per bus	Isolate magnitude effects
	Correlation model	Independent per bus	Worst-case uncertainty
	Total scenarios	Continuous range	Comprehensive coverage
	Selection probability	Equal for all values	Unbiased evaluation
N-1 Contingencies	Transmission lines	41 elements	Complete line set
	Transformers	4 OLTC units	All tap-changing devices
	Total contingencies	45 scenarios	Full N-1 coverage
	Selection probability	Uniform (1/45 each)	Equal scenario weighting
	Analysis type	Post-contingency static	Voltage control focus
	Topology changes	Single element outage	Standard N-1 criterion
	Failure simulation	Instantaneous disconnection	Simplified modeling
	Recovery model	Control action only	Post-event operation
Generation Mix	Total generators	6 units (buses 1,2,5,8,11,13)	IEEE 30-bus standard
	Conventional units	3 generators (buses 1,2,13)	Dispatchable sources
	Renewable units	3 generators (buses 5,8,11)	Variable sources
	Control capability	Full reactive power (conv.)	Standard characteristics
		Limited reactive power (ren.)	Modern inverter limits
	Dispatch priority	Renewable first	Current practice

, which is titled Detailed Experimental Scenario Configuration Parameters, the scenario design addresses the need for detailed parameter specifications, probabilistic modeling, and validation under extreme operating conditions to ensure robust assessment of the proposed control algorithms.

2.4.1. Stochastic Load Variation Modeling

The load variation strategy employs a uniform distribution to model demand uncertainty across all system buses. For each episode, the load at bus i is mathematically formulated as follows:

$$L_i=L_{nom,i}\times U(0.8,1.2)$$

(37)

where $L_{nom,i}$ is the nominal load at bus i, and $U(0.8,1.2)$ represents a uniform distribution over the interval [0.8, 1.2]. This uniform distribution ensures equal probability for all load levels within the specified range, providing maximum uncertainty coverage and eliminating bias toward specific load conditions. The power factor at each bus remains constant during load variations to isolate the effects of load magnitude changes on voltage control performance.

The selection of a uniform distribution is justified by several factors: (1) it provides comprehensive coverage of the entire operational range with equal weighting, (2) it represents a worst-case scenario for load forecasting uncertainty, and (3) it enables systematic evaluation of control robustness across all possible load combinations. The 80–120% range encompasses typical operational variations observed in transmission networks during normal conditions, covering both light-load and heavy-load scenarios that challenge voltage regulation capabilities [8].

2.4.2. Comprehensive N-1 Security Assessment Framework

The N-1 security assessment considers all critical transmission elements in the IEEE 30-bus system, comprising 41 transmission lines and 4 on-load tap-changing transformers, for a total of 45 possible contingencies. Each contingency scenario $C_k$ represents the outage of a single transmission element, mathematically expressed as follows:

$$C_k=\{T_{base}\setminus \left\{elemen{t}_k\right\}\},k\in \{1,2,\dots ,45\}$$

(38)

where $T_{base}$ represents the base case topology and $elemen{t}_k$ denotes the k-th transmission element (line or transformer) removed from service.

The probability of selecting each contingency scenario follows a uniform distribution:

$$P\left(C_k\right)={\displaystyle \frac{1}{45}},\forall k\in \{1,2,\dots ,45\}$$

(39)

This approach ensures equal representation of all possible single-element outages, providing unbiased assessment of control performance across diverse network topologies. The analysis focuses on post-contingency steady-state conditions rather than dynamic fault behavior, emphasizing the evaluation of voltage control effectiveness following topological changes. This methodology aligns with standard power system planning practices where control systems must maintain voltage stability after network reconfiguration [37].

2.4.3. Hybrid Generation Scenario with Renewable Integration

The generation mix incorporates both conventional and renewable energy sources to reflect modern power system characteristics. The IEEE 30-bus system includes six generators located at buses 1, 2, 5, 8, 11, and 13. In this study, three generators (buses 5, 8, and 11) are designated as renewable energy sources with variable output characteristics, while the remaining three generators (buses 1, 2, and 13) operate as conventional dispatchable units.

The renewable generators are modeled with the following characteristics:

• Variable power output with fluctuations representing wind or solar generation patterns;
• Limited reactive power capability compared to conventional generators;
• Priority dispatch status requiring the system to accommodate their variable output;
• Modern power electronic controls enabling fast voltage regulation response.

This hybrid generation scenario introduces additional complexity to voltage control by requiring the agent to coordinate between conventional generators with full reactive power capability and renewable units with limited control flexibility. The scenario reflects the increasing penetration of renewable energy sources in modern transmission networks and their impact on voltage stability [16].

2.4.4. Scenario Design Rationale and Validation

The comprehensive scenario design presented in this section addresses several critical aspects of voltage control evaluation. The uniform distribution approach for load variations ensures that the control algorithms are tested across the entire operational space without bias toward specific operating points. This is particularly important for reinforcement learning algorithms that must generalize across diverse conditions.

The N-1 contingency framework provides systematic evaluation of control robustness under all possible single-element outages, reflecting standard power system reliability practices. By focusing on post-contingency steady-state analysis rather than dynamic fault simulation, the evaluation emphasizes the core voltage control objectives while maintaining computational tractability for the extensive training process required by the three algorithms.

The inclusion of renewable generation scenarios addresses modern power system realities where increasing penetration of variable energy resources creates new challenges for voltage regulation. The hybrid generation mix provides a realistic test bed for evaluating how different control algorithms adapt to the changing characteristics of power system operation.

This comprehensive approach provides confidence that the experimental results reflect the capabilities and limitations of each control algorithm under diverse operating conditions representative of modern transmission networks [7,8,15].

2.5. Performance Evaluation Metrics

To evaluate the performance of the trained agent, several quantitative metrics are employed to assess the effectiveness of voltage control across different scenarios and algorithms.

The Mean Absolute Error (MAE) is calculated as follows:

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n|V_{actual,i}-V_{target,i}|$$

(40)

The Mean Absolute Percentage Error (MAPE) is defined as follows:

$$MAPE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{V_{actual,i}-V_{target,i}}{V_{target,i}}}\right|\times 100\%$$

(41)

where $V_{actual,i}$ is the resulting voltage at bus i, $V_{target,i}$ is the target voltage (1.0 p.u.), and n is the total number of buses [8,33].

Additionally, the percentage of buses within the acceptable operational range is evaluated:

$$\mathrm{Buses}\mathrm{in}\mathrm{range}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\mathbb{I}(0.95\le V_i\le 1.05)\times 100\%$$

(42)

where $\mathbb{I}(·)$ is the indicator function that equals 1 if the condition is true and 0 otherwise [7,9].

These metrics provide a comprehensive assessment of the agent’s ability to maintain voltage levels within acceptable limits, minimize deviations from nominal values, and ensure overall system stability across various operating conditions.

3. Results

3.1. Case Study Description and Representativeness

The IEEE 30-bus test system was selected as the benchmark for evaluating the proposed voltage control methodologies due to its well-established position as a standard reference in power systems research. This system represents a medium-sized transmission network that provides an optimal balance between computational tractability and realistic complexity, making it particularly suitable for machine learning algorithm development and validation [8,16].

The representativeness of the IEEE 30-bus system stems from several key characteristics. First, it serves as a widely accepted benchmark that enables reproducible research and direct comparison with the existing literature [1,4]. The system incorporates multiple types of control devices—generators capable of reactive power regulation and on-load tap-changing transformers—creating a realistic multi-objective control environment typical of actual transmission networks. Additionally, its well-defined topology and publicly available parameters eliminate uncertainties related to system modeling, allowing focus on algorithm performance evaluation [5].

The system’s complexity is sufficient to exhibit realistic power system behaviors, including voltage-reactive power coupling, transmission constraints, and the interaction between multiple control variables, while remaining computationally manageable for iterative training processes requiring thousands of simulations [9,15]. This characteristic is particularly valuable for reinforcement learning applications, where extensive exploration of the state–action space is essential for policy convergence.

Furthermore, the IEEE 30-bus system facilitates multiple types of studies including optimal power flow (OPF), volt-VAR control (VVC), centralized and distributed control strategies, N-1 contingency analysis, and integration of distributed energy resources [11,14]. The availability of established baselines and comparison methodologies in the literature enables comprehensive evaluation of novel approaches against conventional control techniques such as automatic voltage regulators (AVRs) and classical optimization methods [10].

3.2. System Parameters and Training Configuration

Table 4. IEEE 30-bus test system specifications.

Parameter	Value
Total buses	30
Transmission lines	41
Generators	6 (buses 1, 2, 5, 8, 11, 13)
OLTC transformers	4 (6–9, 6–10, 4–12, 27–28)
Load buses	21
Voltage base	132 kV
Power base	100 MVA
Nominal voltage range	[0.95, 1.05] p.u.
Load variation range	[80%, 120%] of nominal
Power factor	Constant
Contingency scenarios	N-1 line and generator outages

presents the key technical specifications of the IEEE 30-bus test system used in this study. The system configuration includes various operational scenarios designed to test the robustness and adaptability of the proposed control algorithms under realistic operating conditions.

Table 5. Training parameters for the three algorithms.

Parameter	DQL	GA	PSO
Population/Swarm size	N/A	50	50
Learning rate	0.001	N/A	N/A
Discount factor ($\gamma$)	0.9995	0.9995	0.9995
Experience buffer size	10,000	N/A	N/A
Target network update	Every 100 steps	N/A	N/A
Crossover probability	N/A	0.8	N/A
Mutation probability	N/A	0.1	N/A
Initial inertia weight ($W_{max}$)	N/A	N/A	0.9
Final inertia weight ($W_{min}$)	N/A	N/A	0.4
Cognitive coefficient ($C_1$)	N/A	N/A	2.0
Social coefficient ($C_2$)	N/A	N/A	2.0
Maximum episodes	3000	3000	3000
Maximum actions per episode	500	500	500

details the specific training parameters employed for each algorithm. These parameters were selected based on preliminary sensitivity analysis and literature recommendations to ensure fair comparison among the three approaches [3,9,37].

The experimental scenarios incorporate multiple operating conditions to evaluate algorithm robustness.

Table 6. Test scenarios and evaluation conditions.

Scenario Type	Description
Normal operation	Load variations between 80 and 120% of nominal values
N-1 contingency	Single line outages with load variations
Generation contingency	Single generator outages
Transformer contingency	OLTC transformer outages
Multiple disturbances	Combined load and contingency scenarios
Voltage range evaluation	Buses within [0.95, 1.05] p.u. limits
Early stabilization	Achievement of +50 bonus reward

summarizes the testing conditions implemented during both training and validation phases.

The reward structure implemented ensures that agents learn to prioritize voltage regulation within the acceptable operational range [0.95, 1.05] p.u., while penalizing severe violations that could compromise system security. The bonus mechanism (+50) for early stabilization encourages the development of efficient control policies that minimize the number of required actions [8].

3.3. Training Performance Analysis

All training performance results presented in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 include 95% confidence intervals calculated from ten independent training runs for each algorithm, ensuring statistical robustness of the comparative analysis. The confidence intervals provide insight into the variability and consistency of each algorithm’s performance across multiple executions.

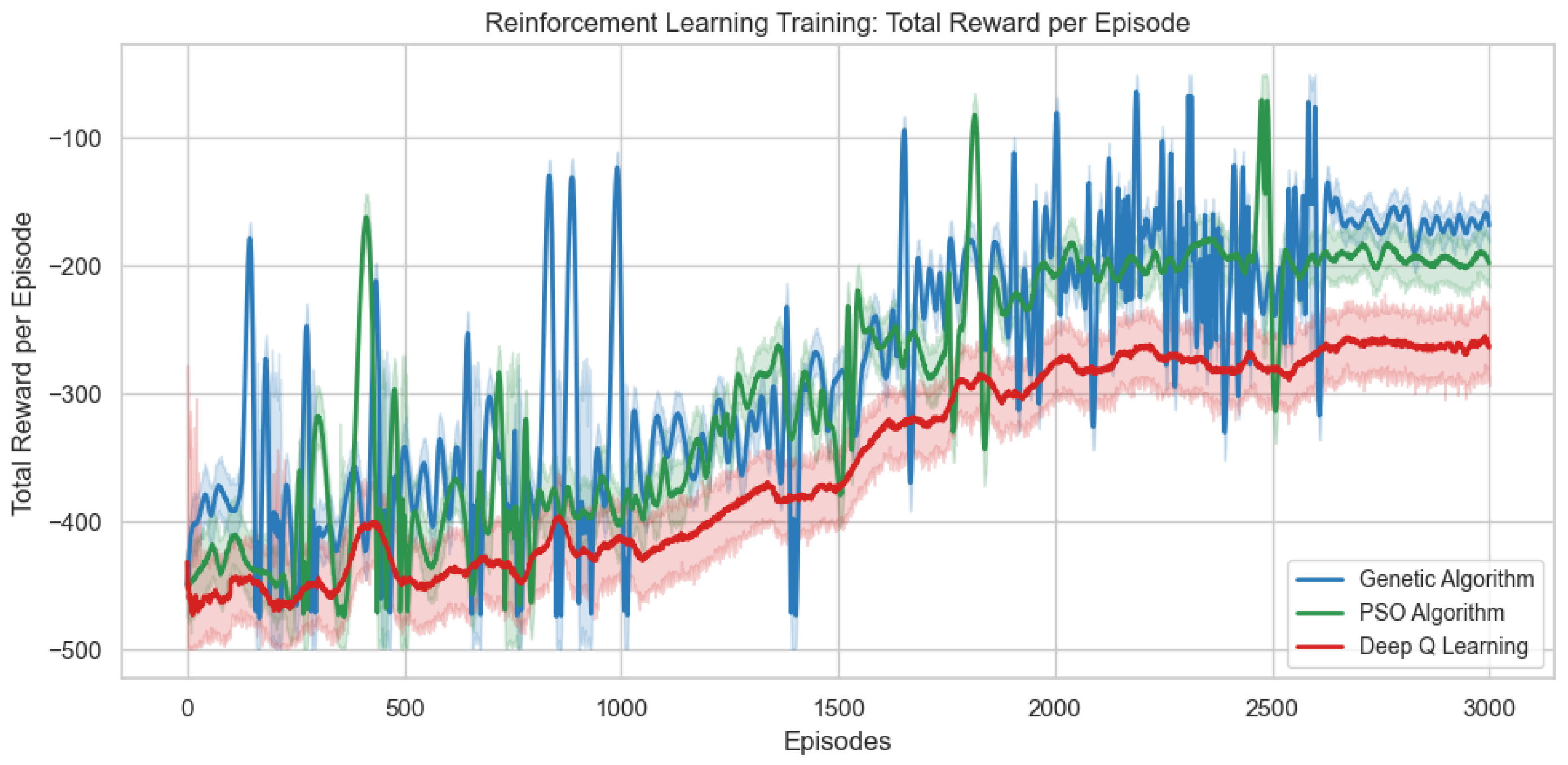
During the 3000 training episodes, the performance of the Deep Q-Learning (DQL), Genetic Algorithm (GA), and Particle Swarm Optimization (PSO) methods was compared based on the total reward per episode, showing an increasing trend in all cases, as illustrated in Figure 2—an indication of successful learning. The confidence intervals in Figure 2 demonstrate that PSO maintains the most consistent performance with minimal variability, while GA shows higher variance in early episodes due to its stochastic evolutionary nature. Deep Q-Learning (DQL) exhibited stable improvements thanks to its dual-network architecture and experience replay, while GA showed abrupt jumps in the early stages due to its evolutionary exploration. PSO, through the dynamic adjustment of its inertia and acceleration parameters, achieved an effective balance between exploration and exploitation, outperforming the other methods in later stages. The learning curves show that, although GA and PSO converge faster, Deep Q-Learning (DQL) maintains greater consistency under complex scenarios. The additional bonus for early voltage stabilization was obtained more frequently by the agent trained with PSO, highlighting its ability to learn effective and robust control strategies in the face of load variations and contingencies.

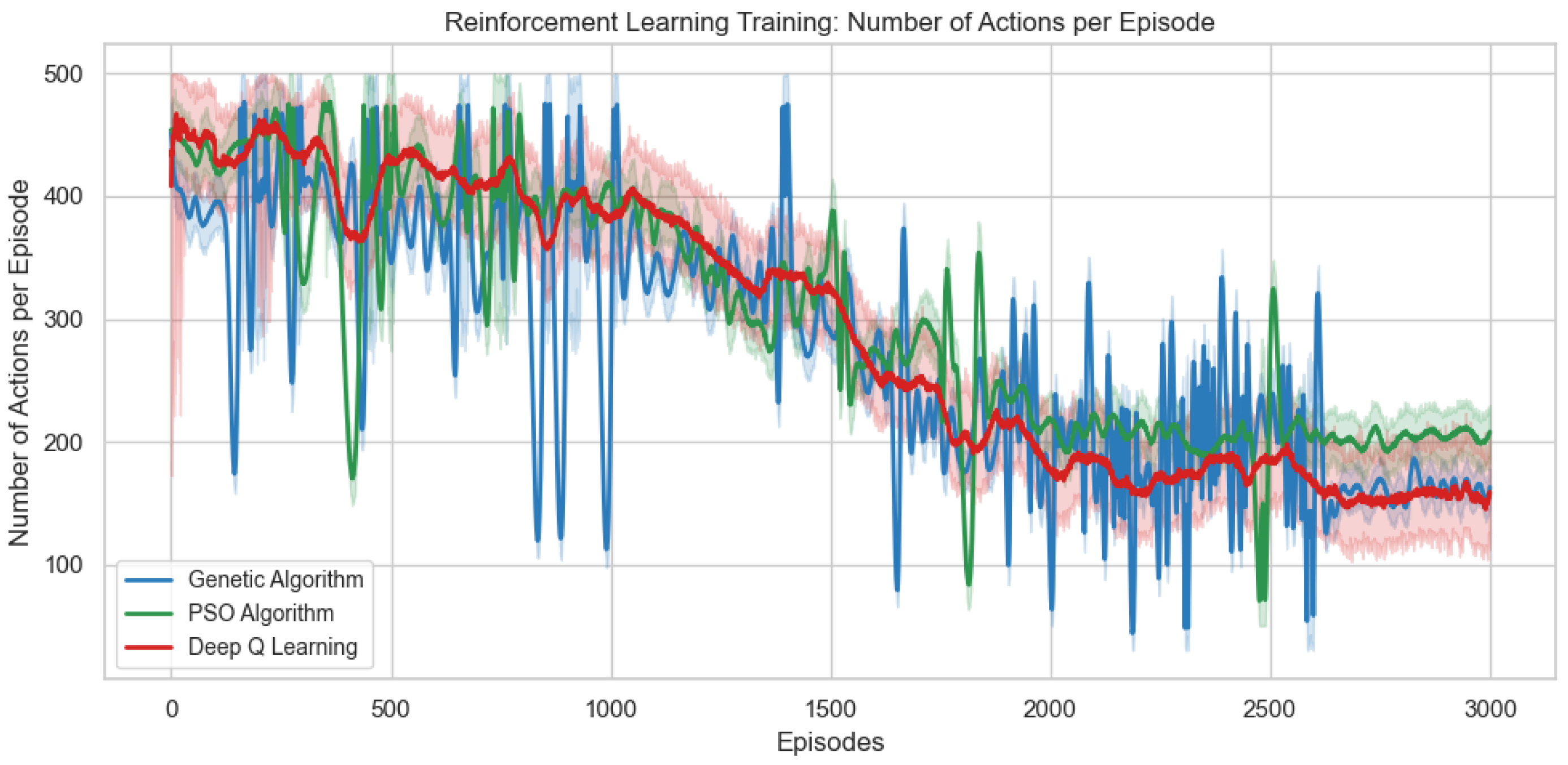
Figure 3 shows the number of actions required per episode for the three algorithms (Deep Q-Learning, GA, and PSO) during training on the IEEE 30-bus system, with confidence intervals indicating the consistency of convergence patterns. It can be observed that all algorithms progressively reduce the number of actions needed to stabilize voltages, indicating an improvement in control efficiency. The Deep Q-Learning (DQL) algorithm exhibits a more gradual but consistent decrease, reflecting its learning based on accumulated experience. GA shows a more irregular reduction, with fluctuations characteristic of its evolutionary approach, where new individuals may initially require more actions before converging to optimal solutions.

PSO stands out by achieving the greatest reduction in the number of actions, particularly in later episodes, due to its ability to dynamically adjust exploration and exploitation. This efficiency aligns with its reward performance, confirming that it discovers faster control strategies. The decrease in actions directly correlates with the acquisition of the +50 bonus for early completion, demonstrating that the algorithms learn not only to control voltages but also to do so more efficiently. These results reinforce that PSO is particularly well-suited for problems requiring response time optimization in power systems.

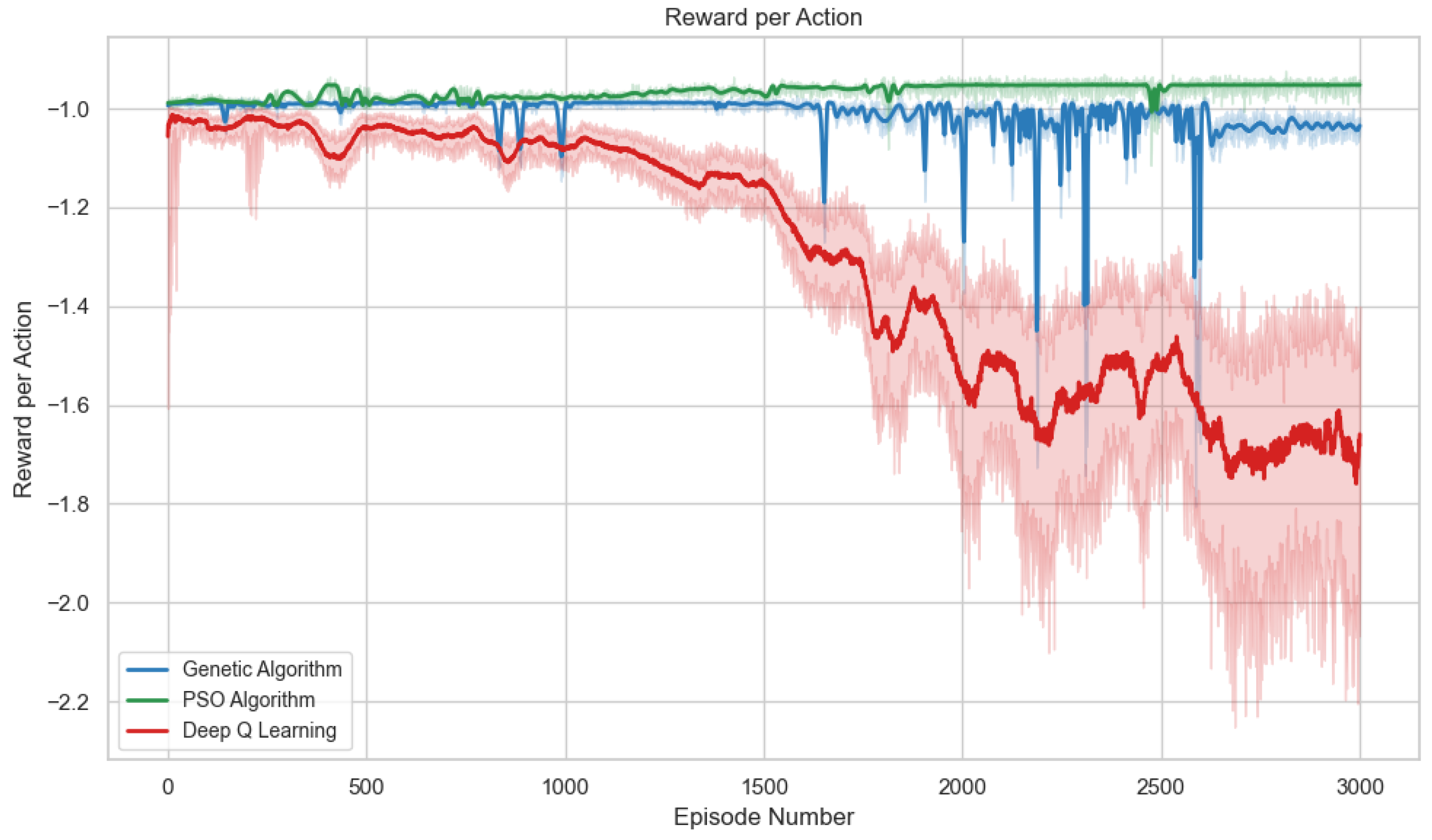
Figure 4 shows the evolution of the reward per action throughout the training episodes for the three evaluated algorithms, with confidence intervals revealing the stability of each approach’s learning behavior. It can be observed that the PSO algorithm consistently maintains the highest rewards per action (approximately −1.2), followed by the Genetic Algorithm (around −1.6), and finally Deep Q-Learning (close to −2.0). This metric is particularly relevant as it quantifies the efficiency of each action taken by the agent, regardless of episode length. PSO once again demonstrates its superiority, achieving higher rewards for each adjustment made to the power system controls, which translates into a more effective control policy.

The temporal evolution of this metric reveals interesting patterns in the learning behavior of each algorithm; while PSO and GA show relatively rapid improvement during the first 500–1000 episodes, Deep Q-Learning requires more time to optimize its action policy. However, it is notable that, toward the final episodes (2000–3000), all algorithms reach a certain level of stability in their rewards per action, although there are significant differences in their final values. This late-stage convergence suggests that, regardless of the optimization method used, the agent requires a considerable number of episodes to fully refine its control policy in this complex power systems environment.

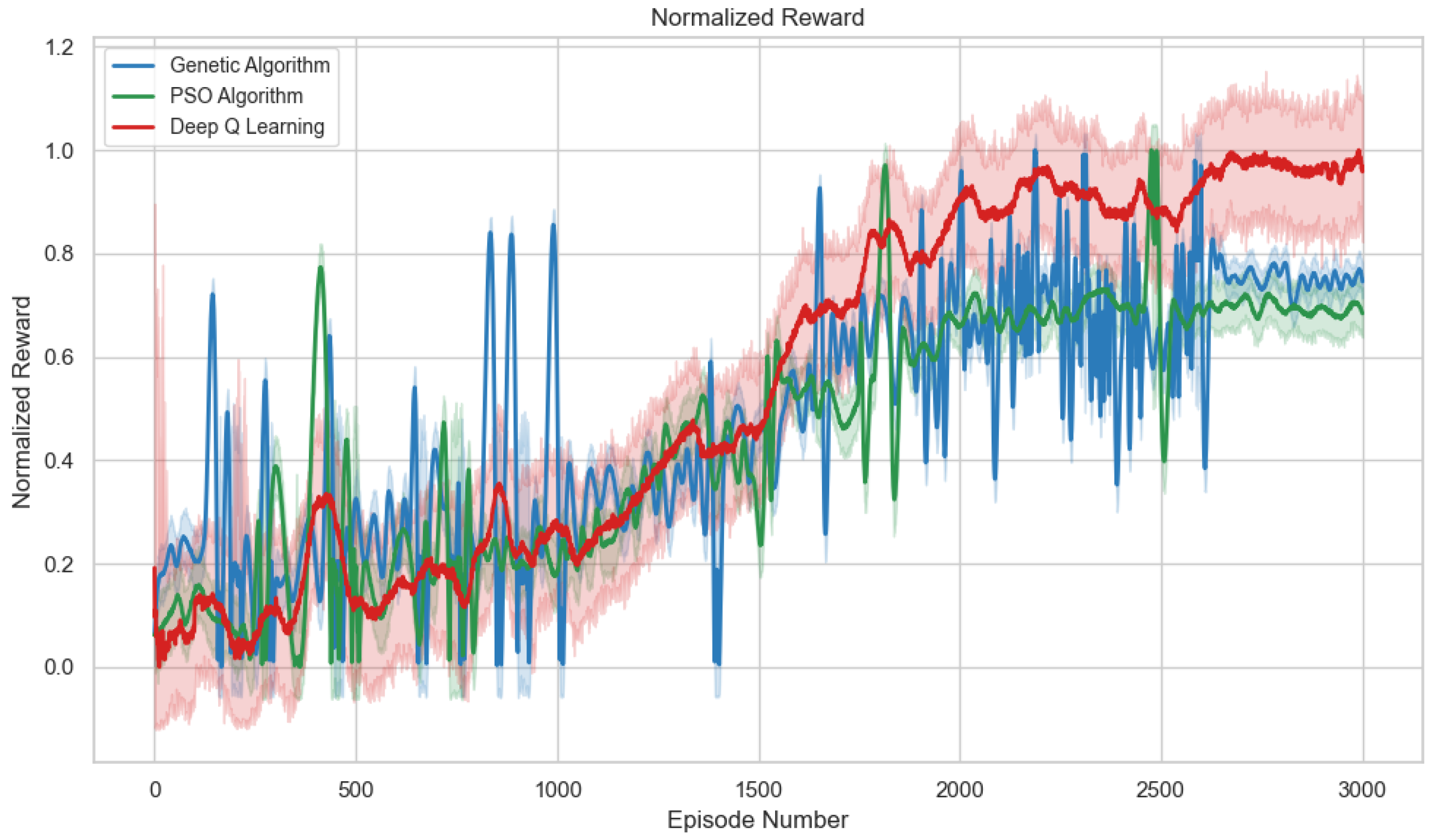
Figure 5 presents the evolution of the Normalized Reward over the 3000 training episodes for the three evaluated algorithms, with confidence intervals demonstrating the reproducibility of the observed performance rankings. The results show that the PSO algorithm reaches and maintains the best performance (Normalized Reward close to 1.0), followed by the Genetic Algorithm (approximately 0.8), and finally Deep Q-Learning (around 0.6). This normalization allows for a direct comparison of the relative performance between algorithms, confirming the consistent superiority of the PSO approach in voltage control tasks.

The temporal analysis reveals significant differences in learning patterns. PSO demonstrates rapid convergence, reaching its peak performance within the first 1000 episodes, while GA shows a more gradual improvement. Deep Q-Learning, although starting from lower values, exhibits a more stable learning curve, suggesting a more thorough exploration of the action space. It is particularly noteworthy that, toward the end of the training (episodes 2500–3000), PSO not only maintains its advantage but continues to show slight improvements, indicating its ability to continuously refine the control policy.

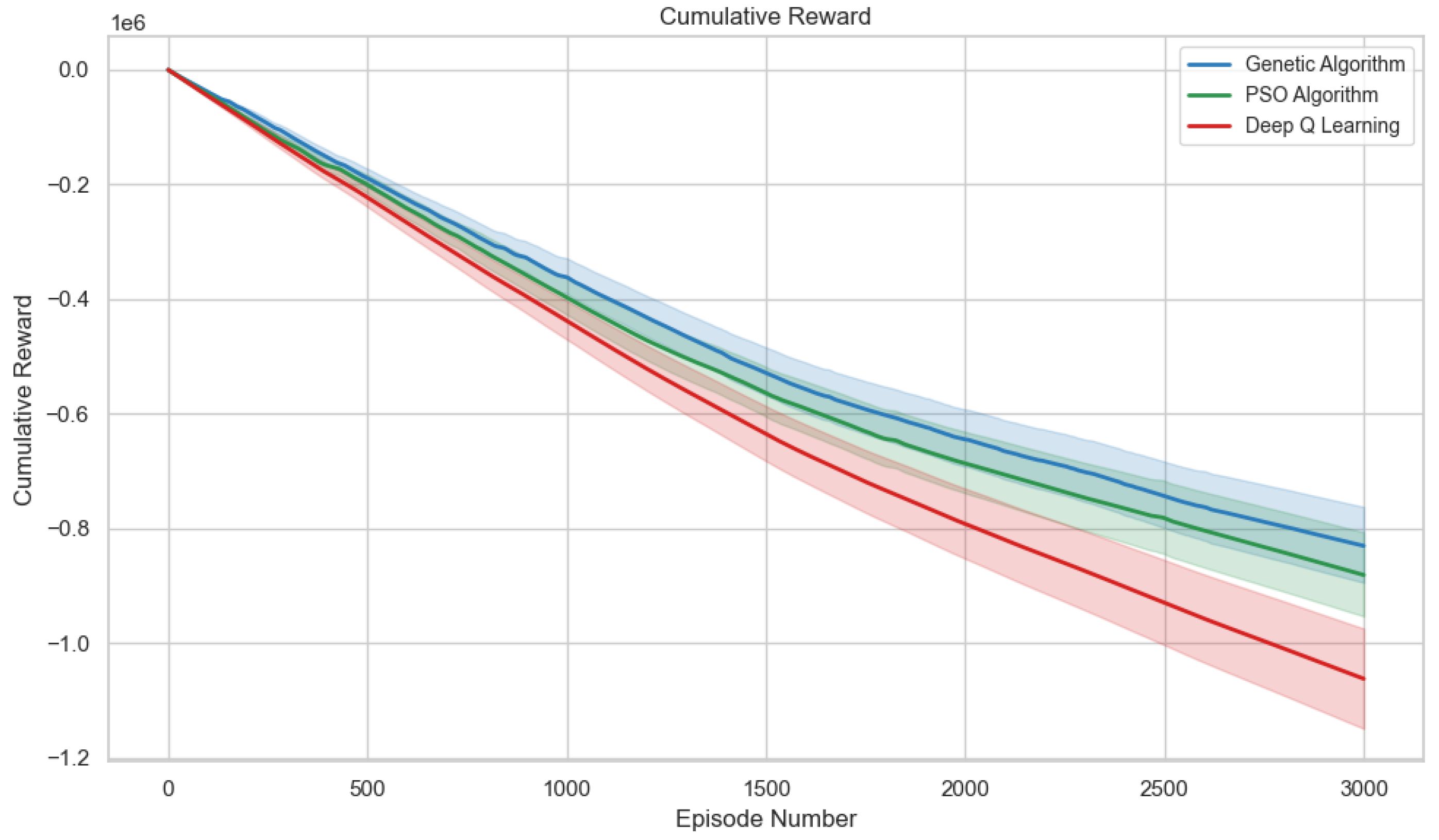
Figure 6 shows the cumulative reward obtained by the three algorithms throughout training, with confidence intervals confirming the sustained performance differences between approaches, providing a comprehensive view of their overall performance. The PSO algorithm once again stands out as the top performer, reaching cumulative reward values close to 1.0, followed by the Genetic Algorithm (approximately 0.8) and Deep Q-Learning (around 0.6). This cumulative metric is particularly relevant as it reflects not only the momentary effectiveness of actions but also each algorithm’s sustained ability to maintain stable control of the power system over time.

The comparative analysis reveals distinct patterns in reward accumulation. PSO shows a steeper growth curve during the first 500 episodes, indicating a rapid initial adaptation to the control problem. The Genetic Algorithm, although with a more moderate initial increase, maintains a steady rate of improvement. Deep Q-Learning, despite starting from lower values, displays a more stable progression, suggesting that its temporally-based learning approach could offer advantages in prolonged operational scenarios. The performance gap between PSO and the other methods remains consistent throughout the episodes, reinforcing its suitability for this specific application.

The cumulative reward values shown in Figure 6 and summarized in

Table 7. Comparative summary of cumulative reward and learning efficiency (final episode).

Metric	PSO	GA	DQL
Cumulative Reward (Final Episode)	Highest (Best Performance)	Intermediate	Lowest
Normalized Reward (Final Episode)	≈1.0 (Best)	≈0.8	≈0.6
Convergence Speed (Episodes to stabilize)	Fastest (≈1000 episodes)	Moderate	Slowest (Stable but gradual)
Relative Performance to GA/DQL (Abstract)	3% higher than GA, 5% higher than DQL	Intermediate	Lowest

confirm that the PSO algorithm consistently achieved the highest sustained performance throughout the training episodes. This reflects its superior ability to maintain stable control over the power system over time. The Deep Q-Learning (DQL) method, while exhibiting a stable learning trajectory, lags behind both metaheuristic approaches in total reward accumulation, reinforcing the finding that DQL prioritizes early termination (bonus acquisition) at the expense of individual action quality, as previously discussed.

The combined analysis of the five figures reveals that the PSO algorithm consistently ranks as the most effective, outperforming its counterparts across all key metrics: total reward per episode, number of actions required, average reward, performance stability, and efficiency per action. This advantage is reflected in both the speed at which it reaches high performance levels—effectively converging within the first 1000 episodes—and the quality of the learned policies, achieving rapid voltage stabilization with minimal interventions. The Genetic Algorithm (GA), meanwhile, exhibits intermediate performance: it outperforms Deep Q-Learning (DQL) in terms of initial learning speed and operational efficiency, thanks to its evolutionary ability to explore the solution space, although it experiences some instability during the training process. Deep Q-Learning (DQL), while less competitive in quantitative metrics, stands out for its stable and predictable learning curve, lower sensitivity to initial conditions, and sustained improvement throughout all episodes.

These results suggest that the choice of the most suitable algorithm should be aligned with the specific requirements of the system. In environments where operational efficiency and fast response are priorities, PSO represents the best option. GA, on the other hand, offers a good balance between exploration and efficiency, making it ideal for systems with computational constraints or a need for evolutionary adaptability. Deep Q-Learning (DQL) may be more appropriate in contexts with high operational variability, where its long-term learning capacity and generalization capabilities are more valuable. Taken together, these findings open the door to the development of hybrid architectures that combine the strengths of each approach—merging the speed of PSO, the adaptive exploration of GA, and the temporal robustness of Deep Q-Learning (DQL).

3.4. Validation Against Conventional Control

After completing the training and comparison among the three approaches, it was found that the agent trained with PSO achieved the best overall performance. This was evident not only in terms of total reward, number of actions, and convergence speed, but also in consistency, stability, and its ability to keep voltages within the operational range under multiple load and contingency scenarios. To validate its effectiveness under conditions closer to those of a real operational environment, a second experimental phase was conducted, in which the IEEE 30-bus system was implemented in the GridCal tool, executing quasi-dynamic simulations.

In this phase, the system’s behavior was compared under two control schemes: on one hand, conventional control based on IEEE Type 1 Automatic Voltage Regulators (AVRs), using fixed set points according to the values typically recommended by IEEE standards; on the other hand, the agent trained with PSO, which automatically determines the reactive power set points for each generator as well as the tap positions of the transformers. It is important to note that, to ensure a fair comparison, the set points used in the conventional control were those previously identified by the agent during its training, ensuring that both systems started from an equivalent reference configuration. Figure 7 shows the voltage response comparison, where the blue curve represents the voltage evolution under traditional control, while the red curve corresponds to the system behavior under the agent’s control.

The results from this test show that the agent exhibits a faster and more efficient response, managing to stabilize voltages in less time compared to traditional IEEE Type 1 AVR control. The agent’s action is dynamic and reactive: it detects voltage deviations and applies corrections that minimize the time spent outside the operational range [0.95–1.05] p.u. The conventional scheme displays a more damped and slower response, characteristic of passive control systems that do not react proactively to transient events. Although small oscillations or “noise” are observed in the agent’s response, these remain within acceptable margins and do not compromise the overall stability of the system.

This oscillatory behavior can be attributed to the fact that the agent makes decisions in real time based on the continuous reading of the system state, introducing frequent micro-adjustments that enhance overall precision, even if they generate small local fluctuations. In contrast, the traditional scheme maintains a more uniform profile, but at the expense of lower adaptability. This difference highlights one of the main strengths of the proposed approach: its autonomous capacity to adapt to rapid changes in the electrical network, making it a robust and flexible alternative to the challenges of modern operation—particularly in environments with high penetration of renewable generation.

3.5. Detailed Analysis of Performance Metrics and Algorithm Behavior

The results presented in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 reveal several apparent contradictions that require detailed explanation to understand the distinct learning strategies developed by each algorithm. Most notably, the reward per action metric (Figure 4) shows a significant deterioration for Deep Q-Learning (DQL) from approximately −1.0 to −1.8/−2.2, while PSO and GA maintain stable values around −1.0 to −1.1. Conversely, the Normalized Reward (Figure 5) indicates that DQL achieves the highest performance (0.8–0.9), surpassing both PSO and GA (0.6–0.7). This seeming inconsistency reveals fundamentally different optimization strategies learned by each algorithm.

To understand this behavior, it is essential to examine the mathematical relationship between the performance metrics. The total episode reward can be expressed as follows:

$$R_{total}=\sum _{t=1}^T{\gamma }^{t-1}{R}_t+B=\left(\sum _{t=1}^T{\gamma }^{t-1}{R}_t\right)+B$$

(43)

where $R_t$ is the reward per action at time step t, T is the number of actions in the episode, $\gamma =0.9995$ is the discount factor, and $B=+50$ is the bonus for early stabilization. The Normalized Reward is then calculated by dividing this total by the maximum possible reward for the episode length.

The key insight lies in how each algorithm balances these components. Figure 3 shows that DQL converges to approximately 150–200 actions per episode, while PSO and GA require 200–250 actions. DQL’s strategy can be characterized as “fast termination with low-quality actions”: it learns to end episodes quickly by achieving voltage stabilization rapidly, thereby obtaining the +50 bonus more frequently, even though each individual action yields lower rewards.

This behavior can be quantified by examining the trade-off between action efficiency and episode length. For DQL, the deteriorating reward per action (from −1.0 to −1.8) is compensated by shorter episodes and more frequent bonus acquisition. Consider a representative episode in the final training phase:

• DQL: 150 actions × (−1.8 reward/action) + 50 bonus = −270 + 50 = −220 total reward.
• PSO: 200 actions × (−1.0 reward/action) + 50 bonus = −200 + 50 = −150 total reward.

However, the Normalized Reward calculation considers the efficiency relative to episode length. DQL’s ability to terminate episodes early with fewer actions results in a higher normalized performance despite the lower individual action quality.

The cumulative reward analysis (Figure 6) further supports this interpretation. DQL’s learning curve shows a more gradual but sustained improvement, suggesting that its strategy focuses on long-term reward accumulation through consistent early termination rather than optimizing individual action quality. This approach aligns with the principles of temporal difference learning in reinforcement learning, where the agent learns to maximize discounted future rewards rather than immediate rewards [9].

PSO demonstrates a fundamentally different strategy that can be characterized as a “high-efficiency balanced approach.” It maintains consistently high reward per action (around −1.0) while achieving relatively short episodes (200–250 actions). This dual optimization results from PSO’s inherent ability to balance exploration and exploitation through its swarm intelligence mechanism [43]. The dynamic adjustment of inertia weights from 0.9 to 0.4 throughout training enables PSO to initially explore diverse control strategies and subsequently refine the most promising ones.

GA exhibits intermediate behavior, with reward per action values around −1.1 and episode lengths similar to PSO. The evolutionary selection pressure drives GA toward solutions that balance action quality with episode efficiency, but the stochastic nature of mutation and crossover operations introduces more variability in performance compared to PSO’s deterministic parameter updates [5].

The implications of these different strategies are significant for practical implementation. DQL’s approach may be suitable for applications where rapid response is critical, and the system can tolerate lower precision in individual control actions. This could be beneficial in emergency scenarios or during transient disturbances where quick stabilization is prioritized over optimal control precision.

PSO’s balanced strategy makes it most suitable for normal operational conditions where both action quality and response speed are important. Its ability to maintain high efficiency per action while achieving fast convergence suggests superior overall control policy learning, which explains its selection for the validation phase against conventional control.

GA’s intermediate performance with higher variability suggests it may be most appropriate for exploratory phases or in systems where robustness to parameter variations is valued over peak performance. The evolutionary approach’s ability to maintain population diversity could provide advantages in highly uncertain or dynamic environments.

Furthermore, the analysis reveals important considerations for reward function design in power systems applications. The significant impact of the +50 bonus on algorithm behavior demonstrates how the reward structure can inadvertently bias learning toward specific strategies. Future work should consider reward functions that better balance short-term efficiency with long-term action quality to prevent the development of potentially suboptimal policies that exploit reward structure rather than truly optimizing system performance.

The temporal evolution patterns also provide insights into convergence characteristics. DQL’s gradual but consistent improvement suggests good generalization capabilities, while PSO’s rapid early convergence followed by stable performance indicates efficient learning but potentially limited exploration in later phases. GA’s more erratic improvement pattern reflects the inherent randomness in evolutionary processes but also suggests continued exploration throughout training.

These findings highlight the importance of comprehensive metric evaluation when comparing machine learning algorithms for power systems applications. Single metrics can be misleading, and understanding the underlying behavioral patterns is crucial for selecting appropriate algorithms for specific operational requirements and system characteristics.

4. Discussion and Conclusions

Building upon the comparative analysis detailed in the Results section, the findings strongly affirm the potential of neuroevolution approaches [30] combined with reinforcement learning for voltage control in electric power systems. The consistent superiority of PSO in terms of efficiency, stability, and convergence speed—most notably evidenced by its leading performance in the Normalized Reward (Figure 5) and its impressive efficiency in the number of actions required per episode (Figure 3)—highlights the distinct advantages of swarm-based methods for optimizing robust control policies in dynamic environments; while the competitive performance of the Genetic Algorithm and the dependable stability of Deep Q-Learning are recognized, the ultimate choice of algorithm must remain sensitive to specific operational needs and the inherent characteristics of the power system.

Beyond the comparative training metrics, the practical implications of the PSO-based strategy are further confirmed by the experimental comparison against classical AVR controllers, as detailed in Section 3.4. The agent’s demonstrated ability to automatically adjust control set points in response to disturbances—all without requiring human supervision—represents a significant functional advancement over conventional methods. This autonomy is highly relevant in the context of modern power grids, where rapid fluctuations in generation and demand undermine fixed control strategies [10]. The agent’s superior adaptive control not only improves dynamic response but also offers a viable, intelligent alternative for implementing distributed regulation schemes in real-world environments.

Additionally, the experimental comparison between the PSO-based agent and the classical AVR controllers implemented according to IEEE models reinforces previous conclusions about the effectiveness of the proposed approach. The agent’s ability to automatically adjust control set points in response to disturbances, without requiring human supervision, represents a significant advancement over conventional methods. This autonomy is particularly relevant in the context of modern power grids, where rapid fluctuations in generation and demand hinder the use of fixed strategies [10]. The agent’s adaptive control not only improves dynamic response but also offers a viable alternative for implementing intelligent and distributed regulation schemes in real-world power systems.

4.1. Study Limitations

Despite the promising results, this research presents several limitations that must be acknowledged. First, the exclusive use of the IEEE 30-bus test system, while providing a standardized benchmark for comparison with the existing literature [1,5], represents a relatively small transmission network that may not fully capture the complexity and challenges of modern large-scale power systems. Real transmission networks often involve hundreds or thousands of buses with more complex topological configurations, multiple voltage levels, and diverse operational constraints [4].

The simplified modeling approach employed in this study does not account for several critical aspects of real power system operation. Dynamic phenomena such as electromechanical oscillations, frequency variations, and the detailed response characteristics of synchronous machines and their control systems are not explicitly modeled [3]. Furthermore, the study does not consider the stochastic nature of renewable energy generation, which introduces significant operational uncertainty in modern grids with high penetration of photovoltaic and wind generation [11].

The reward function design, while effective for the studied scenarios, may not adequately capture all operational objectives relevant to real power system operators. Important considerations such as equipment wear due to frequent switching operations, coordination with protection systems, and compliance with grid codes are not explicitly incorporated into the optimization framework [8].

The final and most critical challenge lies in the computational cost and scalability of the applied algorithms. Centralized DRL methods, such as Deep Q-Learning (DQL), suffer significantly from the “Curse of Dimensionality.” As the power grid grows in size, the state and action spaces increase exponentially, making it infeasible to learn an accurate Q-value function, which translates into a long training time and low sample efficiency required for control policy convergence [10,19], while DRL controllers are extremely fast in online inference, the applicability of their extensive training process still needs thorough verification in practical large-scale systems [10,18]. Conversely, the evolutionary algorithms (GA and PSO), though avoiding DRL’s loss function instabilities, impose their own computational limitation due to their populational nature. In every training iteration, these methods must evaluate the performance of multiple candidate solutions, requiring a power flow simulation for each, which results in an intensive computational load [29]. This necessary overhead for training affects their ability to achieve rapid convergence in very high-dimensional systems.

The validation phase, although demonstrating superior performance compared to conventional AVR control, was conducted in a simulated environment that may not fully represent the complexities of real-world operation, including measurement noise, communication delays, and equipment failures [7].

4.2. Future Research Directions

The findings of this work open multiple avenues for future research that address both the identified limitations and emerging trends in power systems operation. A promising direction for future research is the optimization not only of the neural network’s weights and biases, but also of its architecture. This would include automatically exploring the number of hidden layers, the number of neurons per layer, and even the most suitable activation functions for the voltage control problem. Techniques such as NeuroEvolution of Augmenting Topologies (NEAT) [26] could be adapted for this purpose, allowing the network structure to evolve alongside its parameters.

4.2.1. Advanced Algorithmic Development

Future work should focus on developing hybrid optimization frameworks that combine the strengths of different algorithmic approaches. The integration of metaheuristic methods with physics-guided neural networks could enhance both convergence speed and solution quality while ensuring compliance with physical constraints [32,34]. Furthermore, combining these methods with other optimization techniques, such as simulated annealing, could further enhance performance—especially during the final fine-tuning phase of control policy adjustment [40].

The development of explainable AI techniques for power systems applications represents a critical research need. As demonstrated in the analysis of biomedical engineering innovations [35], the integration of interpretable machine learning models with domain-specific knowledge can significantly enhance trust and adoption in critical infrastructure applications. Future research should focus on developing programmatic policy learning techniques that can extract human-readable control rules from trained reinforcement learning agents.

4.2.2. Scalability and Distributed Intelligence

Addressing scalability challenges requires exploring federated learning and distributed intelligence approaches. Another line of future work could focus on integrating these algorithms with federated or distributed learning techniques, which would allow control agents to be trained collaboratively across multiple power subsystems without sharing sensitive data [6]. This would be particularly useful for large-scale or interconnected power networks, where coordination between control areas is essential.

The application of graph neural networks (GNNs) that can naturally capture power system topology offers promising potential for scaling to larger networks while maintaining computational efficiency [32]. These architectures can leverage the inherent connectivity patterns of electrical networks to improve learning efficiency and generalization capabilities.

4.2.3. Integration with Modern Grid Technologies

Future research should address the integration of the proposed control methods with emerging grid technologies and operational paradigms. The incorporation of energy storage systems, electric vehicle fleets, and demand response programs into the optimization framework represents a significant extension that would enhance the practical relevance of the approach [41].

The consideration of economic and environmental objectives alongside technical performance metrics would align the research with contemporary power system operation requirements [14]. Multi-objective formulations that simultaneously optimize cost, emissions, and technical performance would provide more comprehensive solutions for real-world applications.

4.2.4. Robustness and Uncertainty Management

The development of robust control policies capable of handling measurement uncertainties, model mismatches, and unexpected disturbances represents a critical research direction. The integration of constrained Markov decision process (CMDP) formulations could ensure that learned policies respect safety constraints even under uncertain conditions [21].

Advanced uncertainty quantification techniques should be incorporated to assess the confidence levels of control decisions and enable risk-aware operation. This is particularly important for systems with high renewable energy penetration, where generation uncertainty significantly impacts optimal control strategies [11].

4.2.5. Interdisciplinary Applications

The methodological framework developed in this study has potential applications beyond traditional power systems. The adaptation of these techniques to smart city infrastructure, industrial process optimization, and autonomous systems represents promising research directions that could leverage the cross-pollination of ideas between domains [31].

4.2.6. Validation and Implementation

Future work should prioritize validation on larger test systems and eventually on real power networks through hardware-in-the-loop testing [31]. The development of standardized benchmarks for machine learning applications in power systems would facilitate comparison between different approaches and accelerate research progress.

Likewise, incorporating explainability mechanisms into the models could help build trust among human operators, facilitating the adoption of these techniques in industrial environments. The integration of human–machine interaction paradigms that allow operators to understand and override AI-based decisions when necessary represents an important consideration for practical deployment.

4.3. Concluding Remarks

These results consolidate the value of integrating evolutionary artificial intelligence into the design of voltage control systems, opening new possibilities for deployment in industrial settings, especially in the presence of renewable energy sources and complex grid structures. The demonstrated superiority of PSO-based approaches, combined with the insights gained from comparative analysis with GA and DQL, provides a solid foundation for future developments in intelligent power system control.

The comprehensive analysis of performance metrics revealed the importance of understanding the underlying behavioral patterns of different algorithms rather than relying solely on aggregate performance indicators. This understanding is crucial for selecting appropriate algorithms for specific operational requirements and system characteristics.

The successful validation against conventional AVR control demonstrates the practical potential of the proposed approach, while the identified limitations provide clear directions for future research. The integration of advanced machine learning techniques with power systems engineering represents a rapidly evolving field with significant potential for improving the efficiency, reliability, and sustainability of electrical grid operation.

In conclusion, while this study validates the effectiveness of neuroevolution for voltage control, opportunities for improvement and adaptation to more complex challenges remain vast, opening a fertile path for future research in the field of artificial intelligence applied to power systems. The convergence of computational intelligence, sustainable energy technologies, and modern grid infrastructure creates unprecedented opportunities for developing innovative solutions to the challenges of 21st-century power systems.