Time-Series Forecasting Patents in Mexico Using Machine Learning and Deep Learning Models
Abstract
1. Introduction
2. Materials and Methods
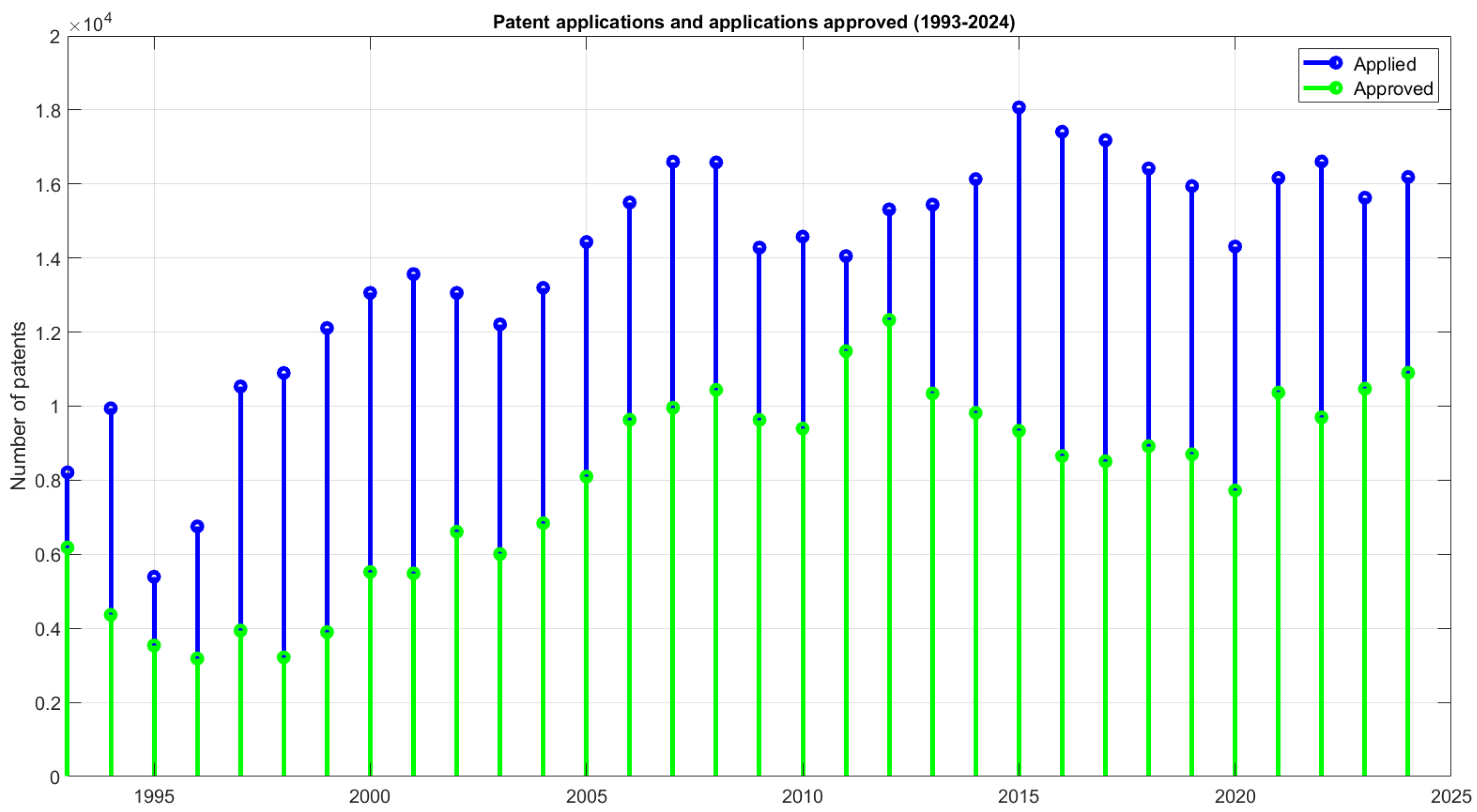
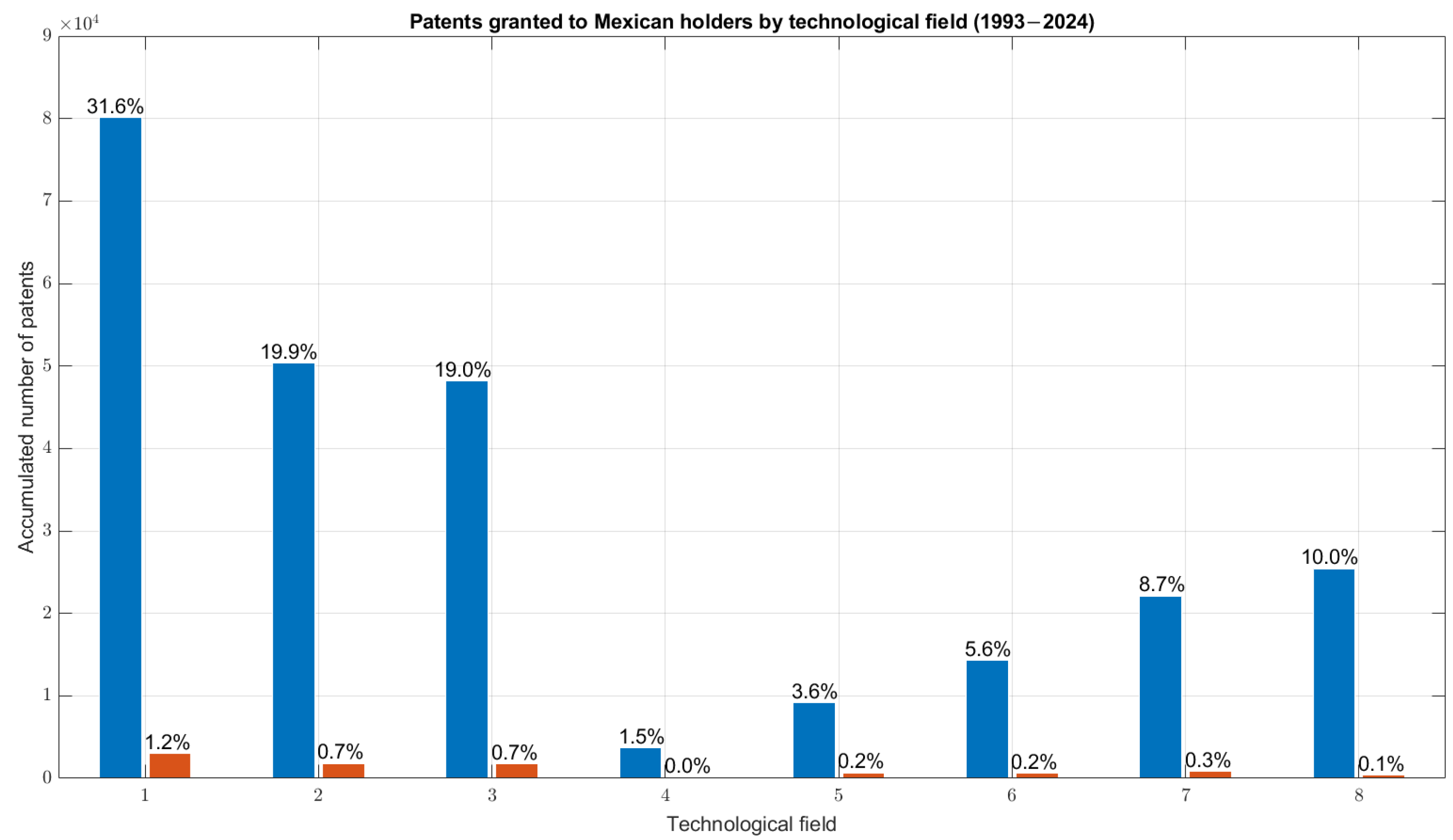
2.1. Exploratory Data Analysis
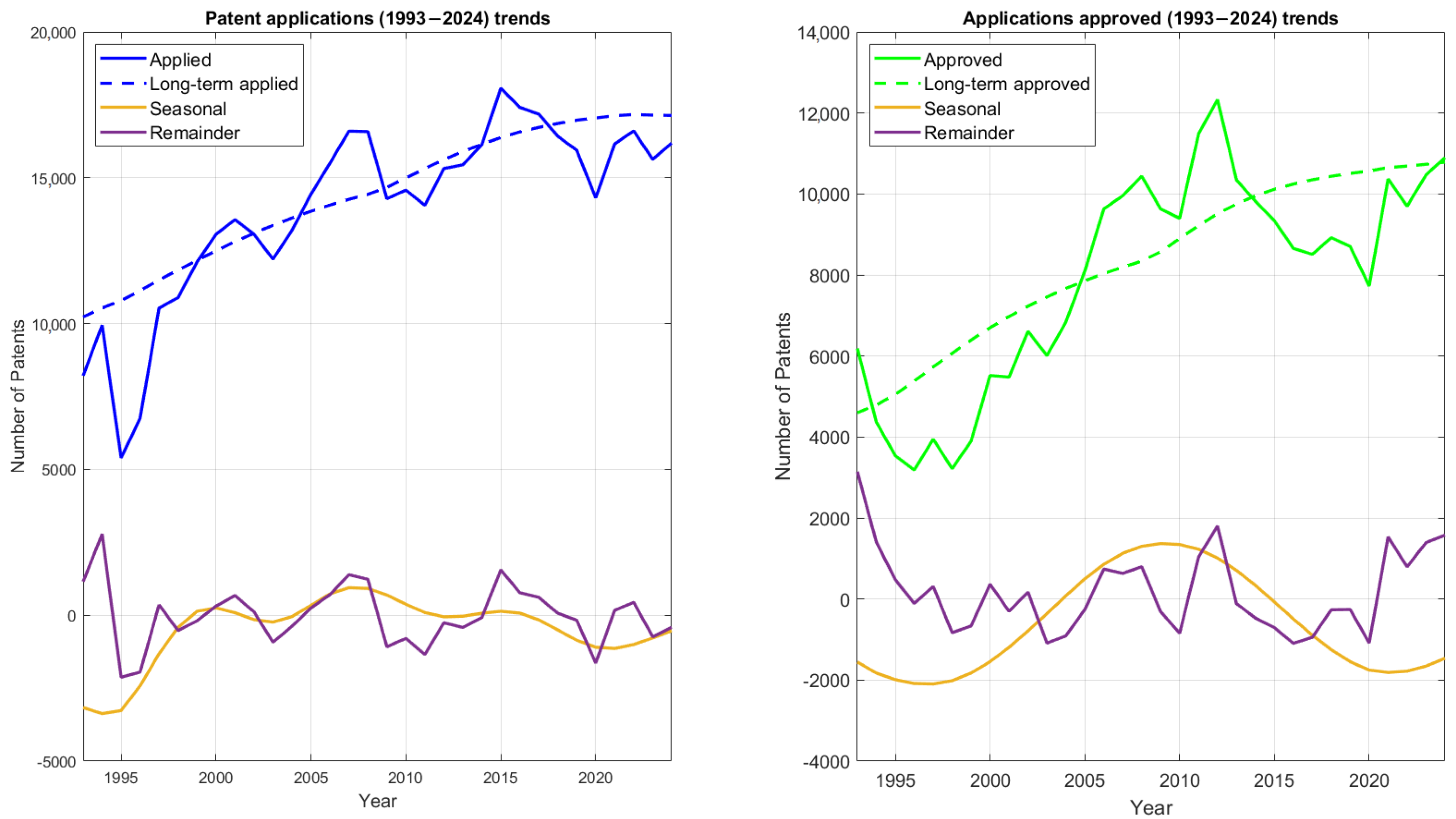
2.2. Decomposition
2.3. Model Selection and Fitting
2.3.1. ARIMA
2.3.2. Regression Tree
2.3.3. Random Forest
2.3.4. Support Vector Machines (SVMs)
2.3.5. Long Short-Term Memory
2.4. Model Prediction and Forecasting
2.5. Model Evaluation
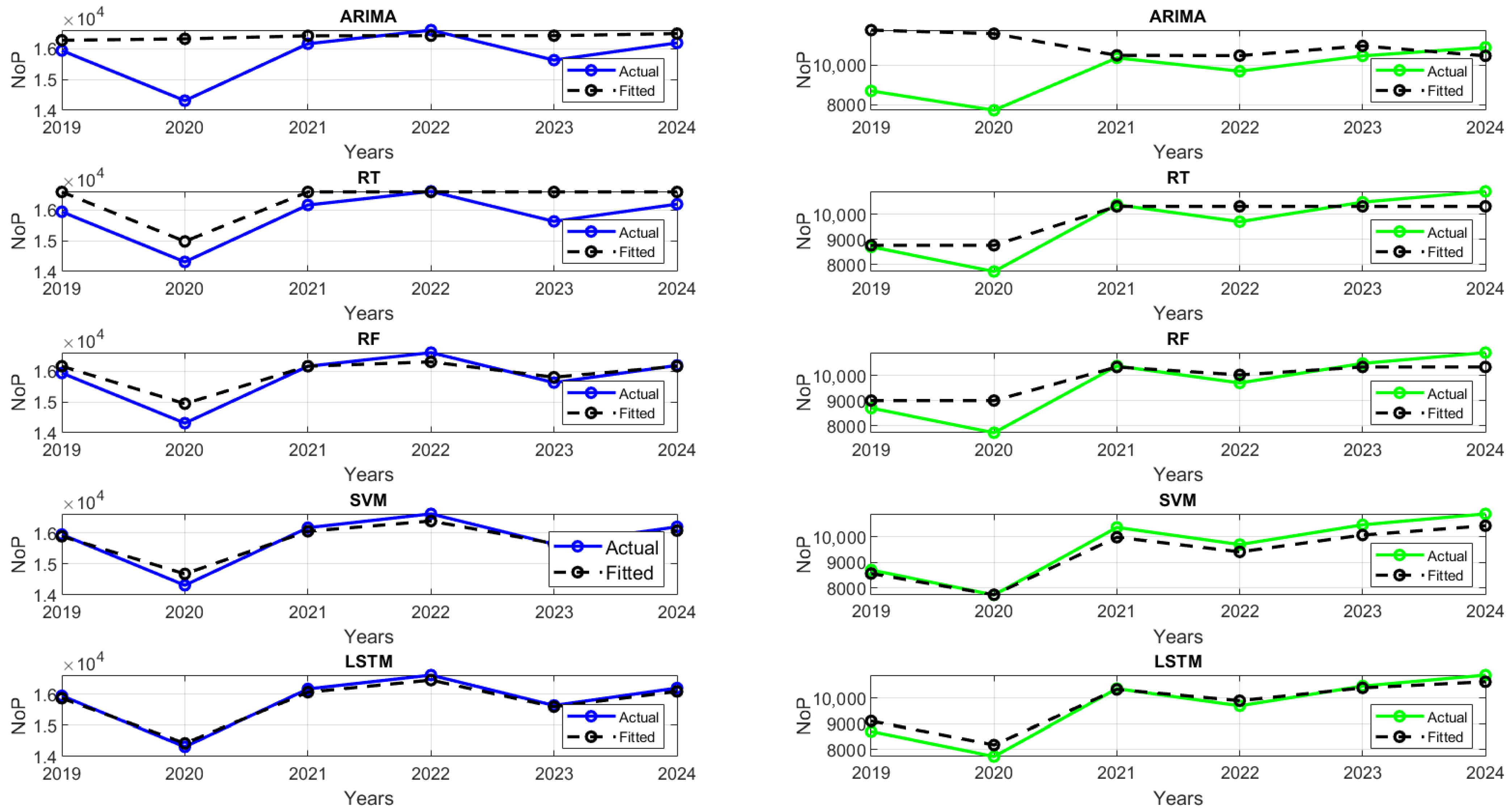
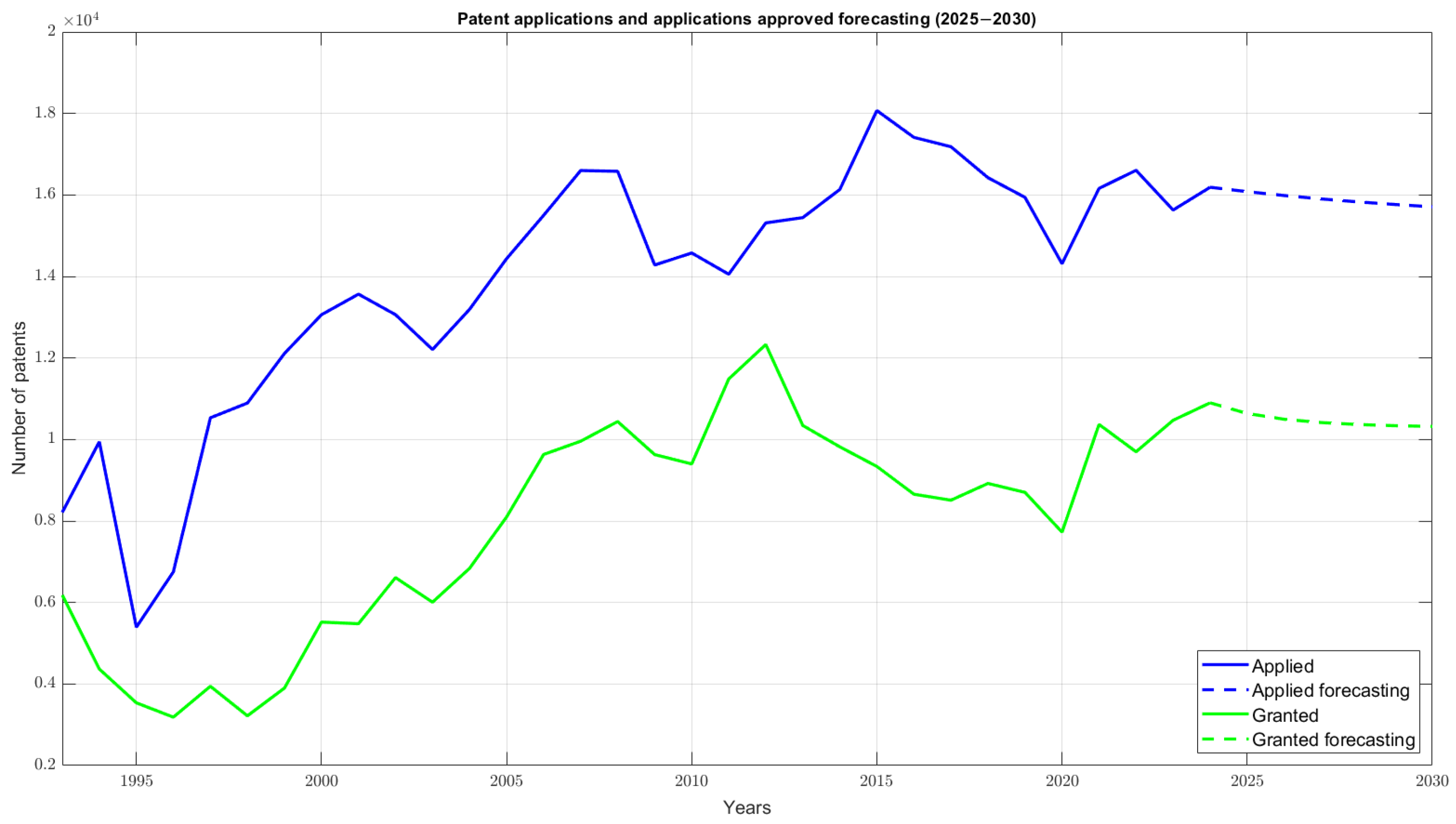
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beltrán-Urvina, L.I.; Acosta-Andino, B.F.; Gallegos-Varela, M.C.; Vallejos-Orbe, H.M. Intellectual Property as a Strategy for Business Development. Laws 2025, 14, 18. [Google Scholar] [CrossRef]
- Ponta, L.; Puliga, G.; Manzini, R. A measure of innovation performance: The Innovation Patent Index. Manag. Decis. 2021, 59, 73–98. [Google Scholar] [CrossRef]
- Gassmann, O.; Bader, M.A.; Thompson, M.J. Patent Management: Protecting Intellectual Property and Innovation; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Pérez Hernández, C.C.; Hernández Calzada, M.A.; Mendoza Moheno, J. Towards a knowledge economy in Mexico: Failures and Challenges. Econ. UNAM 2020, 17, 147–164. [Google Scholar]
- Takwi, F.M. Business management and innovation: A critical analysis of small business success. Am. J. Oper. Manag. Inf. Syst. 2020, 5, 62–73. [Google Scholar] [CrossRef]
- WIPO. Patents. Available online: https://www.wipo.int/en/web/patents/ (accessed on 2 September 2025).
- OECD. OECD Economic Surveys: Mexico 2024. Available online: https://www.oecd.org/en/publications/oecd-economic-surveys-mexico-2024_b8d974db-en.html (accessed on 2 September 2025).
- Díaz-Bautista, A.; González, E.D.; Andrade, S.G. Nearshoring, Comercio Internacional y Desarrollo Económico en México: Las Oportunidades de México en la Reestructuración Económica Mundial; Comunicacion Científica: Ciudad de México, Mexico, 2025. [Google Scholar]
- Guzmán, A.; Gómez Víquez, H.; López Herrera, F. Patents and economic growth: The case of Mexico during NAFTA. Econ. Teor. y Pract. 2018, 177–213. [Google Scholar]
- IMPI. La Contribucion Economica de la Propiedad Intelectual en Mexico. Available online: https://www.gob.mx/cms/uploads/attachment/file/663632/IP-Key-LA_Impact-Study-Mexico-2020_Report.pdf (accessed on 2 September 2025).
- Mejía, C.; Kajikawa, Y. Patent research in academic literature: Landscape and trends with a focus on patent analytics. Front. Res. Metrics Anal. 2025, 9, 1484685. [Google Scholar] [CrossRef]
- Ampornphan, P.; Tongngam, S. Exploring technology influencers from patent data using association rule mining and social network analysis. Information 2020, 11, 333. [Google Scholar] [CrossRef]
- Han, S.; Huang, H.; Huang, X.; Li, Y.; Yu, R.; Zhang, J. Core patent forecasting based on graph neural networks with an application in stock markets. Technol. Anal. Strateg. Manag. 2024, 36, 1680–1694. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, F.; Liu, Y.; Li, Z.; Du, J.; Zhang, L. Forecasting emerging technologies using data augmentation and deep learning. Scientometrics 2020, 123, 1–29. [Google Scholar] [CrossRef]
- Yao, L.; Ni, H. Prediction of patent grant and interpreting the key determinants: An application of interpretable machine learning approach. Scientometrics 2023, 128, 4933–4969. [Google Scholar] [CrossRef]
- Lee, C.; Kwon, O.; Kim, M.; Kwon, D. Early identification of emerging technologies: A machine learning approach using multiple patent indicators. Technol. Forecast. Soc. Change 2018, 127, 291–303. [Google Scholar] [CrossRef]
- Jiang, H.; Fan, S.; Zhang, N.; Zhu, B. Deep learning for predicting patent application outcome: The fusion of text and network embeddings. J. Inf. 2023, 17, 101402. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q. Patent prediction based on long short-term memory recurrent neural network. In Proceedings of the 9th International Conference on Computer Engineering and Networks, Changsha, China, 18–20 October 2021; Springer: Singapore, 2021; pp. 291–299. [Google Scholar]
- Tsai, M.C. A homogenous forecast model based on the hybrid imputation method for forecasting national patent application numbers. Multimed. Tools Appl. 2024, 83, 41137–41169. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Ji, N.; Ding, Q.; Zhang, F.; Long, Y.; Ye, X.; Chen, Y. Enhancing patent text classification with Bi-LSTM technique and alpine skiing optimization for improved diagnostic accuracy. Multimed. Tools Appl. 2025, 84, 9257–9286. [Google Scholar] [CrossRef]
- Miller, J.A.; Aldosari, M.; Saeed, F.; Barna, N.H.; Rana, S.; Arpinar, I.B.; Liu, N. A survey of deep learning and foundation models for time series forecasting. arXiv 2024, arXiv:2401.13912. [Google Scholar] [CrossRef]
- Maragakis, M.; Rouni, M.A.; Mouza, E.; Kanetidis, M.; Argyrakis, P. Tracing technological shifts: Time-series analysis of correlations between patent classes. Eur. Phys. J. Plus 2023, 138, 776. [Google Scholar] [CrossRef]
- Instituto Mexicano de la Propiedad Industrial (IMPI). IMPI in Numbers. Available online: https://docs.google.com/spreadsheets/d/11DJblFCsGsH_PxKFambn3uxF289r7l3w/edit?gid=1930750129#gid=1930750129 (accessed on 2 September 2025).
- Soto-Rubio, M.; Germán-Soto, V.; Gutiérrez Flores, L. Patentes, tamaño de empresa y financiamiento público en México: Análisis regional con modelos de datos de conteo. Rev. Mex. Econ. Finanz. 2023, 18, e569. [Google Scholar] [CrossRef]
- Meisenbacher, S.; Turowski, M.; Phipps, K.; Rätz, M.; Müller, D.; Hagenmeyer, V.; Mikut, R. Review of automated time series forecasting pipelines. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2022, 12, e1475. [Google Scholar] [CrossRef]
- Zhang, X.; Li, R. A novel decomposition and combination technique for forecasting monthly electricity consumption. Front. Energy Res. 2021, 9, 792358. [Google Scholar] [CrossRef]
- Golyandina, N.; Korobeynikov, A.; Zhigljavsky, A. Singular Spectrum Analysis with R; Springer: Berlin/Heidelberg, Germany, 2018; p. 83. [Google Scholar]
- Matamoros, A.A.; Nieto-Reyes, A.; Agostinelli, C. nortsTest: An R Package for Assessing Normality of Stationary Processes. R J. 2025, 16, 135–156. [Google Scholar] [CrossRef]
- Kwon, K.; Jun, S.; Lee, Y.J.; Choi, S.; Lee, C. Logistics technology forecasting framework using patent analysis for technology roadmap. Sustainability 2022, 14, 5430. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Kim, H.; Lee, D.; Yoon, S. A comprehensive survey of deep learning for time series forecasting: Architectural diversity and open challenges. Artif. Intell. Rev. 2025, 58, 1–95. [Google Scholar] [CrossRef]
- Park, M.J.; Yang, H.S. Comparative study of time series analysis algorithms suitable for short-term forecasting in implementing demand response based on AMI. Sensors 2024, 24, 7205. [Google Scholar] [CrossRef]
- Fathi, S.; Srinivasan, R.; Fenner, A.; Fathi, S. Machine learning applications in urban building energy performance forecasting: A systematic review. Renew. Sustain. Energy Rev. 2020, 133, 110287. [Google Scholar] [CrossRef]
- Masini, R.P.; Medeiros, M.C.; Mendes, E.F. Machine learning advances for time series forecasting. J. Econ. Surv. 2023, 37, 76–111. [Google Scholar] [CrossRef]
- Lin, T.Y.; Chou, L.C. A systematic review of artificial intelligence applications and methodological advances in patent analysis. World Pat. Inf. 2025, 82, 102383. [Google Scholar] [CrossRef]
- Wang, M.; Pan, J.; Li, X.; Li, M.; Liu, Z.; Zhao, Q.; Luo, L.; Chen, H.; Chen, S.; Jiang, F.; et al. ARIMA and ARIMA-ERNN models for prediction of pertussis incidence in mainland China from 2004 to 2021. BMC Public Health 2022, 22, 1447. [Google Scholar] [CrossRef]
- Erciyes, K. Algebraic Graph Algorithms; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Hu, J.; Szymczak, S. A review on longitudinal data analysis with random forest. Briefings Bioinform. 2023, 24, bbad002. [Google Scholar] [CrossRef] [PubMed]
- Eom, H.; Choi, S.; Choi, S.O. Marketable value estimation of patents using ensemble learning methodology: Focusing on US patents for the electricity sector. PLoS ONE 2021, 16, e0257086. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.H.; Che, H.C. Intellectual capital forecasting for invention patent through machine learning model. J. Intellect. Cap. 2024, 25, 129–150. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Tong, H. Data Mining: Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2022. [Google Scholar]
- She, Y.; Hong, Y.; Shen, S.; Yang, B.; Zhang, L.; Wang, J. Consistency regularization for few shot multivariate time series forecasting. Sci. Rep. 2025, 15, 14195. [Google Scholar] [CrossRef] [PubMed]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Athiyarath, S.; Paul, M.; Krishnaswamy, S. A comparative study and analysis of time series forecasting techniques. SN Comput. Sci. 2020, 1, 175. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. M5 accuracy competition: Results, findings, and conclusions. Int. J. Forecast. 2022, 38, 1346–1364. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2015, 104, 148–175. [Google Scholar] [CrossRef]
- Sasaki, H.; Sakata, I. Identifying potential technological spin-offs using hierarchical information in international patent classification. Technovation 2021, 100, 102192. [Google Scholar] [CrossRef]
- Gürler, M. The effect of the researchers, research and development expenditure as innovation inputs on patent grants and high-tech exports as innovation outputs in OECD and emerging countries especially in BRIICS. Avrupa Bilim Teknol. Derg. 2021, 32, 1140–1149. [Google Scholar] [CrossRef]
- Romero-Betancur, J.D. Colombian technological panorama: An approach from pa-tent applications in Colombia between 2000 and 2018. Rev. Cient. 2021, 40, 89–101. [Google Scholar] [CrossRef]
- Olvera, S.G. Paradojas de la innovación y la migración calificada de inventores en el contexto neoliberal: Reflexiones en torno al caso mexicano. Migr. y Desarro. 2021, 19, 143–175. [Google Scholar] [CrossRef]
- Mondragón, J.J.P. Propiedad intelectual y comercio internacional. Rev. Fac. Derecho Mex. 2019, 69, 855–878. [Google Scholar] [CrossRef]
- Pérez Hernández, C.C. Determinantes de la capacidad tecnológica en México: Factores meso económicos que impulsan los productos tecno-científicos. Contad. y Adm. 2020, 65, e158. [Google Scholar]
- Zou, T.; Yu, L.; Sun, L.; Du, B.; Wang, D.; Zhuang, F. Event-based dynamic graph representation learning for patent application Trend Prediction. IEEE Trans. Knowl. Data Eng. 2023, 36, 1951–1963. [Google Scholar] [CrossRef]
- Dehghani, A.; Moazam, H.M.Z.H.; Mortazavizadeh, F.; Ranjbar, V.; Mirzaei, M.; Mortezavi, S.; Ng, J.L.; Dehghani, A. Comparative evaluation of LSTM, CNN, and ConvLSTM for hourly short-term streamflow forecasting using deep learning approaches. Ecol. Inform. 2023, 75, 102119. [Google Scholar] [CrossRef]
- Shobayo, O.; Adeyemi-Longe, S.; Popoola, O.; Okoyeigbo, O. A Comparative Analysis of Machine Learning and Deep Learning Techniques for Accurate Market Price Forecasting. Analytics 2025, 4, 5. [Google Scholar] [CrossRef]
- Kamateri, E.; Stamatis, V.; Diamantaras, K.; Salampasis, M. Automated single-label patent classification using ensemble classifiers [Conference paper]. In Proceedings of the 2022 14th International Conference on Machine Learning and Computing, Suzhou, China, 18–21 February 2022; pp. 324–330. [Google Scholar]
- Lahboub, K.; Benali, M. Assessing the predictive power of transformers, ARIMA, and LSTM in forecasting stock prices of Moroccan credit companies. J. Risk Financ. Manag. 2024, 17, 293. [Google Scholar] [CrossRef]
- Castillo-Esparza, M.M.G.C.; Cuevas-Pichardo, L.J.; Montejano-García, S. Innovation in Mexico: Patents, R&D expenditure and human capital. Sci. Prax. 2022, 2, 82–103. [Google Scholar]

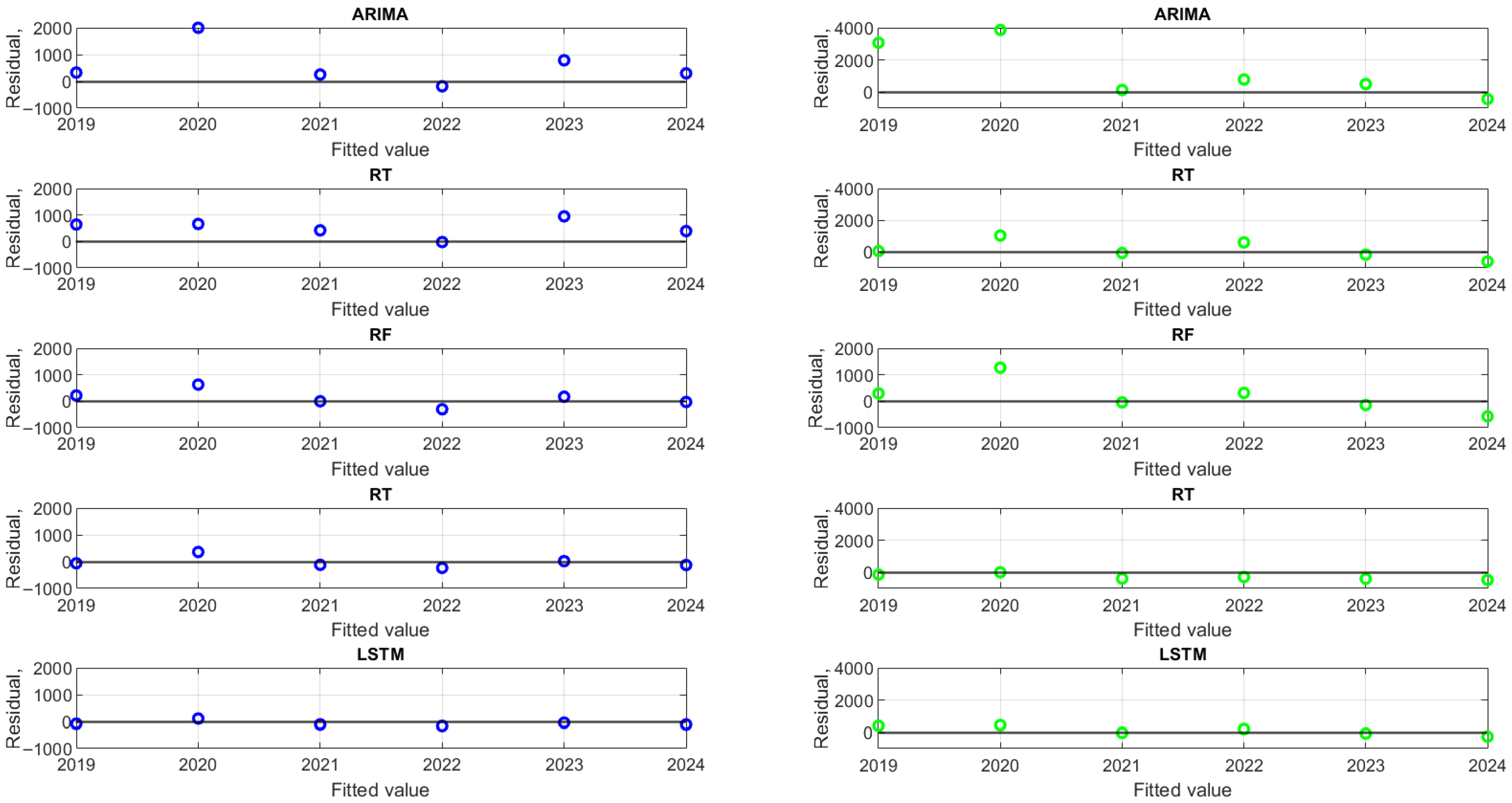
| Models | Optimized Hyperparameters |
|---|---|
| ARIMA | Order of the autoregressive component (p = 3), degree of differentiation (d = 1), and order of the moving average component (q = 3) |
| Regression trees | Minimum leaf size = 4, maximum number of splits = 24, minimum parent size = 10, and split criterion = mse |
| Random forest | Kernel function = linear, kernel scale = 1, epsilon = 0.0115, and solver = SMO |
| Support vector machines | Method = Bag and number of learning cycles = 10 |
| Long short-term memory | One LSTM layer with number of hidden units = 16, dropout layer = 0.2776, and fully connected layer = 1. Training options: solver name = adam, maximum epochs = 686, gradient threshold= 1, initial learn rate = 0.0951, and batch size = 40 |
| Models | Optimized Hyperparameters |
|---|---|
| ARIMA | Order of the autoregressive component (p = 3), degree of differentiation (d = 1), and order of the moving average component (q = 3) |
| Regression trees | Minimum leaf size = 4, maximum number of splits = 24, minimum parent size = 10, and split criterion = mse |
| Random forest | Kernel function=linear, kernel scale = 0.1118, epsilon = 0.0025, and solver = SMO |
| Support vector machines | Method = Bag and number of learning cycles = 12 |
| Long short-term memory | Two LSTM layers with number of hidden units = 87, dropout layer = 0.2776, and fully connected layer = 1. Training options: solver name = adam, maximum epochs = 996, gradient threshold = 1, initial learn rate = 0.0951, and batch size = 400 |
| Models | RMSE | MAPE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Best | Median | SD | Mean | Best | Median | SD | Mean | Best | Median | SD | |
| ARIMA | 803.70 | 18.00 | 589.50 | 781.50 | 0.84 | 0.99 | 0.96 | 0.31 | 5.11 | 0.10 | 3.74 | 5.09 |
| RTs | 1077.60 | 35.88 | 960.42 | 961.31 | 0.58 | 0.99 | 0.90 | 0.80 | 6.60 | 0.25 | 5.70 | 5.66 |
| RF | 1176.15 | 135.83 | 1022.06 | 860.22 | 0.68 | 0.99 | 0.80 | 0.46 | 7.14 | 0.93 | 6.69 | 4.83 |
| SVMs | 894.75 | 1.77 | 664.61 | 746.67 | 0.29 | 0.99 | 0.92 | 1.38 | 5.76 | 0.01 | 4.04 | 5.08 |
| LSTM | 1194.30 | 273.85 | 1120.06 | 817.07 | 0.78 | 0.99 | 0.93 | 0.28 | 9.63 | 1.42 | 6.96 | 7.63 |
| Models | RMSE | MAPE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Best | Median | SD | Mean | Best | Median | SD | Mean | Best | Median | SD | |
| ARIMA | 827.50 | 147.00 | 602.50 | 675.05 | 0.90 | 0.99 | 0.95 | 0.12 | 7.98 | 1.72 | 6.09 | 6.03 |
| RTs | 1065.11 | 97.25 | 996.96 | 900.05 | 0.56 | 0.99 | 0.80 | 0.66 | 10.25 | 1.01 | 11.61 | 7.83 |
| RF | 1366.51 | 67.28 | 1055.98 | 1021.76 | 0.18 | 0.99 | 0.75 | 1.51 | 13.32 | 0.65 | 11.83 | 9.01 |
| SVMs | 1033.06 | 2.60 | 719.15 | 956.37 | 0.81 | 0.99 | 0.91 | 0.22 | 9.77 | 0.03 | 7.74 | 8.53 |
| LSTM | 1730.93 | 62.02 | 1136.45 | 2351.94 | 0.20 | 0.99 | 0.77 | 1.28 | 28.30 | 0.64 | 11.22 | 56.44 |
| Models | RMSE | MAPE | |
|---|---|---|---|
| ARIMA | 910.08 | −0.5 | 4.29 |
| RTs | 593.27 | 0.33 | 3.33 |
| RF | 308.69 | 0.82 | 1.48 |
| SVMs | 190.48 | 0.93 | 0.98 |
| LSTM | 106.91 | 0.97 | 0.63 |
| Models | RMSE | MAPE | |
|---|---|---|---|
| ARIMA | 2058.1 | −1.02 | 17.22 |
| RTs | 552.8 | 0.75 | 4.67 |
| RF | 599.96 | 0.70 | 5.02 |
| SVMs | 322.91 | 0.91 | 2.73 |
| LSTM | 283.20 | 0.93 | 2.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Islas, J.-C.; Bolaños-Rodriguez, E.; Dominguez-Ramirez, O.-A.; Márquez-Grajales, A.; Guadarrama-Atrizco, V.-H.; Pedraza-Amador, E.-M. Time-Series Forecasting Patents in Mexico Using Machine Learning and Deep Learning Models. Inventions 2025, 10, 102. https://doi.org/10.3390/inventions10060102
Gonzalez-Islas J-C, Bolaños-Rodriguez E, Dominguez-Ramirez O-A, Márquez-Grajales A, Guadarrama-Atrizco V-H, Pedraza-Amador E-M. Time-Series Forecasting Patents in Mexico Using Machine Learning and Deep Learning Models. Inventions. 2025; 10(6):102. https://doi.org/10.3390/inventions10060102
Chicago/Turabian StyleGonzalez-Islas, Juan-Carlos, Ernesto Bolaños-Rodriguez, Omar-Arturo Dominguez-Ramirez, Aldo Márquez-Grajales, Víctor-Hugo Guadarrama-Atrizco, and Elba-Mariana Pedraza-Amador. 2025. "Time-Series Forecasting Patents in Mexico Using Machine Learning and Deep Learning Models" Inventions 10, no. 6: 102. https://doi.org/10.3390/inventions10060102
APA StyleGonzalez-Islas, J.-C., Bolaños-Rodriguez, E., Dominguez-Ramirez, O.-A., Márquez-Grajales, A., Guadarrama-Atrizco, V.-H., & Pedraza-Amador, E.-M. (2025). Time-Series Forecasting Patents in Mexico Using Machine Learning and Deep Learning Models. Inventions, 10(6), 102. https://doi.org/10.3390/inventions10060102









