1. Introduction
In recent years, the deterioration of social infrastructure, including bridges, has become a significant issue around the world, with reported incidents of damage and collapse [
1]. Many developed nations constructed a large number of bridges during periods of rapid economic growth, and these structures are now aging. Japan, for instance, intensively built many bridges from the 1950s to the 1970s. As a result, bridge deterioration is progressing, and countermeasures such as maintenance and renewal are required. However, rebuilding bridges involves large-scale work and substantial costs, making it unrealistic. Therefore, the Japanese government has mandated regular inspections every five years. By performing preventive maintenance on damaged areas, the government aims to preserve and continue using existing bridges over the long term [
2]. Currently, for these periodic inspections, inspectors rely on scaffolding or special crane vehicles. However, these methods require significant time and cost, and pose challenges such as ensuring the safety of inspectors working in hazardous locations. To address these issues, the introduction of inspection robots is attracting attention.
In recent years, various bridge inspection robots have been developed, including suction-based robots [
3,
4,
5,
6,
7,
8], flying robots [
9,
10,
11,
12,
13,
14,
15,
16], and wire-driven robots [
17]. Among these, the author focused on wire-driven robots.
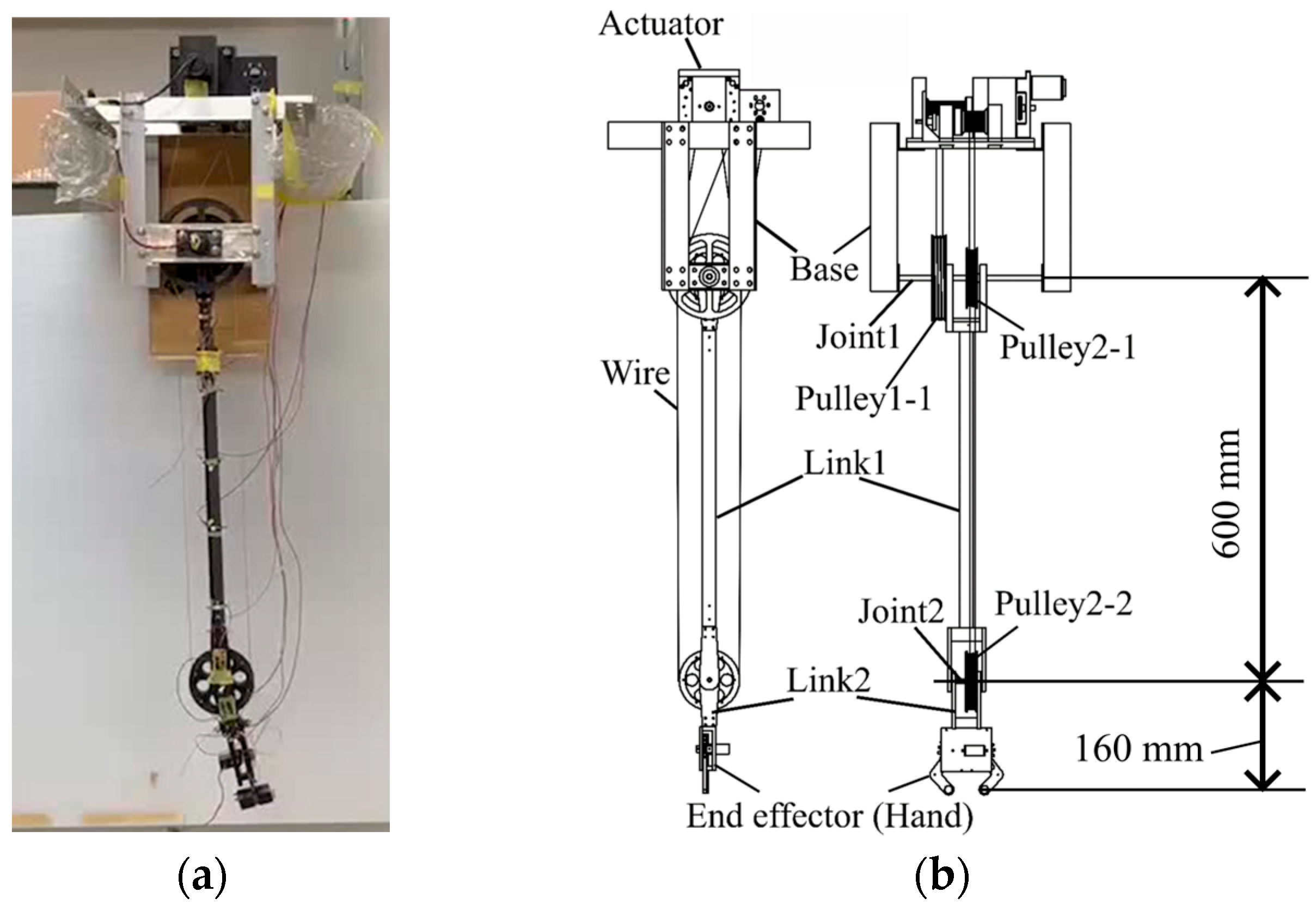
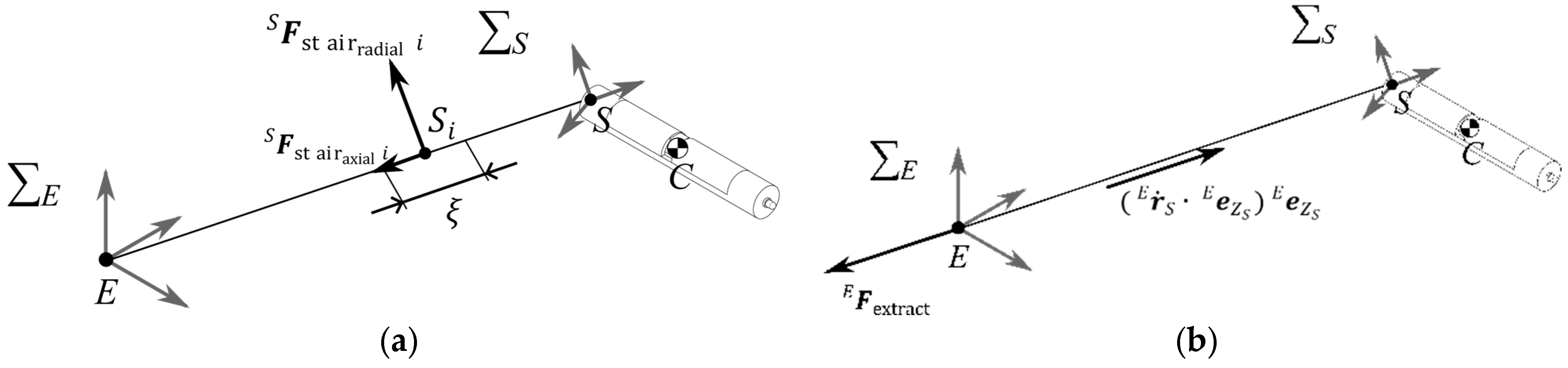
Wire-driven robots operate by attaching a winch to the bridge structure and using wires installed beneath the bridge to move and conduct inspections. Compared to flying or suction-based robots, they have a lower risk of falling and can move stably. Additionally, depending on the suspension method, various inspection techniques can be applied, allowing inspections to be conducted on a wide range of bridges, including concrete and steel bridges, regardless of material. However, using these robots presents wire installation challenges. If people can access under the bridge, manual wire installation is possible. However, when a bridge is located over a road or river, it becomes difficult for workers to set up the wires.
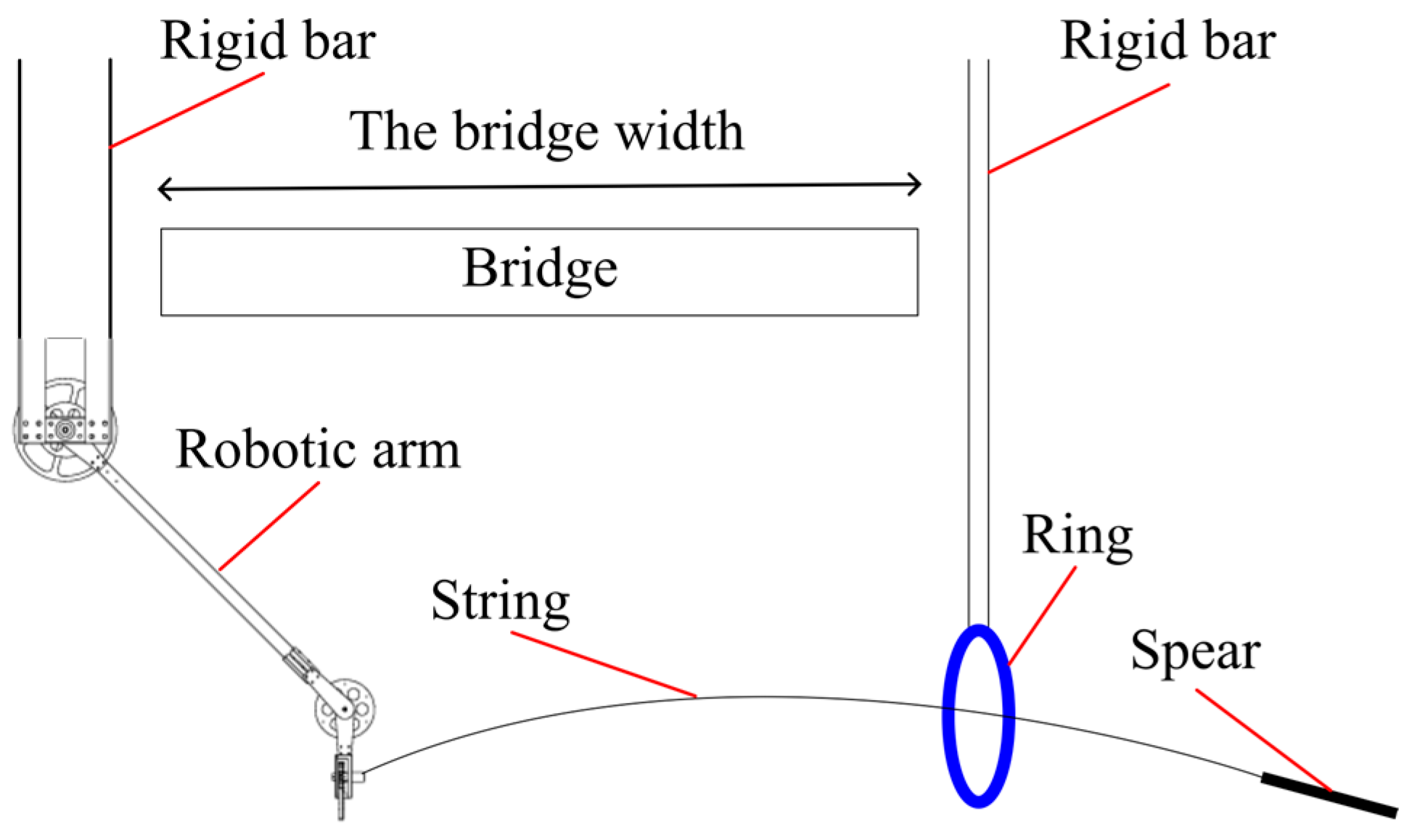
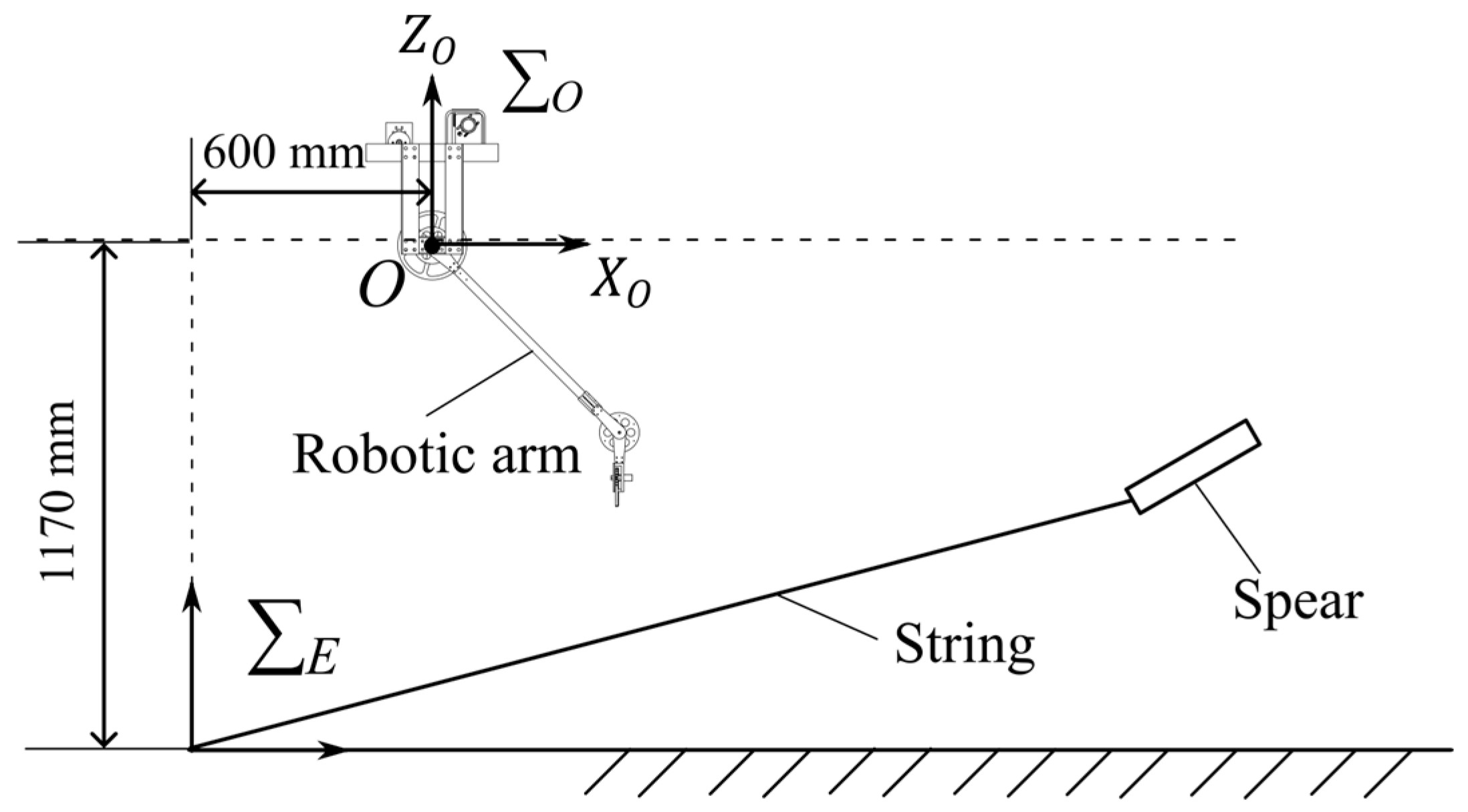
Therefore, this study aims to install wires beneath bridge girders using a wire installation device. With the goal of wire installation, Ishida et al. developed a slingshot system [
18], while Ohara et al. proposed a spring-type shooting device [
19]. However, these devices lack the capability to adjust the shooting velocity arbitrarily. Since the width of actual bridges varies, it is desirable to adjust the shooting velocity according to the distance to the ring in order to suppress excessive shooting force. Accordingly, a spear-throwing approach utilizing a robotic arm is proposed in this study. The use of a robotic arm enables arbitrary adjustment of the shooting velocity, making it possible to adapt to varying bridges. The outline of the wire installation method is shown in
Figure 1, where a robotic arm-type wire installation device, attached to a rigid rod, is lowered from one side of the bridge. Next, a ring is placed on the opposite side beneath the girder. A spear with a string attached is then thrown toward the ring, passing through it. Afterward, the ring is retrieved along with the spear and string. The wire is then attached to the retrieved spear. Finally, by pulling the string from the device side, the wire is installed beneath the girder. For explanatory purposes, the sizes in
Figure 1 do not reflect actual proportions.
A variety of studies have been carried out on the throwing of objects and robotic end effectors. Okada et al. [
20] investigated the manipulation of objects beyond the operational range of a robotic arm by throwing them from an arm mounted on the ground. In this case, the thrown object is not equipped with a thread. Additionally, Arisumi et al. [
21] and Adriano et al. [
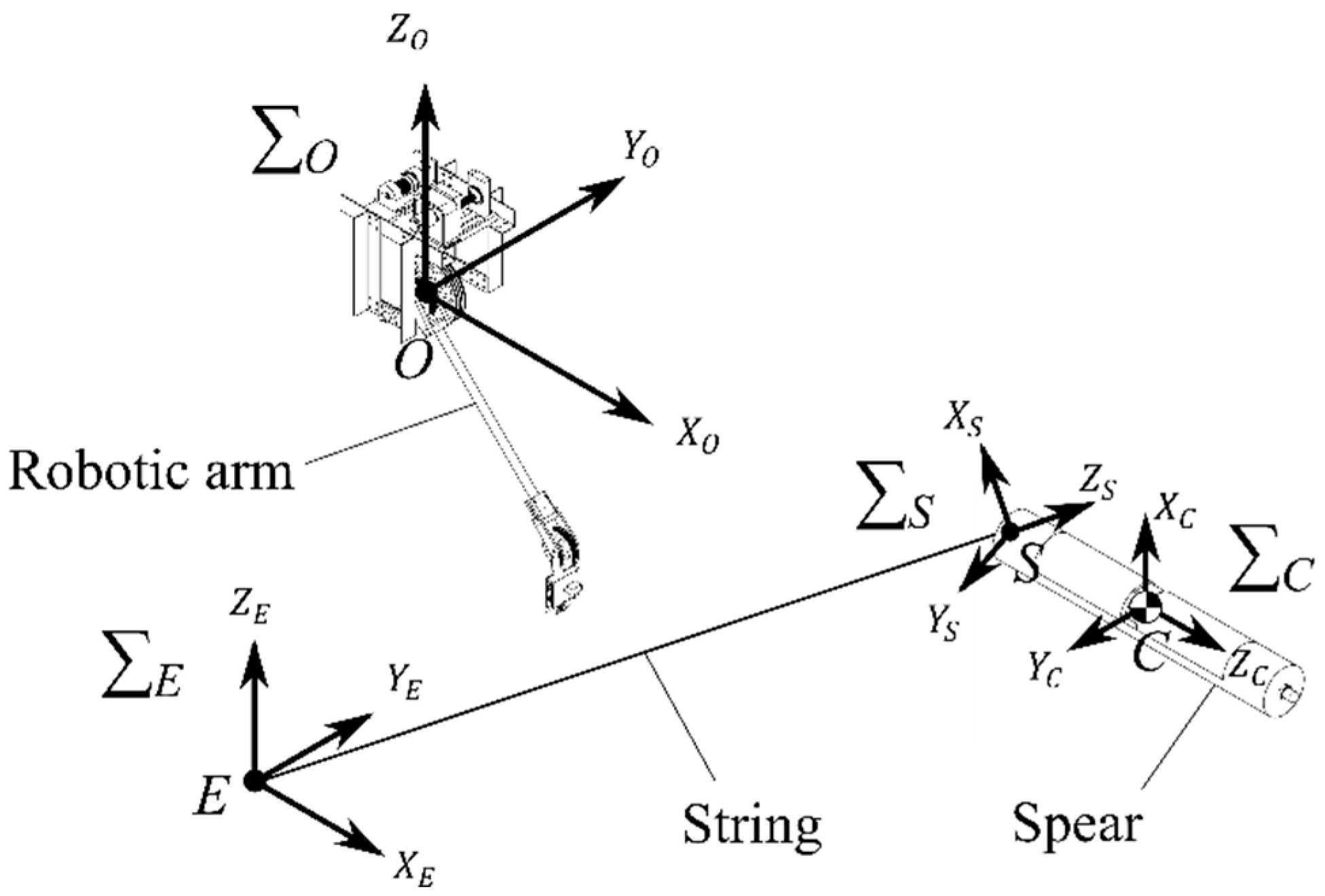
22] proposed a method known as casting manipulation, in which an end effector tethered with a thread is thrown to expand the manipulable workspace. As shown in
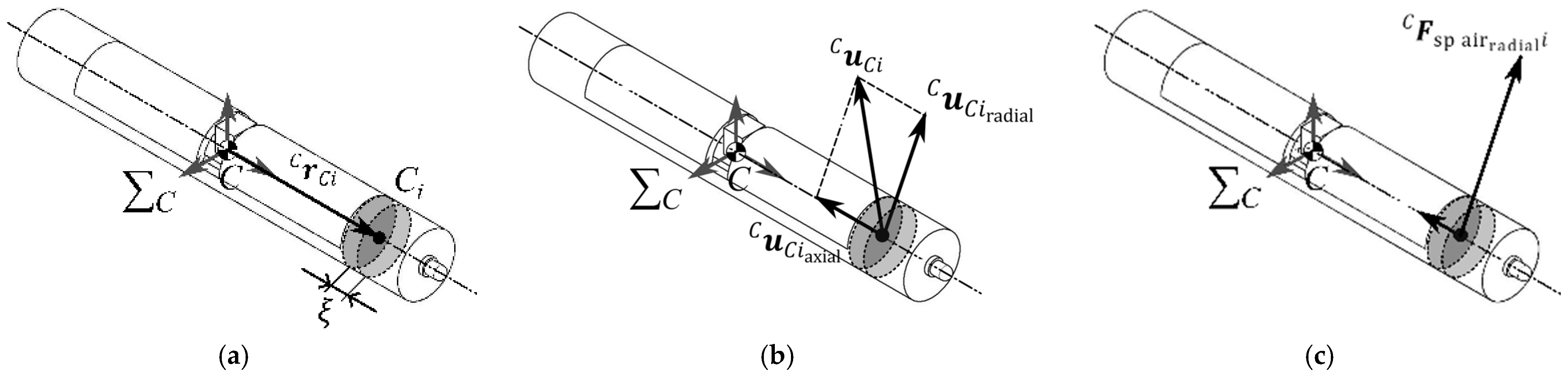
Table 1, while these studies analyze the landing position of the thrown end effector considering the frictional force of the string, they do not take into account the air resistance acting on either the end effector or the string. However, since the object thrown by the wire installation device is lightweight, the effect of air resistance is significant and cannot be neglected. Therefore, in this study, a three-dimensional dynamic model considering air resistance acting on both the thrown spear and the string was constructed. After validating the model under conditions with varying shooting velocities, trajectory analysis was performed. Furthermore, the initial conditions such as the throwing angle and velocity, obtained from the analysis results, are input into the device to throw the spear, and the successful passage of the spear through the ring is experimentally verified.
3. Result
Using the throwing conditions obtained in
Section 2.4 (throwing angle: 50 degrees, throwing angular velocity: 492 degrees/s) as target values, 11 throwing experiments toward the ring were conducted.
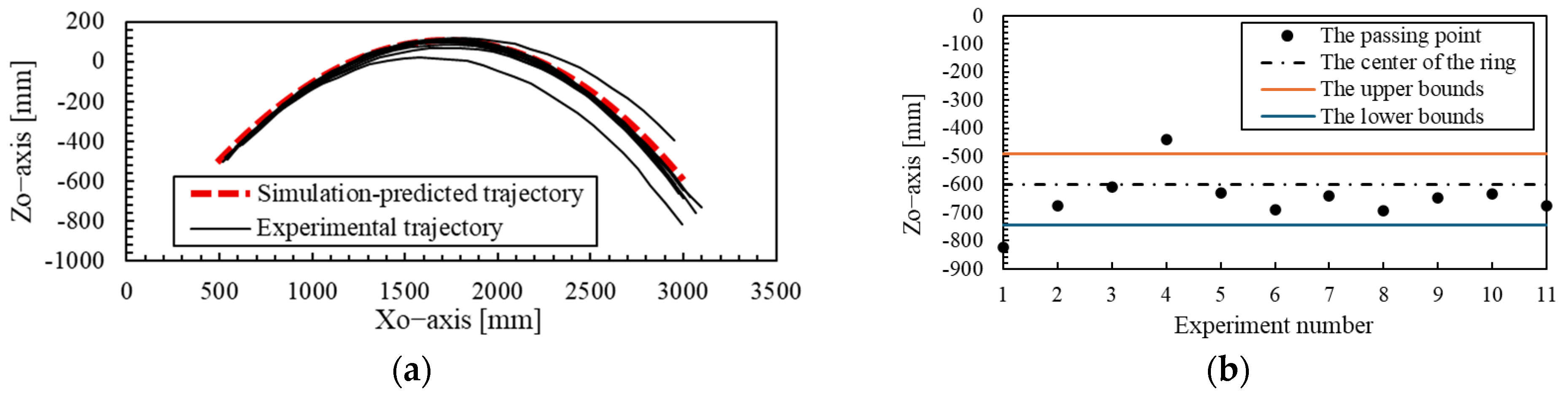
Figure 14a shows the estimated trajectory from the simulation model as well as the actual trajectories of the spear observed in the experiments. The coordinates of the spear’s passing point are also shown in
Figure 14b. The horizontal axis represents the number of experimental trials, and the dashed line indicates the center position of the ring. The initial values measured in each trial are shown in
Table 6 and
Table 7. In addition, the throwing conditions obtained from trajectory estimation, as well as the sample means and 95% confidence intervals of the measured values in the experiment, are also presented in
Table 8. Note that the initial values in the third experiment could not be measured due to a failure.
From
Table 8, it can be seen that the spear was thrown with approximately the target throwing angle and angular velocity.
Figure 14a shows that the experimentally obtained spear trajectory generally agrees with the predicted trajectory from the simulation model. As shown in
Figure 14b, excluding the first and fourth trials, the passing points of the spear fell within the upper and lower bounds resulting from variations in
.
Based on the above, it was confirmed that this trajectory estimation method provides sufficient accuracy and reproducibility, as long as the spear is thrown under conditions close to the target throwing parameters. In particular, when the ring is placed at a horizontal distance of 3 m, it was found that if the ring has an inner diameter of at least 250 mm, nearly all spears can be passed through the ring.
4. Discussion
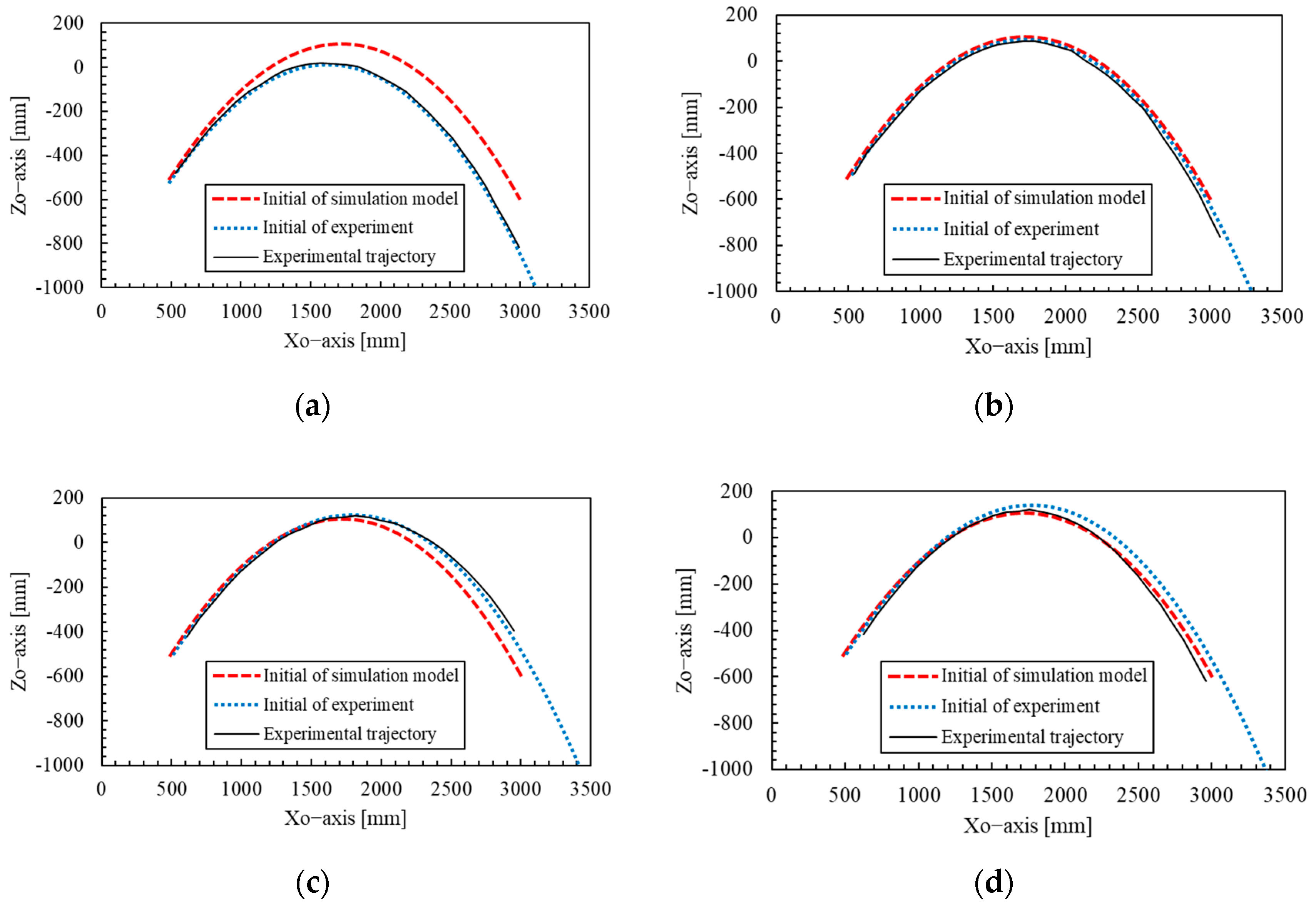
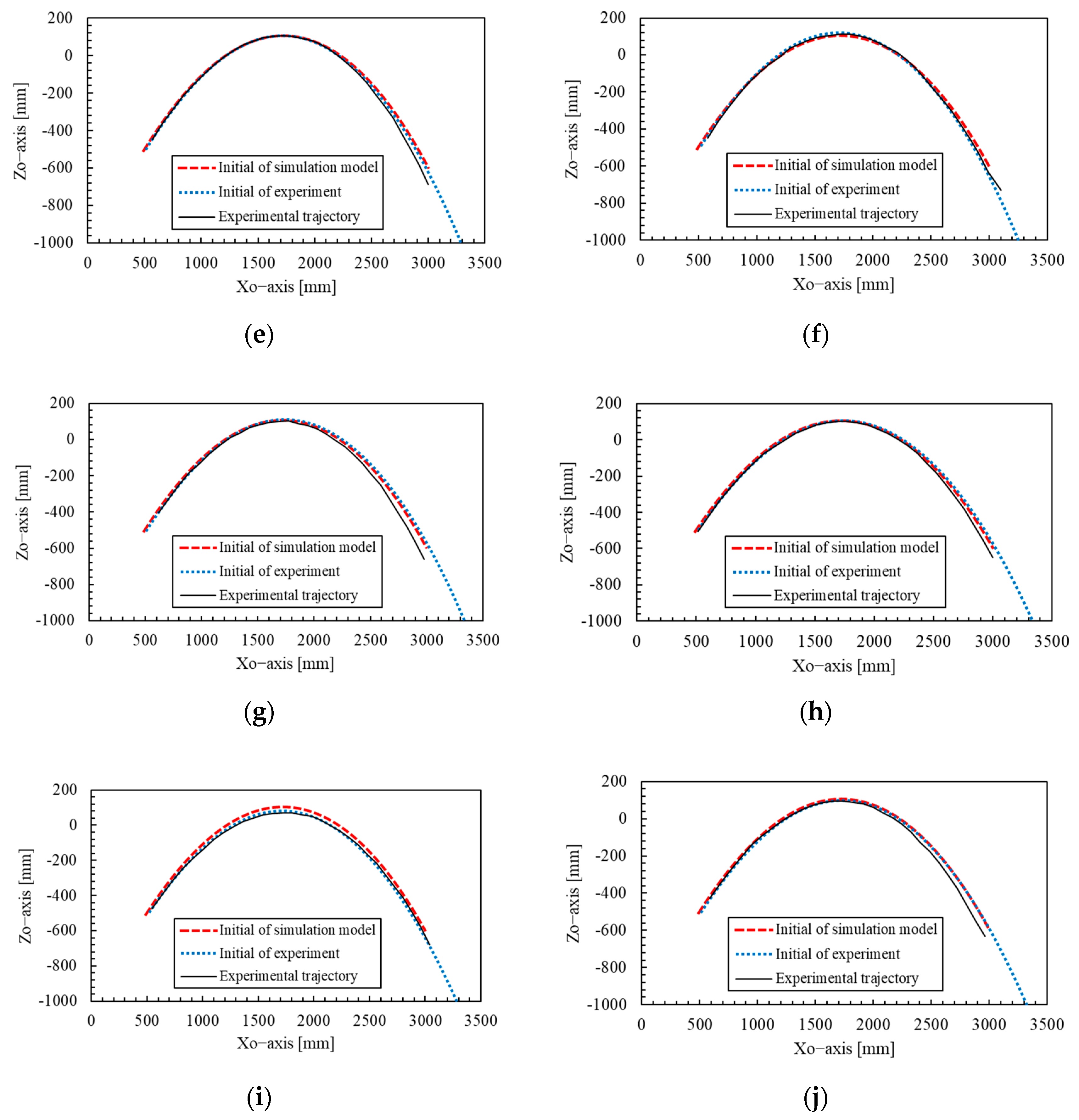
The cause of the deviation of the passing point from the center of the ring is discussed. First, the error in the initial conditions between the simulation model and the experiment is considered as a possible cause. In the simulation model, the initial conditions were set using Equations (28)–(31). However, the initial conditions measured in the experiment are shown in
Table 5 and 6, and discrepancies are observed between the model and the actual measurements. Therefore, two types of flight simulations of the spear were conducted: one using the initial conditions of the simulation model shown in
Table 8, and the other using the initial conditions obtained from each individual experiment in
Table 6 and 7. The results are shown in
Figure 15.
From
Figure 15, it was confirmed that when all experimentally obtained initial conditions were used, the simulated trajectories became closer to the actual experimental trajectories in many trials compared to those predicted using the original model parameters. In particular, for the first and fourth trials, where the passing points deviated from the predicted intervals, it was confirmed that the trajectories better matched the experimental results when the initial values obtained from experiments were applied, as shown in
Figure 15a,c. Therefore, it is suggested that discrepancies in the initial conditions between the simulation model and the actual experiment influence the trajectory and the passing point. To reduce the deviation of the passing point, it is important to realize initial conditions in the actual system that are as close as possible to those used in the trajectory prediction model. While the throwing angle and angular velocity can be made to closely follow the target values by improving the control performance of the robotic arm, the shooting angle, shooting velocity, posture angle, and angular velocity are affected by slippage between the spear and the robotic hand. As a result, it is currently difficult to specify these values in advance. In order to allow all initial values to be predetermined, it is necessary to elucidate the dynamics of the transition from the contact state between the robot hand and the spear to the separation state. On the other hand, the fact that the trajectory error was reduced by adjusting the model’s initial values based on the experimental initial values indicates that the prediction of the spear’s trajectory after release using the present model was valid. Even in this case, discrepancies remained between the experimental and simulated trajectories, which are considered to be due to modeling errors in
obtained from Equation (27) based on
Figure 10.
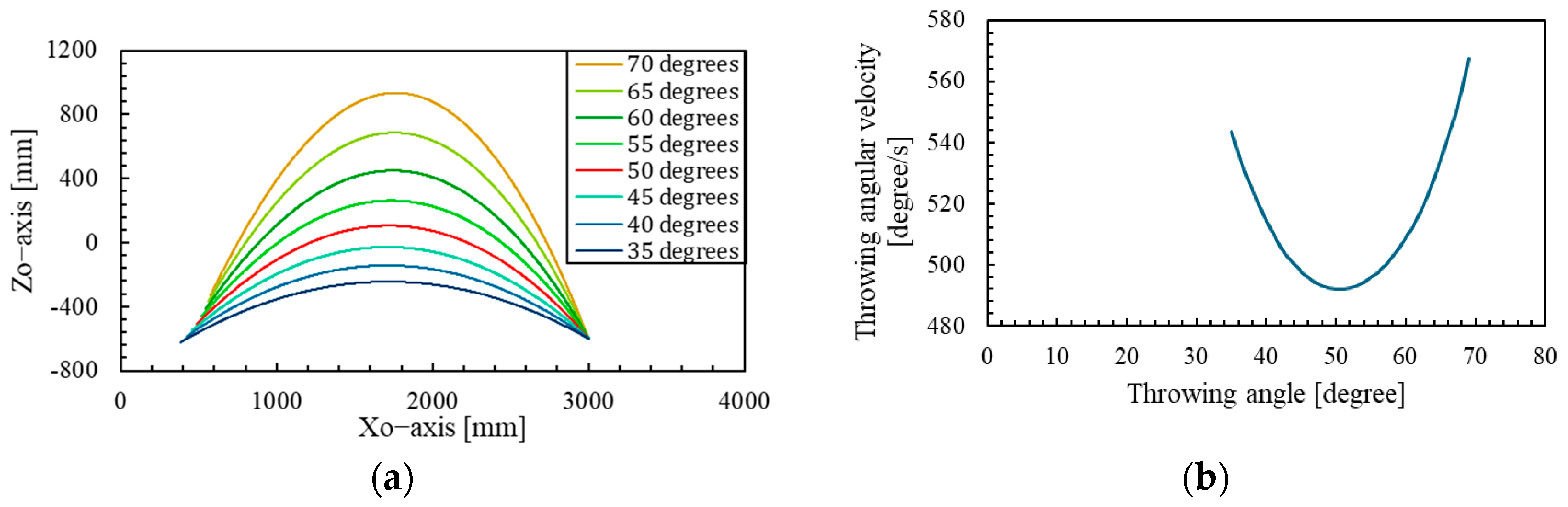
Next, we discuss the practical applicability of the device developed in this study. According to a survey conducted by CTI Engineering Co., Ltd. targeting 421 bridges within Japan, 49.3% of the bridges have a width of 10 m or more, and 41.0% of the bridges have a girder clearance height between 2 and 5 m [
18]. Thus, actual bridges generally have a wider width than the 3-m width assumed in this study, and there are also constraints on the girder clearance height in the vertical direction. In this study, the throwing conditions were selected based on the trajectory corresponding to the minimum throwing angular velocity indicated by the red line in
Figure 13a. However, in practice, it is necessary to consider the girder clearance height of the bridge and examine trajectories from
Figure 13a that ensure the spear does not contact the bridge. Therefore, scenarios where the spear is thrown along a trajectory lower than the red line trajectory can be considered, and in such cases, the throwing angular velocity increases as the trajectory deviates further from the red line, as shown in
Figure 13b. From
Table 3, it can be confirmed that when the target throwing angular velocity reaches the maximum of 600 degrees/s, the measured variations in the throwing angle and angular velocity increase. This is considered to be due to the rapid acceleration and deceleration of the robotic arm, which reduces its ability to follow the commanded values. As discussed above, variations in the initial conditions lead to deviations in the spear’s trajectory and passing position. Therefore, the lower the clearance height under the girder, the more the robotic arm tends to throw at a low trajectory. This low trajectory requires a higher angular velocity, which consequently leads to decreased throwing accuracy. Similarly, as the width of the bridge increases, the distance to the ring becomes larger, requiring a higher angular velocity for the throw and potentially reducing throwing accuracy. In other words, if the robotic arm’s tracking performance to the commanded values can be improved even under conditions of high angular velocity, throwing accuracy is expected to improve. This will be a subject of future work.
We discuss the potential applicability of the device to alternative uses. Considering its capability to throw objects and thereby extend the operational range of a robotic arm, the device may be applicable to picking tasks [
30]. In this task, a robotic hand attached to a thread is thrown toward a distant target object to capture it, and the object is then retrieved by pulling the thread back.
In this study, a model of a spear attached with a string was constructed, and it was verified that the trajectory prediction enables accurate throwing to the target position. Based on these results, it is demonstrated that trajectory analysis of an end effector equipped with a string is feasible even when air resistance cannot be neglected, and that by predicting the trajectory to a distant target object, the end effector can be accurately thrown to the object’s location. Therefore, it is considered feasible to apply this device to picking tasks and similar operations.
5. Conclusions
The author developed a robotic arm-based wire installation device. A simulation model of the spear was created to estimate the required throwing angle and angular velocity based on the position of the ring, and experiments were conducted to throw the spear toward the ring. The following findings were obtained:
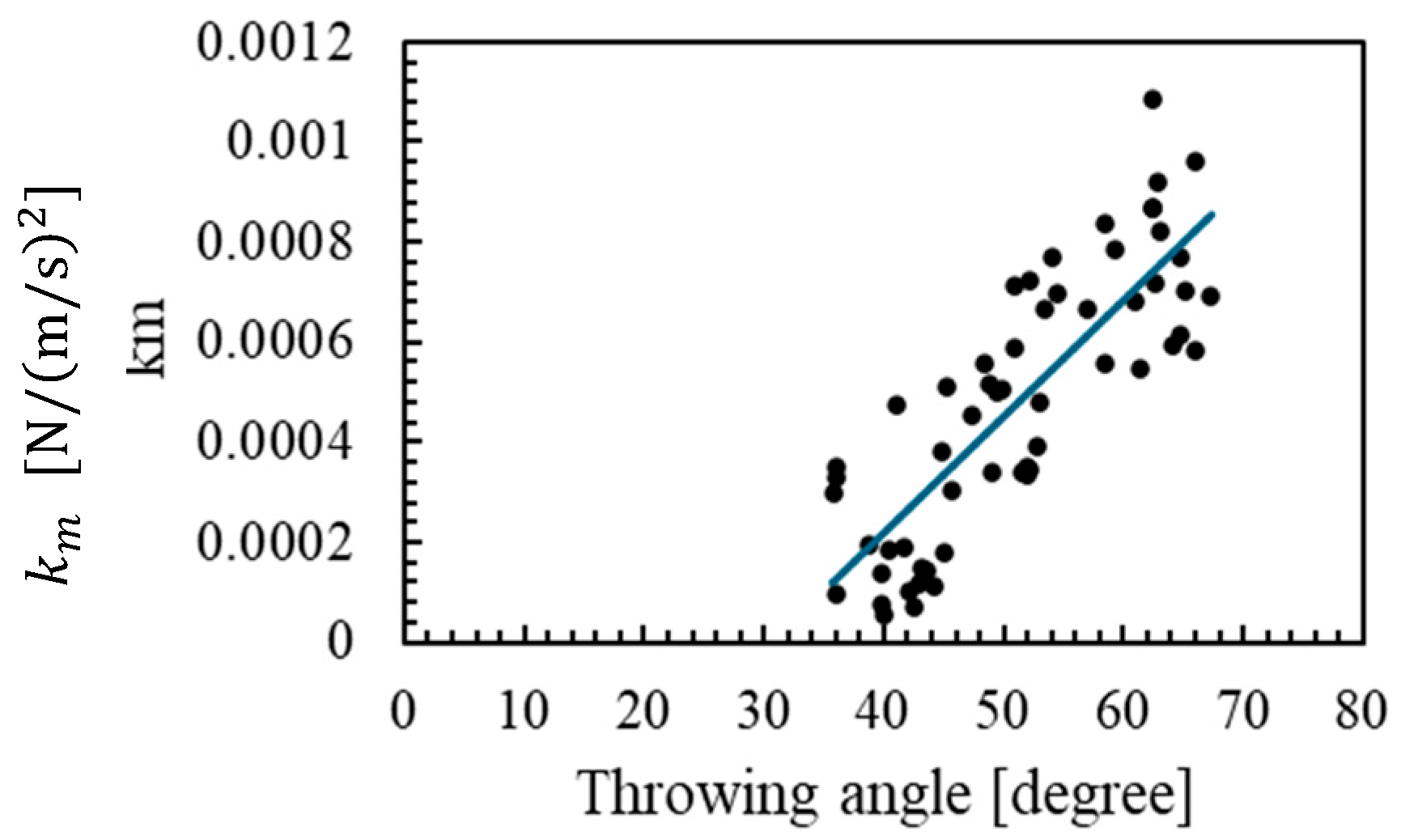
The dependence of the extraction tension coefficient on the throwing angular velocity was not observed within the range of the present experiments, whereas a dependence on the throwing angle was confirmed. In particular, for throwing angles of 35 degrees or more, the extraction tension coefficient exhibited a monotonically increasing trend with respect to the throwing angle, and a linear approximation was found to be applicable. This approximation allowed the estimation error of the extraction tension coefficient to be reduced to a maximum of 0.000340 .
The throwing angle and angular velocity required for the spear to pass through the target ring position were estimated using the simulation model. In the experiment conducted under these conditions, it was confirmed that the spear passed through the ring with high reproducibility, achieving success in 9 out of 11 trials. In particular, it was demonstrated that when the ring with an inner diameter of 250 mm was placed 3 m away, nearly all spears were able to pass through the ring.
Future challenges and prospects are as follows: In this research, experiments were conducted in a windless environment free from external disturbances, thereby establishing the foundation of a model that accounts for the effects of the string and air resistance, and verifying its validity. Since wind is expected to be present in the actual space beneath bridges, future work should apply the model developed in this study to examine the accuracy of trajectory prediction under windy conditions. Furthermore, it was confirmed that discrepancies in initial values between the simulation and the actual system affected errors in the spear’s trajectory and passing points. To reduce such initial value errors, it is necessary to elucidate the dynamic effects such as slipping and friction that occur when the spear is released from the robotic hand, and to improve the tracking performance of the robotic arm to its target values.