Intelligent Damage Prediction During Vehicle Collisions Based on Simulation Datasets
Abstract
1. Introduction
2. Implementation and Reliability Verification of Finite Element Model for Collision Simulation
2.1. Implementation of Collision Simulation Models
2.2. Reliability Verification
3. Establishment of Collision Damage Datasets
3.1. Setting of Collision Scenarios
3.2. Selection of Dataset Points
3.2.1. Damage Points on Energy-Absorbing Components
3.2.2. Damage Points on Cab-Related Components
3.3. Extraction of Collision Damage Datasets
4. Collision Damage Prediction Model
4.1. RF Algorithm
4.2. RF Prediction Model
4.2.1. Correction of Abnormal Data
4.2.2. Data Normalization
4.2.3. Training and Test Sets
4.2.4. Parameter Setting and Construction of RF Model
4.2.5. Analysis of Characteristic Variable Importance
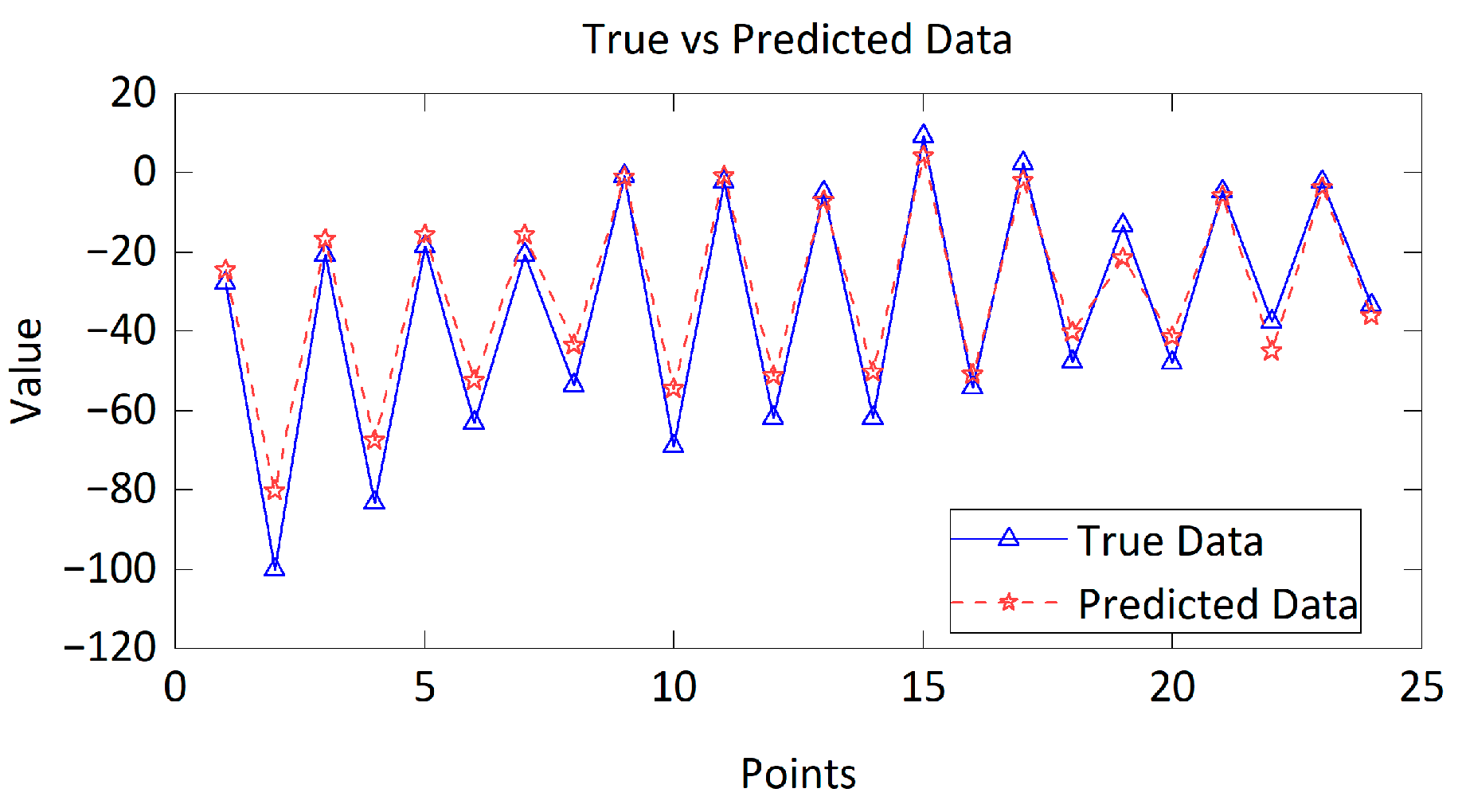
4.3. Analysis of Prediction Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| pre-normalized offset distance | number of trees in random forest | ||
| normalized offset distance | number of features considered for node splitting | ||
| maximum offset distance | minimum node size | ||
| minimum offset distance | number of samples | ||
| initial collision speed | simulated collision damage value at -th point | ||
| normalized collision speed | predicted collision damage value at -th point | ||
| maximum initial collision speed | simulated value at -th point | ||
| minimum initial collision speed | predicted value at -th point |
References
- Wang, Y.; Zhang, F.; Feng, Q.; Kang, K. Strategic analysis of intelligent connected vehicle industry competitiveness: A comprehensive evaluation system integrating rough set theory and projection pursuit. Complex Intell. Syst. 2024, 10, 7033–7038. [Google Scholar] [CrossRef]
- Aleksa, M.; Schaub, A.; Erdelean, I.; Wittmann, S.; Soteropoulos, A.; Fürdös, A. Impact analysis of advanced driver assistance systems (ADAS) regarding road safety—Computing reduction potentials. Eur. Transp. Res. Rev. 2024, 1, 39. [Google Scholar] [CrossRef]
- Ding, S.; Qu, J. Research on multi-tasking smart cars based on autonomous driving systems. Comput. Sci. 2023, 4, 292. [Google Scholar] [CrossRef]
- Wang, Q.; Gan, S.; Chen, W.; Li, Q.; Nie, B. A data-driven, kinematic feature-based, near real-time algorithm for injury severity prediction of vehicle occupants. Accid. Anal. Prev. 2021, 156, 106149. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Wang, B.; Liu, H.; Zhao, K. Model construction and simulation analysis of vehicle collision on steep road section in mountainous area. Green Connected Automated Transportation and Safety. In Proceedings of the 11th International Conference on Green Intelligent Transportation Systems and Safety, Singapore, 17–19 October 2022; pp. 333–348. [Google Scholar]
- Lee, J.; Kim, H.K.; Heo, S.J.; Lee, S.J. Equivalent stiffness modeling method of a battery system for evaluating vehicle rear-end collision performance. Int. J. Automot. Technol. 2023, 24, 1325–1330. [Google Scholar] [CrossRef]
- Sheikh, M.S.; Peng, Y. A collision avoidance model for on-ramp merging of autonomous vehicles. J. Civ. Eng. 2023, 27, 1323–1326. [Google Scholar] [CrossRef]
- Deva Hema, D.; Rajeeth Jaison, T. Efficient collision risk prediction model for autonomous vehicle using novel optimized LSTM based deep learning framework. Int. J. Intell. Transp. Syst. Res. 2024, 22, 352–354. [Google Scholar] [CrossRef]
- Farhat, W.; Ben Rhaiem, O.; Faiedh, H.; Souani, C. A novel cooperative collision avoidance system for vehicular communication based on deep learning. Int. J. Inf. Technol. 2024, 16, 1661–1664. [Google Scholar] [CrossRef]
- Zulherman, D.; Yang, J.; Shimizu, K.; Yokota, Y. Deep Q-learning network-based imbalanced classification for fatality prediction of single-vehicle motorcycle crashes. Int. J. Intell. Transp. Syst. Res. 2025, 23, 175–191. [Google Scholar] [CrossRef]
- Zhu, G.; Chen, J.; Liu, X.; Sun, T.; Lai, X.; Zheng, Y.; Guo, Y.; Bhagat, R. Intelligent lithium plating detection and prediction method for Li-ion batteries based on random forest model. Green Energy Intell. Transp. 2025, 4, 100167. [Google Scholar] [CrossRef]
- Li, Y.L.; Yin, Q.G.; Zhang, Y.; Zhou, H. Deformation prediction model of concrete face rockfill dams based on an improved random forest model. Water Sci. Eng. 2023, 16, 390–398. [Google Scholar] [CrossRef]
- Gaaloul, Y.; Bel Hadj Brahim Kechiche, O.; Oudira, H.; Chouder, A.; Hamouda, M.; Silvestre, S.; Kichou, S. Faults detection and diagnosis of a Large-Scale PV system by analyzing power losses and electric indicators computed using random forest and KNN-Based prediction models. Energies 2025, 18, 2482. [Google Scholar] [CrossRef]
- Grigorie, L.D.; Dima, D.S.; Romanescu, A.E.; Marin, M. Reconstruction of rollover collision using PC Crash 11.1 and 3D scanner. In The 30th SIAR International Congress of Automotive and Transport Engineering: Science and Management of Automotive and Transportation Engineering; Springer Nature: Berlin/Heidelberg, Germany, 2020; pp. 265–272. [Google Scholar]
- Tianbo, W.; Guofu, T.; Tao, W. Simulation analysis of side impact safety of a passenger car. J. Auto Sci. Technol. 2021, 1, 82–86. [Google Scholar]
- Shinagam, R.K.; Maruvada, T.; Janjeti, S.; Talari, R.M.D.; Shinaga, R.V. Development of a machine learning algorithm for efficient localization of damage in a composite structure using random forest technique. IJST-T Civ. Eng. 2024, 48, 4793–4799. [Google Scholar] [CrossRef]
- Assou, S.; Tourbier, Y.; Gstalter, E.; Charrier, M.; Dessombz, O.; Jézéquel, L. A reduced model using random forest: Application on car crash optimization. SeMA J. 2021, 78, 193–195. [Google Scholar] [CrossRef]
- Mejbel, B.G.; Sarow, S.A.; Al-Sharify, M.T.; Al-Haddad, L.A.; Ogaili, A.A.F.; Al-Sharify, Z.T. A data fusion analysis and random forest learning for enhanced control and failure diagnosis in rotating machinery. J. Fail. Anal. Prev. 2024, 24, 2979–2985. [Google Scholar] [CrossRef]
- Puxing, L.; Hong, Z.; Xiaolei, W. Application of safety level approach on deliberation of structural strength criteria of lifeboat in SOLAS. J. Ship Eng. 2018, 40, 6–11. [Google Scholar]
- Rama Krishna, S.; Sathish, J.; Tarun, M.; Sruthi Jones, V.; Raghu Vamsi, S.; Janu Sree, S. A support vector machine-based intelligent system for real-time structural health monitoring of port tower cranes. J. Fail. Anal. Prev. 2024, 24, 2543–2549. [Google Scholar] [CrossRef]
- Kashifi, M.T.; Al-Sghan, I.Y.; Rahman, S.M.; Al-Ahmadi, H.M. Spatiotemporal grid-based crash prediction—Application of a transparent deep hybrid modeling framework. Neural Comput. Appl. 2022, 34, 20655–20678. [Google Scholar] [CrossRef]

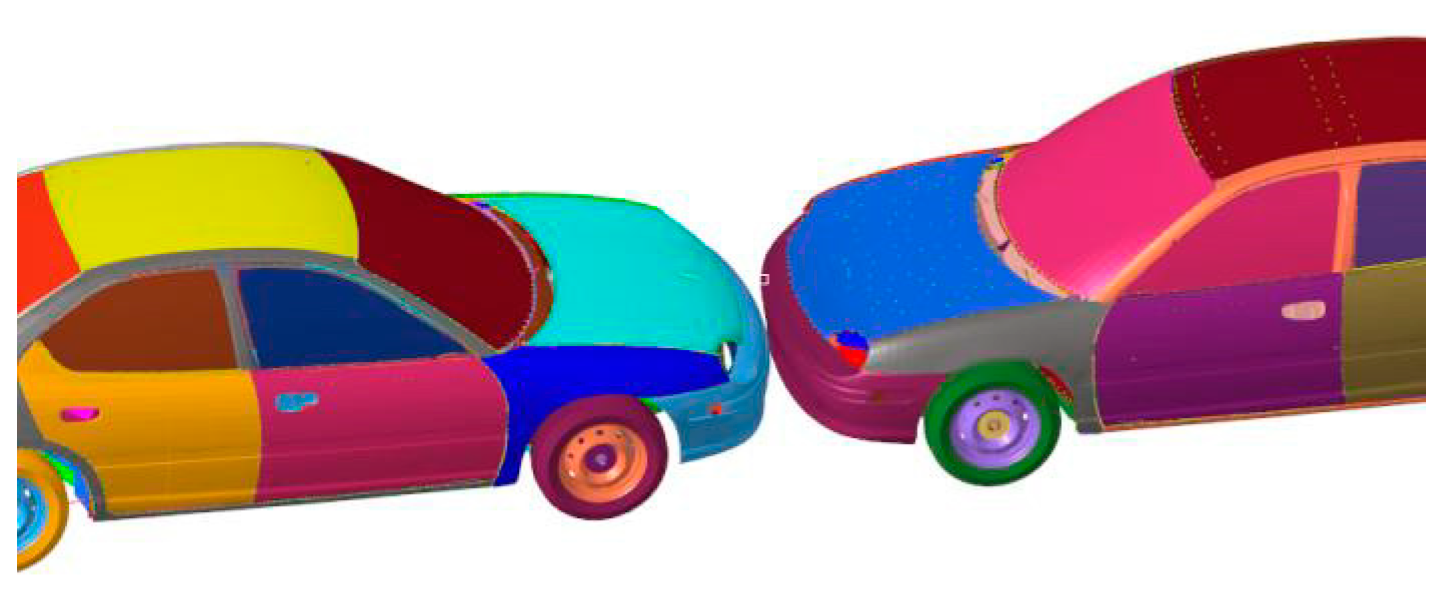






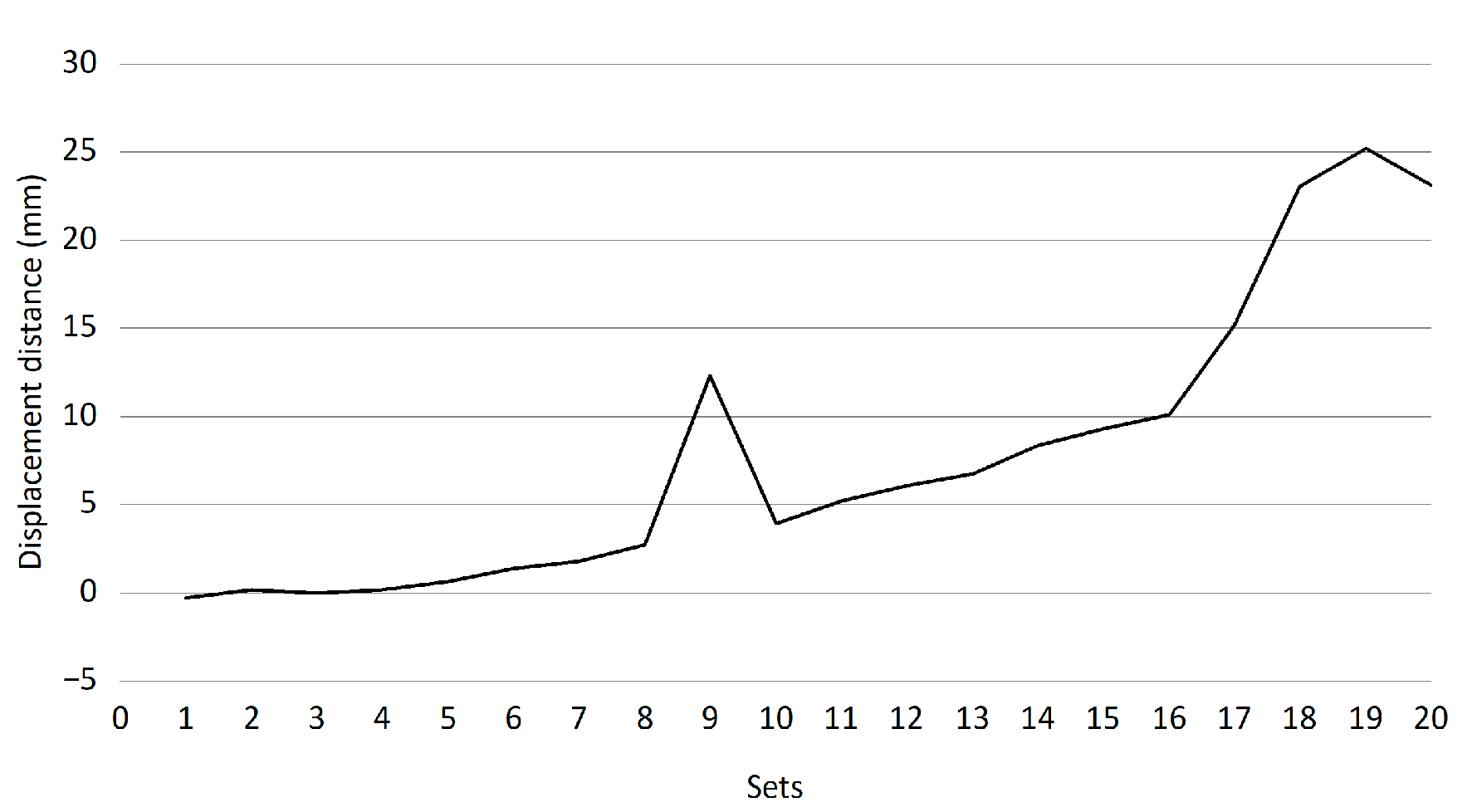
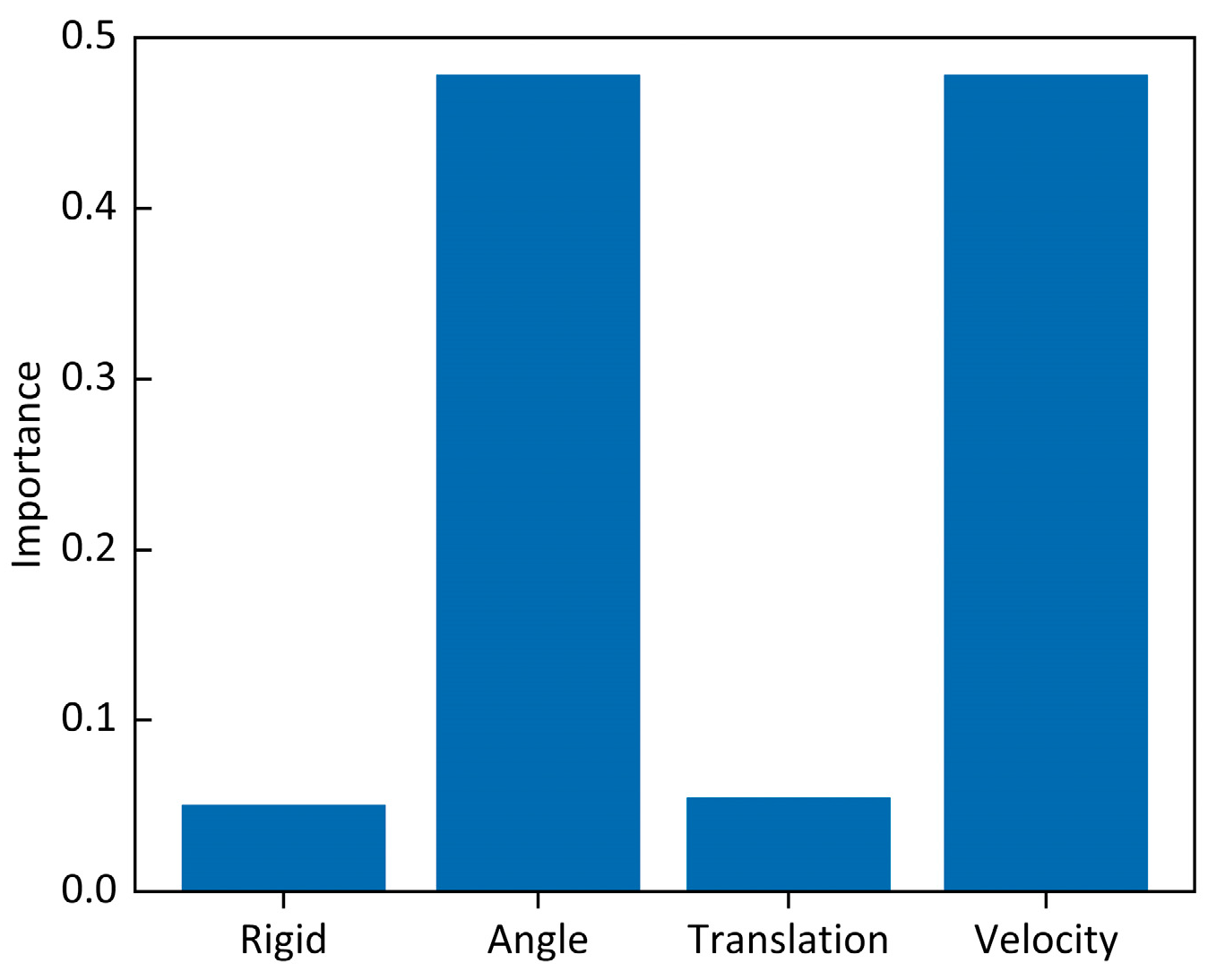
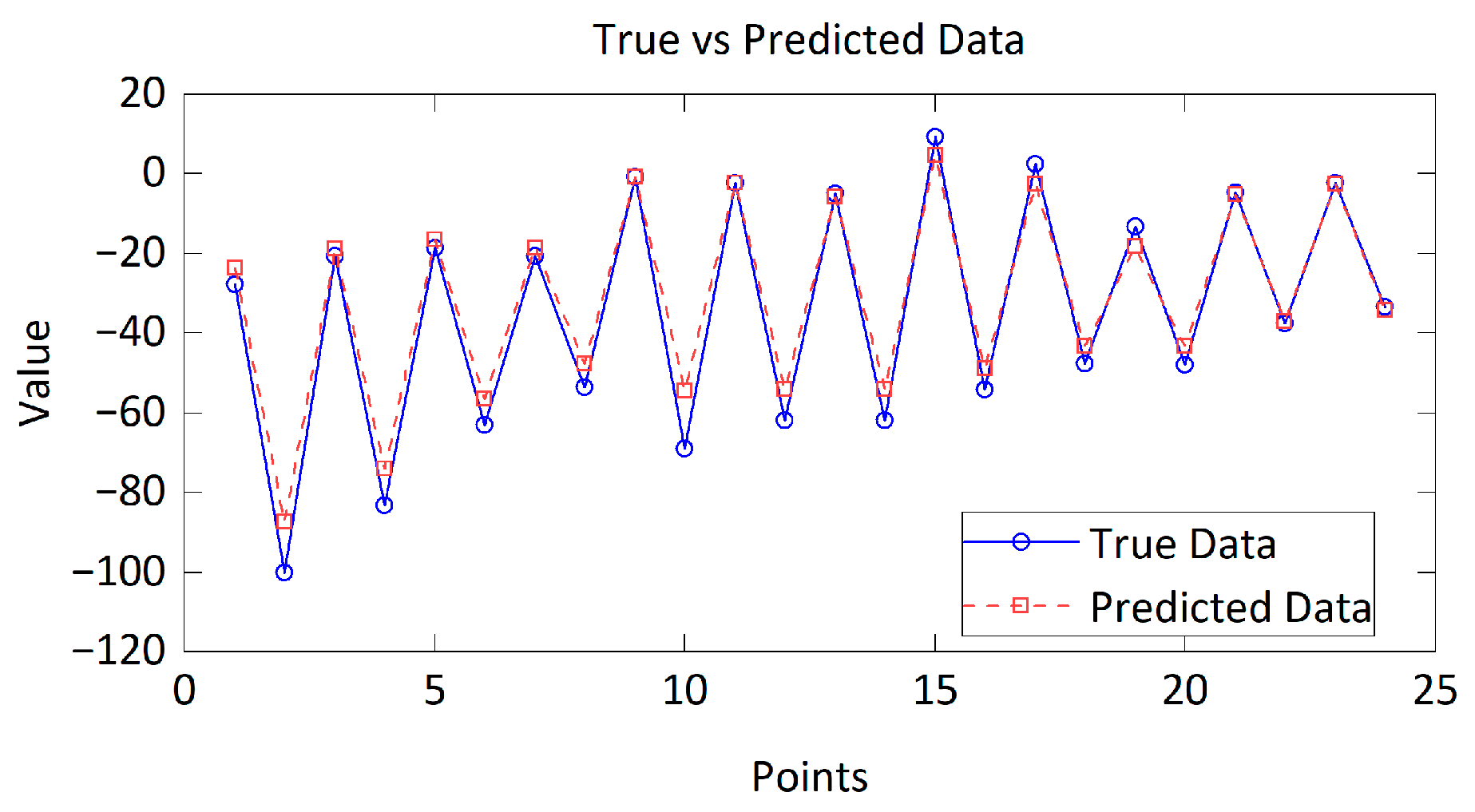
| No. | Collision Scenario |
|---|---|
| 1 | Frontal Collision (100%) of Vehicle with Rigid Wall |
| 2 | Frontal Collision (100%) of Two Vehicles |
| 3 | Frontal Collision (50%) of Two Vehicles |
| 4 | Side Collision of Two Vehicles |
| Collision Object | Collision Angle | Collision Offset (mm) | Collision Speed (km/h) |
|---|---|---|---|
| 1 | 0 | 0 | 2.5 |
| 1 | 0 | 0 | 7.5 |
| 0 | 0 | 0 | 12.5 |
| 0 | 0 | 0 | 17.5 |
| 0 | 0 | −500 | 22.5 |
| 0 | 0 | −500 | 27.5 |
| 0 | 90 | 0 | 32.5 |
| 0 | 90 | 0 | 37.5 |
| … | … | … | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … | 24 |
|---|---|---|---|---|---|---|---|
| −2.14 | 1.02 | −35.82 | −2.02 | 0.49 | −35.52 | … | −50.56 |
| −2.55 | 0.52 | −39.88 | −2.33 | 0.44 | −39.44 | … | −45.4 |
| −22.19 | 6.98 | −62.01 | −18.16 | −0.14 | −51.66 | … | −26.66 |
| −51.33 | 8.11 | −78.68 | −39.87 | −7.28 | −63.87 | … | −27.99 |
| −42.98 | 18.67 | −94.59 | −32.66 | 1.76 | −71.77 | … | −50.86 |
| −79.69 | 31.62 | −127.44 | −46.7 | −6.81 | −75.3 | … | −50.15 |
| −34.88 | −82.347 | −65.496 | −34.03 | −72.563 | −66.232 | … | −122.02 |
| −43.975 | −97.68 | −57.338 | −43.679 | −85.5 | −60.643 | … | −43.325 |
| … | … | … | … | … | … | … | … |
| Point | Simulated Displacement (mm) | Predicted Displacement by RF (mm) | Predicted Displacement by SVMR (mm) |
|---|---|---|---|
| 1 | −27.79 | −23.61 | −24.63 |
| 2 | −100.03 | −87.38 | −80.27 |
| 3 | −20.72 | −18.78 | −16.91 |
| 4 | −83.1 | −73.96 | −67.64 |
| 5 | −18.43 | −16.55 | −15.62 |
| 6 | −63.08 | −56.63 | −52.48 |
| 7 | −20.54 | −18.63 | −15.58 |
| 8 | −53.63 | −47.48 | −43.39 |
| 9 | −0.81 | −0.71 | −1.02 |
| 10 | −69.12 | −54.52 | −54.57 |
| 11 | −2.15 | −2.22 | −0.72 |
| 12 | −62.01 | −54.17 | −51.18 |
| 13 | −4.95 | −5.712 | −7.09 |
| 14 | −61.74 | −54.04 | −50.16 |
| 15 | 9.28 | 4.65 | 4.30 |
| 16 | −54.15 | −48.9 | −50.76 |
| 17 | 2.39 | −2.66 | −2.07 |
| 18 | −47.74 | −43.12 | −40.18 |
| 19 | −13.2 | −18.38 | −21.47 |
| 20 | −47.8 | −43.30 | −41.28 |
| 21 | −4.48 | −5.19 | −5.81 |
| 22 | −37.44 | −37.05 | −45.04 |
| 23 | −2.21 | −2.56 | −3.81 |
| 24 | −33.47 | −34.2 | −36.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Liu, C.; An, X.; Liu, X.; Hao, L. Intelligent Damage Prediction During Vehicle Collisions Based on Simulation Datasets. Inventions 2025, 10, 40. https://doi.org/10.3390/inventions10030040
Liu S, Liu C, An X, Liu X, Hao L. Intelligent Damage Prediction During Vehicle Collisions Based on Simulation Datasets. Inventions. 2025; 10(3):40. https://doi.org/10.3390/inventions10030040
Chicago/Turabian StyleLiu, Sheng, Conghao Liu, Xunan An, Xin Liu, and Liang Hao. 2025. "Intelligent Damage Prediction During Vehicle Collisions Based on Simulation Datasets" Inventions 10, no. 3: 40. https://doi.org/10.3390/inventions10030040
APA StyleLiu, S., Liu, C., An, X., Liu, X., & Hao, L. (2025). Intelligent Damage Prediction During Vehicle Collisions Based on Simulation Datasets. Inventions, 10(3), 40. https://doi.org/10.3390/inventions10030040










