Designing a Femtosecond-Resolution Bunch Length Monitor Using Coherent Transition Radiation Images

Abstract

Ultrashort bunch length measurements are crucial for characterizing electron beams in short-pulse accelerators, including novel accelerators like EuPRAXIA and those used for free-electron lasers (FELs). This work provides an overview of the design process and the current status of a single-shot bunch length monitor prototype based on a broadband spatial imaging system for coherent transition radiation (CTR), which was recently installed at the MAX IV short-pulse facility (SPF). The THz-based imaging system was designed using optical system simulation software for full bunch simulation. CTR images were captured experimentally, followed by image analysis for comparison with reference bunch length data from the transverse deflecting cavity (TDC). This paper presents the conceptualization and design choices for the optical system of the bunch length monitor, the current experimental set-up, the installation details, and preliminary positive observations confirming the potential of this method as a novel approach to bunch length monitoring using spatial CTR images and a scalar technique, with potential for future bunch profile measurements.

1. Introduction

Modern short-pulse accelerators, such as high-gradient plasma-based accelerators, are driving the requirements for bunch length measurements to ultrashort ranges. In recent years, advances in plasma acceleration have positioned it as a potential alternative to overcome the limitations of conventional radiofrequency (RF) acceleration, where the limits of the accelerating field (to the order of few hundred MeV m⁻¹) imposed by the breakdown effect on the materials of the accelerating structures result in long structures and high costs for achieving high energy values. Plasma-based accelerators can produce field gradients of tens of GeV m⁻¹, thus achieving high particle energy values with accelerating distances of only a few centimeters, therefore potentially reducing costs and making it feasible to attain specific applications that require high-energy beams but in facilities with smaller footprints compared with their conventional RF acceleration counterparts.

At present, there are two main types of plasma-based particle accelerators: laser-driven (LWFAs) and beam-driven plasma wakefield accelerators (PWFAs). In the case of strongly nonlinear LWFAs [1,2,3,4], capture, entrapment, and acceleration of the electrons of the surrounding plasma can be achieved, resulting in bunch lengths of a few femtoseconds with sub-fs microstructures, kA peak currents, energy spread of a few percent, and mrad divergence [5], with the need for shot-to-shot diagnostics derived from the instability introduced by the nonlinear nature of the accelerating mechanism. These resulting parameters for LWFAs pose a challenge to the diagnostics available to conventional accelerators, in contrast to PWFAs, which can utilize these diagnostics more often since the properties of the accelerated beams are primarily determined by the RF accelerator used for injection [5].

Developing diagnostics for these ultrashort electron bunches produced in LWFAs (bunches measuring from a few femtoseconds to a few hundred femtoseconds long, with sub-fs resolutions to resolve microstructures) is also beneficial for other machines, like free electron lasers (FELs) and projected future colliders (such as the Compact Linear Collider (CLIC) [6]), since these have requirements in similar ranges [7]. In particular, light sources like FELs operating in the X-ray region require short-pulse electron beams with high brightness, and longitudinal diagnostics are key for their operation and optimization, where it is necessary to determine the high peak current, bunch shape, microstructures, and duration, which directly influence the lasing process [8,9,10].

1.1. Longitudinal Bunch Profile Monitoring

Transverse deflecting structures (TDSs) or cavities (TDCs) are the gold standard solution for studying the longitudinal phase space (LPS) and, consequently, also for longitudinal bunch profile measurements. This method has demonstrated resolutions in the sub-to-few-femtosecond ranges [9,11,12,13]. However, these structures are costly to produce and operate, with considerable physical footprints, whereas LWFA-based facilities aim for smaller footprints and lower costs in comparison. They might be more suitable for conventional RF accelerators as space is less likely to be a limitation, and they can utilize the already available operational infrastructure. They are also destructive to the electron beam, which is acceptable for specific set-ups where they are located at the end of the beamline or when online monitoring is not required. However, this is undesirable for measurements at intermediate accelerating stages, which would benefit from minimally invasive and online methods. Thus, there is a motivation to develop a diagnostic solution that can achieve comparable resolution using alternative methods, in searching for a minimally invasive, single-shot online method for monitoring the bunch length or profile.

Longitudinal diagnostics are broadly divided into (1) direct particle techniques and (2) radiative techniques [7]. TDCs [9,11,12,13] and passive streakers [14] are examples of the former, where the longitudinal bunch profile is typically streaked horizontally onto the transverse plane and then observed as an image on a screen. For the latter technique, the Coulomb field of the electron bunches is used to produce radiation from which the bunch profile can be inferred [15], typically from its coherent components (all wavelengths greater than or equal to the bunch length). In both cases, the techniques have resolution ranges that depend on the physical phenomenon used for the diagnostics, allowing for the choice of one technique over the others to be used in specific machines, depending on the particular requirements and set-up.

The techniques that analyze coherent radiation, such as coherent Cherenkov diffraction radiation [16] and coherent Smith–Purcell radiation [17], are among the noninvasive methods for studying ultrashort bunch lengths using radiative methods. Coherent transition radiation (CTR) [18,19,20] is another option that serves the same purpose but is more widely studied due to its simplicity in implementation. Even though it can be destructive to the beam, it can be set up for minimally invasive operation (for high enough energies), and single-shot studies are possible under certain circumstances that allow temporarily blocking the beam for the bunch length measurement, thereby avoiding the continuous disturbance of downstream users.

The longitudinal charge distribution (or bunch profile) can be reconstructed from the frequency-dependent form factor information in the CTR spectrum using phase retrieval algorithms [18,21,22]. However, this approach has its challenges, since there is a need for a (broadband) calibrated spectrometer, high spectral resolution, and high dynamic range [15].

1.2. Scope

As an alternative approach, a CTR imaging system is proposed, and a conventional image analysis implementation is used to study the bunch length through the spatial image distribution of CTR. For this method, a point-to-point spatial imaging system is set up to focus on the broadband radiation from the transition radiation (TR) source plane. This CTR imaging method operates on the principle that the CTR spatial image distribution depends on the bunch profile, which has been previously demonstrated to work as a longitudinal compression monitor [23,24]. A CTR monitor is considered for its simplicity in implementation as it supports the study of coherent radiation (CXR), and the results have the potential to be applied to the study of CXR variants in the future for less invasive monitoring, such as synchrotron radiation. Although invasiveness is expected from the proposed set-up, the results will serve as the basis for the future development of online, noninvasive diagnostics that follow a similar working principle.

2. Materials and Methods

The MAX IV short-pulse facility (SPF) was considered for the design and deployment of the monitor. The requirements for the bunch length monitor were based on the expected bunch lengths falling in the range of 20–100 fs FWHM at 3 GeV, with a ≤150 pC bunch charge, 10 Hz repetition rate, ≈2 mm mrad normalized emittance, and a ≤0.1% energy spread.

The monitor concept could be tested later with laser-plasma-based accelerators where the requirements overlap, such as EuPRAXIA, where the parameter ranges (as per the conceptual design report) are for electron beams with bunch lengths <30 fs FWHM at 1–5 GeV, with a 5–100 pC bunch charge, 20–100 Hz repetition rate, ≤1 mm mrad normalized emittance, and a ≤1% energy spread [25].

2.1. Generation of Coherent Transition Radiation

Coherent radiation occurs when the particle bunch is emitted coherently due to its size. All wavelengths equal to or larger than the bunch size (in both the transverse and longitudinal dimensions) will be emitted coherently. Specifically, there is a wavelength transition range between the incoherent and coherent spectral regions centered at the wavelength cutoff ${\lambda }_{\mathrm{cutoff}}$ determined by the bunch duration $\tau$, where $\tau \approx {\lambda }_{\mathrm{cutoff}}/c$ [15]. This description applies to several phenomena of radiation production, known as polarization radiation [26], which are used for beam diagnostics, including transition radiation, diffraction radiation, Cherenkov radiation, and Smith–Purcell radiation.

Transition radiation is produced when charged particles pass a boundary between two media with different dielectric properties, such as when the beam hits a conducting or dielectric plate or foil like the one shown in Figure 1a, corresponding with the one used in the proposed set-up. For relativistic particles ($\gamma >>1$), the forward TR is emitted in a narrow cone around the direction of particle propagation, as shown in Figure 1b, and in the direction of reflection, which is used for observing this backward or “reflected” TR through a window perpendicular to the beam path [27,28].

In the set-up, the TR target had a 25 mm diameter and 5 mm-thick aluminum substrate with a 200 nm gold layer finish on the surface. It was moved by an actuator in and out of the beam path at a fixed $45°$ incidence. The TR target’s insertion into the beamline was integrated into the general control system. It could be easily manipulated from the control room to temporarily block the beam for CTR image collection. This method is invasive, as the current thickness results in the electron beam being strongly scattered. However, the set-up could be made less invasive by using thinner targets (in the range of a few tens of $\mathsf{\mu }$m, or several skin depths of the radiation being measured), since these are effectively transparent in the range of a few GeV of energy.

2.2. Study of Coherent Transition Radiation

For retrieving the longitudinal bunch profile and the bunch length from coherent transition radiation, two approaches are discussed in this paper. The spectral techniques are briefly described first, focusing on the study of the power spectrum of the radiation. However, the proposed method falls under the second approach of scalar techniques, as it is based on the analysis of an integral quantity, such as the intensity in a broadband image.

2.2.1. Spectral Techniques

When assuming full transverse coherence, meaning that the transverse RMS size ${\sigma }_r<<\gamma \lambda /2\pi$ [29], the power spectrum of the CTR for an individual bunch is given by [30]

$$S_{\mathrm{CTR}}(\rho \left(z\right),\omega )=S_p\left(\omega \right)N^2{F}_z(\rho \left(z\right),\omega )$$

(1)

where $\rho \left(z\right)$ is the normalized charge distribution of the electron bunch or longitudinal bunch profile, $\omega$ is the angular frequency, $S_p\left(\omega \right)$ is the single-particle TR power spectrum, N is the number of particles in the bunch, and $F_z(\rho \left(z\right),\omega )$ is the longitudinal form factor, defined as

$$F_z(\rho \left(z\right),\omega )={\left|{\int }_{-\infty }^{\infty }\rho \left(z\right)e^{-i{\displaystyle \frac{\omega }{c}}z}dz\right|}^2.$$

(2)

The longitudinal particle distribution $\rho \left(z\right)$ can be reconstructed from the spectral distribution of the CTR by using iterative phase retrieval algorithms, although the solutions are nonunique [29]. In practice, however, a spectrometer has a limited resolution and bandwidth, and there is a need for interpolation and extrapolation on the measured spectra to attempt reconstruction. There have been demonstrations for bunches hundreds of femtoseconds in length (∼600 fs) [31] down to microstructures tens of ficoseconds long [18] or a few ficoseconds long (3–60 fs) [29], as well as sub-ficosecond resolution microstructures [15].

2.2.2. Scalar Techniques

The angular distribution of the CTR carries information about the bunch length. However, collecting the angular distribution (by placing the detector in the focal plane of a focusing element) will not only capture rays from the source plane but also any from upstream sources sharing the same angular properties, which can make the result unsuitable for diagnostic purposes. The approach used in this work has been proposed as an alternative, which uses the spatial distribution instead and also carries the dependence on the longitudinal bunch profile [23,24].

The method involves implementing an imaging system to focus on the source plane of the TR (since no other radiation sources are located in this plane) and placing a detector on the image plane. With this approach, synchrotron radiation from the bends and possible diffraction radiation from limiting apertures on the beamline become only background radiation, as they typically originate from outside the TR source plane and are thus defocused and flattened in the image’s background, resulting in a better signal-to-noise ratio for capturing the TR.

The image distribution for an electron bunch $I_{\mathrm{bunch}}^i$ for a specific bandwidth is given by the image distribution for a single electron $I_e^i$ multiplied by the longitudinal form factor $F_z$ and integrated over said bandwidth $\Delta \omega$ [23]:

$${\displaystyle \frac{d{I}_{\mathrm{bunch}}^i}{dr}}\approx N_e^2{\int }_{\Delta \omega }{\displaystyle \frac{d^2{I}_e^i}{d\omega dr}}{F}_z(\rho \left(z\right),\omega )d\omega$$

(3)

where $N_e$ is the number of electrons in the bunch. In practice, however, the resulting images will also be modulated by the added transmittance $T\left(\omega \right)$ of the optical elements (vacuum viewport, mirrors, lenses, etc.) and an atmosphere of propagation (i.e., air absorption). They are also modulated by the detector response $D\left(\omega \right)$. Both modulations should be taken into account for designs, calculations, and measurements [32], giving

$${\displaystyle \frac{d{I}_{\mathrm{bunch}}^i}{dr}}\approx N_e^2{\int }_{\Delta \omega }{\displaystyle \frac{d^2{I}_e^i}{d\omega dr}}{F}_z(\rho \left(z\right),\omega )D\left(\omega \right)T\left(\omega \right)d\omega .$$

(4)

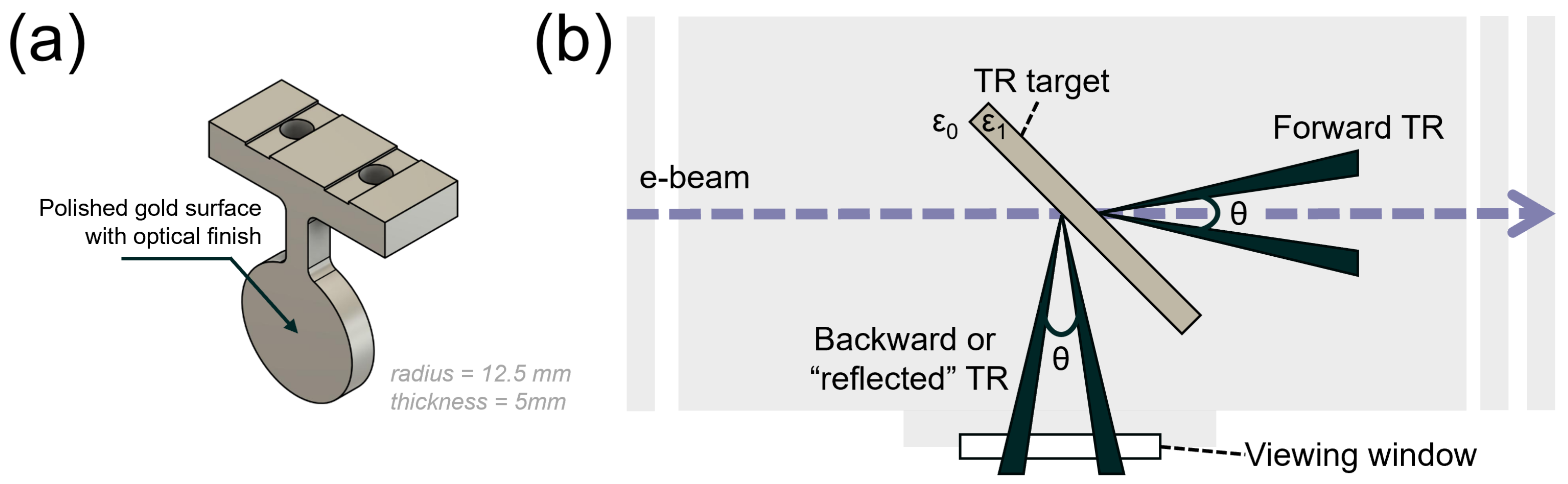
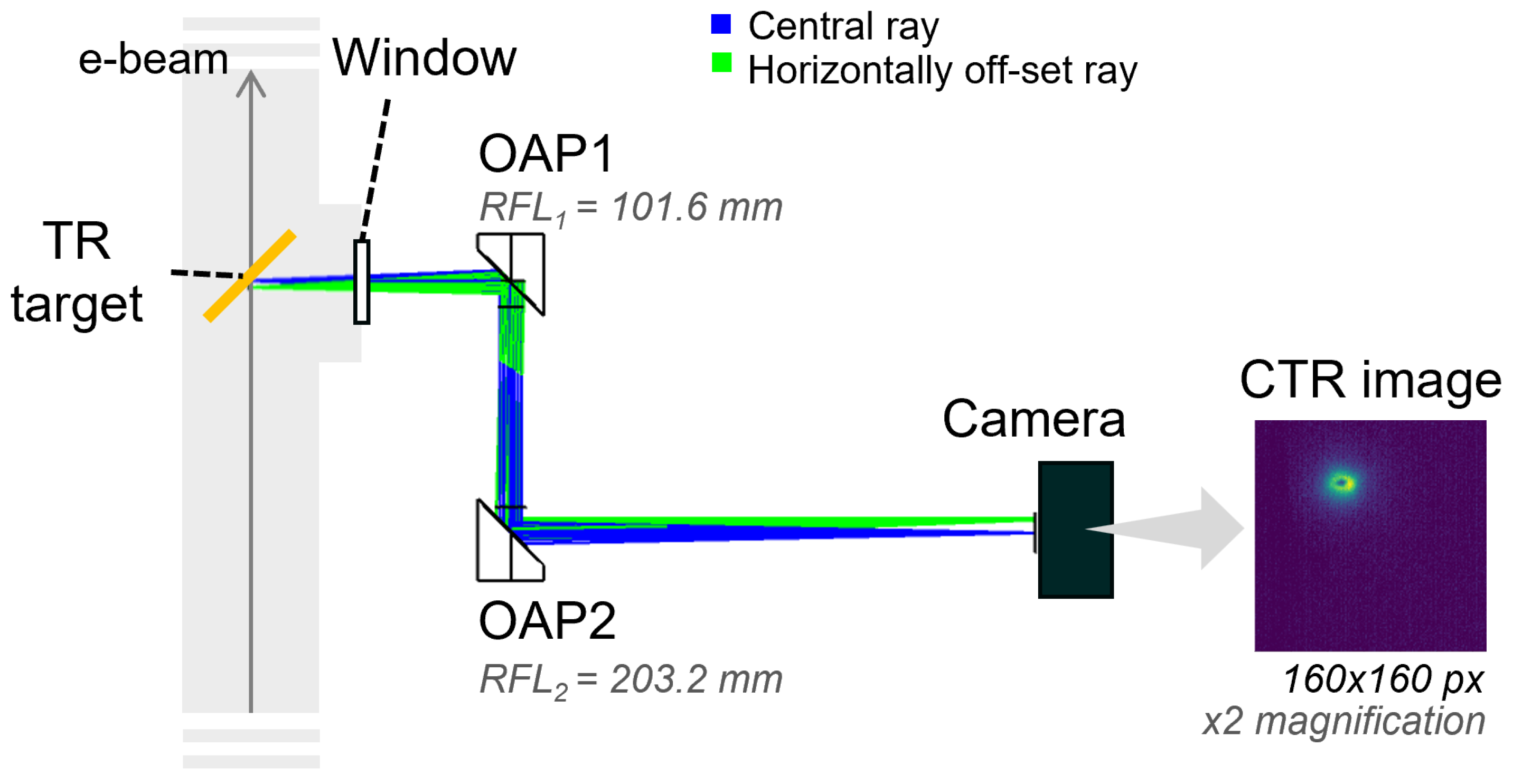
2.3. Device Concept and Design

Based on the discussions to this point, it is evident that the requirements for the CTR imaging system are primarily determined by the need to cover the wavelength range defined by the bunch lengths of interest, where $\lambda \ge {\lambda }_{\mathrm{cutoff}}$ and there is a need for it to be broadband.

The expected bunch length range at the MAX IV SPF of 20–100 fs FWHM translates to a requirement for an imaging system covering $\lambda ⪆3$ $\mathsf{\mu }$m. The condition of full transverse coherence ${\sigma }_r<<\gamma \lambda /2\pi$ is met, since ${\sigma }_r$ at the CTR target location is to the order of a few hundred micrometers and $\gamma \lambda /2\pi \approx 2800$ $\mathsf{\mu }$m at ${\lambda }_{\min }=$ 3 $\mathsf{\mu }$m.

When considering the longer wavelengths, diffraction radiation effects start to appear as the transverse extent of the TR field, scaling with $\gamma \lambda /2\pi$, begins to be comparable to or exceed the transverse dimension of the TR target [30,33], truncating the emitted field at the target boundaries and modifying the field distribution in the image plane. To account for these effects, the physical size and shape of the TR target must be modeled in the simulations, as there is no sharp cutoff in the spectral response but rather a gradual effect with nonlinear distortions in the spectral amplitude that become more evident (with significant attenuation) when longer wavelengths become dominant, i.e., while measuring longer bunch lengths.

The proposed design consists of a reflective optics imaging system with off-axis parabolic mirrors (OAPs), known for their ability to collimate and focus without chromatic aberrations, which makes them suitable for a broadband system. These mirrors help overcome some of the limitations imposed by the lens systems studied in previous works (see [23,24]).

The OAP system enhances the image intensity with the high reflectivity of the metallic coatings (>90% in the 450 nm–20 $\mathsf{\mu }$m range [34]) on the mirrors, which also enables higher magnifications, in contrast with the transmissive materials in the $\mathsf{\mu }$m or THz range, which can introduce significant losses in specific frequency ranges [35], resulting in reduced intensities for frequencies where transmittance is low and even information loss when there is close to complete absorption. The OAP mirrors also reduce the information losses due to their relatively flat reflectance in a broad frequency range. However, they can introduce geometric aberrations and pose challenges related to the complexity and alignment requirements of the set-up.

The use of OAPs is common for imaging and focusing in THz systems. Their use has been studied to find the best configurations for minimizing the aberrations introduced by their geometry. When using two OAP mirrors (see Figure 2a), the symmetric configuration is preferred over the anti-symmetric configuration [36,37]; however, taking into account the layout with respect to the beamline, only the anti-symmetric configuration would be feasible with the available space, and thus this one was selected for the first prototype installation. The use of standard kinematic mounts and a cage system proved sufficient to achieve alignment.

When more mirrors are included (see Figure 2b), the S shape and step shape are preferred, since those keep the symmetry to counter the aberrations from single mirrors. Still, only the step shape would be possible in the current location with the beamline layout, and thus it would be the layout used in future designs if more mirrors were to be included. The U-shaped configuration would be possible under current conditions, but it is discouraged as it contributes to wavefront distortions [38].

The actual elements used and their properties of interest are discussed below and presented in Figure 3:

• The high-resistivity float-zone silicon (HRFZ-Si) window (TYDEX, LLC.: St. Petersburg, Russia) was installed at the vacuum viewport. HRFZ-Si is one of the most commonly used materials in THz optics and is suitable for a wide range of wavelengths, ranging from near-infrared (≥1.2 $\mathsf{\mu }$m) to >1000 mm [35].
• The $Ø25.4$ mm (Ø1″) protected silver-coated OAPs with reflected focal lengths ${\mathrm{RFL}}_1=$ $101.6$ mm (4″) and ${\mathrm{RFL}}_2=$ $203.2$ mm (8″) (Thorlabs Inc.: Newton, NJ, USA), resulting in a $2\times$ magnification [34].
• The $160\times 160$ pyroelectric broadband array Pyrocam™ IIIHR GigE (Ophir Optronics Solutions Ltd.: Jerusalem, Israel) [39], namely PY-III-HR-C-A-PRO, has a spectral range of 13–355 nm and 1.06–3000 $\mathsf{\mu }$m, an active area of $12.8\times 12.8$ mm, a dynamic range of 60 dB, and a frame rate with a maximum resolution of 100 fps.

The set-up was initially simulated using Ansys Zemax OpticStudio^® (ANSYS, Inc: Canonsburg, PA, USA) [41] with the layout shown in Figure 4, tested in the laboratory, and later installed in the facility for experimental data collection.

3. Results

3.1. Installation

The tests of the CTR imaging system were conducted at the MAX IV SPF, with the specific location being SP02 (see Figure 5). During the beamtime, data collection was performed while running at 3 GeV to study bunches in the 35–100 fs range (as per the reference TDC bunch length measurements) and at approximately 100 pC. The imaging system, as shown in Figure 6, was installed in the designated location for image acquisition.

An example simulated output of the CTR image for a single wavelength is presented in Figure 7a. It predicted the presence of a horizontal geometric distortion (from the anti-symmetric configuration) that can also be observed in the experimental images (see Figure 7b).

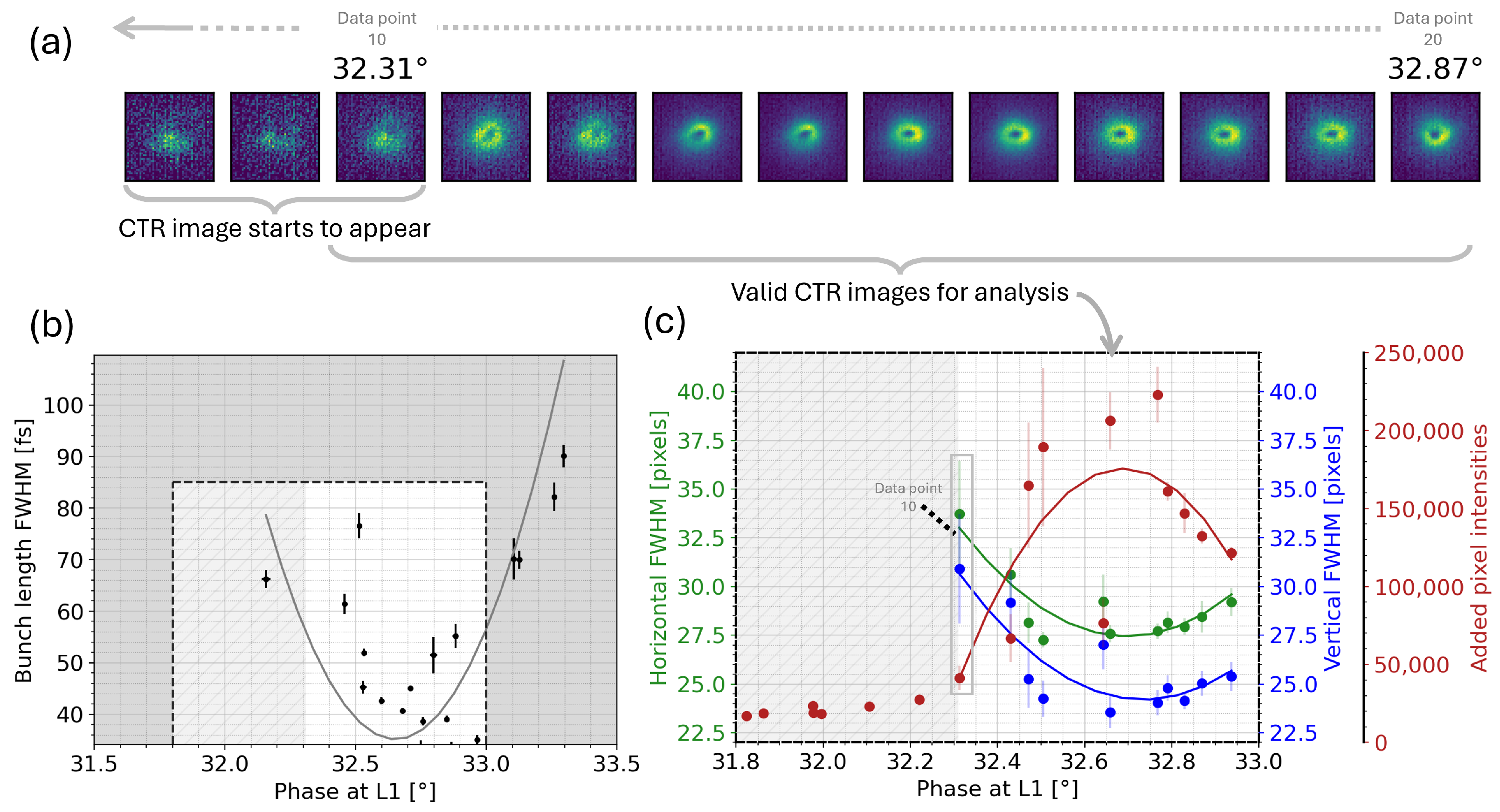
3.2. Data Collection and Preprocessing

Multiple scans were performed, and the CTR images were acquired at SP02.

Phase scans were performed by manipulating the fill times on the klystrons (KXXs), feeding the linear acceleration stages (LXs) highlighted in Figure 5. The fill times determine the phase of the RF, effectively varying the linear compression with the scans. Specifically, K01 was scanned for L1, and all klystrons downstream of K02 (fed through the main drive line (MDL)) were scanned to change the phases throughout the main linacs L2–L19.

Similarly, sextupole scans to study nonlinear compression were performed by varying the current on the sextupoles (SXXXs) in the bunch compressors (BCXs), SX01 in BC1, and SX02 in BC2, as seen in Figure 5.

The scans included 1D scans and 2D scans for combinations of the different parameters.

Figure 8a features an example set of three images cropped to ROI single-shot CTR images for three points in a 1D phase scan at L1. For the study of the CTR images, after preprocessing and data extraction, an analysis of the 1D image profiles (obtained by summing the pixel values in the horizontal and vertical directions) was performed to determine how the CTR images changed with variations in the phase during the scan. For this purpose, the horizontal and vertical profiles (Figure 8b,c, respectively) were fitted to Gaussians, and the resulting FWHM in pixels was used as the feature of interest.

The CTR image profile’s FWHM was selected as the feature of interest because previous works have shown how the FWHM of the normalized 1D cross-section of the spatial distribution of simulated CTR images is dependent on the bunch length [24]. It was expected that the image’s FWHM would change accordingly and that the change would be observed within the limits of what the proposed optical system and detector could image.

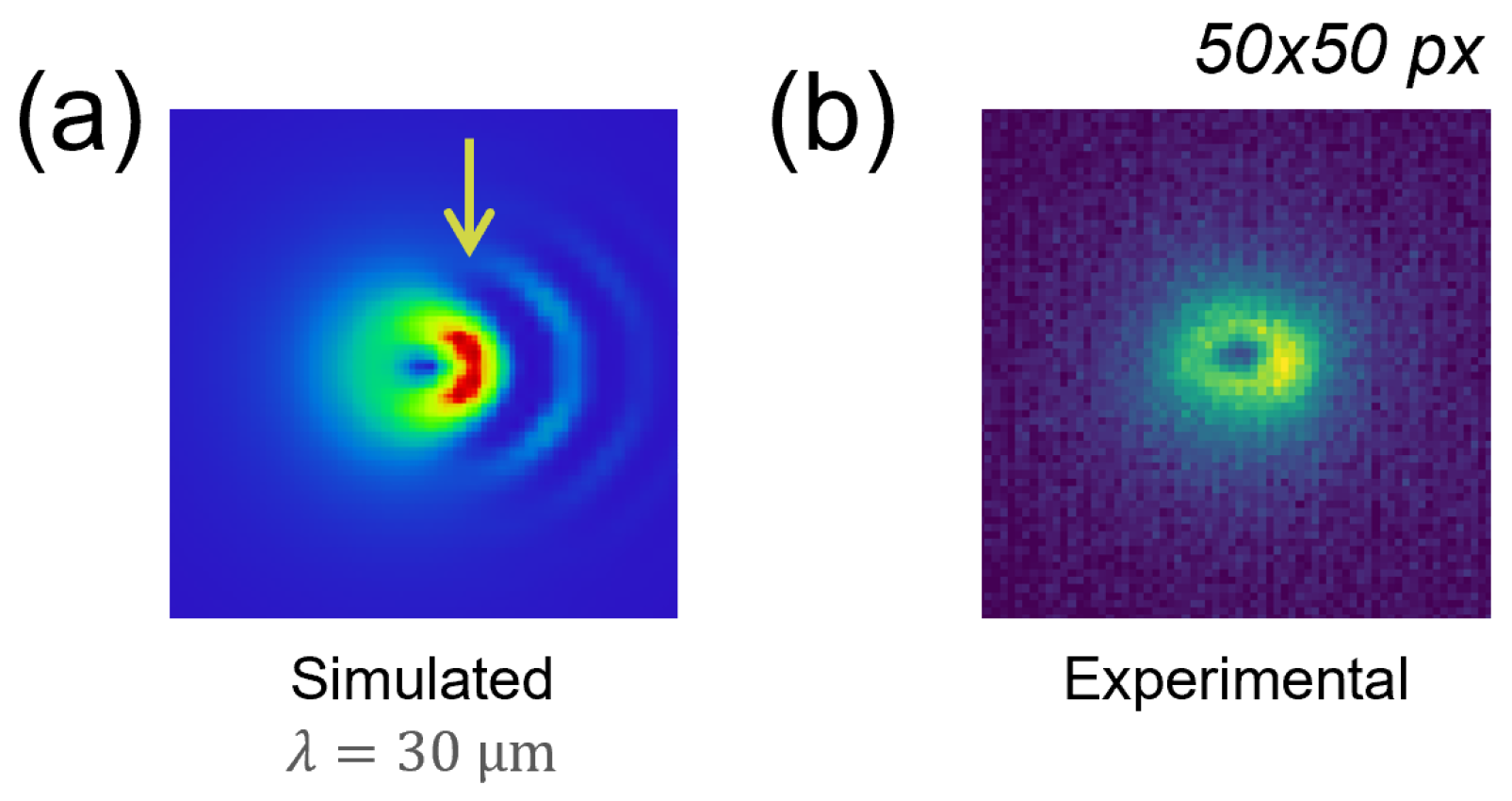
3.3. CTR Image Analysis and the Bunch Length

To contrast the information extracted from the CTR images, the scans were replicated in SP01 to obtain TDC measurements of the bunch profiles. The TDC bunch profiles were extracted, and from there, the FWHM bunch lengths were determined to use as a reference.

However, due to restrictions on the times for operation of the TDC and the overall data collection schedule, it was not possible to perform most of the benchmark TDC scans immediately before or after the CTR scans. Since TDC scans could only occur during a limited time window during the day, alternating the beam between SP01 and SP02 would waste some of this already limited time. Therefore, most of the CTR scans and the reference TDC data were collected with a difference of up to one day (≈12–20 h).

The results for a 20-point 1D phase scan of L1 are shown in Figure 9. The CTR images are shown in Figure 9a; however, only the 11 shots in the range of $\left[32.31°, 32.87°\right]$ were actually visible with this optical system.

For a given phase point, 10 shots were recorded, with each containing the machine parameters of interest and the corresponding CTR or TDC image. Nevertheless, since the actual parameter being scanned was the fill time in K01, the resulting phases at L1 were not fully matched between the CTR and TDC scans, which is thought to be due to the varying conditions of the accelerator between the two scans. Figure 9b shows the FWHM bunch length reference values derived from the TDC scan at SP01; the lighter rectangle highlights the region that would correspond with the phase range covered by the scan at the CTR location at SP02, depicted in Figure 9c.

4. Discussion

The reference bunch length data in Figure 9b indicate that the electron bunch was undergoing a point of maximum compression in the range of this scan, also referred to as a waist, meaning that a similar behavior should have been expected in the FWHM CTR image profiles, which was observed and presented in Figure 9c. The CTR images were analyzed separately in both horizontal and vertical dimensions, and the results appear to be self-consistent, as they both show similarity with the behavior of the reference TDC data. Additionally, the total image intensity was analyzed, as also shown in Figure 9c, confirming that the optical system could not detect the CTR image until around data point 10, and the intensity reached a maximum at maximum compression.

Data point 10, where the CTR image started to become more visible but was not yet fully visible, had higher error bars; however, the errors improved when sharper images were captured. The range of visible CTR images would suggest an upper limit on the optical system’s ability to capture the CTR images at approximately 60–70 fs FWHM, which fell within ${\lambda }_{\mathrm{cutoff}}\approx$ 8–9 $\mathsf{\mu }$m.

The CTR image analysis results align with previous works that predicted the FWHM and intensity behaviors [23,24], and they are positive indicators for the development of this monitoring technique for determining the bunch length from CTR image distributions. However, the current prototype does not yet enable accurate measurements of the bunch length, and further improvements are needed in subsequent iterations of both the image acquisition system and the data analysis techniques.

4.1. Image Acquisition System Improvements

Straightforward improvement for the image analysis can be expected by implementing a step-shaped configuration (see Figure 2b) for the OAP optical system to reduce the geometric aberrations on the horizontal plane that are observed currently and choosing the additional mirrors such that the final magnification is higher (e.g., ${\mathrm{RFL}}_3=4$″ and ${\mathrm{RFL}}_4=8$″ yield $4\times$ magnification overall). However, there would be a trade-off due to the larger magnification reducing the individual pixel intensities (doubling the intensity of the magnification decrease by four) and the added reflections resulting from the mirror coating reflectances, resulting in a lower final intensity when compared with the two-mirror system, implying a reduced measurement range overall for the monitor.

If both changes are implemented, then new CTR image acquisitions with an ROI of approximately $100\times 100$ pixels would allow for a more detailed look at the CTR image profiles for rerunning the presented analysis and, additionally, potentially enabling observation of the effects on the resulting CTR image of microstructures in the electron bunch under conditions of overcompression, for example.

In the presented 1D phase scan at L1, there was no evident lower limit to the bunch length from which the CTR image was lost. To determine this lower limit, the next step is to perform a similar CTR image analysis for scans reaching maximum compression to try to find a minimum FWHM. Then, the beam can also be studied in overcompression, where substructures may become visible at this lower limit, in an attempt to test the system resolution, as the CTR features are expected to change with the presence of higher-frequency components in the image.

Some changes may be necessary to fully explore the smaller bunch lengths and structures as the coherent TR cutoff ${\lambda }_{\mathrm{cutoff}}$ for electron bunches of a few femtoseconds (1–9 fs) falls within the optical and near-infrared 0.3–2.7 $\mathsf{\mu }$m range, and thus they might not be resolvable with the current bandwidth. The current system utilizes an HRFZ-Si viewing window, which is not fully transparent in this range of a few femtoseconds (only at wavelengths $\ge 1.2$ $\mathsf{\mu }$m or bunch lengths $\ge 4$ fs). An ideal option would be a diamond window, but it is costly to implement. Alternatively, options like TPX could be considered, although other wavelength ranges would be attenuated [35].

Even after replacing the window with a new material, the system would also require additional cameras to effectively cover the new spectral ranges not currently covered by the Pyrocam. The OAP system would require further development with beam splitters and added mirrors to split different frequency bands into the various sensors. Additionally, since high-frequency components (closer to the CTR image center) would dominate the image for shorter bunch lengths, the current magnification ($2\times$) could be insufficient to observe enough detail in the CTR images.

4.2. Image Analysis Improvements

The presented image analysis, although illustrative for studying the physical phenomenon, lacks the required rigor to extract sufficient information for fully characterizing the relationship between the CTR image distributions and bunch length measurements. CTR images are complex and carry information about the main structure and the substructures present on the electron bunch profile. To find, study, and model these, two approaches could be considered.

First, by simulating CTR images from realistic simulated profiles (for example, from particle tracking simulations), it may be possible to compare experimental images directly to find these relationships. However, the effect of substructures and the high-frequency components that dominate the CTR images when present in the electron bunch profile could limit the ability to generalize this type of analysis due to increased complexity.

The second approach to consider is the use of deep learning techniques for image analysis and computer vision, as these can more easily learn the patterns and complexity of the CTR images. Both approaches could be combined, as the second method would also benefit from the use of simulated profiles and corresponding CTR spatial images to train the models, since deep learning models require thousands of samples for training. With this approach, determining the bunch length would be possible; however, it also opens up the possibility of full bunch profile reconstructions, provided that the correct models are trained, as preliminary work with Gaussian profiles has shown [43].

5. Conclusions

Taken together, the prototype design process and the preliminary results presented in the previous sections both support continued work toward the development of a fully functional bunch length monitor based on the analysis of coherent transition radiation images. The design-to-data collection process required a deep understanding of the CTR and all the considerations for effectively acquiring relevant data to test the technique at MAX IV SPF for bunches $<70$ fs FWHM at 3 GeV and $\approx 100$ pC. The data analysis stage consolidated this knowledge, making it possible to define the following steps for new iterations of the prototype (improvements in magnification, widening the bandwidth by replacing optical components, or the addition of new sensors for new frequency ranges) and image analysis techniques (simulated CTR comparisons and deep learning) toward a single-shot online bunch length monitor.