Real-Time Dose Monitoring via Non-Destructive Charge Measurement of Laser-Driven Electrons for Medical Applications
Abstract
1. Introduction
2. Real-Time Dose Monitoring System
3. Calibration of Dose Monitoring System with Standard RCF Dosimetry
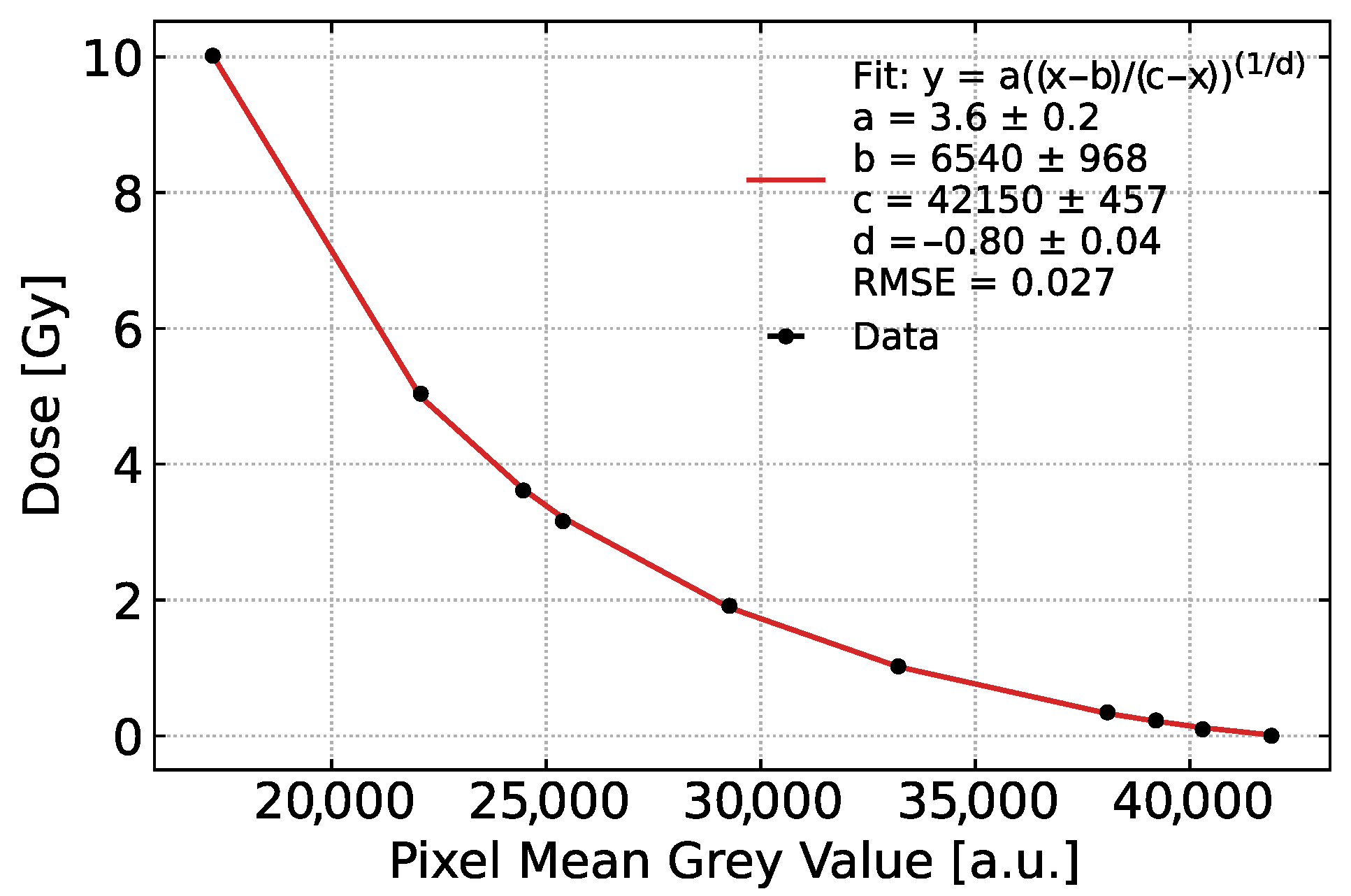
3.1. Experimental Calibration of Dose Versus Charge
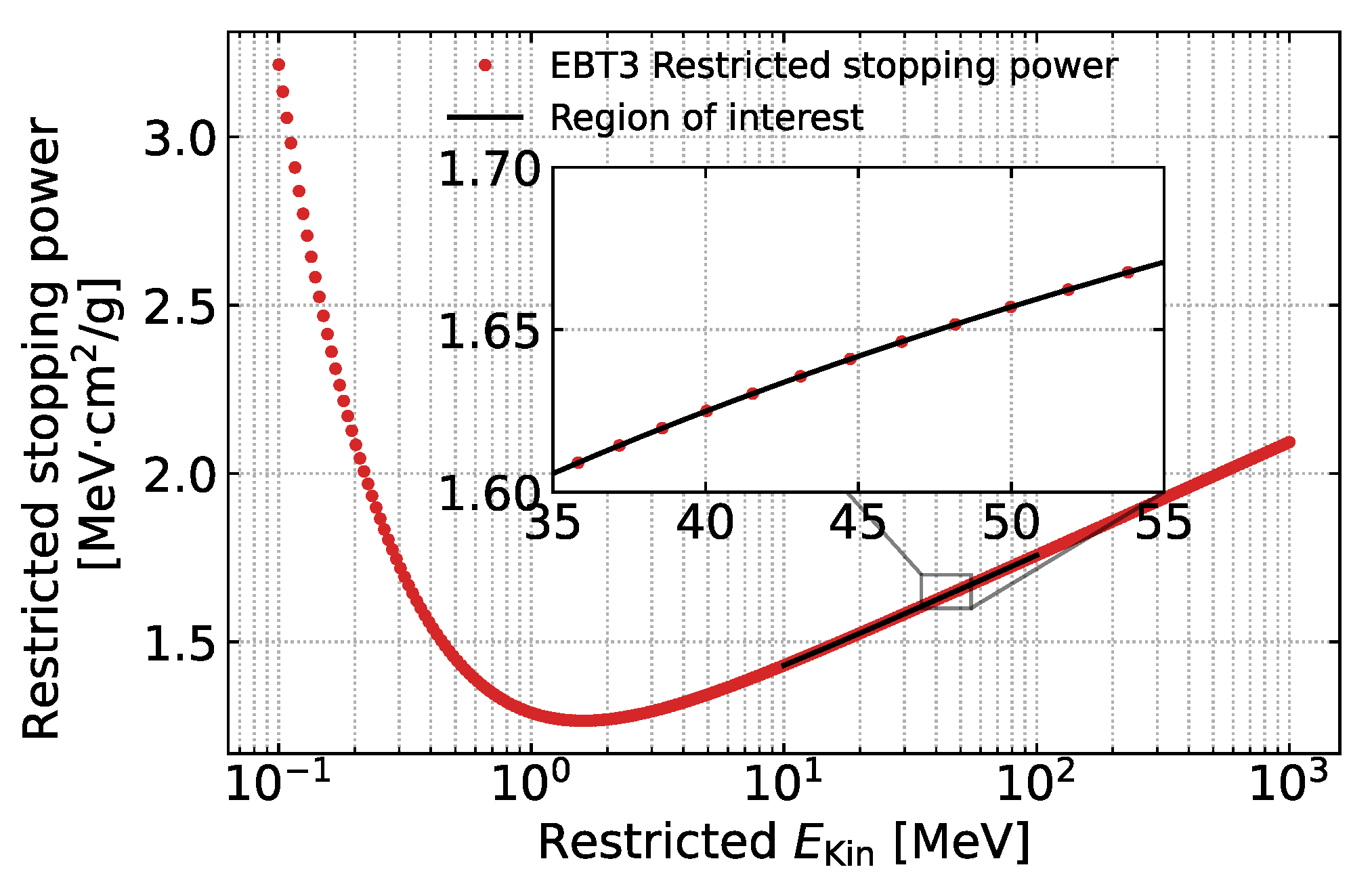
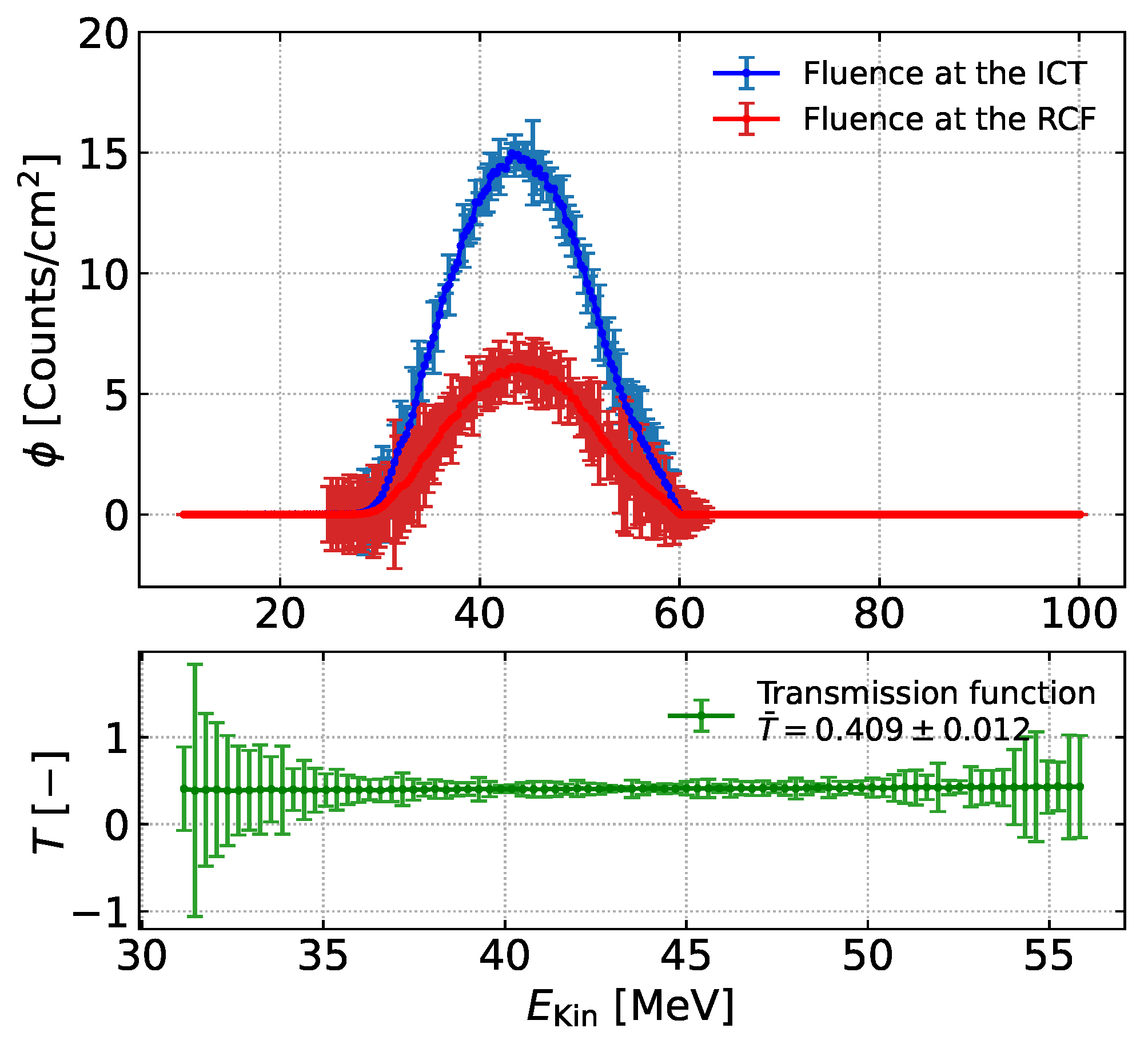
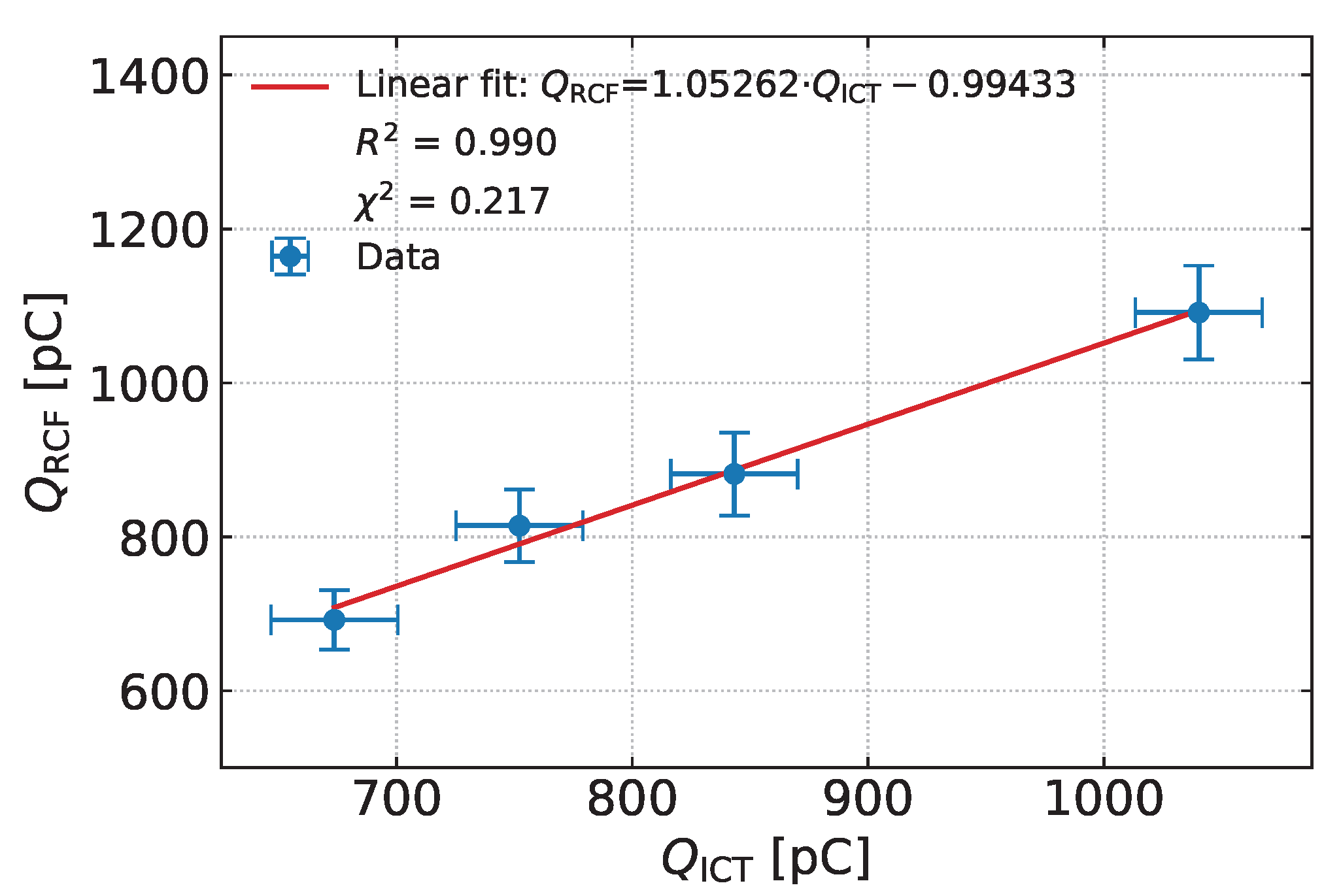
3.2. Cross-Validation of the Dose Monitoring System
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tajima, T.; Dawson, J.M. Laser Electron Accelerator. Phys. Rev. Lett. 1979, 43, 267–270. [Google Scholar] [CrossRef]
- Mangles, S.P.D.; Murphy, C.D.; Najmudin, Z.; Thomas, A.G.R.; Collier, J.L.; Dangor, A.E.; Divall, E.J.; Foster, P.S.; Gallacher, J.G.; Hooker, C.J.; et al. Monoenergetic beams of relativistic electrons from intense laser–plasma interactions. Nature 2004, 431, 535–538. [Google Scholar] [CrossRef]
- Geddes, C.G.R.; Toth, C.; van Tilborg, J.; Esarey, E.; Schroeder, C.B.; Bruhwiler, D.; Nieter, C.; Cary, J.; Leemans, W.P. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 2004, 431, 538–541. [Google Scholar] [CrossRef] [PubMed]
- Faure, J.; Glinec, Y.; Pukhov, A.; Kiselev, S.; Gordienko, S.; Lefebvre, E.; Rousseau, J.P.; Burgy, F.; Malka, V. A laser–plasma accelerator producing monoenergetic electron beams. Nature 2004, 431, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Leemans, W.P.; Nagler, B.; Gonsalves, A.J.; Toth, C.; Nakamura, K.; Geddes, C.G.R.; Esarey, E.; Schroeder, C.B.; Hooker, S.M. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2006, 2, 696–699. [Google Scholar] [CrossRef]
- Nakamura, K.; Nagler, B.; Toth, C.; Geddes, C.G.R.; Schroeder, C.B.; Esarey, E.; Leemans, W.P.; Gonsalves, A.J.; Hooker, S.M. GeV electron beams from a centimeter-scale channel guided laser wakefield accelerator. Phys. Plasmas 2007, 14, 056708. [Google Scholar] [CrossRef]
- Labate, L.; Andreassi, M.G.; Baffigi, F.; Bizzarri, R.; Borghini, A.; Bussolino, G.C.; Fulgentini, L.; Ghetti, F.; Giulietti, A.; Köster, P.; et al. TLESM: A laser-driven sub-MeV electron source delivering ultra-high dose rate on thin biological samples. J. Phys. D Appl. Phys. 2016, 49, 275401. [Google Scholar] [CrossRef]
- Lagzda, A.; Angal-Kalinin, D.; Jones, J.; Aitkenhead, A.; Kirkby, K.J.; MacKay, R.; Herk, M.V.; Farabolini, W.; Zeeshan, S.; Jones, R.M. Influence of heterogeneous media on Very High Energy Electron (VHEE) dose penetration and a Monte Carlo-based comparison with existing radiotherapy modalities. Nucl. Instrum. Methods Phys. Res. B. 2020, 482, 70–81. [Google Scholar] [CrossRef]
- Labate, L.; Palla, D.; Panetta, D.; Avella, F.; Baffigi, F.; Brandi, F.; Martino, F.D.; Fulgentini, L.; Giulietti, A.; Köster, P.; et al. Toward an effective use of laser-driven very high energy electrons for radiotherapy: Feasibility assessment of multi-field and intensity modulation irradiation schemes. Sci. Rep. 2020, 10, 17307. [Google Scholar] [CrossRef]
- Panaino, C.M.V.; Piccinini, S.; Andreassi, M.G.; Bandini, G.; Borghini, A.; Borgia, M.; Naro, A.D.; Labate, L.; Maggiulli, E.; Portaluri, M.G.A.; et al. Very High-Energy Electron Therapy Toward Clinical Implementation. Cancers 2025, 17, 181. [Google Scholar] [CrossRef]
- Favaudon, V.; Caplier, L.; Monceau, V.; Pouzoulet, F.; Sayarath, M.; Fouillade, C.; Poupon, M.F.; Brito, I.; Hupe, P.; Bourhis, J.; et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci. Transl. Med. 2014, 6, 245ra93. [Google Scholar] [CrossRef]
- Montay-Gruel, P.; Petersson, K.; Jaccard, M.; Boivin, G.; Germond, J.F.; Petit, B.; Doenlen, R.; Favaudon, V.; Bochud, F.; Bourhis, C.B.J.; et al. Irradiation in a flash: Unique sparing of memory in mice after whole brain irradiation with dose rates above 100Gy/s. Radiother. Oncol. 2017, 124, 365–369. [Google Scholar] [CrossRef]
- Montay-Gruel, P.; Acharya, M.M.; Petersson, K.; Alikhani, L.; Yakkala, C.; Allen, B.D.; Ollivier, J.; Petit, B.; Jorge, P.G.; Syage, A.R.; et al. Long-term neurocognitive benefits of FLASH radiotherapy driven by reduced reactive oxygen species. Proc. Natl. Acad. Sci. USA 2019, 116, 10943–10951. [Google Scholar] [CrossRef]
- Vozenin, M.C.; Fornel, P.D.; Petersson, K.; Favaudon, V.; Jaccard, M.; Germond, J.F.; Petit, B.; Burki, M.; Ferrand, G.; Patin, D.; et al. The Advantage of FLASH Radiotherapy Confirmed in Mini-pig and Cat-cancer Patients. Clin. Cancer Res. 2019, 25, 35–42. [Google Scholar] [CrossRef]
- Bourhis, J.; Sozzi, W.J.; Jorge, P.G.; Gaide, O.; Bailat, C.; Duclos, F.; Patin, D.; Ozsahin, M.; Bochud, F.; Germond, J.F.; et al. Treatment of a first patient with FLASH-radiotherapy. Radiother. Oncol. 2019, 139, 18–22. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Liu, S.; Qiu, J.; Hu, A.; Zhou, W.; Wang, J.; Gu, W.; Zhu, Y.; Zha, H.; Xiang, R.; et al. Instantaneous dose rate as a crucial factor in reducing mortality and normal tissue toxicities in murine total-body irradiation: A comparative study of dose rate combinations. Mol. Med. 2025, 31, 79. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.B.; Leemans, W.P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229–1285. [Google Scholar] [CrossRef]
- Laschinsky, L.; Baumann, M.; Beyreuther, E.; Enghardt, W.; Kaluza, M.; Karsch, L.; Lessmann, E.; Naumburger, D.; Nicolai, M.; Richter, C.; et al. Radiobiological Effectiveness of Laser Accelerated Electrons in Comparison to Electron Beams from a Conventional Linear Accelerator. J. Radiat. Res. 2012, 53, 395–403. [Google Scholar] [CrossRef]
- Vojnovic, B.; Tullis, I.D.C.; Newman, R.G.; Petersson, K. Monitoring beam charge during FLASH irradiations. Front. Phys. 2023, 11, 1185237. [Google Scholar] [CrossRef]
- Arjomandy, B.; Tailor, R.; Zhao, L.; Devic, S. EBT2 film as a depth-dose measurement tool for radiotherapy beams over a wide range of energies and modalities. Med. Phys. 2012, 39, 912–921. [Google Scholar] [CrossRef]
- Sipila, P.; Ojala, J.; Kaijaluoto, S.; Jokelainen, I.; Kosunen, A. Gafchromic EBT3 film dosimetry in electron beams-energy dependence and improved film read-out. J. Appl. Clin. Med. Phys. 2016, 17, 360–373. [Google Scholar] [CrossRef]
- Kokurewicz, K.; Schüller, A.; Brunetti, E.; Subiel, A.; Kranzer, R.; Hackel, T.; Meier, M.; Kapsch, R.P.; Jaroszynski, D.A. Dosimetry for New Radiation Therapy Approaches Using High Energy Electron Accelerators. Front. Phys. 2020, 8, 568302. [Google Scholar] [CrossRef]
- Clements, N.; Bazalova-Carter, M. Monte Carlo calculated absorbed-dose energy dependence of EBT3 and EBT4 films for 5–200 MeV electrons and 100 keV–15 MeV photons. J. Appl. Clin. Med. Phys. 2024, 25, 14529. [Google Scholar] [CrossRef] [PubMed]
- Fainstein, C.; Winkler, E.; Saravi, M. ESR/Alanine γ-dosimetry in the 10–30 Gy range. Appl. Radiat. Isot. 2000, 52, 1195–1196. [Google Scholar] [CrossRef] [PubMed]
- Gondre, M.; Jorge, P.G.; Vozenin, M.C.; Bourhis, J.; Bochud, F.; Bailat, C.; Moeckli, R. Optimization of Alanine Measurements for Fast and Accurate Dosimetry in FLASH Radiation Therapy. Radiat. Res. 2020, 194, 573–579. [Google Scholar] [CrossRef]
- Francescon, P.; Kilby, W.; Noll, J.M.; Masi, L.; Satariano, N.; Russo, S. Monte Carlo simulated corrections for beam commissioning measurements with circular and MLC shaped fields on the CyberKnife M6 System: A study including diode, microchamber, point scintillator, and synthetic microdiamond detectors. Phys. Med. Biol. 2017, 62, 1076. [Google Scholar] [CrossRef]
- Consoli, F.; De-Angelis, R.; Andreoli, P.; Cipriani, M.; Cristofari, G.; Giorgio, G.D.; Ingenito, F. Experiments on electromagnetic pulse (EMP) generated by laser-plasma interaction in nanosecond regime. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 182–187. [Google Scholar] [CrossRef]
- He, Q.Y.; Yan, W.; Liu, Z.P.; Yan, Y.; Fang, Y.L.; Li, C.T.; Wu, Q.F.; Song, T.; Li, T.S.; Lin, C.; et al. Measurement of electromagnetic pulse in laser acceleration enhanced by near-critical density targets. Phys. Plasmas 2024, 31, 103303. [Google Scholar] [CrossRef]
- Glinec, Y.; Faure, J.; Guemnie-Tafo, A.; Malka, V.; Monard, H.; Larbre, J.P.; Waele, V.D.; Marignier, J.L.; Mostafavi, M. Absolute calibration for a broad range single shot electron spectrometer. Rev. Sci. Instrum. 2006, 77, 103301. [Google Scholar] [CrossRef]
- Hidding, B.; Pretzler, G.; Clever, M.; Brandl, F.; Zamponi, F.; Lubcke, A.; Kampfer, T.; Uschmann, I.; Forster, E.; Schramm, U.; et al. Novel method for characterizing relativistic electron beams in a harsh laser-plasma environment. Rev. Sci. Instrum. 2007, 78, 083301. [Google Scholar] [CrossRef]
- Nakamura, K.; Gonsalves, A.J.; Lin, C.; Smith, A.; Rodgers, D.; Donahue, R.; Byrne, W.; Leemans, W.P. Electron beam charge diagnostics for laser plasma accelerators. Phys. Rev. ST Accel. Beams 2011, 14, 062801. [Google Scholar] [CrossRef]
- Lazurik, V.; Moskvin, V.; Tabata, T. Average depths of electron penetration: Use as characteristic depths of exposure. IEEE Trans. Nucl. Sci. 1997, 45, 626–631. [Google Scholar] [CrossRef]
- Galimberti, M.; Giulietti, A.; Giulietti, D.; Gizzi, L.A. SHEEBA: A spatial high energy electron beam analyzer. Rev. Sci. Instrum. 2005, 76, 053303. [Google Scholar] [CrossRef]
- Gizzi, L.A.; Labate, L.; Baffigi, F.; Brandi, F.; Bussolino, G.; Fulgentini, L.; Koster, P.; Palla, D. Overview and specifications of laser and target areas at the Intense Laser Irradiation Laboratory. High Power Laser Sci. Eng. 2021, 9, e10. [Google Scholar] [CrossRef]
- Paelinck, L.; Ebongue, A.; Neve, W.D.; Wagter, C.D. Radiochromic EBT film dosimetry: Effect of film orientation and batch on the lateral correction of the scanner. Radiother. Oncol. 2007, 84, 194–195. [Google Scholar]
- Chung, H.; Lynch, B.; Samant, S. High-precision GAFCHROMIC EBT film-based absolute clinical dosimetry using a standard flatbed scanner without the use of a scanner non-uniformity correction. J. Appl. Clin. Med. Phys. 2010, 11, 3112. [Google Scholar] [CrossRef]
- Ali, I.; Costescu, C.; Vicic, M.; Dempsey, J.F.; Williamson, J.F. Dependence of radiochromic film optical density post-exposure kinetics on dose and dose fractionation. Med. Phys. 2003, 30, 1958–1967. [Google Scholar] [CrossRef] [PubMed]
- Papaconstadopoulos, P.; Hegyi, G.; Seuntjens, J.; Devic, S. A protocol for EBT3 radiochromic film dosimetry using reflection scanning. Med. Phys. 2014, 41, 122101. [Google Scholar] [CrossRef]
- Howard, M.E.; Herman, M.G.; Grams, M.P. Methodology for radiochromic film analysis using FilmQA Pro and ImageJ. PLoS ONE 2020, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jorge, P.G.; Grilj, V.; Bourhis, J.; Vozenin, M.C.; Germond, J.F.; Bochud, F.; Bailat, C.; Moeckli, R. Technical note: Validation of an ultrahigh dose rate pulsed electron beam monitoring system using a current transformer for FLASH preclinical studies. Med. Phys. 2022, 49, 1831–1838. [Google Scholar] [CrossRef] [PubMed]
- Kranzer, R.; Schuller, A.; Bourgouin, A.; Hackel, T.; Poppinga, D.; Lapp, M.; Looe, H.K.; Poppe, B. Response of diamond detectors in ultra-high dose-per-pulse electron beams for dosimetry at FLASH radiotherapy. Phys. Med. Biol. 2022, 67, 075002. [Google Scholar] [CrossRef]
- Oesterle, R.; Jorge, P.G.; Grilj, V.; Bourhis, J.; Vozenin, M.C.; Germond, J.F.; Bochud, F.; Bailat, C.; Moeckli, R. Implementation and validation of a beam-current transformer on a medical pulsed electron beam LINAC for FLASH-RT beam monitoring. J. Appl. Clin. Med. Phys. 2021, 22, 165–171. [Google Scholar] [CrossRef]
- Geulig, L.D.; Obst-Huebl, L.; Nakamura, K.; Bin, J.; Ji, Q.; Steinke, S.; Snijders, A.M.; Mao, J.H.; Blakely, E.A.; Gonsalves, A.J.; et al. Online charge measurement for petawatt laser-driven ion acceleration. Rev. Sci. Instrum. 2022, 93, 103301. [Google Scholar] [CrossRef] [PubMed]
- Vlachos, S.G.; Labate, L.; Baffigi, F.; Bandini, G.; Brandi, F.; Fulgentini, L.; Gregocki, D.; Köster, P.; Palla, D.; Piccinini, S.; et al. Single-shot spectrometer with pointing angle correction for laser-driven electron beams featuring pointing instability and transverse inhomogeneity. Nucl. Instrum. Methods Phys. Res. A 2026, 1082, 171038. [Google Scholar] [CrossRef]
- McParland, B.J. Medical Radiation Dosimetry; Springer: London, UK, 2013; Chapter 10; Available online: https://link.springer.com/book/10.1007/978-1-4471-5403-7 (accessed on 18 August 2025).
- Palmer, A.L.; Dimitriadis, A.; Nisbet, A.; Clark, C.H. Evaluation of Gafchromic EBT-XD film, with comparison to EBT3 film, and application in high dose radiotherapy verification. Phys. Med. Biol. 2015, 60, 8741. [Google Scholar] [CrossRef] [PubMed]
- Ahdida, C.; Bozzato, D.; Calzolari, D.; Cerutti, F.; Charitonidis, N.; Cimmino, A.; Coronetti, A.; D’Alessandro, G.L.; Servelle, A.D.; Esposito, L.S.; et al. New Capabilities of the FLUKA Multi-Purpose Code. Front. Phys. 2022, 9, 788253. [Google Scholar] [CrossRef]
- Battistoni, G.; Boehlen, T.; Cerutti, F.; Chin, P.W.; Esposito, L.S.; Fasso, A.; Ferrari, A.; Lechner, A.; Empl, A.; Mairani, A.; et al. Overview of the FLUKA code. Ann. Nucl. Energy 2015, 82, 10–18. [Google Scholar] [CrossRef]





| [ pC] | ||||
|---|---|---|---|---|
| Shot No. | Set 1 | Set 2 | Set 3 | Set 4 |
| 1 | 78.6 | 56.3 | 87.3 | 117.8 |
| 2 | 67.9 | 90.8 | 82.5 | 99.9 |
| 3 | 101.3 | 55.4 | 40.4 | 93.2 |
| 4 | 62.2 | 42.6 | 83.3 | 98.3 |
| 5 | 30.1 | 82.4 | 76.2 | 120.3 |
| 6 | 59.0 | 113.7 | 111.8 | 103.4 |
| 7 | 73.6 | 76.7 | 83.0 | 56.8 |
| 8 | 53.6 | 83.7 | 80.5 | 135.2 |
| 9 | 91.0 | 91.3 | 84.9 | 103.6 |
| 10 | 56.3 | 59.2 | 113.4 | 111.8 |
| Sum: | 673.6 ± 26.9 | 752.1 ± 26.9 | 843.3 ± 26.9 | 1040.3 ± 26.9 |
| Average ± STD: | 67.4 ± 19.2 | 75.2 ± 20.4 | 84.3 ± 19.0 | 104.0 ± 19.7 |
| RCF Dose: | 0.1578 ± 0.0722 | 0.1857 ± 0.0891 | 0.2010 ± 0.1042 | 0.2488 ± 0.1134 |
| Thickness | Density | Mass Composition [%] | |||||
|---|---|---|---|---|---|---|---|
| Layer | [m] | [g/cm3] | H | Li | C | O | Al |
| Polyester | 125 | 1.35 | 4.2 | 0.0 | 62.5 | 33.3 | 0.0 |
| Active layer | 25 | 1.2 | 8.8 | 0.6 | 51.1 | 32.8 | 6.7 |
| Polyester | 125 | 1.35 | 4.2 | 0.0 | 62.5 | 33.3 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gregocki, D.; Köster, P.; Labate, L.U.; Piccinini, S.; Avella, F.; Baffigi, F.; Bandini, G.; Brandi, F.; Fulgentini, L.; Palla, D.; et al. Real-Time Dose Monitoring via Non-Destructive Charge Measurement of Laser-Driven Electrons for Medical Applications. Instruments 2025, 9, 25. https://doi.org/10.3390/instruments9040025
Gregocki D, Köster P, Labate LU, Piccinini S, Avella F, Baffigi F, Bandini G, Brandi F, Fulgentini L, Palla D, et al. Real-Time Dose Monitoring via Non-Destructive Charge Measurement of Laser-Driven Electrons for Medical Applications. Instruments. 2025; 9(4):25. https://doi.org/10.3390/instruments9040025
Chicago/Turabian StyleGregocki, David, Petra Köster, Luca Umberto Labate, Simona Piccinini, Federico Avella, Federica Baffigi, Gabriele Bandini, Fernando Brandi, Lorenzo Fulgentini, Daniele Palla, and et al. 2025. "Real-Time Dose Monitoring via Non-Destructive Charge Measurement of Laser-Driven Electrons for Medical Applications" Instruments 9, no. 4: 25. https://doi.org/10.3390/instruments9040025
APA StyleGregocki, D., Köster, P., Labate, L. U., Piccinini, S., Avella, F., Baffigi, F., Bandini, G., Brandi, F., Fulgentini, L., Palla, D., Salvadori, M., Vlachos, S. G., & Gizzi, L. A. (2025). Real-Time Dose Monitoring via Non-Destructive Charge Measurement of Laser-Driven Electrons for Medical Applications. Instruments, 9(4), 25. https://doi.org/10.3390/instruments9040025








