Combining Wave and Particle Effects in the Simulation of X-ray Phase Contrast—A Review

Abstract

X-ray phase-contrast imaging (XPCI) is a family of imaging techniques that makes contrast visible due to phase shifts in the sample. Phase-sensitive techniques can potentially be several orders of magnitude more sensitive than attenuation-based techniques, finding applications in a wide range of fields, from biomedicine to materials science. The accurate simulation of XPCI allows for the planning of imaging experiments, potentially reducing the need for costly synchrotron beam access to find suitable imaging parameters. It can also provide training data for recently proposed machine learning-based phase retrieval algorithms. The simulation of XPCI has classically been carried out using wave optics or ray optics approaches. However, these approaches have not been capable of simulating all the artifacts present in experimental images. The increased interest in dark-field imaging has also prompted the inclusion of scattering in XPCI simulation codes. Scattering is classically simulated using Monte Carlo particle transport codes. The combination of the two perspectives has proven not to be straightforward, and several methods have been proposed. We review the available literature on the simulation of XPCI with attention given to particular methods, including the scattering component, and discuss the possible future directions for the simulation of both wave and particle effects in XPCI.

1. Introduction

X-ray phase-contrast imaging has proven to be a useful technique in many fields, ranging from material science to biomedical imaging, mainly due to the benefit of producing images with higher sensitivity than traditional attenuation-based imaging regarding both X-ray energies and resolutions. In medical imaging, this has led to the development of the first prototypes for clinical use [1,2,3,4,5,6]. The higher sensitivity is due to the physical quantity, the real part of the refractive index responsible for phase shift, which can be over three orders of magnitude larger than the imaginary part responsible for attenuation. For example, the clinical X-ray images used as standard will have relatively low contrast for soft tissues, as opposed to phase contrast images.

Different ways to achieve phase contrast in X-ray imaging have been developed. The techniques discussed in this review are GBI, MoBI, and PBI. GBI uses diffraction gratings to generate phase contrast. The phase shift induced by the sample distorts the pattern from a first grating, and a second grating can be used to measure the displacements created by the distortions. From this, the phase and amplitude of the wave can be reconstructed [7,8,9]. MoBI works on a similar principle as GBI but uses a random or coded mask in front of the sample instead to induce a modulation pattern. This pattern is then similarly distorted by the phase shift in the object. The displacements of the modulation pattern can then be measured and used to reconstruct the phase shift. On the other hand, PBI requires no additional optical elements but uses free-space propagation instead to yield phase contrast. When measured in this way, the image corresponds to a Fresnel diffraction pattern. The simplicity of this technique makes it suitable for high-resolution imaging, theoretically limited by the wavelength of the X-rays. The previous two techniques, however, seem more appropriate for lower-resolution imaging; for example, in a clinical setting, since PBI would require prohibitively large propagation distances for the usual image resolutions used in medical imaging, it would require a small X-ray source, i.e., coherent X-rays. At the same time, XPCI is interesting in its own right in terms of yielding a truly useful imaging modality, with an additional step for reconstructing the phase shift (and possibly the attenuation), known as phase retrieval. The different applications of phase-contrast propagation-based imaging range from clinical applications to high-resolution studies of biological samples within synchrotron experiments. These realizations were possible due to upstream simulations that allowed for the precise definition and improvement of such approaches.

In 2010 and 2012, Chen et al. [10] and Bravin et al. [11] reviewed the different methods to simulate XPCI. Ten years later, Quénot et al. [12] reviewed the state-of-the-art and compared ray optical and Monte Carlo method simulations; Berujon et al. [13] reviewed imaging using random modulation masks. The previous reviews were consistent and thorough; however, some date back a while, and the last review (from 2021) details the different methods for simulation but does not focus on the combination of wave and particle effects. In the present review, we demonstrate, investigate, and analyze how simulations of XPCI have improved in recent years. We review methods that combine wave and Monte Carlo simulations.

There are several motivations for accurately simulating X-ray phase contrast images. For example, access to synchrotron facilities is limited. The ability to simulate an imaging experiment beforehand can make the use of available “beam-time” more efficient by allowing for the pre-selection of imaging conditions, such as X-ray energy, detector position, or the grating parameters. Classically, phase contrast has been simulated mainly using wave optics or, in some simpler cases, ray optics [14]. Another motivation for the accurate simulation of phase contrast is that in the classical approaches, all the effects that contribute to the final image are not accounted for, for example, incoherent scattering. A common limitation of the phase retrieval step, especially in PBI, is the sensitivity to noise in the low spatial frequency range. The sensitivity itself is due to the physical characteristics of the imaging system, but it is increasingly thought that the low-frequency contributions are due to the effects that are not accounted for by the classical methods.

The utilization of XPCI simulations for clinical purposes is not limited solely to this technology, as various research initiatives have focused on enhancing various related aspects. These include improving the detection of small-angle scattering, such as was conducted by Modregger et al. [15], and dark-field imaging, such as in the works of Weber et al. [16], Gureyev et al. [17], and Spindler et al. [18], as well as phase retrieval in the works of Burvall et al. and Lohr et al. [19,20].

Incoherent scattering has classically been simulated using the Monte Carlo (MC) method of image simulation. The MC method offers accurate particle-based simulation for the modeling of photon-matter interactions (scattering, photoelectric effect, and pair creation). In MC image simulation, virtual particles are created in a random manner and are then transported through a model of a sample in a stepwise manner. The path of each particle through the object is determined based on the probabilities of scattering and absorption obtained from the corresponding physical cross-sections of the material.

In order to correctly account for both the phase contrast and scattering effects in images, the two effects should be combined into one simulator. To this end, several methods to achieve this combination of wave and particle effects have recently been proposed [21,22,23]. Therefore, in this review, we explore the classical approaches to the simulation of phase contrast and scattering separately, followed by a more detailed review of the recent techniques for combining the two effects. We discuss the apparent merits and limitations of these techniques and make the connection to the Wigner distribution function-based methods that are used in visible light optics. This type of method seems to represent a promising direction of research for the simulation of XPCI.

2. Wave Optics Simulation of X-ray Phase-Contrast Imaging

The classical approach to the simulation of XPCI is based on the classical wave optical diffraction formulas: either the Fresnel (nearfield) or Fraunhofer (farfield) regime. The regimes are differentiated by the relative propagation distance with respect to the imaging parameters, such as pixel size and X-ray wavelength. Mathematically, both regimes can be derived as linear approximations of Kirchhoff’s diffraction formula and, thus, provide straightforward linear relationships for light propagation.

In the near field case, the contrast generated on the detector from a given object described by its complex refractive index is

$$n=1-{\delta }_n(x,y,z)-i{\beta }_n(x,y,z)$$

(1)

with ${\delta }_n(x,y,z)$ as the refractive index decrement, and ${\beta }_n(x,y,z)$ as the attenuation index at position $(x,y,z)$. The phase $\varphi$ and amplitude B of the wave are usually considered straight-line projections through the refractive index,

$$\varphi (x,y)=-\frac{2\pi }{\lambda }\int {\delta }_n(x,y,z)\mathrm{d}z,$$

(2)

$$B(x,y)=\frac{2\pi }{\lambda }\int {\beta }_n(x,y,z)\mathrm{d}z,$$

(3)

so that the exit wave (4) is

$${\psi }_0(x,y)=\psi (x,y,z=0)=exp[-B(x,y)]exp\left[i\varphi (x,y)\right].$$

(4)

The propagation of light over a distance D is then given as a linear filtering of the exit wave (5):

$${\psi }_D(x,y)=\psi (x,y,z=D)={\psi }_0(x,y)★P_D(x,y)$$

(5)

where $P_D$ is the so-called Fresnel propagator (6):

$${\widehat{P}}_D(f_x,f_y)=exp\left[-i\pi \lambda D\left(f_x^2+f_y^2\right)\right].$$

(6)

The intensity on the detector (7) is the squared modulus of the wave in the detector plane:

$$I_D(x,y)={\left|{\psi }_D(x,y)\right|}^2.$$

(7)

When the propagation distance is sufficiently large, the diffraction pattern can be calculated through Fraunhofer diffraction. Mathematically, this corresponds to the Fourier transform of the wave exiting the object in the spatial co-ordinates of the detector plane, assuming the object is thin enough that no diffraction occurs inside it. We focus here on the Fresnel case.

Wave-based approaches have advantages in terms of implementation simplicity and rapid calculation. They involve either the intensity of the Fourier transform of the wave or the intensity of a convolution of the wave with a propagator function. The formulas are available in standard textbooks, such as [24]. The calculated intensity represents the probability of photon reception at a certain position. In order to simulate unwanted random contributions, noise has to be added to the ideal pattern. The noise can take the form of a Poisson process for low-imaging statistics, additive Gaussian white noise for more abundant photons, or some intermediate distribution, reflecting the image after a specific counting time to form the complete diffraction pattern.

The wave optics approach is, on the surface, very simple. One subtle difference, however, is that the formulation is not discrete. Therefore, to obtain reasonable results, the images corresponding to the wave must be appropriately oversampled [14,25].

Peterzol et al. [14] showed how the sampling process affects ray and wave optics: For ray optics, in the reviewed articles, the sampling is not critical; it depends on the spatial resolution of the detector and the propagation distance. For wave optics, higher energies and smaller propagation distances induce finer fringes and, therefore, more oversampling. Langer et al. [26] demonstrate that oversampling is necessary for correct results. More recently, Häggmark et al. [27,28] show that combining the simulations of higher X-ray energies and detailed object models exists. The articles discuss the sampling requirements for the wave propagation simulations of phase-contrast X-ray imaging. The sampling requirement for wave propagation simulations includes very high wavefront sampling, which limits simulations to small idealized objects. The paper suggests that the upsampling strategy will make structures smooth and rounded compared to real microstructures that may have more edges. The proposed solution would be to adjust each material separately, but for biological tissue, the result suffices. This sampling requirement should, therefore, depend on the requirements of the simulation in itself.

For the purpose we investigate here, a limitation is that while the wave formulation is mathematically exact, it cannot take into account particle effects, such as scattering. Particle effects may be simulated separately, and the results combined into a posteriori, but the two simulations must then be appropriately weighted, which is not straightforward. In a complete simulation, the image should be constructed so as to account for all the considered physical effects simultaneously, ideally in a photon-by-photon manner, such as in the MC approaches in Section 3.

The early usage of wave-based approaches in XPCI was reported by Lagomarsino et al. [29]. Vidal et al. [30] investigated artifact sources in synchrotron micro-tomography based on a computer code [31] that was developed to simulate an X-ray imaging system. The physical principles were the X-ray attenuation law and the detecting probability based on deterministic methods. The code uses CAD models to describe complex 3D objects and allows for the adjustment of the imaging chain’s geometry. Initially, the deterministic computed images have no photon noise, but Gaussian random fluctuations can be added if needed. Later on, such techniques were implemented in open source software, such as GATE [26].

Several works offer studies on the extent of imaging systems and the specific phenomena to be recreated. Zdora et al. [32] presented a simulation study on the effects of a polychromatic X-ray spectrum on the performance of modulation-based, dark-field, and phase-contrast imaging. This was carried out through a simulation study on polychromatic X-ray speckle-based imaging and the characterization of the beam-hardening artefacts and their effects.

An example of simulation based on the Fresnel diffraction integral is the one by Chang et al. [33]. It is used to calculate the propagated wave to obtain a refraction map (after the object) by differentiating the phase in the direction of refraction analysis. The simulator can be used for testing and developing highly sensitive X-ray imaging techniques based on X-ray refraction analysis prior to experimentation. It was validated by comparing the CT reconstruction of a virtual phantom with its map of a refractive index, showing deviations below 0.7% for soft tissues.

Another approach to wave optics simulation is the method proposed by Dey et al. [34]. The paper describes a novel single-phase-grating phase-contrast system that has been simulated using Sommerfield-Rayleigh diffraction integrals. The particularity of the grating is that it is linear-quadratic. A deliberate spatial dependence of phase was introduced in addition to a linear grating to build up a slow, varying fringe pattern on a standard X-ray detector. The Sommerfield-Rayleigh integral simulation is of a single-grating X-ray system with an alternating linear and linear-quadratic grating function. Chirp grating is assumed to introduce a transmission and phase delay. This allows for the interference pattern to be tuned to different applications depending on the detector resolution.

Wave-based simulations can be used for different purposes and with different technologies. He et al. [35] demonstrated a method using a wire mesh to produce a periodic intensity pattern in the illumination to generate phase-contrast images. They also presented a technique using wider windowing functions during Fourier processing to improve spatial resolution in mesh-based phase-contrast imaging. Bewick et al. [36] proposed a method using the “T-matrix” to simulate coherent light propagation through biological tissue, which is more efficient than existing methods. Sung et al. [37] used a wave optics approach to simulate a GBI system to image a 4D whole mouse body (MOBY) phantom. The phantom was defined using non-uniform rational B-splines. Vignero et al. [38] offered an approach where the measured summary metrics were applied to generate transmission and differential phase images with large fields of view.

An alternative to full wave optics simulations is the paraxial wave propagation model. It is a fast and accurate model that has been proposed for forward modeling in XPCI, capable of modeling arbitrary objects and multi-scattering [39]. The model incorporates geometric cone beam effects into the multi-slice beam-propagation method. The multi-slice beam-propagation method (MSBPM) is a numerical simulation technique used in the field of optics and photonics to model the propagation of light through complex structures, such as photonic devices and waveguides. It is an extension of the traditional beam-propagation method (BPM), which is a widely used approach for simulating light propagation in planar waveguides. All simulations were performed in MATLAB, and the implementations of the Mie solution were carried out through parallel beam geometry for a multiple scattering effect. The simulations were performed on different objects and proved efficient, with a computation time depending on the number of pixels and how many slices the objects were divided into.

Another approach is ray optics, which is based on tracing curves that are perpendicular to the wavefront. This type of simulation will only consider refraction (in the object) as the mechanism for phase contrast; however, interference effects are not accounted for. Ray-based simulation for X-ray phase contrast was pioneered by Peterzol et al. (2005) [14]. The ray optical method adequately approximates the wave optical approach when there are restrictions on the spatial frequencies present in the final image without any limitation on the maximum phase shift. The ray optical approximation describes the phase-contrast formation mechanism as the refraction of X-rays in an object due to variations in the thickness and refractive index of the sample. This approximation can be used when the pixel size of the imaging system is sufficiently large.

Hassan et al. [40] proposed a ray tracing method to develop simulations for a mesh-based X-ray phase imaging system. Mesh-based XPCI has the particularity of using a mesh detector. The mesh detector is capable of measuring the phase shift of the X-rays with high sensitivity. It does this by analyzing the interference patterns created by the mesh as the X-rays pass through it. The phase shift information is extracted from these interference patterns. The simulation is based on a forward model using ray tracing to produce accurate images; their aim is to prove that this is a promising technique for system optimization.

Quénot et al. [41] presented a comparison of different simulation methods, including a ray tracing method. Their own PARESIS software allows for computing the intensity images obtained during modulation-based XPCI. The evaluation presented a comparison of different simulation codes: MC, analytical ray tracing, and wave optics Fresnel propagation. The simulators were contrasted against synchrotron and conventional imaging experiments. The codes were mainly for MoBI, but they also work for PBI.

The main limitation of the ray optics approach is that interference phenomena cannot be accounted for. In the sub-micron range, interference effects start to dominate in phase contrast. It is straightforward to combine ray optics and scattering, as well as combine ray tracing followed by Fresnel propagation [22,42,43]. It is the combinations with coherent effects that are difficult. These effects exist due to the interference of the X-rays when radiation exhibits wave-like properties; they can have both positive and negative implications: enhancing image contrast, reducing artifacts, optimizing the radiation parameters, dose reductions, and improving phase retrieval and image analysis.

3. Monte Carlo Simulation of X-ray Phase-Contrast Imaging

As mentioned previously, improving propagation-based phase-contrast (XPCI) imaging will improve resolution, reduce radiation exposure, and enhance contrast. This is because XPCI can reveal the fine details in various objects that traditional X-ray methods might miss. The wave optics, ray tracing, and paraxial approximation methods reached their limit regarding the effects that could be reproduced in a simulation compared to the experiments. Monte Carlo (MC) is a powerful computational tool that allows for focusing on some of those effects, such as scattering. MC is a particle-based approach that models the behaviour of photons as they traverse a sample during simulation. The inclusion of refraction in the model makes it possible to simulate phase-contrast images with the same limitations as those in ray-based methods.

While MC methods are generally time-consuming, recent work has demonstrated the possibility of accelerating them using machine learning-based approaches [44]. Therefore, in the future, it might be possible to accelerate combined wave and particle approaches using machine learning.

Sanctorum et al. [45,46,47] used GATE (based on Geant4) and Matlab to simulate XPCI. Firstly, a GB-XPCI was introduced for a simulation focused on phantoms with fibrous microstructures; secondly, the framework was extended to model more interactions and combine the MC simulations of GATE with numerical wave propagation; thirdly, the GI aspect of the simulation is focused on by replacing the original ones with virtual ones to reduce simulation time and optimize their study of GB-XPCI simulations. The different studies prove the efficiency and improvement of the technique via the introduction of new physics-based tools for accurate XPCI simulations using the GATE framework, focusing on the edge illumination method.

Langer et al. [42] implemented an MC process for the refraction and total reflection of X-rays. The technique results in a precise and complete simulation of XPCI in GATE. It includes absorption, scattering, and refraction and directly integrates wave optics into GATE. Refraction is implemented by using a boundary process within GATE and can be adapted to imaging methods by altering certain parameters of the source and detectors.

Yan et al. [48] used Geant4 for an XPCI simulation focused on cryogenic implosions and inertial confinement fusion rather than a medical situation. The MC model implements photoelectric effects, such as scattering and absorption, through the direct use of Geant4 modules, and refraction is implemented by using a boundary process according to Snell’s law.

Wang et al. [49] used Geant4 to implement X-ray refraction for XPCI. The simulation uses 5 million particles and considers only the refraction effect; it is implemented in Geant4 by defining the refraction indexes manually regarding material properties.

Brombal et al. [50] presented an X-ray differential phase-contrast imaging simulation using Geant4. It aims to define the optimal design of the experimental setup, which includes a custom X-ray refraction process. It focuses on edge illumination XPCI, as well as propagation-based XPCI. The refraction is implemented by using a boundary process according to Snell’s law. The propagation-based image is formed by tracking the refracted X-rays from the sample to the detector. Edge illumination is implemented by using Wiener filter-based integration in the Fourier space. The MC simulation is run using Geant4 processes with different detectors and parameters for the different types of imaging.

Several approaches exist for simulation imaging using MC methods [42,45,46,47,48,49,50] and are seemingly identical in methodology because they implement Geant4 for different case scenarios. It is apparent that MC simulation toolkits/frameworks (mainly GATE and Geant4 in the literature) are improved when put through different implementations. The study shows that having so many methods implementing similar approaches will finally lead to efficient computer code. The main drawback of the MC approaches to the simulation of XPCI (described above) is that they cannot account for interference effects, only refraction. Further, they still separate wave- and particle-based simulations into separate simulators and combine the results by weighting and adding them a posteriori.

4. Combined Wave-Optics and Monte Carlo Simulation of X-ray Phase Contrast

The attempts to combine particle and wave aspects typically involve separate simulations that are then combined. There are different limitations to implementing such types of combinations. Classical wave methods have certain limitations when it comes to accurately simulating all aspects of XPCI. Shanblatt et al. [39] mentioned different limitations regarding wave optics simulations, such as reliance on paraxial approximation, which may not hold for high numerical aperture objectives or strong phase gradients. With ray tracing, the implementation would require a substantial number of paths through the sample to achieve convergence to obtain physically relevant results. During the simulations, it is only with a very large number of particles that the desired effects can be achieved. A simulation based on ray tracing, including particle effects such as scattering and wave effects such as diffraction, would need very high computational capacity, as mentioned in the previous section.

A combination of wave and particle effects would promise a single simulation, a more realistic simulation of noise, and a simulation that is more physically accurate; it would also avoid the ad hoc weighting of the images and “thin” object assumptions. Partially coherent illumination would be more easily simulated due to particle effects accounting for multiple scattering.

Several attempts at combining the simulation of particle and wave effects have been presented in the literature [21,22,23,38,43,51]. Cipiccia et al. [51] discussed the implementation of the Huygens-Fresnel principle, alongside refraction and absorption, using the FLUKA MC code, for the first time. The simulation framework is adapted for X-ray GI and is based on a two-part method to capture both particle and wave effects. Wave optical propagation is implemented through the application of the Huygens-Fresnel principle. The MC part is modeled using FLUKA. This accounts for the refractive index, applying Snell’s law for the simulated materials. It uses discretization to approximate continuous processes; this is carried out by dividing them into discrete steps or intervals, allowing the tracking of individual particles or photons and calculating the interaction. Firstly, a ray tracing approach is validated by simulating the scattering for relaxed coherent conditions through a sample. Secondly, a wave optical approach is validated by simulating diffraction and interference via the application of the Huygens Fresnel principle and verification using the double slit experiment. The simulated models were then further validated for both edge illumination XPCI experiments in the context of the ray tracing approach and a Talbot interferometer experiment for a wave optical approach. The framework was used to compare the formation of phase-contrast images for the wave optical and the ray tracing approaches; both are implemented by using FLUKA and, therefore, are a working combination of wave and particle effects for XPCI techniques.

In 2009, Bartl et al. [21] presented the first MC-based simulation of XPCI, simulating GB-XPCI through wave optics combined with a separate MC simulation of incoherent scattering. The paper is further detailed in Section 4.1.

In 2016, Peter et al. [43] employed ray tracing to simulate absorption, scattering, and refraction. The method transforms particles into waves through a heuristic, but it does not detail the scattering’s image impact. The framework combines both the particle and wave-like properties of X-rays to model the physical interaction processes occurring in GI alongside numerical simulations of phase-sensitive X-ray imaging using MC Methods. The paper is further detailed in Section 4.2.

In 2018, Vignero et al. [38] described the development of a hybrid simulation framework for GB-XPCI that combines analytical and empirical input data. The framework offers full wave simulations combined with MC refraction and reflection. Firstly, the phase and attenuation properties are calculated, followed by convolving the object with a Gaussian filter with a standard deviation equal to the scaled focal spot blur to account for the finite source size; finally, noise is added for the correct texture. From there, they compute the expected signal based on theory instead of modeling the wave interactions. Transmission imaging is predicted by the Beer-Lambert law. The differential phase signal is based on the intensity shift depending on the refraction angle.

In 2022, Tessarini et al. [23] described a semi-classical MC algorithm for the simulation of X-ray-phase contrast, using grating interferometry as an example within the publication. The framework is inspired by different works that include coherent effects into MC simulations, such as full MC using FLUKA, ray tracing-based MC, and hybrid models. The paper is further detailed in Section 4.3.

4.1. Simulation of GB-XPCI by Combining Fresnel Propagation and MC Scattering

Bartl et al. [21] presented a technique that adds together a wave simulation and a particle simulation (Figure 1). The framework incorporates all contributing physical aspects, especially the particle and the wave behaviors of X-ray photons, realistic noise, and a detailed X-ray source and detector description.

The framework is adapted to a differential phase-contrast imaging type, which is grating interferometry. It simulates coherent X-ray propagation, interference, and incoherent particle scattering. It is structured in the following way: a wave optics part defines the source and propagates it through space and through the object until it reaches the detector, and then adds the scattering contributions at said detector.

The wave optics part of the simulation starts with a characterization of the sources, which are coherent waves. Two types of waves are implemented: plane or spherical. The transmitted wavefront is calculated based on the thin-sample approximation, both for the object (in case there is one) and for the phase-grating. The thin-sample approximation simplifies the imaging process by assuming that the sample being imaged is very thin compared to the wavelength of the radiation used for imaging. By using this approximation, the initial wave is calculated behind the phase grating at $z=0$. This wave is then forward-propagated along z using the Fresnel propagator (6). The propagation through the geometry is based on the solution of the Helmholtz equation in free space.

The scattering part of the simulation is based on the Monte Carlo simulation tool RoSi [52]. It is used to calculate the scattered incoherent parts of the intensity distribution immediately in front of the detector.

This framework combines the two effects by adding them to the detector. The detection is also simulated using the Monte Carlo simulation tool RoSi [52]. It is based on the generation of the point spread function for the Medipix detector. The point spread function is also known as impulse response; it is the response of a focused optical imaging system to a point source or point object. The addition of scattered photons with the resulting wave is added based on weights. The article does not specify how these weights are computed.

The framework is validated by the verification of the reconstructed image of the simulated grating-interferometry setup. The simulated object (a cylindrical human vessel filled with blood) proves valid compared to the expected calculations respecting the grating-interferometry dimensions.

The simulation parameters used in the work of Bartl et al. [21] were a point-like mono-energetic source of energy $30\mathrm{k}\mathrm{e}\mathrm{V}$ and a phase grating of size $4\mathsf{\mu }\mathrm{m}$, and the intensities were calculated until the third Talbot order.

4.2. Combining MC with Coherent Wave Optics via a Step-by-Step Simulation of GI XPCI

Peter et al. [22] presented a simulation framework of phase-sensitive X-ray imaging that takes both the particle- and wave-like properties of X-rays into consideration. It is a split approach that includes a three-step simulation, making the framework adaptable to different phase-sensitive X-ray imaging methods (Figure 2).

The framework is adapted to many types of imaging but is specifically tested for propagation-based imaging and grating interferometry phase-contrast imaging. It simulates coherent X-ray propagation, interference, refraction, and incoherent particle scattering. It is structured as such: first, the Monte Carlo part provides the diffraction, interference, refraction, and scattering events through space and through the sample. A transition part follows, adapting the MC results to be used in the wave optics part. The wave-optics part propagates the resulting contributions of the source passing through the sample onto the detector.

The simulation starts with the MC part of the split approach by using egs++, which is the C++ interface for EGSnrc. Particle transport follows stepwise transport from the source section of the geometry through the interaction site (which is the object) until it reaches the edge of the MC part. For each step, the path is determined, and the respective phase shift is added to the optical path length of the photon. The optical path length describes the distance traveled through a medium from one point to another; it takes into account not only the physical distance between the two points but also the effects of the refractive index of the material on the path of the light. These interactions, therefore, include scattering, refraction, and interference. All particles that did not undergo any interactions will have the same optical path length. It is the phase space that is then passed on to the transition part.

The underlying algorithm on which the simulation is based is not explicitly mentioned; however, regarding the aforementioned part, we can identify a ray tracing algorithm.

The MC part produces a phase space for each particle. Within the second part of the split approach, the transition part produces a complex amplitude via the association of each particle with a wave. These resulting waves, if they correspond to particles that fell into the same area, will be summed up under consideration of their phase. This reduces computation time for the wave optics part. The resulting waves are, therefore, the wavefront after the sample. The wavefront is then passed on to the wave optics part.

The wave optics part of the simulation is the last part of the split approach. It uses the wavefront from the transition part to calculate the intensity obtained at the detector.

This framework combines the particle and wave effects by consecutively passing from the first to the latter through the use of calculations. The detection is represented by the calculation of the intensity from the resulting complex amplitude wave. However, as it is an adaptable framework depending on the types of imaging, the detection will differ based on the chosen technique. As mentioned above, the framework was validated by a comparison with a propagation-based imaging simulation and a GI simulation.

For propagation-based imaging, the simulation propagates the wave to a plane at a distance d from the sample. This is carried out through convolution with the free-space propagator. Calculating the square of the absolute value of the propagated wave gives the intensity of the signal on the detector. For GI imaging, the simulation propagates the wave through the two gratings: firstly, the phase grating and, secondly, the absorption grating. The amplitude is multiplied by the phase shift of the phase grating. The result is then propagated to the absorption grating via a convolution with the free space propagator. What results is then multiplied with the transmission function of the absorption grating. The intensity is the integral over the whole area of the pixel of the square of the absolute value of the wave. This procedure is repeated for all phase-step positions. The projection images are then obtained from the intensity using a Fourier-based approach.

The validation of the propagation-based imaging simulation was carried out through a comparison of two results. The first comparison was with the data obtained from the projection approximation; the other comparison was with the measured data from the TOMCAT beamline. Comparisons were carried out for three different distances. The images show a comparison of the line profiles from the measurement signal, the MC signal, and the PA signal. The fringes observed in the experiment are much better approximated by the MC signal than the PA signal for the smaller sample detector distances.

The validation of the GI imaging simulation was carried out through a comparison of the data measured using a GI setup for two different phantoms. The qualitative agreement of the reconstructed phase images shows the validation of the technique by showing that the phase signal is simulated realistically. The correlation coefficient for the two images is 0.96, and the normalized mean square error is 0.06%.

The parameters used by Peter et al. [22] were a finite-size divergent source with an energy of $10\mathrm{k}\mathrm{e}\mathrm{V}$ and an object consisting of a hollow cylinder with an outer radius of $5.5\mathrm{m}\mathrm{m}$ and am inner radius of $4.5\mathrm{m}\mathrm{m}$, consisting of polypropylene. The cavities in the cylinder were filled with different liquids to test different levels of absorption. The source-to-sample distance was $25\mathrm{m}$.

4.3. Semi-Classical Monte Carlo Algorithm for the Simulation of X-ray Grating Interferometry

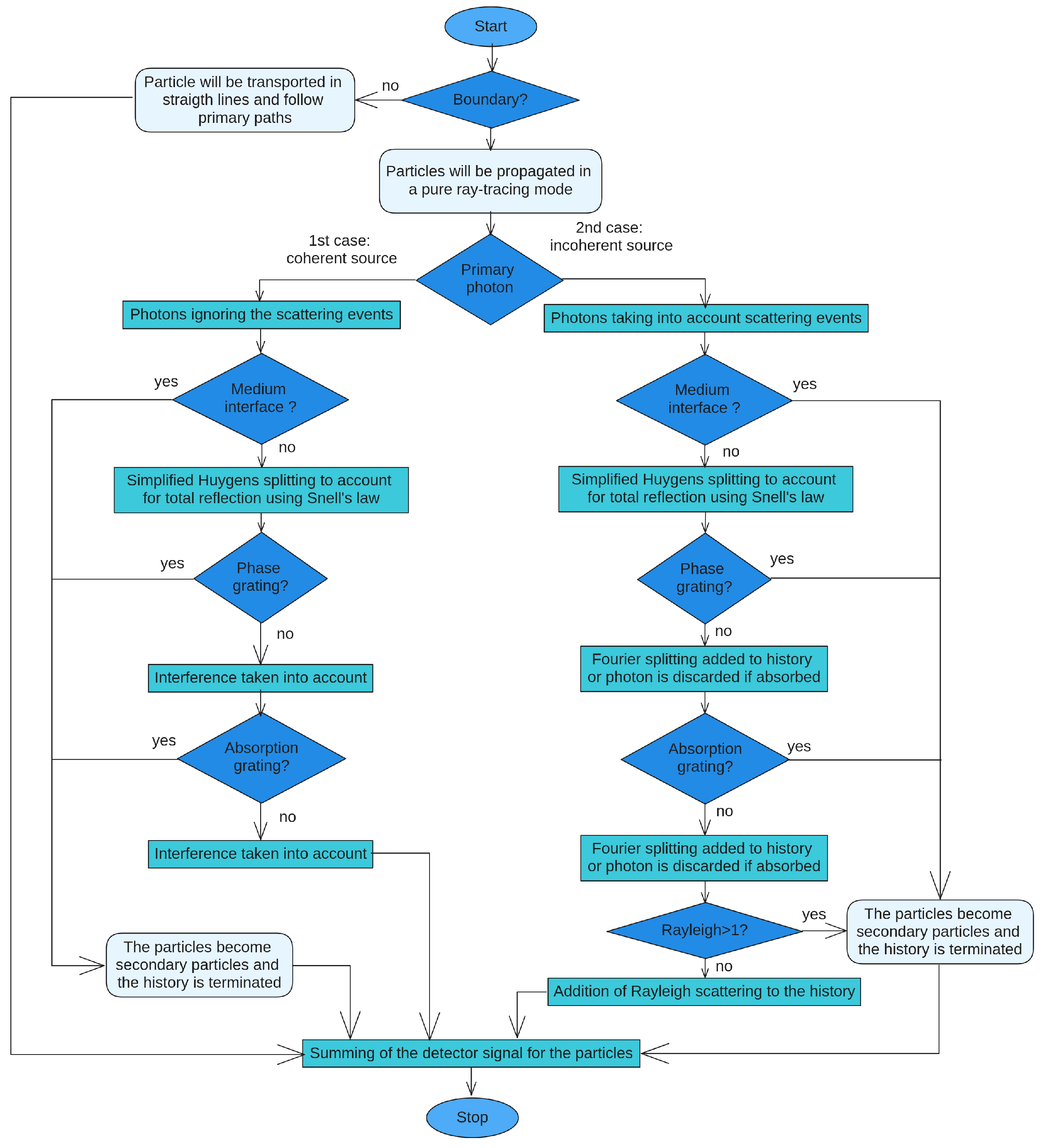
Tessarini et al. [23] presented a simulation framework of phase-sensitive X-ray imaging that is based on semi-classical properties of particles, allowing for the combination of particle- and wave-like effects (Figure 3).

The framework is adapted to simulate grating-interferometry phase-contrast imaging. It simultaneously accounts for interference, refraction, diffraction, and scattering processes. It is structured as such: the general implementation of the system is carried out through complex amplitudes that are modified according to the different elements they come across through the geometry. It is based on the rules of quantum mechanics, where the addition of these photon amplitudes becomes a sum over the smooth surfaces of the system (medium interfaces, phase gratings, and absorption gratings), characterizing an overall amplitude between the source and the detector. Propagation through the system follows the ray tracing algorithm. The simulation of photon transport is carried out using the definition of single photon amplitude in real space, resulting in the aforementioned overall amplitude that represents the propagated wave source. Combining wave and particle effects is based on the full path integral of quantum mechanics. The full path integral [53] replaces the classical notion of a single, unique classical trajectory for a system with a sum or functional integral over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude. As it is such a complex approach, it is simplified to achieve acceptable simulation times; this simplification brings the definition and calculation of probabilities. These probabilities are introduced in the photon-based ray tracing to be calculated for when the system reaches specific events. These events are interference, diffraction, refraction, and scattering.

The ray tracing algorithm is used for the calculation of the probability of a primary photon. The calculation follows conventional MC particle transport, implemented with EGSnrc, and is approximated classically with sharply defined position and momentum. The scattering events, with their own probability, are introduced in the algorithm through a second step. During the calculation of the primary photon, scattering events may happen along every photon path. The Beer-Lambert law governs the probability of the appearance of a scattering event within a straight path segment, as in conventional MC.

Similarly to Bartl et al. [21], the simulation has distinct events depending on the coherence of the source. The different sources affect the primary signal probability; they can either be a planar wave or a spherical wave.

Photons are simulated one by one; either one leaves the geometry or its amplitude must be added to the total detector signal before a new photon history is started. Thus, the photons are treated independently, each creating a detector signal.

The simulation starts with a coherent source, and the photons are to ignore the scattering events. This translates to the conventional particle history of MC particle transport. During these trajectories, the algorithm keeps track of the amplitude of the ray. This propagation follows a pure ray tracing mode; it allows for the accounting of interference patterns due to primary events. A second simulation with scattering events enabled is calculated and will add potential secondary particles to the particle stack if such events should occur.

If there is neither a sample nor gratings, they will have a single trajectory and will go in a single direction. The trajectory and direction remain unchanged, in a straight line, until it reaches the detector.

The introduction of optical elements will impact the manner in which the photon leaves the simulation geometry.

If the simulation starts with a coherent source and there are interfaces, such as a sample, a phase grating, or an absorption grating, the ray tracing algorithm translates this into multiple particles crossing the geometry and its contents.

The initial approach introduced uniform path splitting based on the Huygens-Fresnel principle; however, the resulting calculation would be much too demanding due to an unfeasible amount of paths. It is with variance reduction in mind that within the simulation, different probabilities were assigned for the different interfaces, with the aim being to facilitate the computation of the algorithm. For the case of reflection, only total reflection is of importance for the simulation; therefore, Snell’s law is applied as a classical approximation for medium interfaces. Fourier splitting procedures for phase and absorption gratings improved simulation time, as their function was to restrict the transport to the relevant paths and give the user a way to define a maximum angle to be considered in the simulation. In the case of absorption gratings, the photon is discarded if the classical photon path hits an absorbing section of the grating and is transmitted otherwise. In the case of phase gratings, the transmission consists of a discrete sum over the Fourier coefficients, defining the probability of the transmission amplitude. There are cases where photon paths have no position-dependent phase term. These are directly transported through the grating with no modification, and a weight is applied to each path.

Here, the Fourier splitting and the adapted Huygens splitting are made similar to the MC particle splitting. The weights of secondary particles are multiplied according to a specific value depending on the interface that created the scattering. If Rayleigh scattering occurs, then the path is considered primary on the particle stack. This would increase computation time; therefore, the number of these coherent events is limited to one per path. If any other propagation of secondary particles happens, no extra interference should be calculated, and its history is terminated by sending the photon ray to the detector.

Regarding detection, the detector signal is calculated depending on the hits received and the amplitudes that were associated with the particles that reached it. The detector signal is constructed based on the probabilities associated with either a photon or a scattered photon. The final detector signal is an addition of all the recorded hits. It is defined for both the coherent and incoherent cases. However, to simplify the simulation, the only case scenario investigated is the single-scattering one. The probability of finding a scattered photon having a specific energy within a specific pixel will depend on the source type.

The simulation is validated using five comparisons. Four are simulations in academic cases: the double-slit for interference validation, the Talbot carpet for Huygens and Fourier splitting validation, a polystyrene and silicon cylinder with GI for absorption and differential phase validation, and a cylinder with GI for deposited energy validation. The final comparison is with an experimental tabletop GI setup. All verify that the simulations are realistic.

The simulation parameters used by Tessarini et al. [23] were an incoherent source: three gratings with a 0.5 duty cycle and periods of $1\mathsf{\mu }\mathrm{m}$, $1.5\mathsf{\mu }\mathrm{m}$, and $3\mathsf{\mu }\mathrm{m}$, respectively. The space between G1 and G2 was $20.1\mathrm{c}\mathrm{m}$, and between G0 and G1, it was $60.3\mathrm{c}\mathrm{m}$.

5. Discussion and Conclusions

Since XPCI is usually considered a wave phenomenon, the simulation of phase contrast has historically been carried out by mainly using a wave perspective and the well-known Fresnel diffraction formulas. The ray optical approach was originally introduced as a way to simplify the simulation of XPCI. This approach more easily accounts for scattering and other effects and can include refraction and reflection on interfaces, but it is only valid for slowly varying phase relative to the spatial resolution of the imaging system and does not account for interference effects.

An MC-based (pure and/or combined) XPCI simulation should be chosen when needed to incorporate phenomena specific to particles, such as scattering. Pure wave approaches are specific for a simulation aiming to recreate the effects of phase contrast without correctly including reflection or scattering.

What both techniques show is that they can work for the same X-ray energies, resolutions, and samples. However, the pure MC method allows for additional geometries to be incorporated. The combined MC method allows for a distinction of the different parts of a simulation, making the parameters more adjustable.

MC simulators (pure and/or combined) will permit the study of the relationship between the dark-field signal and the SAXS signal. The dark-field signal illuminates the specimen with oblique or scattered light for small pixel sizes, and the SAXS signal allows for the quantification of nanoscale density differences with a small-angle scattering technique.

With the rise of dark-field imaging, the contribution of scattering to the image formation process has received increasing attention. It is also thought that the scattering component can contribute to the low spatial frequency noise often observed in images after phase retrieval [26]. This has sparked an interest in methods that allow for simulation at the same time as the wave effects of phase contrast and the particle effects of incoherent scattering. These methods, however, remain separate simulations that are combined in an ad hoc manner into a final image, not allowing for the precise estimation of noise in the phase-contrast component, which is possible with the use of MC methods.

The different simulation methods for phase-contrast imaging described in this review differ in their technical complexity, the use of X-ray optical elements, the readout process, and the method of propagating the signals within the framework, as well as how they detect and measure the different phenomena that alter X-rays. However, few direct comparisons of different methods have been performed so far. As a summary, a visual comparison is given in

Table 1. Comparison of the benefits and limitations of each method.

Comparison of XPCI Simulation Methods
Classical Methods		Pure MC Methods		Combination
Benefits	Limitations	Benefits	Limitations	Benefits	Limitations
Considers refraction and absorption	Formulations are not discrete	Photon by photon image construction possible	Interference and diffraction are not fully taken into account	Interference and scattering are possible in addition to refraction and absorption
Numerous simulations offer different implementations	Interference, diffraction and scattering are not taken into account	Scattering can be taken into account	Nonlinear effects and the complexities of modern optical systems can challenge accuracy	Two-part simulation can save time
Easy to implement: involves either the intensity of the Fourier transform of the wave or the intensity of a convolution of the wave with a propagator function	Images cannot be constructed photon by photon	Accurate simulation of phase-sensitive X-ray imaging		Photon-by-photon image construction possible
		Nonlinear effects and the complexities of modern optical systems can challenge accuracy	Assumption of independence	Accurate simulation of phase-sensitive X-ray imaging
			Convergence issues	Good agreement between measurements and simulations

.