An Ultra-Compact X-ray Regenerative Amplifier Free-Electron Laser
Abstract
1. Introduction
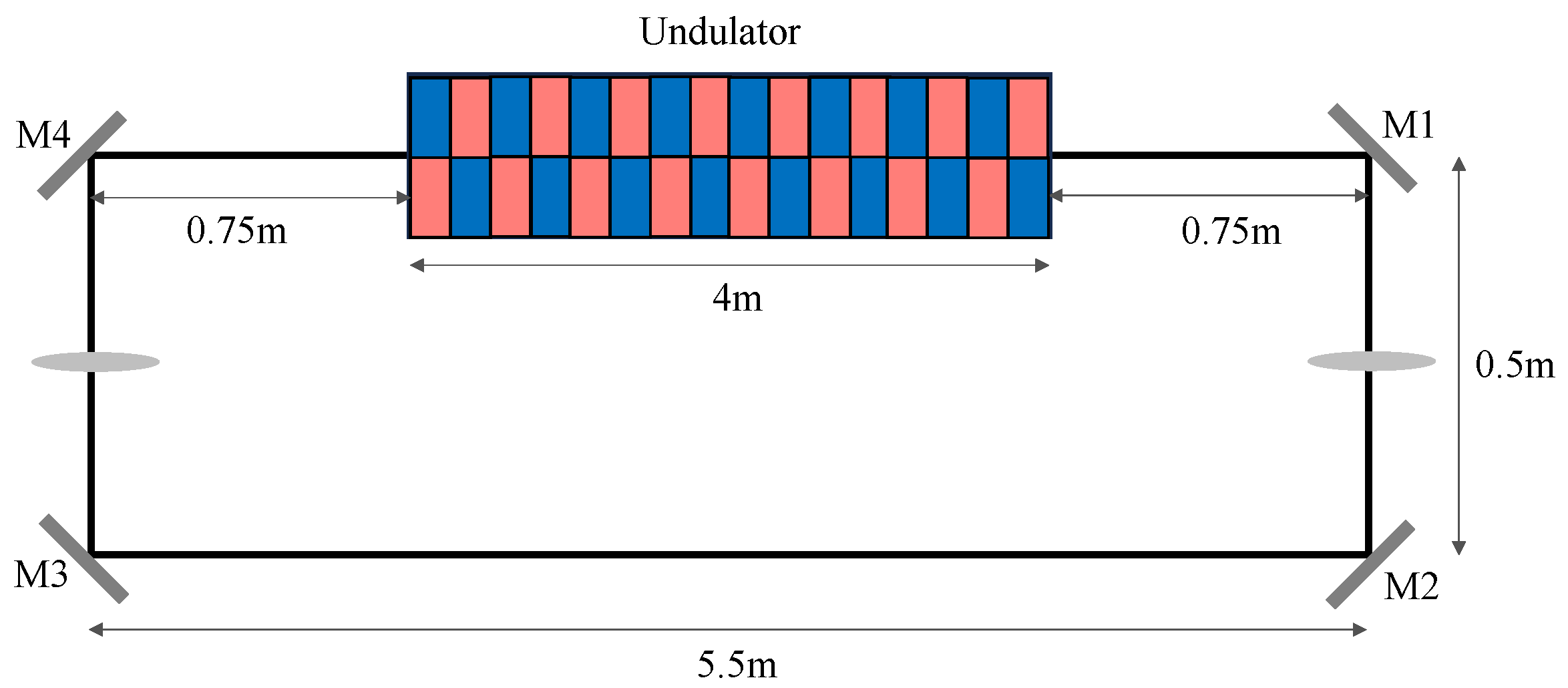
2. XRAFEL and Beam Configuration
3. One-Dimension Study
3.1. Three-Dimension Study
3.1.1. 1 μm Current
3.1.2. 3 μm Current
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEL | Free-electron laser |
| XFEL | X-ray free-electron laser |
| XRAFEL | X-ray regenerative amplifier free-electron laser |
| UC-XFEL | Ultra-compact X-ray free-electron laser |
| UC-XRAFEL | Ultra-Compact X-ray regenerative amplifier free-electron laser |
| SASE | Self-amplified spontaneous emission |
| SLAC | Stanford Linear Accelerator Center |
Appendix A. Stability of the Input SASE Seed on the Spectra

References
- Cornacchia, M. Linac Coherent Light Source (LCLS) Design Study Report; Technical Report No. SLAC-R-521; SLAC National Accelerator Lab.: Menlo Park, CA, USA, 1998. [Google Scholar] [CrossRef]
- Eom, I.; Chun, S.H.; Lee, J.H.; Nam, D.; Ma, R.; Park, J.; Park, S.; Park, S.H.; Yang, H.; Nam, I.; et al. Recent Progress of the PAL-XFEL. Appl. Sci. 2022, 12, 1010. [Google Scholar] [CrossRef]
- Abela, R.; Aghababyan, A.; Altarelli, M.; Altucci, C.; Amatuni, G.; Anfinrud, P.; Audebert, P.; Ayvazyan, V.; Baboi, N.; Baehr, J.; et al. XFEL: The European X-ray Free-Electron Laser-Technical Design Report; DESY: Hamburg, Germany, 2006. [Google Scholar] [CrossRef]
- Pandey, S.; Bean, R.; Sato, T.; Poudyal, I.; Bielecki, J.; Cruz Villarreal, J.; Yefanov, O.; Mariani, V.; White, T.A.; Kupitz, C.; et al. Time-resolved serial femtosecond crystallography at the European XFEL. Nat. Methods 2020, 17, 73–78. [Google Scholar] [CrossRef] [PubMed]
- Sobolev, E.; Zolotarev, S.; Giewekemeyer, K.; Bielecki, J.; Okamoto, K.; Reddy, H.K.N.; Andreasson, J.; Ayyer, K.; Barak, I.; Bari, S.; et al. Megahertz single-particle imaging at the European XFEL. Commun. Phys. 2020, 3, 97. [Google Scholar] [CrossRef]
- Berrah, N.; Fang, L.; Murphy, B.; Osipov, T.; Ueda, K.; Kukk, E.; Feifel, R.; van der Meulen, P.; Salen, P.; Schmidt, H.T.; et al. Double-core-hole spectroscopy for chemical analysis with an intense X-ray femtosecond laser. Proc. Natl. Acad. Sci. USA 2011, 108, 16912–16915. [Google Scholar] [CrossRef] [PubMed]
- Suga, M.; Akita, F.; Sugahara, M.; Kubo, M.; Nakajima, Y.; Nakane, T.; Yamashita, K.; Umena, Y.; Nakabayashi, M.; Yamane, T.; et al. Light-induced structural changes and the site of O=O bond formation in PSII caught by XFEL. Nature 2017, 543, 131–135. [Google Scholar] [CrossRef] [PubMed]
- Lehmkühler, F.; Dallari, F.; Jain, A.; Sikorski, M.; Möller, J.; Frenzel, L.; Lokteva, I.; Mills, G.; Walther, M.; Sinn, H.; et al. Emergence of anomalous dynamics in soft matter probed at the European XFEL. Proc. Natl. Acad. Sci. USA 2020, 117, 24110–24116. [Google Scholar] [CrossRef] [PubMed]
- Kao, C.C. Challenges and opportunities for the next decade of XFELs. Nat. Rev. Phys. 2020, 2, 340–341. [Google Scholar] [CrossRef]
- Nanni, E.; Graves, W.; Moncton, D. Nanomodulated electron beams via electron diffraction and emittance exchange for coherent x-ray generation. Phys. Rev. Accel. Beams 2018, 21, 014401. [Google Scholar] [CrossRef]
- Rosenzweig, J.B.; Majernik, N.; Robles, R.R.; Andonian, G.; Camacho, O.; Fukasawa, A.; Kogar, A.; Lawler, G.; Miao, J.; Musumeci, P.; et al. An ultra-compact X-ray free-electron laser. New J. Phys. 2020, 22, 093067. [Google Scholar] [CrossRef]
- Wang, W.; Feng, K.; Ke, L.; Yu, C.; Xu, Y.; Qi, R.; Chen, Y.; Qin, Z.; Zhang, Z.; Fang, M.; et al. Free-electron lasing at 27 nanometres based on a laser wakefield accelerator. Nature 2021, 595, 516–520. [Google Scholar] [CrossRef]
- Rosenzweig, J.B.; Andonian, G.; Agustsson, R.; Anisimov, P.M.; Araujo, A.; Bosco, F.; Carillo, M.; Chiadroni, E.; Giannessi, L.; Huang, Z.; et al. A high-flux compact X-ray free-electron laser for next generation chip metrology needs. Preprints 2023, 2023111639. [Google Scholar] [CrossRef]
- Huang, Z.; Ruth, R.D. Fully Coherent X-ray Pulses from a Regenerative-Amplifier Free-Electron Laser. Phys. Rev. Lett. 2006, 96, 144801. [Google Scholar] [CrossRef]
- Marcus, G.; Halavanau, A.; Huang, Z.; Krzywinski, J.; MacArthur, J.; Margraf, R.; Raubenheimer, T.; Zhu, D. Refractive Guide Switching a Regenerative Amplifier Free-Electron Laser for High Peak and Average Power Hard X rays. Phys. Rev. Lett. 2020, 125, 254801. [Google Scholar] [CrossRef]
- Rauer, P.; Decking, W.; Lipka, D.; Thoden, D.; Wohlenberg, T.; Bahns, I.; Brueggmann, U.; Casalbuoni, S.; Di Felice, M.; Dommach, M.; et al. Cavity based X-ray free electron laser demonstrator at the European X-ray Free Electron Laser facility. Phys. Rev. Accel. Beams 2023, 26, 020701. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Z.; Morgan, J.; Hemsing, E.; Huang, Z. Active Q-Switched X-ray Regenerative Amplifier Free-Electron Laser. Phys. Rev. Lett. 2023, 131, 055001. [Google Scholar] [CrossRef] [PubMed]
- Shvyd’ko, Y.V.; Stoupin, S.; Cunsolo, A.; Said, A.H.; Huang, X. High-reflectivity high-resolution X-ray crystal optics with diamonds. Nat. Phys. 2010, 6, 196–199. [Google Scholar] [CrossRef]
- Shvyd’Ko, Y.; Stoupin, S.; Blank, V.; Terentyev, S. Near-100% Bragg reflectivity of X-rays. Nat. Photonics 2011, 5, 539–542. [Google Scholar] [CrossRef]
- Kim, K.J.; Shvyd’ko, Y.; Reiche, S. A Proposal for an X-ray Free-Electron Laser Oscillator with an Energy-Recovery Linac. Phys. Rev. Lett. 2008, 100, 244802. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.; Huang, S.; Liu, K.X.; Kim, K.J.; Lindberg, R.R.; Bane, K.L.F.; Ding, Y.; Huang, Z.; Marcus, G.; Maxwell, T.J. Start-to-End Simulations for an X-ray FEL Oscillator at the LCLS-II and LCLS-II-HE. In Proceedings of the 38th International Free Electron Laser Conference (FEL'17), Santa Fe, NM, USA, 20–25 August 2017; JACoW: Geneva, Switzerland, 2018; pp. 247–250. [Google Scholar] [CrossRef]
- Huang, N.S.; Liu, Z.P.; Deng, B.J.; Zhu, Z.H.; Li, S.H.; Liu, T.; Qi, Z.; Yan, J.W.; Zhang, W.; Xiang, S.W.; et al. The MING proposal at SHINE: Megahertz cavity enhanced X-ray generation. Nucl. Sci. Tech. 2023, 34, 6. [Google Scholar] [CrossRef]
- Margraf, R.; Robles, R.; Halavanau, A.; Kryzywinski, J.; Li, K.; MacArthur, J.; Osaka, T.; Sakdinawat, A.; Sato, T.; Sun, Y.; et al. Low-loss stable storage of 1.2 Å X-ray pulses in a 14 m Bragg cavity. Nat. Photonics 2023, 17, 878–882. [Google Scholar] [CrossRef]
- Wollenweber, L.; Preston, T.R.; Descamps, A.; Cerantola, V.; Comley, A.; Eggert, J.H.; Fletcher, L.B.; Geloni, G.; Gericke, D.O.; Glenzer, S.H.; et al. High-resolution inelastic X-ray scattering at the high energy density scientific instrument at the European X-ray Free-Electron Laser. Rev. Sci. Instruments 2021, 92, 013101. [Google Scholar] [CrossRef]
- Kowalewski, M.; Fingerhut, B.P.; Dorfman, K.E.; Bennett, K.; Mukamel, S. Simulating Coherent Multidimensional Spectroscopy of Nonadiabatic Molecular Processes: From the Infrared to the X-ray Regime. Chem. Rev. 2017, 117, 12165–12226. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, U.; Kern, J.; Schoenlein, R.W.; Wernet, P.; Yachandra, V.K.; Yano, J. Using X-ray free-electron lasers for spectroscopy of molecular catalysts and metalloenzymes. Nat. Rev. Phys. 2021, 3, 264–282. [Google Scholar] [CrossRef]
- Aquila, A.; Barty, A.; Bostedt, C.; Boutet, S.; Carini, G.; dePonte, D.; Drell, P.; Doniach, S.; Downing, K.H.; Earnest, T.; et al. The linac coherent light source single particle imaging road map. Struct. Dyn. 2015, 2, 041701. [Google Scholar] [CrossRef] [PubMed]
- Glover, T.E.; Fritz, D.M.; Cammarata, M.; Allison, T.K.; Coh, S.; Feldkamp, J.M.; Lemke, H.; Zhu, D.; Feng, Y.; Coffee, R.N.; et al. X-ray and optical wave mixing. Nature 2012, 488, 603–608. [Google Scholar] [CrossRef] [PubMed]
- Adams, B.W.; Buth, C.; Cavaletto, S.M.; Evers, J.; Harman, Z.; Keitel, C.H.; Pálffy, A.; Picón, A.; Röhlsberger, R.; Rostovtsev, Y.; et al. X-ray quantum optics. J. Mod. Opt. 2013, 60, 2–21. [Google Scholar] [CrossRef]
- Reiche, S. Numerical Studies for a Single Pass High Gain Free Electron Laser. Ph.D. Thesis, Hamburg University, Hamburg, Germany, 2000. [Google Scholar]
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Schreiber, S.; Faatz, B.; Feldhaus, J.; Honkavaara, K.; Treusch, R. FEL User Facility FLASH. Proc. IPAC 2010, 10, 2149–2151. [Google Scholar]
- Kim, K.J.; Huang, Z.; Lindberg, R. Synchrotron Radiation and Free-Electron Lasers: Principles of Coherent X-ray Generation; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Piovella, N.; Volpe, L. A Review of High-Gain Free-Electron Laser Theory. Atoms 2021, 9, 28. [Google Scholar] [CrossRef]
- Schmüser, P.; Dohlus, M.; Dohlus, J. Refinements of the One-Dimensional FEL Theory. In Ultraviolet and Soft X-ray Free-Electron Lasers: Introduction to Physical Principles, Experimental Results, Technological Challenges; Schmüser, P., Dohlus, M., Rossbach, J., Eds.; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 83–101. [Google Scholar] [CrossRef]
- Anisimov, P. Canonical Formulation of 1D FEL Theory Revisited, Quantized and Applied to Electron Evolution. In Proceedings of the 38th International Free Electron Laser Conference, FEL2017, Santa Fe, NM, USA, 20–25 August 2017. [Google Scholar] [CrossRef]
- Kroll, N.; Morton, P.; Rosenbluth, M. Free-electron lasers with variable parameter wigglers. IEEE J. Quantum Electron. 1981, 17, 1436–1468. [Google Scholar] [CrossRef]
- Pound, B.A.; Candler, R.; Crisp, S.; Ody, A.; Musumeci, P.; Rosenzweig, J. Focusing of a relativistic electron beam with a microfabricated quadrupole magnet. Phys. Rev. Accel. Beams 2023, 26, 042401. [Google Scholar] [CrossRef]
- Lindberg, R.R.; Shvyd’ko, Y.V. Time dependence of Bragg forward scattering and self-seeding of hard x-ray free-electron lasers. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 050706. [Google Scholar] [CrossRef]








| Parameter | Units | Value |
|---|---|---|
| Energy | GeV | 2.44 |
| Energy spread | % | 0.03 |
| Normalized transverse emittance | nm-rad | 75 |
| Peak current | kA | 4.0 |
| Undulator parameter, K | 0.50 | |
| Undulator period | mm | 6.5 |
| Undulator length | m | 4.0 |
| Radiation wavelength | Å | 1.783 |
| Photon energy | keV | 6.95 |
| Cavity roundtrip length, | m | 12 |
| CRL focal length, f | m | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singleton, M.; Rosenzweig, J.; Tang, J.; Huang, Z. An Ultra-Compact X-ray Regenerative Amplifier Free-Electron Laser. Instruments 2024, 8, 2. https://doi.org/10.3390/instruments8010002
Singleton M, Rosenzweig J, Tang J, Huang Z. An Ultra-Compact X-ray Regenerative Amplifier Free-Electron Laser. Instruments. 2024; 8(1):2. https://doi.org/10.3390/instruments8010002
Chicago/Turabian StyleSingleton, Madison, James Rosenzweig, Jingyi Tang, and Zhirong Huang. 2024. "An Ultra-Compact X-ray Regenerative Amplifier Free-Electron Laser" Instruments 8, no. 1: 2. https://doi.org/10.3390/instruments8010002
APA StyleSingleton, M., Rosenzweig, J., Tang, J., & Huang, Z. (2024). An Ultra-Compact X-ray Regenerative Amplifier Free-Electron Laser. Instruments, 8(1), 2. https://doi.org/10.3390/instruments8010002








