Measuring the Beam Energy in Proton Therapy Facilities Using ATLAS IBL Pixel Detectors
Abstract
1. Introduction
2. Materials and Methods
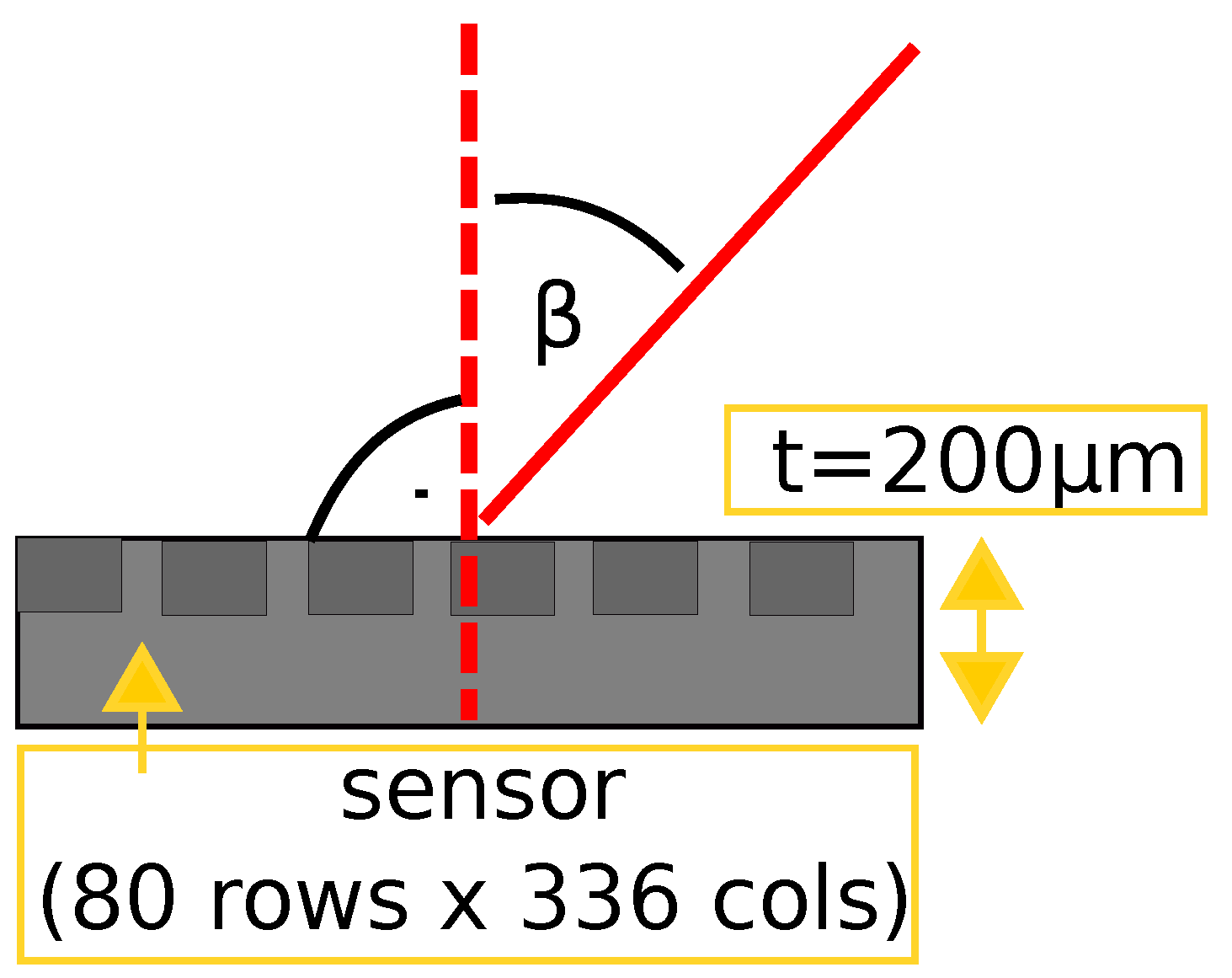
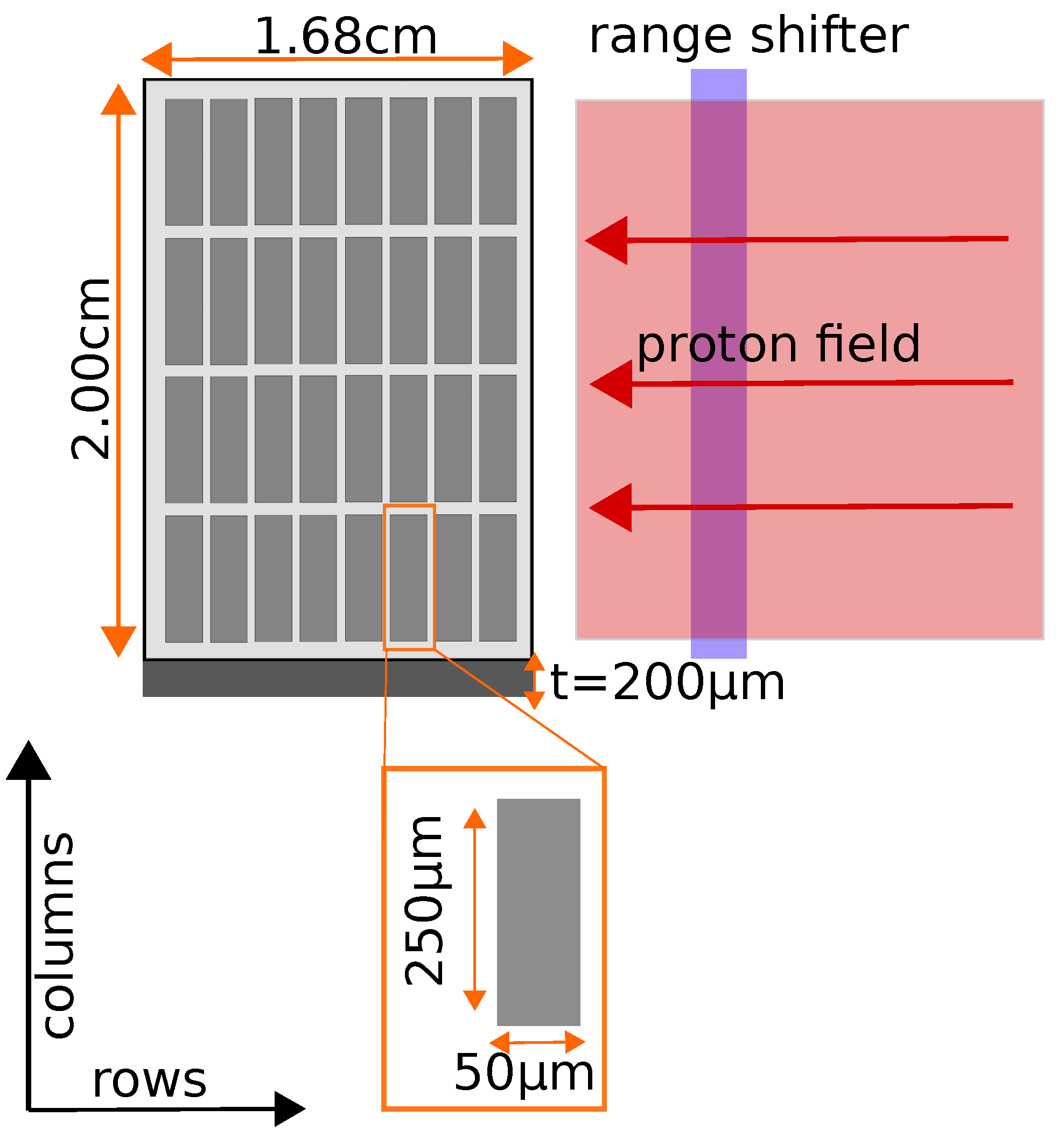
2.1. ATLAS IBL Pixel Detector
2.2. Beam Characteristics
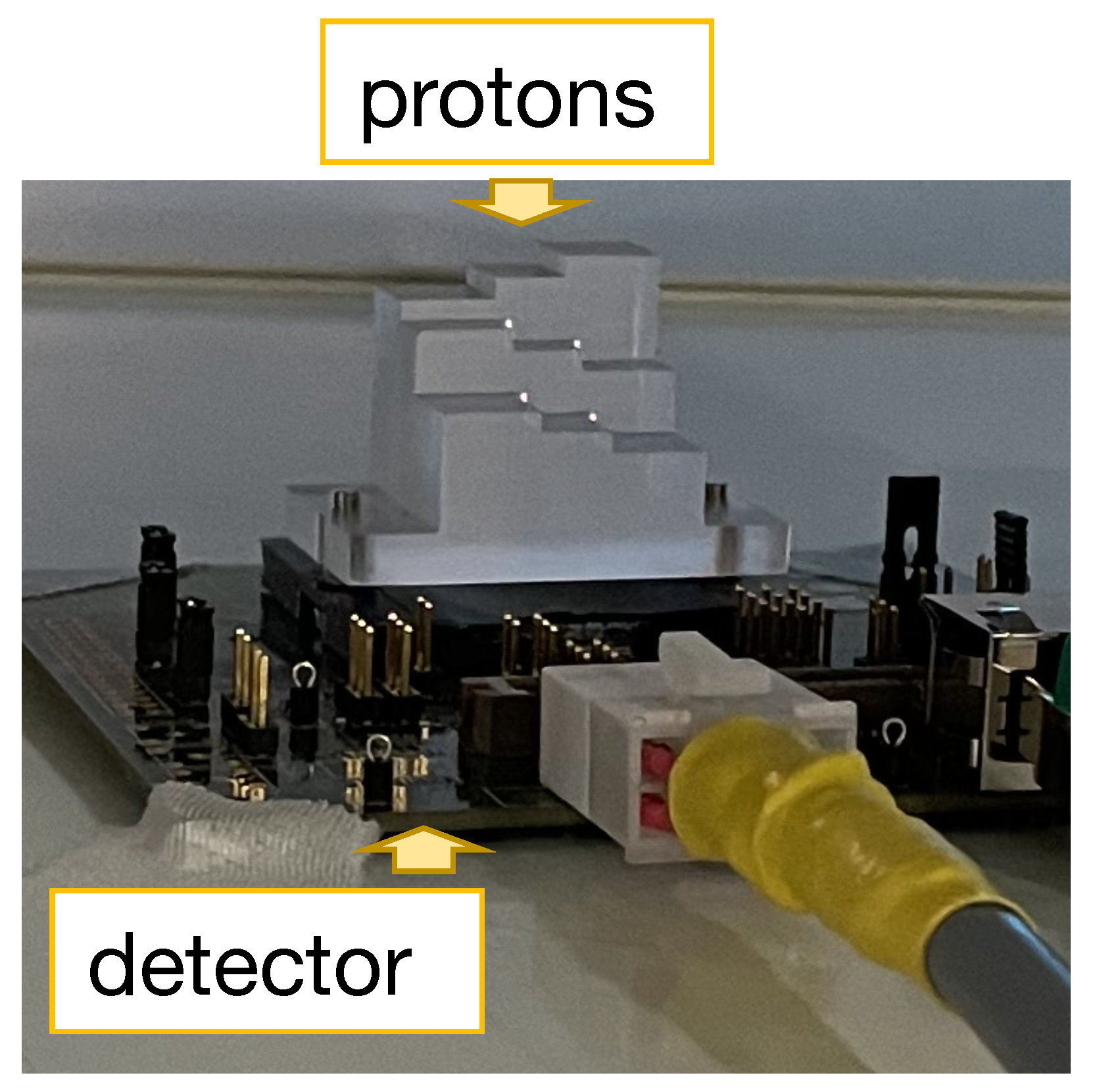
2.3. Experimental Setup
- : initial proton energy delivered by the accelerator;
- : proton energy downstream of the variable thickness of RW3 slabs;
- : proton energy incident on the silicon sensor.
2.3.1. Clustering and Cluster Charge
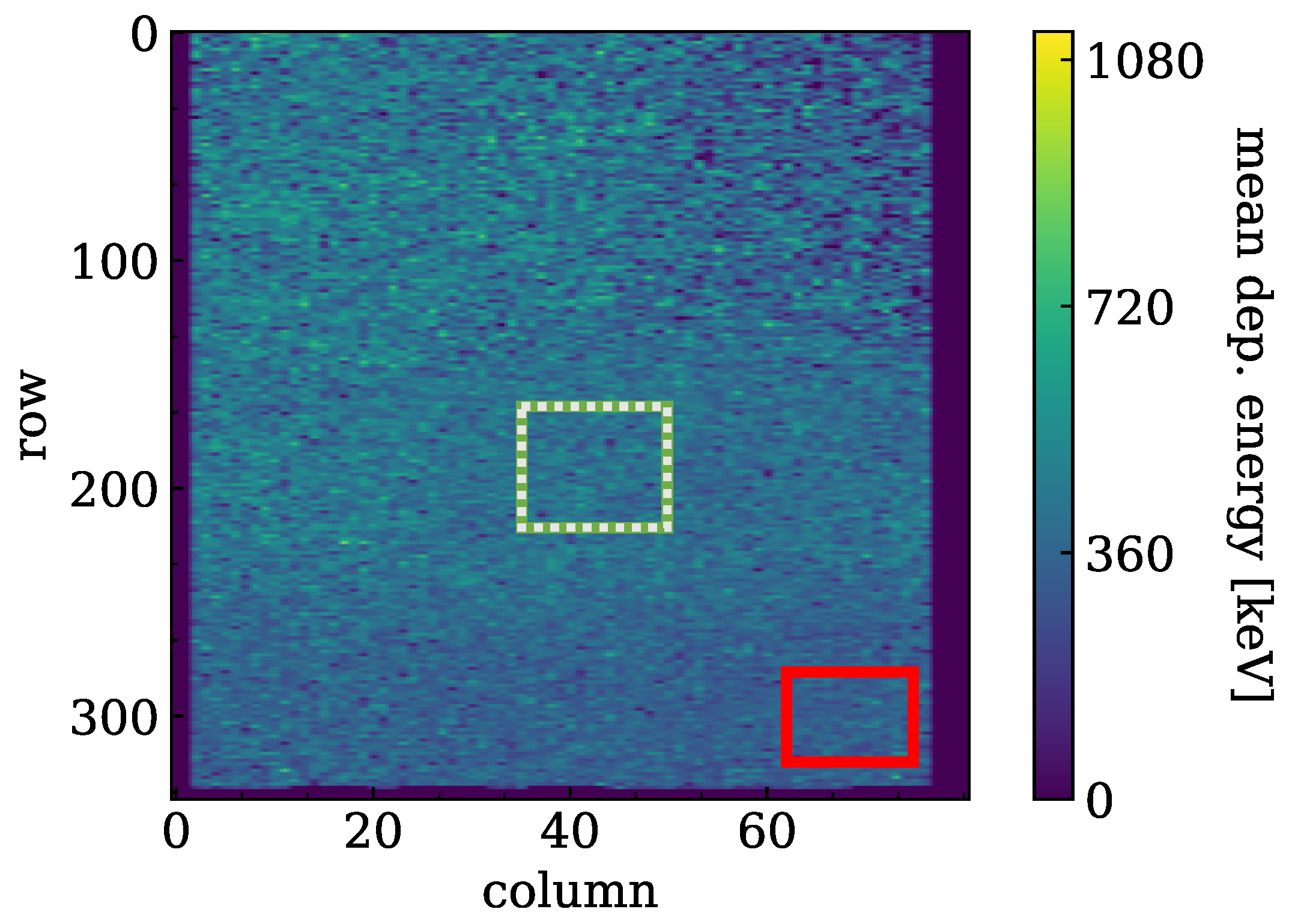
2.3.2. Regions of Interest
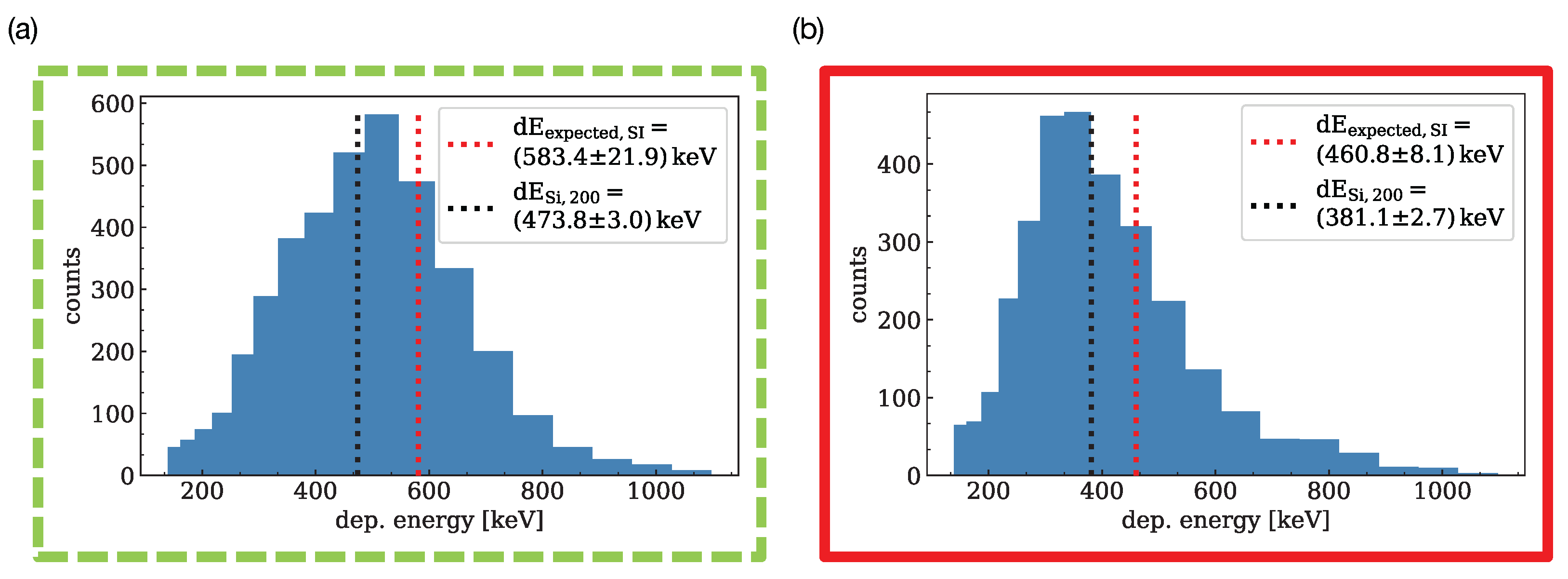
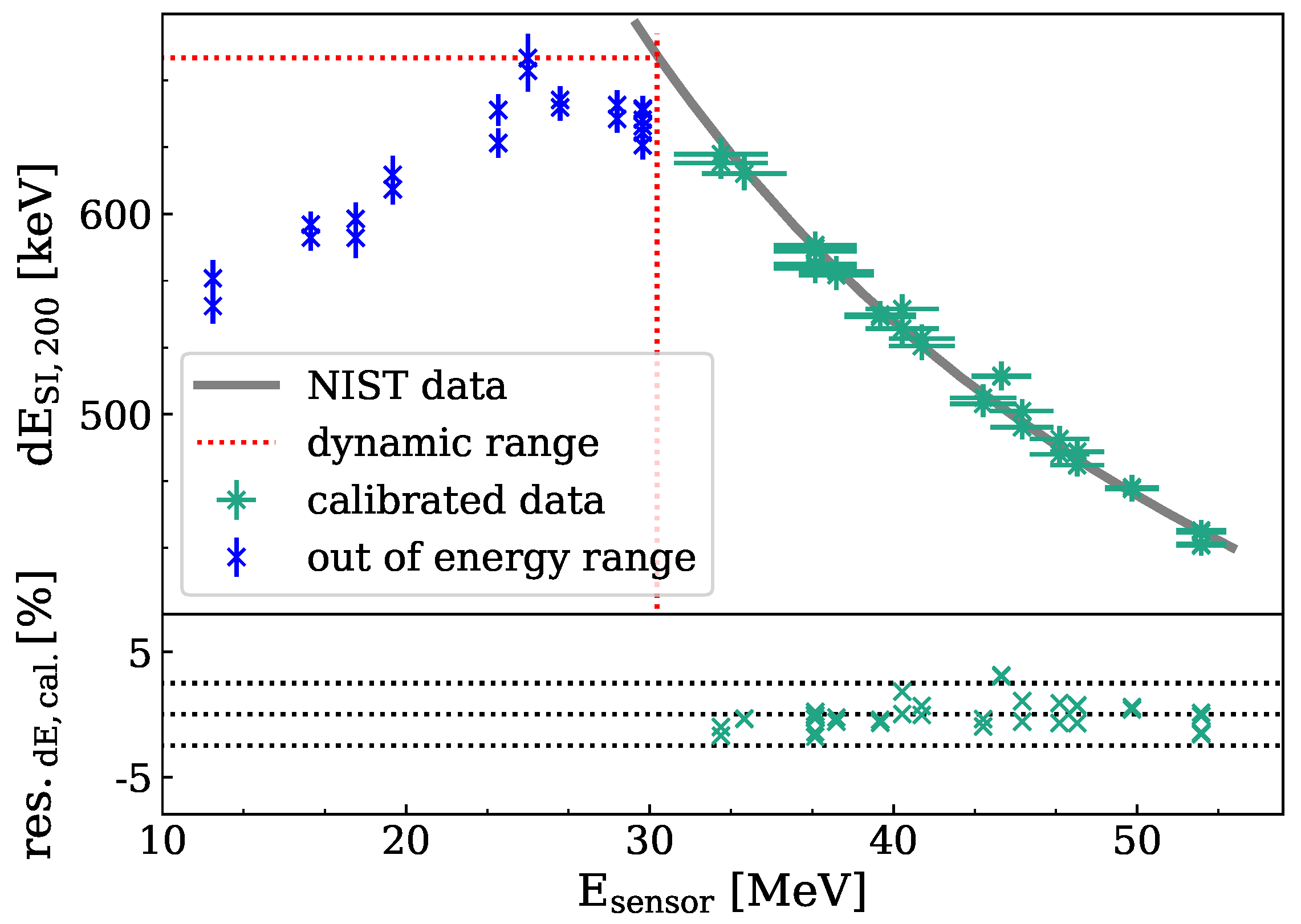
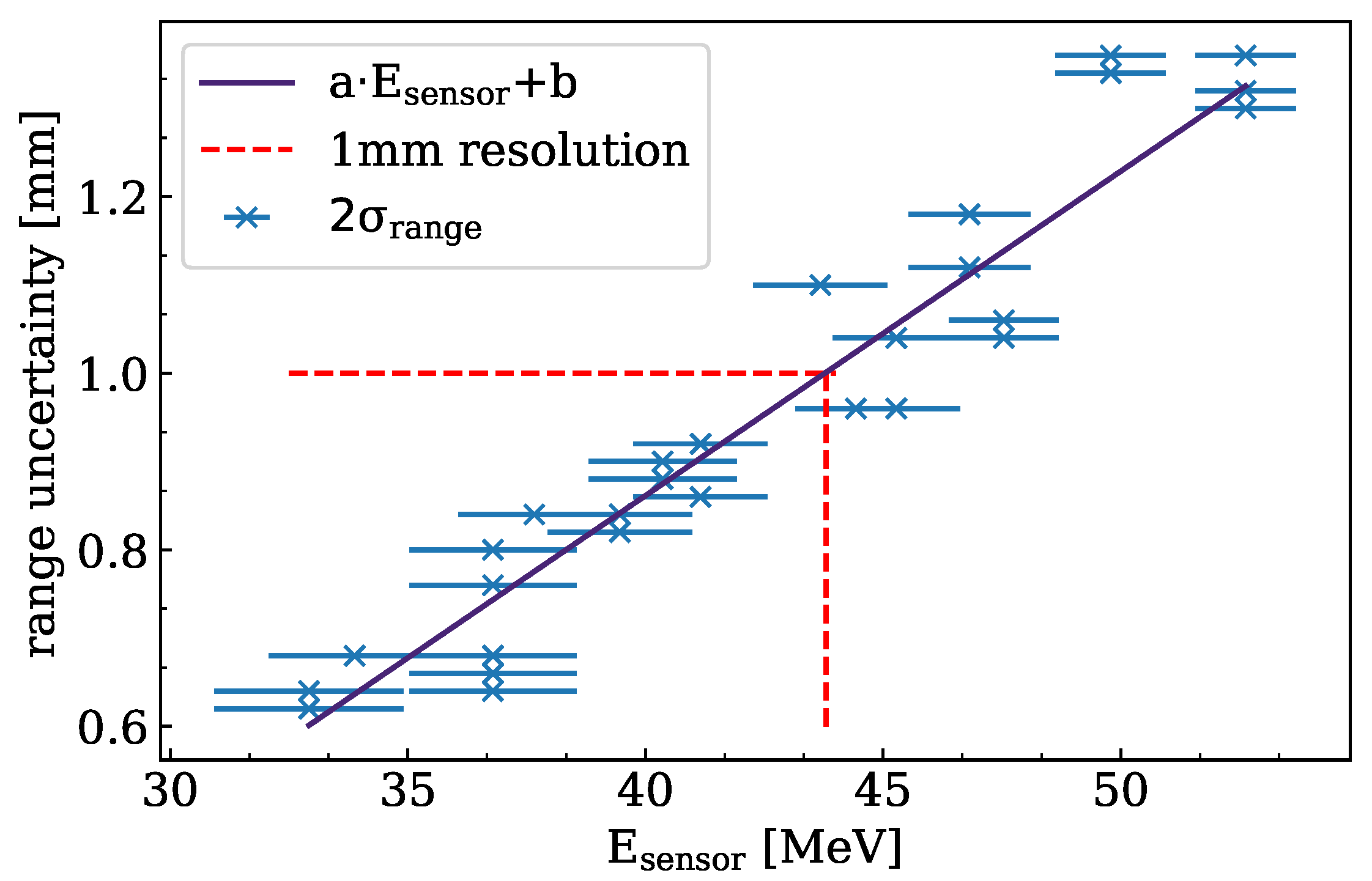
2.4. Let Spectra Measurement
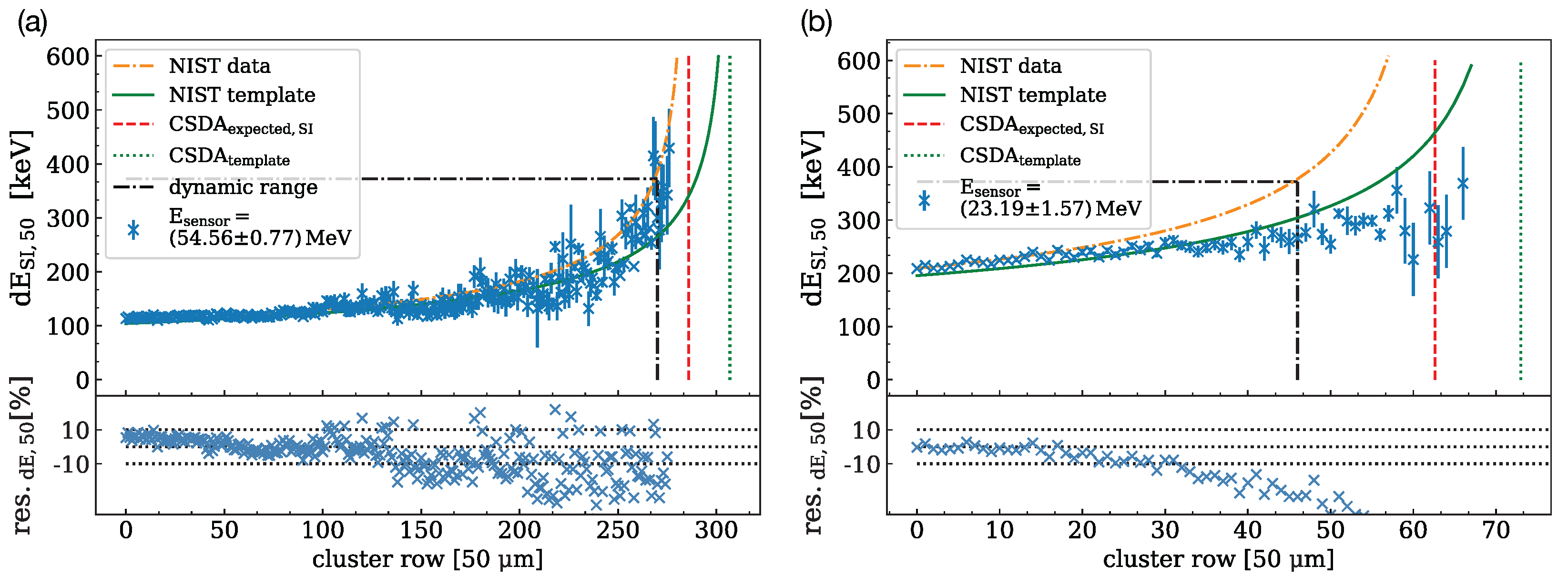
2.5. Track LET Measurement
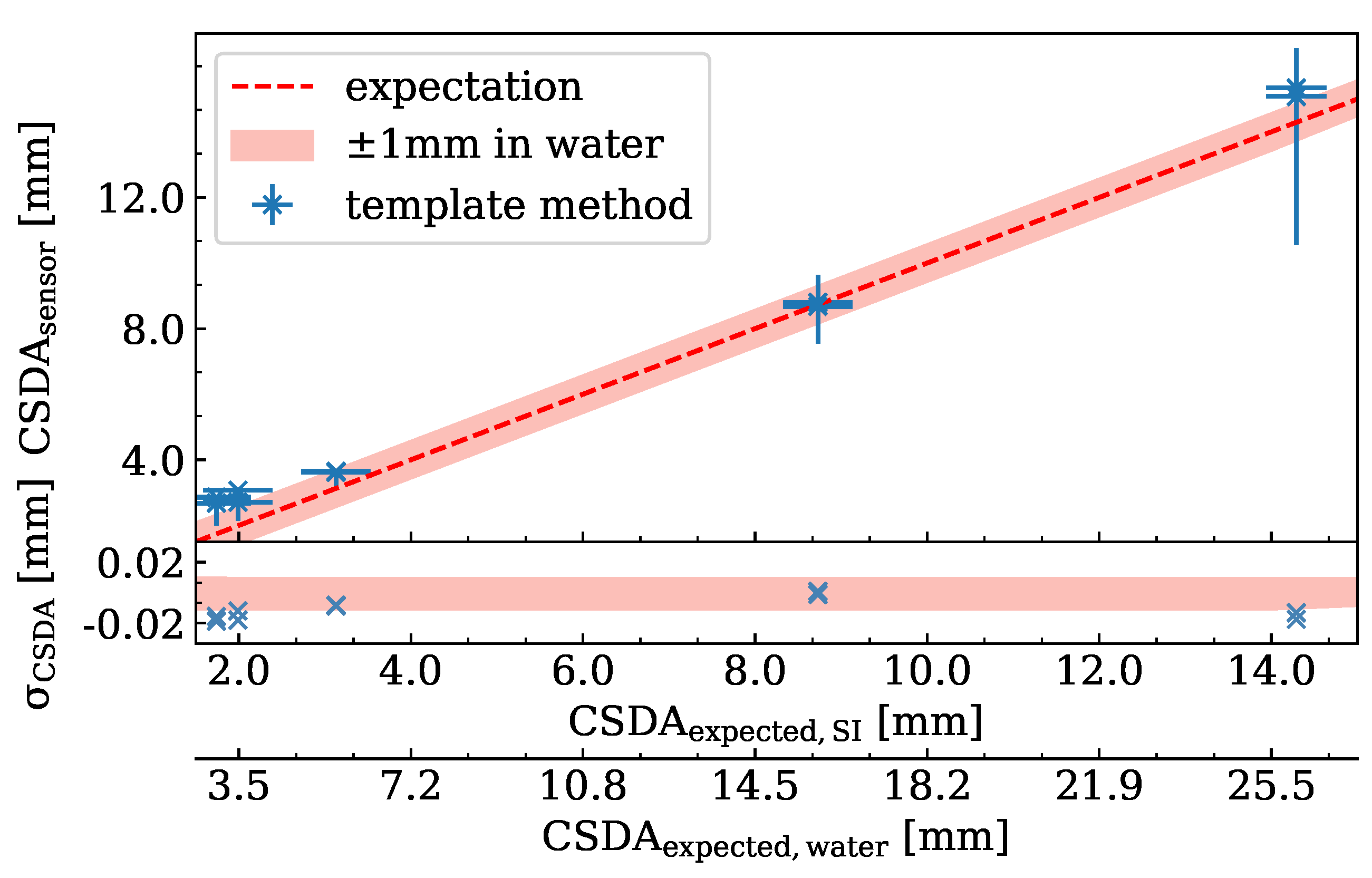
- As the sensor is only 200 μ wide perpendicular to the direction of the proton track, a considerable number of protons is scattered out of the sensor before being stopped. Figure 10 shows the distributions of cluster lengths for measurements at different proton energies. Both distributions show a decline in the number of clusters towards large cluster lengths due to multiple Coulomb scattering. This increases the statistical uncertainty of the track length for high-energy protons, as very few protons reach the end of their range inside the sensor.
- The probability for an elastic interaction to result in a large scattering angle depends on the thickness of the material traversed and the inverse of the proton energy [26]. This leads to an underestimation of the track length, which increases for longer tracks, i.e., higher proton energy. This effect can also be seen in Figure 10, where the measured track length is significantly smaller than the expected proton range for high-energy protons, while for lower proton energy track lengths are close to the expected range. Track lengths exceeding the CSDA range or falling below can appear due to range straggling.
- Protons scattered out of the sensor can travel for a distance before being scattered back into the sensor. These create a track in the silicon that has a gap where several pixels do not register hits. As these protons lose less energy while traveling through the air outside the silicon sensor, these tracks are longer than the proton range in silicon, leading to an overestimation of the proton range. Tracks that display this kind of gap are referred to as split tracks and are excluded from the analysis.
3. Results
3.1. Let Spectra Measurement
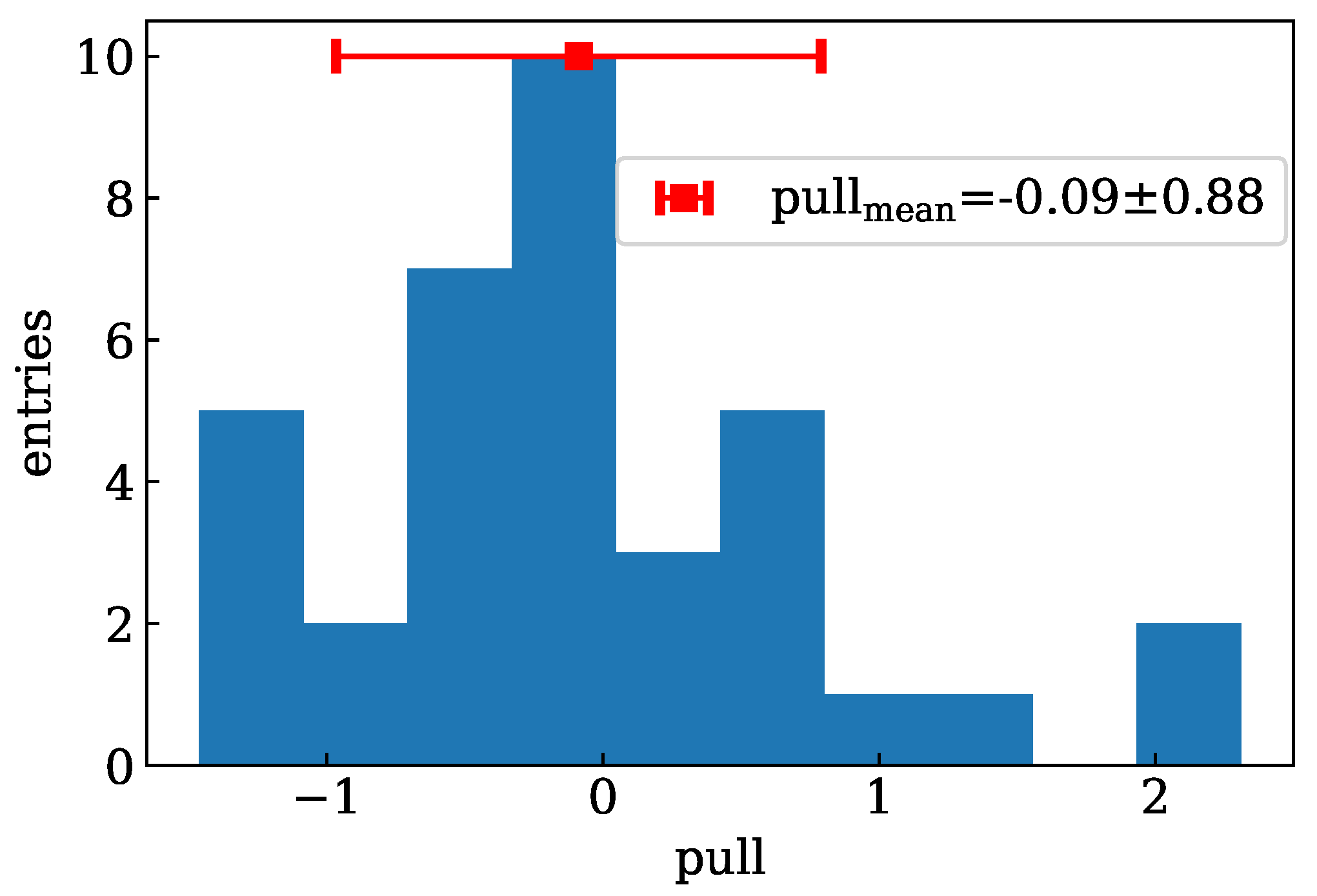
3.2. Track LET Measurement
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LET | Linear Energy Transfer |
| QA | Quality Assurance |
| HEP | High-Energy Physics |
| IBL | Insertable B-Layer |
| ToT | Time over Threshold |
| ROI | Region Of Interest |
| WER | Water-Equivalent Ratio |
| CSDA | Continuous Slowing Down Approximation |
| WET | Water-Equivalent Thickness |
| NIST | National Institute of Standards and Technology |
References
- Arjomandy, B.; Taylor, P.; Ainsley, C.; Safai, S.; Sahoo, N.; Pankuch, M.; Farr, J.B.; Yong Park, S.; Klein, E.; Flanz, J.; et al. AAPM task group 224: Comprehensive proton therapy machine quality assurance. Med. Phys. 2019, 46, e678–e705. [Google Scholar] [CrossRef]
- Granja, C.; Oancea, C.; Jakubek, J.; Marek, L.; Benton, E.; Kodaira, S.; Miller, J.; Rucinski, A.; Gajewski, J.; Stasica, P.; et al. Wide-range tracking and LET-spectra of energetic light and heavy charged particles. Nucl. Instrum. Methods 2021, 988, 164901. [Google Scholar] [CrossRef]
- Gehrke, T.; Burigo, L.; Aricó, G.; Berke, S.; Jakubek, J.; Turecek, D.; Tessonnier, T.; Mairani, A.; Martišíková, M. Energy deposition measurements of single 1H, 4He and 12C ions of therapeutic energies in a silicon pixel detector. JINST 2017, 12, P0402. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Alnaghy, S.; Petasecca, M.; Cutajar, D.; Lerch, M.; Pospisil, S.; Giacometti, V.; Schulte, R.; Rosso, V.; Würl, M.; et al. Medipix detectors in radiation therapy for advanced quality-assurance. Radiat. Meas. 2020, 130, 106211. [Google Scholar] [CrossRef]
- Vignati, A.; Giordanengo, S.; Milian, F.M.; Ganjeh, Z.A.; Donetti, M.; Fausti, F.; Ferrero, M.; Ali, O.H.; Villarreal, O.M.; Mazza, G.; et al. A new detector for the beam energy measurement in proton therapy: A feasibility study. Phys. Med. Biol. 2020, 65, 215030. [Google Scholar] [CrossRef] [PubMed]
- Grinstein, S. ATLAS Collaboration. Overview of the ATLAS insertable B-layer (IBL) project. Nucl. Instr. Meth. A 2013, 699, 61–66. [Google Scholar] [CrossRef]
- Schilling, I.; Bäcker, C.M.; Bäumer, C.; Behrends, C.; Kröninger, K.; Timmermann, B.; Weingarten, J. Characterization of pixelated silicon detectors for daily quality assurance measurements in proton therapy. arXiv 2022, arXiv:2204.02060. [Google Scholar]
- Bäumer, C.; Koska, B.; Lambert, J.; Timmermann, B.; Mertens, T.; Talla, P.T. Evaluation of detectors for acquisition of pristine depth-dose curves in pencil beam scanning. J. Appl. Clin. Med. Phys. 2015, 16, 151–163. [Google Scholar] [CrossRef] [PubMed]
- Granja, C.; Jakubek, J.; Martisikova, M.; Kodaira, S.; Polansky, S.; Krist, P.; Zach, V.; Matlocha, T. Dynamic range and resolving power of the Timepix detector to heavy charged particles. JINST 2018, 13, C11003. [Google Scholar] [CrossRef]
- Bergmann, B.; Pichotka, M.; Pospisil, S.; Vycpalek, J.; Burian, P.; Broulim, P.; Jakubek, J. 3D track reconstruction capability of a silicon hybrid active pixel detector. Eur. Phys. J. C 2017, 77, 1–9. [Google Scholar] [CrossRef]
- Giordanengo, S.; Palmans, H. Dose detectors, sensors, and their applications. Med. Phys. 2018, 45, e1051–e1072. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sciveres, M.; Arutinov, D.; Barbero, M.; Beccherle, R.; Dube, S.; Elledge, D.; Fleury, J.; Fougeron, D.; Gensolen, F.; Gnani, D.; et al. The FE-I4 Pixel Readout Integrated Circuit. Nucl. Instr. Meth. A 2011, 636, 155–159. [Google Scholar] [CrossRef]
- Weingarten, J. ATLAS IBL sensor qualification. JINST A 2012, 7, C01039. [Google Scholar] [CrossRef][Green Version]
- Klein, C.A. Bandgap Dependence and Related Features of Radiation Ionization Energies in Semiconductors. J. Appl. Phys. 1968, 39, 2029–2038. [Google Scholar] [CrossRef]
- Mohammadian-Behbahani, M.R.; Monaco, V.; Abujami, M.; Bersani, D.; Data, E.M.; Galeone, C.; Giordanengo, S.; Ali, O.H.; Villarreal, O.A.; Milian, F.M.; et al. Two-channel combination methods for count-loss correction in radiation measurements at high rates and with pulsed sources. Nucl. Instrum. Methods Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2022, 1040, 167195. [Google Scholar] [CrossRef]
- Petzoldt, J.; Roemer, K.E.; Enghardt, W.; Fiedler, F.; Golnik, C.; Hueso-Gonzalez, F.; Helmbrecht, S.; Kormoll, T.; Rohling, H.; Smeets, J.; et al. Characterization of the microbunch time structure of proton pencil beams at a clinical treatment facility. Phys. Med. Biol. 2016, 61, 2432. [Google Scholar] [CrossRef]
- Bäumer, C.; Bäcker, C.M.; Gerhardt, M.; Grusell, E.; Koska, B.; Kröninger, K.; Nitsch, C.; Rullkötter, H.; Siregar, H.M.; Timmermann, B.; et al. Measurement of absolute activation cross sections from carbon and aluminum for proton therapy. Nucl. Instrum. Methods Phys. Res. B 2019, 440, 75–81. [Google Scholar] [CrossRef]
- Behrends, C.; Bäcker, C.M.; Schilling, I.; Zwiehoff, S.; Weingarten, J.; Kröninger, K.; Rehbock, C.; Barcikowski, S.; Wulff, J.; Bäumer, C.; et al. The radiosensitizing effect of platinum nanoparticles in proton irradiations is not caused by an enhanced proton energy deposition at the macroscopic scale. Phys. Med. Biol. 2022, 67, 155023. [Google Scholar] [CrossRef]
- Campbell, M.; Havranek, V.; Heijne, E.; Holy, T.; Idarraga, J.; Jakubek, J.; Lebel, C.; Leroy, C.; Llopart, X.; Novotny, J.; et al. Charge collection from proton and alpha particle tracks in silicon pixel detector devices. IEEE Nucl. Sci. Symp. Conf. Rec. 2007, 2, 1047–1050. [Google Scholar]
- Olsansky, V.; Granja, C.; Oancea, C.; Mackova, A.; Havranek, V.; Chvatil, D.; Bila, J. Spectral-sensitive proton radiography of thin samples with the pixel detector Timepix3. JINST 2022, 17, C04016. [Google Scholar] [CrossRef]
- Kroupa, M.; Bahadori, A.; Campbell-Ricketts, T.; Empl, A.; Hoang, S.M.; Idarraga-Munoz, J.; Rios, R.; Semones, E.; Stoffle, N.; Tlustos, L.; et al. A semiconductor radiation imaging pixel detector for space radiation dosimetry. Life Sci. Space Res. 2015, 6, 69–78. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Radiation Units and Measurements. Linear Energy Transfer; ICRU Report: Bethesda, MD, USA, 1970; Volume 16. [Google Scholar]
- Berger, M.; Coursey, J.S.; Zucker, M.A.; Chang, J. ESTAR, PSTAR, and ASTAR: Computer Programs for Calculating Stopping-Power and Range Tables for Electrons, Protons, and Helium Ions (Version 1.2.3). [Online]. 2005. Available online: http://physics.nist.gov/Star (accessed on 15 June 2022).
- Parisi, A.; Olko, P.; Swakoń, J.; Horwacik, T.; Jabłoński, H.; Malinowski, L.; Nowak, T.; Struelens, L.; Vanhavere, F. Microdosimetric characterization of a clinical proton therapy beam: Comparison between simulated lineal energy distributions in spherical water targets and experimental measurements with a silicon detector. Phys. Med. Biol. 2022, 67, 015006. [Google Scholar] [CrossRef]
- Behrends, C.; Bäumer, C.; Verbeek, N.; Ehlert, J.; Prasad, R.; Wulff, J.; Lühr, A.; Timmermann, B. Providing proton fields down to the few-MeV level at clinical pencil beam scanning facilities for radiobiological experiments. Phys. Med. Phys. 2022, 49, 666–674. [Google Scholar] [CrossRef]
- Paganetti, H. Proton Therapy Physics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- International Commission on Radiation Units and Measurements. Stopping Powers and Ranges for Protons and Alpha Particles; ICRU Report: Bethesda, MD, USA, 1993; Volume 49. [Google Scholar]
- Sigmund, P.; Schinner, A.; Paul, H. Errata and addenda for ICRU report 73, stopping of ions heavier than helium. J. ICRU 2009, 5, 1–10. [Google Scholar]
- Dhanesar, S.; Sahoo, N.; Kerr, M.; Taylor, M.B.; Summers, P.; Zhu, X.R.; Poenisch, F.; Gillin, M. Quality assurance of proton beams using a multilayer ionization chamber system. Med. Phys. 2013, 40, 092102. [Google Scholar] [CrossRef] [PubMed]
- Catalano, R.; Petringa, G.; Cuttone, G.; Bonanno, V.P.; Chiappara, D.; Musumeci, M.S.; Puglia, S.M.; Stella, G.; Scifoni, E.; Tommasino, F.; et al. Transversal dose profile reconstruction for clinical proton beams: A detectors inter-comparison. Phys. Med. 2020, 70, 133–138. [Google Scholar] [CrossRef]
- Debrot, E.; Mundy, D.; Guatelli, S.; Petasecca, M.; Perevertaylo, V.; Beltran, C.; Rosenfeld, A.B. The dose magnifying glass quality assurance system for daily proton therapy range verification. Phys. Med. Biol. 2021, 66, 094001. [Google Scholar] [CrossRef]
- Placidi, L.; Togno, M.; Weber, D.C.; Lomax, A.J.; Hrbacek, J. Range resolution and reproducibility of a dedicated phantom for proton PBS daily quality assurance. Z. Med. Phys. 2018, 28, 310–317. [Google Scholar] [CrossRef] [PubMed]
- Rana, S.; Bennouna, J.; Samuel, E.J.; Gutierrez, A.N. Development and long-term stability of a comprehensive daily QA program for a modern pencil beam scanning (PBS) proton therapy delivery system. J. Appl. Clin. Med. Phys. 2019, 20, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Bäumer, C.; Fuentes, C.; Janson, M.; Matic, A.; Timmermann, B.; Wulff, J. Stereotactical fields applied in proton spot scanning mode with range shifter and collimating aperture. Phys. Med. Biol. 2019, 65, 155003. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schilling, I.; Bäcker, C.M.; Bäumer, C.; Behrends, C.; Hötting, M.; Hohmann, J.; Kröninger, K.; Timmermann, B.; Weingarten, J. Measuring the Beam Energy in Proton Therapy Facilities Using ATLAS IBL Pixel Detectors. Instruments 2022, 6, 80. https://doi.org/10.3390/instruments6040080
Schilling I, Bäcker CM, Bäumer C, Behrends C, Hötting M, Hohmann J, Kröninger K, Timmermann B, Weingarten J. Measuring the Beam Energy in Proton Therapy Facilities Using ATLAS IBL Pixel Detectors. Instruments. 2022; 6(4):80. https://doi.org/10.3390/instruments6040080
Chicago/Turabian StyleSchilling, Isabelle, Claus Maximilian Bäcker, Christian Bäumer, Carina Behrends, Marius Hötting, Jana Hohmann, Kevin Kröninger, Beate Timmermann, and Jens Weingarten. 2022. "Measuring the Beam Energy in Proton Therapy Facilities Using ATLAS IBL Pixel Detectors" Instruments 6, no. 4: 80. https://doi.org/10.3390/instruments6040080
APA StyleSchilling, I., Bäcker, C. M., Bäumer, C., Behrends, C., Hötting, M., Hohmann, J., Kröninger, K., Timmermann, B., & Weingarten, J. (2022). Measuring the Beam Energy in Proton Therapy Facilities Using ATLAS IBL Pixel Detectors. Instruments, 6(4), 80. https://doi.org/10.3390/instruments6040080





