Metrological Characterization of a CO2 Laser-Based System for Inscribing Long-Period Gratings in Optical Fibers
Abstract
1. Introduction
2. Materials and Methods
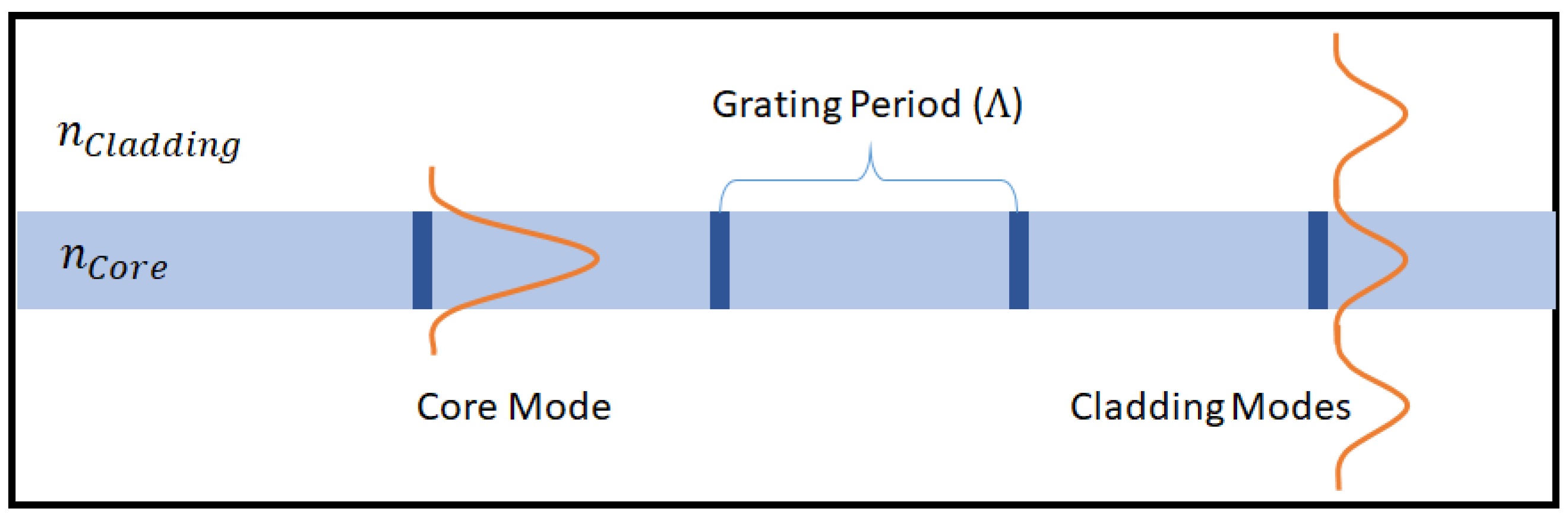
2.1. Operating Principle
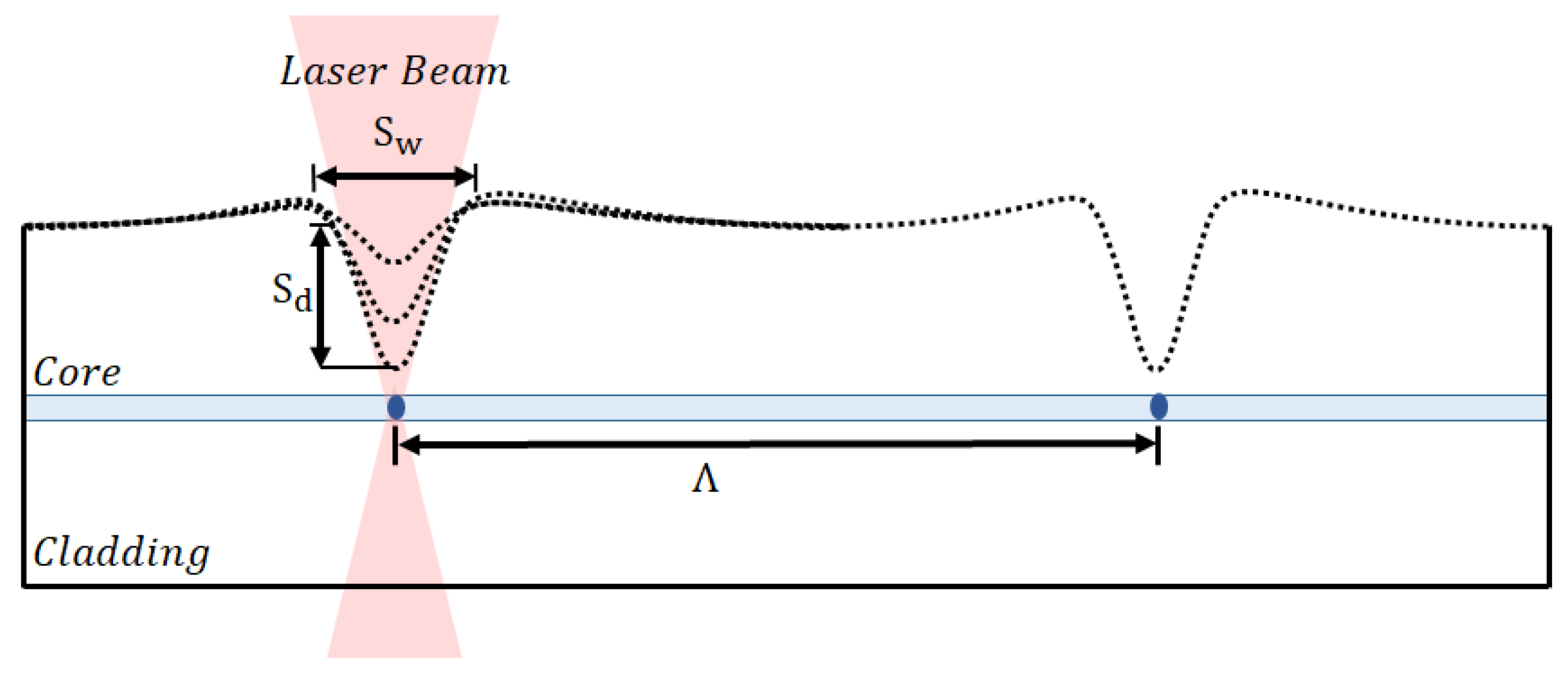
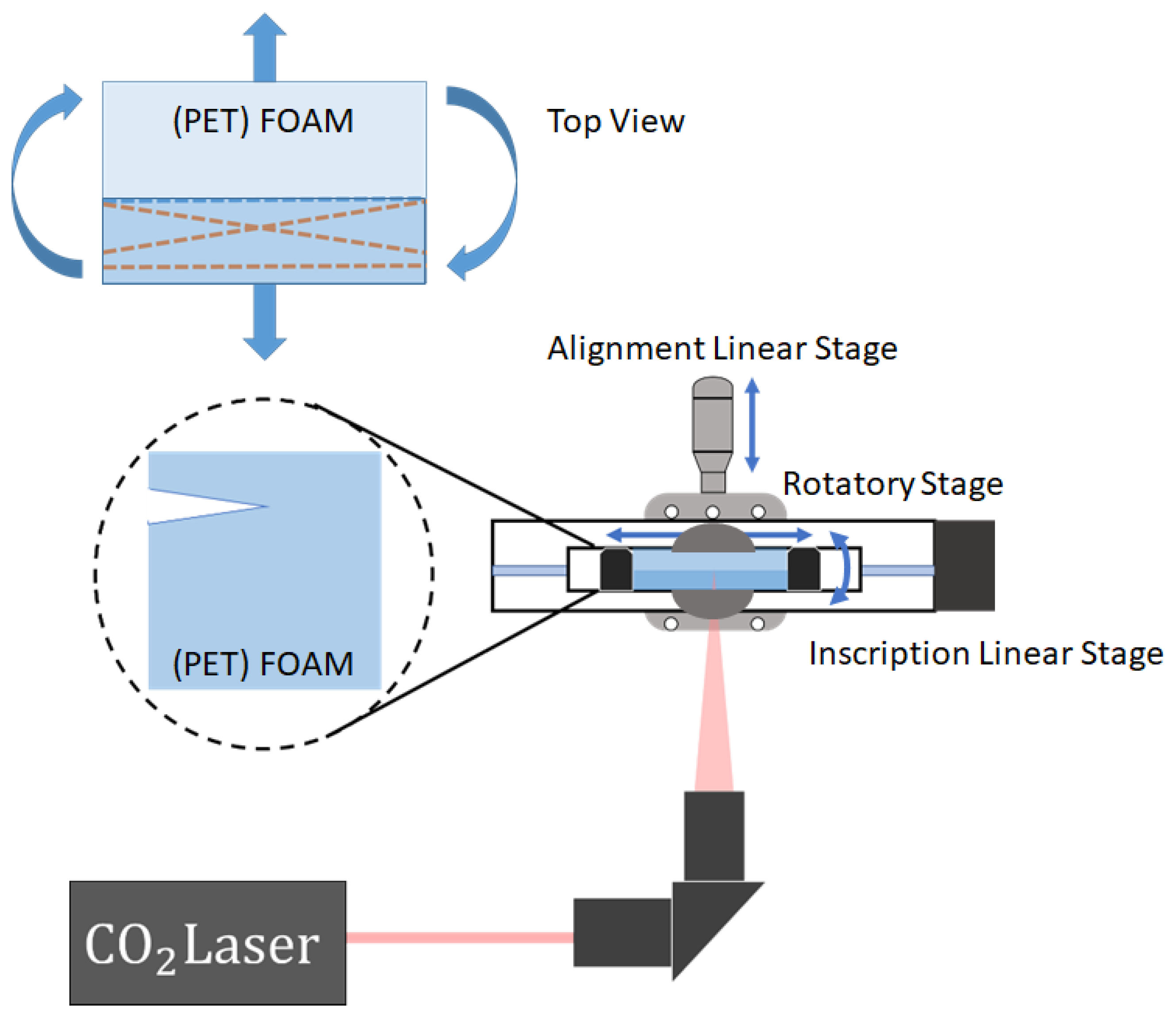
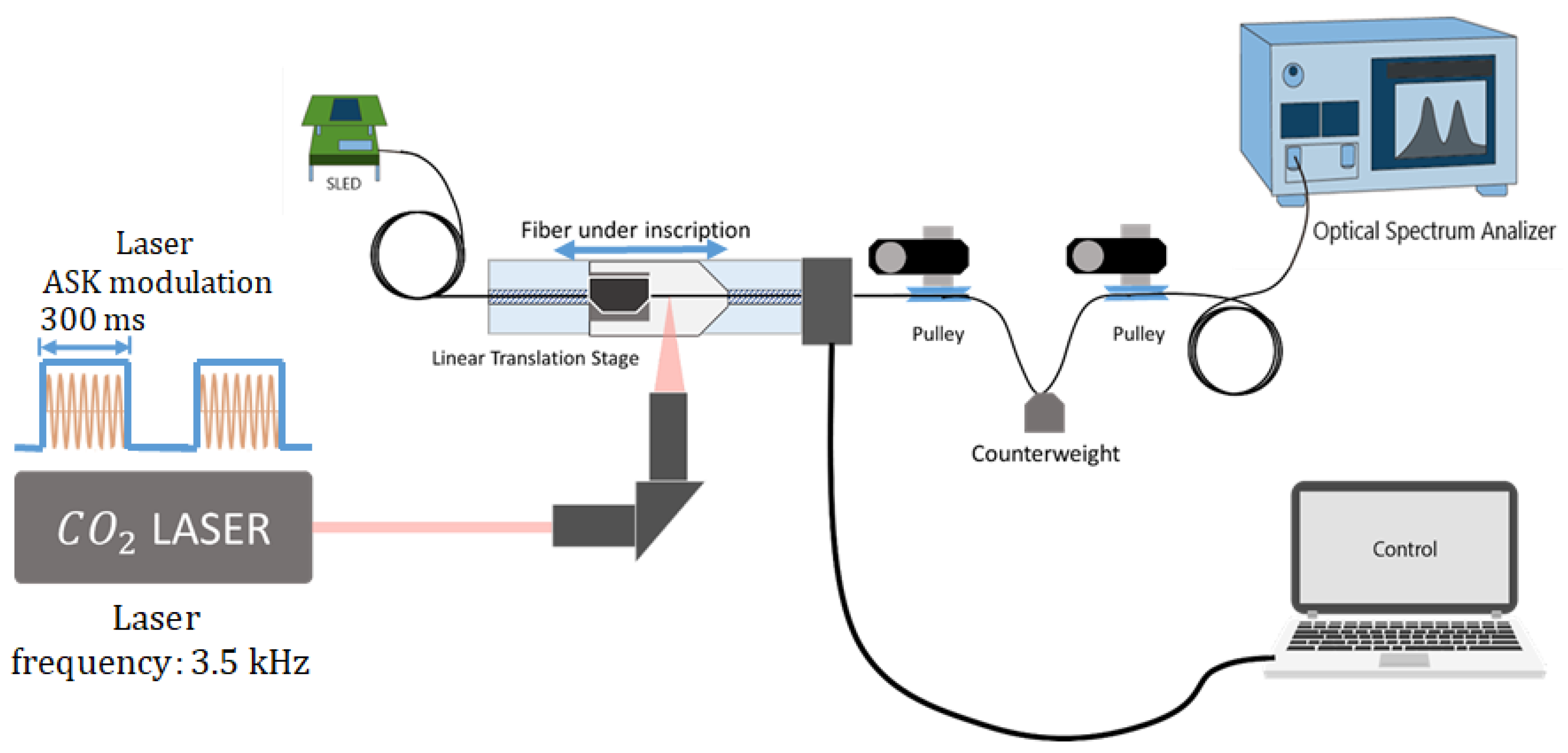
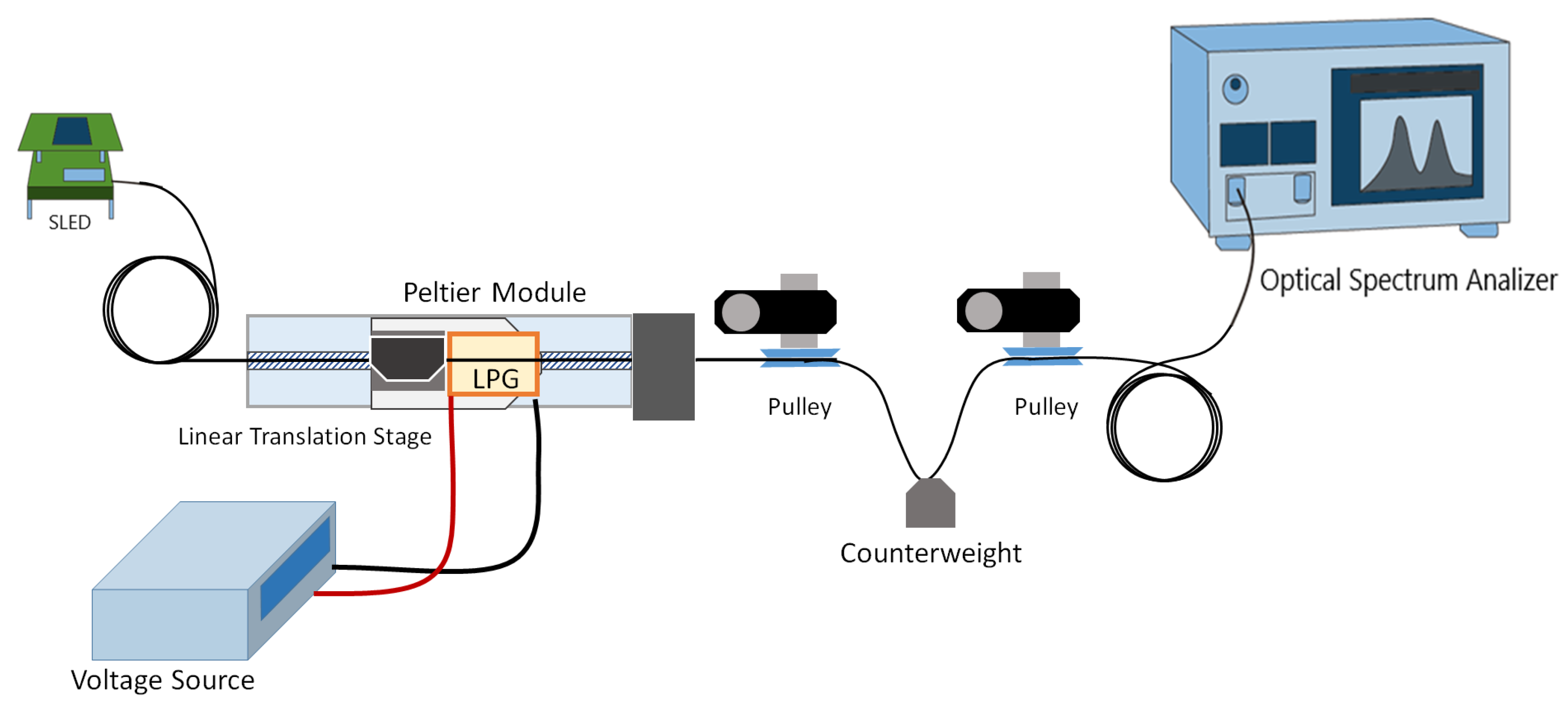
2.2. Fabrication of LPFGs Using CO Laser Technique
2.3. Uncertainty Model
3. Results
4. Discussion
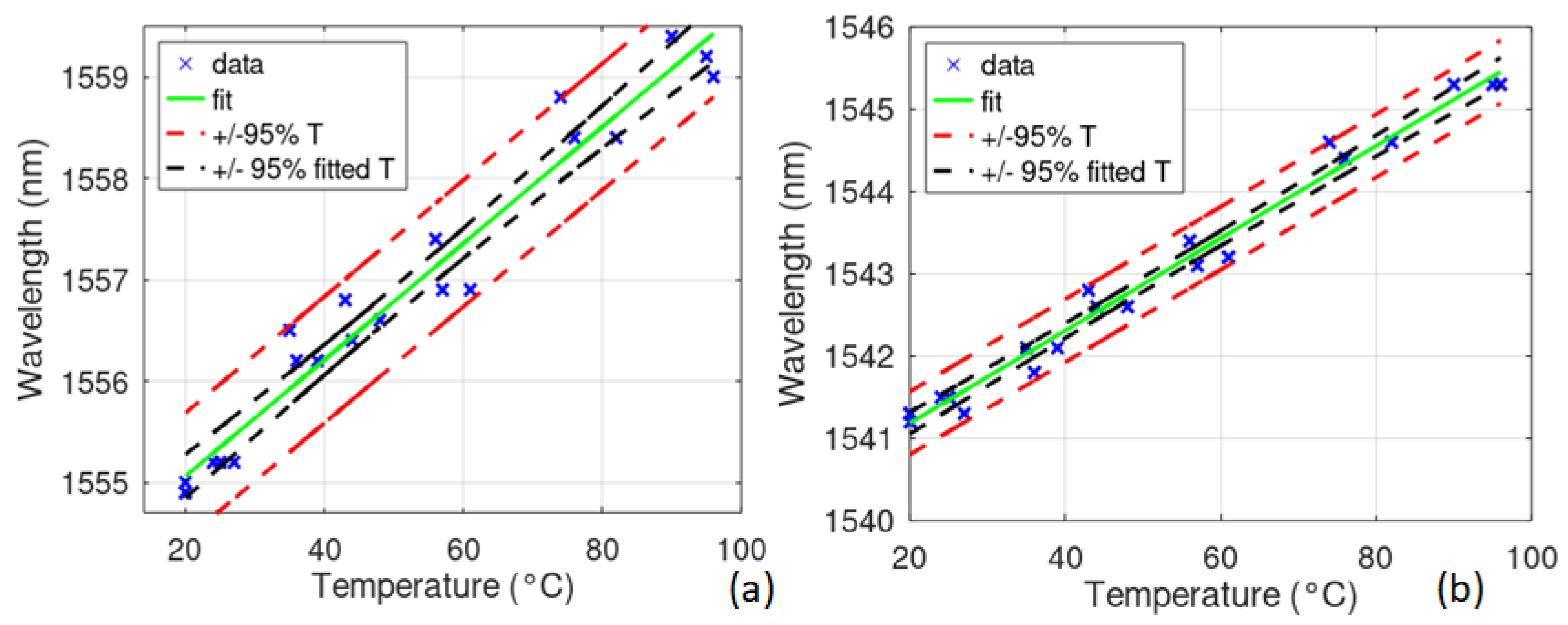
4.1. Thermal Characterization
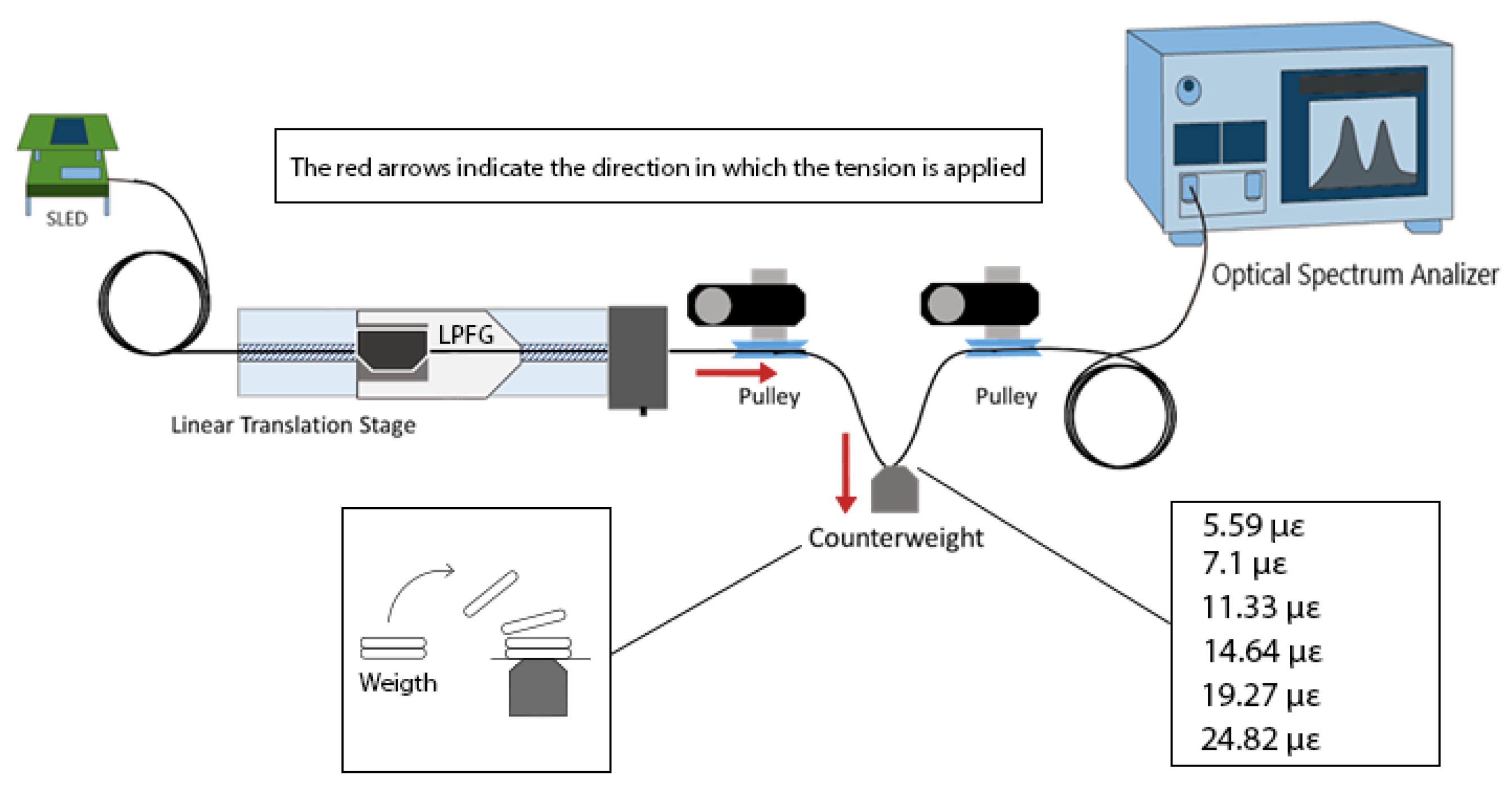
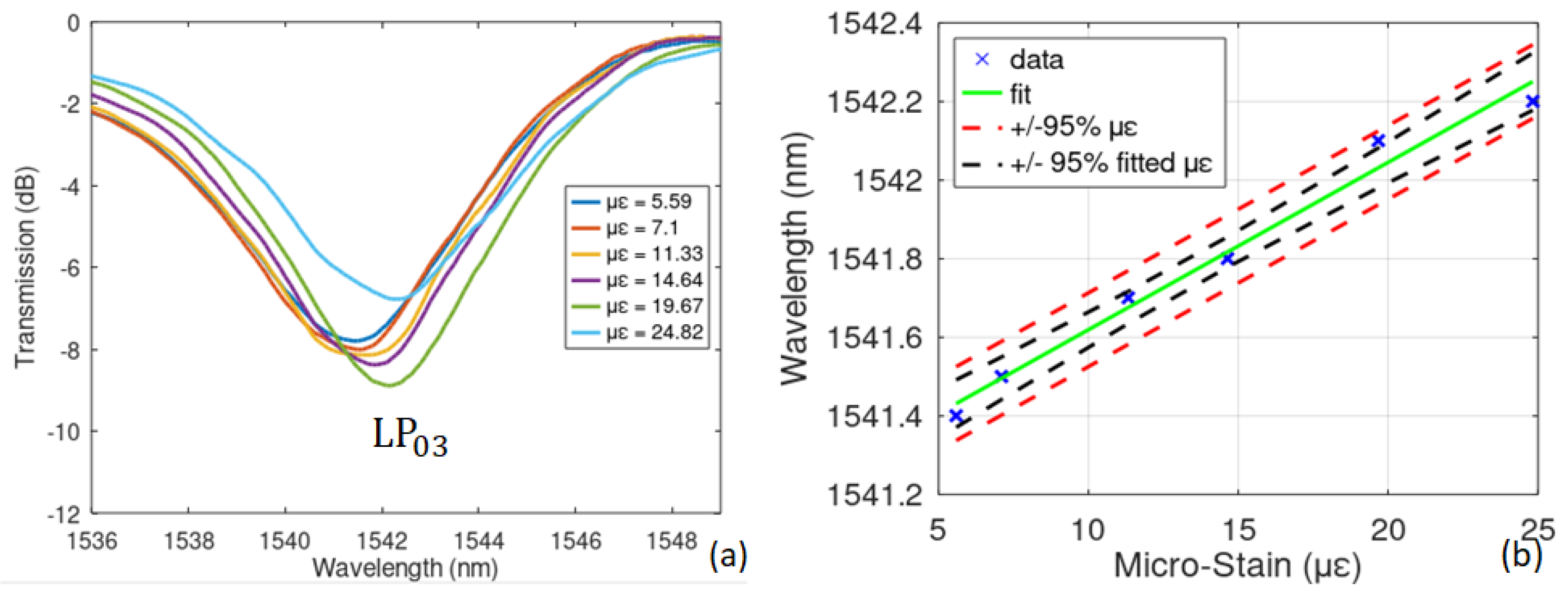
4.2. Strain Characterization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rojas, J.F.; Valencia, S.; Montoya-Cardona, J.A.; Galvis, J.L.; Gomez-Cardona, N.D. Long-period fiber grating sensors fabrication at high-frequency carbon dioxide laser pulses. J. Phys. Conf. Ser. 2020, 1547, 012005. [Google Scholar] [CrossRef]
- Urrutia, A.; Villar, I.D.; Zubiate, P.; Zamarreño, C.R. A Comprehensive Review of Optical Fiber Refractometers: Toward a Standard Comparative Criterion. Laser Photonics Rev. 2019, 13, 1900094. [Google Scholar] [CrossRef]
- Gómez-Cardona, N.; Jiménez-Durango, C.; Usuga-Restrepo, J.; Torres, P.; Reyes-Vera, E. Thermo-optically tunable polarization beam splitter based on selectively gold-filled dual-core photonic crystal fiber with integrated electrodes. Opt. Quantum Electron. 2021, 53, 68. [Google Scholar] [CrossRef]
- Gomez-Cardona, N.; Reyes-Vera, E.; Torres, P. High sensitivity refractive index sensor based on the excitation of long-range surface plasmon polaritons in H-shaped optical fiber. Sensors 2020, 20, 2111. [Google Scholar] [CrossRef] [PubMed]
- Galvis-Arroyave, J.L.; Villegas-Aristizabal, J.; Montoya-Cardona, J.; Montoya-Villada, S.; Reyes-Vera, E. Experimental characterization of a tuneable all-fiber mode converter device for mode-division multiplexing systems. J. Phys. Conf. Ser. 2020, 1547, 012004. [Google Scholar] [CrossRef]
- Wang, W.C.; Zhou, B.; Xu, S.H.; Yang, Z.M.; Zhang, Q.Y. Recent advances in soft optical glass fiber and fiber lasers. Prog. Mater. Sci. 2019, 101, 90–171. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Light. Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Zhao, X.W.; Wang, Q. Mini review: Recent advances in long period fiber grating biological and chemical sensors. Instrum. Sci. Technol. 2019, 47, 140–169. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, L.; Bennion, I. Sensitivity characteristics of long-period fiber gratings. J. Light. Technol. 2002, 20, 255–266. [Google Scholar] [CrossRef]
- Baptista, F.D.; Guerreiro, A.; Gomes, L.A.; Caldas, P. Simulation of long period fibre gratings and applications. AIP Conf. Proc. 2015, 1648, 710010. [Google Scholar] [CrossRef]
- Kim, S.; Jeong, Y.; Kim, S.; Kwon, J.; Park, N.; Lee, B. Control of the characteristics of a long-period grating by cladding etching. Appl. Opt. 2000, 39, 2038–2042. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhang, W.; Bai, Z.; Wang, L.; Zhang, L.; Zhou, Q.; Chen, L.; Yan, T. CO2-laser-induced long period fiber gratings in few mode fibers. IEEE Photonics Technol. Lett. 2015, 27, 145–148. [Google Scholar] [CrossRef]
- Hu, Q.; Zhao, X.; Tian, X.; Li, H.; Wang, M.; Wang, Z.; Xu, X. Raman suppression in 5 kW fiber amplifier using long period fiber grating fabricated by CO2 laser. Opt. Laser Technol. 2022, 145, 107484. [Google Scholar] [CrossRef]
- Dandapat, K.; Tripathi, S.M. Highly sensitive long-period fiber-grating-based biosensor inherently immune to temperature and strain. J. Opt. Soc. Am. B 2021, 38, 3601–3607. [Google Scholar] [CrossRef]
- Imas, J.J.; Zamarreño, C.R.; Villar, I.D.; Matias, I.R. Optimization of fiber bragg gratings inscribed in thin films deposited on d-shaped optical fibers. Sensors 2021, 21, 4056. [Google Scholar] [CrossRef] [PubMed]
- Vengsarkar, A.; Lemaire, P.; Judkins, J.; Bhatia, V.; Erdogan, T.; Sipe, J. Long-period fiber gratings as band-rejection filters. J. Light. Technol. 1996, 14, 58–65. [Google Scholar] [CrossRef]
- Rego, G.; Okhotnikov, O.; Dianov, E.; Sulimov, V. High-temperature stability of long-period fiber gratings produced using an electric arc. J. Light. Technol. 2001, 19, 1574. [Google Scholar] [CrossRef]
- Lancry, M.; Niay, P.; Douay, M. Comparing the properties of various sensitization methods in H2-loaded, UV hypersensitized or OH-flooded standard germanosilicate fibers. Opt. Express 2005, 13, 4037–4043. [Google Scholar] [CrossRef]
- Savin, S.; Digonnet, M.J.F.; Kino, G.S.; Shaw, H.J. Tunable mechanically induced long-period fiber gratings. Opt. Lett. 2000, 25, 710. [Google Scholar] [CrossRef]
- Wang, Y. Review of long period fiber gratings written by CO2 laser. J. Appl. Phys. 2010, 108, 081101. [Google Scholar] [CrossRef]
- Wang, Y.P.; Wang, D.N.; Jin, W.; Rao, Y.J.; Peng, G.D. Asymmetric long period fiber gratings fabricated by use of CO2 laser to carve periodic grooves on the optical fiber. Appl. Phys. Lett. 2006, 89, 151105. [Google Scholar] [CrossRef]
- Villar, I.D.; Fuentes, O.; Chiavaioli, F.; Corres, J.M.; Matias, I.R. Optimized strain long-period fiber grating (LPFG) sensors operating at the dispersion turning point. J. Light. Technol. 2018, 36, 2240–2247. [Google Scholar] [CrossRef]
- Rao, Y.J.; Wang, Y.P.; Ran, Z.L.; Zhu, T. Novel fiber-optic sensors based on long-period fiber gratings written by high-frequency CO2 laser pulses. J. Light. Technol. 2003, 21, 1320. [Google Scholar] [CrossRef]
- Davis, D.D.; Gaylord, T.K.; Glytsis, E.N.; Kosinski, S.G.; Mettler, S.C.; Vengsarkar, A.M. Long-period fibre grating fabrication with focused CO2 laser pulses. Electron. Lett. 1998, 34, 302–303. [Google Scholar] [CrossRef]
- Chan, H.M.; Perez, E.; Alhassen, F.; Tomov, I.V.; Lee, H.P. Ultra-compact long-period fiber grating and grating pair fabrication using a modulation-scanned CO2 laser. In Proceedings of the OFC/NFOEC 2007—2007 Conference on Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007; IEEE: Anaheim, CA, USA, 2007; pp. 1–3. [Google Scholar] [CrossRef]
- Jin, X.; Sun, C.; Duan, S.; Liu, W.; Li, G.; Zhang, S.; Chen, X.; Zhao, L.; Lu, C.; Yang, X.; et al. High strain sensitivity temperature sensor based on a secondary modulated tapered long period fiber grating. IEEE Photonics J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, J.; Wang, C.; Feng, M.; Zheng, Y.; Wang, T.; Wang, Z. Critical grating period behavior of a sensitivity enhanced LPFG sensor written in a few-mode fiber. Opt. Commun. 2021, 490, 126904. [Google Scholar] [CrossRef]
- Lee, D.L. Electromagnetic Principles of Integrated Optics, 1st ed.; Wiley: Hoboken, NJ, USA, 1986; p. 331. [Google Scholar]
- Jin, L.; Jin, W.; Ju, J.; Wang, Y. Coupled local-mode theory for strongly modulated long period gratings. J. Light. Technol. 2010, 28, 1745–1751. [Google Scholar] [CrossRef]
- Singh, A.; Engles, D.; Sharma, A.; Singh, M. Temperature sensitivity of long period fiber grating in SMF-28 fiber. Optik 2014, 125, 457–460. [Google Scholar] [CrossRef]
- Bai, Z.; Zhang, W.; Gao, S.; Zhang, H.; Wang, L.; Liu, F. Bend-insensitive long period fiber grating-based high temperature sensor. Opt. Fiber Technol. 2015, 21, 110–114. [Google Scholar] [CrossRef]
- Ansari, F.; Libo, Y. Mechanics of Bond and Interface Shear Transfer in Optical Fiber Sensors. J. Eng. Mech. 1998, 124, 385–394. [Google Scholar] [CrossRef]
- Rao, Y.; Zhu, T.; Ran, Z.; Wang, Y.; Jiang, J.; Hu, A. Novel long-period fiber gratings written by high-frequency CO2 laser pulses and applications in optical fiber communication. Opt. Commun. 2004, 229, 209–221. [Google Scholar] [CrossRef]
- Black, R.J.; David, Z.; Levy, O.; Park, Y.L.; Moslehi, B.; Neslen, C. On the gage factor for optical fiber grating strain gages. In Proceedings of the 53rd International SAMPE Symposium and Exhibition (SAMPE 2008), Augsburg, Germany, 18–19 September 2008; Society for the Advancement of Material and Process Engineering: Long Beach, CA, USA, 2008. [Google Scholar]

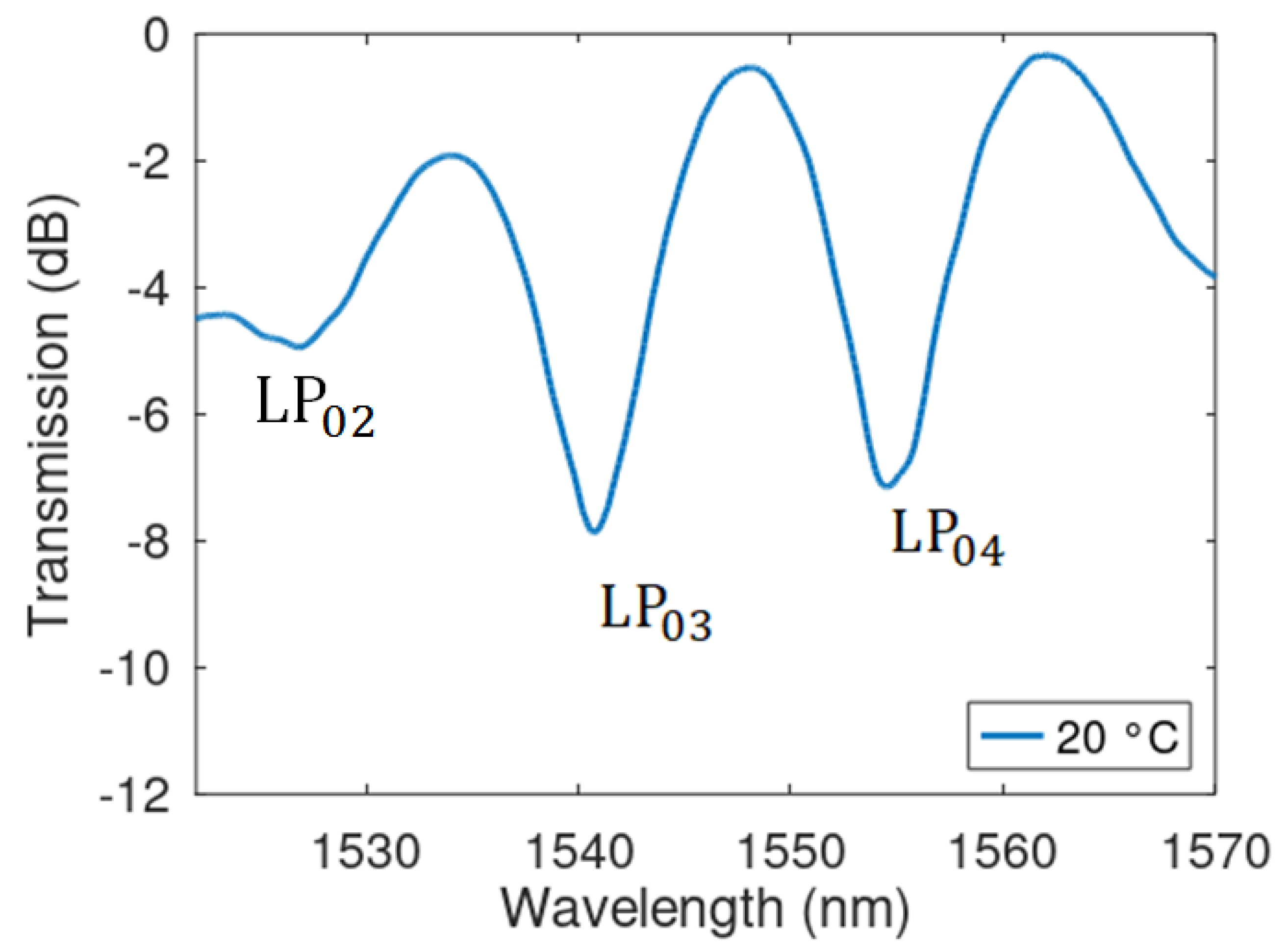
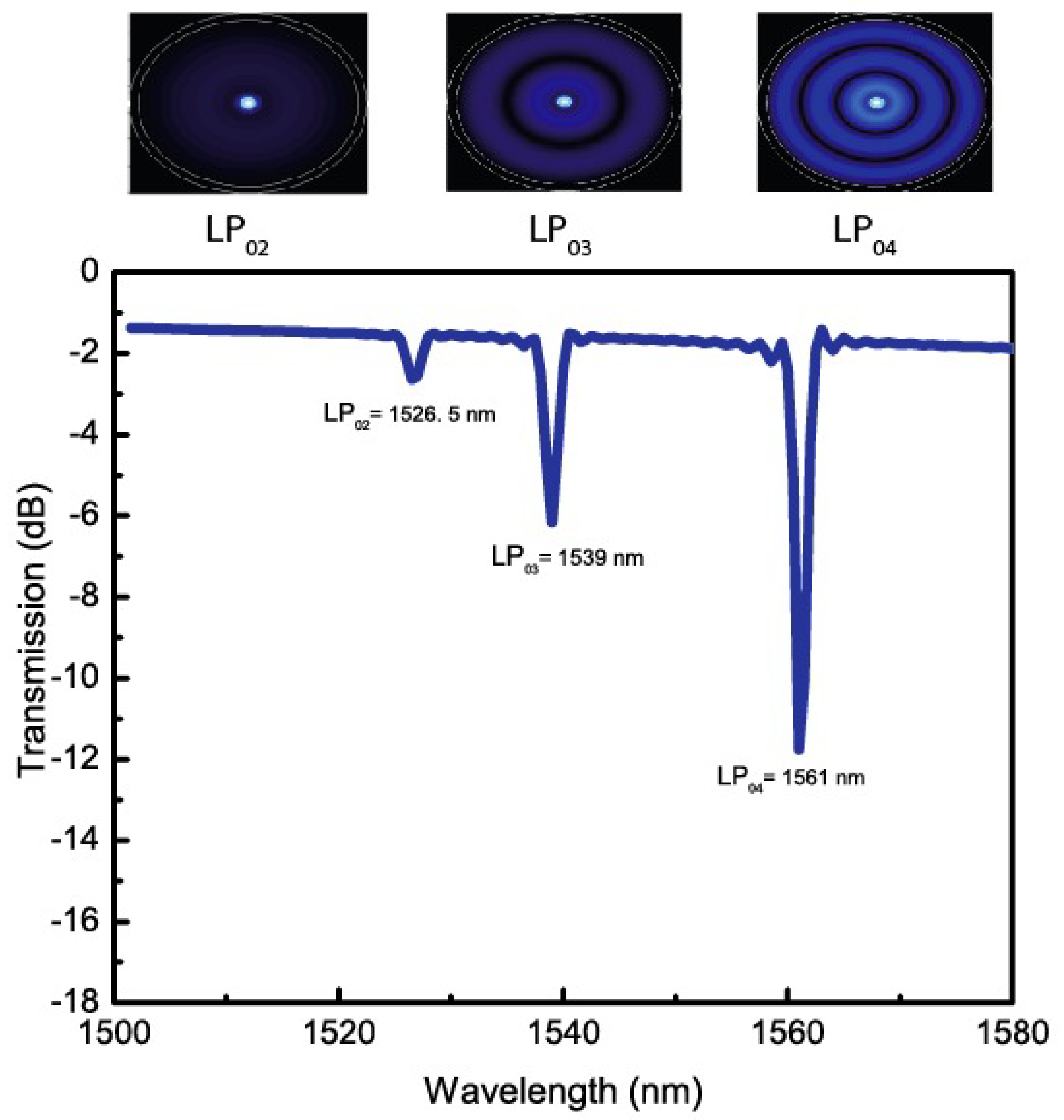
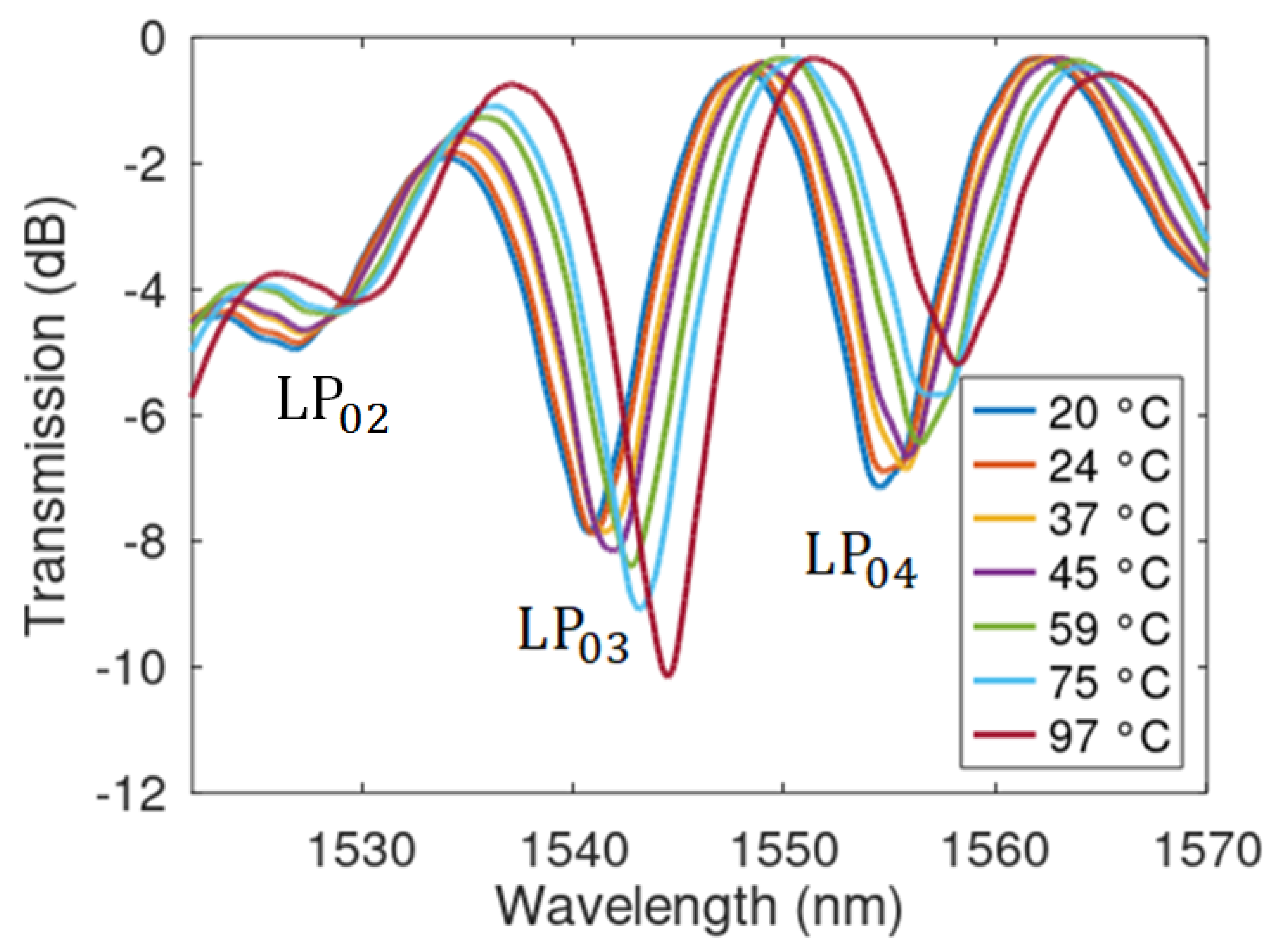
| Programmed Value (m) | l (m) | Error (m) | U (m) |
|---|---|---|---|
| 620.0 | 619.0 | −1.0 | 4.0 |
| Geometry Parameter | Mean Value (m) | U (m) |
|---|---|---|
| S | 49.4 | 1.2 |
| S | 50.3 | 3.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valencia-Garzón, S.; Reyes-Vera, E.; Galvis-Arroyave, J.; Montoya, J.P.; Gomez-Cardona, N. Metrological Characterization of a CO2 Laser-Based System for Inscribing Long-Period Gratings in Optical Fibers. Instruments 2022, 6, 79. https://doi.org/10.3390/instruments6040079
Valencia-Garzón S, Reyes-Vera E, Galvis-Arroyave J, Montoya JP, Gomez-Cardona N. Metrological Characterization of a CO2 Laser-Based System for Inscribing Long-Period Gratings in Optical Fibers. Instruments. 2022; 6(4):79. https://doi.org/10.3390/instruments6040079
Chicago/Turabian StyleValencia-Garzón, Sebastian, Erick Reyes-Vera, Jorge Galvis-Arroyave, Jose P. Montoya, and Nelson Gomez-Cardona. 2022. "Metrological Characterization of a CO2 Laser-Based System for Inscribing Long-Period Gratings in Optical Fibers" Instruments 6, no. 4: 79. https://doi.org/10.3390/instruments6040079
APA StyleValencia-Garzón, S., Reyes-Vera, E., Galvis-Arroyave, J., Montoya, J. P., & Gomez-Cardona, N. (2022). Metrological Characterization of a CO2 Laser-Based System for Inscribing Long-Period Gratings in Optical Fibers. Instruments, 6(4), 79. https://doi.org/10.3390/instruments6040079








