Energy Resolution Studies in Simulation for the IDEA Dual-Readout Calorimeter Prototype
Abstract
1. Introduction
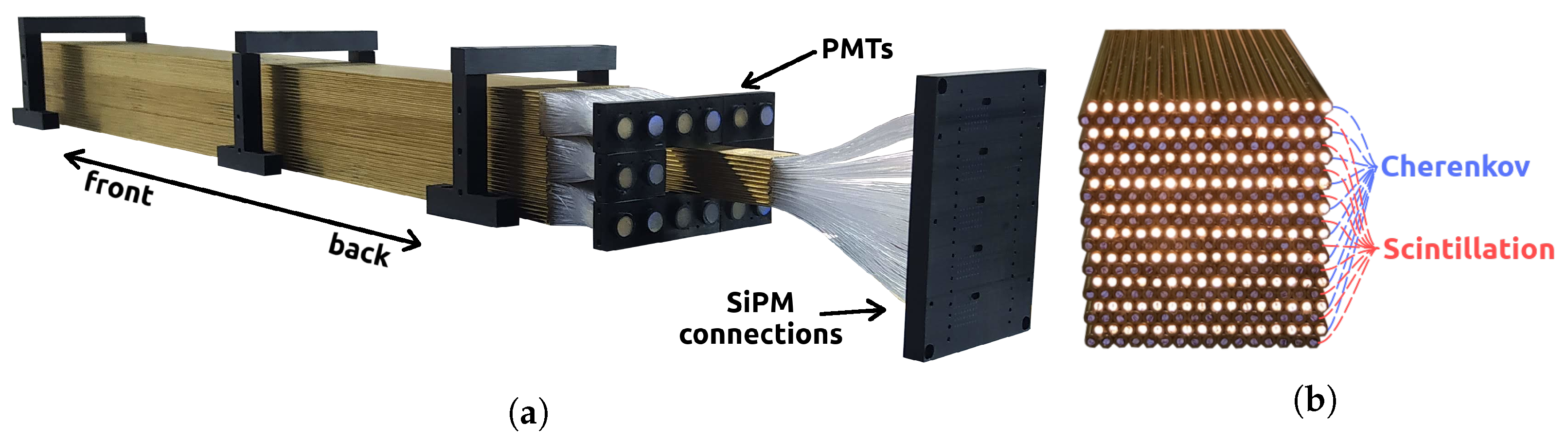
2. Prototype for Testbeams
3. Electromagnetic Energy Resolution
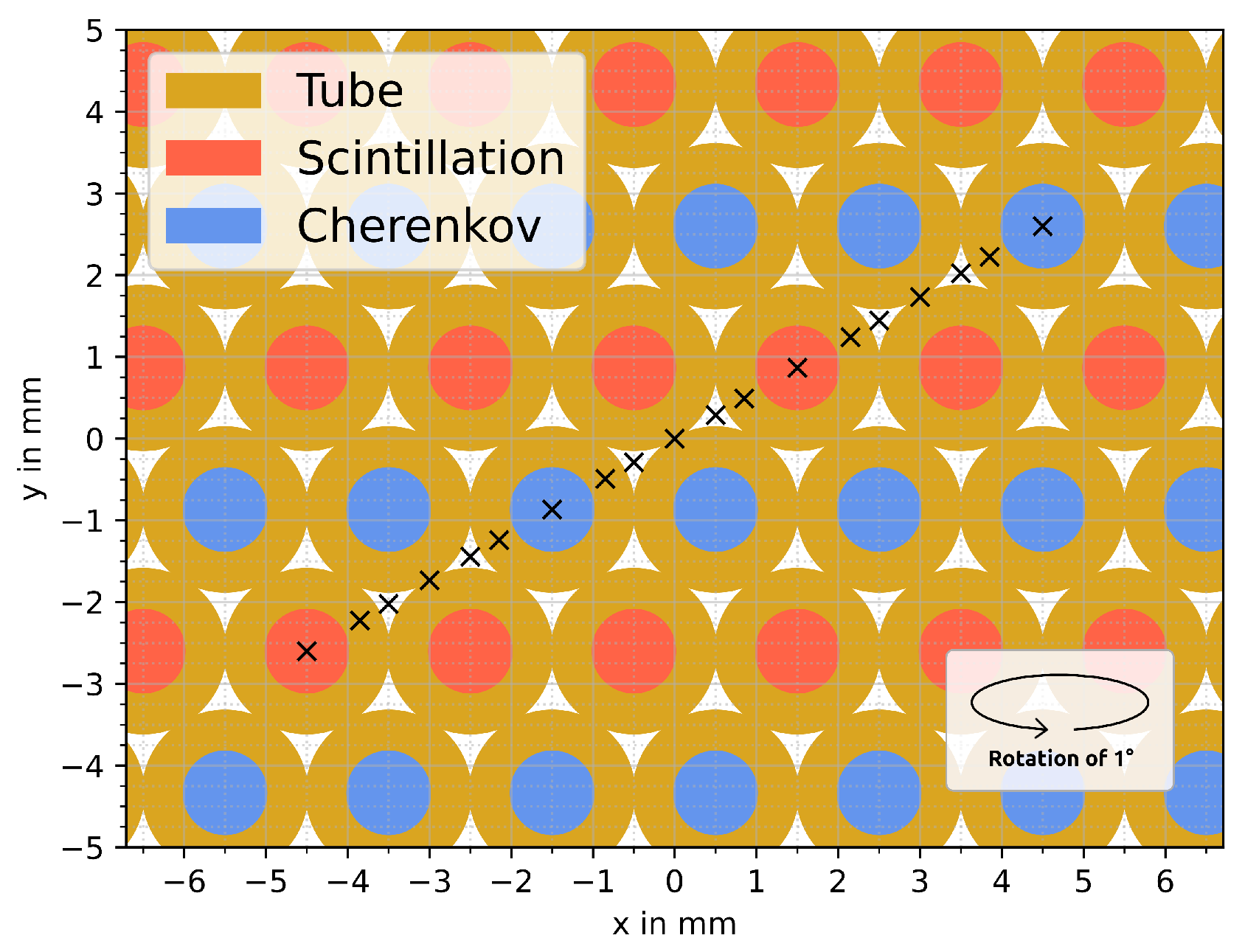
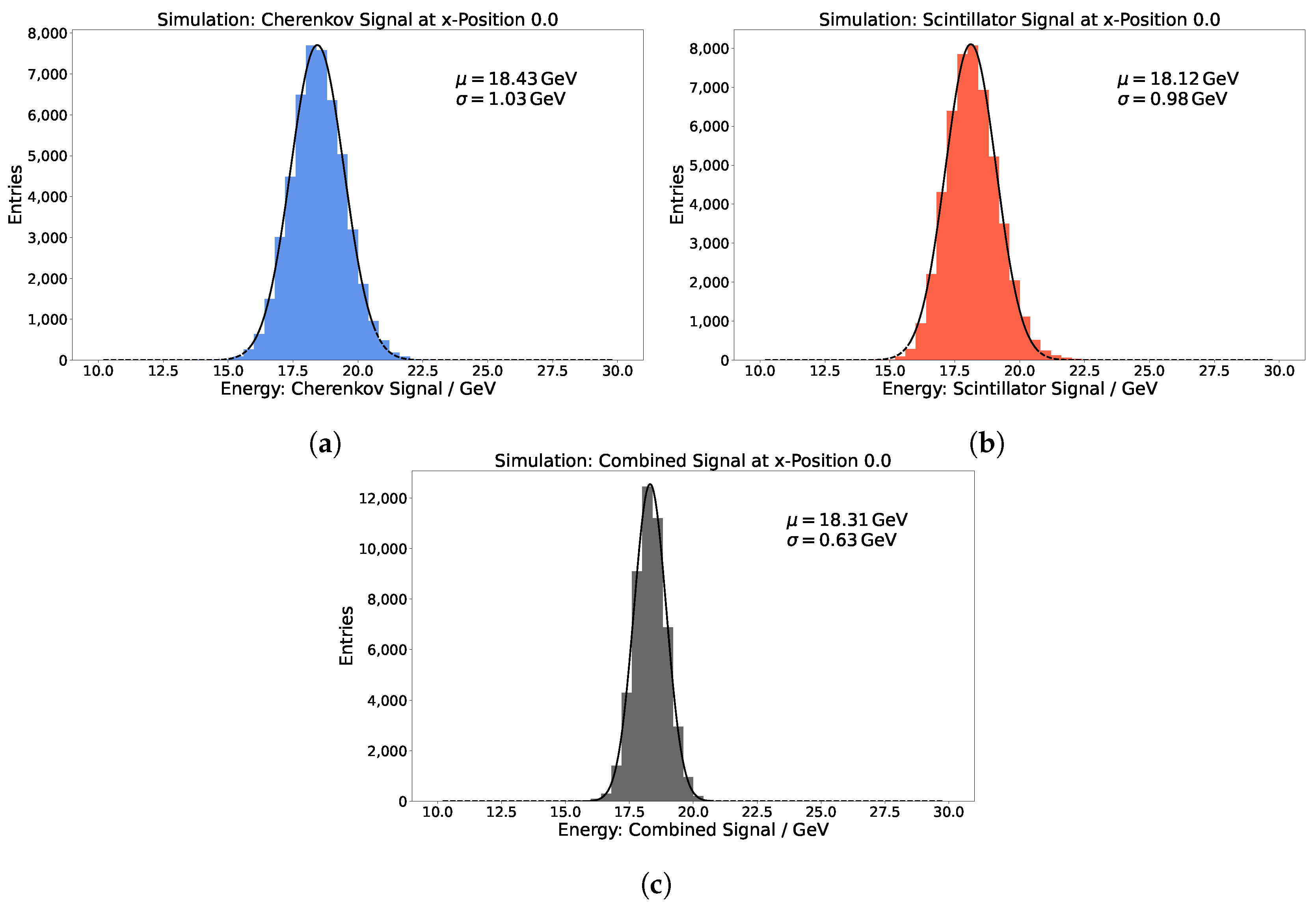
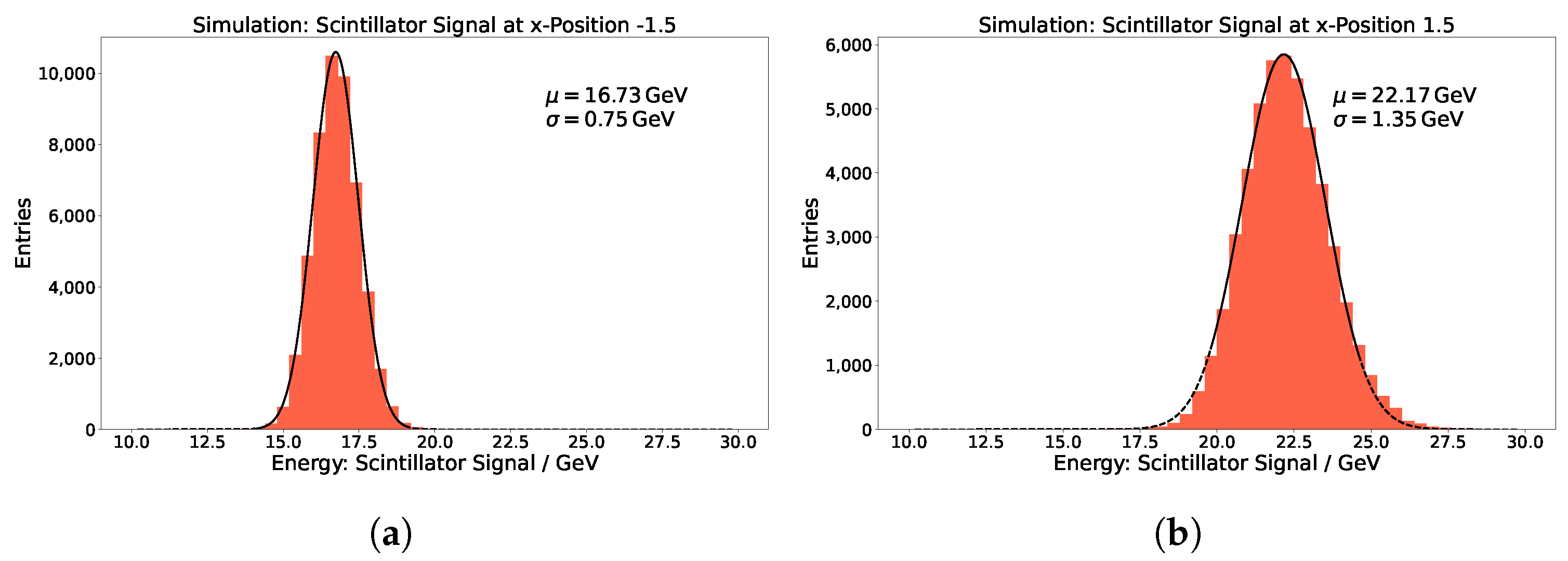
3.1. Simulation Setup
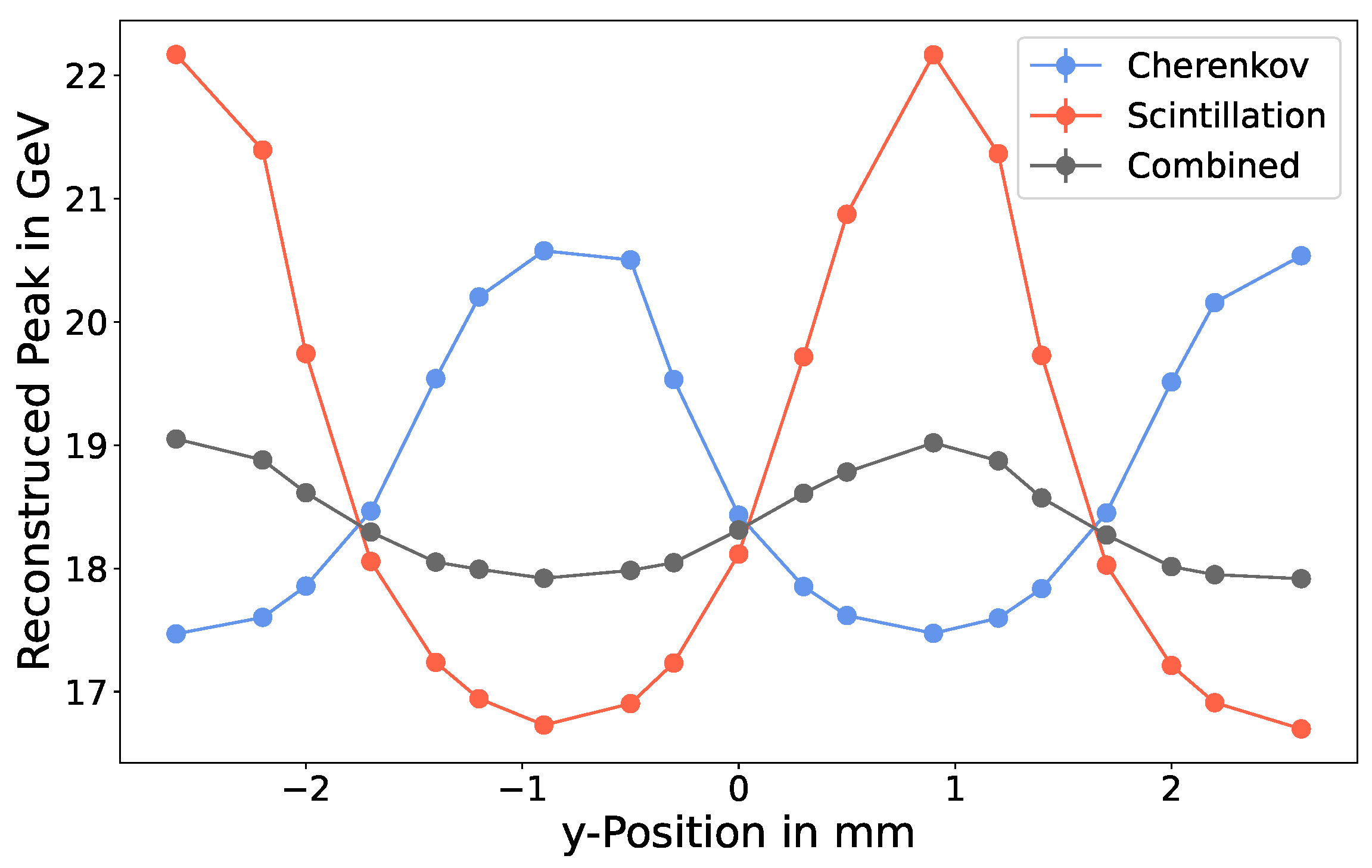
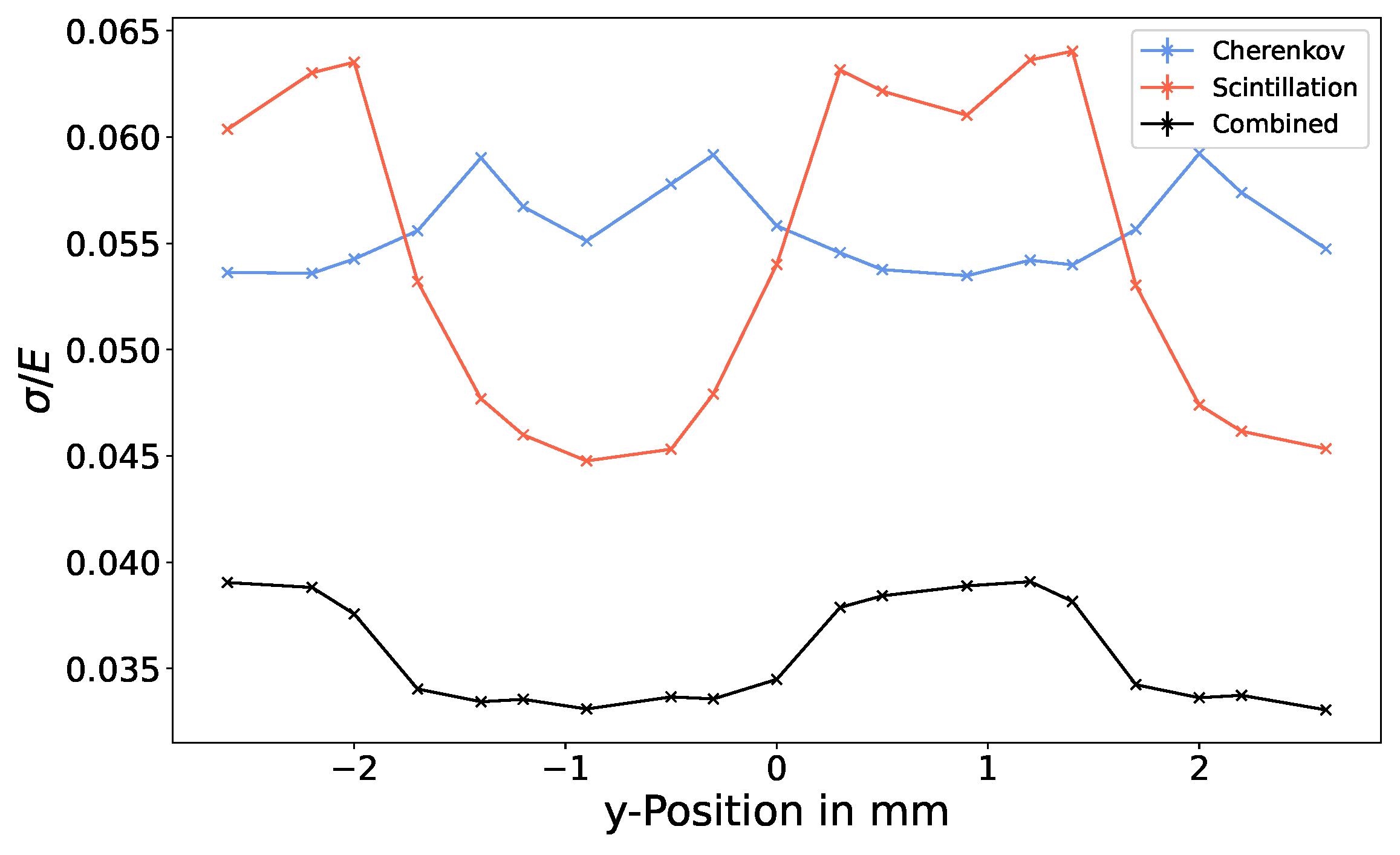
3.2. Impact Point Dependence
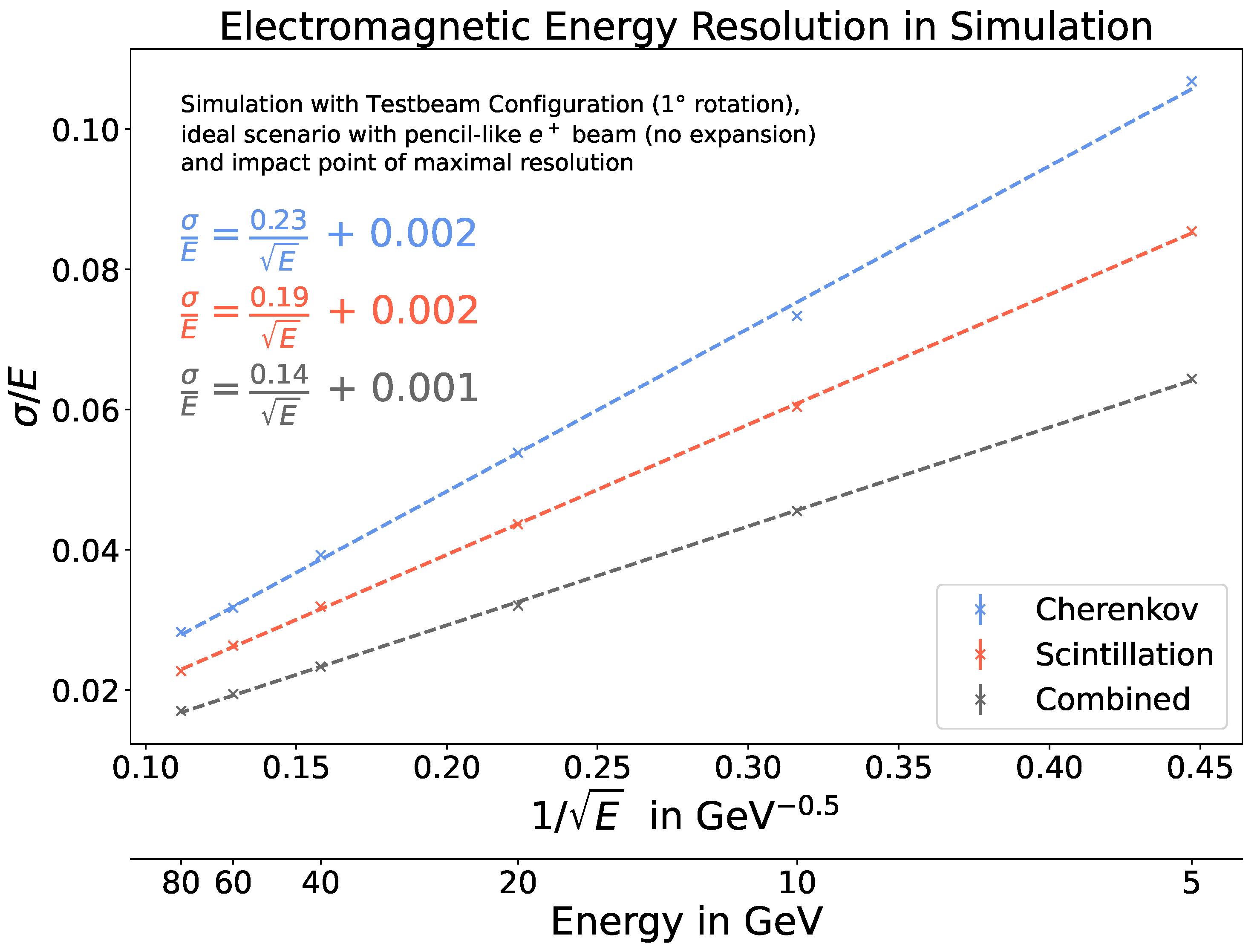
3.3. Energy Dependence
4. Conclusions
Funding
 This project has received funding from the European Union’s Horizon 2020 Research and Innovation programme under grant agreement No 101004761.
This project has received funding from the European Union’s Horizon 2020 Research and Innovation programme under grant agreement No 101004761.Data Availability Statement
Conflicts of Interest
Abbreviations
| EM | Electromagnetic |
| SiPM | Silicon Photomultiplier |
| PMT | Photomultiplier |
References
- Akchurin, N.; Bedeschi, F.; Cardini, A.; Cascella, M.; Cei, F.; De Pedis, D.; Ferrari, R.; Fracchia, S.; Franchino, S.; Fraternali, M.; et al. The electromagnetic performance of the RD52 fiber calorimeter. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2014, 735, 130–144. [Google Scholar] [CrossRef]
- Lee, S.; Livan, M.; Wigmans, R. Dual-readout calorimetry. Rev. Mod. Phys. 2018, 90, 025002. [Google Scholar] [CrossRef]
- Derrick, M.; Gacek, D.; Hill, N.; Musgrave, B.; Noland, R.; Petereit, E.; Repond, J.; Stanek, R.; Sugano, K. Design and construction of the ZEUS barrel calorimeter. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1991, 309, 77–100. [Google Scholar] [CrossRef]
- Antonello, M. IDEA: A detector concept for future leptonic colliders. Nuovo Cim. C 2020, 43, 27. [Google Scholar] [CrossRef]
- First Beam Tests for Highly Granular Dual-Readout Calorimeter Prototype. Available online: https://aidainnova.web.cern.ch/first-beam-tests-highly-granular-dual-readout-calorimeter-prototype (accessed on 31 July 2022).
- DREMTubes—GitHub Repository. Available online: https://github.com/lopezzot/DREMTubes (accessed on 31 July 2022).
- Pezzotti, L. Including Calorimeter Test-Beams into Geant-Val. CALOR 2022. Available online: https://indi.to/rT6st (accessed on 31 July 2022).
- Brient, J.C.; Videau, H. The Calorimetry at the Future e+ e− Linear Collider. arXiv 2002, arXiv:hep-ex/0202004. [Google Scholar] [CrossRef]
- Antonello, M.; Caccia, M.; Cascella, M.; Dunser, M.; Ferrari, R.; Franchino, S.; Gaudio, G.; Hall, K.; Hauptman, J.; Jo, H.; et al. Tests of a dual-readout fiber calorimeter with SiPM light sensors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2018, 899, 52–64. [Google Scholar] [CrossRef]
- Kolanoski, H.; Wermes, N. Particle Detectors: Fundamentals and Applications; Oxford University Press: Oxford, UK, 2020; pp. 603–604. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loeschcke Centeno, A., on behalf of the IDEA Dual-Readout Collaboration. Energy Resolution Studies in Simulation for the IDEA Dual-Readout Calorimeter Prototype. Instruments 2022, 6, 44. https://doi.org/10.3390/instruments6040044
Loeschcke Centeno A on behalf of the IDEA Dual-Readout Collaboration. Energy Resolution Studies in Simulation for the IDEA Dual-Readout Calorimeter Prototype. Instruments. 2022; 6(4):44. https://doi.org/10.3390/instruments6040044
Chicago/Turabian StyleLoeschcke Centeno, Andreas on behalf of the IDEA Dual-Readout Collaboration. 2022. "Energy Resolution Studies in Simulation for the IDEA Dual-Readout Calorimeter Prototype" Instruments 6, no. 4: 44. https://doi.org/10.3390/instruments6040044
APA StyleLoeschcke Centeno, A., on behalf of the IDEA Dual-Readout Collaboration. (2022). Energy Resolution Studies in Simulation for the IDEA Dual-Readout Calorimeter Prototype. Instruments, 6(4), 44. https://doi.org/10.3390/instruments6040044





