DOME: Discrete Oriented Muon Emission in GEANT4 Simulations
Abstract
:1. Introduction
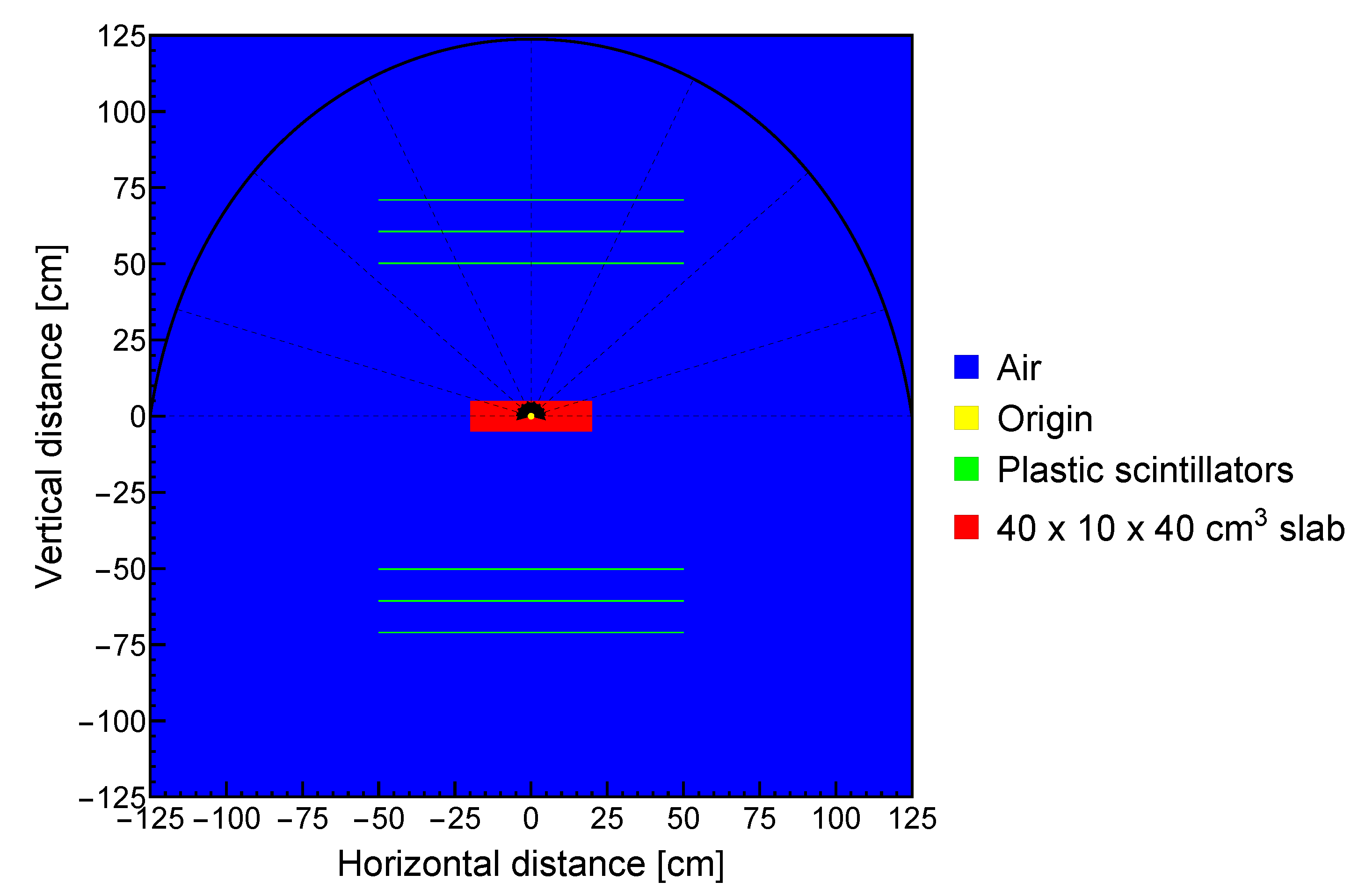
2. Central Focus Scheme
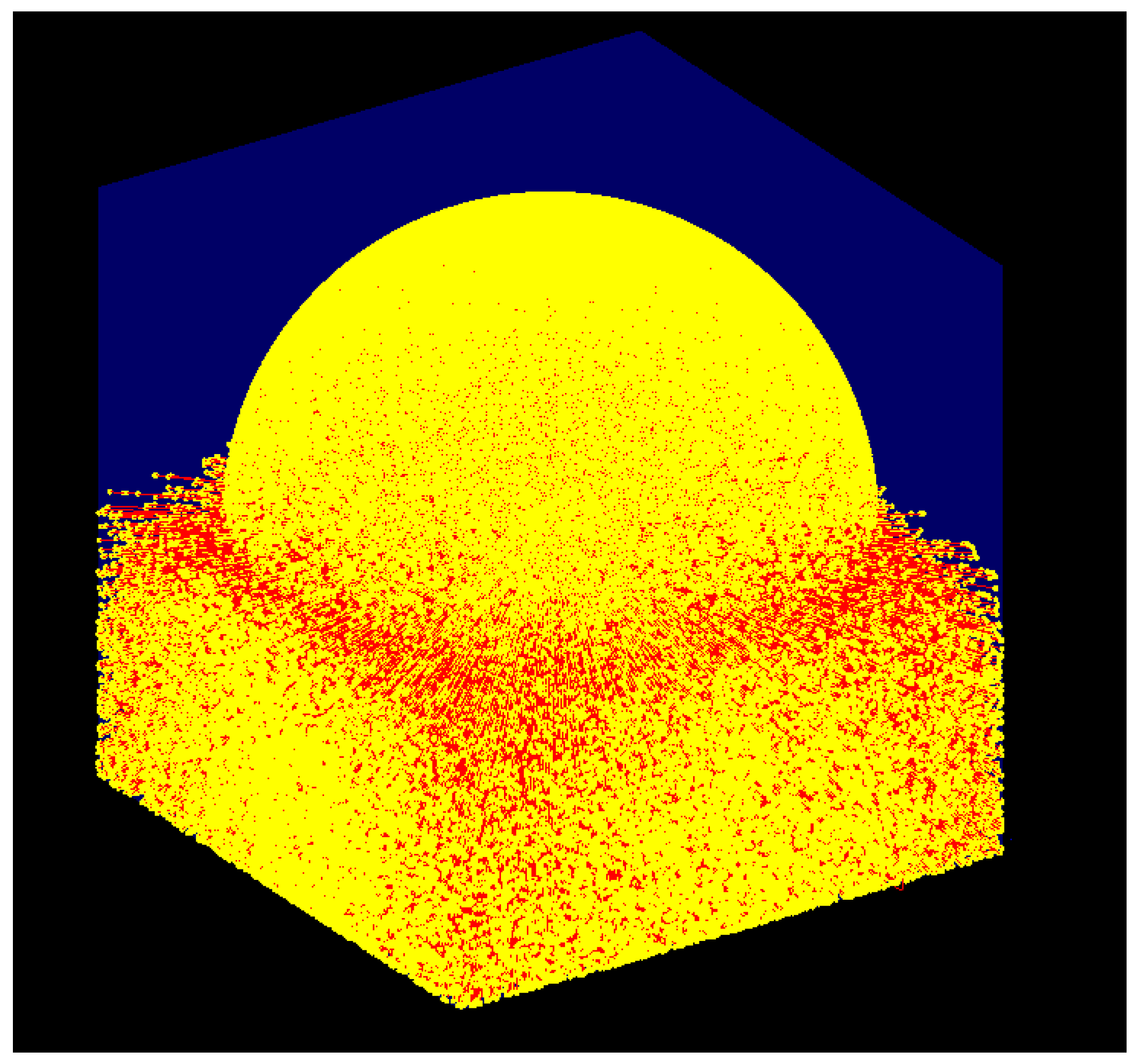
2.1. Generation through Gaussian Distributions
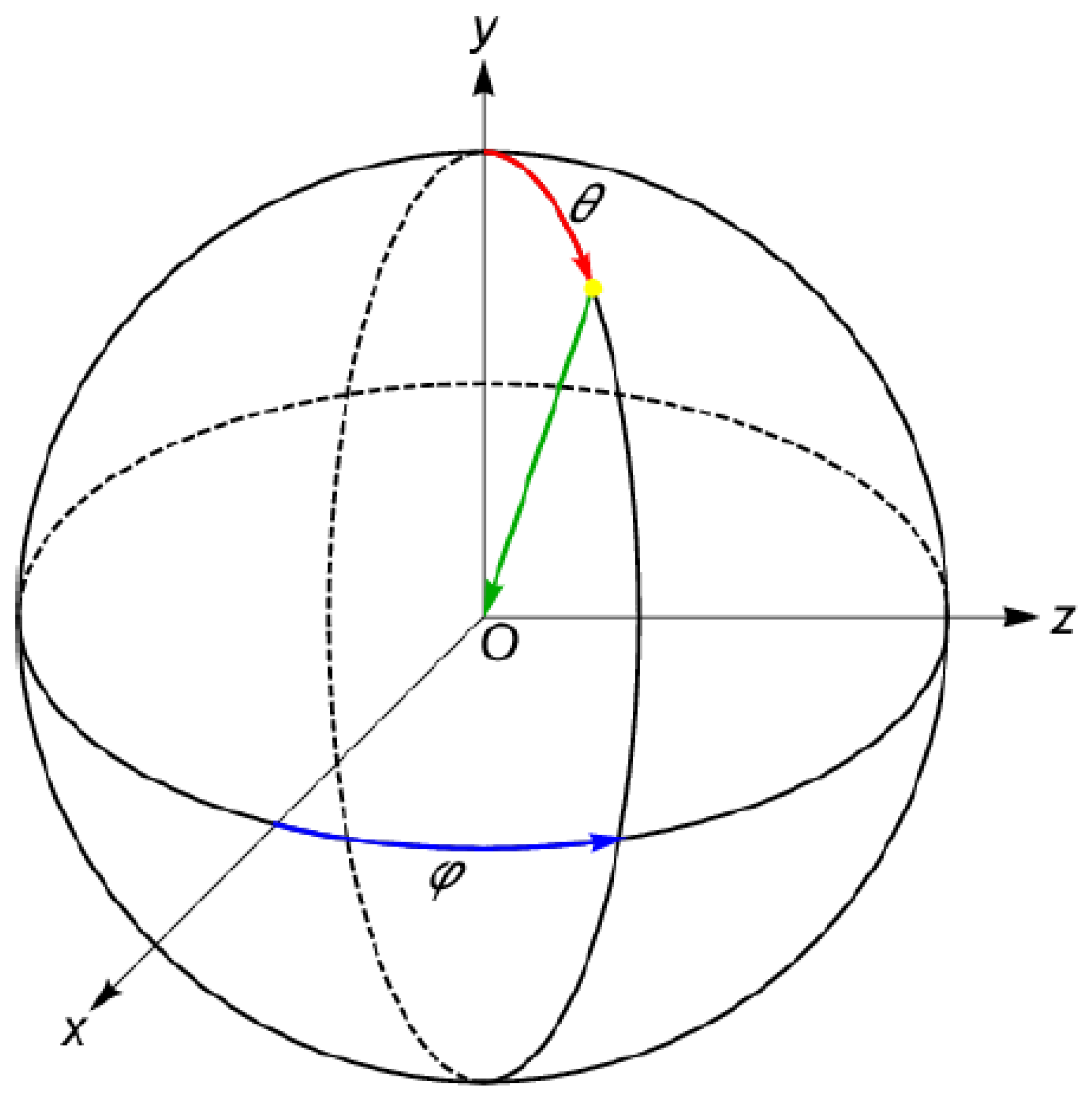
2.2. Generation via Coordinate Transformation
3. Restrictive Planar Focus Scheme
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Generation via Gaussian Distributions
#include "B1PrimaryGeneratorAction.hh"
#include "G4LogicalVolumeStore.hh"
#include "G4LogicalVolume.hh"
#include "G4Box.hh"
#include "G4RunManager.hh"
#include "G4ParticleGun.hh"
#include "G4ParticleTable.hh"
#include "G4ParticleDefinition.hh"
#include "G4SystemOfUnits.hh"
#include "Randomize.hh"
#include <iostream>
using namespace std;
B1PrimaryGeneratorAction::B1PrimaryGeneratorAction()
: G4VUserPrimaryGeneratorAction(),
fParticleGun(0)
// fEnvelopeBox(0)
{
G4int n_particle = 1;
fParticleGun = new G4ParticleGun(n_particle);
// default particle kinematic
G4ParticleTable* particleTable = G4ParticleTable::GetParticleTable();
G4String particleName;
G4ParticleDefinition* particle
= particleTable->FindParticle(particleName="mu-");
fParticleGun->SetParticleDefinition(particle);
}
B1PrimaryGeneratorAction::~B1PrimaryGeneratorAction()
{
delete fParticleGun;
}
//80-bin Discrete CRY Energy Spectrum
void B1PrimaryGeneratorAction::GeneratePrimaries(G4Event* anEvent)
{
//Discrete probabilities
double A[]= {0.0, 0.01253639, 0.02574546, 0.02802035, 0.02706636, 0.03528534, 0.02826496,
0.03157946, 0.03078447, 0.02777574, 0.02546415, 0.03150608, 0.02815489,
0.02580661, 0.02364179, 0.02170935, 0.02152589, 0.02348279, 0.02134243,
0.0196913, 0.02036398, 0.01841931, 0.01718402, 0.01700056, 0.01624226,
0.01539835, 0.01536166, 0.01471344, 0.01422421, 0.01412637, 0.01284215,
0.01260977, 0.01213278, 0.0129033, 0.01248746, 0.01196155, 0.01064064,
0.01057949, 0.0096255, 0.0103838, 0.00928304, 0.00879382, 0.00884274,
0.00793767, 0.00786429, 0.00769306, 0.00709376, 0.00736283, 0.0071916,
0.00721607, 0.00692253, 0.00643331, 0.00678799, 0.00673907, 0.00618869,
0.00634769, 0.00665346, 0.00650669, 0.00561385, 0.00589516, 0.00589516,
0.00578508, 0.00557716, 0.00550378, 0.00434187, 0.0043541, 0.00408503,
0.00364472, 0.00399941, 0.00388934, 0.00396272, 0.00431741, 0.00368142,
0.00363249, 0.00362026, 0.00410949, 0.00336342, 0.00358357, 0.00362026,
0.00348573, 0.0035958};
//Discrete energies
double B[]= {0.0, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000,
1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000,
2100, 2200, 2300, 2400, 2500, 2600, 2700, 2800, 2900, 3000,
3100, 3200, 3300, 3400, 3500, 3600, 3700, 3800, 3900, 4000,
4100, 4200, 4300, 4400, 4500, 4600, 4700, 4800, 4900, 5000,
5100, 5200, 5300, 5400, 5500, 5600, 5700, 5800, 5900, 6000,
6100, 6200, 6300, 6400, 6500, 6600, 6700, 6800, 6900, 7000,
7100, 7200, 7300, 7400, 7500, 7600, 7700, 7800, 7900, 8000};
G4int SizeEnergy=sizeof(B)/sizeof(B[0]);
G4int SizeProbability=sizeof(A)/sizeof(A[0]);
G4double Grid[sizeof(B)/sizeof(B[0])];
double sum=0;
for(int x=0; x < 81; x++){
sum=sum+A[x];
Grid[x]=sum;
std::ofstream GridFile;
GridFile.open("Probability_grid.txt", std::ios::app);
GridFile << Grid[x] << G4endl;
GridFile.close();
}
G4double radius=100*cm; //radius of sphere
for (int n_particle = 1; n_particle < 100000; n_particle++){
G4double x0=G4RandGauss::shoot();
std::ofstream GaussFile;
GaussFile.open("Gauss_x.txt", std::ios::app); //in mm
GaussFile << x0 << G4endl;
GaussFile.close();
//Centerally focused semi-spherical source via Gauss distributions
G4double y0=G4RandGauss::shoot();
G4double z0=G4RandGauss::shoot();
G4double n0=sqrt(pow(x0,2)+pow(y0,2)+pow(z0,2));
//Coordinates on sphere
x0 = radius*(x0/n0);
y0 = radius*abs(y0/n0);
z0 = radius*(z0/n0);
std::ofstream SphereFile;
SphereFile.open("coordinates_on_sphere.txt", std::ios::app); //in mm
SphereFile << x0 << " "<< y0 << " " << z0 << " " << G4endl;
SphereFile.close();
fParticleGun->SetParticlePosition(G4ThreeVector(x0,y0,z0));
//Aimed at origin
G4double x1=0;
G4double y1=0;
G4double z1=0;
G4double mx = x1-x0;
G4double my = y1-y0;
G4double mz = z1-z0;
G4double mn = sqrt(pow(mx,2)+pow(my,2)+pow(mz,2));
mx = mx/mn;
my = my/mn;
mz = mz/mn;
fParticleGun->SetParticleMomentumDirection(G4ThreeVector(mx,my,mz));
G4double Energy=0; //Just for initialization
G4double pseudo=G4UniformRand();
for (int i=0; i < 81; i++){
if(pseudo > Grid[i] && pseudo <= Grid[i+1]){
Energy=B[i+1];
std::ofstream EnergyFile;
EnergyFile.open("Energy.txt", std::ios::app);
EnergyFile << Energy << G4endl;
EnergyFile.close();
}
}
fParticleGun->SetParticleEnergy(Energy);
fParticleGun->GeneratePrimaryVertex(anEvent);
}
}
Appendix B. Generation by Means of Coordinate Transformation
#include "B1PrimaryGeneratorAction.hh"
#include "G4LogicalVolumeStore.hh"
#include "G4LogicalVolume.hh"
#include "G4Box.hh"
#include "G4RunManager.hh"
#include "G4ParticleGun.hh"
#include "G4ParticleTable.hh"
#include "G4ParticleDefinition.hh"
#include "G4SystemOfUnits.hh"
#include "Randomize.hh"
#include <iostream>
using namespace std;
B1PrimaryGeneratorAction::B1PrimaryGeneratorAction()
: G4VUserPrimaryGeneratorAction(),
fParticleGun(0)
// fEnvelopeBox(0)
{
G4int n_particle = 1;
fParticleGun = new G4ParticleGun(n_particle);
// default particle kinematic
G4ParticleTable* particleTable = G4ParticleTable::GetParticleTable();
G4String particleName;
G4ParticleDefinition* particle
= particleTable->FindParticle(particleName="mu-");
fParticleGun->SetParticleDefinition(particle);
}
B1PrimaryGeneratorAction::~B1PrimaryGeneratorAction()
{
delete fParticleGun;
}
//80-bin Discrete CRY Energy Spectrum
void B1PrimaryGeneratorAction::GeneratePrimaries(G4Event* anEvent)
{
//Discrete probabilities
double A[]= {0.0, 0.01253639, 0.02574546, 0.02802035, 0.02706636, 0.03528534, 0.02826496,
0.03157946, 0.03078447, 0.02777574, 0.02546415, 0.03150608, 0.02815489,
0.02580661, 0.02364179, 0.02170935, 0.02152589, 0.02348279, 0.02134243,
0.0196913, 0.02036398, 0.01841931, 0.01718402, 0.01700056, 0.01624226,
0.01539835, 0.01536166, 0.01471344, 0.01422421, 0.01412637, 0.01284215,
0.01260977, 0.01213278, 0.0129033, 0.01248746, 0.01196155, 0.01064064,
0.01057949, 0.0096255, 0.0103838, 0.00928304, 0.00879382, 0.00884274,
0.00793767, 0.00786429, 0.00769306, 0.00709376, 0.00736283, 0.0071916,
0.00721607, 0.00692253, 0.00643331, 0.00678799, 0.00673907, 0.00618869,
0.00634769, 0.00665346, 0.00650669, 0.00561385, 0.00589516, 0.00589516,
0.00578508, 0.00557716, 0.00550378, 0.00434187, 0.0043541, 0.00408503,
0.00364472, 0.00399941, 0.00388934, 0.00396272, 0.00431741, 0.00368142,
0.00363249, 0.00362026, 0.00410949, 0.00336342, 0.00358357, 0.00362026,
0.00348573, 0.0035958};
//Discrete energies
double B[]= {0.0, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000,
1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000,
2100, 2200, 2300, 2400, 2500, 2600, 2700, 2800, 2900, 3000,
3100, 3200, 3300, 3400, 3500, 3600, 3700, 3800, 3900, 4000,
4100, 4200, 4300, 4400, 4500, 4600, 4700, 4800, 4900, 5000,
5100, 5200, 5300, 5400, 5500, 5600, 5700, 5800, 5900, 6000,
6100, 6200, 6300, 6400, 6500, 6600, 6700, 6800, 6900, 7000,
7100, 7200, 7300, 7400, 7500, 7600, 7700, 7800, 7900, 8000};
G4int SizeEnergy=sizeof(B)/sizeof(B[0]);
G4int SizeProbability=sizeof(A)/sizeof(A[0]);
G4double Grid[sizeof(B)/sizeof(B[0])];
double sum=0;
for(int x=0; x < 81; x++){
sum=sum+A[x];
Grid[x]=sum;
std::ofstream GridFile;
GridFile.open("Probability_grid.txt", std::ios::app);
GridFile << Grid[x] << G4endl;
GridFile.close();
}
G4double radius=100*cm; //radius of sphere
for (int n_particle = 1; n_particle < 100000; n_particle++){
//Centerally focused semi-spherical source via coordinate transformation
G4double rand1=G4UniformRand();
G4double rand2=G4UniformRand();
G4double theta=acos(2*rand1-1);
G4double phi=2*3.14159265359*rand2;
//Coordinates on sphere
G4double x0=radius*sin(theta)*cos(phi);
G4double y0=radius*abs(cos(theta));
G4double z0=radius*sin(theta)*sin(phi);
std::ofstream SphereFile;
SphereFile.open("coordinates_on_sphere.dat", std::ios::app); //in mm
SphereFile << x0 << " "<< y0 << " " << z0 << G4endl;
SphereFile.close();
fParticleGun->SetParticlePosition(G4ThreeVector(x0,y0,z0));
//Aimed at origin
G4double x1=0;
G4double y1=0;
G4double z1=0;
G4double mx = x1-x0;
G4double my = y1-y0;
G4double mz = z1-z0;
G4double mn = sqrt(pow(mx,2)+pow(my,2)+pow(mz,2));
mx = mx/mn;
my = my/mn;
mz = mz/mn;
fParticleGun->SetParticleMomentumDirection(G4ThreeVector(mx,my,mz));
G4double Energy=0; //Just for initialization
G4double pseudo=G4UniformRand();
for (int i=0; i < 81; i++){
if(pseudo > Grid[i] && pseudo <= Grid[i+1]){
Energy=B[i+1];
std::ofstream EnergyFile;
EnergyFile.open("Energy.txt", std::ios::app);
EnergyFile << Energy << G4endl;
EnergyFile.close();
}
}
fParticleGun->SetParticleEnergy(Energy);
fParticleGun->GeneratePrimaryVertex(anEvent);
}
}
References
- Pagano, D.; Bonomi, G.; Donzella, A.; Zenoni, A.; Zumerle, G.; Zurlo, N. EcoMug: An Efficient COsmic MUon Generator for cosmic-ray muon applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2021, 1014, 165732. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Topuz, A.I.; Kiisk, M.; Giammanco, A. Particle generation trough restrictive planes in GEANT4 simulations for potential applications of cosmic ray muon tomography. arXiv 2022, arXiv:2201.07068. [Google Scholar]
- Topuz, A.I.; Kiisk, M. Towards energy discretization for muon scattering tomography in GEANT4 simulations: A discrete probabilistic approach. arXiv 2022, arXiv:2201.08804. [Google Scholar]
- Marsaglia, G. Choosing a point from the surface of a sphere. Ann. Math. Stat. 1972, 43, 645–646. [Google Scholar] [CrossRef]
- Tashiro, Y. On methods for generating uniform random points on the surface of a sphere. Ann. Inst. Stat. Math. 1977, 29, 295–300. [Google Scholar] [CrossRef]
- Weisstein, E.W. “Disk Point Picking”. From MathWorld-A Wolfram Web Resource. 2011. Available online: http://mathworld.wolfram.com/ (accessed on 22 May 2022).
- Georgadze, A.; Kiisk, M.; Mart, M.; Avots, E.; Anbarjafari, G. Method and Apparatus for Detection and/or Identification of Materials and of Articles Using Charged Particles. US Patent 16/977,293, 7 January 2021. [Google Scholar]
- Borozdin, K.N.; Hogan, G.E.; Morris, C.; Priedhorsky, W.C.; Saunders, A.; Schultz, L.J.; Teasdale, M.E. Radiographic imaging with cosmic-ray muons. Nature 2003, 422, 277. [Google Scholar] [CrossRef] [PubMed]
- Frazão, L.; Velthuis, J.; Maddrell-Mander, S.; Thomay, C. High-resolution imaging of nuclear waste containers with muon scattering tomography. J. Instrum. 2019, 14, P08005. [Google Scholar] [CrossRef]
- Frazão, L.; Velthuis, J.; Thomay, C.; Steer, C. Discrimination of high-Z materials in concrete-filled containers using muon scattering tomography. J. Instrum. 2016, 11, P07020. [Google Scholar] [CrossRef]
- Bonechi, L.; D’Alessandro, R.; Giammanco, A. Atmospheric muons as an imaging tool. Rev. Phys. 2020, 5, 100038. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Topuz, A.I.; Kiisk, M.; Giammanco, A. DOME: Discrete Oriented Muon Emission in GEANT4 Simulations. Instruments 2022, 6, 42. https://doi.org/10.3390/instruments6030042
Topuz AI, Kiisk M, Giammanco A. DOME: Discrete Oriented Muon Emission in GEANT4 Simulations. Instruments. 2022; 6(3):42. https://doi.org/10.3390/instruments6030042
Chicago/Turabian StyleTopuz, Ahmet Ilker, Madis Kiisk, and Andrea Giammanco. 2022. "DOME: Discrete Oriented Muon Emission in GEANT4 Simulations" Instruments 6, no. 3: 42. https://doi.org/10.3390/instruments6030042
APA StyleTopuz, A. I., Kiisk, M., & Giammanco, A. (2022). DOME: Discrete Oriented Muon Emission in GEANT4 Simulations. Instruments, 6(3), 42. https://doi.org/10.3390/instruments6030042





