Atmospheric and Geodesic Controls of Muon Rates: A Numerical Study for Muography Applications
Abstract
1. Introduction
- MUPAGE [24] is a fast Monte Carlo generator of bundles of atmospheric muons for underwater/ice neutrino telescopes. It is based on parametric formulas obtained from Monte Carlo simulations of cosmic ray showers generating muons in bundle, with constraints from measurements of the muon flux with underground experiments. The range of validity extends from 1.5 km to 5.0 km of water vertical depth, and from 0° up to 85° for the zenith angle.
- Matrix Cascade equation MCeq [25,26,27,28,29] uses numerical equation cascades to study fluxes. It is a complete Monte Carlo calculation scheme, capable of calculating neutrino, electron and muon fluxes up to 100 TeV, with a statistical accuracy of about a few percent. All particles have their own cascades of equations that represent the evolution of the energy spectrum as a function of atmospheric depth.
- PARMA (PHITS-based Analytical Radiation Model in the Atmosphere) allows to estimate the terrestrial cosmic ray fluxes of neutrons, protons and ions, muons, electrons, positrons and photons almost anywhere on Earth and in the Earth’s atmosphere [30]. The model is based on analytical numerical functions whose parameter values are adjusted to reproduce the EAS results. The accuracy of the EAS simulation has been well verified with various experimental data.
- CRY (Cosmic-ray Shower Library) generates showers distributions for three observation levels (sea level, 2100 m and 11,300 m) and for primary particles from 1 GeV to GeV according to Hagmann et al. [31], and secondary particles from to GeV. The showers are generated in a specific area (maximum size ) from pre-computed tables as explained in Hagmann et al. [32] and primary protons are produced at an altitude of 31 km in the 1976 US atmosphere [33]. In this generator, the east–west effect is not taken into account but the latitude dependence with the geomagnetic cutoff and the CR spectrum modulation are provided. It is possible to set the type of secondary particles to be studied, the altitude, the latitude, the date, the number of particles and the size of the surface of interest. The date allows to take into account the solar modulation described by Papini et al. [34]. It is possible to use pre-calculated tables from GEANT4 to take into account the configuration of the detector [35]. CRY has limitations when you investigate multi-track events in a cosmic ray experiment or identifying background events in muography.
- CORSIKA (COsmic Ray SImulations for KAscade) [36,37] is a Monte Carlo code for simulating atmospheric particle showers initiated by high-energy cosmic ray particles. Primary particles (protons or light nuclei) are tracked in the atmosphere until they interact, decay or are absorbed. All secondary particles are explicitly followed along their trajectories and their parameters are stored when they reach an observational level.
2. Materials and Methods
2.1. Standard Use Cases
2.2. Simulation’s Configuration
2.2.1. Primaries at the Top of the Atmosphere
- Number of simulated showers and energy ranges
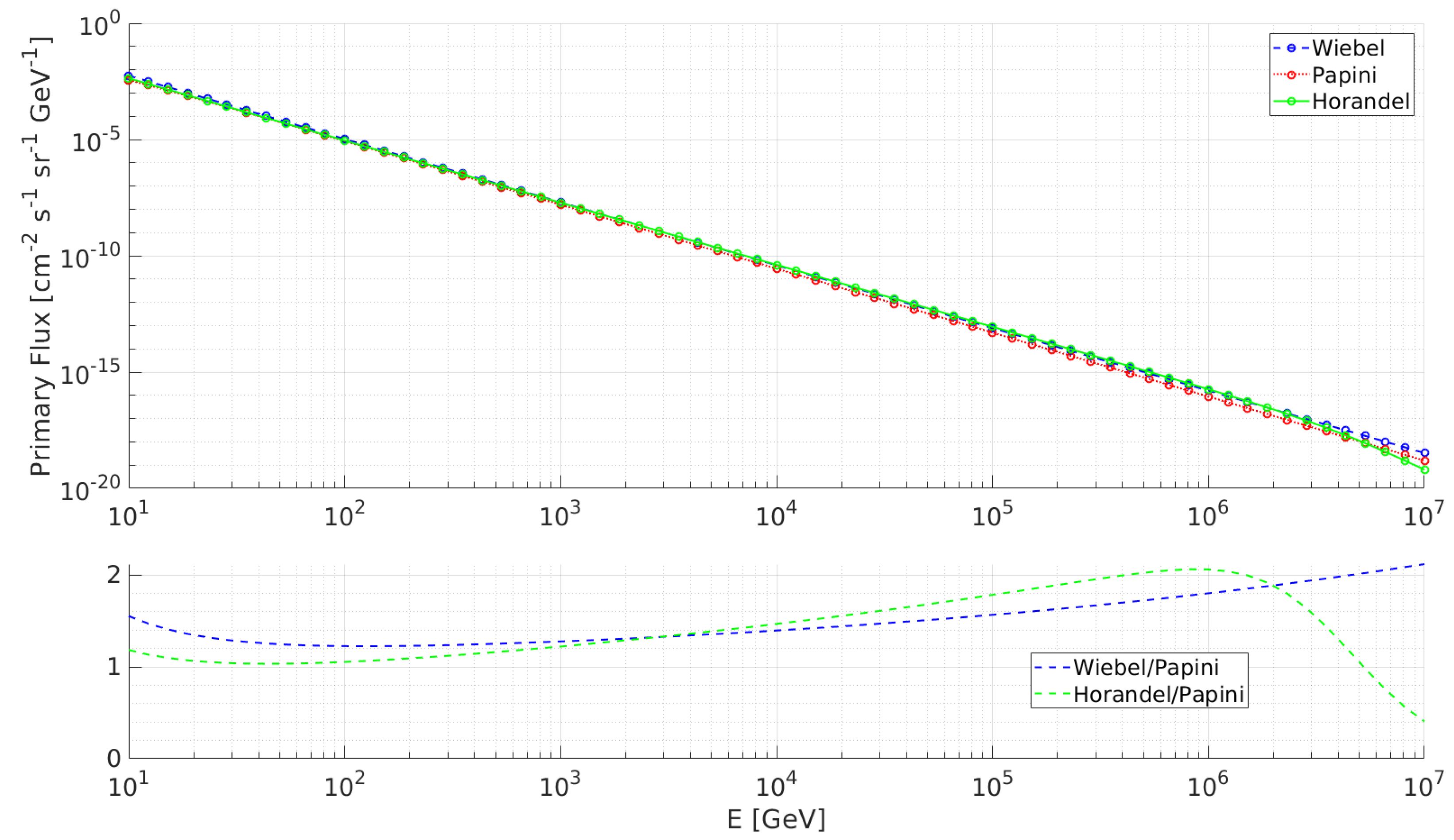
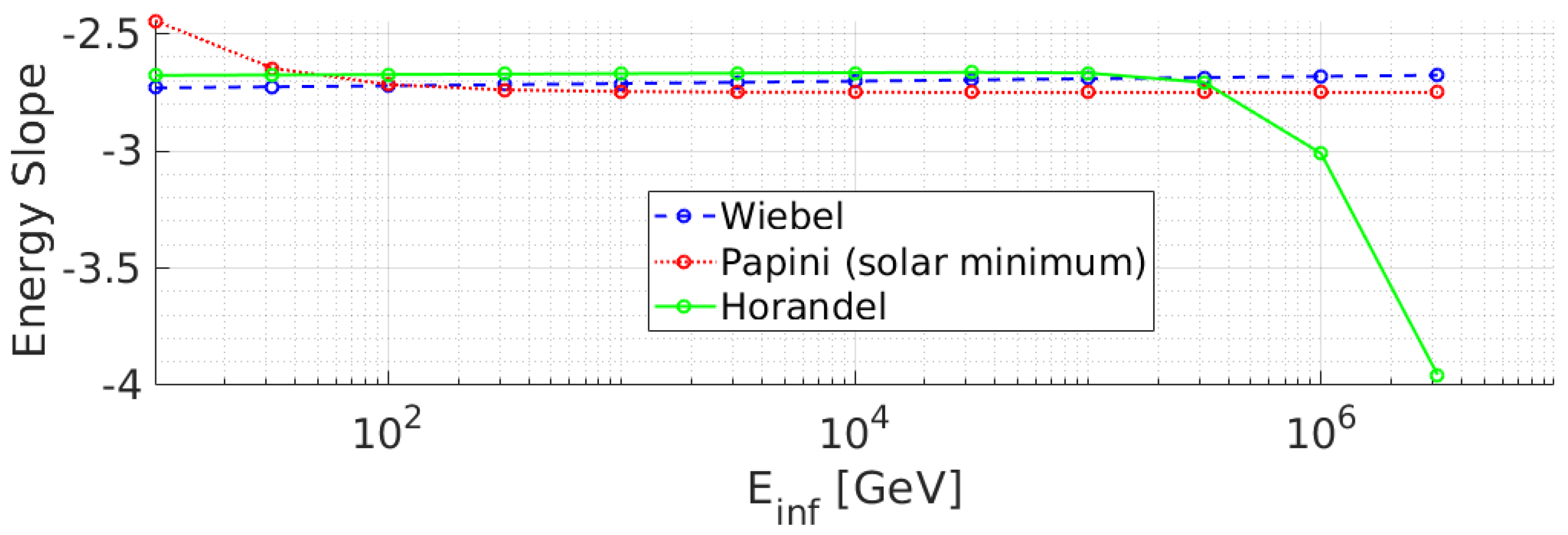
- Slope of the primary spectra
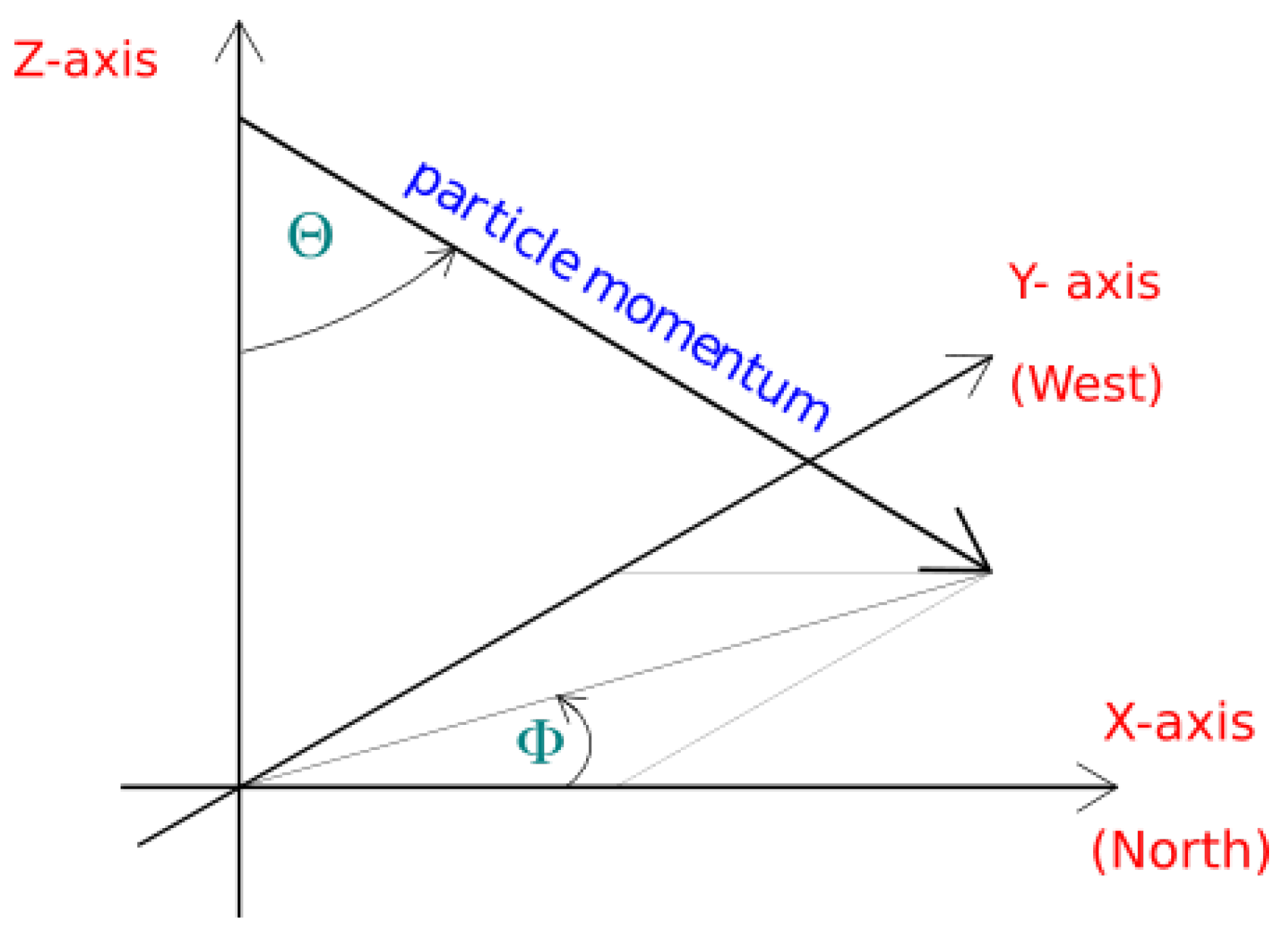
- Particles angles trajectories
2.2.2. Hadronic Interaction Models
2.2.3. Particles Energy Thresholds
2.2.4. Detector Geometry and Observation Levels
2.3. External Parameters
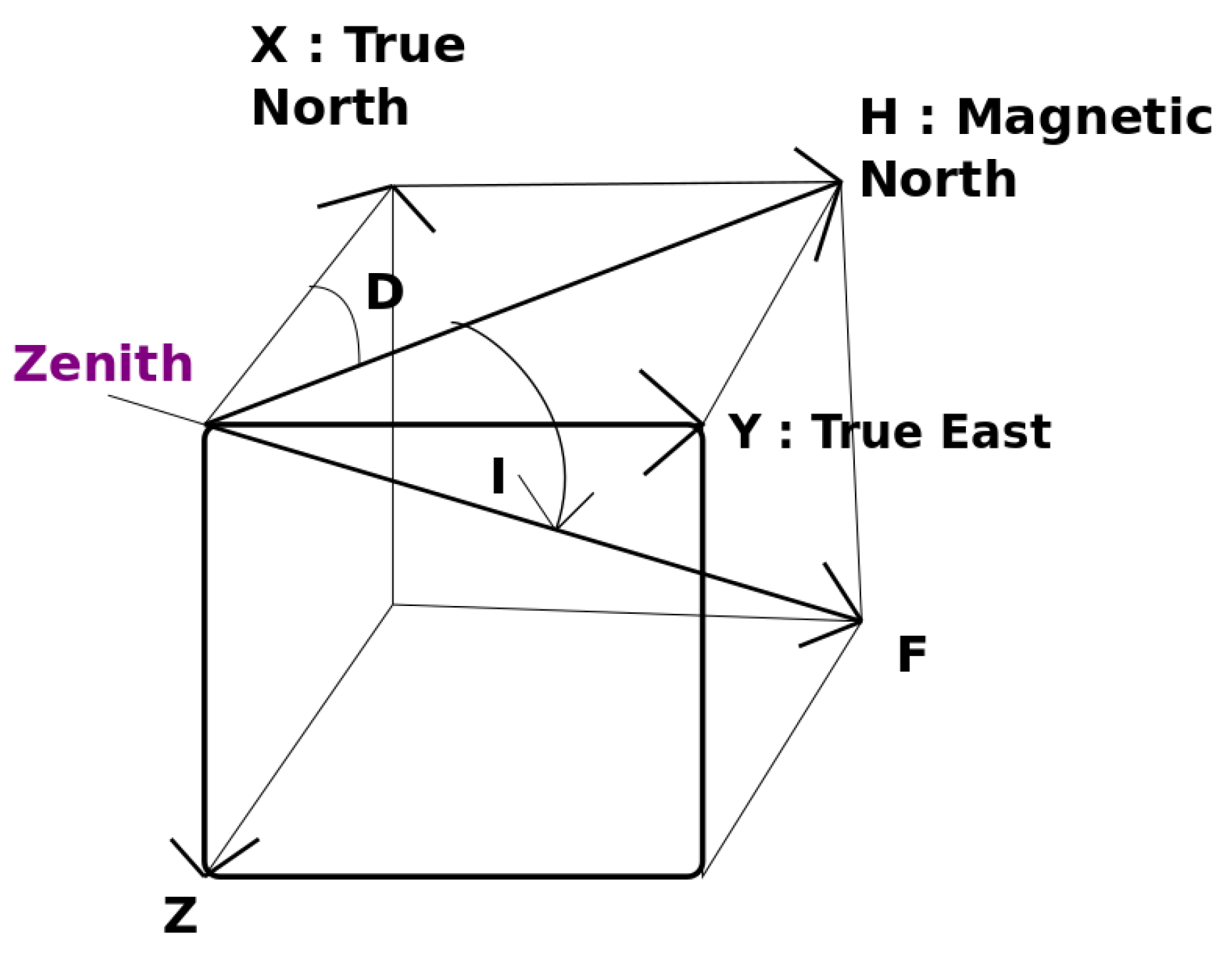
2.3.1. Earth’s Magnetic Field
2.3.2. Atmosphere Parameters
2.3.3. Physical Validity Range
2.4. Normalization Issues
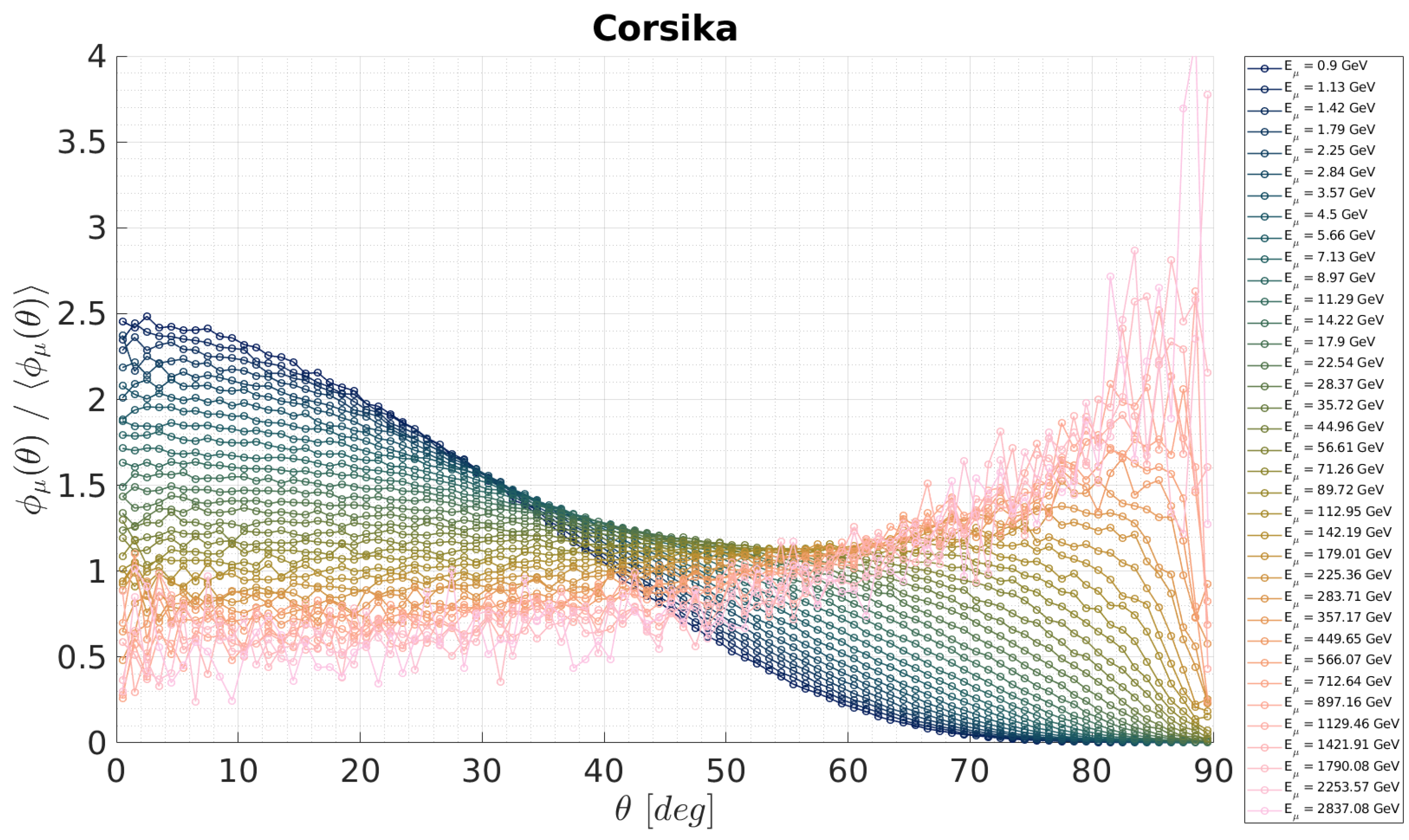
3. Results
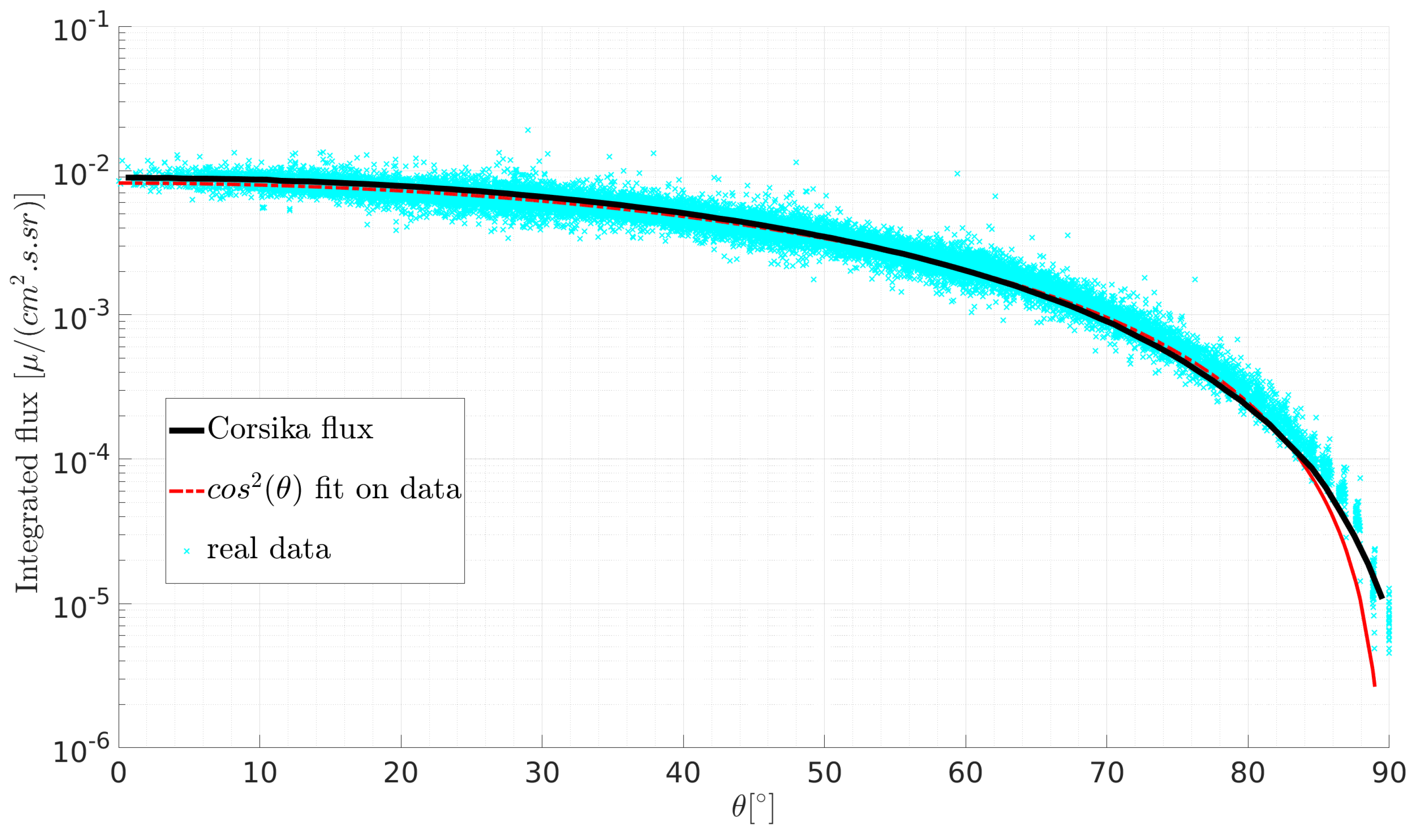
3.1. Comparison with Analytical Models
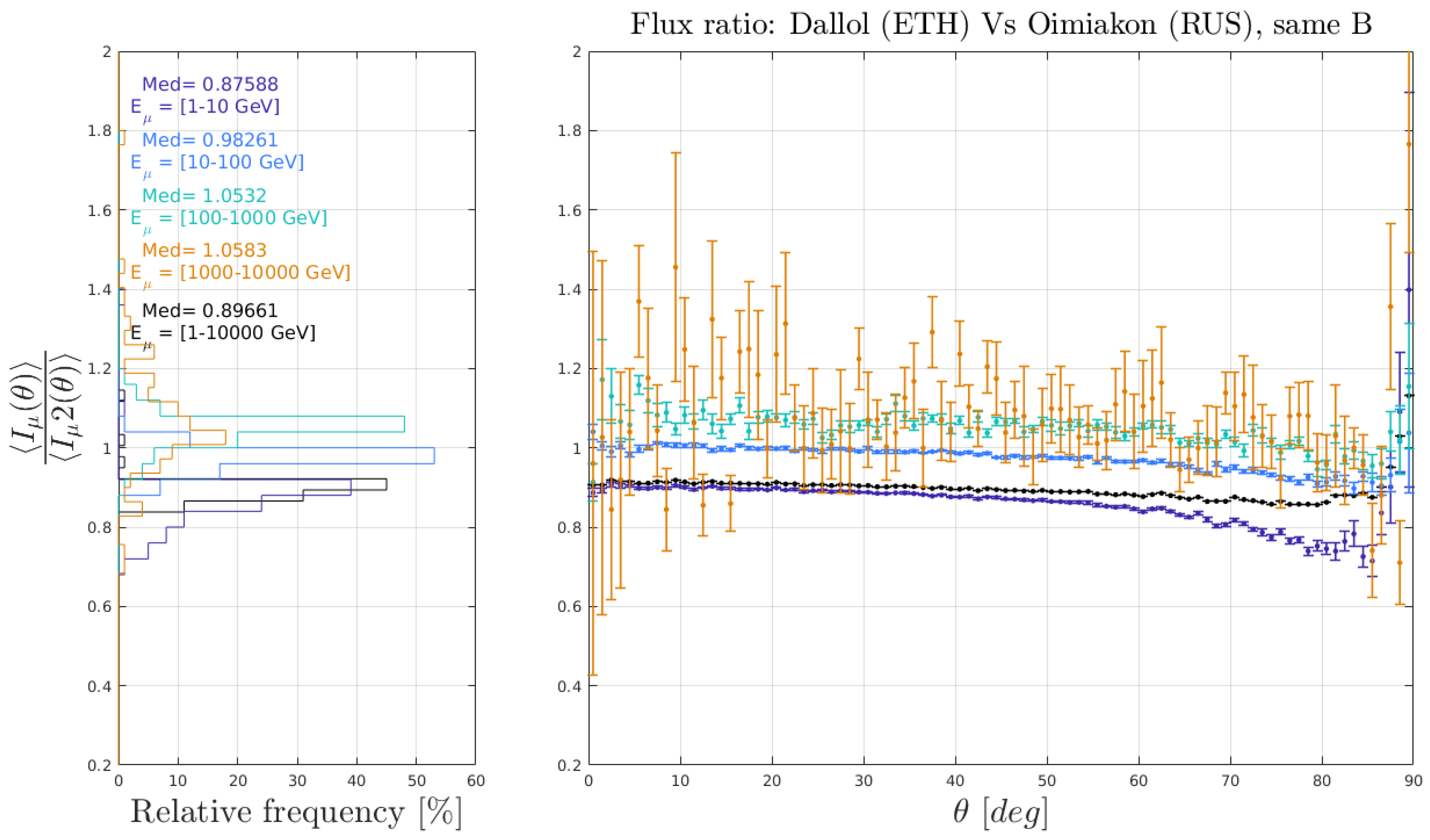
3.2. Comparison with Real Data
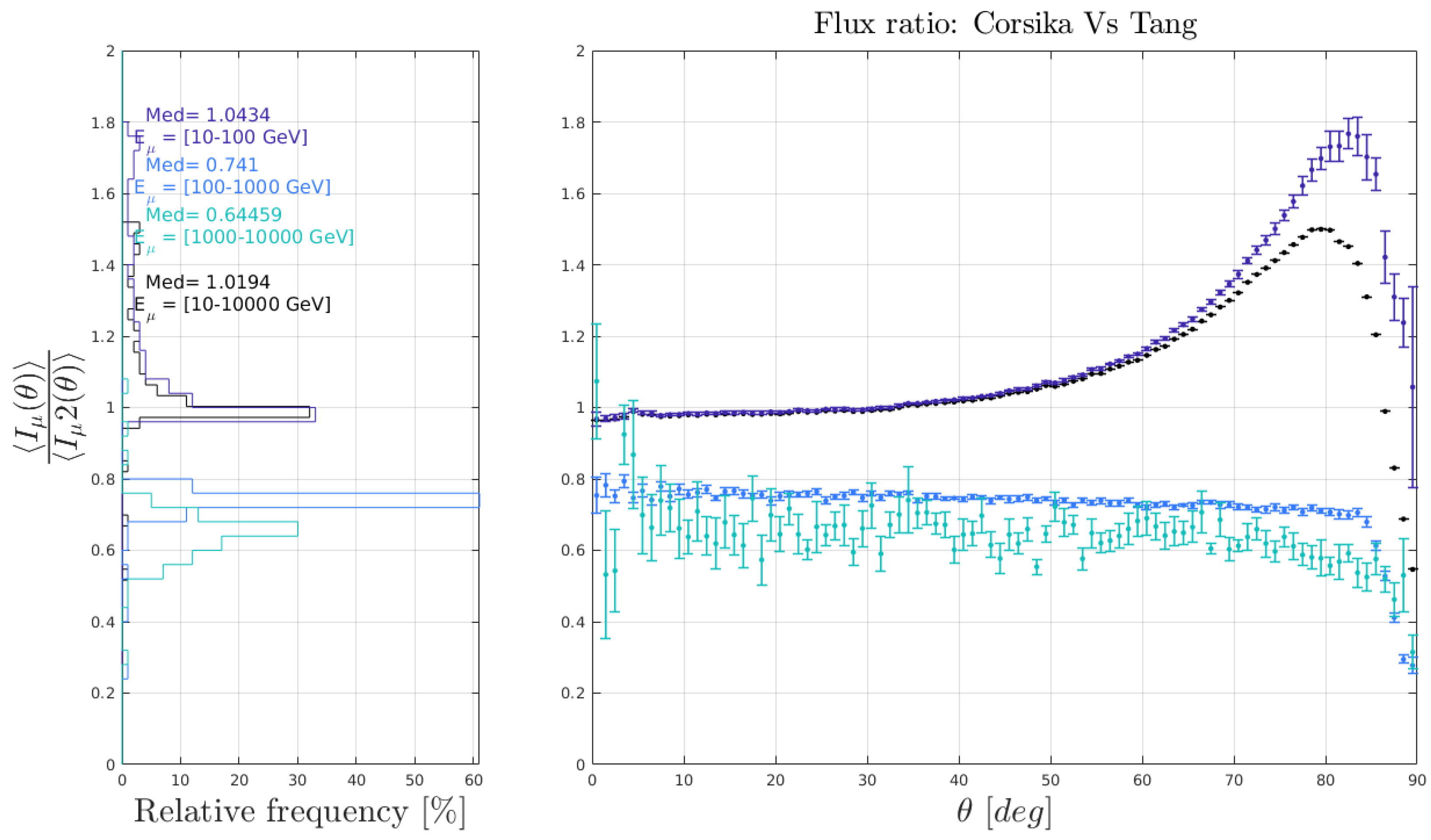
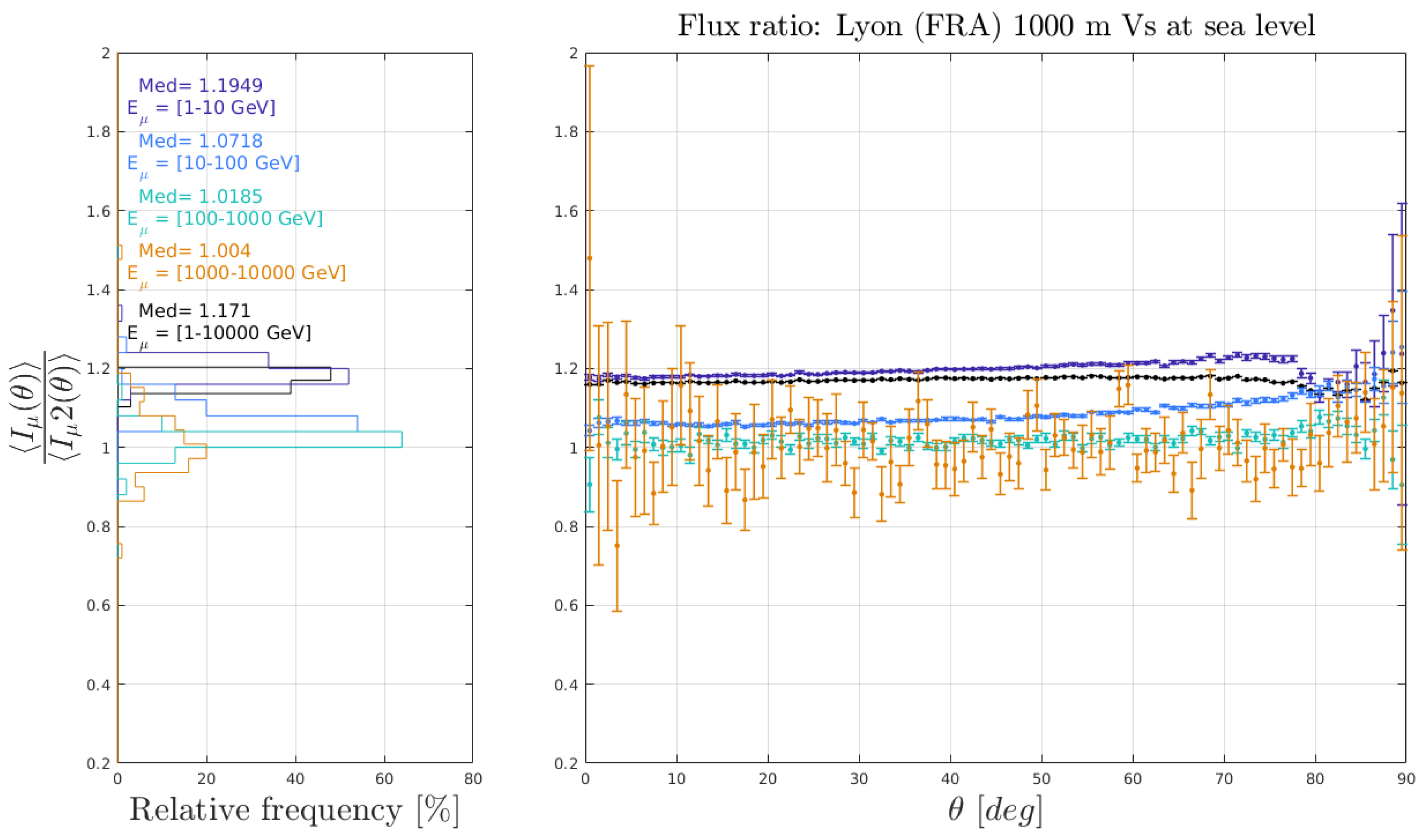
3.3. Geodesic and Atmospheric Factors
3.3.1. Altitude Effects
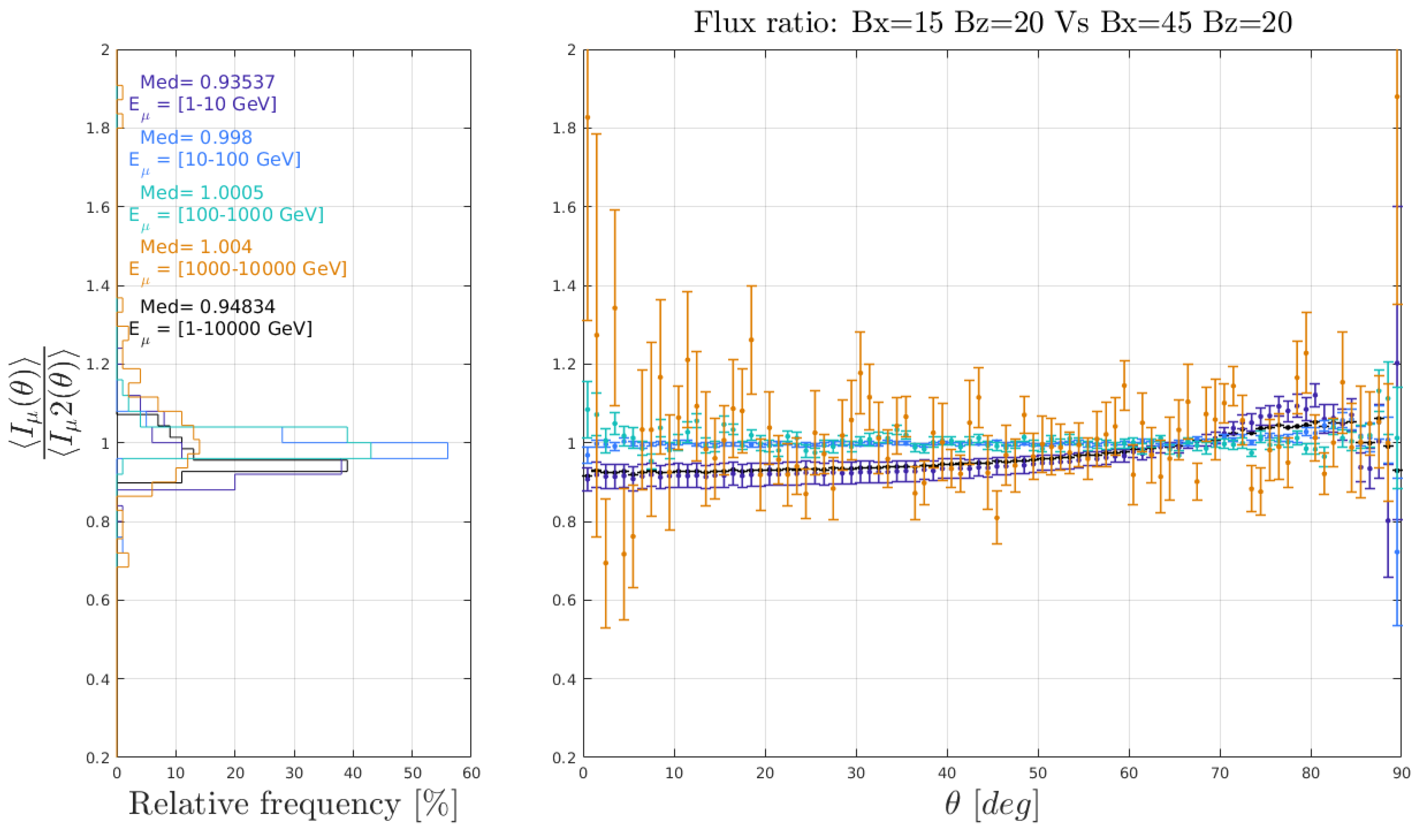
3.3.2. Geomagnetic Field Effects
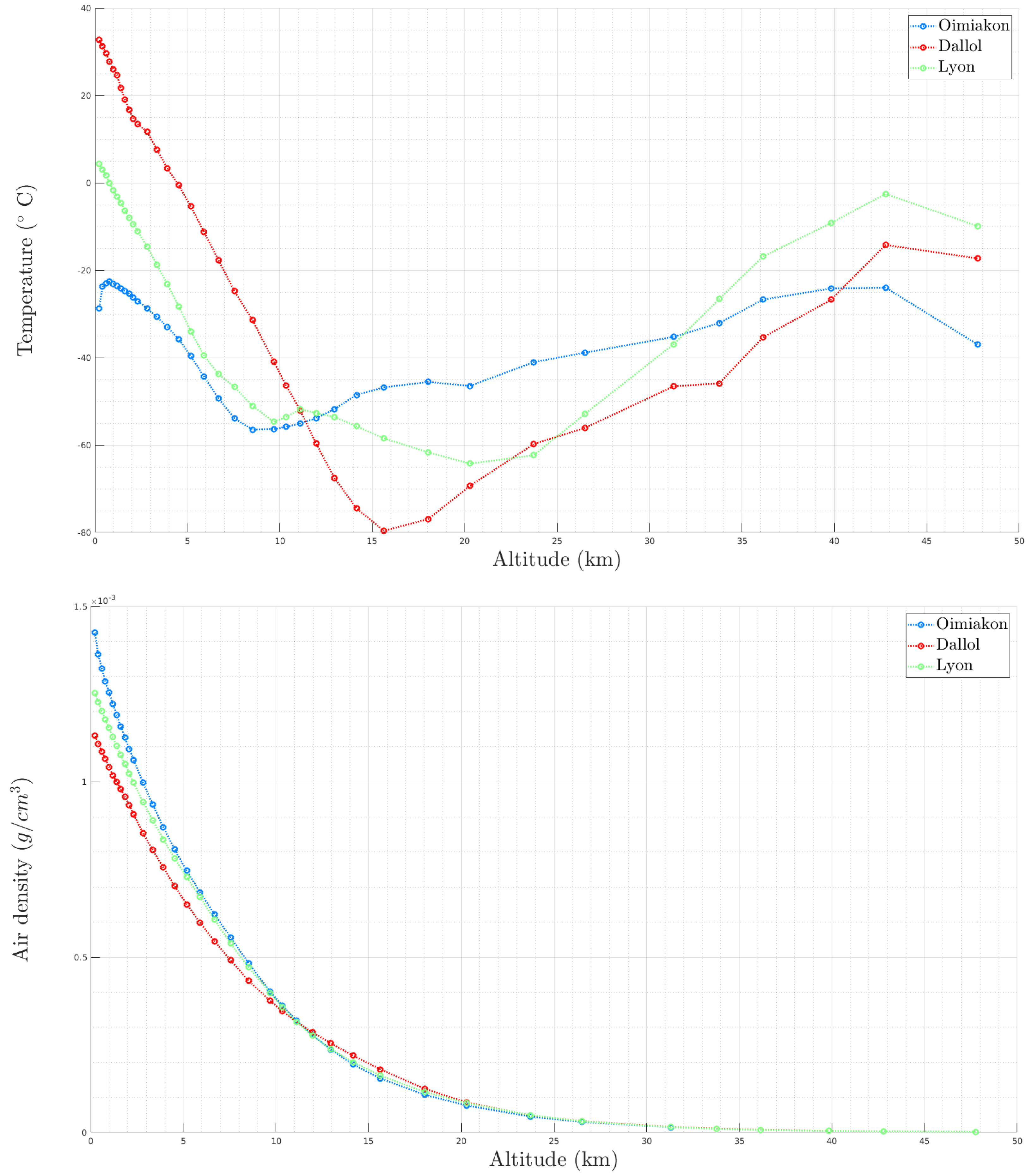
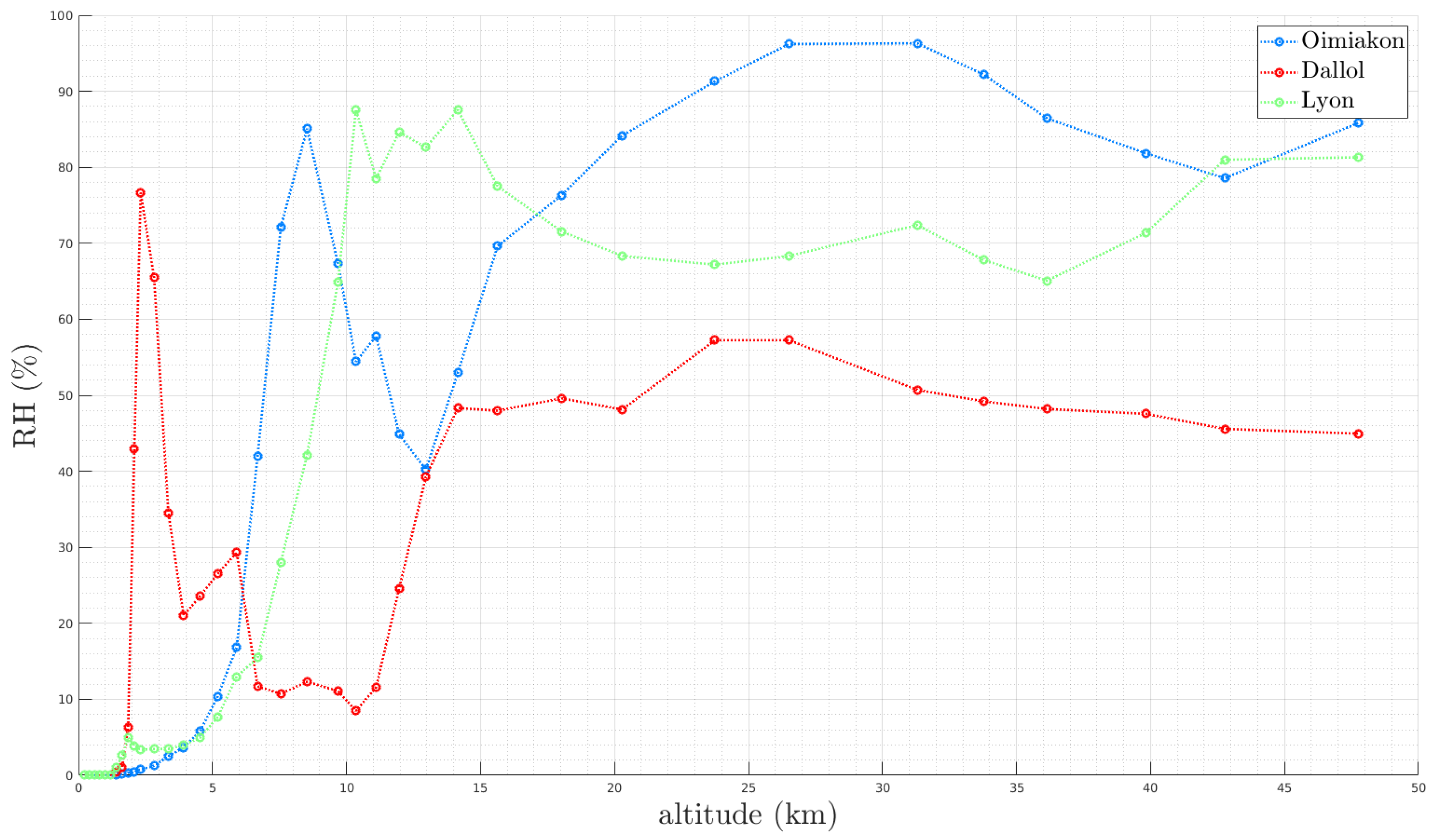
3.3.3. Atmospheric Thermodynamics Effects
- Atmosphere simple parametrization
- Atmosphere properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adamson, P.; Andreopoulos, C.; Arms, K.; Armstrong, R.; Auty, D.; Ayres, D.; Backhouse, C.; Barnett, J.; Barr, G.; Barrett, W.; et al. Observation of muon intensity variations by season with the MINOS far detector. Phys. Rev. D 2010, 81, 012001. [Google Scholar] [CrossRef]
- Tramontini, M.; Rosas-Carbajal, M.; Nussbaum, C.; Gibert, D.; Marteau, J. Middle-atmosphere dynamics observed with a portable muon detector. Earth Space Sci. 2019, 6, 1865–1876. [Google Scholar] [CrossRef]
- Jourde, K.; Gibert, D.; Marteau, J.; de Bremond d’Ars, J.; Gardien, S.; Girerd, C.; Ianigro, J.C. Monitoring temporal opacity fluctuations of large structures with muon radiography: A calibration experiment using a water tower. Sci. Rep. 2016, 6, 23054. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H.K.; Kusagaya, T.; Shinohara, H. Radiographic visualization of magma dynamics in an erupting volcano. Nat. Commun. 2014, 5, 3381. [Google Scholar] [CrossRef]
- Fehr, F.; The TOMUVOL Collaboration. Density imaging of volcanos with atmospheric muons. J. Phys. Conf. Ser. 2012, 375, 052019. [Google Scholar] [CrossRef]
- Lesparre, N.; Gibert, D.; Marteau, J.; Komorowski, J.C.; Nicollin, F.; Coutant, O. Density muon radiography of La Soufrière of Guadeloupe volcano: Comparison with geological, electrical resistivity and gravity data. Geophys. J. Int. 2012, 190, 1008–1019. [Google Scholar] [CrossRef]
- Jourde, K.; Gibert, D.; Marteau, J.; de Bremond d’Ars, J.; Komorowski, J.C. Muon dynamic radiography of density changes induced by hydrothermal activity at the La Soufrière of Guadeloupe volcano. Sci. Rep. 2016, 6, 33406. [Google Scholar] [CrossRef]
- Rosas-Carbajal, M.; Jourde, K.; Marteau, J.; Deroussi, S.; Komorowski, J.C.; Gibert, D. Three-dimensional density structure of La Soufrière de Guadeloupe lava dome from simultaneous muon radiographies and gravity data. Geophys. Res. Lett. 2017, 44, 6743–6751. [Google Scholar] [CrossRef]
- Morishima, K.; Kuno, M.; Nishio, A.; Kitagawa, N.; Manabe, Y.; Moto, M.; Takasaki, F.; Fujii, H.; Satoh, K.; Kodama, H.; et al. Discovery of a big void in Khufu’s Pyramid by observation of cosmic-ray muons. Nature 2017, 552, 386–390. [Google Scholar] [CrossRef]
- Procureur, S.; Attié, D. Development of high-definition muon telescopes and muography of the Great Pyramid. Comptes Rendus Phys. 2019, 20, 521–528. [Google Scholar] [CrossRef]
- Avgitas, T.; Elles, S.; Goy, C.; Karyotakis, Y.; Marteau, J. Mugraphy applied to archaelogy. arXiv 2022, arXiv:2203.00946. [Google Scholar]
- Alfaro, R.; Belmont-Moreno, E.; Cervantes, A.; Grabski, V.; López-Robles, J.; Manzanilla, L.; Martínez-Dávalos, A.; Moreno, M.; Menchaca-Rocha, A. A muon detector to be installed at the Pyramid of the Sun. Rev. Mex. Física 2003, 49, 54–59. [Google Scholar]
- Alvarez, L.W.; Anderson, J.A.; El Bedwei, F.; Burkhard, J.; Fakhry, A.; Girgis, A.; Goneid, A.; Hassan, F.; Iverson, D.; Lynch, G.; et al. Search for hidden chambers in the pyramids. Science 1970, 167, 832–839. [Google Scholar] [CrossRef] [PubMed]
- Guardincerri, E.; Rowe, C.; Schultz-Fellenz, E.; Roy, M.; George, N.; Morris, C.; Bacon, J.; Durham, M.; Morley, D.; Plaud-Ramos, K.; et al. 3D cosmic ray muon tomography from an underground tunnel. Pure Appl. Geophys. 2017, 174, 2133–2141. [Google Scholar] [CrossRef]
- Marteau, J.; de Bremond d’Ars, J.; Gibert, D.; Jourde, K.; Ianigro, J.C.; Carlus, B. DIAPHANE: Muon tomography applied to volcanoes, civil engineering, archaelogy. J. Instrum. 2017, 12, C02008. [Google Scholar] [CrossRef]
- Chevalier, A.; Rosas-Carbajal, M.; Gibert, D.; Cohu, A.; Carlus, B.; Ianigro, J.C.; Bouvier, F.; Marteau, J. Using mobile muography on board a Tunnel boring machine to detect man-made structures. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2019; Volume 2019, p. NS43B-0839. [Google Scholar]
- Borozdin, K.; Greene, S.; Lukić, Z.; Milner, E.; Miyadera, H.; Morris, C.; Perry, J. Cosmic ray radiography of the damaged cores of the Fukushima reactors. Phys. Rev. Lett. 2012, 109, 152501. [Google Scholar] [CrossRef]
- Baccani, G.; Bonechi, L.; Borselli, D.; Ciaranfi, R.; Cimmino, L.; Ciulli, V.; D’Alessandro, R.; Fratticioli, C.; Melon, B.; Noli, P.; et al. The MIMA project. Design, construction and performances of a compact hodoscope for muon radiography applications in the context of archaeology and geophysical prospections. J. Instrum. 2018, 13, P11001. [Google Scholar] [CrossRef]
- Tang, A.; Horton-Smith, G.; Kudryavtsev, V.A.; Tonazzo, A. Muon simulations for Super-Kamiokande, KamLAND, and CHOOZ. Phys. Rev. D 2006, 74, 053007. [Google Scholar] [CrossRef]
- Shukla, P.; Sankrith, S. Energy and angular distributions of atmospheric muons at the Earth. Int. J. Mod. Phys. A 2018, 33, 1850175. [Google Scholar] [CrossRef]
- Honda, M.; Kajita, T.; Kasahara, K.; Midorikawa, S.; Sanuki, T. Calculation of atmospheric neutrino flux using the interaction model calibrated with atmospheric muon data. Phys. Rev. 2007, D75, 043006. [Google Scholar] [CrossRef]
- Guan, M.; Chu, M.C.; Cao, J.; Luk, K.B.; Yang, C. A parametrization of the cosmic-ray muon flux at sea-level. arXiv 2015, arXiv:1509.06176. [Google Scholar]
- Gaisser, T.K. Cosmic Rays and Particle Physics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Carminati, G.; Bazzotti, M.; Margiotta, A.; Spurio, M. Atmospheric MUons from PArametric formulas: A fast GEnerator for neutrino telescopes (MUPAGE). Comput. Phys. Commun. 2008, 179, 915–923. [Google Scholar] [CrossRef]
- Fedynitch, A.; Engel, R.; Gaisser, T.K.; Riehn, F.; Stanev, T. MCEq—Numerical code for inclusive lepton flux calculations. In Proceedings of the 34th International Cosmic Ray Conference PoS(ICRC2015), Hague, The Netherlands, 30 July–6 August 2015; p. 1129. [Google Scholar] [CrossRef]
- Fedynitch, A.; Becker Tjus, J.; Desiati, P. Influence of hadronic interaction models and the cosmic ray spectrum on the high energy atmospheric muon and neutrino flux. Phys. Rev. D 2012, 86, 114024. [Google Scholar] [CrossRef]
- Fedynitch, A.; Dembinski, H.; Engel, R.; Gaisser, T.K.; Riehn, F.; Stanev, T. A state-of-the-art calculation of atmospheric lepton fluxes. In Proceedings of the 35th International Cosmic Ray Conference (ICRC2017), Busan, Korea, 10–20 July 2017; p. 1019. [Google Scholar] [CrossRef]
- Fedynitch, A.; Riehn, F.; Engel, R.; Gaisser, T.K.; Stanev, T. Hadronic interaction model Sibyll 2.3 c and inclusive lepton fluxes. Phys. Rev. D 2019, 100, 103018. [Google Scholar] [CrossRef]
- Fedynitch, A.; Engel, R.; Gaisser, T.K.; Riehn, F.; Stanev, T. Calculation of conventional and prompt lepton fluxes at very high energy. arXiv 2015, arXiv:1503.00544. [Google Scholar] [CrossRef]
- Sato, T. Analytical model for estimating terrestrial cosmic ray fluxes nearly anytime and anywhere in the world: Extension of PARMA/EXPACS. PLoS ONE 2015, 10, e0144679. [Google Scholar] [CrossRef]
- Hagmann, C.; Lange, D.; Wright, D. Monte Carlo Simulation of Proton-Induced Cosimc Ray Cascades in the Atmosphere; Technical Report; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 2007. [Google Scholar]
- Hagmann, C.; Lange, D.; Verbeke, J.; Wright, D. Cosmic-Ray Shower Library (CRY); Lawrence Livermore National Laboratory Document UCRL-TM-229453; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2012. [Google Scholar]
- Olàh, L.; Varga, D. Investigation of soft component in cosmic ray detection. Astropart. Phys. 2017, 93, 17–27. [Google Scholar] [CrossRef]
- Papini, P.; Grimani, C.; Stephens, S. An estimate of the secondary-proton spectrum at small atmospheric depths. Il Nuovo Cimento C 1996, 19, 367–387. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.a.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Heck, D.; Schatz, G.; Knapp, J.; Thouw, T.; Capdevielle, J. CORSIKA: A Monte Carlo Code to Simulate Extensive Air Showers; Technical Report; Citeseer: State College, PA, USA, 1998; 6019. [Google Scholar]
- Heck, D.; Pierog, T. Extensive Air Shower Simulation with CORSIKA: A User’s Guide; Version 7.6300 from 22 September 2017; Institut für Kernphysik: Mainz, Germany, 2017. [Google Scholar]
- Clay, J. Penetrating radiation II. Proc. R. Acad. Sci. Amst. 1928, 31, 1091–1097. [Google Scholar]
- Biallass, P.; Hebbeker, T. Parametrization of the cosmic muon flux for the generator CMSCGEN. arXiv 2009, arXiv:0907.5514. [Google Scholar]
- Wentz, J.; Brancus, I.M.; Bercuci, A.; Heck, D.; Oehlschläger, J.; Rebel, H.; Vulpescu, B. Simulation of Atmospheric Muon and Neutrino Fluxes with CORSIKA. Phys. Rev. D 2003, 67, 073020. [Google Scholar] [CrossRef]
- Mitrica, B.; Brancus, I.; Rebel, H.; Wentz, J.; Bercuci, A.; Toma, G.; Aiftimiei, C.; Duma, M. Experimentally guided Monte Carlo calculations of the atmospheric muon and neutrino flux. Nucl. Phys. B-Proc. Suppl. 2006, 151, 295–298. [Google Scholar] [CrossRef]
- Pethuraj, S.; Majumder, G.; Datar, V.; Mondal, N.; Mondal, S.; Nagaraj, P.; Ravindran, K.; Saraf, M.; Satyanarayana, B.; Shinde, R.; et al. Azimuthal Dependence of Cosmic Muon Flux by 2 m × 2 m RPC Stack at IICHEP-Madurai and Comparison with CORSIKA and HONDA Flux. In Proceedings of the XXIII DAE High Energy Physics Symposium, Chennai, India, 10–15 December 2018; pp. 807–812. [Google Scholar]
- Kovylyaeva, A.; Dmitrieva, A.; Tolkacheva, N.; Yakovleva, E. Calculations of temperature and barometric effects for cosmic ray flux on the Earth surface using the CORSIKA code. Phys. Conf. Ser. 2013, 409, 012128. [Google Scholar] [CrossRef]
- Useche, J.; Avila, C. Estimation of cosmic-muon flux attenuation by Monserrate Hill in Bogota. arXiv 2018, arXiv:1810.04712. [Google Scholar]
- Hörandel, J.R. On the knee in the energy spectrum of cosmic rays. Astropart. Phys. 2003, 19, 193–220. [Google Scholar] [CrossRef]
- Wiebel-Sooth, B.; Biermann, P.L.; Meyer, H. Cosmic Rays VII. Individual element spectra: Prediction and data. arXiv 1997, arXiv:astro-ph/9709253. [Google Scholar]
- Spurio, M. The cosmic rays and our galaxy. In Particles and Astrophysics; Springer: Berlin/Heidelberg, Germany, 2015; pp. 23–54. [Google Scholar]
- Nesterenok, A. Numerical calculations of cosmic ray cascade in the Earth’s atmosphere -Results for nucleon spectra. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2013, 295, 99–106. [Google Scholar] [CrossRef]
- Pethuraj, S.; Datar, V.; Majumder, G.; Mondal, N.; Ravindran, K.; Satyanarayana, B. Measurement of azimuthal dependent cosmic muon flux by 2mx2m RPC stack near Equator at IICHEP-Madurai. arXiv 2019, arXiv:1905.00739. [Google Scholar]
- Heck, D. The CURVED Version of the Air Shower Simulation Program CORSIKA; Technical Report; Forschungszentrum Karlsruhe: Karlsruhe, Germany, 2004. [Google Scholar]
- Usoskin, I.G.; Kovaltsov, G.A. Cosmic ray induced ionization in the atmosphere: Full modeling and practical applications. J. Geophys. Res. 2006, 111, D21206. [Google Scholar] [CrossRef]
- Apel, W.; Asch, T.; Badea, A.; Bahren, L.; Bekk, K.; Bercuci, A.; Bertaina, M.; Biermann, P.; Blumer, J.; Bozdog, H.; et al. Progress in air shower radio measurements: Detection of distant events. Astropart. Phys. 2006, 26, 332–340. [Google Scholar] [CrossRef][Green Version]
- Heck, D. Extensive Air Shower Simulations with CORSIKA and the Influence of High-Energy Hadronic Interaction Models. arXiv 2001, arXiv:astro-ph/0103073. [Google Scholar]
- Engel, R.; Heck, D.; Pierog, T. Extensive Air Showers and Hadronic Interactions at High Energy. Annu. Rev. Nucl. Part. Sci. 2011, 61, 467–489. [Google Scholar] [CrossRef]
- Tapia, A.; Dueñas, D.; Rodriguez, J.; Betancourt, J.; Caicedo, D. First Monte Carlo Simulation Study of Galeras Volcano Structure Using Muon Tomography. In Proceedings of the 38th International Conference on High Energy Physics, ICHEP 2016, Chicago, IL, USA, 3–10 August 2016. [Google Scholar]
- Atri, D. Hadronic interaction models and the angular distribution of cosmic ray muons. arXiv 2013, arXiv:1309.5874. [Google Scholar]
- Klepser, S. CORSIKA: Extensive Air Shower Simulation; Springer: Berlin, Germany, 2006; p. 29. [Google Scholar]
- Mitrica, B.; Petcu, M.; Saftoiu, A.; Brancus, I.; Sima, O.; Rebel, H.; Haungs, A.; Toma, G.; Duma, M. Investigation of cosmic ray muons with the WILLI detector compared with the predictions of theoretical models and with semi-analytical formulae. Nucl. Phys. B-Proc. Suppl. 2009, 196, 462–465. [Google Scholar] [CrossRef]
- Cazon, L.; Conceicao, R.; Pimenta, M.; Santos, E. A model for the transport of muons in extensive air showers. Astropart. Phys. 2012, 36, 211–223. [Google Scholar] [CrossRef]
- Velinov, P.; Mishev, A. Cosmic ray induced ionization in the atmosphere estimated with CORSIKA code simulations. C. R. Acad. Bulg. Des Sci. 2007, 60, 493. [Google Scholar]
- Abreu, P.; Aglietta, M.; Ahlers, M.; Ahn, E.; Albuquerque, I.F.d.M.; Allard, D.; Allekotte, I.; Allen, J.; Allison, P.; Almela, A.; et al. Description of atmospheric conditions at the Pierre Auger Observatory using the global data assimilation system (GDAS). Astropart. Phys. 2012, 35, 591–607. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service Climate Data Store (CDS). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate; CCCS: Singapore, 2017; Volume 15.
- Gaisser, T.K.; Engel, R.; Resconi, E. Cosmic Rays and Particle Physics; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Grashorn, E.; De Jong, J.; Goodman, M.; Habig, A.; Marshak, M.L.; Mufson, S.; Osprey, S.; Schreiner, P. The atmospheric charged kaon/pion ratio using seasonal variation methods. Astropart. Phys. 2010, 33, 140–145. [Google Scholar] [CrossRef]
| E Threshold | Hadrons | Muons | Electrons | Photons |
|---|---|---|---|---|
| 1. [57] | 0.1 GeV | 0.1 GeV | 0.1 MeV | 0.1 MeV |
| 2. [58] | 0.2 GeV | 0.2 GeV | 0.1 MeV | 0.1 MeV |
| 3. [59] | 0.05 GeV | 0.05 GeV | 0.003 GeV | 0.003 GeV |
| 4. [52] | 300 MeV | 100 MeV | 250 keV | 250 keV |
| 5. [60] | 0.05 GeV | 50 keV | 50 keV | 50 keV |
| 6. This study | 0.05 GeV | 0.01 GeV | 0.001 GeV | 0.001 GeV |
| 1–10,000 GeV | 1–10 GeV | 1000–10,000 GeV | |
|---|---|---|---|
| Magnetic field | 5 (±4)% | 6 (±1)% | 0.2 (±1)% |
| Altitude: - 1000 m/0 m - 5000 m/0 m | 15 (±1)% 115 (±10)% | 17 (±2.5)% 106 (±25)% | 7 (±2.7)% 2 (±1)% |
| Atmosphere: - Extreme - Seasonal | 10 (±7)% 8 (±1)% | 13 (±10)% 9 (±3)% | 5 (±10)% 2 (±10)% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cohu, A.; Tramontini, M.; Chevalier, A.; Ianigro, J.-C.; Marteau, J. Atmospheric and Geodesic Controls of Muon Rates: A Numerical Study for Muography Applications. Instruments 2022, 6, 24. https://doi.org/10.3390/instruments6030024
Cohu A, Tramontini M, Chevalier A, Ianigro J-C, Marteau J. Atmospheric and Geodesic Controls of Muon Rates: A Numerical Study for Muography Applications. Instruments. 2022; 6(3):24. https://doi.org/10.3390/instruments6030024
Chicago/Turabian StyleCohu, Amélie, Matias Tramontini, Antoine Chevalier, Jean-Christophe Ianigro, and Jacques Marteau. 2022. "Atmospheric and Geodesic Controls of Muon Rates: A Numerical Study for Muography Applications" Instruments 6, no. 3: 24. https://doi.org/10.3390/instruments6030024
APA StyleCohu, A., Tramontini, M., Chevalier, A., Ianigro, J.-C., & Marteau, J. (2022). Atmospheric and Geodesic Controls of Muon Rates: A Numerical Study for Muography Applications. Instruments, 6(3), 24. https://doi.org/10.3390/instruments6030024






