Abstract
Twenty-five years ago, at the CALOR1997 conference in Tucson, the idea of dual-readout calorimetry was first presented. In this talk, I discuss the considerations that led to that proposal, and describe the developments that have since taken place, to the point where dual-readout calorimetry is now considered a major candidate for experiments at future colliders.
In 1997, at the seventh edition of the CALOR conference series, I introduced what was to become dual-readout calorimetry. After describing the potential advantages of simultaneous detection of and the Čerenkov light generated in the absorption of high-energy hadrons, I ended my presentation with the following sentence (Paper 1, Table 1):
“I am convinced that resources for a dedicated R&D program to investigate these possibilities may turn out to be extremely well spent”.
In my talk today, I will demonstrate that this prediction has turned out to be correct. I will, in a chronological way, describe the R&D efforts that have been carried out in the past 25 years. These efforts have led to the point that today dual-readout calorimetry is considered a major candidate for future experiments in particle physics. However, let me start by providing some context by summarizing the developments in our understanding of calorimetry that took place in the decade preceding the 1997 conference:
- Hadron showers consist of an electromagnetic (em) and a non-em component.
- The non-em component involves nuclear reactions; the nuclear binding energy of nucleons released in these reactions does not contribute to the calorimeter signals. This is what is usually referred to as invisible energy.
- The hadronic energy resolution of a calorimeter is usually determined by fluctuations in invisible energy.
- The relative effect of such fluctuations does not become smaller as at increasing energy, unlike in em calorimeters, where sampling fluctuations and fluctuations in the number of signal quanta dominate.
- The average value of the em shower fraction increases with energy. This is the reason for the non-linearity typical for most hadron calorimeters.
- A crucial calorimeter performance parameter is , the ratio of the calorimeter response (i.e., average signal/GeV) to the em and non-em shower components. Typically, , because of invisible energy. If , a major performance improvement can be obtained. Such calorimeters are called compensating.
So how can these facts be used to improve hadron calorimeter performance?
- By designing a calorimeter in such a way that . This works only for sampling calorimeters.
- In sampling calorimeters, different classes of shower particles may be sampled very differently. The electrons and positrons that make up the em shower component are sampled according to 1. In the non-em component, neutrons produced in nuclear breakup may be sampled much (10–100 times) more efficiently, when the active medium contains hydrogen. There is little or no competition for elastic scattering in that case.
- The total kinetic neutron energy is correlated with the invisible energy loss, especially in high-Z materials.
- The amplification factor for neutron signals should be chosen such that it compensates for the invisible energy loss: . This amplification factor is determined by the sampling fraction for charged shower particles in the calorimeter, e.g., ∼2% for Pb/plastic scintillator, ∼6% for U/plastic scintillator structures.
Figure 1 illustrates the importance of the value for the performance of hadron calorimeters. Diagram c shows that the compensating calorimeter is nicely linear, while the calorimeters with exhibit substantial non-linearities. A comparison of diagrams Figure 1a,b illustrates the importance for the hadronic energy resolution. At high energy, the resolution of the 2% sampling device (Figure 1b) was measured to be 3 times better than that of the homogeneous (i.e., sampling fraction 100%) calorimeter (Figure 1a), and the difference in energy dependence is also very striking.
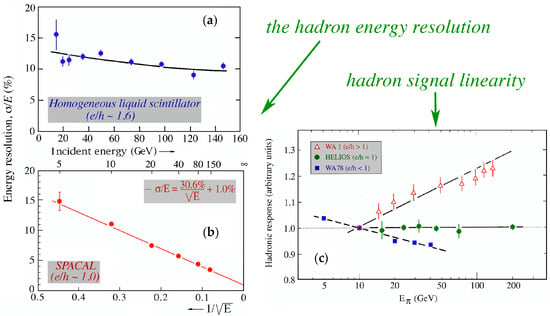
Figure 1.
The effects of compensation for the performance of hadron calorimeters.
Despite the obvious advantages offered by compensating calorimeters (hadronic energy resolution, signal linearity, Gaussian response functions, as well as the fact that calibration becomes very easy since there are no more differences between electrons and hadrons) there are also some disadvantages. The small sampling fraction that is needed limits the em energy resolution, and the crucial reliance on detecting neutrons requires larger integration volumes and integration times than may be practical. However, the most important disadvantage may concern the jet performance. Typically, a substantial energy fraction of jets comes in the form of relatively low-energy particles. As illustrated by Figure 2a, the response to hadrons gradually decreases for kinetic energies below 5 GeV, since an increasing fraction of the hadrons range out before initiating a nuclear interaction, and thus only lose energy by ionizing the absorber medium, just like muons. Furthermore, since the value may be quite different from 1.0 (e.g., 0.6 in the case of the uranium calorimeter shown in this figure), response non-linearity is thus also an issue for jet detection in this compensating calorimeter. Figure 2b shows that this problem could be mitigated by using a lower-Z absorber medium. Dual-readout calorimetry offers that option. It is also not bound by the small sampling fractions required for compensation. These were important considerations for the proposal to study the possibilities of this alternative method to improve the performance of hadron calorimeters.
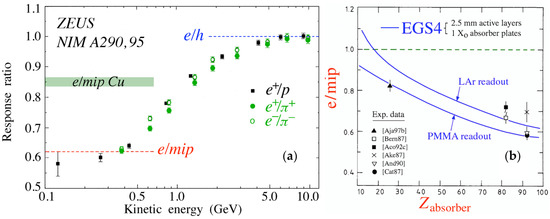
Figure 2.
The low-energy response of the compensating ZEUS calorimeter (a) and the values measured for sampling calorimeters with different Z absorber material (b).
Having a good idea is one thing, finding the money to test it experimentally is a completely different issue, especially when there is no immediate application, e.g., in an approved future experiment. However, in this case NASA came to the rescue, thanks to a former postdoc of mine who was working on a project to detect ultra-high cosmic hadrons outside the Earth’s atmosphere. NASA was considering an experiment at the International Space Station, called ACCESS, and had issued a call for proposals for a suitable detector. In the TeV-PeV energy region, calorimetry was one of very few viable options. However, mass restrictions (<2000 kg) and the required large aperture made this an extremely challenging proposition, since how could one expect to do any meaningful measurements with an instrument that was only 2 nuclear interactions lengths deep (or even less) on a particle that needed at least 10 interaction lengths to be absorbed?
The properties of such a thin calorimeter would be completely determined by leakage fluctuations. Furthermore, unless one could get a handle on these fluctuations, event by event, no acceptable performance should be expected. We argued (successfully) that dual-readout calorimetry could provide such a handle. The argument went as follows. At a depth of 2 , the overwhelming majority of the hadrons will initiate a nuclear interaction in the calorimeter. In this interaction, some fraction of the energy will be used for production. If that fraction is large, there will, on average, be relatively little energy leakage, since the em showers developed by the s may be contained, to a large extent, in the absorber, especially if this is made of high-Z material (/ in lead). On the other hand, if the em fraction is low, the energy that leaks out of the thin calorimeter is relatively large. It was already known from the prototype studies for the CMS very-forward calorimeter, which uses quartz fibers as active material, that the Čerenkov light produced in these fibers is overwhelmingly generated by the em components of the hadron showers. For these reasons, simultaneous detection of Čerenkov light and scintillation light (a measure for ) would provide not only information about the energy deposited in the calorimeter, but also on the relative fraction of em shower energy and, therefore, about the undetected energy leaking out.
We tested the validity of these ideas (Paper 2, Table 1) with the calorimeter depicted in Figure 3. The absorber material was lead, 39 plates, each 6.4 mm thick, for a total depth of 1.4 . In between these plates, layers of ribbons of fibers were inserted. These fibers were alternatingly made of plastic scintillator and quartz. The fibers from each layer were read out by small photomultiplier tubes. As shown in the figure, these PMTs were arranged in such a way that x-y granularity was achieved for both types of readout. Essentially, in this way we constructed two calorimeters that provided completely independent scintillator (S) and Čerenkov (Q) signals from the same events.
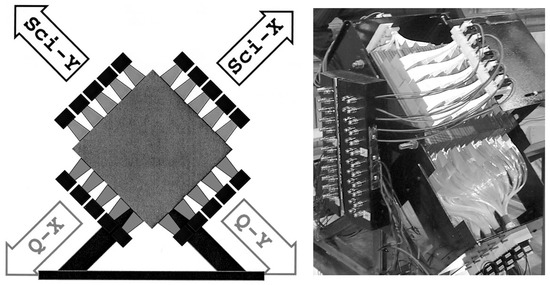
Figure 3.
The first dual-readout calorimeter, a prototype for the ACCESS experiment at the International Space Station.
In order to study whether the ideas described above worked in practice, this instrument was exposed to beams of high-energy pions at the CERN SPS. Figure 4 shows some results from measurements with 375 GeV . The energy scale for both types of signals was set with a beam of electrons. Figure 4a shows a scatter plot of the signals from the pions recorded in the quartz (vertical scale) and scintillation (horizontal scale) fibers. If there was no extra information in the Čerenkov signals, the data points would cluster around the diagonal in this plot. However, the observed banana shape indicates otherwise. A straight line through the origin of this plot describes data with a fixed ratio of the two types of signals. In Figure 4c,d, the scintillation signal distributions are shown for cuts and , respectively. These distributions are subsets of the total scintillation signal distribution, which is shown in Figure 4b. Clearly, small values select events with relatively little content, and thus large shower energy leakage and a relatively small total signal. On the other hand, events with relatively large values are indicative for showers with a relatively large em fraction, and hence relatively little energy leakage and a correspondingly large calorimeter signal. This is precisely what we hoped to achieve with this dual-readout calorimeter.
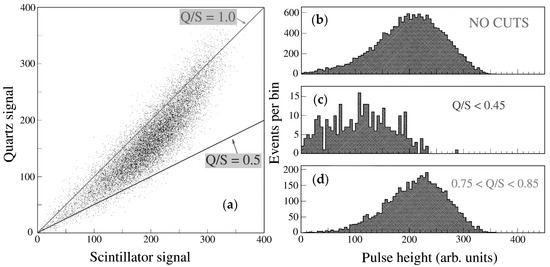
Figure 4.
Results from measurements of the signals from 375 GeV sent into the 1.4 thick ACCESS dual-readout calorimeter. See text for details.
Encouraged by the fact that the dual-readout principle worked already so well in this extremely thin calorimeter2, we started to plan for a much larger instrument for particle physics experiments, here on Earth where the mass limitations imposed by NASA do not apply. To contain high-energy hadron showers, such a detector needed to be at least 10 deep. We chose copper absorber, which has many advantages over lead (weight, machinability, ratio,...). Based on the mentioned results, we convinced US-DOE (our funding agency) to support us financially (160 k$). To save money, we used as much material from previous projects as possible (e.g., quartz fibers from CMS-HFCAL, PMTs, etc.). The DREAM calorimeter, shown in Figure 5, was built at TTU in 2003 and tested at the CERN SPS with beams of high-energy electrons, pions and muons (Paper 3, Paper 4, Table 1), by a small group of TTU people, with help from some friends (Hans Paar, John Hauptman, Aldo Penzo).

Figure 5.
The DREAM calorimeter. See text for details.
The basic building block was a 2 m long copper rod with a central hole in it. In this hole were inserted seven optical fibers, three scintillating and four undoped ones (quartz in the central region, PMMA in the periphery). The calorimeter consisted of 5150 such rods, arranged in a pattern of 19 hexagonal cells. The fibers from each cell were split into two bunches, one for each type of fiber. Each bunch was connected to a PMT, so that there were thus 19 + 19 = 38 signals recorded for every shower developing in this instrument, which had a total fiducial mass of 1030 kg.
Figure 6b shows the first surprise encountered when we tested this detector with muons of different energies (Paper 3, Table 1). Even though the calorimeter was calibrated with a beam of high-energy electrons, the signals for muons, which also exclusively lose energy through the em interaction, were different for the two types of signals provided by the calorimeter. The S signals were, on average, larger than the C ones, by a constant amount. The reason for this is the fact that the direct Čerenkov light emitted as the muons travel in the direction of the fibers through the calorimeter, falls outside the numerical aperture of the fibers, and thus does not contribute to the signals. For the S signals, this is inconsequential, but the C fibers only produce a signal from the radiative energy losses. Since the relative importance of these processes increases with the muon energy, so do the signals, both in the S and the C channels. The constant difference between these two signals thus makes it possible to measure (event by event) the fractions of the measured scintillation signal due to direct ionization and to higher-order em processes: A unique feature.
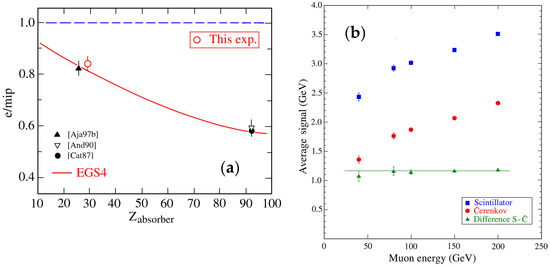
Figure 6.
Results of muon detection with the DREAM calorimeter.
Measurement of the ratio (Figure 6a) confirmed that the value for this copper calorimeter (0.82) was indeed considerably closer to 1 than the values typical for calorimeters based on lead or uranium absorber.
Additionally, the results obtained for the hadronic performance (Paper 4, Table 1) confirmed the beneficial effects of the dual-readout method. Figure 7a shows that the response became linear and equal to that of electrons when the information from both types of signals was used to reconstruct the particle energy. The hadronic energy resolution also improved in this process, especially at high energies, because the deviation from scaling (almost) disappeared (Figure 7b).
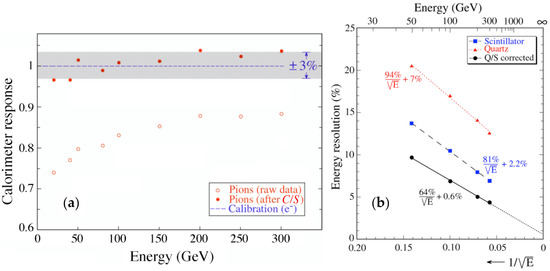
Figure 7.
Results of pion detection with the DREAM calorimeter.
The method we used to determine the em shower fraction and the energy of the hadron is illustrated in Figure 8a, which shows the scatter plot of the two types of signals recorded for each event. The two signals, S and C, can each be described in terms of an em plus a non-em component. The latter is weighed by a factor . The crucial point of the method is that these factors () are different for the S and C components, otherwise all data points would be scattered around the diagonal, and the method to determine the em fraction and the hadron energy from the signal ratio, as described in this figure, would not work. It turns out that the total signal distribution, which may be obtained by projecting the scatter plot on either the horizontal (S) or vertical axis (C), is non-Gaussian, which is typical for calorimeters with (Figure 8b). However, is turns out that this distribution is in fact a superposition of many distributions with different fixed em fractions (Figure 8c), and the overall signal distribution just reflects the extent to which these different fractions occur in practice. The dual-readout method eliminates these differences and results in Gaussian signal distributions with the correct average value, i.e., the same as the value for electrons of the same energy.
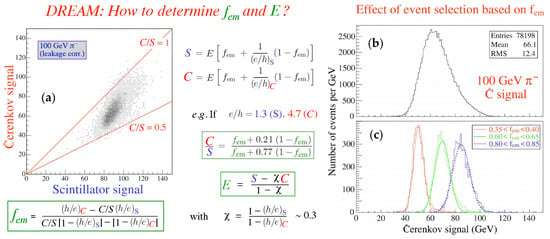
Figure 8.
The dual-readout method used to determine the em shower fraction and the hadron energy, based on the S and C signals (a). The non-Gaussian 100 GeV signal distribution (b) is a superposition of Gaussian distributions with different values (c).
A closer look at the (energy normalized) [] scatter plot reveals several other interesting features (Figure 9). All experimental data points are located on a straight line that connects the points [] and [1,1]. The larger the value, the closer the data point is to [1,1], i.e., the point where the electron data congregate (). The distribution of the hadron data points on this line reflects the distribution of the values. The distributions may be different for different types of hadrons (e.g., for pions the average value is larger than for protons of the same energy, see Figure 9), but the data points cluster around the same line. The same is true for hadrons of different energy, where the average increases with energy. The parameter , which was introduced in Figure 8, is equivalent to the cotangent of the angle that defines the direction of the line around which the data points cluster in Figure 9. This leads to the important conclusion that both and , which form the essence of the dual-readout method, are independent of the hadron energy and the type of hadron (Paper 10, Table 1).
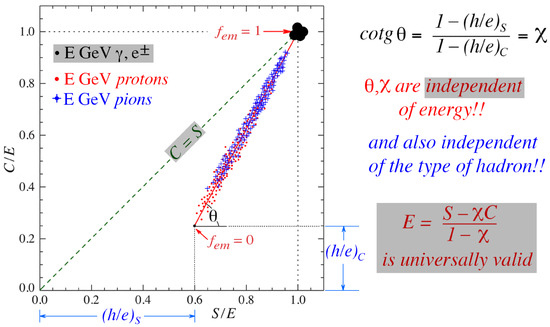
Figure 9.
The dual-readout method is independent of the energy and the type of hadron. It also works well for jets.
After the successes obtained with the DREAM calorimeter, a new collaboration was formed that further pursued the possibilities of this novel concept in the context of CERN’s R&D program. This RD52 Collaboration consisted of American, Italian and South Korean scientists. The dual-readout technique does not necessarily require a sampling calorimeter. However, it is essential that the signals provided by the detector can be separated into Čerenkov and scintillation components. RD52 demonstrated the possibility to achieve that in a number of high-density crystals (Paper 5, Table 1), e.g., PbWO, which is being used in CMS and other hep experiments. It turned out that a substantial fraction of the signals produced by this type of crystal is actually the result of Čerenkov light, and that it can be distinguished from the scintillation component in a variety of ways, including the time structure, the spectral properties and the polarization characteristics of the signals.
The Collaboration also built a substantial em calorimeter section consisting of BGO crystals and used this in conjunction with the DREAM detector, which served as the hadronic section. Figure 10 shows some results of tests of this configuration. By using UV filters, the signals from the BGO section exhibited both a Čerenkov and a scintillation component, which could be extracted with two separated time gates (Figure 10a). Figure 10b shows that it even turned out to be possible to obtain information on the production of neutrons in the shower development, which manifested itself as a slow tail in the scintillation signals. This tail was absent for tests with electrons and in all Čerenkov signals. It was demonstrated that by using the neutron information event-by-event a similar unraveling of the overall signal distribution could be obtained as on the basis of the value (Figure 8b,c).
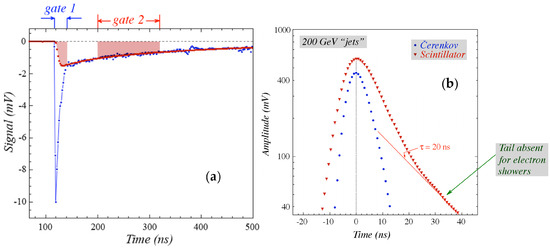
Figure 10.
RD52 results on tests of the DREAM calorimeter preceded by a BGO em section. See text for details.
The RD52 Collaboration also built and tested fiber sampling calorimeters with a much finer sampling than the DREAM one. Figure 11 shows a copper based instrument that was primarily tested with electrons (Paper 7, Table 1). A larger, 1350 kg calorimeter using lead as absorber material was built by the Pavia group, and was tested with beams of high-energy electrons, muons, pions and protons at CERN.

Figure 11.
A fine-sampling copper-fiber calorimeter built by the Pisa group of the RD52 Collaboration.
These measurements were also used to test the predictions depicted in Figure 9, i.e., the fact that the dual-readout method yields results that are independent on the type of hadron. Figure 12a shows excellent signal linearity, both for pions and protons, over the full energy range of the measurements (Paper 9, Table 1). The average signals per GeV were within ∼2% equal for electrons, protons and pions. Figure 12b shows that the response functions were extremely well described by a Gaussian function, and the width of this function scaled within experimental errors with , without any need for additional resolution terms, both for pions and for protons. To obtain these results, the calorimeter was surrounded by large slabs of plastic scintillator, whose signals were used to determine the side leakage of the hadron showers, event by event.
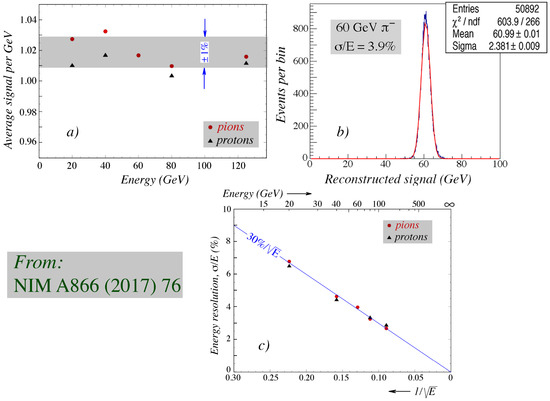
Figure 12.
Results on pion and proton detection with a fine-sampling lead based dual-readout calorimeter built by the RD52 Collaboration. Shown are results on hadron signal linearity (a), response function (b) and energy resolution (c).
Side leakage fluctuations were still a significant remaining contribution to this record setting resolution performance. Other factors were the Čerenkov light yield and sampling fluctuations. However, the ultimate limit that can be achieved is determined by the correlation between the reconstructed hadron energy and the nuclear binding energy loss in the shower development. Our Monte Carlo studies (Paper 8, Table 1) revealed that this ultimate limit is actually better than that achievable with compensation techniques, both for copper and lead absorber (Figure 13).
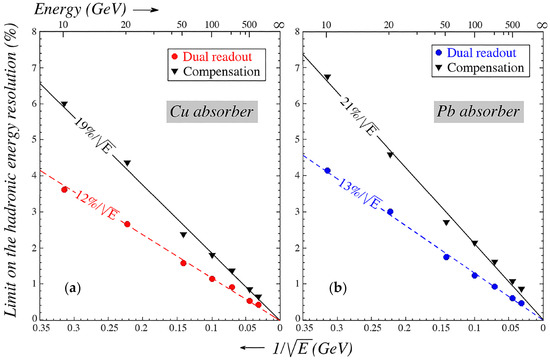
Figure 13.
The limit on the hadronic energy resolution derived from the correlation between nuclear binding energy losses and the parameters measured in dual-readout or compensating calorimeters, as a function of the particle energy. Results from GEANT Monte Carlo simulations of pion showers developing in a massive block of copper (a) or lead (b).
In summary, dual-readout fiber calorimetry offers potentially a spectacular performance improvement over the calorimeters used in past and present hep experiments. It is often assumed that the fact that the fiber structure prevents longitudinal segmentation is a significant disadvantage, especially when it comes to electron identification. Actually, this is a myth. Not only does the very fine lateral segmentation allowed by the fibers offer fantastic alternative options, but the time structure of the signals also turns out to make it possible to determine the depth of the light production in the fibers with a precision of ∼1 . We have demonstrated (Paper 6, Table 1) that a combination of the various available options made it possible to identify electrons with >99% efficiency, with <0.2% pion misidentification, in a mixed electron/pion beam. Apart from that, the fiber geometry allows for a very compact structure without significant dead space, while the absence of longitudinal segmentation avoids the huge and often unsolvable problems encountered when intercalibrating the different longitudinal sections of a segmented device. This fiber calorimeter can be calibrated with electrons and that is all that is needed to obtain the correct energy scale for all hadrons, and jets.
Table 1 lists some significant publications from 25 years of dual-readout calorimetry, in chronological order. A complete list can be found in the Rev. Mod. Phys. article (Paper 11, Table 1), indicated by the red arrows.

Table 1.
A chronological selection of publications on dual-readout calorimetry.
Conflicts of Interest
The author declares no conflict of interest.
| 1 | in the last stages of an EM shower, sampling of soft photons depends on the Z value of the absorber medium, which may lead to . |
| 2 | Unfortunately, NASA cancelled the ACCESS project after the accident with the Columbia Space Shuttle (2003). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).