Abstract
We present a concept that enables the determination of the complex refractive index of attenuating media from two critical angles, measured sequentially at two interfaces between a single sample and two different prisms. The proposed method is general in that it applies with s and p polarisation states, thus it is suited for the characterisation of isotropic as well as anisotropic media. Uncertainty analysis indicates that relative error in the determination of the real (imaginary) index can be less than (in the order of ), respectively.
1. Introduction
The refractive index of a medium derives from the reflectance profile at an interface between the sample and a front reference medium, which is typically a transparent prism [1,2]. When the sample is transparent, the refractive index is a real number that can be determined from just one out of several features of the reflectance profile, such as the critical angle of total internal reflection () [3,4,5] or the Brewster angle () [6,7,8,9]. When the sample attenuates light, the refractive index becomes a complex quantity, the imaginary part of which incorporates light extinction properties (absorption and/or scattering). Then, a pair of input values is needed to recover the real and imaginary component. This pair may comprise, for example, the critical angle of attenuated total reflection along with the reflectance at that point () [10,11], the pseudo-Brewster angle together with the reflectance at that point () [12], or the the pseudo-Brewster angle and the reflectance at normal incidence () [13].
Typical prism-coupling refractometers [14,15,16,17] are equipped with high resolution rotary tables (see Figure 1a). Hence, the angular features of the reflectance profile (e.g., ) can be resolved with high accuracy [18]. On the contrary, accuracy in the measurement of reflectance (e.g., ) is seriously compromised by unavoidable laser power fluctuations [18,19]. In that respect, it is advantageous to devise methods whereby the complex refractive index results from an input pair that contains two angles.
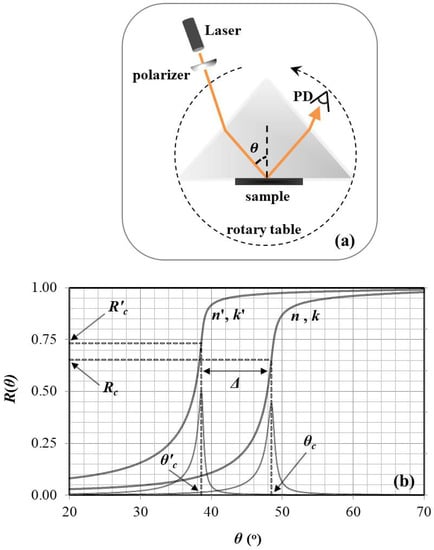
Figure 1.
(a) A typical prism-coupling refractometer. The sample is attached to the base of a transparent reference prism, which sits on a rotary table. Incoming through the prism’s front facet, a collimated linearly polarized laser beam hits the interface at a variable incidence angle . The reflected light exits the prism through its rear facet, heading towards a photodiode (PD), where the reflectance profile is monitored. (b) Fresnel reflectance profiles at two interfaces between a sample and two different prisms. Bell-like curves are corresponding derivatives , peaking at and . Calculations assume s polarisation and , , .
Here, we demonstrate how to retrieve the complex optical constant of an attenuating medium from the critical angle pair () measured at two interfaces between the same sample and two different prisms. The real indices of the prisms are and , such that . To obtain a first insight, Figure 1b depicts corresponding reflectance profiles. Calculations are based on the Fresnel equation for the exemplary case of s polarised light, while parameters
assume the values that are indicated in the figure’s caption. Located at the maximum of the respective reflectance derivative , which is also plotted in Figure 1b, critical angles and are separated by . Reflectances and are also tracked in Figure 1b.
The sample’s complex refractive index derives from the input pair () as the unique numerical solution of a well-posed equation system that is fully described next. The proposed method is general in the sense that it applies with s and p polarised light, hence it is suited for isotropic as well as anisotropic media. Uncertainty analysis indicates that within an extinction range, say, , which includes several material families of interest, the real (or the imaginary) index can be determined with relative error less than ∼ (or ∼), respectively.
The proposed method resembles the two prism, two angle approach introduced by Azzam several decades ago [20], utilizing the pseudo-Brewster angle pair () as input. Despite the conceptual similarity, Azzam’s routine was found to be inaccurate (or even unusable) when , a condition that automatically excludes most non-metal samples (The review of literature within the space limits of this letter is not exhaustive. For example, the interested reader should be referred to Hirschfeld’s two prism method, which is based on the measurement of two reflectances () at preset angles [21]. Another report on single prism two angle method [22] was also published recently, lacking however generality, since it applies only to isotropic media. Finally, we acknowledge a conceptually different route to determine the complex optical constants of attenuating samples, which depends on fitting experimental data to Fresnel equations [23,24,25,26,27,28]. This approach is not a “point” method and has been proven sensitive to the choice of fit range [29,30]. An indepth comparison of the proposed method to Fresnel fitting is beyond our current scopes).
2. Background Theory
We start by recalling the mathematical framework that is derived from Fresnel equations in Ref. [10]. The involved formulas are compactly expressed in terms of the real dielectric constant of the prism and the complex dielectric constant of the sample . Shorthands t and , which relate to and via
are also convenient. Then, it is
Parameters and depend on polarisation. Analytic solutions exist for s polarisation. These are
The situation is slightly more complicated for p polarization, in which case and can be numerically obtained as solutions of two algebraic equations. Originally reported in [10] and reduced to an equivalent but more appealing notation in [22], these equations are:
Equations (4) and (5) for s polarisation and Equations (6) and (7) for p polarisation enable the calculation of and (equivalently, and ) at either polarisation state, from experimental input values (. This procedure is fully described in Ref. [10]. In what follows, we show how to eliminate reflectance from the input, via its replacement by an additional critical angle , which may be accurately measured at an interface with a second prism.
3. Method’s Description
Collecting two reflectance profiles by use of two different prisms introduces additional conditions to the problem. These conditions are already stated in Equation (1) ( and ). By use of Equation (3), they can be written in the alternative form
Throughout, accent marks denote parameters that relate to the second prism.
Parameters and in Equations (8) and (9) are essentially functions of and (equivalently, and ). These functions are given explicitly by Equations (4) and (5) for s polarisation, or implicitly by Equations (6) and (7) for p polarisation. In that sense, Equations (8) and (9) define a system of two equations on four independent variables. Two of them are the measured input quantities (). The other two are the unknowns to be determined (). Solving numerically this system is the method’s first step. To that end, we performed extensive numerical studies using Wolfram Mathematica’s noniterative global solver NSolve, to conclude that the real roots are always unique, at least within the physically meaningful range .
Then, in the method’s second step, the directly measured along with the numerically retrieved enable the calculation of the complex optical constants via Equation (3). Exactly the same result is obtained by use of and , instead.
Figure 2a depicts graphically the method’s operating principle. Therein, the iso- curve is plotted in the () plane, representing the hypothetical measurement of a critical angle with the first prism; the critical angle measured with the second prism (or equivalently, the angular shift ) varies in steps of , an amount that simulates the resolution of state-of-the-art rotary tables. Any given value of defines a single point in the plot; its coordinates yield the sample’s optical constants.
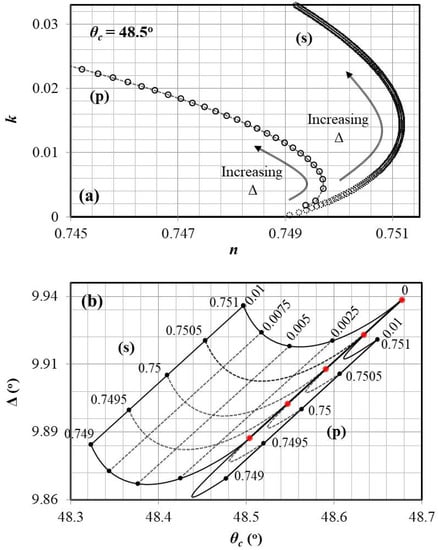
Figure 2.
(a) Iso- curves in the () plane () arrows mark the direction of increasing in steps of , starting from a base for s (p) polarisation. (b) Iso-n and iso-k curves in the () plane. Parameter n assumes constant values and for both polarisations. Parameter k assumes constant values and for s polarisation, as well as 0 and for p polarisation. The common transparency line () separates the s polarisation grid on the left, from the p polarisation grid on the right.
A complementary picture is drawn in Figure 2b, where families of iso-n and iso-k curves are plotted in the () plane. Examining Figure 2 leads to several conclusions, the most important of which are the following. (1) For constant , k increases monotonically with increasing ; n does the same for low-k values, eventually reaching a characteristic turning point past which, n decreases with increasing . (2) At the transparency limit (), curves for s and p polarisation converge into a single point (Figure 2a) or a single line (Figure 2b); there, the polarisation independent condition of total internal reflection holds true, that is and . (3) The density of points in Figure 2a is lower for p polarisation than it is for s polarisation. This observation is reflected in Figure 2b, where the grid pattern for p polarisation is more squeezed than it is for s polarisation. These facts are first indications that the method’s sensitivity is generally higher with s polarised light, as we shall further discuss next.
4. Uncertainty Assessment
The distinctive advantage of the proposed method is that in its first step, reflectance can be numerically computed from experimental input data () with higher accuracy than it can be directly measured. Uncertainty in this computation can be expressed in terms of the input (P) and output (S) sensitivity matrices [31]
where functions and are defined in Equations (8) and (9), respectively. The former definitions assume independence between the input variables and , which is reasonable, since these measurands are obtained via separate experimental runs. Then, it is
where , are the experimental uncertainties in the measurement of the respective critical angles, while , are the first row elements in the overall sensitivity matrix [31]
Since the same experimental setup is to be used with both prisms, it is reasonable to assume that . We may thus define the normalised (with respect to ) uncertainty
The preceding expressions can be used to evaluate under what circumstances errors in the numerical determination of are (as we claim) smaller than corresponding errors in its direct measurement (the latter should be typically ). We shall skip this exercise to proceed right away with the investigation of a more interesting problem: the calculation of uncertainties in the determination of the complex optical constants from the directly measured and the indirectly retrieved , during the method’s second step. Based on standard error propagation rules and assuming zero covariance between and , we may write for the relative uncertainties of (or n) and (or k)
It is now more convenient to define the normalised (with respect to ) relative uncertainties of the real () and the imaginary () index which, by use of Equation (13), read:
For any given sample and prism pair, that is for fixed and , normalised relative uncertainties and can be calculated via Equation (Section 4). Figure 3 depicts such calculations for indicative values and variable k. In agreement with the interpretation of Figure 2, we observe that the proposed method is generally more accurate for s, than it is for p polarisation. Another striking observation is that, within the k range we account for, the method’s accuracy generally improves with increasing attenuation (that is, with increasing k). This seems to be a unique feature of our technique, since other approaches are typically expected to behave in the opposite way. Exceptionally, uncertainty for p polarisation decreases with increasing k only up to a characteristic local minimum, thereafter increasing as attenuation grows. The local minimum may be interpreted as the equivalent of the turning point observed in Figure 2a. S polarisation exhibits the same behaviour at k values beyond the scale of the horizontal axis in Figure 3.
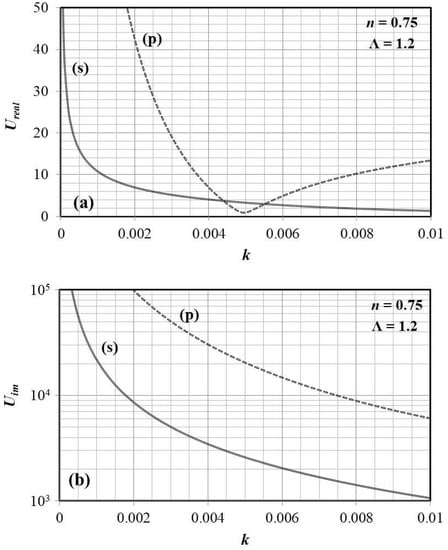
Figure 3.
Normalized relative error (a) and (b) as a function of k, for both polarisation states. Throughout, we assume constant values for and .
Modern refractometers equipped with high resolution rotary tables measure critical angles with an uncertainty between and (that is, between 20 µrad and 100 µrad). This uncertainty range is commonly assumed to be reasonable in the bibliography [22,32], suggesting that is primarily limited by the minimal incremental motion of the rotary table and remains practically insensitive to other factors, such as the divergence of the input laser beam or random noise (e.g., due to laser power fluctuations and the electronic detection system). It is also assumed that systematic errors in the measurement of critical angles, such as those resulting from the off-axis placement of the prism on the rotary table, have been properly removed (to that end, we remark that it is possible to calibrate the experimental setup with the use of a refractive index certified reference material).
Therefore, to estimate the magnitude of relative errors and we need to multiply and by a factor ranging from to , respectively. As k approaches for s polarisation (or the local minimum at for p polarisation), it is , indicating that can be as low as , or at least remain below . Similarly, as k approaches , it is , suggesting that should be in the range of to for s polarisation (increased five-fold for p polarisation).
Up to now, our assessment assumed fixed n and . There exists some space for further error optimisation by proper choice of first and second prism, so as to tune n and , respectively. In general, higher n and higher values reduce the real and imaginary index error for s polarised light. For p polarisation, higher values have the same effect; yet, a smaller n shifts the observed local minimum of the real index error to a lower k, an effect that might be desirable in several situations.
We shall not elaborate further on these dependencies, which however attest that the proposed method can determine the complex optical constants with relative uncertainties and , within a spectral range that extends from to . These specifications compare well to standard refractometry with transparent samples (in terms of the real index), as well as ellipsometry (in terms of the imaginary index).
5. Limitations and Further Insights
The evident limitation in the practical use of our method relates to the confined attenuation span for which it remains highly accurate. However, even the narrow window, say, , contains several material families of great scientific interest, ranging from food products and fuel oils to semiconductors, water and aqueous solutions (towards infrared wavelengths), as well as nearly the entirety of biological matter.
A second limitation that should be accounted for relates to the validity of Fresnel equations from which, the proposed mathematical framework originates. It is commonly accepted that, if light attenuation comes from absorption, Fresnel equations apply unconditionally. On the contrary, as is further elaborated in the bibliography [33,34], if light attenuation rises from scattering effects (that is, with inhomogeneus samples) Fresnel equations are valid only when the size of the scatterers remains small compared to the wavelength of light. Moreover, the applicability of the proposed method with inhomogeneous samples is further complicated by the fact that the same spot on the sample surface should be irradiated with both prisms.
A final aspect worth commenting on is the time duration of measurement; at first instance, one might assume that performing separate measurements on two different prisms may cause unwelcome delays. In reality, however, the proposed method spares the need for reflectance callibration, which is commonly required in prism coupling refractometry of attenuating media and involves a follow-up measurement at the prism–air interface. This simplification is due to the fact that critical angles and can be determined by differentiating directly the uncalibrated reflectance profile, as is measured (in arbitrary units) by the photodiode.
6. Conclusions
This letter introduces two prism critical angle refractometry as a novel method for determining the complex optical constants of attenuating media, by means of a well-posed nonlinear equation system that can be solved numerically. The proposed method exhibits several appealing features, the most important of which are summarised below.
- 1.
- A pair of angles () is all that the method needs as input. To the benefit of precision, reflectance values are not required in the computational process.
- 2.
- The routine is general, since it applies with s and p polarised light, facilitating the characterisation of optically isotropic and anisotropic samples.
- 3.
- Uncertainty in the determination of the output quantities () decreases as attenuation grows from zero, which is ideally suited for analysing media that attenuate light as much as, for example, most forms of biological matter.
Uncertainty assessment indicated that the real (or the imaginary) index can be determined with a relative error ∼ (or ∼), respectively. The method’s specifications meet the needs of several application in various fields, such as biomedical optics, analytical chemistry and quality control.
Author Contributions
Conceptualization, K.M.; Formal analysis, S.K., P.G. and K.M.; Investigation, S.K. and P.G.; Methodology, K.M.; Writing—original draft, S.K. and K.M.; Writing—review and editing, S.K. and P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bond, W.L. Measurement of the Refractive Indices of Several Crystals. J. Appl. Phys. 1965, 36, 1674–1677. [Google Scholar] [CrossRef]
- Shukla, R.; Srivastava, A.; Srivastava, A.; Srivastava, M.; Dixit, S.; Misra, D. Design of an optoelectronic refractometer having an adjustable range of refractive index measurement. Opt. Laser Technol. 2008, 40, 692–696. [Google Scholar] [CrossRef]
- Onodera, H.; Awai, I.; Ikenoue, J.I. Refractive-index measurement of bulk materials: Prism coupling method. Appl. Opt. 1983, 22, 1194. [Google Scholar] [CrossRef] [PubMed]
- Russo, N.; Tonso, A.; Sicre, E. Liquid refractometry: An approach for a continuous measurement. Opt. Laser Technol. 1993, 25, 109–112. [Google Scholar] [CrossRef]
- Sun, T.Q.; Ye, Q.; Wang, X.W.; Wang, J.; Deng, Z.C.; Mei, J.C.; Zhou, W.Y.; Zhang, C.P.; Tian, J.G. Scanning focused refractive-index microscopy. Sci. Rep. 2014, 4, 5647. [Google Scholar] [CrossRef] [PubMed]
- Elshazly-Zaghloul, M.; Azzam, R.M.A. Brewster and pseudo-Brewster angles of uniaxial crystal surfaces and their use for determination of optical properties. J. Opt. Soc. Am. 1982, 72, 657. [Google Scholar] [CrossRef]
- Luna-Moreno, D.; De la Rosa-Cruz, E.; Cuevas, F.; Regalado, L.; Salas, P.; Rodríguez, R.; Castaño, V. Refractive index measurement of pure and Er3+–doped ZrO2–SiO2 sol–gel film by using the Brewster angle technique. Opt. Mater. 2002, 19, 275–281. [Google Scholar] [CrossRef]
- Pabitha, G.; Dhanasekaran, R. Investigation on the linear and nonlinear optical properties of a metal organic complex—Bis thiourea zinc acetate single crystal. Opt. Laser Technol. 2013, 50, 150–154. [Google Scholar] [CrossRef]
- D’silva, E.; Podagatlapalli, G.K.; Rao, S.V.; Dharmaprakash, S. Structural, optical and electrical characteristics of a new NLO crystal. Opt. Laser Technol. 2012, 44, 1689–1697. [Google Scholar] [CrossRef]
- Koutsoumpos, S.; Giannios, P.; Stavrakas, I.; Moutzouris, K. The derivative method of critical-angle refractometry for attenuating media. J. Opt. 2020, 22, 075601. [Google Scholar] [CrossRef]
- Matiatou, M.; Giannios, P.; Koutsoumpos, S.; Toutouzas, K.G.; Zografos, G.C.; Moutzouris, K. Data on the refractive index of freshly-excised human tissues in the visible and near-infrared spectral range. Results Phys. 2021, 22, 103833. [Google Scholar] [CrossRef]
- Humphreys-Owen, S.P.F. Comparison of Reflection Methods for Measuring Optical Constants without Polarimetric Analysis, and Proposal for New Methods based on the Brewster Angle. Proc. Phys. Soc. 1961, 77, 949–957. [Google Scholar] [CrossRef]
- Azzam, R.M.A.; Ugbo, E.E. Contours of constant pseudo-Brewster angle in the complex ϵ plane and an analytical method for the determination of optical constants. Appl. Opt. 1989, 28, 5222. [Google Scholar] [CrossRef] [PubMed]
- Tioua, B.; Soltani, M.T.; Khechekhouche, A.; Wondraczek, L. Physical properties and luminescence of highly stable erbium-doped antimony glasses for NIR broadband amplification. Opt. Laser Technol. 2022, 152, 108152. [Google Scholar] [CrossRef]
- Neethish, M.; Kumar, V.R.K.; Nalam, S.A.; Harsha, S.S.; Kiran, P.P. Effect of chirp on supercontinuum generation from Barium Zinc Borate glasses. Opt. Laser Technol. 2022, 149, 107890. [Google Scholar] [CrossRef]
- Mahadevan, M.; Sankar, P.; Vinitha, G.; Arivanandhan, M.; Ramachandran, K.; Anandan, P. Non linear optical studies on semiorganic single crystal: L-arginine 4-nitrophenalate 4-nitrophenol dihydrate (LAPP). Opt. Laser Technol. 2017, 92, 168–172. [Google Scholar] [CrossRef]
- Zheng, J.; Jiang, J.; Chen, H.; Zheng, R.; Shen, X.; Yu, K.; Wei, W. Optical nonlinearity and supercontinuum generation of tellurite glass at 1.064 μm. Opt. Laser Technol. 2021, 138, 106832. [Google Scholar] [CrossRef]
- Koutsoumpos, S.; Giannios, P.; Moutzouris, K. Extended derivative method of critical-angle refractometry for attenuating media: Error analysis. Meas. Sci. Technol. 2021, 32, 105007. [Google Scholar] [CrossRef]
- Koutsoumpos, S.; Giannios, P.; Moutzouris, K. Critical Angle Refractometry for Lossy Media with a Priori Known Extinction Coefficient. Physics 2021, 3, 569–578. [Google Scholar] [CrossRef]
- Azzam, R.M.A. Analytical determination of the complex dielectric function of an absorbing medium from two angles of incidence of minimum parallel reflectance. J. Opt. Soc. Am. A 1989, 6, 1213. [Google Scholar] [CrossRef][Green Version]
- Hirschfeld, T. Accuracy and Optimization of the Two Prism Technique for Calculating the Optical Constants from ATR Data. Appl. Spectrosc. 1970, 24, 277–282. [Google Scholar] [CrossRef]
- Koutsoumpos, S.; Giannios, P.; Moutzouris, K. Critical angle refractometry with optically isotropic attenuating media. Appl. Phys. B 2022, 128, 91. [Google Scholar] [CrossRef]
- Giannios, P.; Toutouzas, K.G.; Matiatou, M.; Stasinos, K.; Konstadoulakis, M.M.; Zografos, G.C.; Moutzouris, K. Visible to near-infrared refractive properties of freshly-excised human-liver tissues: Marking hepatic malignancies. Sci. Rep. 2016, 6, 27910. [Google Scholar] [CrossRef] [PubMed]
- Giannios, P.; Koutsoumpos, S.; Toutouzas, K.G.; Matiatou, M.; Zografos, G.C.; Moutzouris, K. Complex refractive index of normal and malignant human colorectal tissue in the visible and near-infrared. J. Biophotonics 2016, 10, 303–310. [Google Scholar] [CrossRef]
- Niskanen, I.; Räty, J.; Peiponen, K.E. Complex refractive index of turbid liquids. Opt. Lett. 2007, 32, 862. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Wang, J.; Liu, Y.; Ye, Q.; Zeng, H.; Zhou, W.; Mei, J.; Zhang, C.; Tian, J. Effect of the gradient of complex refractive index at boundary of turbid media on total internal reflection. Opt. Express 2015, 23, 7320. [Google Scholar] [CrossRef] [PubMed]
- Räty, J.; Pääkkönen, P.; Peiponen, K.E. Assessment of wavelength dependent complex refractive index of strongly light absorbing liquids. Opt. Express 2012, 20, 2835. [Google Scholar] [CrossRef]
- Calhoun, W.R.; Maeta, H.; Combs, A.; Bali, L.M.; Bali, S. Measurement of the refractive index of highly turbid media. Opt. Lett. 2010, 35, 1224. [Google Scholar] [CrossRef]
- Goyal, K.G.; Dong, M.L.; Nguemaha, V.M.; Worth, B.W.; Judge, P.T.; Calhoun, W.R.; Bali, L.M.; Bali, S. Empirical model of total internal reflection from highly turbid media. Opt. Lett. 2013, 38, 4888. [Google Scholar] [CrossRef]
- Guo, W.; Xia, M.; Li, W.; Dai, J.; Zhang, X.; Yang, K. A local curve-fitting method for the complex refractive index measurement of turbid media. Meas. Sci. Technol. 2012, 23, 047001. [Google Scholar] [CrossRef]
- Beck, B.T.; Peterman, R.J.; Wu, C.H.J. The Uncertainty in Solutions to Implicit Equation Systems. J. Fluids Eng. 2019, 142, 014502. [Google Scholar] [CrossRef]
- Garcia-Valenzuela, A.; Pena-Gomar, M.; Fajardo-Lira, C. Measuring and sensing a complex refractive index by laser reflection near the critical angle. Opt. Eng. 2002, 41, 1704–1716. [Google Scholar] [CrossRef]
- García-Valenzuela, A.; Barrera, R.G.; Sánchez-Pérez, C.; Reyes-Coronado, A.; Méndez, E.R. Coherent reflection of light from a turbid suspension of particles in an internal-reflection configuration: Theory versus experiment. Opt. Express 2005, 13, 6723. [Google Scholar] [CrossRef] [PubMed]
- Morales-Luna, G.; Contreras-Tello, H.; García-Valenzuela, A.; Barrera, R.G. Experimental Test of Reflectivity Formulas for Turbid Colloids: Beyond the Fresnel Reflection Amplitudes. J. Phys. Chem. B 2016, 120, 583–595. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).