Beyond the
Abstract
:1. Introduction
2. A Simple Gaussian Model and the Linear Growth
3. The Schematic Model
4. The Lucky Model
The Linear Growth in the Lucky Model
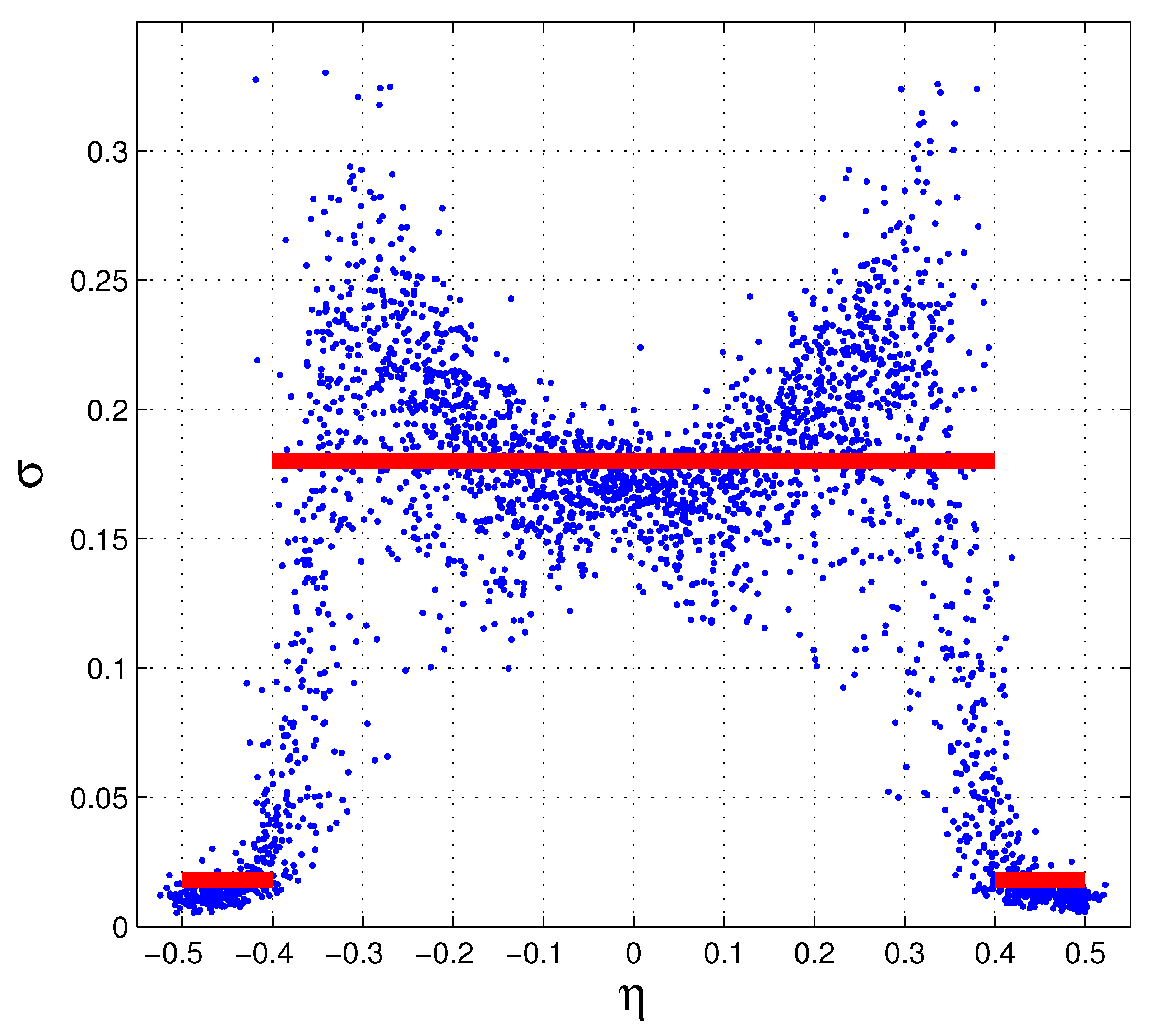
5. Hints for an Experimental Verification
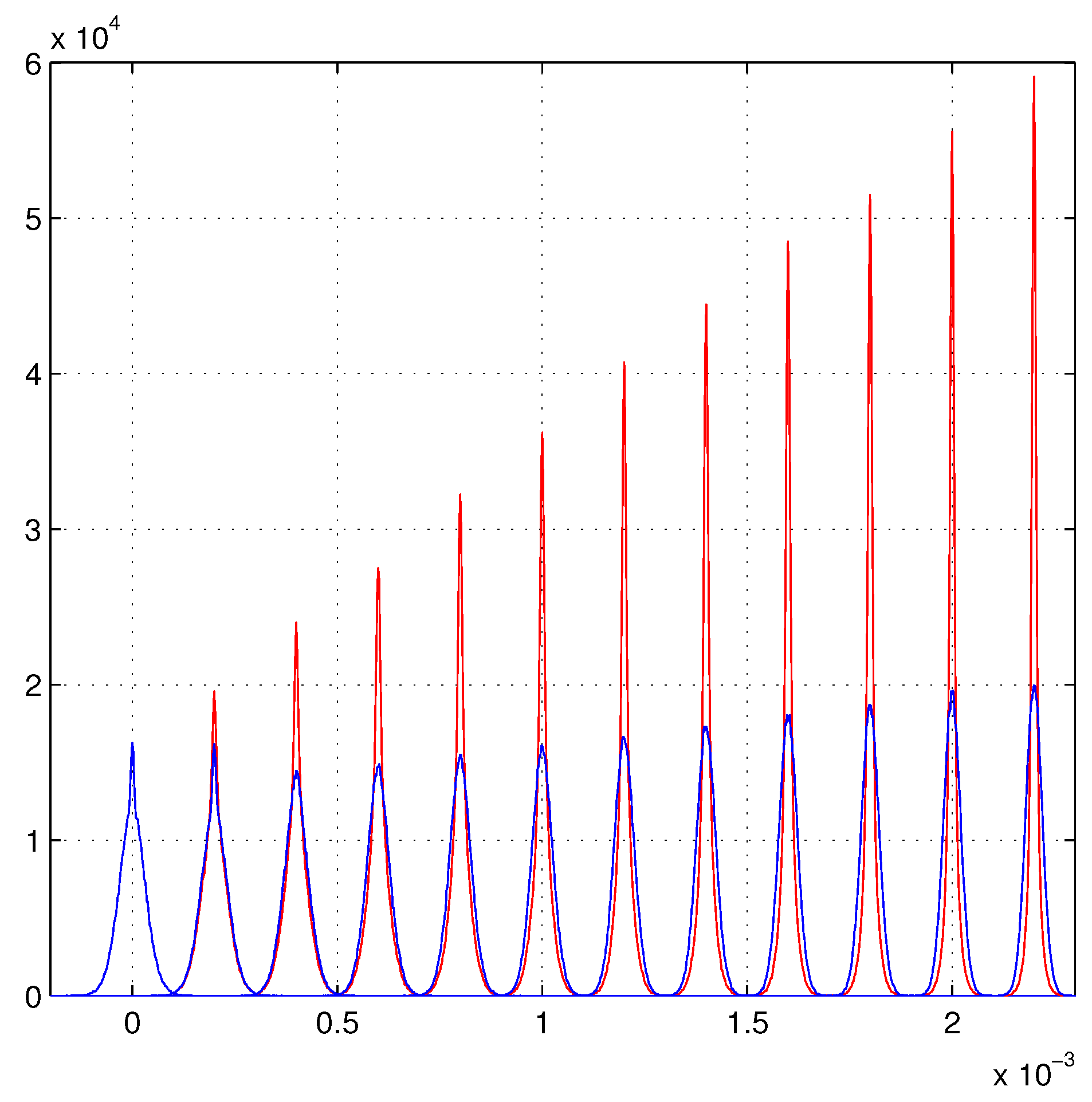
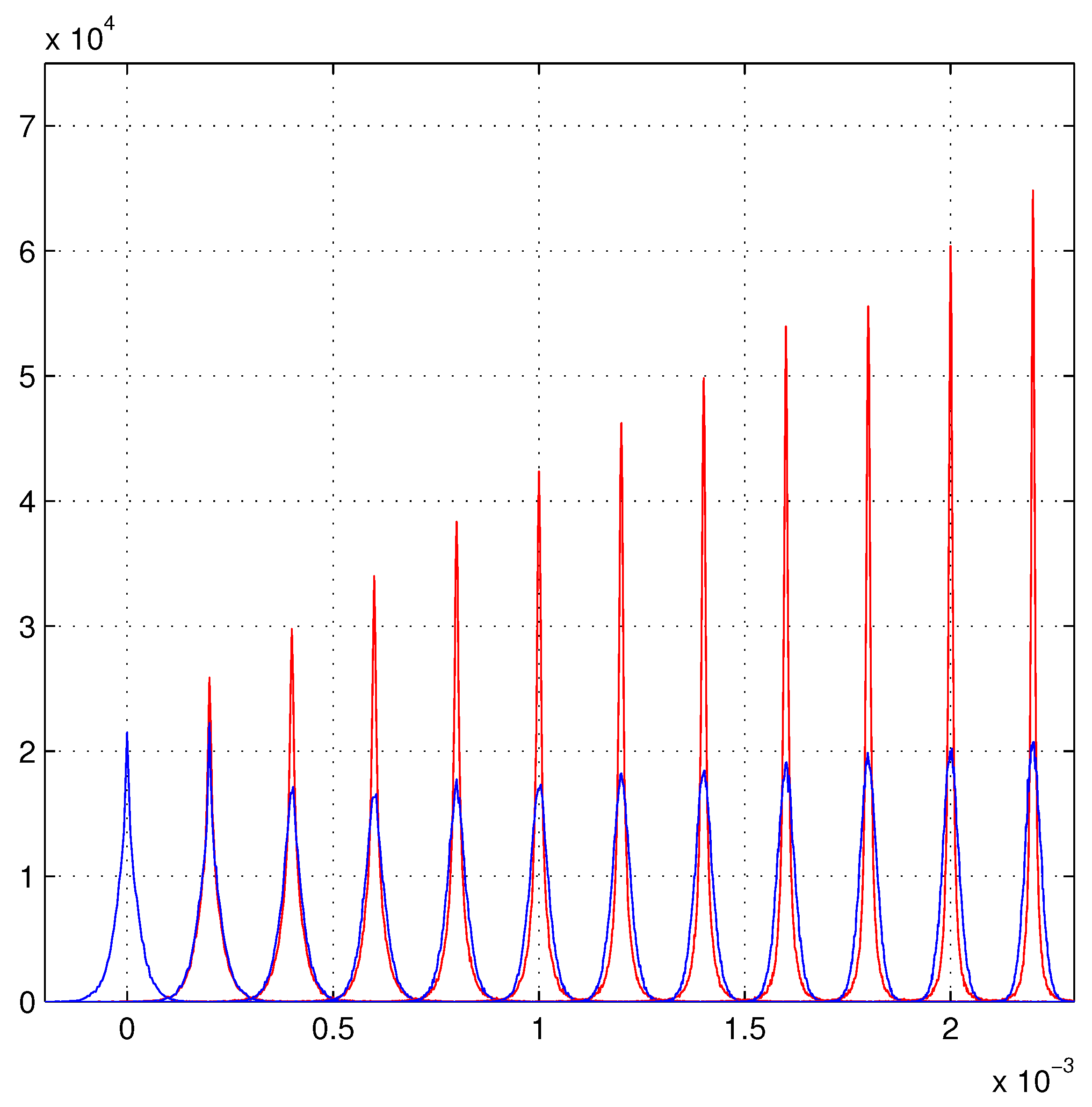
6. Linear Growth of the Maximum Likelihood Evaluations
Beyond the Present Maximum Likelihood Evaluations
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| probability density function | |
| MIP | minimum ionizing particle |
| COG | center of gravity |
| COG | center of gravity algorithm with n-strips |
References
- Landi, G.; Landi, G.E. Improvement of track reconstruction with well tuned probability distributions. J. Instrum. 2014, 9, P10006. [Google Scholar] [CrossRef] [Green Version]
- Landi, G.; Landi, G.E. Optimizing momentum resolution with a new fitting method for silicon-strip detectors. Instruments 2018, 2, 22. [Google Scholar] [CrossRef] [Green Version]
- Landi, G.; Landi, G.E. The Cramer-Rao inequality to improve of the resolution of the least-squares method in track fitting. Instruments 2020, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Landi, G.; Landi, G.E. Generalized inequelities to optimizing the fitting method for track reconstructions. Physics 2020, 2, 35. [Google Scholar] [CrossRef]
- Landi, G.; Landi, G.E. Probability Distributions of Positioning Errors for Some Forms of Center-of-Gravity Algorithms. Part II. arXiv 2020, arXiv:2011.14474. [Google Scholar]
- Landi, G.; Landi, G.E. Silicon Micro-strip Detectors. Encyclopedia 2021, 1, 82. [Google Scholar] [CrossRef]
- Ivchenko, G.; Medvedev, Y. Mathematical Statistics; Mir Publishers: Moscow, Russia, 1990. [Google Scholar]
- Devore, J.L.; Berk, K.N. Modern Mathematical Statistics with Applications; Springer: New York, NY, USA, 2018. [Google Scholar]
- Olive, K.A.; Agashe, K.; Amsler, C.; Antonelli, M.; Arguin, J.-F.; Asner, D.M.; Baer, H.; Band, H.R.; Barnett, R.M.; Basaglia, T.; et al. Particle Data Group. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- ALICE Collaboration. The ALICE experiment at the CERN Large Hadron Collider. J. Instrum. JINST 2008, 3, S08002. [Google Scholar] [CrossRef]
- ATLAS Collaboration. The ATLAS experiment at the CERN Large Hadron Collider. J. Instrum. 2008, 3, S08003. [Google Scholar] [CrossRef] [Green Version]
- CMS Collaboration. The CMS experiment at the CERN Large Hadron Collider. J. Instrum. 2008, 3, S08004. [Google Scholar] [CrossRef] [Green Version]
- Gauss, C.F. Méthode des Moindres Carrés. Mémoires sur la Combination des Observations; Franch translation by J. Bertrand; Revised by the Author; Mallet-Bachelier: Paris, France, 1855; Available online: https://books.google.it/books?id=_qzpB3QqQkQC (accessed on 1 September 2018).
- CMS Collaboration. The performance of the CMS muon detector in proton-proton collision at = 7 TeV at the LHC. J. Instrum. 2013, 8, P11002. [Google Scholar] [CrossRef]
- MATLAB 2020; The MathWorks Inc.: Natick, MA, USA, 2020.
- Adriani, O.; Bongi, M.; Bonechi, L.; Bottai, S.; Castellini, G.; Fedele, D.; Grandi, M.; Landi, G.; Papini, P.; Ricciarini, S.; et al. In-flight performance of the PAMELA magnetic spectrometer. In Proceedings of the 16th International Workshop on Vertex Detectors, (PoS(Vertex 2007)048), Lake Placid, NY, USA, 23–28 September 2007. [Google Scholar]
- Belau, E.; Klanner, R.; Lutz, G.; Neugebauer, E.; Seebrunner, H.J.; Wylie, A. Charge collection in silicon strip detector. Nucl. Instrum. Method Phys. Res. A 1983, 214, 253–260. [Google Scholar] [CrossRef]
- Landi, G. Properties of the center of gravity as an algorithm for position measurements. Nucl. Instrum. Methods Phys. Res. A 2002, 485, 698–719. [Google Scholar] [CrossRef] [Green Version]
- Landi, G. Problems of position reconstruction in silicon microstrip detectors. Nucl. Instr. Methods Phys. Res. A 2005, 554, 226. [Google Scholar] [CrossRef]
- Landi, G.; Landi, G.E. Asymmetries in Silicon Microstrip Response Function and Lorentz Angle. arXiv 2014, arXiv:1403.4273. [Google Scholar]
- Scandale, W.; Arduini, G.; Cerutti, F.; D’Andrea, M.; Esposito, L.S.; Garattini, M.; Gilardoni, S.; Mirarchi, D.; Montesano, S.; Natochii, A. Double-crystal measurements at the CERN SPS. Nucl. Instr. Methods Phys. Res. A 2021, 1015, 165747. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landi, G.; Landi, G.E.
Beyond the
Landi G, Landi GE.
Beyond the
Landi, Gregorio, and Giovanni E. Landi.
2022. "Beyond the
Landi, G., & Landi, G. E.
(2022). Beyond the




