GHz Superconducting Single-Photon Detectors for Dark Matter Search
Abstract
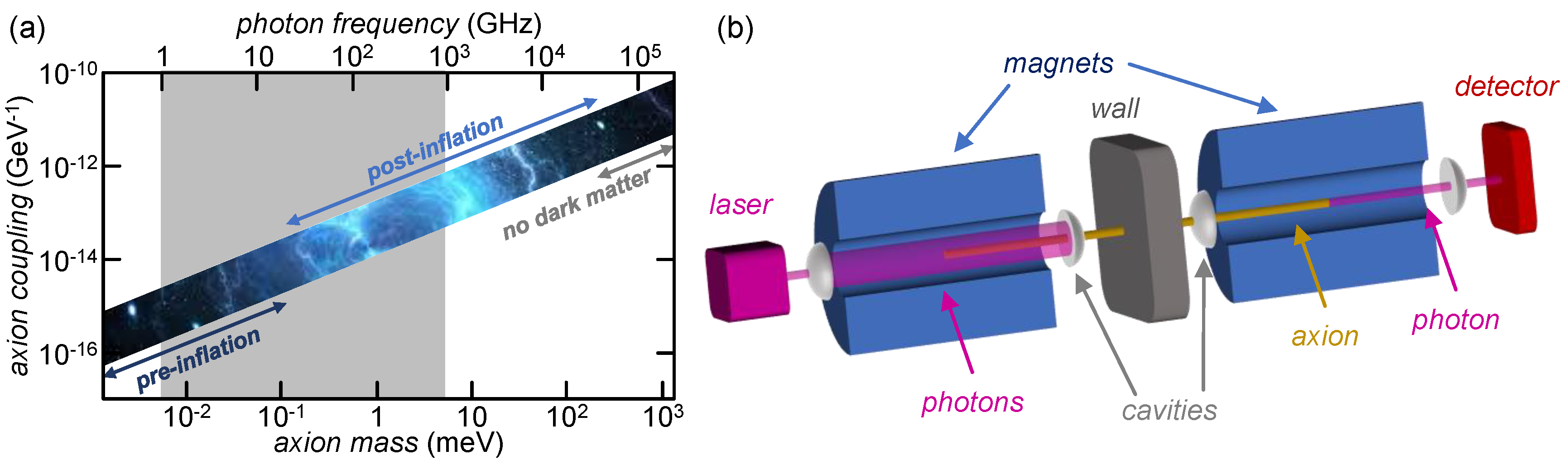
1. Introduction
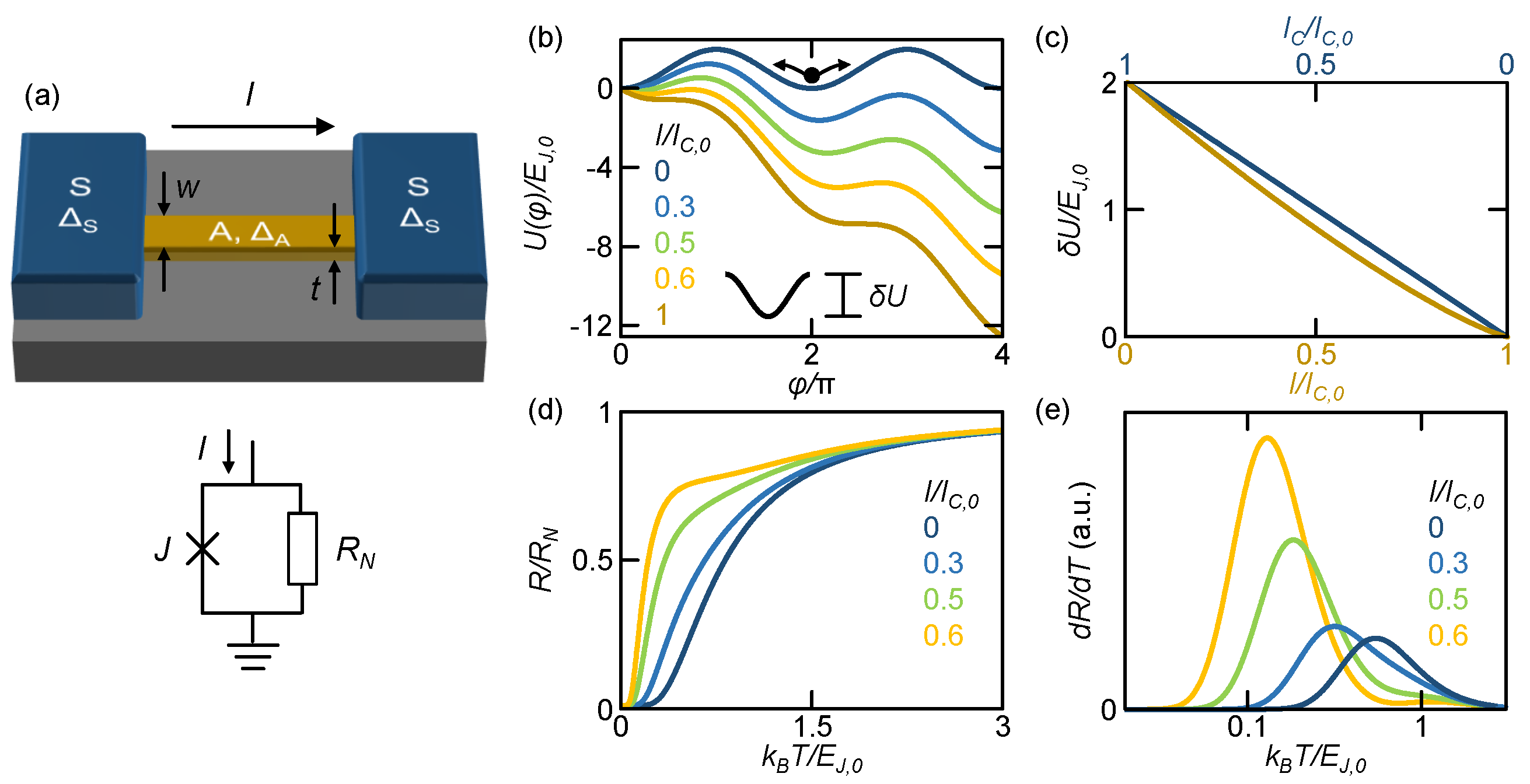
2. Theoretical Modeling of a One-Dimensional Fully Superconducting Josephson Junction
- a thin insulating barrier forming a superconductor/insulator/superconductor SIS-JJ;
- a short section of normal metal creating superconductor/normal metal/superconductor SNS-JJ;
- a physical constriction in the superconductor producing an SsS-JJ (known as Dayem bridge);
- a short section of lower energy gap superconductor realizing a SS’S-JJ.
3. Experimental Demonstration of a 1DJ
3.1. Density of States and One-Dimensionality
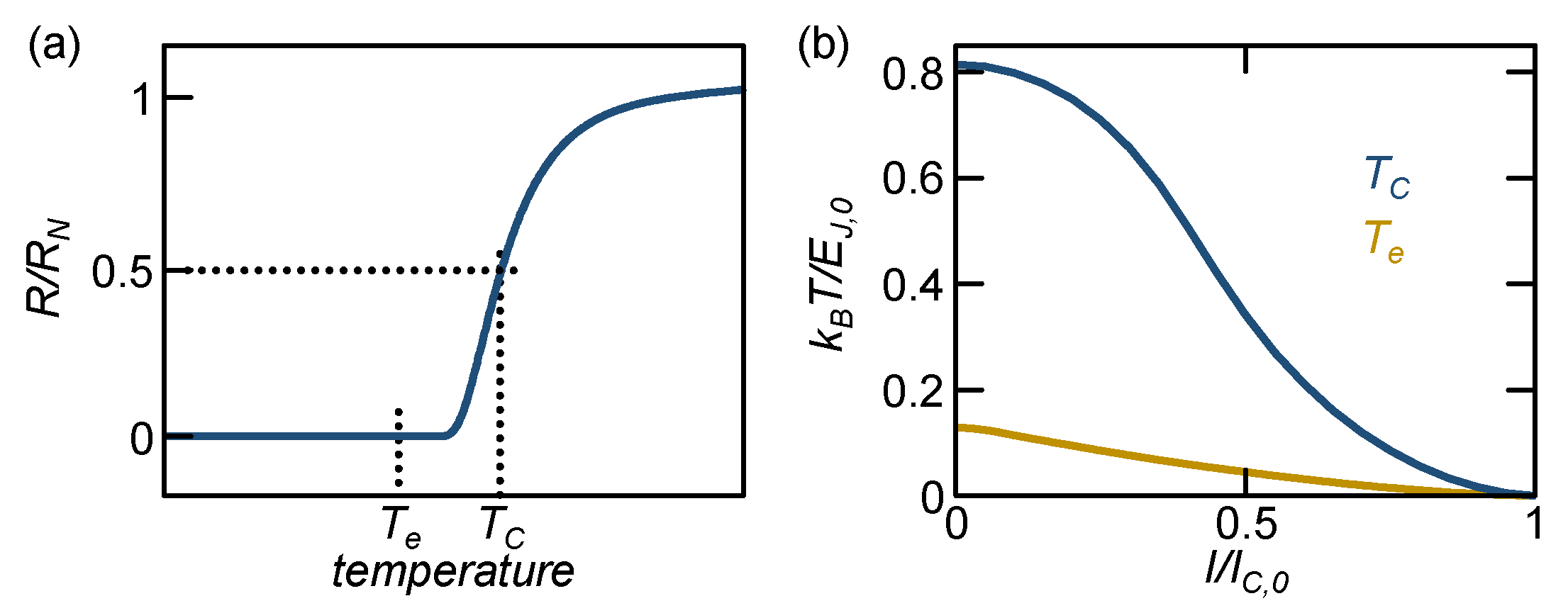
3.2. Current Control of the R vs T
4. Operation Principle of the Nano-TES and JES
5. Single-Photon Detection Performance of the Nano-TES and the JES
5.1. Modeling of the Nano-TES
5.2. Modeling of the JES
5.3. Performance Deduced from the Experimental Data
6. Materials and Methods
6.1. Fabrication Procedure
6.2. Measurement Setups
6.3. Basic Properties of the Active Region
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Preskill, J.; Wise, B.M.; Wilczek, F. Cosmology of the invisible axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef]
- Abbott, L.F.; Sikivie, P. A cosmological bound on the invisible axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar] [CrossRef]
- Peccei, D.R.; Quinn, H. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440. [Google Scholar] [CrossRef]
- Dine, M.; Fischler, W.; Srednicki, M. A Simple Solution to the Strong CP Problem with a Harmless Axion. Phys. Lett. B 1981, 104, 199. [Google Scholar] [CrossRef]
- Kim, J.E. Weak Interaction Single and Strong CP Invariance. Phys. Rev. Lett. 1979, 43, 103. [Google Scholar] [CrossRef]
- Zioutas, K.; Tsagri, M.; Semertzidis, Y.; Papaevangelou, T.; Dafni, T.; Anastassopoulos, V. Axion searches with helioscopes and astrophysical signatures for axion(-like) particles. New J. Phys. 2009, 11, 105020. [Google Scholar] [CrossRef]
- Sikivie, P. Experimental Tests of the ”Invisible” Axion. Phys. Rev. Lett. 1983, 51, 1415. [Google Scholar] [CrossRef]
- Van Bibber, K.; McIntyre, P.M.; Morris, D.E.; Raffelt, G.G. Design for a practical laboratory detector for solar axions. Phys. Rev. D 1989, 39, 2089. [Google Scholar] [CrossRef]
- Arik, M.; Aune, S.; Barth, K.; Belov, A.; Bräuninger, H.; Bremer, J. New solar axion search using the CERN Axion Solar Telescope with 4He filling. Phys. Rev. D 2015, 92, 021101. [Google Scholar] [CrossRef]
- Armengaud, E.; Avignone, F.T.; Betz, M.; Brax, P.; Brun, P.; Cantatore, G.; Zioutas, K. Conceptual Design of the International Axion Observatory (IAXO). JINST 2014, 9, T05002. [Google Scholar] [CrossRef]
- Asztalos, S.J.; Carosi, G.; Hagmann, C.; Kinion, D.; Van Bibber, K.; Hotz, M.; Clarke, J. A SQUID-based microwave cavity search for dark-matter axions. Phys. Rev. Lett. 2010, 104, 041301. [Google Scholar] [CrossRef] [PubMed]
- Barbieri, R.; Braggio, C.; Carugno, G.; Gallo, C.S.; Lombardi, A.; Ortolan, A.; Speake, C.C. Searching for galactic axions through magnetized media: The QUAX proposal. Phys. Dark Univ. 2017, 15, 135–141. [Google Scholar] [CrossRef]
- Graham, P.W.; Irastorza, I.G.; Lamoreaux, S.K.; Lindner, A.; van Bibber, K.A. Experimental Searches for the Axion and Axion-Like Particles. Ann. Rev. Nuc. Part. Sci. 2016, 65, 485–514. [Google Scholar] [CrossRef]
- Ehret, K.; Frede, M.; Ghazaryan, S.; Hildebrandt, M.; Knabbe, E.A.; Kracht, D.; Willke, B. New ALPS Results on Hidden-Sector Lightweights. Phys. Lett. B 2010, 689, 149. [Google Scholar] [CrossRef]
- Capparelli, L.M.; Cavoto, G.; Ferretti, J.; Giazotto, F.; Polosa, A.D.; Spagnolo, P. Axion-like particle searches with sub-THz photons. Phys. Dark Univ. 2016, 12, 37–44. [Google Scholar] [CrossRef]
- Alesini, D.; Babusci, D.; Barone, C.; Buonomo, B.; Beretta, M.M.; Bianchini, L.; Torrioli, G. Status of the SIMP Project: Toward the Single Microwave Photon Detection. J. Low Temp. Phys. 2020, 199, 348–354. [Google Scholar] [CrossRef]
- Alesini, D.; Babusci, D.; Barone, C.; Buonomo, B.; Beretta, M.M.; Bianchini, L.; Torrioli, G. Development of a Josephson junction based single photon microwave detector for axion detection experiments. J. Phys. Conf. Ser. 2020, 1559, 012020. [Google Scholar] [CrossRef]
- Irwin, K.D. An application of electrothermal feedback for high resolution cryogenic particle detection. Appl. Phys. Lett. 1995, 66, 1998–2000. [Google Scholar] [CrossRef]
- Irwin, K.D. Seeing with Superconductors. Sci. Am. 2006, 295, 86–94. [Google Scholar] [CrossRef]
- Khosropanah, P.; Dirks, B.; Parra-Borderias, M.; Ridder, M.; Hijmering, R.; Van der Kuur, J.; Hoevers, H. Low noise transition edge sensor (TES) for the SAFARI Instrument on SPICA. In Proceedings of the SPIE 7741, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy V, San Diego, CA, USA, 27 June– 2 July 2010; p. 77410L. [Google Scholar]
- De Visser, P.J.; Baselmans, J.J.A.; Bueno, J.; Llombart, N.; Klapwijk, T.M. Fluctuations in the electron system of a superconductor exposed to a photon flux. Nat Commun. 2014, 5, 3130. [Google Scholar] [CrossRef]
- Monfardini, A.; Baselmans, J.; Benoit, A.; Bideaud, A.; Bourrion, O.; Catalano, A.; Macias-Perez, J. Lumped element kinetic inductance detectors for space applications. In Proceedings of the SPIE 9914, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VIII, Edinburgh, UK, 28 June–1 July 2016; Volume 2016, p. 99140N. [Google Scholar]
- Josephson, B.D. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Solinas, P.; Giazotto, F.; Pepe, G.P. Proximity SQUID Single-Photon Detector via Temperature-to-Voltage Conversion. Phys. Rev. Applied 2018, 10, 024015. [Google Scholar] [CrossRef]
- Guarcello, C.; Braggio, A.; Solinas, P.; Pepe, G.P.; Giazotto, F. Josephson-Threshold Calorimeter. Phys. Rev. Appl. 2019, 11, 054074. [Google Scholar] [CrossRef]
- Giazotto, F.; Heikkilä, T.T.; Pepe, G.P.; Helistö, P.; Luukanen, T.T.; Pekola, J.P. Ultrasensitive proximity Josephson sensor with kinetic inductance readout. Appl. Phys. Lett. 2008, 92, 162507. [Google Scholar] [CrossRef]
- Virtanen, P.; Ronzani, A.; Giazotto, F. Josephson Photodetectors via Temperature-to-Phase Conversion. Phys. Rev. Appl. 2018, 9, 054027. [Google Scholar] [CrossRef]
- Natarajan, C.M.; Tanner, M.G.; Hdfield, R.H. Superconducting nanowire single-photon detectors: Physics and applications. Supercond. Sci. Technol. 2012, 25, 063001. [Google Scholar] [CrossRef]
- Oelsner, G.; Revin, L.S.; Il’Ichev, E.; Pankratov, A.L.; Meyer, H.G.; Grönberg, L.; Kuzmin, L.S. Underdamped Josephson junction as a switching current detector. Appl. Phys. Lett. 2013, 103, 142605. [Google Scholar] [CrossRef]
- Oelsner, G.; Andersen, C.K.; Rehák, M.; Schmelz, M.; Anders, S.; Grajcar, M.; Il’ichev, E. Detection of weak microwave fields with an underdamped Josephson junction. Phys. Rev. Appl. 2017, 7, 014012. [Google Scholar] [CrossRef]
- Kuzmin, L.S.; Sobolev, A.S.; Gatti, C.; Di Gioacchino, D.; Crescini, N.; Gordeeva, A.; Il’ichev, E. Single Photon Counter Based on a Josephson Junction at 14 GHz for Searching Galactic Axions. IEEE Trans. Appl. Supercond. 2018, 28, 2400505. [Google Scholar] [CrossRef]
- Paolucci, F.; Buccheri, V.; Germanese, G.; Ligato, N.; Paoletti, R.; Signorelli, G.; Bitossi, M.; Spagnolo, P.; Falferi, P.; Rajteri, M.; et al. Highly sensitive nano-TESs for gigahertz astronomy and dark matter search. J. Appl. Phys. 2020, 128, 194502. [Google Scholar] [CrossRef]
- Paolucci, F.; Ligato, N.; Buccheri, V.; Germanese, G.; Virtanen, P.; Giazotto, F. Hypersensitive tunable Josephson escape sensor for gigahertz astronomy. Phys. Rev. Appl. 2020, 14, 034055. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Barone, A.; Paternò, G. Physics and Applications of the Josephson Effect; Wiley-VCH: New York, NY, USA, 1982. [Google Scholar]
- Bezryadin, A. Superconductivity in Nanowires: Fabrication and Quantum Transport; Wiley-VCH: New York, NY, USA, 2012. [Google Scholar]
- Ivanchenko, Y.M.; Zil’berman, L.A. The Josephson effect in small tunnel contacts. Sov. Phys. JETP 1969, 28, 1272. [Google Scholar]
- Cochran, J.F.; Mapother, D.E. Superconducting Transition in Aluminum. Phys. Rev. 1958, 111, 132. [Google Scholar] [CrossRef]
- Giazotto, F.; Heikkilä, T.T.; Luukanen, A.; Savin, A.M.; Pekola, J.P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 2006, 78, 217–274. [Google Scholar] [CrossRef]
- Golubov, A.A.; Kupriyanov, M.Y.; Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411–479. [Google Scholar] [CrossRef]
- De Gennes, P.G. Boundary Effects in Superconductors. Rev. Mod. Phys. 1964, 36, 225. [Google Scholar] [CrossRef]
- Kogan, V.G. Coherence length of a normal metal in a proximity system. Phys. Rev. B 1982, 26, 88. [Google Scholar] [CrossRef]
- Courtois, H.; Meschke, M.; Peltonen, J.T.; Pekola, J.P. Hysteresis in a Proximity Josephson Junction. Phys. Rev. Lett. 2008, 101, 067002. [Google Scholar] [CrossRef]
- Andreev, A.F. The Thermal Conductivity of the Intermediate State in Superconductors. JETP 1964, 66, 1228–1231. [Google Scholar]
- Timofeev, A.V.; Pascual Giarcía, C.; Kopnin, N.B.; Savin, A.M.; Meschke, M.; Giazotto, F.; Pekola, J.P. Recombination-Limited Energy Relaxation in a Bardeen-Cooper-Schrieffer Superconductor. Phys. Rev. Lett. 2009, 102, 017003. [Google Scholar] [CrossRef]
- Heikkilä, T.T.; Silaev, M.; Virtanen, P.; Bergeret, F.S. Thermal, electric and spin transport in superconductor/ferromagnetic-insulator structures. Progr. Surf. Sci. 2019, 94, 100540. [Google Scholar]
- Rabani, H.; Taddei, F.; Bourgeois, O.; Fazio, R.; Giazotto, F. Phase-dependent electronic specific heat in mesoscopic josephson junction. Phys. Rev. B 2008, 78, 012503. [Google Scholar] [CrossRef]
- O’brien, J.L. Optical Quantum Computing. Science 2007, 318, 1567–1570. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbiden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Tittel, W. Quantum key distribution breaking limits. Nat. Photonics 2019, 13, 310–311. [Google Scholar] [CrossRef]




| Sample | |||||
|---|---|---|---|---|---|
| (mK) | () | () | (GHz) | 100 GHz 300 GHz | |
| 1 | 128 | 6 | 0.01 | 100 | 1 3 |
| 2 | 139 | 5 | 0.2 | 540 | 0.18 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paolucci, F.; Giazotto, F. GHz Superconducting Single-Photon Detectors for Dark Matter Search. Instruments 2021, 5, 14. https://doi.org/10.3390/instruments5020014
Paolucci F, Giazotto F. GHz Superconducting Single-Photon Detectors for Dark Matter Search. Instruments. 2021; 5(2):14. https://doi.org/10.3390/instruments5020014
Chicago/Turabian StylePaolucci, Federico, and Francesco Giazotto. 2021. "GHz Superconducting Single-Photon Detectors for Dark Matter Search" Instruments 5, no. 2: 14. https://doi.org/10.3390/instruments5020014
APA StylePaolucci, F., & Giazotto, F. (2021). GHz Superconducting Single-Photon Detectors for Dark Matter Search. Instruments, 5(2), 14. https://doi.org/10.3390/instruments5020014







