Can We Extract Production Cross-Sections from Thick Target Yield Measurements? A Case Study Using Scandium Radioisotopes
Abstract
:1. Introduction
2. Materials and Methods
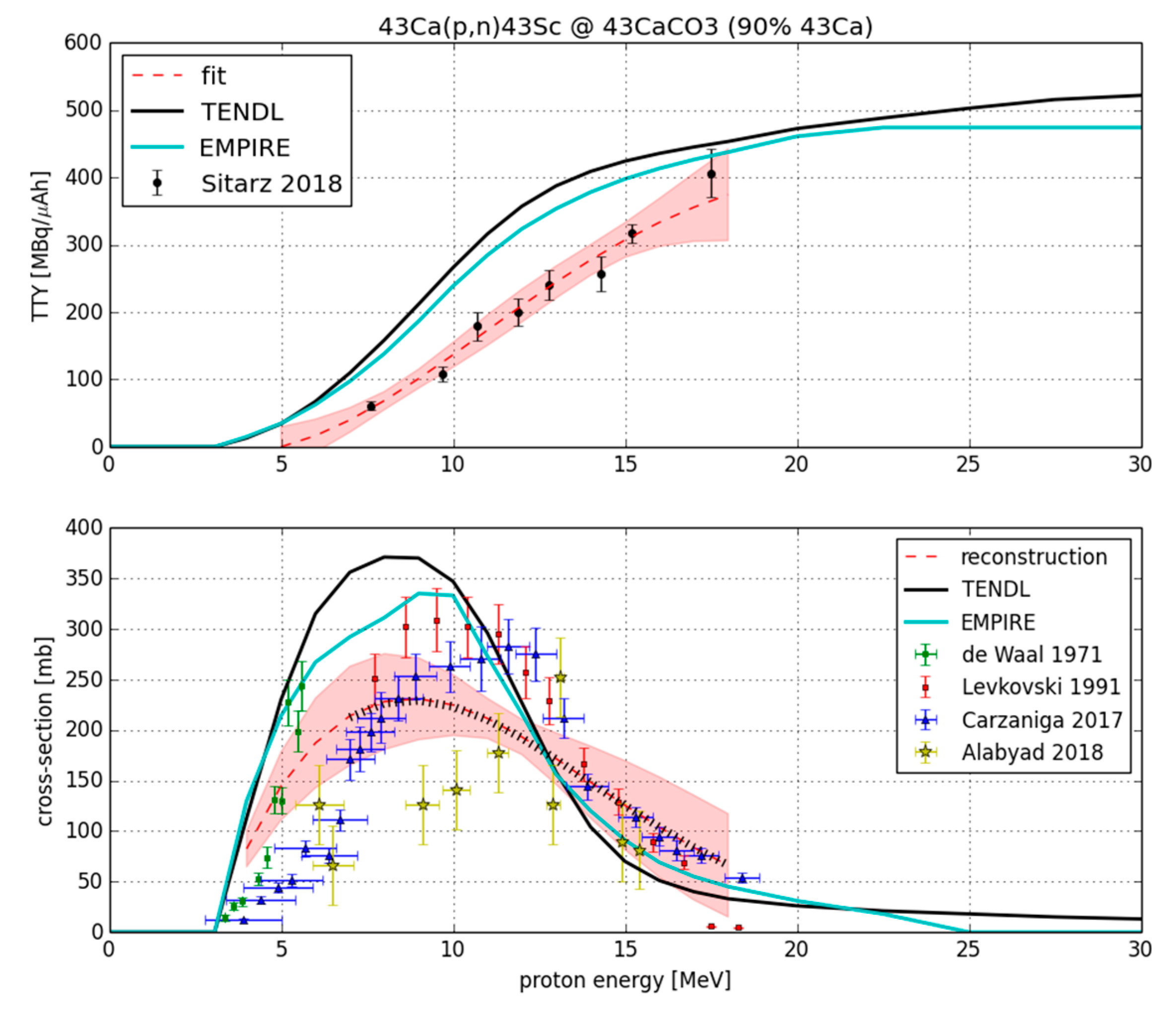
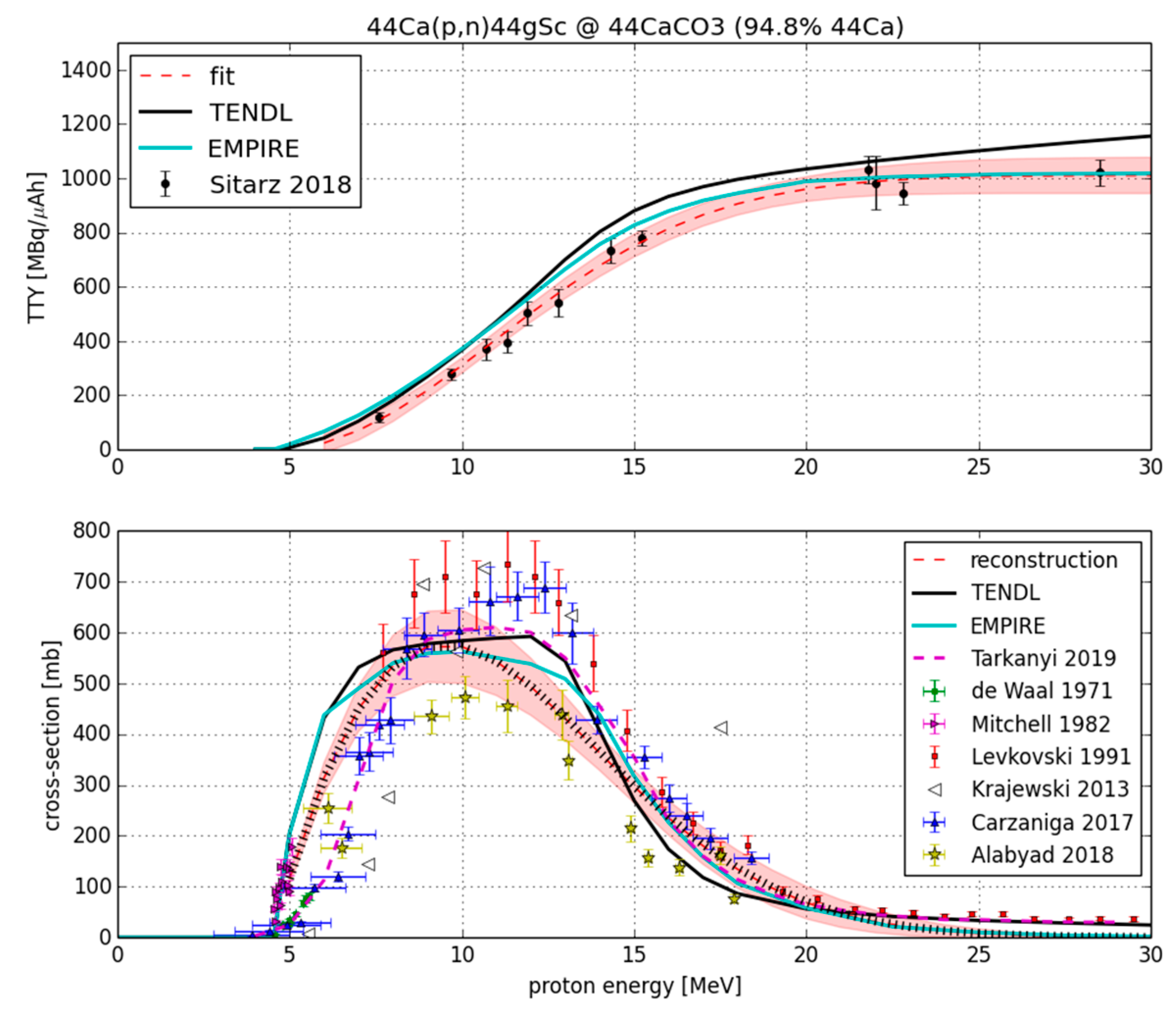
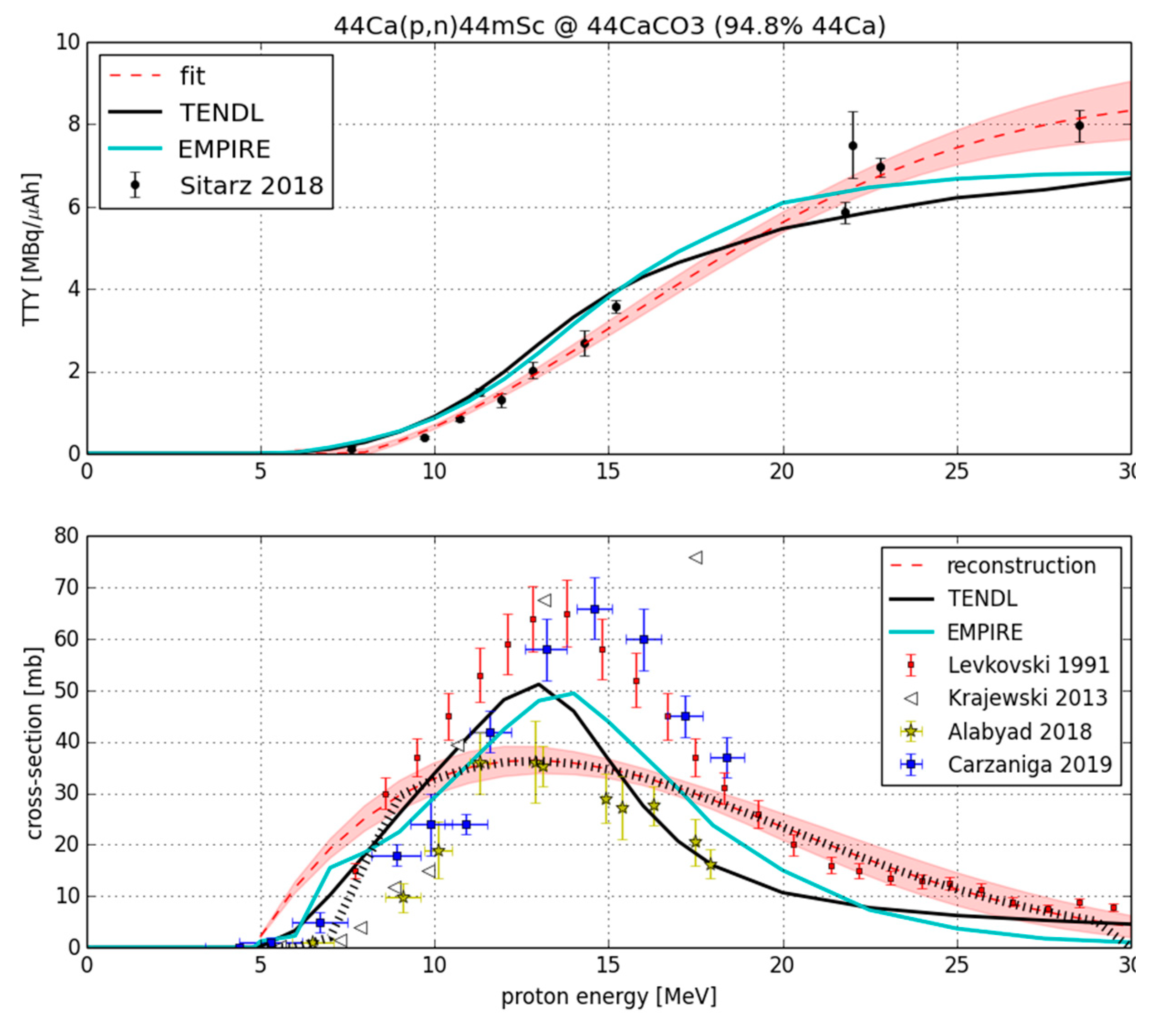
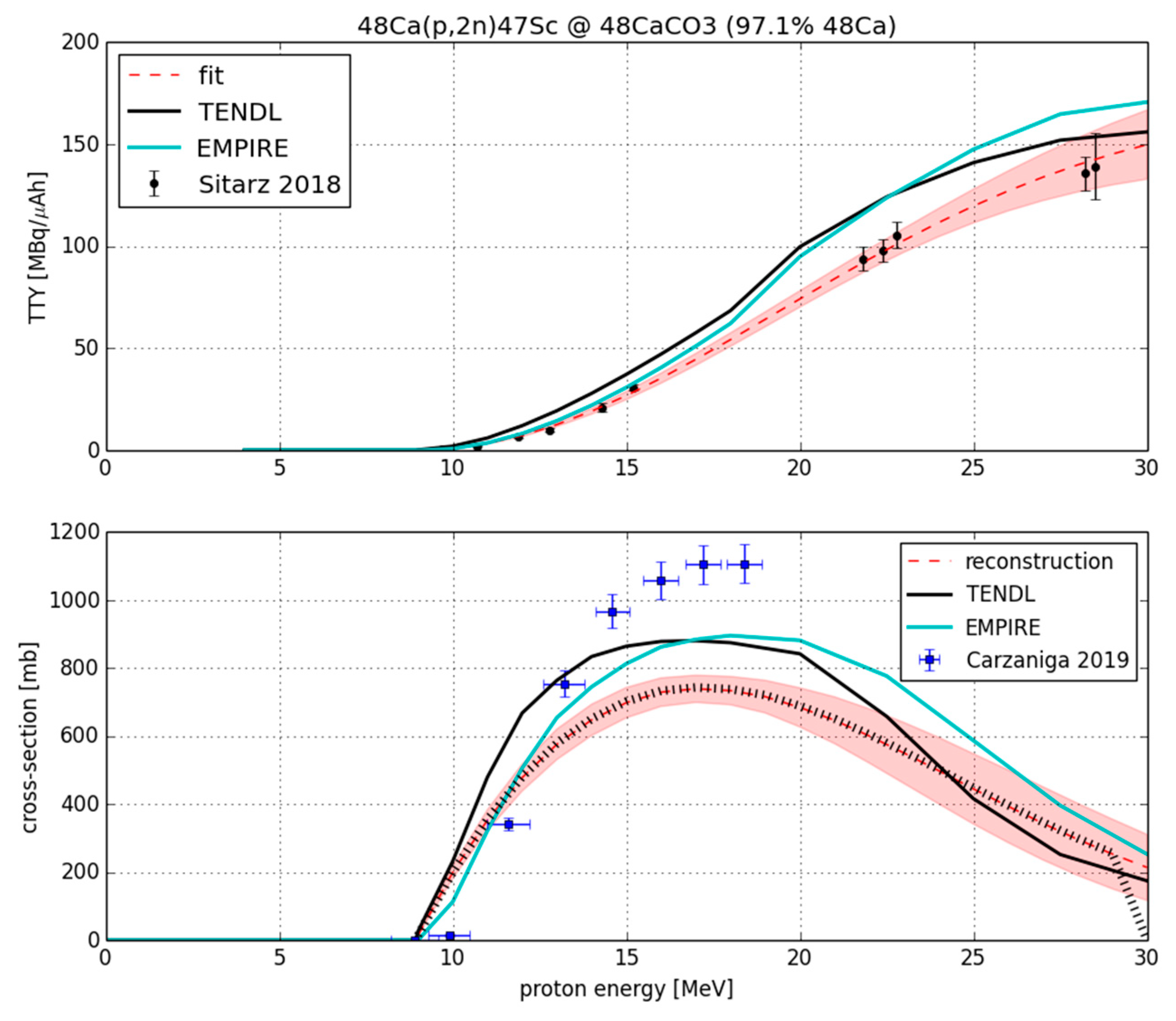
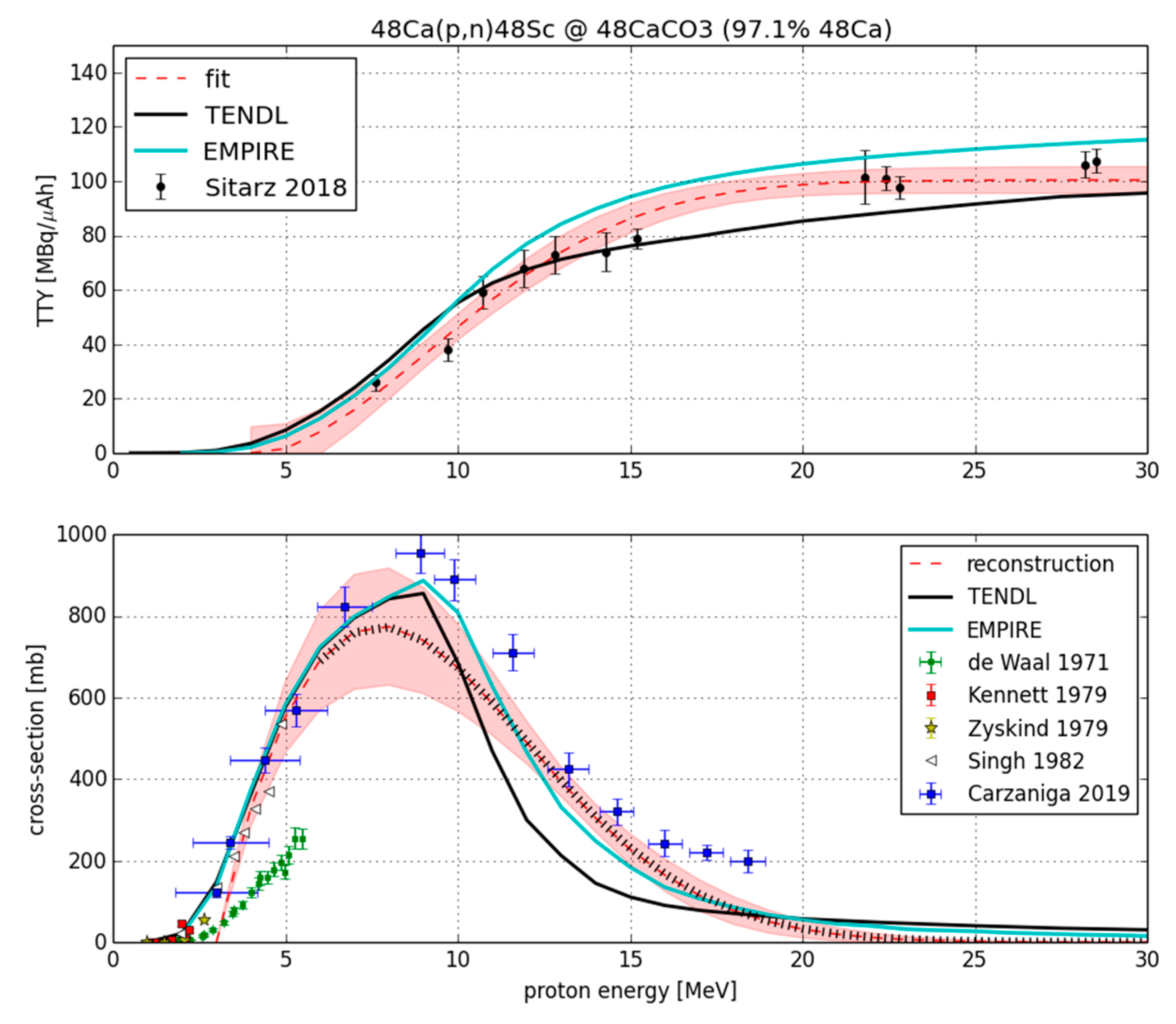
3. Results and Discussion
4. Conclusions and Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Koumarianou, E.; Pawlak, D.; Korsak, A.; Mikolajczak, R. Comparison of receptor affinity of natSc-DOTA-TATE versus natGa-DOTA-TATE. Nucl. Med. Rev. 2011, 14, 85–89. [Google Scholar] [CrossRef]
- Walczak, R.; Krajewski, S.; Szkliniarz, K.; Sitarz, M.; Abbas, K.; Choiński, J.; Jakubowski, A.; Jastrzębski, J.; Majkowska, A.; Simonelli, F.; et al. Cyclotron production of 43Sc for PET imaging. EJNMMI Phys. 2015. [Google Scholar] [CrossRef] [PubMed]
- Bunka, M.; Müller, C.; Vermeulen, C.; Haller, S.; Türler, A.; Schibli, R.; van der Meulen, N.P. Imaging quality of 44Sc in comparison with five other PET radionuclides using Derenzo phantoms and preclinical PET. Appl. Radiat. Isot. 2016, 110, 129–133. [Google Scholar] [CrossRef] [PubMed]
- Domnanich, K.A.; Müller, C.; Farkas, R.; Schmid, R.M.; Ponsard, B.; Schibli, R.; Türler, A.; van der Meulen, N.P. 44Sc for labeling of DOTA- and NODAGA-functionalized peptides: Preclinical in vitro and in vivo investigations. EJNMMI Radiopharm. Chem. 2016. [Google Scholar] [CrossRef]
- Domnanich, K.A.; Eichler, R.; Müller, C.; Jordi, S.; Yakusheva, V.; Braccini, S.; Behe, M.; Schibli, R.; Türler, A.; van der Meulen, N.P. Production and separation of 43Sc for radiopharmaceutical purposes. EJNMMI Radiopharm. Chem. 2017. [Google Scholar] [CrossRef] [PubMed]
- Grignon, C.; Barbet, J.; Bardiès, M.; Carlier, T.; Chatal, J.F.; Couturier, O.; Cussonneau, J.P.; Faivre, A.; Ferrer, L.; Girault, S.; et al. Nuclear medical imaging using β+ γ coincidence from 44Sc radio-nuclide with liquid xenon as detection medium. Nucl. Instrum. Meth. A 2017, 571, 142–145. [Google Scholar] [CrossRef]
- Lang, C.; Habs, D.; Parodi, K.; Thirolf, P.G. Sub-millimeter nuclear medical imaging with reduced dose application in positron emission tomography using β+ γ coincidences. JINST 2013, 9, P01008. [Google Scholar] [CrossRef]
- Thirolf, P.G.; Lang, C.; Parodi, K. Perspectives for Highly-Sensitive PET-Based Medical Imaging Using β+γ Coincidences. Acta Phys. Pol. A 2015, 127, 1441–1444. [Google Scholar] [CrossRef]
- Huclier-Markai, S.; Kerdjoudj, R.; Alliot, C.; Bonraisin, A.C.; Michel, N.; Haddad, F.; Barbet, J. Optimization of reaction conditions for the radiolabeling of DOTA and DOTA-peptide with 44m/44Sc and experimental evidence of the feasibility of an in vivo PET generator. Nucl. Med. Biol. 2014, 41, e36–e43. [Google Scholar] [CrossRef] [PubMed]
- Alliot, C.; Audouin, N.; Barbet, J.; Bonraisin, A.C.; Bossé, V.; Bourdeau, C.; Bourgeois, M.; Duchemin, C.; Guertin, A.; Haddad, F.; et al. Is there an interest to use deuteron beams to produce non-conventional radionuclides? Front. Med. 2015. [Google Scholar] [CrossRef]
- Alliot, C.; Kerdjoudj, R.; Michel, N.; Haddad, F.; Huclier-Markai, S. Cyclotron production of high purity 44m,44Sc with deuterons from 44CaCO3 targets. Nucl. Med. Biol. 2015, 42, 524–529. [Google Scholar] [CrossRef]
- Duchemin, C.; Guertin, A.; Haddad, F.; Michel, N.; Métivier, V. Production of scandium-44m and scandium-44g with deuterons on calcium-44: Cross-section measurements and production yield calculations. Phys. Med. Biol. 2015, 60, 17. [Google Scholar] [CrossRef]
- Domnanich, K.A.; Müller, C.; Benešová, M.; Dressler, R.; Haller, S.; Köster, U.; Ponsard, B.; Schibli, R.; Türler, A.; van der Meulen, N.P. 47Sc as useful β- emitter for the radiotheragnostic paradigm: A comparative study of feasible production routes. EJNMMI Radiopharm. Chem. 2017. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Call for Coordinated Research Project “Therapeutic Radiopharmaceuticals Labelled with New Emerging Radionuclides (67Cu, 186Re, 47Sc)”. 2015. Available online: https://www.iaea.org/projects/crp/f22053 (accessed on 13 May 2019).
- International Atomic Energy Agency. 2015. Available online: http://cra.iaea.org/cra/stories/2015-09-30-F22053-New_Emerging_Radionuclides.html (accessed on 13 May 2019).
- Müller, C.; Bunka, M.; Haller, S.; Köster, U.; Groehn, V.; Bernhardt, P.; van der Meulen, N.P.; Türler, A.; Schibli, R. Promising Prospects for 44Sc-/47Sc-Based Theragnostics: Application of 47Sc for Radionuclide Tumor Therapy in Mice. J. Nucl. Med. 2014, 55, 1658–1664. [Google Scholar] [CrossRef]
- Müller, C.; Domnanich, K.A.; Umbricht, C.A.; van der Meulen, N.P. Scandium and terbium radionuclides for radiotheranostics: Current state of development towards clinical application. Br. J. Radiol. 2018. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Live Chart of Nuclides. Available online: https://www-nds.iaea.org/relnsd/vcharthtml/VChartHTML.html (accessed on 12 May 2019).
- Szkliniarz, K.; Sitarz, M.; Walczak, R.; Jastrzębski, J.; Bilewicz, A.; Choiński, J.; Jakubowski, A.; Majkowska, A.; Stolarz, A.; Trzcińska, A.; Zipper, W. Production of medical Sc radioisotopes with an alpha particle beam. Appl. Radiat. Isot. 2016, 118, 182–189. [Google Scholar] [CrossRef]
- Sitarz, M.; Szkliniarz, K.; Jastrzębski, J.; Choiński, J.; Guertin, A.; Haddad, F.; Jakubowski, A.; Kapinos, K.; Kisieliński, M.; Majkowska, A.; et al. Production of Sc medical radioisotopes with proton and deuteron beams. Appl. Radiat. Isot. 2018, 142, 104–112. [Google Scholar] [CrossRef]
- Nagatsu, K.; Fukumura, T.; Takei, M.; Szelecsényi, F.; Kovács, Z.; Suzuki, K. Measurement of thick target yields of the natS(α,x)34mCl nuclear reaction and estimation of its excitation function up to 70 MeV. Nucl. Inst. Meth. Phys. Res. B 2008, 266, 709–713. [Google Scholar] [CrossRef]
- Phelps, M.E. PET: Molecular Imaging and Its Biological Applications; Springer: New York, NY, USA, 2004. [Google Scholar]
- Pedroso de Lima, J.J. Nuclear Medicine Physics Series in Medical Physics and Biomedical Engineering, Cyclotron and Radionuclide Production, Series in Medical and Biomedical Engineering; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Jose, K.K.; Naik, S.R. On the q-Weibull Distribution and Its Applications. Com. Stat. Th. Meth. 2009, 38, 912–926. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM Code, Version 2008.04. Available online: http://www.srim.org/ (accessed on 12 May 2019).
- de Waal, T.J.; Peisach, M.; Pretorius, R. Activation cross sections for proton-induced reactions on calcium isotopes up to 5.6 MeV. J. Inorg. Nucl. Chem. 1971, 33, 2783–2789. [Google Scholar] [CrossRef]
- Kennett, S.R.; Switkowski, Z.E.; Paine, B.M.; Sargood, D.G. Yield Measurements in the Reactions 48Ca(p,γ)49Sc and 48Ca(p,n)48Sc. J. Phys. G 1979, 5, 399. [Google Scholar] [CrossRef]
- Zyskind, J.L.; Davidson, J.M.; Esat, M.T.; Spear, R.H.; Shapiro, M.H.; Fowler, W.A.; Barnes, C.A. Cross Section Measurements and Thermonuclear Reaction Rates for 48Ca(p,γ)49Sc and 48Ca(p,n)48Sc. Nucl. Phys. A 1979, 315, 430–444. [Google Scholar] [CrossRef]
- Mitchell, L.W.; Anderson, M.R.; Kennett, S.R.; Sargood, D.G. Cross-sections and thermonuclear reaction rates for 42Ca(p,γ)43Sc, 44Ca(p,γ)45Sc, 44Ca(p,n)44Sc and 45Sc(p,n)45Ti. J. Nucl. Phys. A 1982, 380, 318–334. [Google Scholar] [CrossRef]
- Singh, G.; Kailas, S.; Saini, S.; Chatterjee, A.; Balakrishnan, M.; Mehta, M.K. Reaction 48Ca(p,n)48Sc from E(p) = 1.885 to 5.1 MeV. Pramana 1982, 19, 565–577. [Google Scholar] [CrossRef]
- Levkovskij, V.N. Cross-section of medium mass nuclide activation (A=40-100) by medium energy protons and alpha-particles (E=10-50 MeV); Inter-Vesi: Moscow, Russia, 1991. [Google Scholar]
- Krajewski, S.; Cydzik, I.; Abbas, K.; Bulgheroni, A.; Simonelli, F.; Holzwarth, U.; Bilewicz, A. Cyclotron production of 44Sc for clinical application. J. Radiochim. Acta 2013. [Google Scholar] [CrossRef]
- Carzaniga, T.S.; Auger, M.; Braccini, S.; Bunka, M.; Ereditato, A.; Nesteruk, K.P.; Scampoli, P.; Türler, A.; van der Meulen, N. Measurement of 43Sc and 44Sc production cross-section with an 18 MeV medical PET cyclotron. Appl. Radiat. Isot. 2017, 129, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Alabyad, M.; Mohamed, G.V.; Hassan, H.E.; Takács, S.; Ditrói, F. Experimental measurement and theoretical calculations for proton, deuteron and α-particle induced nuclear reactions on calcium: Special relevance to the production of 43,44Sc. J. Radioan. Nucl. Chem. 2018, 316, 119–128. [Google Scholar] [CrossRef]
- Carzaniga, T.S.; Braccini, S. Cross-section measurement of 44mSc, 47Sc, 48Sc and 47Ca for an optimized 47Sc production with an 18 MeV medical PET cyclotron. Appl. Radiat. Isot. 2019, 143, 18–23. [Google Scholar] [CrossRef]
- Tárkányi, F.T.; Ignatyuk, A.V.; Hermanne, A.; Capote, R.; Carlson, B.V.; Engle, J.W.; Kellett, M.A.; Kibédi, T.; Kim, G.N.; Kondev, F.G.; et al. Recommended nuclear data for medical radioisotope production: diagnostic positron emitters. J. Radioan. Nucl. Chem 2019, 319, 533–666. [Google Scholar] [CrossRef]
- Herman, M.; Capote, R.; Carlson, B.V.; Obložinský, P.; Sin, M.; Trkov, A.; Wienke, H.; Zerkin, V. EMPIRE: Nuclear Reaction Model Code System for Data Evaluation. Nucl. Data Sheets 2007, 108, 2655–2715. [Google Scholar] [CrossRef]
- Koning, A.J.; Rochman, D. Modern Nuclear Data Evaluation with The TALYS Code System. Nucl. Data Sheets 2012, 113, 2841–2934. [Google Scholar] [CrossRef]
| Radio-Nuclide | T1/2 | Eaverage β- or β+ | Branching or Transition | Main γ-Lines [keV] and Intensities |
|---|---|---|---|---|
| 43Sc | 3.89 h | β+ 476 keV | β+ 88% | 373 (22.5%) |
| 44gSc | 3.97 h | β+ 632 keV | β+ 95% | 1157 (99.9%) |
| 44mSc | 58.61 h | N/A | IT 99% | 271 (86.7%), 1002 (1.2%), 1126 (1.2%), 1157 (1.2%) |
| 47Sc | 3.35 d | β- 162 keV | β- 100% | 159 (68.3%) |
| 48Sc | 43.67 h | β- 220 keV | β- 100% | 175 (7.5%), 984 (100%), 1038 (97.6%), 1213 (2.4%), 1312 (100%) |
| Parameter | 43Ca(p,n)43Sc | 44Ca(p,n)44gSc | 44Ca(p,n)44mSc | 48Ca(p,2n)47Sc | 48Ca(p,n)48Sc |
|---|---|---|---|---|---|
| Ethr [MeV] | 3.07 | 4.54 | 4.81 | 8.93 | theory: 0.51 adopted: 3.0 |
| a [MeV] | 10(2) | 8.8(6) | 13.7(7) | 14.7(9) | 8.0(8) |
| b [MeV] | 4.5(6) | 4.8(1.0) | 7.0(1) | 9.05(14) | 4.2(7) |
| c [MBq(μAh)−1 (MeV)−2] | 7.1(9) | 24.5(1.2) | 0.075(3) | 1.57(6) | 2.5(2) |
| d [MBq/μAh] | 348 | 952 | 6.82 | 169 | 79.4 |
| χ2/dof | 1.30 | 0.57 | 6.11 | 1.05 | 1.79 |
| E [MeV] | σ [mb] | ||||
|---|---|---|---|---|---|
| 43Ca(p,n)43Sc | 44Ca(p,n)44gSc | 44Ca(p,n)44mSc | 48Ca(p,2n)47Sc | 48Ca(p,n)48Sc | |
| 5 | 145(20) | 115(6) | 2.11(8) | 0 | 552(48) |
| 6 | 187(26) | 314(13) | 11.7(5) | 0 | 692(66) |
| 7 | 214(29) | 450(20) | 19.2(8) | 0 | 761(77) |
| 8 | 228(28) | 534(26) | 25.1(1.1) | 0 | 744(78) |
| 9 | 231(24) | 572(31) | 29.6(1.3) | 14.2(6) | 740(71) |
| 10 | 225(18) | 572(32) | 32.9(1.4) | 199(7) | 674(58) |
| 11 | 211(12) | 543(30) | 35.0(1.4) | 353(14) | 586(43) |
| 12 | 193(10) | 493(25) | 36.2(1.3) | 478(18) | 490(29) |
| 13 | 172(15) | 431(19) | 36.4(1.2) | 576(20) | 393(20) |
| 14 | 148(21) | 363(15) | 35.9(1.0) | 647(20) | 304(18) |
| 15 | 125(26) | 297(14) | 34.7(8) | 698(20) | 228(21) |
| 16 | 104(29) | 235(15) | 33.1(7) | 729(19) | 164(22) |
| 17 | 84(30) | 180(16) | 31.0(7) | 739(18) | 115(21) |
| 18 | 66(30) | 134(16) | 28.7(8) | 734(18) | 78(19) |
| 19 | 97(16) | 26.1(1.0) | 716(21) | 51(15) | |
| 20 | 68(14) | 23.4(1.1) | 684(26) | 32(12) | |
| 21 | 47(12) | 20.8(1.3) | 647(31) | 20(9) | |
| 22 | 31(10) | 18.2(1.4) | 600(35) | 12(6) | |
| 23 | 20(7) | 15.7(1.4) | 550(40) | 7(4) | |
| 24 | 13(6) | 13.5(1.4) | 499(43) | 4(3) | |
| 25 | 8(4) | 11.3(1.4) | 445(46) | 2.0(1.6) | |
| 26 | 5(3) | 9.5(1.4) | 393(47) | 1.0(9) | |
| 27 | 2.7(1.8) | 7.8(1.3) | 343(48) | 0.5(5) | |
| 28 | 1.5(1.1) | 6.4(1.2) | 297(47) | 0.3(3) | |
| 29 | 0.8(7) | 5.1(1.1) | 253(45) | 0.12(16) | |
| 30 | 0.4(4) | 4.0(9) | 213(43) | 0.05(8) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sitarz, M.; Jastrzębski, J.; Haddad, F.; Matulewicz, T.; Szkliniarz, K.; Zipper, W. Can We Extract Production Cross-Sections from Thick Target Yield Measurements? A Case Study Using Scandium Radioisotopes. Instruments 2019, 3, 29. https://doi.org/10.3390/instruments3020029
Sitarz M, Jastrzębski J, Haddad F, Matulewicz T, Szkliniarz K, Zipper W. Can We Extract Production Cross-Sections from Thick Target Yield Measurements? A Case Study Using Scandium Radioisotopes. Instruments. 2019; 3(2):29. https://doi.org/10.3390/instruments3020029
Chicago/Turabian StyleSitarz, Mateusz, Jerzy Jastrzębski, Férid Haddad, Tomasz Matulewicz, Katarzyna Szkliniarz, and Wiktor Zipper. 2019. "Can We Extract Production Cross-Sections from Thick Target Yield Measurements? A Case Study Using Scandium Radioisotopes" Instruments 3, no. 2: 29. https://doi.org/10.3390/instruments3020029
APA StyleSitarz, M., Jastrzębski, J., Haddad, F., Matulewicz, T., Szkliniarz, K., & Zipper, W. (2019). Can We Extract Production Cross-Sections from Thick Target Yield Measurements? A Case Study Using Scandium Radioisotopes. Instruments, 3(2), 29. https://doi.org/10.3390/instruments3020029





