Undamped Higgs Modes in Strongly Interacting Superconductors

Abstract

In superconductors, gauge $U\left(1\right)$ symmetry is spontaneously broken. According to Goldstone’s theorem, this breaking of a continuous symmetry establishes the existence of the Bogoliubov phase mode while the gauge-invariant response also includes the amplitude fluctuations of the order parameter. The latter, which are also termed ‘Higgs’ modes in analogy with the standard model, appear at the energy of the spectral gap $2\Delta$, when the superconducting ground state is evaluated within the weak-coupling BCS theory, and, therefore, are damped. Previously, we have shown that, within the time-dependent Gutzwiller approximation (TDGA), Higgs modes appear inside the gap with a finite binding energy relative to the quasiparticle continuum. Here, we show that the binding energy of the Higgs mode becomes exponentially small in the weak-coupling limit converging to the BCS solution. On the other hand, well-defined undamped amplitude modes exist in strongly coupled superconductors when the interaction energy becomes of the order of the bandwidth.

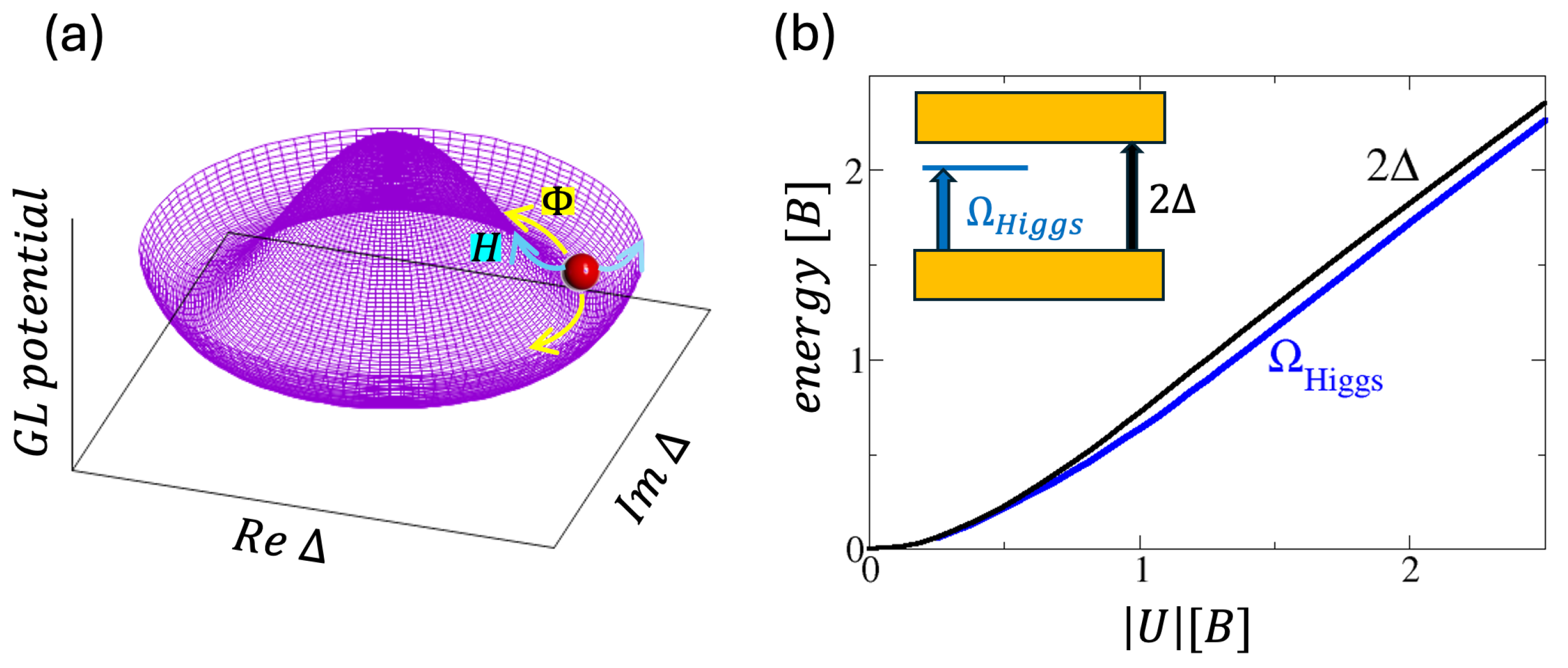
1. Introduction

There exists a close analogy between the mechanism at the heart of the mass generation for scalar and vector bosons in the standard model [1,2] and the mechanism responsible for superconductivity [3,4]. In both cases, the spontaneous breaking of a continuous symmetry comes along with the emergence of new elementary excitations. In the context of superconductors, they are identified with the collective fluctuations of the macroscopic (complex) order parameter. These comprise the massless phase fluctuations, which, in a charged superconductor, are pushed to the plasma frequency via the Anderson–Higgs mechanism [5]. In addition, amplitude fluctuations are the analog of the Higgs field in the ‘standard model’ and are, therefore, also referred to as “Higgs” modes in a superconducting system, cf. Figure 1a. In conventional (weakly-coupled or BCS) superconductors, the energy of the Higgs mode coincides with the spectral gap $2\Delta$ for single-particle excitations. The latter influence the dynamics of the Higgs excitation, leading to a non-relativistic strongly overdamped mode. In addition, the effects can hardly be probed experimentally, unless the system is strongly perturbed from its equilibrium [6,7,8,9,10,11,12].

It has been discussed in the literature (see, e.g., Refs. [13,14,15]) that amplitude fluctuations of the superconducting order parameter can give rise to in-gap excitations when the quantum critical point of the superconducting phase transition is approached. In this spirit, the subgap absorption, observed in strongly disordered NbN and InO films [16], has been taken as evidence for Higgs modes, which appear below the spectral gap $2\Delta$. However, this interpretation, which relies on the validity of Lorentz-invariant $\mathcal{O}\left(2\right)$ models, has been questioned in Ref. [17] and, instead, it has been shown that the subgap absorption, observed in Ref. [16] and also Ref. [18], is most likely due to phase modes, which, due to the low superfluid density (and, thus, low energy plasma excitation), can be active at energies below the spectral gap.

In a recent paper [19], we have shown that, in the limit of strong coupling, the Higgs mode is shifted inside the spectral gap, even in the clean system, which leads to undamped Higgs oscillations, cf. Figure 1b. This theory is relevant for systems where the interaction becomes of the same order than that of the bandwidth. Such a situation could be realized in cold atomic Fermion condensates and, in fact, a well-defined collective mode throughout the entire crossover from BCS to Bose–Einstein condensation has been observed recently [20] in a system with weak modulation of the confinement. Our previous work was based on the time-dependent Gutzwiller approximation (TDGA) [21,22,23,24,25,26,27,28,29], which allows for the investigation of dynamical properties of systems with a strong local interaction U (i.e., Hubbard-type models). By evaluating the spectral gap $2\Delta$ and the energy of the Higgs mode, it could be shown that both quantities begin to separate when the magnitude of the local attraction $\left|U\right|$ becomes larger than the bandwidth. However, within this numerical approach, it is difficult to analyze the situation at weak coupling. In particular, it is difficult to distinguish between the situation where a critical coupling must be exceeded to push the Higgs mode into the spectral gap, and a scenario where, at weak coupling, the difference between the energy of the Higgs mode and $2\Delta$ becomes exponentially small.

Here, we analyze the situation in the weak-coupling limit of the TDGA and show that the latter scenario is realized in this case. Section 2 introduces the model and first discusses the appearance of amplitude modes within the standard BCS + RPA approach. The analysis of the Higgs excitation within the TDGA is then performed in Section 4 in the weak-coupling limit and we finally conclude our discussion in Section 5.

2. Model and BCS Approximation

We exemplify the evaluation of amplitude modes within the single-band attractive Hubbard Hamiltonian

$$\begin{array}{ccc}\hfill H& =& \sum _{ij}{t}_{ij}{c}_{i,\sigma }^{†}{c}_{j,\sigma }-\mu \sum _i{n}_i-\left|U\right|\sum _i{n}_{i,\uparrow }{n}_{i,\downarrow }\hfill \end{array}$$

(1)

where, in the following, we denote the Fourier transform of $t_{ij}$ as the dispersion ${\epsilon }_k$.

Decoupling in the pair channel yields the usual BCS Hamiltonian

$$H=\sum _{k,\sigma }{\xi }_k{c}_{k,\sigma }^{†}{c}_{k,\sigma }+\sum _k\left({\Delta }^{*}{c}_{-k,\downarrow }{c}_{k,\uparrow }+\Delta c_{k,\uparrow }^{†}{c}_{-k,\downarrow }^{†}\right)+N{\displaystyle \frac{{|\Delta |}^2}{\left|U\right|}}$$

(2)

with $\Delta =-\left|U\right|\langle c_{-k,\downarrow }{c}_{k,\uparrow }\rangle$, ${\xi }_k={\epsilon }_k-\mu$, and N denotes the number of lattice sites.

Equation (2) can be diagonalized with the Bogoljubov transformation,

$$\begin{array}{ccc}\hfill c_{k,\uparrow }& =& {\alpha }_k{\gamma }_{k,0}-{\beta }_k^{*}{\gamma }_{k,1}^{†}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill c_{-k,\downarrow }& =& {\beta }_k{\gamma }_{k,0}^{†}+{\alpha }_k{\gamma }_{k,1}\hfill \end{array}$$

(4)

and one obtains

$$H=\sum _k{E}_K\left({\gamma }_{k,0}^{†}{\gamma }_{k,0}+{\gamma }_{k,1}^{†}{\gamma }_{k,1}\right)+\sum _k({\xi }_k-E_k)+N{\displaystyle \frac{|{\Delta }^2|}{\left|U\right|}}$$

(5)

where $E_k=\sqrt{{\xi }_k^2+{\Delta }^2}$, ${\alpha }_k^2={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{{\xi }_k}{E_k}}\right)$, and ${\beta }_k^2={\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{{\xi }_k}{E_k}}\right)$. The self-consistency condition (zero temperature) reads

$${\displaystyle \frac{1}{\left|U\right|}}={\displaystyle \frac{1}{N}}\sum _k{\displaystyle \frac{1}{2E_k}}.$$

(6)

3. Collective Modes beyond Weak-Coupling BCS Theory

The mean-field decoupling neglects the following fluctuation contributions in the pairing channel:

$$V_{fl}^{pair}=-\left|U\right|{\displaystyle \frac{1}{N}}\sum _q\delta {\Delta }_q^{†}\delta {\Delta }_q$$

(7)

with

$$\begin{array}{ccc}\hfill \delta {\Delta }_q& =& \sum _k\left[c_{-k+q/2,\downarrow }{c}_{k+q/2,\uparrow }-\langle c_{-k+q/2,\downarrow }{c}_{k+q/2,\uparrow }\rangle \right]\hfill \\ & =& \sum _k\left[{\alpha }_k^{+}{\alpha }_k^{-}{\gamma }_{k-q/2,1}{\gamma }_{k+q/2,0}-{\beta }_k^{+}{\beta }_k^{-}{\gamma }_{k-q/2,0}^{†}{\gamma }_{k+q/2,1}^{†}\right.\hfill \\ & +& \left.{\alpha }_k^{+}{\beta }_k^{-}{\gamma }_{k-q/2,0}^{†}{\gamma }_{k+q/2,0}+{\beta }_k^{+}{\alpha }_k^{-}{\gamma }_{k+q/2,1}^{†}{\gamma }_{k-q/2,1}\right]\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \delta {\Delta }_q^{†}& =& \left[c_{k+q/2,\uparrow }^{†}{c}_{-k+q/2,\downarrow }^{†}-\langle c_{k+q/2,\uparrow }^{†}{c}_{-k+q/2,\downarrow }^{†}\rangle \right]\hfill \\ & =& \sum _k\left[{\alpha }_k^{+}{\alpha }_k^{-}{\gamma }_{k+q/2,0}^{†}{\gamma }_{k-q/2,1}^{†}-{\beta }_k^{+}{\beta }_k^{-}{\gamma }_{k+q/2,1}{\gamma }_{k-q/2,0}\right.\hfill \\ & +& \left.{\alpha }_k^{+}{\beta }_k^{-}{\gamma }_{k+q/2,0}^{†}{\gamma }_{k-q/2,0}+{\beta }_k^{+}{\alpha }_k^{-}{\gamma }_{k-q/2,1}^{†}{\gamma }_{k+q/2,1}\right],\hfill \end{array}$$

(9)

and we have defined ${\alpha }_k^{\pm }={\alpha }_{k\pm q/2}$ and ${\beta }_k^{\pm }={\beta }_{k\pm q/2}$.

In the same way, the fluctuation contribution in the charge channel is obtained as

$$V_{fl}^{charge}=-{\displaystyle \frac{\left|U\right|}{2}}{\displaystyle \frac{1}{2N}}\sum _q\delta {\rho }_q\delta {\rho }_{-q}$$

(10)

with

$$\begin{array}{ccc}\hfill \delta {\rho }_q& =& \sum _k\left[({\alpha }_k^{+}{\beta }_k^{-}+{\alpha }_k^{-}{\beta }_k^{+})({\gamma }_{k-q/2,1}^{†}{\gamma }_{k+q/2,0}^{†}+{\gamma }_{k-q/2,0}{\gamma }_{k+q/2,1})\right.\hfill \\ & +& \left.({\alpha }_k^{+}{\alpha }_k^{-}-{\beta }_k^{+}{\beta }_k^{-})({\gamma }_{k-q/2,1}^{†}{\gamma }_{k+q/2,1}+{\gamma }_{k+q/2,0}^{†}{\gamma }_{k-q/2,0})\right].\hfill \end{array}$$

(11)

3.1. Correlation Functions and RPA Resummation

We denote correlation functions by

$${\chi }_{nm}(\widehat{A},\widehat{B})=-i\int dt{e}^{i\omega t}\langle \mathcal{T}{\widehat{A}}_n\left(t\right){\widehat{B}}_m\left(0\right)\rangle$$

(12)

where, in the following, $\widehat{A}$ and $\widehat{B}$ correspond to either pair or charge fluctuations in Equations (8), (9), and (11).

It is convenient to define the $3\times 3$ matrices

$$\underline{{\chi }_q^0}\left(\omega \right)=\left(\begin{array}{ccc}{\chi }_q^0(\delta {\Delta }_{-q}^{†},\delta {\Delta }_q^{†})& {\chi }_q^0(\delta {\Delta }_{-q}^{†},\delta {\Delta }_{-q})& {\chi }_q^0(\delta {\Delta }_{-q}^{†},\delta {\rho }_{-q})\\ {\chi }_q^0(\delta {\Delta }_q,\delta {\Delta }_q^{†})& {\chi }_q^0(\delta {\Delta }_q,\delta {\Delta }_{-q})& {\chi }_q^0(\delta {\Delta }_q,\delta {\rho }_{-q})\\ {\chi }_q^0(\delta {\rho }_q,\delta {\Delta }_q^{†})& {\chi }_q^0(\delta {\rho }_q,\delta {\Delta }_{-q})& {\chi }_q^0(\delta {\rho }_q,\delta {\rho }_{-q})\end{array}\right)$$

where the superscript ‘0’ indicates that the elements are computed with the bare BCS wave function and are given in Appendix A.

The correlations of the interacting system are then defined by an analogous matrix $\underline{{\chi }_q}\left(\omega \right)$ but without superscript. From Equations (7) and (10), the matrix for the local interaction is given by

$$\underline{V}=\left(\begin{array}{ccc}0& -\left|U\right|& 0\\ -\left|U\right|& 0& 0\\ 0& 0& -\left|U\right|/2\end{array}\right).$$

(13)

The RPA resummation can then be written as

$$\underline{\chi }=\underline{{\chi }^0}+\underline{{\chi }^0}\underline{V}\underline{\chi }$$

which is solved by

$$\underline{\chi }={\left[\underline{1}-\underline{{\chi }^0}\underline{V}\right]}^{-1}\underline{{\chi }^0}.$$

(14)

3.2. Amplitude and Phase Correlations

Introducing amplitude $A_q\equiv (\delta {\Delta }_q+\delta {\Delta }_{-q}^{†})/\sqrt{2}$ and phase operators ${\Phi }_q\equiv (\delta {\Delta }_q-\delta {\Delta }_{-q}^{†})/\sqrt{2}$, the amplitude and phase correlation functions are obtained from

$$\begin{array}{ccc}\hfill {\chi }_q^{AA}& \equiv & {\chi }_q(A_q,A_{-q})={\displaystyle \frac{1}{2}}\left[{\chi }_q(\delta {\Delta }_{-q}^{†},\delta {\Delta }_q^{†})+{\chi }_q(\delta {\Delta }_{-q}^{†},\delta {\Delta }_{-q})\right.\hfill \\ & +& \left.{\chi }_q(\delta {\Delta }_q,\delta {\Delta }_q^{†})+{\chi }_q(\delta {\Delta }_q,\delta {\Delta }_{-q})\right]\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\chi }_q^{\Phi \Phi }& \equiv & {\chi }_q({\Phi }_q,{\Phi }_{-q})={\displaystyle \frac{1}{2}}\left[{\chi }_q(\delta {\Delta }_{-q}^{†},\delta {\Delta }_q^{†})-{\chi }_q(\delta {\Delta }_{-q}^{†},\delta {\Delta }_{-q})\right.\hfill \\ & -& \left.{\chi }_q(\delta {\Delta }_q,\delta {\Delta }_q^{†})+{\chi }_q(\delta {\Delta }_q,\delta {\Delta }_{-q})\right]\hfill \end{array}$$

(16)

and analogously for the mixed correlations between amplitude, phase, and charge.

The susceptibility and interaction matrices can now be transformed into the amplitude-phase representation by introducing the matrix

$$\underline{\gamma }=\left(\begin{array}{ccc}{\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}& 0\\ {\displaystyle \frac{1}{\sqrt{2}}}& -{\displaystyle \frac{1}{\sqrt{2}}}& 0\\ 0& 0& 1\end{array}\right)$$

(17)

so that

$$\begin{array}{ccc}\hfill \underline{\gamma }{\underline{\chi }}_q\underline{\gamma }& =& \left(\begin{array}{ccc}{\chi }_q^{AA}& {\chi }_q^{A\Phi }& {\chi }_q^{A\rho }\\ {\chi }_q^{\Phi A}& {\chi }_q^{\Phi \Phi }& {\chi }_q^{\Phi \rho }\\ {\chi }_q^{\rho A}& {\chi }_q^{\Phi \rho }& {\chi }_q^{\rho \rho }\end{array}\right)\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill \underline{\gamma }\underline{V}\underline{\gamma }& =& \left(\begin{array}{ccc}-\left|U\right|& 0& 0\\ 0& \left|U\right|& 0\\ 0& 0& -\left|U\right|/2\end{array}\right)\hfill \end{array}$$

(19)

and the RPA equation, Equation (14), also holds in the transformed representation. Therefore, the interaction in the amplitude channel is attractive, whereas it is repulsive in the phase channel.

3.3. The ph-Symmetric Case in the Limit q = 0

In the case of particle-hole symmetry and for $q=0$ (where ${\alpha }_k^{\pm }={\alpha }_k$, and ${\beta }_k^{\pm }={\beta }_k$), one finds a decoupling of amplitude from phase and charge fluctuations, i.e.,

$$\begin{array}{ccc}\hfill {\chi }_q^{\left(0\right),A\Phi }\left(\omega \right)& =& -{\displaystyle \frac{1}{2N}}\sum _k{\displaystyle \frac{{\xi }_k}{E_k}}\left[{\displaystyle \frac{1}{\omega -2E_k}}+{\displaystyle \frac{1}{\omega +2E_k}}\right]=0\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\chi }_q^{\left(0\right),A\rho }\left(\omega \right)& =& -{\displaystyle \frac{\Delta }{\sqrt{2}N}}\sum _k{\displaystyle \frac{{\xi }_k}{E_k^2}}\left[{\displaystyle \frac{1}{\omega -2E_k}}-{\displaystyle \frac{1}{\omega +2E_k}}\right]=0.\hfill \end{array}$$

(21)

As a consequence, the amplitude correlations decouple from the phase-charge sector in the RPA equation, Equation (14), and one finds

$${\chi }_{q=0}^{AA}\left(\omega \right)={\displaystyle \frac{{\chi }_{q=0}^{\left(0\right)AA}\left(\omega \right)}{1+\left|U\right|{\chi }_{q=0}^{\left(0\right)AA}\left(\omega \right)}}$$

(22)

and, from Equation (15) together with the bare correlation functions listed in Appendix A, one obtains

$${\chi }_{q=0}^{\left(0\right)AA}\left(\omega \right)={\displaystyle \frac{2}{N}}\sum _k{\displaystyle \frac{{\xi }_k^2}{E_k}}{\displaystyle \frac{1}{{\omega }^2-4E_k^2}}.$$

(23)

Noting that

$${\chi }_{q=0}^{\left(0\right)AA}(\omega =2\Delta )={\displaystyle \frac{2}{N}}\sum _k{\displaystyle \frac{{\xi }_k^2}{E_k}}{\displaystyle \frac{1}{4{\Delta }^2-4E_k^2}}=-{\displaystyle \frac{1}{N}}\sum _k{\displaystyle \frac{1}{2E_k}}$$

(24)

it becomes apparent that the ‘pole’ of Equation (22) is given by

$$1+\left|U\right|{\chi }_{q=0}^{\left(0\right)AA}(\omega =2\Delta )=1-{\displaystyle \frac{\left|U\right|}{N}}\sum _k{\displaystyle \frac{1}{2E_k}}=0$$

(25)

because this is identical to the self-consistency equation, Equation (6).

Therefore, the energy of the amplitude mode at $q=0$ is given by $\omega =2\Delta$ and coincides with the onset of quasiparticle excitations. Thus, it is not a pole but rather a branch cut in the amplitude correlation function.

It should also be noted that a similar result appears in the case of the repulsive Hubbard model where the amplitude excitations of the SDW order parameter appear at the energy of the SDW gap, as has been shown in Ref. [30].

Figure 2 visualizes the condition to find the Higgs pole in Equation (22) for a two-dimensional system. As a function of $\omega$, the (negative) bare amplitude correlation function Equation (24) is a continuously decreasing function, which, at $\omega =2\Delta$, reaches the value ${\chi }_{q=0}^{\left(0\right)AA}(\omega =2\Delta )=-1/\left|U\right|$, which leads to the Higgs pole at exactly $\omega =2\Delta$. This can change if we hypothesize an interaction between quasiparticles V different from the static interaction U that appears in the BCS equation. In case V would be more negative than U (blue dashed line in Figure 2), the pole of Equation (22) would occur at $\omega <2\Delta$ and, therefore, would correspond to a bound state inside the spectral gap. We will show, in the following section, that this is exactly the situation that is realized within the TDGA because, in this variational scheme, the denominator of Equation (22) is not related to the self-consistency condition for the spectral gap when $\omega =2\Delta$. This can be understood as vertex corrections in the effective interaction between quasiparticles in the same spirit as Ref. [31].

4. TDGA

The TDGA ground state is obtained by optimizing the number of doubly occupied sites in the underlying BCS state $|BCS\rangle$ by applying the ‘Gutzwiller projector’ ${\widehat{P}}_G$, i.e.,

$$|{\Psi }_G\rangle ={\widehat{P}}_G|BCS\rangle .$$

The variational energy $E^{GA}(D,J^{-})=\langle {\Psi }_G|\widehat{H}|{\Psi }_G\rangle /\langle {\Psi }_G|{\Psi }_G\rangle$ depends on the double occupancy D and the anomalous correlations $J^{-}\equiv \langle c_{i\downarrow }{c}_{i\uparrow }\rangle$, cf., e.g., [32]. A first step in the application of the TDGA is the evaluation of the so-called Gutzwiller Hamiltonian, defined as the derivative of $E^{GA}(D,J^{-})$ with respect to the density matrix [21,22]. One obtains (for the homogeneous system, N lattice sites) [32]

$$\begin{array}{ccc}\hfill H^{GA}& =& \sum _k{E}_k\left[{\gamma }_{k,0}^{†}{\gamma }_{k,0}+{\gamma }_{k,1}^{†}{\gamma }_{k,1}\right]+\sum _k({\xi }_k-E_k)-2N\Delta J^{-}-N\left|U\right|D.\hfill \end{array}$$

where, now, the quasiparticle energy in ${\xi }_k=z^2{\epsilon }_k-\mu$ is renormalized by

$$z={\displaystyle \frac{\sqrt{\frac{1}{2}-D+J^z}\left(\sqrt{D-J^z-J^{-}}+\sqrt{D-J^z+J^{-}}\right)}{\sqrt{\frac{1}{4}-{\left(J^{-}\right)}^2}}}.$$

(26)

and $J^z$ is related to the density n via $J^z=1/2(n-1)$. In contrast to weak-coupling BCS theory, where the spectral gap parameter is given by $\Delta =-\left|U\right|J^{-}$, in the TDGA, this quantity is obtained from the variational principle as

$$\Delta ={\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathsf{\partial }{z}^2}{\mathsf{\partial }\langle J^{-}\rangle }}{\displaystyle \frac{1}{N}}\sum _k{\epsilon }_k\left[1-{\displaystyle \frac{{\xi }_k}{E_k}}\right].$$

(27)

On the other hand, the equation for the anomalous correlations still resembles the corresponding BCS result and reads

$$\langle J^{-}\rangle =-{\displaystyle \frac{1}{N}}\sum _k{\displaystyle \frac{|\Delta |}{2E_k}}.$$

(28)

4.1. Ground State for the Half-Filled Case

Similar to the BCS case, we focus in the following on the half-filled system where analytical results can be obtained in the weak-coupling limit. The renormalization factor simplifies to

$$z^2={\displaystyle \frac{1-2D}{\frac{1}{4}-{\left(J^{-}\right)}^2}}\left[D+\sqrt{D^2-{\left(J^{-}\right)}^2}\right]$$

(29)

and expanding Equation (29) for small $J^{-}$ (weak coupling) yields

$$z^2=8D(1-2D)+32D(1-2D)(1-{\displaystyle \frac{1}{16D^2}}){\left(J^{-}\right)}^2.$$

(30)

Furthermore, for the half-filled system, we can write $D=1/4+d$ and obtain in the lowest order in $J^{-}$,

$$z^2=1-16d^2+32d{\left(J^{-}\right)}^2.$$

(31)

We proceed by evaluating Equations (27) and (28) for a constant DOS, $\rho \left(\omega \right)=1/\left(2B\right)$ for $-B\le \omega \le B$. For Equation (28), we obtain

$$\begin{array}{ccc}\hfill \Delta & =& -32d{J}^{-}{\displaystyle \frac{1}{2B}}{\int }_{-B}^{B}d\omega {\displaystyle \frac{{\omega }^2}{\sqrt{{\omega }^2+{\Delta }^2}}}\hfill \\ & =& -32d{J}^{-}{\displaystyle \frac{1}{2B}}\left[B\sqrt{B^2+{\Delta }^2}-{\displaystyle \frac{{\Delta }^2}{2}}ln{\displaystyle \frac{\sqrt{1+{\Delta }^2/B^2}+1}{\sqrt{1+{\Delta }^2/B^2}-1}}\right]\hfill \\ & \approx & -16d{J}^{-}\left[B-{\displaystyle \frac{{\Delta }^2}{B}}ln{\displaystyle \frac{2B}{\Delta }}\right]\approx -16Bd{J}^{-},\hfill \end{array}$$

(32)

and, in the last line, we used the limit of weak coupling.

In the same limit, the anomalous correlations Equation (27) are obtained as

$$\begin{array}{ccc}\hfill \langle J^{-}\rangle & =& -{\displaystyle \frac{\Delta }{4B}}{\int }_B^B{\displaystyle \frac{d\omega }{\sqrt{{\omega }^2+{\Delta }^2}}}\hfill \\ & =& -{\displaystyle \frac{\Delta }{4B}}ln{\displaystyle \frac{\sqrt{1+{\Delta }^2/B^2}+1}{\sqrt{1+{\Delta }^2/B^2}-1}}\hfill \\ & \approx & -{\displaystyle \frac{\Delta }{2B}}ln{\displaystyle \frac{2B}{\Delta }}.\hfill \end{array}$$

(33)

Inserting Equation (33) into Equation (32) finally yields

$$\begin{array}{ccc}\hfill \Delta & =& 2B{e}^{-{\displaystyle \frac{1}{8d}}}\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill J^{-}& =& -{\displaystyle \frac{1}{8d}}{e}^{-{\displaystyle \frac{1}{8d}}},\hfill \end{array}$$

(35)

where it should be noted that $B=B_0{z}^2$, with $B_0$ being the bare bandwidth. The dependence of $\Delta$ and $J^{-}$ on U is encoded in the dependence on d with $\Delta \to 0$, $J^{-}\to 0$ when $d\to 0$.

We are now in the position to evaluate the total Gutzwiller approximated energy

$$\begin{array}{ccc}\hfill {\displaystyle \frac{E^{GA}}{N}}& =& -{\displaystyle \frac{1}{2B}}{\int }_{-B}^{B}d\omega \sqrt{{\omega }^2+{\Delta }^2}-2\Delta J^{-}+UD\hfill \\ & =& -{\displaystyle \frac{1}{4B}}\left[2B\sqrt{B^2+{\Delta }^2}+{\Delta }^{2}ln{\displaystyle \frac{\sqrt{B^2+{\Delta }^2}+B}{\sqrt{B^2+{\Delta }^2}-B}}\right]-2\Delta J^{-}+UD\hfill \\ & \approx & -B/2-2\Delta J^{-}+UD\hfill \\ & \approx & -{\displaystyle \frac{B_0}{2}}\left(1-16d^2+32d{\left(J^{-}\right)}^2\right)+{\displaystyle \frac{B_0}{2d}}\left(1-16d^2+32d{\left(J^{-}\right)}^2\right)e^{-{\displaystyle \frac{1}{4d}}}-\left|U\right|\left({\displaystyle \frac{1}{4}}+d\right)\hfill \\ & =& -{\displaystyle \frac{B_0}{2}}\left(1-16d^2+{\displaystyle \frac{1}{2d}}{e}^{-{\displaystyle \frac{1}{4d}}}\right)+{\displaystyle \frac{B_0}{2d}}\left(1-16d^2+{\displaystyle \frac{1}{2d}}{e}^{-{\displaystyle \frac{1}{4d}}}\right)e^{-{\displaystyle \frac{1}{4d}}}-\left|U\right|\left({\displaystyle \frac{1}{4}}+d\right)\hfill \end{array}$$

and the minimization $\mathsf{\partial }{E}^{GA}/\mathsf{\partial }d=0$ leads to the equation

$$\begin{array}{ccc}& & \underset{1}{\underbrace{16d}}\underset{2}{\underbrace{-16e^{-{\displaystyle \frac{1}{4d}}}}}+\underset{3}{\underbrace{{\displaystyle \frac{1}{4d^2}}\left[{\displaystyle \frac{1}{4d}}-1\right]\left[{\displaystyle \frac{1}{d}}{e}^{-{\displaystyle \frac{1}{4d}}}-1\right]e^{-{\displaystyle \frac{1}{4d}}}}}\hfill \\ & +& \underset{4}{\underbrace{{\displaystyle \frac{1}{2d^2}}\left[{\displaystyle \frac{1}{4d}}-1\right]\left[1-16d^2+{\displaystyle \frac{1}{2d}}{e}^{-{\displaystyle \frac{1}{4d}}}\right]e^{-{\displaystyle \frac{1}{4d}}}}}={\displaystyle \frac{\left|U\right|}{B_0}}.\hfill \end{array}$$

(36)

Contribution ‘1’ determines the double occupancy in the absence of SC, i.e., $d_0={\displaystyle \frac{\left|U\right|}{16B_0}}$.

On the other hand, it can be seen from Figure 3 that, for small d, the contributions ‘2–4’ in Equation (36) are exponentially small; so, by setting $d=d_0+ϵ$, the leading correction for small $U/B_0$ is given by

$$ϵ\approx -{\displaystyle \frac{1}{128}}{\displaystyle \frac{e^{-\frac{1}{2d_0}}}{d_0^4}}=-512{\left({\displaystyle \frac{B_0}{\left|U\right|}}\right)}^4{e}^{-{\displaystyle \frac{8B_0}{\left|U\right|}}},$$

(37)

i.e., the double occupancy decreases with the onset of the SC order.

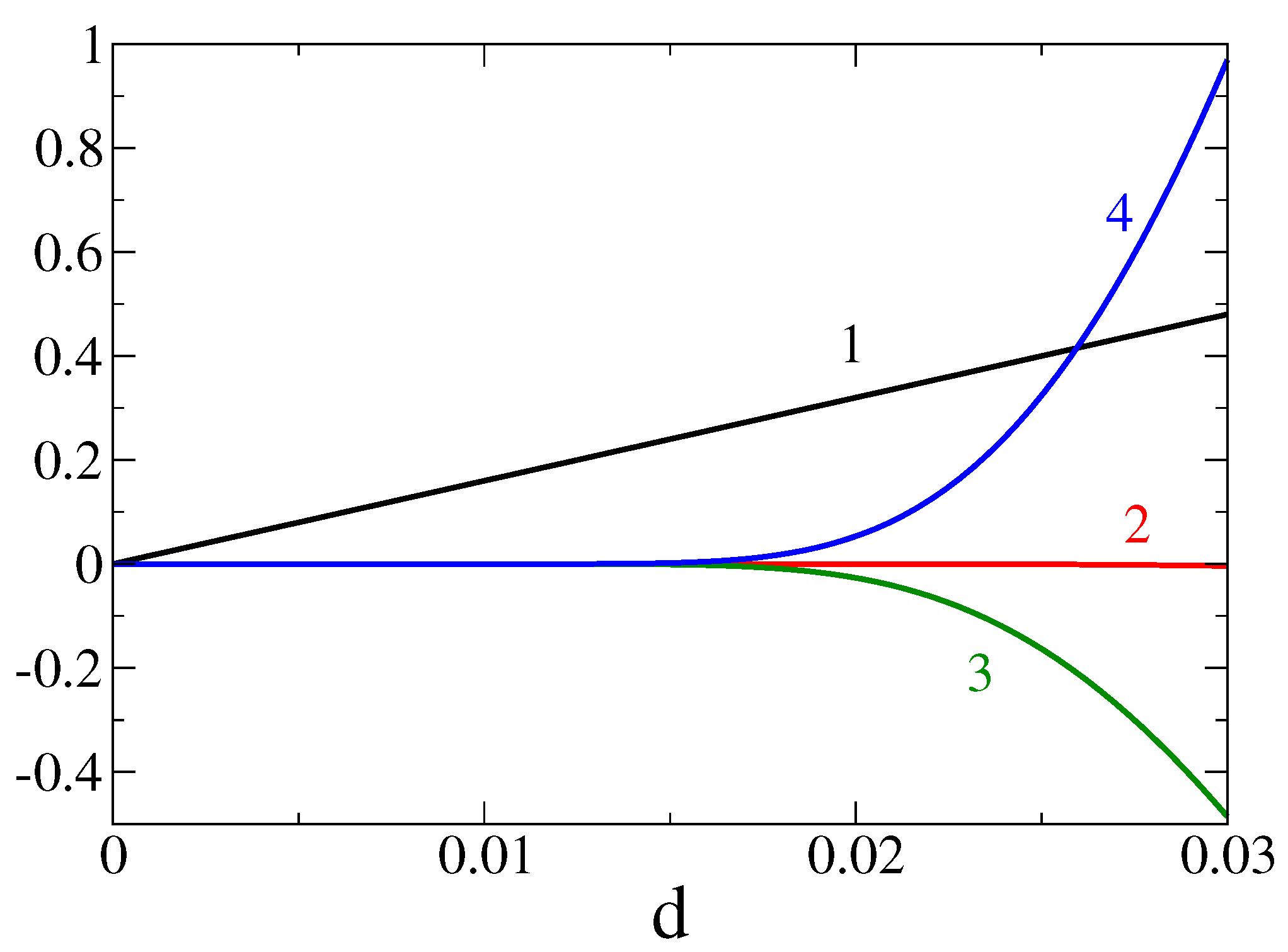
4.2. TDGA for the SC Half-Filled Case

Within the TDGA and employing the weak-coupling limit, the effective interaction in the amplitude channel can be evaluated by expanding the renormalized kinetic energy (per site)

$$e_k=-{\displaystyle \frac{B}{2}}=-{\displaystyle \frac{1}{2}}{B}_0{z}^2=-{\displaystyle \frac{1}{2}}{B}_0\left[1-16d^2+32d{\left(J^{-}\right)}^2\right]$$

(38)

in terms of the fluctuations $\delta d$ and $\delta J^{-}$.

One obtains

$$H^{int}={\displaystyle \frac{1}{2}}\left(\begin{array}{c}\delta d\\ \delta J^{-}\end{array}\right)\left(\begin{array}{cc}16B_0& -32B_0{J}^{-}\\ -32B_0{J}^{-}& -32d{B}_0\end{array}\right)\left(\begin{array}{c}\delta d\\ \delta J^{-}\end{array}\right).$$

(39)

In the spirit of the anti-adiabaticity principle [21], we eliminate the high-energy double occupancy fluctuations from Equation (39) using the condition $\mathsf{\partial }{H}^{int}/\mathsf{\partial }\delta d=0$, which yields $\delta d=2J^{-}\delta J^{-}$. The resulting interaction in the amplitude channel alone (it should be noted that $\delta J^{-}=\sqrt{2}\delta A_{q=0}$, cf. Section 3.2) is given by $H_{int}^{AA}=1/2V_{eff}\delta A_{q=0}\delta A_{q=0}$ with

$$V^{eff}=-16B_0\left[d+2{\left(J^{-}\right)}^2\right]$$

(40)

or, when we use $d=d_0+\epsilon$,

$$V^{eff}=-\left|U\right|-16B_0\left[\epsilon +2{\left(J^{-}\right)}^2\right].$$

(41)

From Equations (35) and (37), it turns out that, in the considered limit (half-filling, weak coupling), the TDGA provides an exponentially small correction to the bare interaction $-\left|U\right|$.

We proceed by investigating the consequences for the resulting Higgs mode within the TDGA. Similar to the BCS + RPA case, the amplitude mode occurs as a pole in Equation (22), $1+|V_0^{eff}|{\chi }_{q=0}^{\left(0\right)AA}\left(\omega \right)=0$ with

$${\chi }_{q=0}^{\left(0\right)AA}\left(\omega \right)={\displaystyle \frac{2}{N}}\sum _k{\displaystyle \frac{{\xi }_k^2}{E_k}}{\displaystyle \frac{1}{{\omega }^2-4E_k^2}}.$$

(42)

where, now, ${\xi }_k$ contains the renormalization of ${\epsilon }_k$ by the GA factors $z^2$.

The comparison of Equation (25) and Equation (27) reveals that the Higgs mode would occur at $\omega =2\Delta$ when the effective interaction would be given by ${\tilde{V}}_{eff}=\Delta /\langle J^{-}\rangle$. From Equation (32), one finds

$${\displaystyle \frac{\Delta }{\langle J^{-}\rangle }}=-16B_{0}d{z}^2=-16B_{0}d\left[1-16d^2+32d{\left(J^{-}\right)}^2\right]$$

(43)

or, when we make use of $d=d_0+\epsilon$,

$${\displaystyle \frac{\Delta }{\langle J^{-}\rangle }}=-\left|U\right|+16d\left|U\right|\left[d-2{\left(J^{-}\right)}^2\right]-16B_0\epsilon \left[1-16d^2+32d{\left(J^{-}\right)}^2\right].$$

(44)

Thus,

$$V^{eff}-{\displaystyle \frac{\Delta }{\langle J^{-}\rangle }}=-32B_0{\left(J^{-}\right)}^2\left[1-16d^2\right]-256B_0{d}^3\approx -256B_0{d}_0^3=-{\displaystyle \frac{1}{16}}{B}_0{\left({\displaystyle \frac{\left|U\right|}{B_0}}\right)}^3<0.$$

(45)

i.e., $V^{eff}$ is more negative than $\Delta /J^{-}$ in the small coupling limit so that, according to the analysis related to Figure 2, one obtains the pole for the Higgs mode below the spectral gap $2\Delta$.

Expanding the amplitude correlation function Equation (42) around the spectral gap

$${\chi }_{q=0}^{\left(0\right)AA}(\omega =2\Delta -\nu )\approx {\chi }_{q=0}^{\left(0\right)AA}(\omega =2\Delta )+{\displaystyle \frac{\pi }{4B_0}}\sqrt{{\displaystyle \frac{\nu }{\Delta }}}$$

(46)

yields the pole from the resonance condition $1+|V^{eff}|{\chi }_{q=0}^{\left(0\right)AA}(\omega =2\Delta -\nu )=0$ at

$$\nu =2\Delta -{\omega }_H\sim \Delta {\displaystyle \frac{\left|U\right|}{B_0}}\sim \left|U\right|exp\left(-{\displaystyle \frac{2B_0}{\left|U\right|}}\right)$$

(47)

i.e., the shift of the Higgs mode inside the spectral gap is exponentially small in weak coupling.

5. Conclusions

We have shown that the TDGA applied to the weak-coupling limit of the attractive Hubbard model leads to amplitude (‘Higgs’) modes which are split off from the quasiparticle continuum at $2\Delta$ but the corresponding binding energy is exponentially small in the attractive interaction. This is different from the BCS + RPA approach, where the ‘Higgs’ excitation always appears at $2\Delta$ and, therefore, is damped due to the interference with quasiparticle excitations. The analysis in the present paper is based on a constant DOS, which allowed for an analytical treatment of the problem in the weak-coupling limit. Using a numerical evaluation, we have already shown [19] that the DOS has some influence on the position of the Higgs mode and it would definitely be interesting to examine this dependency in more detail, and, eventually, also analytically, in future work. When the interaction becomes comparable with the bandwidth, the Higgs binding energy becomes sizeable [19] and, thus, long-lived amplitude modes could be observed in the crossover regime from BCS to BEC. In fact, recent investigations on cold atomic fermion condensates [20] confirm this picture, although, in this experiment, the modulation of the confinement also seems to play a role. Our theory also goes beyond the applicability to superconductors and should also have relevance in magnetic systems where the collective modes comprise the amplitude excitation of the magnetic order. In fact, in Ref. [19], we have proposed an experimental setup where the predicted bound state of the antiferromagnetic amplitude mode in undoped cuprates may be observed via magneto-optical methods. Of course, the main difference between superconducting and magnetic systems is the absence of low-lying excitations in the former due to the Anderson–Higgs mechanism, which pushes the Bogoljubov–Goldstone mode to the plasma energy. On the other hand, in a magnetic system, the decay channel of the amplitude mode into low-lying magnon excitations persists. In this regard, it is interesting that strong correlations can also stabilize quantum matter [33] so that the proposed split-off magnetic amplitude modes may have a lifetime long enough to be detected via a frequency-dependent Faraday rotated optical signal [19].