Josephson Critical Currents and Related Effects in Ultracold Atomic Superfluid Sytems
Abstract
1. Introduction
2. Theoretical Approach
2.1. The NLPDA Approach
2.2. The LPDA Approach
2.3. The mLPDA Approach
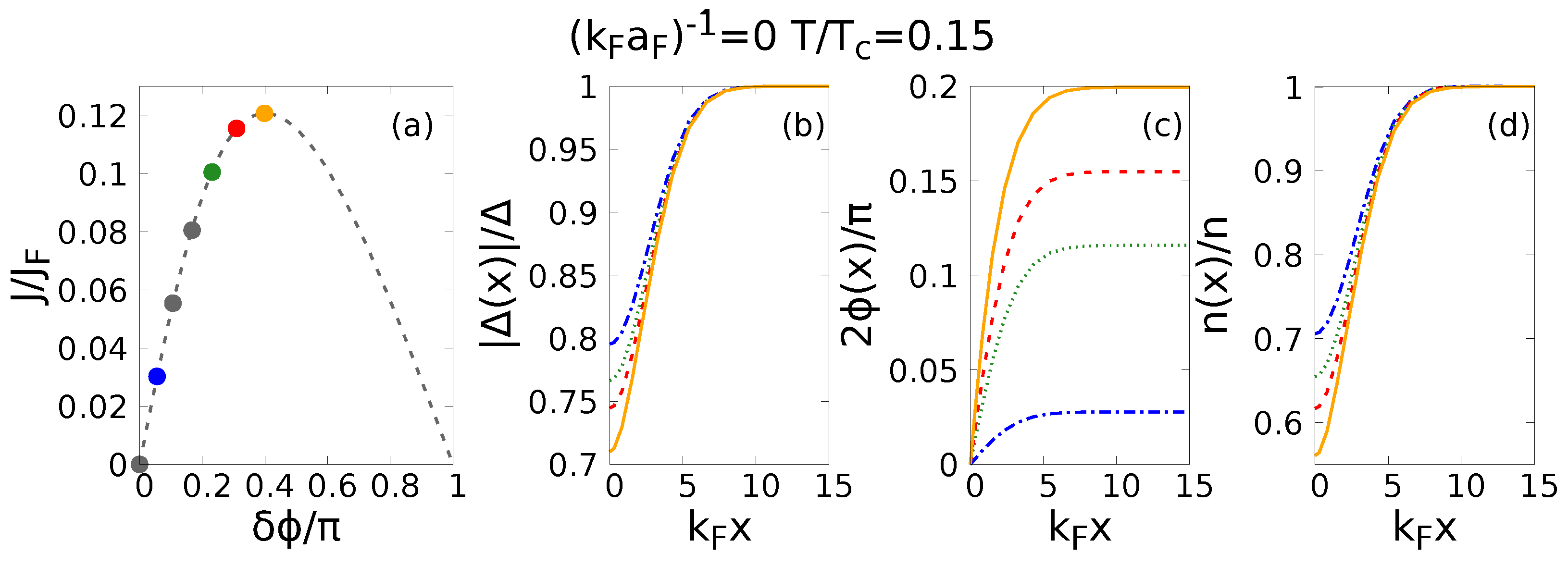
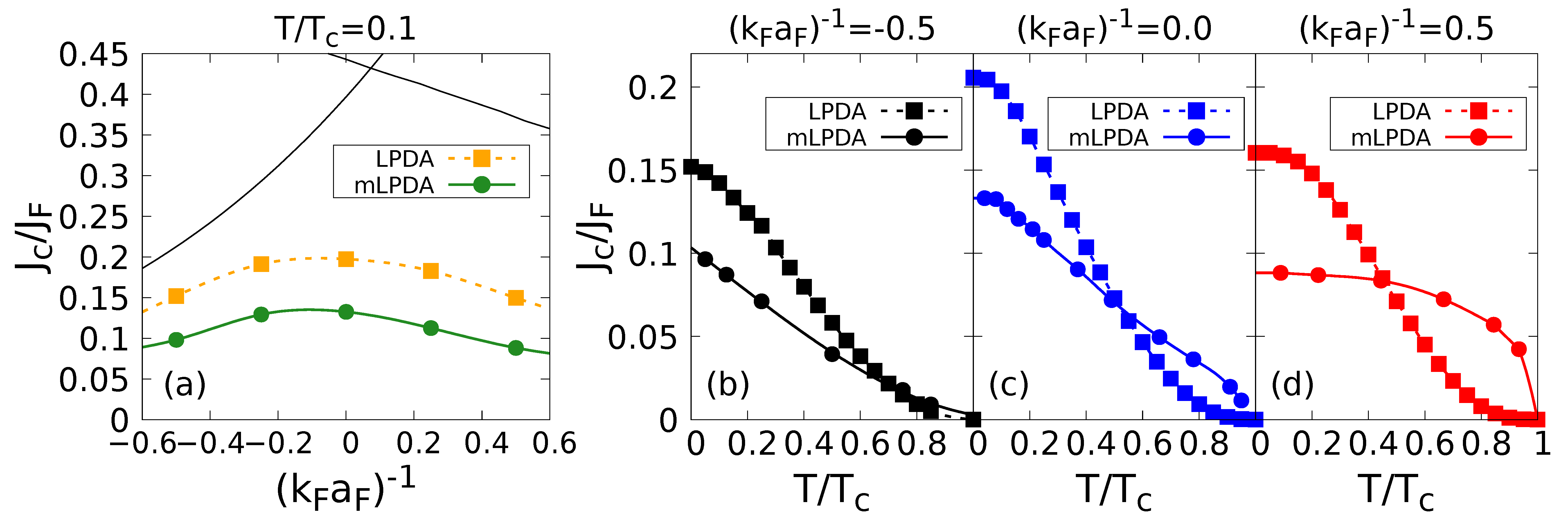
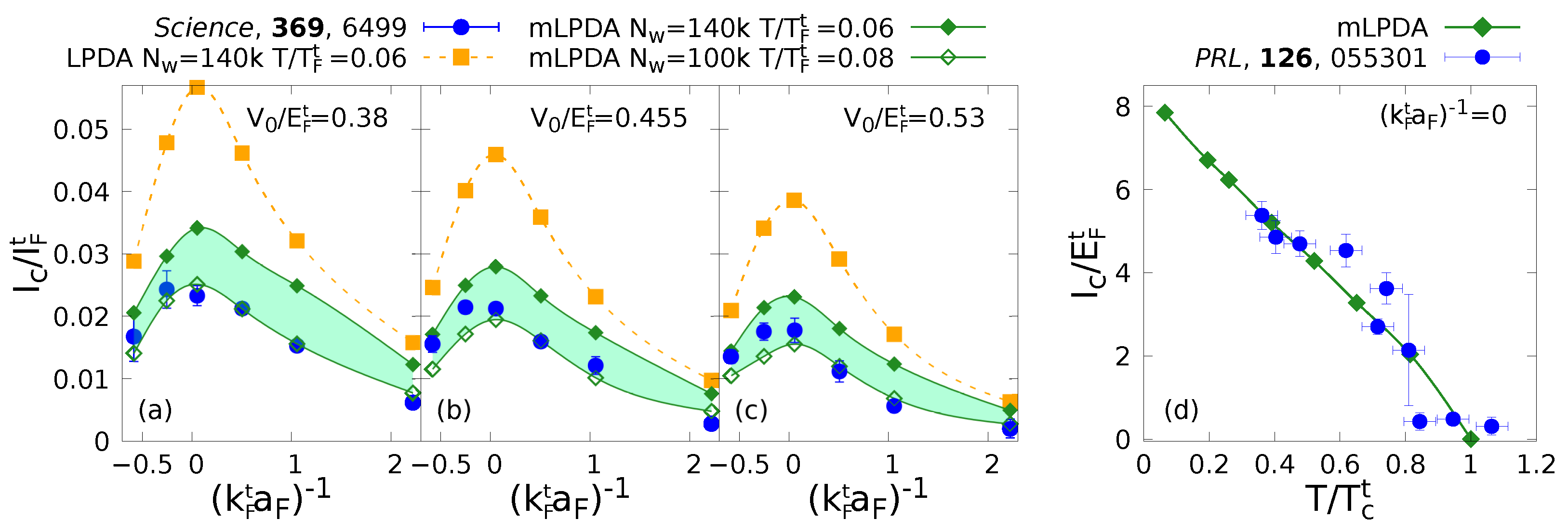
3. Results
3.1. Case of Study: Homogeneous Superfluid
3.2. Case of Study: Trapped Ultracold Atoms
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BCS | Bardeen–Cooper–Schrieffer |
| BdG | Bogoliubov–de Gennes |
| BEC | Bose–Einstein condensation |
| LPDA | Local Phase Density Approximation |
| mLPDA | Local Phase Density Approximation |
| NLPDA | Non-local Phase Density Approximation |
References
- de Gennes, P.G. Superconductivity of Metals and Alloys; Benjamin: Amsterdam, The Netherlands, 1966. [Google Scholar]
- Gor’kov, L.P. Microscopic derivation of the Ginzburg-Landau equations in the theory of Superconductivity. Sov. Phys. JETP 1959, 36, 1364. [Google Scholar]
- Gor’kov, L.P. On the energy spectrum of superconductors. J. Exp. Theor. Phys. (USSR) 1958, 34, 735–739. [Google Scholar]
- Usadel, K.D. Generalized Diffusion Equation for Superconducting Alloys. Phys. Rev. Lett. 1970, 25, 507–509. [Google Scholar] [CrossRef]
- Rammer, J. Quantum Field Theory of Non-Equilibrium States; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Eilenberger, G. Transformation of Gorkov’s equation for type II superconductors into transport-like equations. Z. Physik Hadron. Nucl. 1968, 214, 195. [Google Scholar] [CrossRef]
- Simonucci, S.; Strinati, G.C. Equation for the superfluid gap obtained by coarse graining the Bogoliubov–de Gennes equations throughout the BCS-BEC crossover. Phys. Rev. B 2014, 89, 054511. [Google Scholar] [CrossRef]
- Pieri, P.; Strinati, G.C. Derivation of the Gross-Pitaevskii Equation for Condensed Bosons from the Bogoliubov–de Gennes Equations for Superfluid Fermions. Phys. Rev. Lett. 2003, 91, 030401. [Google Scholar] [CrossRef]
- Piselli, V.; Simonucci, S.; Strinati, G.C. Optimizing the proximity effect along the BCS side of the BCS-BEC crossover. Phys. Rev. B 2018, 98, 144508. [Google Scholar] [CrossRef]
- Simonucci, S.; Strinati, G.C. Nonlocal equation for the superconducting gap parameter. Phys. Rev. B 2017, 96, 054502. [Google Scholar] [CrossRef]
- Taruishi, K.; Schuck, P. Wigner Kirkwood ℏ-expansion of the density matrix in inhomogeneous superfluid Fermi systems. Z. Phys. Hadron. Nucl. 1992, 342, 397–401. [Google Scholar] [CrossRef]
- Schuck, P.; Urban, M.; Viñas, X. Corrections to local-density approximation for superfluid trapped fermionic atoms from the Wigner-Kirkwood ℏ expansion. Eur. Phys. J. A 2023, 59, 164. [Google Scholar] [CrossRef]
- Pei, J.C.; Fei, N.; Zhang, Y.N.; Schuck, P. Generalized second-order Thomas-Fermi method for superfluid Fermi systems. Phys. Rev. C 2015, 92, 064316. [Google Scholar] [CrossRef]
- Fetter, A.L.; Walecka, D.J. Quantum Theory of Many-Particle Systems; Dover Publications: Mineola, NY, USA, 2014. [Google Scholar]
- Pethick, C.J.; Smith, H. Bose-Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Pisani, L.; Piselli, V.; Strinati, G.C. Inclusion of pairing fluctuations in the differential equation for the gap parameter for superfluid fermions in the presence of nontrivial spatial constraints. Phys. Rev. B 2023, 108, 214503. [Google Scholar] [CrossRef]
- Pieri, P.; Pisani, L.; Strinati, G.C. BCS-BEC crossover at finite temperature in the broken-symmetry phase. Phys. Rev. B 2004, 70, 094508. [Google Scholar] [CrossRef]
- Perali, A.; Pieri, P.; Pisani, L.; Strinati, G.C. BCS-BEC Crossover at Finite Temperature for Superfluid Trapped Fermi Atoms. Phys. Rev. Lett. 2004, 92, 220404. [Google Scholar] [CrossRef]
- Piselli, V.; Pisani, L.; Strinati, G.C. Josephson current flowing through a nontrivial geometry: Role of pairing fluctuations across the BCS-BEC crossover. Phys. Rev. B 2023, 108, 214504. [Google Scholar] [CrossRef]
- Kwon, W.J.; Pace, G.D.; Panza, R.; Inguscio, M.; Zwerger, W.; Zaccanti, M.; Scazza, F.; Roati, G. Strongly correlated superfluid order parameters from dc Josephson supercurrents. Science 2020, 369, 84–88. [Google Scholar] [CrossRef]
- Del Pace, G.; Kwon, W.J.; Zaccanti, M.; Roati, G.; Scazza, F. Tunneling Transport of Unitary Fermions across the Superfluid Transition. Phys. Rev. Lett. 2021, 126, 055301. [Google Scholar] [CrossRef]
- Maggio-Aprile, I.; Renner, C.; Erb, A.; Walker, E.; Fischer, Ø. Critical currents approaching the depairing limit at a twin boundary in YBa2Cu3O7-δ. Nature 1997, 390, 487–490. [Google Scholar] [CrossRef]
- Kunchur, M.N. Current-induced pair breaking in magnesium diboride. J. Phys. Condens. Matter 2004, 16, R1183. [Google Scholar] [CrossRef]
- Bergeal, N.; Lesueur, J.; Aprili, M.; Faini, G.; Contour, J.P.; Leridon, B. Pairing fluctuations in the pseudogap state of copper-oxide superconductors probed by the Josephson effect. Nat. Phys. 2008, 4, 608–611. [Google Scholar] [CrossRef]
- Bozovic, I.; Logvenov, G.; Verhoeven, M.A.J.; Caputo, P.; Goldobin, E.; Beasley, M.R. Giant Proximity Effect in Cuprate Superconductors. Phys. Rev. Lett. 2004, 93, 157002. [Google Scholar] [CrossRef] [PubMed]
- Kirzhner, T.; Koren, G. Pairing and the phase diagram of the normal coherence length ξN(T, x) above Tc of La2−xSrxCuO4 thin films probed by the Josephson effect. Sci. Rep. 2014, 4, 6244. [Google Scholar] [CrossRef] [PubMed]
- Deutscher, G.; de Gennes, P. Superconductivity; Parks, R.D., Ed.; Dekker: New York, NY, USA, 1969; Volume 2, Chapter 17. [Google Scholar]
- Polturak, E.; Koren, G.; Coher, D.; Aharoni, E.; Deutscher, G. Proximity Effect in YBa2Cu3O7/Y0.6Pr0.4Ba2Cu3O7/YBa2Cu3O7 Junctions. Phys. Rev. Lett. 1991, 67, 3038. [Google Scholar] [CrossRef] [PubMed]
- Golubov, A.A.; Kupriyanov, M.Y.; Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411–469. [Google Scholar] [CrossRef]
- Piselli, V.; Simonucci, S.; Strinati, G.C. Josephson effect at finite temperature along the BCS-BEC crossover. Phys. Rev. B 2020, 102, 144517. [Google Scholar] [CrossRef]
- Kogan, V.G. Coherence length of a normal metal in a proximity system. Phys. Rev. B 1982, 26, 88–98. [Google Scholar] [CrossRef]
- Fink, H.J. Supercurrents through superconducting-normal-superconducting proximity layers. I. Analytic solution. Phys. Rev. B 1976, 14, 1028–1038. [Google Scholar] [CrossRef]
- Fink, H.J.; Poulsen, R.S. Supercurrents through proximity layers. II. Numerical solution of superconducting-normal-superconducting and superconducting-superconducting-superconducting weak links. Phys. Rev. B 1979, 19, 5716–5724. [Google Scholar] [CrossRef]
- Fink, H.J. Supercurrents through SNS proximity-induced junctions. Phys. Rev. B 1997, 56, 2732–2737. [Google Scholar] [CrossRef]
- Spuntarelli, A.; Pieri, P.; Strinati, G.C. Solution of the Bogoliubov–de Gennes equations at zero temperature throughout the BCS–BEC crossover: Josephson and related effects. Phys. Rep. 2010, 488, 111–167. [Google Scholar] [CrossRef]
- Likharev, K.K. Superconducting weak links. Rev. Mod. Phys. 1979, 51, 101–159. [Google Scholar] [CrossRef]
- Courtois, H.; Gandit, P.; Pannetier, B. Proximity-induced superconductivity in a narrow metallic wire. Phys. Rev. B 1995, 52, 1162–1166. [Google Scholar] [CrossRef] [PubMed]
- Missert, N.; Vale, L.; Ono, R.; Reintsema, C.; Rudman, D.; Thomson, R.; Berkowitz, S. Temperature dependence and magnetic field modulation of critical currents in step-edge SNS YBCO/Au junctions. IEEE Trans. Appl. Superconduct. 1995, 5, 2969–2972. [Google Scholar] [CrossRef]
- Josephson, B. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Varoquaux, E. Anderson’s considerations on the flow of superfluid helium: Some offshoots. Rev. Mod. Phys. 2015, 87, 803–854. [Google Scholar] [CrossRef]
- Sidorenkov, L.A.; Tey, M.K.; Grimm, R.; Hou, Y.H.; Pitaevskii, L.; Stringari, S. Second sound and the superfluid fraction in a Fermi gas with resonant interactions. Nature 2013, 498, 78–81. [Google Scholar] [CrossRef]
- Kuhn, C.C.N.; Hoinka, S.; Herrera, I.; Dyke, P.; Kinnunen, J.J.; Bruun, G.M.; Vale, C.J. High-Frequency Sound in a Unitary Fermi Gas. Phys. Rev. Lett. 2020, 124, 150401. [Google Scholar] [CrossRef]
- Pini, M.; Pieri, P.; Strinati, G.C. Fermi gas throughout the BCS-BEC crossover: Comparative study of t-matrix approaches with various degrees of self-consistency. Phys. Rev. B 2019, 99, 094502. [Google Scholar] [CrossRef]
- Pisani, L.; Piselli, V.; Strinati, G.C. Critical current throughout the BCS-BEC crossover with the inclusion of pairing fluctuations. Phys. Rev. A 2024, 109, 033306. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piselli, V.; Pisani, L.; Strinati, G.C. Josephson Critical Currents and Related Effects in Ultracold Atomic Superfluid Sytems. Condens. Matter 2024, 9, 41. https://doi.org/10.3390/condmat9040041
Piselli V, Pisani L, Strinati GC. Josephson Critical Currents and Related Effects in Ultracold Atomic Superfluid Sytems. Condensed Matter. 2024; 9(4):41. https://doi.org/10.3390/condmat9040041
Chicago/Turabian StylePiselli, Verdiana, Leonardo Pisani, and Giancarlo Calvanese Strinati. 2024. "Josephson Critical Currents and Related Effects in Ultracold Atomic Superfluid Sytems" Condensed Matter 9, no. 4: 41. https://doi.org/10.3390/condmat9040041
APA StylePiselli, V., Pisani, L., & Strinati, G. C. (2024). Josephson Critical Currents and Related Effects in Ultracold Atomic Superfluid Sytems. Condensed Matter, 9(4), 41. https://doi.org/10.3390/condmat9040041







