Abstract
The pursuit of enhanced superconducting device performance has historically focused on minimizing disorder in materials. Recent research, however, challenges this conventional wisdom by exploring the unique characteristics of disordered materials. Following the studies, disorder is currently viewed as a design parameter that can be tuned. This shift in the paradigm has sparked an upsurge in research efforts, which demonstrates that disorder can significantly augment the superconductivity figures of merit. While almost all previous studies attended to the effects related to disorder strength, this article focuses on the impact of short-range disorder correlations that in real materials takes place, for example, due to lattice defects. The study shows that the degree of such correlations can strongly influence the superconducting characteristics.
1. Introduction
Minimizing disorder (static random potential of structural defects, impurities, etc.) in superconducting devices has traditionally been a focal point for enhancing their performance. Nevertheless, recent investigations conducted by multiple research groups [1,2,3] challenge the conventional wisdom, highlighting that the crystalline purity of materials is not the sole determinant for improving superconducting characteristics [4,5,6,7]. Novel strategies to enhance superconductivity now explore the unique characteristics of disordered materials as opposed to the complete elimination of disorder [8,9,10,11]. For instance, the presence of trap states in disordered systems may offer an effective means of enhancing the local order parameter by manipulating the matrix coupling elements, facilitating the concentration of Cooper pairs [12] as in the case of low-dimensional superconducting granular systems [13]. Disorder may also serve as a design parameter to control the local density of states in the vicinity of the Fermi level of superconducting materials [14,15,16]. This duality of the disorder impact has instigated further research to unravel its effects on superconducting characteristics, promising the development of a novel class of materials with highly sought-after attributes. In particular, manipulating the structural disorder can be employed as a controllable tool for tailoring the desired properties of superconducting materials [12,17,18,19,20].
This has led to the recent upsurge in scientific interest for studying the interplay between disorder and superconductivity in both the theoretical and experimental domains [21,22,23,24,25,26,27,28,29]. Prior research predominantly concentrated on investigating the impact of disorder strength to enhance the superconducting characteristics of materials. Consequently, we now acknowledge that disorder can significantly augment various superconductivity figures of merit. In particular, recent investigations demonstrated that remarkable enhancements in the superconducting properties of quasi-one-dimensional single crystals composed of weakly bonded MoSe chains and Na atoms are attributed to disorder [30]. Similarly, strong structural disorder leads to anomalously large improvements in superconductivity in TaS monolayers [31]. Disorder-related effects are believed to contribute to the substantial increase in the critical temperature in recently discovered NbSe superconducting monolayers [19]. Theoretical modeling by numerically solving microscopic theory equations in low-dimensional samples attributes this enhancement to the disorder-induced multi-fractal structure of electronic wave functions [2,3,12,32].
However, certain theoretical aspects of the disorder-related phenomena still remain unexplored. An important question that has received inadequate attention thus far pertains to a possible existence of disorder with spatial correlations (correlations in the positions of the imperfections). The prevailing theory of disordered superconductors heavily relies on spatially uncorrelated disorder, despite the fact that completely random disorder is rare in nature. In most materials, inhomogeneities reveal a certain spatially correlated structure. There is growing appreciation that such correlations can exert a profound influence on the fundamental properties of various disordered systems [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. This problem is of relevance for understanding that the Anderson localization phenomenon in Bose–Einstein condensates, which determines their transport properties, is due to the presence of disorder [60,61,62,63,64].
Recently, the role of the long-range power law disorder correlations for zero-temperature superconducting characteristics was investigated [11]. The calculations have demonstrated that such correlations can alter the statistical properties of the Cooper pair correlations and the superconducting order parameter—the superconducting correlations are enhanced when the degree of the disorder correlations increases. In addition, researchers from the group led by A. Bianconi identified that within the superconductor lanthanum copper oxide, the arrangement of oxygen ions in the interstitial layers adjacent to the copper oxide adheres to a power law distribution. According to them, this distribution is a key determinant of the exceptional conduction characteristics exhibited by cuprates [65].
However, the impact of short-range Gaussian disorder correlations was beyond the scope of our previous work and has not been studied so far. In actual materials, short-range correlated disorder [66,67] can take place when the potential acting on electrons cased by lattice defects is spatially screened [68]. This study focuses on the effects introduced by short-range disorder correlations in superconducting systems. It demonstrates that such correlations significantly influence the superconducting characteristics that depend on the correlation degree. Their influence differs somewhat from that observed for the case of long-range power law correlations [69,70,71,72,73,74].
2. Model
To investigate the phenomenon of superconductivity characterized by s-wave pairing in the presence of correlated on-site disorder, we employ an attractive Hubbard model Hamiltonian, which is given by the following expression [75,76]:
In this equation, represents the chemical potential of the system, and , where () denotes the creation (annihilation) operator for an electron with spin at site i within a two-dimensional lattice. The tunneling amplitude is nonzero only for nearest neighbor sites, where . The parameter represents the on-site coupling strength, and signifies the disorder potential. Our study focuses on a two-dimensional square lattice, and we use vector indices, with , to denote lattice sites. From the Hamiltonian (1), we can derive the Bogoliubov–de Gennes (BdG) equations in a matrix form as shown in refs. [76,77]:
In this context, and are vectors with components and , with representing the position of lattice sites. The operators and have matrix elements defined as follows:
Here, is the Kronecker delta, and the order parameter and Hartree potential are determined through the self-consistency equations [22,78,79]:
The Hartree self-consistency Equation (4) modifies the effective potential experienced by electrons in a disordered system. This modification plays a pivotal role when dealing with strong disorder and cannot be disregarded [21,80] as in the case of weakly disordered systems [81,82].
Disorder Model
Our computations are carried out utilizing a model that takes into consideration structural disorder, wherein the spatial correlations of the disorder potential in reciprocal space exhibit a Gaussian behavior as expressed by the equation:
We generate a spatial disorder potential series, denoted as , indexed by , with a spectral density function that satisfies the relation (5) using an improved version of the Fourier filtering method [83,84,85,86], summarized as the subsequent expression:
where is a discrete inverse space vector with and . Lastly, denotes random phases that follow a uniform distribution in the interval . The amplitude of the disorder potential is characterized by the following quantity:
where
In this context, the numerical averaging represented by the overline is conducted over both lattice sites and the statistical distribution, with angular brackets denoting the statistical ensemble average. By construction, the resulting disorder correlation function has a short-range character. Moreover, it is Gaussian and stationary [83].
3. Results
In our research, we utilized a computational framework based on a square lattice with dimensions represented as , while incorporating periodic boundary conditions. To numerically solve the tight-binding Bogoliubov–de Gennes (BdG) Equation (2), we employed an iterative approach to ensure that the pairing self-consistency Equation (3) was satisfied within a predefined accuracy threshold [77,78]. For details of the numerical procedure employed, one can refer to [87,88,89]. For this study, we maintained a fixed lattice size of , which we determined to be sufficiently large to minimize finite-sample artifacts [11]. We calculated the chemical potential to achieve an average electron density of 0.875 [21].
It is important to note that the fundamental findings in our study remain consistent regardless of the specific choice of , as long as we operate far from the half-filling condition that brings an additional symmetry to the model. Our analysis was conducted within the strong pairing coupling regime and with a very large Debye window, indicating that the coupling interactions encompassed all single-particle states. It is worth emphasizing that all energy quantities in our study are expressed in units of the hopping integral t.
Finally, we statistically averaged observable quantities over 20 independent realizations of disorder, with each set associated with specific values of and . Further details about the numerical procedure used to construct the disorder potential can be found in ref. [11].
We generate various configurations of the disorder profile influenced by the disorder strength and the degree of disorder potential correlation, and address BdG equations to obtain the order parameter profile. For low disorder strength, the system possesses a predominantly uniform order parameter. As we introduce stronger correlations in the disorder, this uniformity becomes more pronounced, aligning with our prior findings on long-range correlations. When the disorder strength amplifies, the patterns exhibit higher contrast, signifying enhanced spatial variations in the order parameter [20]. As the disorder correlations intensify, the wavelength of these variations increases, in accordance with our observations in cases of disorder with power law correlations. Furthermore, comparing the result with the one obtained using a power law correlator, we notice that order parameter clusters are slightly smaller, and order parameter variability is slightly increased in the case of the Gaussian correlations.
As a summary of these observations, Figure 1 displays the distribution of the absolute value of the order parameter for different levels of disorder strength arranged in rows. Different colors represent different values: . This distribution is shown as a function of the relative order parameter , where is the average order parameter. In a superconductor with uncorrelated disorder, this distribution is well described by the log-normal function.
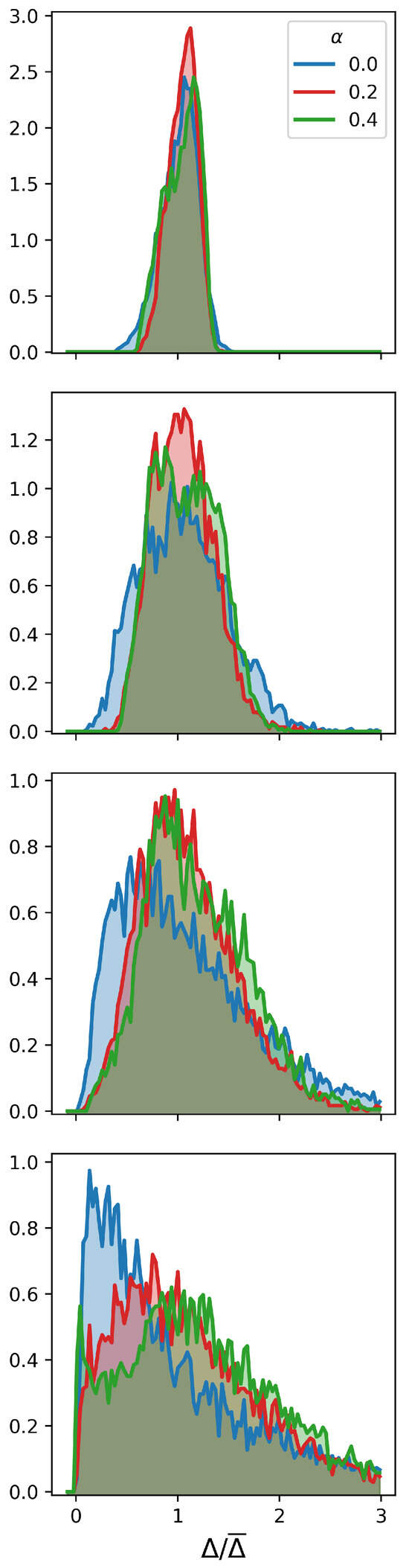
Figure 1.
Statistical distribution of the absolute value of the order parameter , calculated for various values of the disorder strength (from top to bottom: ) and various disorder correlation degree (colors).
At , the distribution exhibits a single peak, with the order parameter approaching 0 as disorder increases. However, as disorder becomes short-range correlated and , even in the presence of weak disorder, a second peak emerges in the distribution, particularly noticeable with larger values. With increasing the disorder strength, both peaks shift towards , but the second peak moves towards at a faster rate than the first peak. This leads to a distribution function with a narrow, prominent peak near and a broader peak at finite order parameter values. These results significantly differ from those obtained using a power law correlator, where a double-peak structure was only observed in cases of high disorder strength and degree of disorder correlations. Thus, for short-range disorder correlations, begins to deviate from the lognormal form at smaller values of disorder strength and degree of correlations. Another distinction between these two correlators is that in the case of a power law correlator, approaches a finite value as approaches 0 and has an opposite slope compared to the log-normal distribution. For the Gaussian correlator, however, tends to 0 as approaches 0.
Figure 2 depicts the order parameter distribution in two models characterized by distinct spatial correlation decay laws: one following a power law and the other adhering to a Gaussian decay. Owing to the divergent physical meaning of in the respective models, their absolute magnitudes differ. However, in both instances, is chosen to ensure an equivalent effective correlation length. The findings reveal that under identical effective correlation lengths and disorder strengths, the model featuring Gaussian-correlated disorder manifests a broader order parameter distribution.
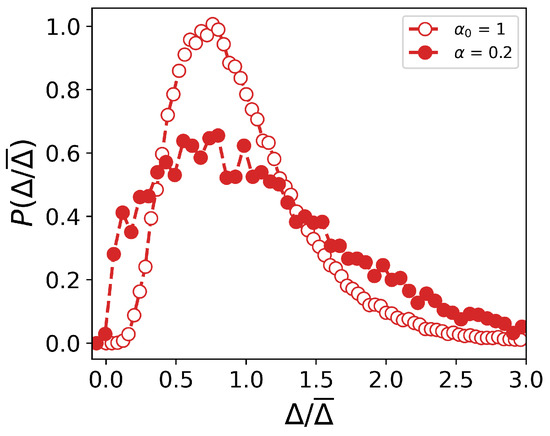
Figure 2.
Statistical distribution of the absolute value of the order parameter in two models calculated for the same effective correlation length. The notations and correspond to the degree of disorder correlation for Gaussian and power law decay, respectively.
To quantify the spatial correlations of the order parameter, we introduce the correlation function defined as
where and are eigenfunctions of the BdG Hamiltonian. In a homogeneous superconductor state, it approaches a constant equal to at large distances, reflecting the off-diagonal long-range order in the mean-field approximation [90]. However, the disorder disrupts this long-range order and global superconducting correlations.
To quantitatively assess these correlations described by , we can analyze its Fourier transform, denoted as . Figure 3 displays this in a logarithmic scale, showing a Gaussian dependence. By fitting the Gaussian dependence
we determine the exponent as a function of as shown in Figure 4. Even in the absence of correlations in disorder, there are correlations in the order parameter with . The introduction of disorder correlations enhances these order parameter correlations. However, this enhancement diminishes at high values, reaching a limit of for significant short-range correlations considered in this work.
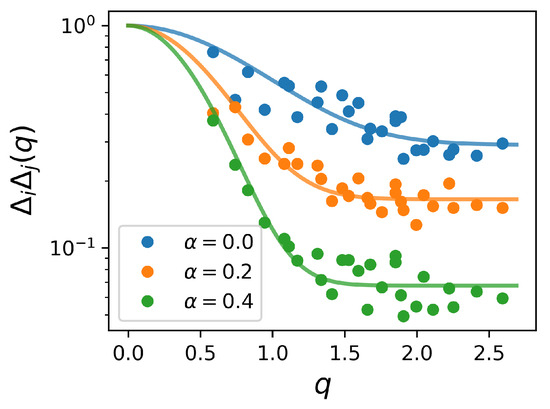
Figure 3.
The Fourier transform of the spatial correlation function of the order parameter for several values of .
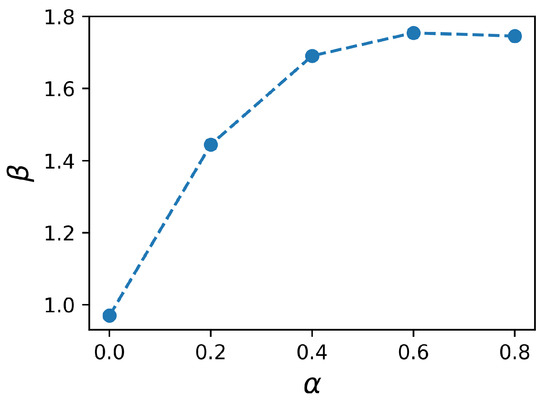
Figure 4.
The order parameter correlation length as a function of .
In weakly disordered samples, the presence of a nonzero order parameter unequivocally signals the onset of superconductivity. However, in the case of strong disorder, the superconductive state becomes strongly nonhomogeneous, forming weakly connected superconductive clusters with randomized phases. This makes it impossible to define superconductivity using local or average order parameters. Instead, the initiation of superconductivity in highly disordered samples can be characterized by the (Meissner) superfluid stiffness, denoted as [91,92]. Within the mean-field theory, the stiffness is determined by the linear response to an externally applied static vector potential,
where represents the long wavelength limit of the transverse current–current correlator, averaged over both the superconductive state and the disorder realizations,
with being the paramagnetic current, and the diamagnetic component being the disorder-averaged kinetic energy along the x direction. Both of these quantities are illustrated in Figure 5, employing a disorder strength of . Figure 6 depicts the stiffness as a function of disorder strength V for various values. As expected, fluctuations decrease the stiffness, consequently suppressing superconductivity. In accordance with our previous work, the stiffness diminishes as the disorder strength V increases. Here, however, for correlated disorder (), an increase in the correlation degree results in the larger stiffness with a consequence that the critical disorder strength, where the stiffness becomes zero, increases at larger .
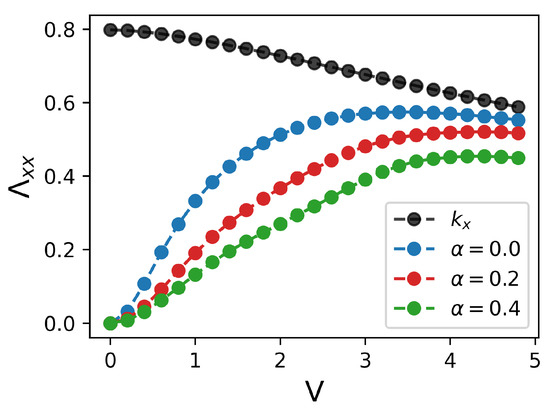
Figure 5.
Diamagnetic and paramagnetic contributions to as functions of V for several values of .
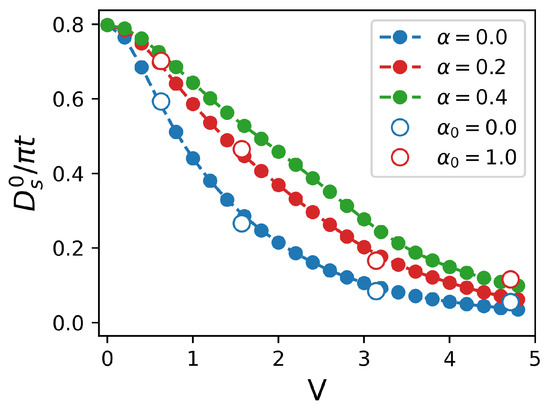
Figure 6.
The superfluid stiffness as a function of V, calculated for several values of .
This figure presents the outcomes of our preceding research concerning two distinct values. Specifically, outcomes associated with the Gaussian correlation law are denoted by filled symbols, whereas those corresponding to the power law model are represented by empty symbols. It is noteworthy that for the presentation of this figure, we deliberately chose values such that both models manifest identical effective disorder correlation lengths.
Moreover, considering our current model, we systematically adjust the disorder strength in the power law correlation model to facilitate a meaningful comparison between the two models. Notably, when is set to zero, a perfect alignment between the results of both models is observed. However, an incremental increase in instigates discernible distinctions in the outcomes, particularly for elevated values of disorder strength.
As depicted in the figure, even for = 1, the superfluid stiffness of the power law model notably surpasses that of the Gaussian correlator in the domain characterized by substantial values of V. Nevertheless, for modest and moderate levels of disorder strength, the distinctions between outcomes for the Gaussian correlator and the power law correlator remain relatively inconspicuous.
4. Discussion
In summary, the results of our study reveal important insights into the impact of the disorder strength and short-range spatial correlations on the superconducting characteristics. The results demonstrate that when the disorder strength increases, the amplitude of the order parameter oscillations also increases, which creates domains where the order parameter is strongly suppressed or enhanced. The introduction of disorder correlations amplifies correlations of the order parameter, with the correlation length reaching the limit of 1.75 for strong short-range disorder correlations.
In highly disordered materials, characterizing superconductivity based on local microscopic properties becomes challenging. In this case, transition to the superconducting state is better characterized by the superfluid stiffness. Our analysis reveals that fluctuations due to disorder make the stiffness decrease, leading to a suppression of superconductivity. However, for correlated disorder, an increase in its correlation degree results in a higher critical disorder strength, where the stiffness vanishes.
Furthermore, an examination of the outcomes achieved for the existing correlated disorder model, in contrast to those derived for the power law decay model, reveals that for identical disorder parameters within a model featuring a Gaussian disorder distribution, the order parameter distribution exhibits increased width on one side. Conversely, in the model incorporating power law correlations, the critical disorder strength leading to the suppression of superconductivity is observed to be greater regarding V than that in the alternative model.
Our findings emphasize the complex interplay between disorder strength and correlations in superconducting systems. Indeed, comparing the results obtained in our theoretical study and the results of the experimental study reported by M. Fratini on the topic “Scale-free structural organization of interstitial oxygen atoms in ” [65], despite the difference that arises from our use of a short-range Gaussian function to model the disorder correlations in our calculations, as opposed to the power law function with an exponential cutoff employed in the experimental work to fit the data, one can glean that these results are in good agreement with the findings outlined in our theoretical framework. Namely, (1) an increase in the disorder correlation length leads to an increase in the order parameter correlations, and (2) the promotion of superconductivity is facilitated by a fractal disorder structure.
These insights are valuable for understanding and characterizing superconductivity in disordered materials, and may have important implications for the development of new materials with tailored superconducting properties. Moreover, it seems that these results are especially of importance for cases where the disorder is detrimental for the observation of certain superconducting states, such as FFLO, etc. [93,94].
Author Contributions
Conceptualization, M.D.C.; methodology, A.V.K., M.D.C. and V.D.N.; software, V.D.N. and A.E.L.; analysis—A.V.K., M.D.C. and A.V.; writing—original draft preparation, M.D.C., A.V.K. and V.D.N.; writing—review and editing, A.V. and M.D.C.; visualization, V.D.N. All authors have read and agreed to the published version of the manuscript.
Funding
V.D.N., A.E.L. and A.V.K. acknowledge support from the Ministry of Science and Higher Education of the Russian Federation (state task project No. FSWU-2023-0031). The calculations were performed with the support of the MEPhI Program Priority 2030. Analytical derivations have been funded within the framework of the HSE University Basic Research Program. A.V. acknowledges support by the Ministry of Science and Higher Education of the Russian Federation (No. FSMG-2023-0014) and the RSF grant 23-72-30004 (https://rscf.ru/project/23-72-30004/, accessed on 21 November 2023) that were used for the analysis of the stiffness.
Data Availability Statement
Correspondence and requests for materials should be addressed to Mihail D. Croitoru.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Feigel’man, M.V.; Ioffe, L.B.; Kravtsov, V.E.; Yuzbashyan, E.A. Eigenfunction Fractality and Pseudogap State near the Superconductor-Insulator Transition. Phys. Rev. Lett. 2007, 98, 27001. [Google Scholar] [CrossRef]
- Burmistrov, I.S.; Gornyi, I.V.; Mirlin, A.D. Enhancement of the Critical Temperature of Superconductors by Anderson Localization. Phys. Rev. Lett. 2012, 108, 17002. [Google Scholar] [CrossRef] [PubMed]
- Stosiek, M.; Lang, B.; Evers, F. Self-consistent-field ensembles of disordered Hamiltonians: Efficient solver and application to superconducting films. Phys. Rev. B 2020, 101, 144503. [Google Scholar] [CrossRef]
- Goldman, A.M.; Marković, N. Superconductor-Insulator Transitions in the Two-Dimensional Limit. Phys. Today 1998, 51, 39–44. [Google Scholar] [CrossRef]
- Ma, M.; Lee, P.A. Localized superconductors. Phys. Rev. B 1985, 32, 5658–5667. [Google Scholar] [CrossRef] [PubMed]
- Gantmakher, V.F.; Dolgopolov, V.T. Superconductor-insulator quantum phase transition. Uspekhi Fizicheskih Nauk 2010, 180, 3. [Google Scholar] [CrossRef]
- Sadovskii, M.V. Superconductivity and localization. Phys. Rep. 1997, 282, 225–348. [Google Scholar] [CrossRef]
- Trivedi, N.; Scalettar, R.T.; Randeria, M. Superconductor-insulator transition in a disordered electronic system. Phys. Rev. B 1996, 54, R3756–R3759. [Google Scholar] [CrossRef]
- Trivedi, N.; Loh, Y.L.; Bouadim, K.; Randeria, M. Emergent granularity and pseudogap near the superconductor-insulator transition. J. Phys. Conf. Ser. 2012, 376, 12001. [Google Scholar] [CrossRef]
- Gastiasoro, M.N.; Andersen, B.M. Enhancing superconductivity by disorder. Phys. Rev. B 2018, 98, 184510. [Google Scholar] [CrossRef]
- Neverov, V.D.; Lukyanov, A.E.; Krasavin, A.V.; Vagov, A.; Croitoru, M.D. Correlated disorder as a way towards robust superconductivity. Commun. Phys. 2022, 5, 177. [Google Scholar] [CrossRef]
- Sacépé, B.; Feigel’man, M.; Klapwijk, T.M. Quantum breakdown of superconductivity in low-dimensional materials. Nat. Phys. 2020, 16, 734–746. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Shanenko, A.A.; Peeters, F.M.; Axt, V.M. Parity-fluctuation induced enlargement of the ratio ΔE/kBTc in metallic grains. Phys. Rev. B 2011, 84, 214518. [Google Scholar] [CrossRef]
- Saini, N.L.; Rossetti, T.; Lanzara, A.; Missori, M.; Perali, A.; Oyanagi, H.; Bianconi, A. Tuning of the Fermi level at the second subband of a superlattice of quantum wires in the CuO2 plane: A possible mechanism to raise the critical temperature. J. Supercond. 1996, 9, 343–348. [Google Scholar] [CrossRef]
- Castro, D.D.; Agrestini, S.; Campi, G.; Cassetta, A.; Colapietro, M.; Congeduti, A.; Continenza, A.; Negri, S.D.; Giovannini, M.; Massidda, S.; et al. European Physical Society Italian Physical Society EDP Sciences The Institute of Physics The amplification of the superconducting Tc by combined effect of tuning of the Fermi level and the tensile micro-strain in Al1-xMgxB2. Europhys. Lett. (EPL) 2002, 58, 278–284. [Google Scholar] [CrossRef]
- Silveira, R.d.L.; Croitoru, M.D.; Pugach, N.G.; Romaguera, A.R.d.C.; Albino Aguiar, J. Engineering low-temperature proximity effect in clean metals by spectral singularities. New J. Phys. 2023, 25, 93009. [Google Scholar] [CrossRef]
- Fang, L.; Jia, Y.; Mishra, V.; Chaparro, C.; Vlasko-Vlasov, V.K.; Koshelev, A.E.; Welp, U.; Crabtree, G.W.; Zhu, S.; Zhigadlo, N.D.; et al. Huge critical current density and tailored superconducting anisotropy in SmFeAsO0.8F0.15 by low-density columnar-defect incorporation. Nat. Commun. 2013, 4, 3655. [Google Scholar] [CrossRef]
- Ghigo, G.; Torsello, D.; Ummarino, G.; Gozzelino, L.; Tanatar, M.; Prozorov, R.; Canfield, P. Disorder-Driven Transition Superconducting Order Parameter in Proton Irradiated Single Crystals. Phys. Rev. Lett. 2018, 121, 107001. [Google Scholar] [CrossRef]
- Zhao, K.; Lin, H.; Xiao, X.; Huang, W.; Yao, W.; Yan, M.; Xing, Y.; Zhang, Q.; Li, Z.X.; Hoshino, S.; et al. Disorder-induced multifractal superconductivity in monolayer niobium dichalcogenides. Nat. Phys. 2019, 15, 904–910. [Google Scholar] [CrossRef]
- Tsai, W.F.; Yao, H.; Läuchli, A.; Kivelson, S.A. Optimal inhomogeneity for superconductivity: Finite-size studies. Phys. Rev. B 2008, 77, 214502. [Google Scholar] [CrossRef]
- Ghosal, A.; Randeria, M.; Trivedi, N. Role of Spatial Amplitude Fluctuations in Highly Disordereds-Wave Superconductors. Phys. Rev. Lett. 1998, 81, 3940–3943. [Google Scholar] [CrossRef]
- Ghosal, A.; Randeria, M.; Trivedi, N. Inhomogeneous pairing in highly disordereds-wave superconductors. Phys. Rev. B 2001, 65, 14501. [Google Scholar] [CrossRef]
- Dubi, Y.; Meir, Y.; Avishai, Y. Nature of the superconductor–insulator transition in disordered superconductors. Nature 2007, 449, 876–880. [Google Scholar] [CrossRef]
- Brun, C.; Cren, T.; Cherkez, V.; Debontridder, F.; Pons, S.; Fokin, D.; Tringides, M.C.; Bozhko, S.; Ioffe, L.B.; Altshuler, B.L.; et al. Remarkable effects of disorder on superconductivity of single atomic layers of lead on silicon. Nat. Phys. 2014, 10, 444–450. [Google Scholar] [CrossRef]
- Lemarié, G.; Kamlapure, A.; Bucheli, D.; Benfatto, L.; Lorenzana, J.; Seibold, G.; Ganguli, S.C.; Raychaudhuri, P.; Castellani, C. Universal scaling of the order-parameter distribution in strongly disordered superconductors. Phys. Rev. B 2013, 87, 184509. [Google Scholar] [CrossRef]
- Noat, Y.; Cherkez, V.; Brun, C.; Cren, T.; Carbillet, C.; Debontridder, F.; Ilin, K.; Siegel, M.; Semenov, A.; Hubers, H.W.; et al. Unconventional superconductivity in ultrathin superconducting NbN films studied by scanning tunneling spectroscopy. Phys. Rev. B 2013, 88, 14503. [Google Scholar] [CrossRef]
- Mondal, M.; Kamlapure, A.; Chand, M.; Saraswat, G.; Kumar, S.; Jesudasan, J.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Phase Fluctuations in a Strongly Disordereds-Wave NbN Superconductor Close to the Metal-Insulator Transition. Phys. Rev. Lett. 2011, 106, 47001. [Google Scholar] [CrossRef]
- Mondal, M.; Kamlapure, A.; Ganguli, S.C.; Jesudasan, J.; Bagwe, V.; Benfatto, L.; Raychaudhuri, P. Enhancement of the finite-frequency superfluid response in the pseudogap regime of strongly disordered superconducting films. Sci. Rep. 2013, 3, 1357. [Google Scholar] [CrossRef]
- Saito, Y.; Nojima, T.; Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2016, 2, 16094. [Google Scholar] [CrossRef]
- Petrović, A.P.; Ansermet, D.; Chernyshov, D.; Hoesch, M.; Salloum, D.; Gougeon, P.; Potel, M.; Boeri, L.; Panagopoulos, C. A disorder-enhanced quasi-one-dimensional superconductor. Nat. Commun. 2016, 7, 12262. [Google Scholar] [CrossRef]
- Peng, J.; Yu, Z.; Wu, J.; Zhou, Y.; Guo, Y.; Li, Z.; Zhao, J.; Wu, C.; Xie, Y. Disorder Enhanced Superconductivity toward TaS2 Monolayer. ACS Nano 2018, 12, 9461–9466. [Google Scholar] [CrossRef]
- Feigel’man, M.; Ioffe, L.; Kravtsov, V.; Cuevas, E. Fractal superconductivity near localization threshold. Ann. Phys. 2010, 325, 1390–1478. [Google Scholar] [CrossRef]
- Weinrib, A.; Halperin, B.I. Critical phenomena in systems with long-range-correlated quenched disorder. Phys. Rev. B 1983, 27, 413–427. [Google Scholar] [CrossRef]
- de Moura, F.A.B.F.; Lyra, M.L. Delocalization in the 1D Anderson Model with Long-Range Correlated Disorder. Phys. Rev. Lett. 1998, 81, 3735. [Google Scholar] [CrossRef]
- Carpena, P.; Bernaola-Galván, P.; Ivanov, P.C.; Stanley, H.E. Metal–insulator transition in chains with correlated disorder. Nature 2002, 418, 955–959. [Google Scholar] [CrossRef] [PubMed]
- Kawarabayashi, T.; Ono, Y.; Ohtsuki, T.; Kettemann, S.; Struck, A.; Kramer, B. Unconventional conductance plateau transitions in quantum Hall wires with spatially correlated disorder. Phys. Rev. B 2007, 75, 235317. [Google Scholar] [CrossRef]
- Pilati, S.; Giorgini, S.; Prokof’ev, N. Superfluid Transition in a Bose Gas with Correlated Disorder. Phys. Rev. Lett. 2009, 102, 150402. [Google Scholar] [CrossRef] [PubMed]
- Liew, S.F.; Cao, H. Optical properties of 1D photonic crystals with correlated and uncorrelated disorder. J. Opt. 2010, 12, 24011. [Google Scholar] [CrossRef]
- Keen, D.A.; Goodwin, A.L. The crystallography of correlated disorder. Nature 2015, 521, 303–309. [Google Scholar] [CrossRef]
- Simonov, A.; Goodwin, A.L. Designing disorder into crystalline materials. Nat. Rev. Chem. 2020, 4, 657–673. [Google Scholar] [CrossRef]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Predictive Self-Assembly of Polyhedra into Complex Structures. Science 2012, 337, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Dzero, M.; Huang, X. Correlated disorder in a Kondo lattice. J. Phys. Condens. Matter 2012, 24, 75603. [Google Scholar] [CrossRef] [PubMed]
- Bonzom, V.; Gurau, R.; Smerlak, M. Universality in p-spin glasses with correlated disorder. J. Stat. Mech. Theory Exp. 2013, 2013, L02003. [Google Scholar] [CrossRef]
- Girschik, A.; Libisch, F.; Rotter, S. Topological insulator in the presence of spatially correlated disorder. Phys. Rev. B 2013, 88, 14201. [Google Scholar] [CrossRef]
- Alamir, A.; Capuzzi, P.; Kashanian, S.V.; Vignolo, P. Probing quantum transport by engineering correlations in a speckle potential. Phys. Rev. A 2014, 89, 23613. [Google Scholar] [CrossRef]
- Pilati, S.; Fratini, E. Ferromagnetism in a repulsive atomic Fermi gas with correlated disorder. Phys. Rev. A 2016, 93, 51604. [Google Scholar] [CrossRef]
- Zierenberg, J.; Fricke, N.; Marenz, M.; Spitzner, F.P.; Blavatska, V.; Janke, W. Percolation thresholds and fractal dimensions for square and cubic lattices with long-range correlated defects. Phys. Rev. E 2017, 96, 62125. [Google Scholar] [CrossRef]
- Campi, G.; Gioacchino, M.D.; Poccia, N.; Ricci, A.; Burghammer, M.; Ciasca, G.; Bianconi, A. Nanoscale Correlated Disorder in Out-of-Equilibrium Myelin Ultrastructure. ACS Nano 2017, 12, 729–739. [Google Scholar] [CrossRef] [PubMed]
- Dikopoltsev, A.; Herzig Sheinfux, H.; Segev, M. Localization by virtual transitions in correlated disorder. Phys. Rev. B 2019, 100, 140202. [Google Scholar] [CrossRef]
- Mangelis, P.; Koch, R.J.; Lei, H.; Neder, R.B.; McDonnell, M.T.; Feygenson, M.; Petrovic, C.; Lappas, A.; Bozin, E.S. Correlated disorder-to-order crossover in the local structure of KxFe2-ySe2-zSz. Phys. Rev. B 2019, 100, 94108. [Google Scholar] [CrossRef]
- Derlet, P.M. Correlated disorder in a model binary glass through a local SU(2) bonding topology. Phys. Rev. Mater. 2020, 4, 125601. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Shan’ko, Y.; Zamkova, N.G.; Bianconi, A. Is There Any Hidden Symmetry in the Stripe Structure of Perovskite High-Temperature Superconductors? J. Phys. Chem. Lett. 2019, 10, 1840–1844. [Google Scholar] [CrossRef]
- Fomin, I.A. Effect of correlated disorder on the temperature of unconventional cooper pairing: 3He in aerogel. JETP Lett. 2008, 88, 59–63. [Google Scholar] [CrossRef][Green Version]
- Fomin, I.A. Anomalous temperature dependence of the order parameter of a superconductor with weakly correlated impurities. JETP Lett. 2011, 93, 144–146. [Google Scholar] [CrossRef]
- Shi, R.; Fang, W.H.; Vasenko, A.S.; Long, R.; Prezhdo, O.V. Efficient passivation of DY center in CH3NH3PbBr3 by chlorine: Quantum molecular dynamics. Nano Res. 2021, 15, 2112–2122. [Google Scholar] [CrossRef]
- Zhao, X.; Vasenko, A.S.; Prezhdo, O.V.; Long, R. Anion Doping Delays Nonradiative Electron–Hole Recombination in Cs-Based All-Inorganic Perovskites: Time Domain ab Initio Analysis. J. Phys. Chem. Lett. 2022, 13, 11375–11382. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, D.; Chu, W.; Wang, B.; Vasenko, A.S.; Prezhdo, O.V. Fluctuations at Metal Halide Perovskite Grain Boundaries Create Transient Trap States: Machine Learning Assisted Ab Initio Analysis. ACS Appl. Mater. Interfaces 2022, 14, 55753–55761. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Chu, W.; Vasenko, A.S.; Prezhdo, O.V. Common Defects Accelerate Charge Carrier Recombination in CsSnI3 without Creating Mid-Gap States. J. Phys. Chem. Lett. 2021, 12, 1948–7185. [Google Scholar] [CrossRef]
- Liu, D.; Wu, Y.; Vasenko, A.S.; Prezhdo, O.V. Grain boundary sliding and distortion on a nanosecond timescale induce trap states in CsPbBr3: ab initio investigation with machine learning force field. Nanoscale 2023, 15, 285–293. [Google Scholar] [CrossRef]
- Clément, D.; Varón, A.F.; Retter, J.A.; Sanchez-Palencia, L.; Aspect, A.; Bouyer, P. Experimental study of the transport of coherent interacting matter-waves in a 1D random potential induced by laser speckle. New J. Phys. 2006, 8, 165. [Google Scholar] [CrossRef]
- Billy, J.; Josse, V.; Zuo, Z.; Bernard, A.; Hambrecht, B.; Lugan, P.; Clément, D.; Sanchez-Palencia, L.; Bouyer, P.; Aspect, A. Direct observation of Anderson localization of matter waves in a controlled disorder. Nature 2008, 453, 891–894. [Google Scholar] [CrossRef] [PubMed]
- Aspect, A.; Inguscio, M. Anderson localization of ultracold atoms. Phys. Today 2009, 62, 30–35. [Google Scholar] [CrossRef]
- Delande, D.; Orso, G. Mobility Edge for Cold Atoms in Laser Speckle Potentials. Phys. Rev. Lett. 2014, 113, 60601. [Google Scholar] [CrossRef] [PubMed]
- Astrakharchik, G.E.; Krutitsky, K.V.; Navez, P. Phase diagram of quasi-two-dimensional bosons in a laser-speckle potential. Phys. Rev. A 2013, 87, 61601. [Google Scholar] [CrossRef]
- Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 2010, 466, 841–844. [Google Scholar] [CrossRef]
- Gurevich, E.; Iomin, A. Generalized Lyapunov exponent and transmission statistics in one-dimensional Gaussian correlated potentials. Phys. Rev. E 2011, 83, 11128. [Google Scholar] [CrossRef]
- Jing-Hui, L. System Driven by Correlated Gaussian Noises Related with Disorder. Chin. Phys. Lett. 2007, 24, 2505–2508. [Google Scholar] [CrossRef]
- Wang, Y.; Nandkishore, R.M. Interplay between short-range correlated disorder and Coulomb interaction in nodal-line semimetals. Phys. Rev. B 2017, 96, 115130. [Google Scholar] [CrossRef]
- Horner, H. Drift, creep and pinning of a particle in a correlated random potential. Zeitschrift für Phys. B Condens. Matter 1996, 100, 243–257. [Google Scholar] [CrossRef][Green Version]
- Izrailev, F.M.; Krokhin, A.A. Localization and the Mobility Edge in One-Dimensional Potentials with Correlated Disorder. Phys. Rev. Lett. 1999, 82, 4062–4065. [Google Scholar] [CrossRef]
- Lugan, P.; Aspect, A.; Sanchez-Palencia, L.; Delande, D.; Grémaud, B.; Müller, C.A.; Miniatura, C. One-dimensional Anderson localization in certain correlated random potentials. Phys. Rev. A 2009, 80, 23605. [Google Scholar] [CrossRef]
- Das, S.K.; Singh, V.N.; Majumdar, P. Magnon spectrum in the domain ferromagnetic state of antisite-disordered double perovskites. Phys. Rev. B 2013, 88, 214428. [Google Scholar] [CrossRef]
- Marcuzzi, M.; Minář, J.; Barredo, D.; de Léséleuc, S.; Labuhn, H.; Lahaye, T.; Browaeys, A.; Levi, E.; Lesanovsky, I. Facilitation Dynamics and Localization Phenomena in Rydberg Lattice Gases with Position Disorder. Phys. Rev. Lett. 2017, 118, 63606. [Google Scholar] [CrossRef] [PubMed]
- Ro, S.; Kafri, Y.; Kardar, M.; Tailleur, J. Disorder-Induced Long-Ranged Correlations in Scalar Active Matter. Phys. Rev. Lett. 2021, 126, 48003. [Google Scholar] [CrossRef] [PubMed]
- Micnas, R.; Ranninger, J.; Robaszkiewicz, S. Superconductivity in narrow-band systems with local nonretarded attractive interactions. Rev. Mod. Phys. 1990, 62, 113–171. [Google Scholar] [CrossRef]
- Zhu, J.X. Bogoliubov-de Gennes Method and Its Applications; Springer: Berlin/Heidelberg, Germany, 2016; Volume 924. [Google Scholar]
- de Braganca, R.H.; Croitoru, M.D.; Shanenko, A.A.; Aguiar, J.A. Effect of Material-Dependent Boundaries on the Interference Induced Enhancement of the Surface Superconductivity Temperature. J. Phys. Chem. Lett. 2023, 14, 5657–5664. [Google Scholar] [CrossRef]
- Hannibal, S.; Kettmann, P.; Croitoru, M.D.; Axt, V.M.; Kuhn, T. Persistent oscillations of the order parameter and interaction quench phase diagram for a confined Bardeen-Cooper-Schrieffer Fermi gas. Phys. Rev. A 2018, 98, 53605. [Google Scholar] [CrossRef]
- Hannibal, S.; Kettmann, P.; Croitoru, M.D.; Axt, V.M.; Kuhn, T. Dynamical vanishing of the order parameter in a confined Bardeen-Cooper-Schrieffer Fermi gas after an interaction quench. Phys. Rev. A 2018, 97, 13619. [Google Scholar] [CrossRef]
- Tarat, S.; Majumdar, P. Charge dynamics across the disorder-driven superconductor-insulator transition. EPL (Europhys. Lett.) 2014, 105, 67002. [Google Scholar] [CrossRef][Green Version]
- Croitoru, M.D.; Shanenko, A.A.; Vagov, A.; Milošević, M.V.; Axt, V.M.; Peeters, F.M. Phonon limited superconducting correlations in metallic nanograins. Sci. Rep. 2015, 5, 16515. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Shanenko, A.A.; Vagov, A.; Vasenko, A.S.; Milošević, M.V.; Axt, V.M.; Peeters, F.M. Influence of Disorder on Superconducting Correlations in Nanoparticles. J. Supercond. Nov. Magn. 2016, 29, 605–609. [Google Scholar] [CrossRef]
- Makse, H.A.; Havlin, S.; Schwartz, M.; Stanley, H.E. Method for generating long-range correlations for large systems. Phys. Rev. E 1996, 53, 5445–5449. [Google Scholar] [CrossRef]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Carpena, P.; Eugene Stanley, H. Effect of trends on detrended fluctuation analysis. Phys. Rev. E 2001, 64, 11114. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Hu, K.; Carpena, P.; Bernaola-Galvan, P.; Stanley, H.E.; Ivanov, P.C. Effect of nonlinear filters on detrended fluctuation analysis. Phys. Rev. E 2005, 71, 11104. [Google Scholar] [CrossRef]
- Coronado, A.V.; Carpena, P. Size Effects on Correlation Measures. J. Biol. Phys. 2005, 31, 121–133. [Google Scholar] [CrossRef] [PubMed]
- Croitoru, M.D.; Gladilin, V.N.; Fomin, V.M.; Devreese, J.T.; Kemerink, M.; Koenraad, P.M.; Sauthoff, K.; Wolter, J.H. Electroluminescence spectra of an STM-tip-induced quantum dot. Phys. Rev. B 2003, 68, 195307. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Gladilin, V.N.; Fomin, V.M.; Devreese, J.T.; Magnus, W.; Schoenmaker, W.; Sorée, B. Quantum transport in a nanosize double-gate metal-oxide-semiconductor field-effect transistor. J. of Appl. Phys. 2003, 96, 2305–2310. [Google Scholar] [CrossRef]
- Kettmann, P.; Hannibal, S.; Croitoru, M.D.; Axt, V.M.; Kuhn, T. Pure Goldstone mode in the quench dynamics of a confined ultracold Fermi gas in the BCS-BEC crossover regime. Phys. Rev. A 2017, 96, 33618. [Google Scholar] [CrossRef]
- Yang, C.N. Concept of Off-Diagonal Long-Range Order and the Quantum Phases of Liquid He and of Superconductors. Rev. Mod. Phys. 1962, 34, 694–704. [Google Scholar] [CrossRef]
- Scalapino, D.J.; White, S.R.; Zhang, S.C. Superfluid density and the Drude weight of the Hubbard model. Phys. Rev. Lett. 1992, 68, 2830–2833. [Google Scholar] [CrossRef]
- Scalapino, D.J.; White, S.R.; Zhang, S. Insulator, metal, or superconductor: The criteria. Phys. Rev. B 1993, 47, 7995–8007. [Google Scholar] [CrossRef] [PubMed]
- Croitoru, M.D.; Buzdin, A.I. The Fulde–Ferrell–Larkin–Ovchinnikov state in layered d-wave superconductors: In-plane anisotropy and resonance effects in the angular dependence of the upper critical field. J. Phys. Condens. Matter 2013, 25, 125702. [Google Scholar] [CrossRef] [PubMed]
- Croitoru, M.; Buzdin, A. In Search of Unambiguous Evidence of the Fulde–Ferrell–Larkin–Ovchinnikov State in Quasi-Low Dimensional Superconductors. Condens. Matter 2017, 2, 30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).